体积表面积计算公式大全[]
几何体的表面积和体积公式大全

几何体的表面积和体积公式大全几何体的表面积,体积计算公式1、圆柱体:表面积:2πRr+2πRh 体积:πR²h (R为圆柱体上下底圆半径,h为圆柱体高)2、圆锥体:表面积:πR²+πR[(h²+R²)的平方根] 体积:πR²h/3 (r为圆锥体低圆半径,h为其高, 3、正方体a-边长,S=6a²,V=a³4、长方体a-长,b-宽,c-高S=2(ab+ac+bc) V=abc5、棱柱S-底面积h-高V=Sh6、棱锥S-底面积h-高V=Sh/37、棱台S1和S2-上、下底面积h-高V=h[S1+S2+(S1S2)^1/2]/38、拟柱体S1-上底面积,S2-下底面积,S0-中截面积h-高,V=h(S1+S2+4S0)/69、圆柱r-底半径,h-高,C—底面周长S底—底面积,S侧—侧面积,S表—表面积C=2πrS底=πr²,S侧=Ch ,S表=Ch+2S底,V=S底h=πr²h10、空心圆柱R-外圆半径,r-内圆半径h-高V=πh(R^2-r^2)11、直圆锥r-底半径h-高V=πr^2h/312、圆台r-上底半径,R-下底半径,h-高V=πh(R²+Rr+r²)/313、球r-半径d-直径V=4/3πr^3=πd^3/614、球缺h-球缺高,r-球半径,a-球缺底半径V=πh(3a²+h²)/6 =πh²(3r-h)/315、球台r1和r2-球台上、下底半径h-高V=πh[3(r1²+r2²)+h²]/616、圆环体R-环体半径D-环体直径r-环体截面半径d-环体截面直径V=2π2Rr²=π2Dd²/417、桶状体D-桶腹直径d-桶底直径h-桶高V=πh(2D²+d²)/12 ,(母线是圆弧形,圆心是桶的中心)V=πh(2D²+Dd+3d²/4)/15 (母线是抛物线形)。
各种形体面积体积计算公式

各种形体面积体积计算公式
一、立体
1.椎体
椎体的表面积公式为:S=2πrh;椎体的体积公式为:V=1/3πr^2h,其中r为椎体半径,h为椎体的高。
2.圆柱体
圆柱体的表面积公式为:S=2πrh+2πr2;圆柱体的体积公式为:
V=πr²h,其中r为圆柱体底面的半径,h为圆柱体的高。
3.球体
球体的表面积公式为:S=4πr²;球体的体积公式为:V=4/3πr³,其中r为球体的半径。
4.圆锥体
圆锥体的表面积公式为:S=πrl+πrs;圆锥体的体积公式为:
V=1/3πr²h,其中r为圆锥体的底面半径,l为圆锥体的底面周长,h为圆锥体的高。
5.正方体
正方体的表面积公式为:S=6a²;正方体的体积公式为:V=a³,其中a为正方体的边长。
6.平行四边体
平行四边体的表面积公式为:S=2a²+2b²;平行四边体的体积公式为:V=a²b,其中a为平行四边体的底面的长度,b为平行四边体的底面的宽度。
二、平面
1.三角形
三角形的面积公式为:S=1/2absinC,其中a、b为三角形的两边,C
为三角形的夹角(以弧度为单位)。
2.矩形
矩形的面积公式为:S=ab,其中a为矩形的长,b为矩形的宽。
3.正方形
正方形的面积公式为:S=a²,其中a为正方形的边长。
4.圆
圆的面积公式为:S=πr²,其中r为圆的半径。
表面积体积的计算公式

表面积体积的计算公式一、正方体。
1. 表面积公式。
- 设正方体的棱长为a,正方体的表面积S = 6a^2。
因为正方体有6个面,且每个面的面积都是a^2。
2. 体积公式。
- 正方体的体积V=a^3。
二、长方体。
1. 表面积公式。
- 设长方体的长、宽、高分别为a、b、c,则表面积S = 2(ab+bc + ac)。
长方体有6个面,相对的面面积相等,其中前面和后面的面积为ac,左面和右面的面积为bc,上面和下面的面积为ab。
2. 体积公式。
- 长方体的体积V=abc。
三、圆柱体。
1. 表面积公式(含两个底面)- 设圆柱体底面半径为r,高为h。
圆柱体的表面积S = 2π r^2+2π rh。
其中2π r^2是两个底面圆的面积,2π rh是侧面展开矩形的面积(矩形的长为底面圆的周长2π r,宽为圆柱的高h)。
2. 体积公式。
- 圆柱体的体积V=π r^2h。
四、圆锥体。
1. 表面积公式(含底面)- 设圆锥底面半径为r,母线长为l。
圆锥的表面积S=π r^2+π rl。
其中π r^2是底面圆的面积,π rl是侧面展开扇形的面积(扇形的弧长为底面圆的周长2π r,半径为母线l)。
2. 体积公式。
- 圆锥体的体积V=(1)/(3)π r^2h(这里h是圆锥的高,根据勾股定理l^2=h^2+r^2,如果已知r和l也可求出h再求体积)。
五、球体。
1. 表面积公式。
- 设球的半径为r,球的表面积S = 4π r^2。
2. 体积公式。
- 球的体积V=(4)/(3)π r^3。
体积表面积计算公式大全

多面体的体积和表面积
图形
尺寸符号
立方体
长方体∧棱柱∨
三棱柱
棱锥
棱台
圆柱和空心圆柱∧管∨
斜线直圆柱
直圆锥
圆台
球
球扇形∧球楔∨
球缺
圆环体∧胎∨
球带体
桶形
椭球体
a,b,c-半轴
交叉圆柱体
梯形体
常用图形求面积公式
图形
尺寸符号
面积(F)表面积(S)
正方形
长方形
三角形
平行四边形
任意四边形
正多边形
菱形
梯形
圆形
椭圆形
a·b-主轴
F= (π/4) a·b
扇形
弓形
圆环
部分圆环
新月形
抛物线形
等多边形
常用形体体积面积计算公式大全

常用形体体积面积计算公式大全以下是常用的形体体积和面积计算公式:
1.立方体:
-体积公式:V=s^3(s为立方体的边长)
-表面积公式:A=6s^2
2.球体:
-体积公式:V=(4/3)πr^3(r为球的半径)
-表面积公式:A=4πr^2
3.圆柱体:
-体积公式:V=πr^2h(r为圆柱的底面半径,h为高)
-表面积公式:A=2πr(r+h)+2πr^2
4.圆锥体:
-体积公式:V=(1/3)πr^2h(r为圆锥的底面半径,h为高) -表面积公式:A=πr(r+√(r^2+h^2))
5.圆环:(两个同心圆之间的区域)
-面积公式:A=π(R^2-r^2)(R为大圆半径,r为小圆半径)
6.正方形:(四边相等,每个角为直角的四边形)
-面积公式:A=a^2(a为边长)
7.长方形:(四边都不相等,每个角为直角的四边形)
-面积公式:A=l×w(l为长,w为宽)
8.三角形:
- 面积公式:A = (1/2)bh (b为底边长,h为高)
9.梯形:(有两个平行的底边)
-面积公式:A=(1/2)(a+b)h(a和b为两个底边的长度,h为高)
10.五边形:
- 面积公式:A = (1/4)sqrt(5(5+2sqrt(5)))a^2 (a为边长)
11.六边形:
-面积公式:A=(3√3)/2a^2(a为边长)
12.椭圆:
- 面积公式:A = πab (a为长轴的一半,b为短轴的一半)
这些是常见的形体体积和面积计算公式,可以帮助你快速计算各种形状的物体的体积和面积。
表面积和体积计算公式

C:周长 S:面积 a:边长周长=边长×4 {C=4a} 面积=边长×边长 {S=a×a}2、正方体V:体积 a:棱长表面积=棱长×棱长×6 {S表=a×a×6} 体积=棱长×棱长×棱长 {V=a×a×a} 3、长方形C:周长 S:面积 a:边长周长=(长+宽)×2 {C=2(a+b)} 面积=长×宽 {S=ab}4、长方体V:体积 s:面积 a:长 b:宽 h:高(1)表面积(长×宽+长×高+宽×高)×2 {S=2(ab+ah+bh)}(2)体积=长×宽×高 {V=abh}5、三角形s:面积 a:底 h:高面积=底×高÷2 {s=ah÷2}三角形高=面积×2÷底三角形底=面积×2÷高6、平行四边形s:面积 a:底 h:高面积=底×高 {s=ah}7、梯形s:面积 a:上底 b:下底 h:高面积=(上底+下底)×高÷2 {s=(a+b)× h÷2}S:面积 C:周长∏ d=直径 r=半径(1)周长=直径×∏=2×∏×半径 {C=∏d=2∏r}(2)面积=半径×半径×∏9、圆柱体v:体积 h:高 s;底面积 r:底面半径 c:底面周长(1)侧面积=底面周长×高 (2)表面积=侧面积+底面积×2 (3)体积=底面积×高(4)体积=侧面积÷2×半径10、圆锥体v:体积 h:高 s;底面积 r:底面半径体积=底面积×高÷3"∏"这个是π。
高中数学的几何体表面积和体积公式是哪些

高中数学的几何体表面积和体积公式是哪些高中数学的几何体表面积和体积公式1、圆柱体:表面积:2πRr+2πRh体积:πR2h(R为圆柱体上下底圆半径,h为圆柱体高)2、圆锥体:表面积:πR2+πR[(h2+R2)的平方根]体积:πR2h/3(r为圆锥体低圆半径,h为其高)3、正方体:表面积:S=6a2,体积:V=a3(a-边长)4、长方体:表面积:S=2(ab+ac+bc)体积:V=abc(a-长,b-宽,c-高)5、棱柱:体积:V=Sh(S-底面积,h-高)6、棱锥:体积:V=Sh/3(S-底面积,h-高)7、棱台:V=h[S1+S2+(S1S2)^1/2]/3(S1上底面积,S2下底面积,h-高)8、拟柱体:V=h(S1+S2+4S0)/6(S1-上底面积,S2-下底面积,S0-中截面积,h-高)9、圆柱:S底=πr2,S侧=Ch,S表=Ch+2S底,V=S底h=πr2h(r-底半径,h-高,C—底面周长,S底—底面积,S侧—侧面积,S表—表面积)10、空心圆柱:V=πh(R^2-r^2)(R-外圆半径,r-内圆半径,h-高)11、直圆锥:V=πr^2h/3(r-底半径,h-高)12、圆台:V=πh(R2+Rr+r2)/3(r-上底半径,R-下底半径,h-高)13、球:V=4/3πr^3=πd^3/6(r-半径,d-直径)14、球缺:V=πh(3a2+h2)/6=πh2(3r-h)/3(h-球缺高,r-球半径,a-球缺底半径)15、球台:V=πh[3(r12+r22)+h2]/6(r1球台上底半径,r2-球台下底半径,h-高)16、圆环体:V=2π2Rr2=π2Dd2/4(R-环体半径,D-环体直径,r-环体截面半径,d-环体截面直径)数学基础差的学生如何提高数学成绩基础薄弱的同学提高数学成绩的方法数学基础打牢,是个非常重要的事,很多及格成绩不到的同学,基本是连计算和公式都不是很过关。
对于这一类学生有以下几点建议。
空间几何体的表面积和体积公式大全
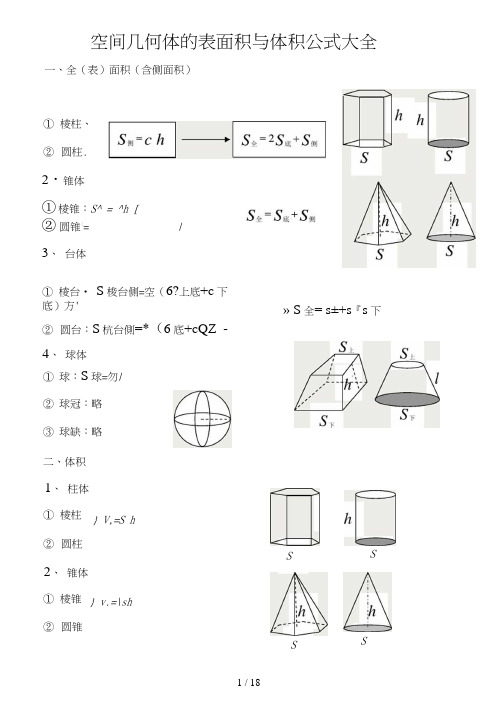
空间几何体的表面积与体积公式大全一、全(表)面积(含侧面积)①棱柱、②圆柱.2・锥体①棱锥:S^ = ^h [②圆锥:= /3、台体①棱台• S梭台侧=空(6?上底+c下底)方'» S全= s±+s『s下②圆台:S杭台側=*(6底+cQZ -4、球体①球:S球=勿/②球冠:略③球缺:略二、体积1、柱体①棱柱} V,=S h②圆柱S S 2、锥体①棱锥} v.=\sh②圆锥S S3、 台体V 台肓//(S 匕+ JS 上S F + S 下)台=齐方(厂上+Jr 上厂下+厂下) 4、 球体①球:V 球② 球冠:略VyT/③ 球缺:略说明:棱锥、棱台计算侧面积时使用侧面的斜高力计算;而圆锥、圆台的 侧面积计算时使用母线/计算。
三、拓展提高1、 祖眶原理:(祖璀:祖冲之的儿子)夹在两个平行平面间的两个几何体,如果它们在任意高度上的平行截面面积都相等,那么这两个几何体的体积相等。
最早推导出球体体积的祖冲之父子便是运用这个原理实现的。
2、 阿基米德原理:(圆柱容球)圆柱容球原理:在一个高和底面直径都是2厂的圆柱形容器内装一个最大 的球体,则该球体的全面积等于圆柱的侧面积,体积等于圆柱体积的?。
①棱台 ②圆台丿分析:圆柱体积:V H1 = s h =(^r)x2r = 2^/圆柱侧面积:S叭削= c/z = (2岔)X2广=4兀/2 彳4 彳因lit :球体体积:|/厅=—x2/r^ =_龙厂球体表面积:S球=4兀厂通过上述分析,我们可以得到一个很重要的关系(如图)即底面直径和高相等的圆柱体积等于与它等底等高的圆锥与同直径的球体积之和3、台体体积公式公式:几冷〃(S上+、恳瓦+ S』证明:如图过台体的上下两底面中心连线的纵切面为梯形ABCD。
延长两侧棱相交于一点P 0设台体上底面积为Si,下底面积为S下高为// °易知:\PDCs 型AB,设卩£ =人,则Pf+h由相似三角形的性质得:孚=袋AB PF即:(相似比等于面积比的算术平方根)、用hi整理得:人=尺刃又因为台体的体积二大锥体体积一小锥体体积u台=§s下(九+力r s上人人(S下-S上)+§s下方即:(、瓦+丫瓦)+扣下力=|/z $ + 应7+S卜)4、球体体积公式推导分析:将半球平行分成相同高度的若干层(兀层),〃越大,每一层越近似于圆柱'"T -HZ)时»每一层都可以看作是一个圆柱。
