一元二次方程根的分布情况归纳总结
一元二次方程根的分布情况归纳总结

一元二次方程根的分布情况归纳总结一元二次方程ax+bx+c=0的根的分布情况可以通过二次函数f(x)=ax^2+bx+c的图象与x轴的交点的横坐标来确定。
设方程的不等两根为x1和x2,且x1<x2.下面分别讨论根的分布情况。
表一:两根与0的大小比较即根的正负情况(a>0)分布情况两个负根即x1<x2<0 两个正根即0<x1<x2 一正根一负根即一个根小于0,一个大于0大致图象结论Δ>0,b0,b>0 f(x)>0 x1和x2都是正数f(0)>0 x1<0<x2表二:两根与k的大小比较(a>0)分布情况两根都小于k即x1x2>k 一个根小于k,一个大于k即x1<k<x2大致图象结论Δ>0,b0 x1<k<x2Δ>0,b>k f(k)>0 x1>x2>kf(k)>0 x1<k<x2表三:根在区间上的分布(a>0)分布情况两根都在(m,n)内一根在(m,n)内,另一根在(p,q)内两根有且仅有一根在(m,n)内,m<n<p<q(图象有两种情况,只画了一种)大致图象结论Δ>0,f(m)>0,f(n)>0 m<n<x1<x2<p<qΔ>0,f(m)>0,f(n)0 x1<m<n<x2<p<qΔ>0,f(m)0,f(p)>0,f(q)<0 m<n<x1<p<q<x2 或x1<m<n<q<p<x2函数与方程思想:1) 方程f(x)=0有根⇔y=f(x)与x轴有交点x⇔函数y=f(x)有零点x2) 若y=f(x)与y=g(x)有交点(x,y)⇔f(x)=g(x)有解x根的分布练题例1、已知二次方程(2m+1)x^2-2mx+(m-1)=0有一正根和一负根,求实数m的取值范围。
一元二次方程根的分布情况归纳总结

1 一元二次方程ax 2• bx • c 二0根的分布情况 2 2 设方程ax • bx • c = 0 a = 0的不等两根为X |,x 2且为:::x 2,相应的二次函数为 f x 二ax bx 0, 方程的根 即为二次函数图象与 x 轴的交点的横坐标(也即是函数的零点),它们的分布情况见下面各表 表一:两根与0的大小比较即根的正负情况(a>0)表二:(两根与k 的大小比较)(a>0) 表三:(根在区间上的分布)(a>0) 两根有且仅有一根在 m, n 内 (图象有两种情况,只画了一种) 一根在 m,n 内,另一根在 p,q 内,m :: n :: p :: q. "■: 0f m .0f n 广0 b m … n 2a大致图象分布情况两个负根即两根都小于 0 X :: 0, x 2 :: 0两个正根即两根都大于 0 x 1 0, x 2 0 一正根一负根即一个根小于 0, 一个大于 0 % ::: 0 ::: 大致图象f 0 ::: 0 分布情况两根都小于k 即x 1 :: k, x 2 :: k两根都大于k 即 x 1 k, x 2 k 一个根小于k ,一个大于k 即 捲::k . x 2 大致图象f k :: 0 分布情况两根都在m, n 内f m f n :: 0 f n :::0 0. "■: 0 f k .0函数与方程思想:(1)方程f(x°)=O有根二y=f(x)与x轴有交点x°=函数y=f(x)有零点X。
(2)若y=f(x)与y = g( x)有交点(x o , y°)= f(x)=g(x)有解x。
根的分布练习题例1、已知二次方程2m 1 x2-2mxrm-1 = 0有一正根和一负根,求实数m的取值范围。
2例2、已知二次函数y = m • 2 x 7:2m - 4 x:「]3m - 3与x轴有两个交点,一个大于1,一个小于1,求实数m的取值范围。
一元二次方程根的分布情况归纳(完整版)

二次方程根的分布与二次函数在闭区间上的最值归纳1、一元二次方程02=++c bx ax 根的分布情况 设方程()200ax bx c a ++=≠的不等两根为12,x x 且12x x <,相应的二次函数为()20f x ax bx c =++=,方程的根即为二次函数图象与x 轴的交点,它们的分布情况见下面各表(每种情况对应的均是充要条件)表一:(两根与0的大小比较即根的正负情况)根在区间上的分布还有一种情况:两根分别在区间()n m ,外,即在区间两侧12,x m x n <>,(图形分别如下)需满足的条件是(1)0a >时,()()00f m f n <⎧⎪⎨<⎪⎩; (2)0a <时,()()0f m f n >⎧⎪⎨>⎪⎩对以上的根的分布表中一些特殊情况作说明: (1)两根有且仅有一根在()n m ,内有以下特殊情况:若()0f m =或()0f n =,则此时()()0f m f n <不成立,但对于这种情况是知道了方程有一根为m 或n ,可以求出另外一根,然后可以根据另一根在区间()n m ,内,从而可以求出参数的值。
如方程()2220mx m x -++=在区间()1,3上有一根,因为()10f =,所以()()()22212mx m x x mx -++=--,另一根为2m,由213m <<得223m <<即为所求;方程有且只有一根,且这个根在区间()n m ,内,即0∆=,此时由0∆=可以求出参数的值,然后再将参数的值带入方程,求出相应的根,检验根是否在给定的区间内,如若不在,舍去相应的参数。
如方程24260x mx m -++=有且一根在区间()3,0-内,求m 的取值范围。
分析:①由()()300f f -<即()()141530m m ++<得出15314m -<<-;②由0∆=即()2164260m m -+=得出1m =-或32m =,当1m =-时,根()23,0x =-∈-,即1m =-满足题意;当32m =时,根()33,0x =∉-,故32m =不满足题意;综上分析,得出15314m -<<-或1m =-根的分布练习题例1、已知二次方程()()221210m x mx m +-+-=有一正根和一负根,求实数m 的取值范围。
二次方程根的分布情况归纳(完整版)

二次方程根的分布与二次函数在闭区间上的最值归纳1、一元二次方程02=++c bx ax 根的分布情况设方程()200ax bx c a ++=≠的不等两根为12,x x 且12x x <,相应的二次函数为()20f x ax bx c =++=,方程的根即为二次函数图象与x 轴的交点,它们的分布情况见下面各表(每种情况对应的均是充要条件)表一:(两根与0的大小比较即根的正负情况)k k k根在区间上的分布还有一种情况:两根分别在区间()n m ,外,即在区间两侧12,x m x n <>,(图形分别如下)需满足的条件是(1)0a >时,()()00f m f n <⎧⎪⎨<⎪⎩; (2)0a <时,()()0f m f n >⎧⎪⎨>⎪⎩对以上的根的分布表中一些特殊情况作说明: (1)两根有且仅有一根在()n m ,内有以下特殊情况:1︒ 若()0f m =或()0f n =,则此时()()0f m f n < 不成立,但对于这种情况是知道了方程有一根为m 或n ,可以求出另外一根,然后可以根据另一根在区间()n m ,内,从而可以求出参数的值。
如方程()2220mx m x -++=在区间()1,3上有一根,因为()10f =,所以()()()22212mx m x x mx -++=--,另一根为2m ,由213m<<得223m <<即为所求; 2︒ 方程有且只有一根,且这个根在区间()n m ,内,即0∆=,此时由0∆=可以求出参数的值,然后再将参数的值带入方程,求出相应的根,检验根是否在给定的区间内,如若不在,舍去相应的参数。
如方程24260x mx m -++=有且一根在区间()3,0-内,求m 的取值范围。
分析:①由()()300f f -< 即()()141530m m ++<得出15314m -<<-;②由0∆=即()2164260m m -+=得出1m =-或32m =,当1m =-时,根()23,0x =-∈-,即1m =-满足题意;当32m =时,根()33,0x =∉-,故32m =不满足题意;综上分析,得出15314m -<<-或1m =-根的分布练习题例1、已知二次方程()()221210m x mx m +-+-=有一正根和一负根,求实数m 的取值范围。
一元二次方程根的分布情况归纳总结(2013.07.22)
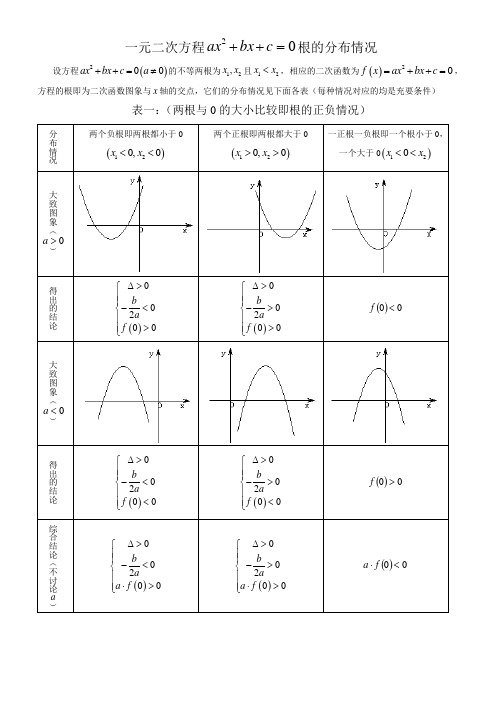
一元二次方程02=++c bx ax 根的分布情况 设方程()200ax bx c a ++=≠的不等两根为12,x x 且12x x <,相应的二次函数为()20f x ax bx c =++=,方程的根即为二次函数图象与x 轴的交点,它们的分布情况见下面各表(每种情况对应的均是充要条件)表一:(两根与0的大小比较即根的正负情况)表二:(两根与k的大小比较)k k k表三:(根在区间上的分布)根在区间上的分布还有一种情况:两根分别在区间()n m ,外,即在区间两侧12,x m x n <>,(图形分别如下)需满足的条件是(1)0a >时,()()00f m f n <⎧⎪⎨<⎪⎩; (2)0a <时,()()0f m f n >⎧⎪⎨>⎪⎩对以上的根的分布表中一些特殊情况作说明: (1)两根有且仅有一根在()n m ,内有以下特殊情况:1︒ 若()0f m =或()0f n =,则此时()()0f m f n <不成立,但对于这种情况是知道了方程有一根为m 或n ,可以求出另外一根,然后可以根据另一根在区间()n m ,内,从而可以求出参数的值。
如方程()2220mx m x -++=在区间()1,3上有一根,因为()10f =,所以()()()22212mx m x x mx -++=--,另一根为2m ,由213m<<得223m <<即为所求; 2︒ 方程有且只有一根,且这个根在区间()n m ,内,即0∆=,此时由0∆=可以求出参数的值,然后再将参数的值带入方程,求出相应的根,检验根是否在给定的区间内,如若不在,舍去相应的参数。
如方程24260x mx m -++=有且一根在区间()3,0-内,求m 的取值范围。
分析:①由()()300f f -<即()()141530m m ++<得出15314m -<<-;②由0∆=即()2164260m m -+=得出1m =-或32m =,当1m =-时,根()23,0x =-∈-,即1m =-满足题意;当32m =时,根()33,0x =∉-,故32m =不满足题意;综上分析,得出15314m -<<-或1m =-函数与方程思想:若y =()f x 与x 轴有交点0x ⇔f (0x )=0 若y =f (x )与y =g (x )有交点(0x ,0y )⇔()f x =()g x 有解0x 。
一元二次方程根的分布情况归纳(完整版)

二次方程根的分布与二次函数在闭区间上的最值归纳1、一元二次方程ax 2 +bx +c = 0根的分布情况设方程ax 2+bx +c =0(a 0)的不等两根为x ,x 且x x ,相应的二次函数为 f (x )=ax 2+bx +c =0,方程的 根即为二次函数图象与 x 轴的交点,它们的分布情况见下面各表(每种情况对应的均是充要条件)表一:(两根与 0 的大小比较即根的正负情况)分布情况小)都根2根x 1大)都根2,根x 1)2小0 一x 1即(根负于一负大根个正一 一大致图象()a得出的结论00b 2a()0-f00b 2a()0-f0 ) (0 (f大致图象()a得出的结论00b 2a()0-f00b 2a ()0-f0 ) (0 f综合结论(不讨论a)0 0 0)b -a2(f 0a0 0 0)b -a2(f 0a0 ) (0 f a表二:(两根与k的大小比较)表三:(根在区间上的分布)两根有且仅有一根在(m , n )内 (图象有两种情况,只画了一种)一根在 (m ,n )内,另一根在(p ,q ) 内, mn p qf (m )f (n ) 0f (p )f (q )根在区间上的分布还有一种情况:两根分别在区间(m ,n )外,即在区间两侧x 1m ,x 2 n ,(图形分别如下)需满 足的条件是大致图象(a得出的结f (m ) 0 f (n ) 0bm - n2af (m ) f (n ) 0或0 00 )m )n )p )q f (m ) f (n ) 0 f (p ) f (q ) 0 0大致图象(a得出的结f (m ) 0 f (n ) 0bm - n2af (m ) f (n ) 0f (m )f (n)0 f (m ) f (n )0 f (p )0 f (p ) f (q )f (q ) 0 分布情况两根都在(m , n )内综合结论(不讨论af (m ) f (n )2g2 f (0)(m +1) - 8mm - 1mm 3-2 2或m 3+2 2m对以上的根的分布表中一些特殊情况作说明:1)两根有且仅有一根在(m ,n )内有以下特殊情况: 若 f(m )=0或 f (n )=0,则此时 f (m )g f (n )0不成立,但对于这种情况是知道了方程有一根为m 或n ,可以 求出另外一根,然后可以根据另一根在区间(m ,n )内,从而可以求出参数的值。
二次方程根的分布情况归纳(完整版)

二次方程根的分布与二次函数在闭区间上的最值归纳1、一元二次方程02=++c bx ax 根的分布情况 设方程()200axbx c a ++=≠的不等两根为12,x x 且12x x <,相应的二次函数为()20f x ax bx c =++=,方程的根即为二次函数图象与x 轴的交点,它们的分布情况见下面各表(每种情况对应的均是充要条件)表一:(两根与0的大小比较即根的正负情况)k k k根在区间上的分布还有一种情况:两根分别在区间()n m ,外,即在区间两侧12,x m x n <>,(图形分别如下)需满足的条件是(1)0a >时,()()00f m f n <⎧⎪⎨<⎪⎩; (2)0a <时,()()0f m f n >⎧⎪⎨>⎪⎩对以上的根的分布表中一些特殊情况作说明: (1)两根有且仅有一根在()n m ,内有以下特殊情况:1︒ 若()0f m =或()0f n =,则此时()()0f m f n <不成立,但对于这种情况是知道了方程有一根为m 或n ,可以求出另外一根,然后可以根据另一根在区间()n m ,内,从而可以求出参数的值。
如方程()2220mx m x -++=在区间()1,3上有一根,因为()10f =,所以()()()22212mx m x x mx -++=--,另一根为2m,由213m <<得223m <<即为所求; 2︒ 方程有且只有一根,且这个根在区间()n m ,内,即0∆=,此时由0∆=可以求出参数的值,然后再将参数的值带入方程,求出相应的根,检验根是否在给定的区间内,如若不在,舍去相应的参数。
如方程24260x mx m -++=有且一根在区间()3,0-内,求m的取值范围。
分析:①由()()300f f -<即()()141530m m ++<得出15314m -<<-;②由∆=即()2164260m m -+=得出1m =-或32m =,当1m =-时,根()23,0x =-∈-,即1m =-满足题意;当32m =时,根()33,0x =∉-,故32m =不满足题意;综上分析,得出15314m -<<-或1m =-根的分布练习题例1、已知二次方程()()221210m x mx m +-+-=有一正根和一负根,求实数m 的取值范围。
二次方程根的分布情况归纳(完整版)

二次方程根的分布
1、一元二次方程
02=++c bx ax 根的分布情况 设方程()2
00ax bx c a ++=≠的不等两根为12,x x 且12x x <,相应的二次函数为()20f x ax bx c =++=,方程的
根即为二次函数图象与x 轴的交点,它们的分布情况见下面各表(每种情况对应的均是充要条件)
表一:(两根与0的大小比较 即根的正负情况)
k k k
根在区间上的分布还有一种情况:两根分别在区间()n m ,外,即在区间两侧12,x m x n <>,(图形分别如下)需满足的条件是
(1)0a >时,()()00f m f n <⎧⎪⎨<⎪⎩; (2)0a <时,()()
0f m f n >⎧⎪⎨>⎪⎩
根的分布练习题
例1、已知二次方程()()221210m x mx m +-+-=有一正根和一负根,求实数m 的取值范围。
例2、已知方程()2210x m x m -++=有两个不等正实根,求实数m 的取值范围。
例3、已知二次函数()()()2
22433y m x m x m =+-+++与x 轴有两个交点,一个大于1,一个小于1,求实数m
的取值范围。
例4、已知二次方程()2
2340mx m x +-+=只有一个正根且这个根小于1,求实数m 的取值范围。
二次函数在闭区间上的最值练习
例2、求函数()[]2
21,1,3f x x ax x =-+∈的最小值。
例3、求函数2
43y x x =-+在区间[],1t t +上的最小值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一元二次方程02
=++c bx ax 根的分布情况
设方程()2
00ax bx c a ++=≠的不等两根为12,x x 且12x x <,相应的二次函数为()20f x ax bx c =++=,
方程的根即为二次函数图象与x 轴的交点,它们的分布情况见下面各表(每种情况对应的均是充要条件)
表一:(两根与0的大小比较即根的正负情况)
分
布情况
两个负根即两根都小于0
()120,0x x << 两个正根即两根都大于0
()120,0x x >>
一正根一负根即一个根小于0,一个大于0()120x x <<
大致图象(
>a )
得出的结论
()00200b a f ∆>⎧⎪⎪
-<⎨⎪>⎪⎩ ()0
0200
b a f ∆>⎧⎪⎪
->⎨⎪>⎪⎩ ()00<f
大
致图象(
<a )
得出的结论
()00200b a f ∆>⎧⎪⎪
-<⎨⎪<⎪⎩ ()0
0200
b a f ∆>⎧⎪⎪
->⎨⎪<⎪⎩ ()00>f
综
合结论(不讨论
a
)
()00200b a a f ∆>⎧⎪⎪-<⎨⎪⋅>⎪⎩ ()0
0200
b a a f ∆>⎧⎪⎪->⎨⎪⋅>⎪⎩ ()00<⋅f a
分
布情况
两根都小于k 即 k x k x <<21, 两根都大于k 即 k x k x >>21, 一个根小于k ,一个大于k 即
21x k x <<
大致图象(
>a )
得出的结论
()020b k a f k ∆>⎧⎪⎪
-<⎨⎪>⎪⎩ ()0
20
b k a f k ∆>⎧⎪⎪
->⎨⎪>⎪⎩ ()0<k f
大
致图象(
<a )
得出的结论
()020b k a f k ∆>⎧⎪⎪
-<⎨⎪<⎪⎩ ()0
20
b k a f k ∆>⎧⎪⎪
->⎨⎪<⎪⎩ ()0>k f
综
合结论(不讨论
a
)
()020b k a a f k ∆>⎧⎪⎪
-
<⎨⎪⋅>⎪⎩ ()0
20
b k a a f k ∆>⎧⎪⎪
-
>⎨⎪⋅>⎪⎩ ()0<⋅k f a
k
k
k
分
布情况两根都在()n
m,内
两根有且仅有一根在()n
m,内
(图象有两种情况,只画了一种)
一根在()n
m,内,另一根在()q
p,
内,q
p
n
m<
<
<
大致图象(
0 > a
)
得出的结论
()
()
2
f m
f n
b
m n
a
∆>
⎧
⎪
>
⎪
⎪
>
⎨
⎪
⎪<-<
⎪⎩
()()0<
⋅n
f
m
f
()
()
()
()
f m
f n
f p
f q
⎧>
⎪
<
⎪
⎨
<
⎪
⎪>
⎩
大
致图象
(
0 < a
)
得
出的结
论
()
()
2
f m
f n
b
m n
a
∆>
⎧
⎪
<
⎪
⎪
<
⎨
⎪
⎪<-<
⎪⎩
()()0<
⋅n
f
m
f
()
()
()
()
f m
f n
f p
f q
⎧<
⎪
>
⎪
⎨
>
⎪
⎪<
⎩
综合结论
(不讨论a )——————()()0<
⋅n
f
m
f
()()
()()
⎪⎩
⎪
⎨
⎧
<
<
q
f
p
f
n
f
m
f
根在区间上的分布还有一种情况:两根分别在区间()n m ,外,即在区间两侧12,x m x n <>,(图形分别如下)需满足的条件是
(1)0a >时,()()00f m f n <⎧⎪⎨<⎪⎩; (2)0a <时,()()0
f m f n >⎧⎪⎨>⎪⎩
对以上的根的分布表中一些特殊情况作说明: (1)两根有且仅有一根在()n m ,内有以下特殊情况:
1︒ 若()0f m =或()0f n =,
则此时()()0f m f n <不成立,但对于这种情况是知道了方程有一根为m 或n ,可以求出另外一根,然后可以根据另一根在区间()n m ,内,从而可以求出参数的值。
如方程()2
220
mx m x -++=在区间()1,3上有一根,因为()10f =,所以()()()2
2212mx m x x mx -++=--,另一根为
2m ,由2
13m
<<得
2
23
m <<即为所求; 2︒ 方程有且只有一根,且这个根在区间()n m ,内,即0∆=,此时由0∆=可以求出参数的值,然后再将参数
的值带入方程,求出相应的根,检验根是否在给定的区间内,如若不在,舍去相应的参数。
如方程
24260x mx m -++=有且一根在区间()3,0-内,求m 的取值范围。
分析:①由()()300f f -<即
()()141530m m ++<得出15314m -<<-
;②由0∆=即()2
164260m m -+=得出1m =-或32
m =,当1m =-时,根()23,0x =-∈-,即1m =-满足题意;当32m =时,根()33,0x =∉-,故3
2
m =不满足题意;
综上分析,得出15
314
m -<<-或1m =-
函数与方程思想:若y =()f x 与x 轴有交点0x ⇔f (0x )=0 若y =f (x )与y =g (x )有交点(0x ,0y )⇔()f x =()g x 有解0x 。
根的分布练习题
例1、已知二次方程()()221210m x mx m +-+-=有一正根和一负根,求实数m 的取值范围。
解:由 ()()2100m f +< 即 ()()2110m m +-<,从而得1
12
m -<<即为所求的范围。
例2、已知二次函数()()()222433y m x m x m =+-+++与x 轴有两个交点,一个大于1,一个小于1,求实数
m 的取值范围。
解:由 ()()210m f +< 即 ()()2210m m ++< ⇒ 1
22
m -<<
即为所求的范围。
例3、已知二次方程()22340mx m x +-+=只有一个正根且这个根小于1,求实数m 的取值范围。
解:由题意有方程在区间()0,1上只有一个正根,则()()010f f < ⇒ ()4310m +< ⇒ 1
3
m <-即为所求范围。
(注:本题对于可能出现的特殊情况方程有且只有一根且这个根在()0,1内,由0∆=计算检验,均不复合题 例4.已知关于x 的二次方程x 2+2mx +2m +1=0.
(1)若方程有两根,其中一根在区间(-1,0)内,另一根在区间(1,2)内,求m 的范围. (2)若方程两根均在区间(0,1)内,求m 的范围
1.若方程4(3)20x x
m m +-•+=有两个不相同的实根,求m 的取值范围。
2.已知函数421x x
y m =+•+有且只有一个零点,求m 的取值范围,并求出该零点
3.关于x 的一元二次方程0222
=++-a ax x ,当a 为何实数时: (1)不同两根在()3,1之间
(2)有一个根大于2,另一个根小于2 (3)在()3,1内有且只有一解
4.已知a 是实数,函数.322)(2
a x ax x f --+=如果)(x f y =在区间[]1,1-上有零点,求a 的取值范围。
