matlab第二讲
合集下载
Matlab第二讲

2.2.3字符串 在Matlab中,字符串是用单引号括起来的字 符序列。MATLAB将字符串当作一个行向 量,每个元素对应一个字符。 例:>>str1=‘hello’ >>str2=‘I like ’’Matlab’’’ %重复单引号 来输入含单引号的字符串须 >>str3=‘你好!’ Matlab存储字符串,一个字符占用2 Byte。
2.2 矩阵和数组
2.2.1矩阵输入 Matlab中的矩阵表示的基本规则: (1)矩阵元素用“[ ]”括住; (2)每行内的元素用逗号或空格隔开; (3)行与行之间用分号或回车键隔开; (4)元素可以是数值或表达式;
通过显式元素输入矩阵: 例:>>c=[1 2;3 4;5 6]或c=[1,2;3,4;5,6] 通过语句生成矩阵: 语句 from: step: to(开始值: 步长: 结束值) step省略时默认步长为1;step省略或step>0 而from>to时为空矩阵,step<0而from<to时 也为空矩阵。 例:x1=2:5 x2=2:0.5:5 x3=5:-1:2 x4=2:-1:3 x5=2:-1:0.5 x6=[1:2:5;1:3:7]
(3)矩阵和数组的除法 矩阵:A\B和A/B分别表示左除和右除。 X=A\B是方程A*X=B的解,A\B=A-1*B X=A/B是方程X*A=B的解,A/B=A*B-1 数组:A.\B和A./B分别表示数组的左除和右除, 表示数组相应元素相除。 例:>>A=[2 -1 3;3 1 -5;4 -1 1] >>B=[5;5;9] >>X=A\B (4)矩阵和数组的乘方 P48 矩阵:A^B 数组:A.^B
MATLAB课件-第二讲
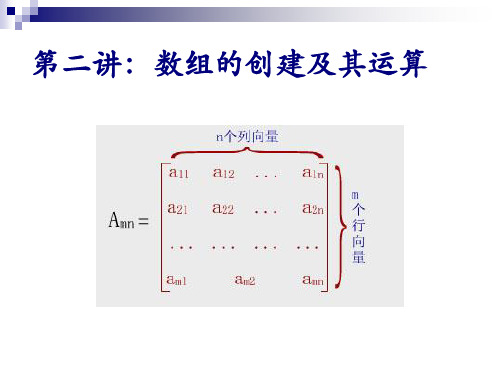
A(r,c)
访问A的由r指定行和c指定列上元素构 成的子数组;r,c可取多行或列
A(r, :)
访问A的r指定行上全部元素构成的子 数组;此处冒号表示全部列
A(:,c)
访问A的c指定列上全部元素的子数 组;此处冒号表示全部行
【例1】单下标的使用 >>a=zeros(2, 5); >>a(:)=-1:8
【例4】>> diag (diag(D)) %外面diag含义为利用一维数组生 成对角阵
ans= 100 010 001
【例5】>>命令栏输入:magic(3) ans =
816 357 492 说明:magic(3)生成一3x3魔方矩阵,即该矩阵横、竖、斜 各列元素总和相等
2.4 数组操作
常见的数组操作函数
命令 permute repmat
reshape
flipud
fliplr
rot90
含义
重排数组的维度次序
按指定的“行数、列数”铺放模块数组,以形成更大 的数组
在总元素数不变的前提下,改变数组的“行数、列 数” 以数组“水平中线”为对称轴,交换上下对称位置上 的数组元素
以数组“垂直中线”为对称轴,交换左右对称位置上 的数组元素
>>a([1 3 5 5 3 1])
ans = 0 5 10 10 5 0
>>a(6)
??? Index exceeds matrix dimensions. 索引超出矩阵维度。 下标值超出了数组的维数,导致错误
>>a(2.1)
??? Subscript indices must either be real positive integers or logicals.
MATLAB讲义第2讲

4
2013-7-27
2.2 命令窗口 (续)
>>who
Your variables are: circle_len area radius
>>whos
Name Size Bytes Class area 1x1 8 double array circle_len 1x1 8 double array radius 1x1 8 double array Grand total is 3 elements using 24 bytes
Matlab Language
20
பைடு நூலகம்
2013-7-27
2.1 数值表示、变量及表达式 (续)
Matlab预定义的变量
变量名 ans eps pi inf i或j NaN 意义 最近的计算结果的变量名 MATLAB定义的正的极小值=2.2204e-16 圆周率π ∞值,无限大 虚数单元,sqrt(-1) 非数,0/0、∞/ ∞
11
2.6 获取在线帮助
MATLAB提供的帮助信息有两类
简单纯文本帮助信息
help
lookfor(条件比较宽松)例:inverse
窗口式综合帮助信息(文字、公式、图形)
doc
helpwin
2013-7-27
Matlab Language
12
〘功能演示-1〙求方程的根
5 3 2 求方程 2 x 3 x 71 x 9 x 13 0 的全部根。
2013-7-27
Matlab Language
6
2.2 命令窗口 (续)
数值显示格式设置 缺省显示格式:简洁的短(short g,7位有效数字)格式 窗口命令及语法格式:format 显示格式关键字 如:format long %15位数字显示 常见通用命令 命令 clc clear who或whos dir cd type help或doc quit或exit
2013-7-27
2.2 命令窗口 (续)
>>who
Your variables are: circle_len area radius
>>whos
Name Size Bytes Class area 1x1 8 double array circle_len 1x1 8 double array radius 1x1 8 double array Grand total is 3 elements using 24 bytes
Matlab Language
20
பைடு நூலகம்
2013-7-27
2.1 数值表示、变量及表达式 (续)
Matlab预定义的变量
变量名 ans eps pi inf i或j NaN 意义 最近的计算结果的变量名 MATLAB定义的正的极小值=2.2204e-16 圆周率π ∞值,无限大 虚数单元,sqrt(-1) 非数,0/0、∞/ ∞
11
2.6 获取在线帮助
MATLAB提供的帮助信息有两类
简单纯文本帮助信息
help
lookfor(条件比较宽松)例:inverse
窗口式综合帮助信息(文字、公式、图形)
doc
helpwin
2013-7-27
Matlab Language
12
〘功能演示-1〙求方程的根
5 3 2 求方程 2 x 3 x 71 x 9 x 13 0 的全部根。
2013-7-27
Matlab Language
6
2.2 命令窗口 (续)
数值显示格式设置 缺省显示格式:简洁的短(short g,7位有效数字)格式 窗口命令及语法格式:format 显示格式关键字 如:format long %15位数字显示 常见通用命令 命令 clc clear who或whos dir cd type help或doc quit或exit
第二讲 MATLAB基础PPT课件
3、MATLAB常用用户文件格式
• M文件:程序文件。文件扩展名为.m。可在File 菜单中创建或打开。也可从历史命令窗口生成。
• MAT文件:数据文件。文件扩展名为.mat。用 于保存工作空间中(内存中)的数据变量。可 用“save”命令生成。
• FIGURE文件:图形文件。文件扩展名为.fig。 可由MATLAB的绘图命令生成,也可在File菜 单中创建或打开。
save — 将全部变量保存到数据文件中 save a b— 将变量a,b保存到数据文件中 save a b-append— 将变量a,b添加到中 clear —— 从内存中删除变量 clear a b —— 从内存中删除变量a,b (clc —— 清屏 ) who —— 显示内存中的变量(只显示变量名) load —— 将变量从 .mat 数据文件中装入内存
Current Directory Browser 窗口
• Workspace Browser(工作空间浏览器窗口)
也是在左上方,可与目录浏览器窗口切换。又称内存浏 览器窗口。用于显示MATLAB工作空间中所有变量的变量名、 数据结构、数据类型、大小和字节数。并可以对变量进行观 察、编辑、提取、保存和图形显示等操作。
Clear Command History % 清除历史命令窗口中的内容
Clear Workspace
% 清除工作空间中的内容
• Desktop: Undock Workspace % 将工作空间窗口从主界面中分离
…ቤተ መጻሕፍቲ ባይዱ
Desktop Layout
% 主界面布局
Command Window % 打开(或关闭)命令窗口
在左上方。可显示当前目录下的M(程序)、 FIG(图形)、 MAT(数据)等文件信息,如文件 类型、文件名、最后修改时间等,并可复制、编辑 和运行M文件以及装载MAT数据文件。选中窗口中 列出的某个文件,单击鼠标右键,即可对其进行打 开、运行、装载等处理和创建、重命名、删除、复 制等常规操作。
MATLAB第二讲__数值计算和符号计算

(4)数值运算中必须先对变量赋值;符号运算无须事先对变 量赋值,但必须先定义,运算结果以标准的符号表达 式形式给出。
Matlab基础应用 21
2.2.2 符号运算中的运算符
(1)基本运算符 符号矩阵:‚+”,‚-”,‚*‛,‚\”, ‚/”, ‚^”, ‚ ’ ” 符号数组:‚.*”,‚./”,‚.\‛,‚.^”, ‚.’ ” (2)关系运算符 运算符只有‚==”,‚~=”。
Matlab基础应用 7
1.3.4 多项式乘除运算(续)
例4: a(x)=x2+2x+3; b(x)=4x2+5x;求c=a(x)*b(x)。 解: >>a=[1 2 3];b=[4 5 0]; >>c=conv(a,b) c= 4 13 22 15 0 >>[d,r]=deconv(c,a) d= 4 5 0 r= 0 0 0 0 0
注意: 方法一只创建了符号表达式,没有创建符号变量; 而方法二既创建了符号表达式,又创建符号变量.
Matlab基础应用 19
2.1.3 创建符号矩阵
使用sym和syms命令创建
例4: A=sym(‘[a,b;c,d]’) A= [ a, b] [ c, d] syms f g h k B=[f,g;h,k] B=
%方法二
Name Size Bytes Class a 1x1 126 sym object b 1x1 126 sym object c 1x1 126 sym object f2 1x1 146 sym object x 1x1 126 sym object Grand total is 20 elements using 650 bytes
matlab-第2讲

函数使用说明: (1) 三角函数以弧度为单位计算。 (2) abs函数可以求实数的绝对值、复数的模、字符串的ASCII 码值. (3) 用于取整的函数有fix、floor、ceil、round,要注意它们的 区别。
• • • •
fix():向0方向靠拢取整 floor():向左取整,即向负无穷方向取整 ceil():返回大于等于指定表达式的最小整数,即向正无穷方向取整 round ():四舍五入 rem(x,y)=x-y.*fix(x./y) mod(x,y) )=x-y.*floor(x./y) rem(x,y)和mod(x,y)要求x,y必须为相同大 小的实矩阵或为标量。
A=
1 1 1 1 8 4 2 1 27 9 3 1 125 25 5 1
(3) 希尔伯特矩阵 在MATLAB中,生成希尔伯特矩阵的函数是hilb(n)。 使用一般方法求逆会因为原始数据的微小扰动而产生不可靠 的计算结果。MATLAB中,有一个专门求希尔伯特矩阵的逆 的函数invhilb(n),其功能是求n阶的希尔伯特矩阵的逆矩阵。
2.1.3 内存变量的管理
1.内存变量的删除与修改 工作空间窗口(Workspace)专门用于内存变量的管理。在 Workspace窗口中可以显示所有内存变量的属性。 当选中某些变量后,再单击Delete按钮,就能删除这些变 量。 当选中某些变量后,再单击Open按钮,将进入变量编辑器。 通过变量编辑器可以直接观察变量中的具体元素,也可修 改变量中的具体元素。
1 4 2 5 3 6
Ex:1. 写出完成下列操作的命令。
a. b.
c.
d. e.
将矩阵A 第2~5 行中的第1,3,5列元素赋给矩阵B。 删除矩阵A的第7号元素。 将矩阵A的每个元素值加30。 求矩阵A的大小和维数(提示:用size函数和ndims函数)。 将含有12个元素的向量x转换成3×4矩阵。
matlab 第二讲

字符与字符串
字符与字符串运算是各种高级语言不可缺少的 部分,Matlab具有强大的字符处理能力。
字符串和字符数组
字符串必须用单引号括起来
str1='Matrix Laboratory'
字符串是由多个字符组成的字符行向量
str2=['M','a','t','r','i','x']
字符数组必须是方的,即每行的字符个数必须相等
>> x=[0:0.2:2*pi];
红色、虚线、 离散点用加号
>> plot(x,cos(x));
>> plot(x,cos(x),’r+:’); 属性可以全部指定,也
>> plot(x,cos(x),’bd-.’); 可以只指定其中某几个 >> plot(x,cos(x),’k*-’); 排列顺序任意
例:>> x=[0:pi/10:2*pi];
>> y=sin(x); >> plot(x,y);
Matlab 二维作图
基本形式
plot(x,y) x, y 都是向量,则以 x 中元素为横坐标, y 中元素为 纵坐标作平面曲线。此时 x, y 必须具有相同长度。 x, y 都是矩阵,则将 x 的列和 y 中相应的列相组合, 绘制多条平面曲线。此时 x, y 必须具有相同的大小。 x 是向量, y 是矩阵,若 x 的长度与 y 的行数相等, 则将 x 与 y 中的各列相对应,绘制多条平面曲线;否 则,若 x 的长度与 y 的列数相等,则将 x 与 y 中的各 行相对应,绘制多条平面曲线。此时 x 的长度必须等 于 y 的行数或列数。
字符与字符串运算是各种高级语言不可缺少的 部分,Matlab具有强大的字符处理能力。
字符串和字符数组
字符串必须用单引号括起来
str1='Matrix Laboratory'
字符串是由多个字符组成的字符行向量
str2=['M','a','t','r','i','x']
字符数组必须是方的,即每行的字符个数必须相等
>> x=[0:0.2:2*pi];
红色、虚线、 离散点用加号
>> plot(x,cos(x));
>> plot(x,cos(x),’r+:’); 属性可以全部指定,也
>> plot(x,cos(x),’bd-.’); 可以只指定其中某几个 >> plot(x,cos(x),’k*-’); 排列顺序任意
例:>> x=[0:pi/10:2*pi];
>> y=sin(x); >> plot(x,y);
Matlab 二维作图
基本形式
plot(x,y) x, y 都是向量,则以 x 中元素为横坐标, y 中元素为 纵坐标作平面曲线。此时 x, y 必须具有相同长度。 x, y 都是矩阵,则将 x 的列和 y 中相应的列相组合, 绘制多条平面曲线。此时 x, y 必须具有相同的大小。 x 是向量, y 是矩阵,若 x 的长度与 y 的行数相等, 则将 x 与 y 中的各列相对应,绘制多条平面曲线;否 则,若 x 的长度与 y 的列数相等,则将 x 与 y 中的各 行相对应,绘制多条平面曲线。此时 x 的长度必须等 于 y 的行数或列数。
Matlab 第二讲:Matlab中的函数

15
MATLAB is column dominant, so when sort is used with a 2-D matrix, each column is sorted in ascending order
16
查看矩阵的大小
查看矩阵的大小:size、length
size(A) size(A,1) size(A,2)
Matlab中的函数
1
函数取值
函数作用在矩阵上的取值
设 x 是变量, f 是一个函数
当 x = a 是标量时,f(x) = f(a) 也是一个标量 当 x = [x1, x2, … , xn ] 是向量时,则 f(x) = [ f(x1), f(x2), … , f(xn)] 是一个与 x 长度相同的向量
f 作用在 x 的每个分量上!
若 A 是矩阵,则 f (A) 是一个与 A 同形状的矩阵
2
函数取值
f ( a11 ) f (a ) 21 f ( A) f ( am1 ) f ( a12 ) f ( a22 ) f ( am 2 ) f ( a1n ) f ( a2 n ) f ( amn )
若参数 x 是矩阵, 则作用在其各列上
6
Function Input can be either scalars or matrices
7
内置函数的使用
Functions consist of
Name Input argument(s) Output In MATLAB sqrt (x)= result sqrt(4) ans = 2
log(x) % ln(x) 自然对数 (以 e 为底) log2(x) % 以 2 为底的对数 log10(x) % 以 10 为底的对数 sqrt(x) abs(x) % 平方根 % 绝对值
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、矩阵的创建
例3、编制一个名为exno1.m的M文件。 %exno1.m %创建一个M文件,用以输入大规模矩阵 Matrix=[12 23 34 25 27 47 46; 21 344 566 43 45 65 45; 423 45 21 23 67 855 45;
123 452 642 64 632 34 26]
四、矩阵的生成
triu(A)——生成一个和A大小相同的上三角矩阵。该矩阵 的主对角线及以上元素取自A中相应元素,其余元素都为 零。 triu(A,k)——生成一个和A大小相同的上三角矩阵。该矩 阵的第k条对角线及以上元素取自A中相应元素,其余元 素都为零。命令triu(A,0)等同于命令triu( A )。 tril(A)——生成一个和A大小相同的下三角矩阵。该矩阵 的主对角线及以下元素取自A中相应元素,其余元素都为 零。 tril(A,k)——生成一个和A大小相同的下三角矩阵。该矩 阵的第k条对角线及以下元素取自A中相应元素,负数k表 示主对角线下的对角线。其余元素都为零。命令 tril(A,0)等同于命令tril(A)
一、矩阵的创建 符号的作用:
逗号和分号的作用 逗号和分号可作为指令间的分隔符,matlab允许多条语句 在同一行出现。 分号如果出现在指令后,屏幕上将不显示结果。 使用逗号时,命令语句的运行结果将显示。 注意:只要是赋过值的变量,不管是否在屏幕上显示过, 都存储在工作空间中,以后可随时显示或调用。变量名尽 可能不要重复,否则会覆盖 。
二、数组的生成
注:以上关于数组生成的命令经常用于作 图,如: x=linspace(0,pi); %生成数组 y=sin(x); %计算函数 plot(x,y); %作图
三、矩阵的裁剪 A(:,j) 返回矩阵A中第j列列向量。 A(i,:) 返回矩阵A中第i行行向量。 A(:,j:k) 返回由矩阵A中的第j列,第j+1列,直到第k列 列向量组成的子阵。 A(i:k,:) 返回由矩阵A中的第i行,第i+1行,直到第k行 行向量组成的子阵。 A(i:k,j:l) 返回由矩阵A中的第i行到第k行行向量和 第j列到第l列列向量组成的子阵。 A(:) 将矩阵A中的每列合并成一个长的列向量。 A(j:k) 返回一个行向量,其中的元素为A(:)中的从第j 个元素到第k个元素。
一、矩阵的创建 2、通过函数创建数值矩阵
MATLAB提供了许多生成和操作矩阵的函数,可 以利用它们去建立矩阵。
例1:x=[0,pi/6,pi/3;pi/2,2*pi/3,5*pi/6]; >> y=sin(x) y= 0 0.5000 0.8660 1.0000 0.8660 0.5000 例2:reshape函数和diag函数等。 reshape函数用于建立数值矩阵。 diag函数用于产生对角阵。
4.导入数据创建矩阵
一、矩阵的创建 1、直接输入 >>a=[1,2,3;4,5,6]; 注:1.必须使用方括号 2.当一行输不完时可以用续行“„” 3.行与行之间用分号或回车符分隔 4.同行元素用空格或逗号分隔 5.矩阵元素可以是任何matlab表达式,可以是 实数,也可是复数,复数可用特殊函数i,j 输入 6.该方法只适合创建小型矩阵
二、数组的生成
2、用Linspace函数构造数组 用Linspace函数构造数组需要指定首尾值和元素总个数。 linspace(a,b) 在区间[a,b]上创建一个有1 0 0个元素 的向量,这1 0 0个数把整个区间线性分隔。 linspace(a,b,n) 在区间[a,b]上创建一个有n个元素的 向量。 这个命令和冒号表示形式相近,但是它直接定义了数 据的个数。
四、矩阵的生成
fliplr(A)——将二维矩阵A左右翻转。这里的‘lr’是 ‘left - right’的缩写。 flipud(A)——将二维矩阵A上下翻转。这里的‘ud’是‘up - down’的缩写。 flipdim(A,n)——沿指定方向翻转矩阵。 注意:这里n=1或2,当=1相当flipud,当n=2相当fliplr. transpose(A) ——沿主对角线翻转矩阵。 ctranspose(A) ——转置矩阵。 rot90(A)——生成一个由矩阵A逆时针旋转90°而得的新阵。 rot90(A,k)——生成一个由矩阵A逆时针旋转k×90°而得到 的新阵。
可以用聚合的方法创建矩阵甚至更多维数组,但不能生成不 规则的形状,必须是矩形的。如果是水平生成矩阵,则每个 子矩阵必须具有相同的行数;如果是垂向生成矩阵,则每个 子矩阵必须具有相同的列数。
四、矩阵的生成
用repmat函数可以利用已有矩阵的多个拷贝来创建矩 阵。键入下面的命令行:
repmat(M,v,h)
四、矩阵的生成
rand——产生在0~1之间均匀分布的随机数;每调用一次 给一个新的数值。 rand+i*rand——产生一个复数随机数。 rand(n)——产生一个nxn的矩阵,其元素为0~1之间均匀 分布随机数。 rand(m,n)——产生一个mxn的矩阵,其元素是0~1之间均 匀分布的随机数。 randn——产生零均值、单位方差的正态分布随机数。 randn(n)——产生一个n×n的矩阵,其元素为零均值、单 位方差的正态分布随机数。 randn(m,n)——产生一个m×n的矩阵,其元素为零均值、 单位方差的正态分布随机数。
四、矩阵的生成
hilb(n)——生成一个n×n的希尔伯特矩阵。 invhilb(n)——生成一个n×n的希尔伯特矩阵的逆矩阵, 其元素都为整数。 magic(n)——给出一个n×n的魔方矩阵。 pascal(n)——返回一个n×n的Pascal矩阵,它是对称、 正定的矩阵,它的元素由Pascal三角组成。它的逆矩阵的 所有元素是整数。 vander(x) ——生成范德蒙矩阵。 如:>>x=[1 2 3 4 5] >>A=vander(x)
三、矩阵的裁剪 A([j1 j2 „ ]) 返回一个行向量,其中的元素为A ( : )中的第j1、j2„元素。 A(:,[j1 j2„]) 返回矩阵A的第j1列、第j2列等的 列向量。 A([i1 i2„] ,:) 返回矩阵A的第i1行、第i2行等 的行向量。 A([i1 i2...],[j1 j2...]) 返回矩阵第i1行、第 i2行等和第j1列、第j2列等的元素。
例如,要将work文件夹中的exno2.xls调入MATLAB中, 可以如下操作。
二、数组的生成
Matlab中的数组在外观上与矩阵毫无差别,也就是说矩阵的 输入方法可以直接移植到数组的输入上。同样,下述关于数 组的生成方法也可以用来生成矩阵。 X=[0 2 3 6 7 8]就构成了一个有6个元素的数组X。 除直接构造外,还有一些常用的构造方法,以下介绍两种: 1、用增量法构造数组 例3、A=10:15 B=-2.5:2.5 默认时,Matlab创建序列时增量总是1.即使最后的值不是 整数。 例4、A=1:6.3
>>a=zeros(4)
>>b=hilb(4) >>a(2,3)=b(2,3) >>a(:,2)=b(:,4) (exno25)
Matlab语言程序设计
理学院
徐屹
东北电力大学
Northeast Dianli College
第二讲 矩阵的输入与生成
ห้องสมุดไป่ตู้一 二
矩阵的创建 数组的生成 矩阵的裁剪
三 3
四 4
矩阵的生成
第二讲 矩阵的输入与生成
一、矩阵的创建
1.直接输入矩阵
矩阵的 创建
2.通过函数创建数值矩阵 3.通过M文件创建矩阵
四、矩阵的生成
diag(A)——生成一个由矩阵A主对角线元素组成的列向量。 主对角线总是从矩阵左上角开始。对于方阵来说它结束 于矩阵的右下角。 diag(x)——生成一个n维的方阵,它的主对角线元素值取 自向量x,其余元素的值都为0。 diag(A ,k)——生成一个由矩阵A第k条对角线的元素组成 的列向量。k=0为主对角线;k<0为下第k对角线;k>0为 上第k对角线。 diag(x ,k)——生成一个(n+abs(k))维的方阵,该矩阵的 第k条对角线元素取自向量x,其余元素都为零。
四、矩阵的生成
矩阵聚合是通过连接一个或多个矩阵来形成一个新的矩阵。 符号[]不仅是一个矩阵构造符,它还是一个Matlab聚合 运算符。表达式C=[A B]在水平方向上聚合矩阵A和B, 表达式C=[A;B]在垂向上聚合它们。 例如:A=ones(2,5)*6, %2*5的矩阵,元素为6. B=rand(3,5), %3*5的矩阵,元素为随机数 C=[A;B] %垂向聚合A和B (exno22)
一、矩阵的创建
例如:>>a3=[2 4 6 8 10];
>>a2=[2,4 6,8,10];
>>a1=[2;4;6;8;10];
Matlab可以在行和列向量之间进行转置,使用“`”,如在 本例中,可以使用如下命令实现上述3个向量的转置,在 “命令”窗口中输入如下命令,并按Enter键确认。
>>a3’ >>a2’ >>a1’
(exno21)
一、矩阵的创建
3、通过M文件建立矩阵 直接输入一个规模比较大的矩阵是很艰苦的工作, 而且出错也不容易修改,这里利用M文件的特点 将所要输入的矩阵按格式先写到一个文本文件中, 然后,将此文件以M为扩展名命名,这就是M文 件。在MATLAB命令窗口中输入此M文件名,则 要输入的大型矩阵就被直接输入到内存中了。
Matlab将矩阵M在垂向上复制v次,在水平方向上复制 h次。例如,下面将已有矩阵A复制到新矩阵B中。
A=[8 1 6;3 5 7;4 9 2]
B=repmat(A,2,4)
(exno23)
四、矩阵的生成
用blkdiag函数创建块对角矩阵
