2018年济南市中考数学试题及答案
2018年济南市中考数学试题及答案
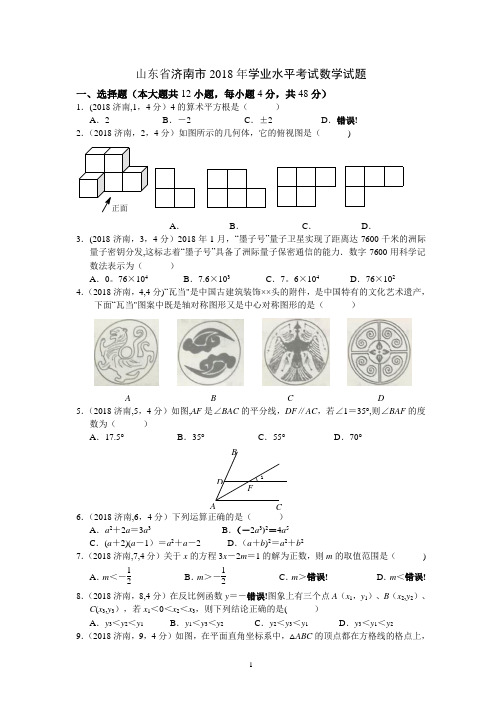
山东省济南市2018年学业水平考试数学试题一、选择题(本大题共12小题,每小题4分,共48分)1.(2018济南,1,4分)4的算术平方根是( )A .2B .-2C .±2D .错误! 2.(2018济南,2,4分)如图所示的几何体,它的俯视图是( )正面A .B .C .D .3.(2018济南,3,4分)2018年1月,“墨子号”量子卫星实现了距离达7600千米的洲际量子密钥分发,这标志着“墨子号”具备了洲际量子保密通信的能力.数字7600用科学记数法表示为( )A .0。
76×104B .7.6×103C .7。
6×104D .76×102 4.(2018济南,4,4分)“瓦当"是中国古建筑装饰××头的附件,是中国特有的文化艺术遗产,下面“瓦当"图案中既是轴对称图形又是中心对称图形的是( )A B C D 5.(2018济南,5,4分)如图,AF 是∠BAC 的平分线,DF ∥AC ,若∠1=35°,则∠BAF 的度数为( ) A .17.5° B .35° C .55° D .70°6.(2018济南,6,4分)下列运算正确的是( ) A .a 2+2a =3a 3 B .(-2a 3)2=4a 5 C .(a +2)(a -1)=a 2+a -2 D .(a +b )2=a 2+b 2 7.(2018济南,7,4分)关于x 的方程3x -2m =1的解为正数,则m 的取值范围是( ) A .m <-12 B .m >-12 C .m >错误! D .m <错误!8.(2018济南,8,4分)在反比例函数y =-错误!图象上有三个点A (x 1,y 1)、B (x 2,y 2)、C (x 3,y 3),若x 1<0<x 2<x 3,则下列结论正确的是( )A .y 3<y 2<y 1B .y 1<y 3<y 2C .y 2<y 3<y 1D .y 3<y 1<y 2 9.(2018济南,9,4分)如图,在平面直角坐标系中,△ABC 的顶点都在方格线的格点上,1A B C DF将△ABC 绕点P 顺时针方向旋转90°,得到△A ′B ′C ′,则点P 的坐标为( ) A .(0,4) B .(1,1) C .(1,2) D .(2,1)xy–1–2–3–412341234567BCA A'C 'B'O10.(2018济南,10,4分)下面的统计图大致反应了我国2012年至2017年人均阅读量的情况.根据统计图提供的信息,下列推断不合理...的是( ) A .与2016年相比,2017年我国电子书人均阅读量有所降低 B .2012年至2017年,我国纸质书的人均阅读量的中位数是4。
2018年山东省济南市中考数学试题及答案-真题试卷

E
M
E
A
A
F
B
C DB
DC
第 26 题图 1
第 26 题图 2
7
27.(2018 济南,27,12 分) 如图 1,抛物线 y=ax2+bx+4 过 A(2,0)、B(4,0)两点,交 y 轴于点 C,过点 C 作 x
轴的平行线与不等式抛物线上的另一个交点为 D,连接 AC、BC.点 P 是该抛物线上一动 点,设点 P 的横坐标为 m(m>4).
=CF,连接 EF 交 BD 于点 O. 求证:OB=OD.
E
A
D
O
B
C
F
22.(2018 济南,22,8 分) 本学期学校开展以“感受中华传统买德”为主题的研学部动,组织 150 名学生多观历史
好物馆和民俗晨览馆,每一名学生只能参加其中全顺活动,共支付票款 2000 元,票价信息 如下:
地点 历史博物馆 民俗展览馆
【答案】B
4.(2018 济南,4,4 分)“瓦当”是中国古建筑装饰××头的附件,是中国特有的文化艺术遗
产,下面“瓦当”图案中既是轴对称图形又是中心对称图形的是(
)
A
B
C
D
【答案】D
5.(2018 济南,5,4 分)如图,AF 是∠BAC 的平分线,DF∥AC,若∠1=35°,则∠BAF
的度数为(
)
2.35 2.48
2
纸质书 电子书
O 2012 2013 2014 2015 2016 2017 年份
11.(2018 济南,11,4 分)如图,一个扇形纸片的圆心角为 90°,半径为 6.如图 2,将这
张扇形纸片折叠,使点 A 与点 O 恰好重合,折痕为 CD,图中阴影为重合部分,则阴
2018年山东省济南市中考数学试卷含解析(完美打印版)

2018年山东省济南市中考数学试卷(含解析)一、选择题(本大题共12小题,每小题4分,共48分)1.(4分)4的算术平方根是()A.2B.﹣2C.±2D.2.(4分)如图所示的几何体,它的俯视图是()A.B.C.D.3.(4分)2018年1月,“墨子号”量子卫星实现了距离达7600千米的洲际量子密钥分发,这标志着“墨子号”具备了洲际量子保密通信的能力.数字7600用科学记数法表示为()A.0.76×104B.7.6×103C.7.6×104D.76×1024.(4分)“瓦当”是中国古建筑装饰檐头的附件,是中国特有的文化艺术遗产,下面“瓦当”图案中既是轴对称图形又是中心对称图形的是()A.B.C.D.5.(4分)如图,AF是∠BAC的平分线,DF∥AC,若∠1=35°,则∠BAF的度数为()A.17.5°B.35°C.55°D.70°6.(4分)下列运算正确的是()A.a2+2a=3a3B.(﹣2a3)2=4a5C.(a+2)(a﹣1)=a2+a﹣2D.(a+b)2=a2+b27.(4分)关于x的方程3x﹣2m=1的解为正数,则m的取值范围是()A.m<﹣B.m>﹣C.m>D.m<8.(4分)在反比例函数y=﹣图象上有三个点A(x1,y1)、B(x2,y2)、C(x3,y3),若x1<0<x2<x3,则下列结论正确的是()A.y3<y2<y1B.y1<y3<y2C.y2<y3<y1D.y3<y1<y29.(4分)如图,在平面直角坐标系中,△ABC的顶点都在方格线的格点上,将△ABC绕点P顺时针方向旋转90°,得到△A′B′C′,则点P的坐标为()A.(0,4)B.(1,1)C.(1,2)D.(2,1)10.(4分)下面的统计图大致反应了我国2012年至2017年人均阅读量的情况.根据统计图提供的信息,下列推断不合理的是()A.与2016年相比,2017年我国电子书人均阅读量有所降低B.2012年至2017年,我国纸质书的人均阅读量的中位数是4.57C.从2014年到2017年,我国纸质书的人均阅读量逐年增长D.2013年我国纸质书的人均阅读量比电子书的人均阅读量的1.8倍还多11.(4分)如图1,一个扇形纸片的圆心角为90°,半径为6.如图2,将这张扇形纸片折叠,使点A与点O恰好重合,折痕为CD,图中阴影为重合部分,则阴影部分的面积为()A.6π﹣B.6π﹣9C.12π﹣D.12.(4分)若平面直角坐标系内的点M满足横、纵坐标都为整数,则把点M叫做“整点”.例如:P(1,0)、Q(2,﹣2)都是“整点”.抛物线y=mx2﹣4mx+4m﹣2(m>0)与x轴交于点A、B两点,若该抛物线在A、B之间的部分与线段AB所围成的区域(包括边界)恰有七个整点,则m的取值范围是()A.≤m<1B.<m≤1C.1<m≤2D.1<m<2二、填空题(本大题共6小题,每小题4分,共24分)13.(4分)分解因式:m2﹣4=.14.(4分)在不透明的盒子中装有5个黑色棋子和若干个白色做子,每个棋子除颜色外都相同,任意摸出一个棋子,摸到黑色棋子的概率是,则白色棋子的个数是.15.(4分)一个正多边形的每个内角等于108°,则它的边数是.16.(4分)若代数式的值是2,则x=.17.(4分)A、B两地相距20km,甲乙两人沿同一条路线从A地到B地.甲先出发,匀速行驶,甲出发1小时后乙再出发,乙以2km/h的速度度匀速行驶1小时后提高速度并继续匀速行驶,结果比甲提前到达.甲、乙两人离开A地的距离y(km)与时间t(h)的关系如图所示,则甲出发小时后和乙相遇.18.(4分)如图,矩形EFGH的四个顶点分别在矩形ABCD的各条边上,AB=EF,FG=2,GC=3.有以下四个结论:①∠BGF=∠CHG;②△BFG≌△DHE;③tan∠BFG=;④矩形EFGH的面积是4.其中一定成立的是.(把所有正确结论的序号填在横线上)三、解答题(本大题共9小题,共78分)19.(6分)计算:2﹣1+|﹣5|﹣sin30°+(π﹣1)0.20.(6分)解不等式组:21.(6分)如图,在▱ABCD中,连接BD,E是DA延长线上的点,F是BC延长线上的点,且AE=CF,连接EF交BD于点O.求证:OB=OD.22.(8分)本学期学校开展以“感受中华传统美德”为主题的研学活动,组织150名学生参观历史博物馆和民俗展览馆,每一名学生只能参加其中一项活动,共支付票款2000元,票价信息如下:(1)请问参观历史博物馆和民俗展览馆的人数各是多少人?(2)若学生都去参观历史博物馆,则能节省票款多少元?23.(8分)如图AB是⊙O的直径,P A与⊙O相切于点A,BP与⊙O相交于点D,C为⊙O上的一点,分别连接CB、CD,∠BCD=60°.(1)求∠ABD的度数;(2)若AB=6,求PD的长度.24.(10分)某校开设了“3D”打印、数学史、诗歌欣赏、陶艺制作四门校本课程,为了解学生对这四门校本课程的喜爱情况,对学生进行了随机问卷调查(问卷调查表如图所示),将调查结果整理后绘制例图1、图2两幅均不完整的统计图表.请您根据图表中提供的信息回答下列问题:(1)统计表中的a=,b=;(2)“D”对应扇形的圆心角为度;(3)根据调查结果,请您估计该校2000名学生中最喜欢“数学史”校本课程的人数;(4)小明和小亮参加校本课程学习,若每人从“A”、“B”、“C”三门校本课程中随机选取一门,请用画树状图或列表格的方法,求两人恰好选中同一门校本课程的概率.25.(10分)如图,直线y=ax+2与x轴交于点A(1,0),与y轴交于点B(0,b).将线段AB先向右平移1个单位长度、再向上平移t(t>0)个单位长度,得到对应线段CD,反比例函数y=(x>0)的图象恰好经过C、D两点,连接AC、BD.(1)求a和b的值;(2)求反比例函数的表达式及四边形ABDC的面积;(3)点N在x轴正半轴上,点M是反比例函数y=(x>0)的图象上的一个点,若△CMN是以CM为直角边的等腰直角三角形时,求所有满足条件的点M的坐标.26.(12分)在△ABC中,AB=AC,∠BAC=120°,以CA为边在∠ACB的另一侧作∠ACM=∠ACB,点D为射线BC上任意一点,在射线CM上截取CE=BD,连接AD、DE、AE.(1)如图1,当点D落在线段BC的延长线上时,直接写出∠ADE的度数;(2)如图2,当点D落在线段BC(不含边界)上时,AC与DE交于点F,请问(1)中的结论是否仍成立?如果成立,请给出证明;如果不成立,请说明理由;(3)在(2)的条件下,若AB=6,求CF的最大值.27.(12分)如图1,抛物线y=ax2+bx+4过A(2,0)、B(4,0)两点,交y轴于点C,过点C作x轴的平行线与抛物线上的另一个交点为D,连接AC、BC.点P是该抛物线上一动点,设点P的横坐标为m (m>4).(1)求该抛物线的表达式和∠ACB的正切值;(2)如图2,若∠ACP=45°,求m的值;(3)如图3,过点A、P的直线与y轴于点N,过点P作PM⊥CD,垂足为M,直线MN与x轴交于点Q,试判断四边形ADMQ的形状,并说明理由.2018年山东省济南市中考数学试卷参考答案与试题解析一、选择题(本大题共12小题,每小题4分,共48分)1.(4分)4的算术平方根是()A.2B.﹣2C.±2D.【分析】算术平方根的定义:一个非负数的正的平方根,即为这个数的算术平方根,由此即可求出结果.【解答】解:∵2的平方为4,∴4的算术平方根为2.故选:A.2.(4分)如图所示的几何体,它的俯视图是()A.B.C.D.【分析】找到从上面看所得到的图形即可.【解答】解:从几何体上面看,2排,上面3个,下面1个,左边2个正方形.故选:D.3.(4分)2018年1月,“墨子号”量子卫星实现了距离达7600千米的洲际量子密钥分发,这标志着“墨子号”具备了洲际量子保密通信的能力.数字7600用科学记数法表示为()A.0.76×104B.7.6×103C.7.6×104D.76×102【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>10时,n是正数;当原数的绝对值<1时,n是负数.【解答】解:7600=7.6×103,故选:B.4.(4分)“瓦当”是中国古建筑装饰檐头的附件,是中国特有的文化艺术遗产,下面“瓦当”图案中既是轴对称图形又是中心对称图形的是()A.B.C.D.【分析】根据轴对称图形与中心对称图形的概念求解.【解答】解:A、不是轴对称图形,也不是中心对称图形;B、不是轴对称图形,是中心对称图形;C、是轴对称图形,不是中心对称图形;D、是轴对称图形,是中心对称图形.故选:D.5.(4分)如图,AF是∠BAC的平分线,DF∥AC,若∠1=35°,则∠BAF的度数为()A.17.5°B.35°C.55°D.70°【分析】根据两直线平行,同位角相等,可得∠F AC=∠1,再根据角平分线的定义可得∠BAF=∠F AC.【解答】解:∵DF∥AC,∴∠F AC=∠1=35°,∵AF是∠BAC的平分线,∴∠BAF=∠F AC=35°,故选:B.6.(4分)下列运算正确的是()A.a2+2a=3a3B.(﹣2a3)2=4a5C.(a+2)(a﹣1)=a2+a﹣2D.(a+b)2=a2+b2【分析】根据多项式的乘法法则、幂的乘方与积的乘方、完全平方公式、合并同类项法则一一判断即可;【解答】解:A、错误.不是同类项不能合并;B、错误.应该是(﹣2a3)2=4a6;C、正确;D、错误.应该是(a+b)2=a2+2ab+b2;故选:C.7.(4分)关于x的方程3x﹣2m=1的解为正数,则m的取值范围是()A.m<﹣B.m>﹣C.m>D.m<【分析】先求出方程的解,再根据题意得出不等式,求出不等式的解集即可.【解答】解:解方程3x﹣2m=1得:x=,∵关于x的方程3x﹣2m=1的解为正数,∴>0,解得:m>﹣,故选:B.8.(4分)在反比例函数y=﹣图象上有三个点A(x1,y1)、B(x2,y2)、C(x3,y3),若x1<0<x2<x3,则下列结论正确的是()A.y3<y2<y1B.y1<y3<y2C.y2<y3<y1D.y3<y1<y2【分析】根据反比例函数图象上点的坐标特征解答.【解答】解:∵A(x1,y1)在反比例函数y=﹣图象上,x1<0,∴y1>0,对于反比例函数y=﹣,在第二象限,y随x的增大而增大,∵0<x2<x3,∴y2<y3<0,∴y2<y3<y1故选:C.9.(4分)如图,在平面直角坐标系中,△ABC的顶点都在方格线的格点上,将△ABC绕点P顺时针方向旋转90°,得到△A′B′C′,则点P的坐标为()A.(0,4)B.(1,1)C.(1,2)D.(2,1)【分析】选两组对应点,连接后作其中垂线,两中垂线的交点即为点P.【解答】解:由图知,旋转中心P的坐标为(1,2),故选:C.10.(4分)下面的统计图大致反应了我国2012年至2017年人均阅读量的情况.根据统计图提供的信息,下列推断不合理的是()A.与2016年相比,2017年我国电子书人均阅读量有所降低B.2012年至2017年,我国纸质书的人均阅读量的中位数是4.57C.从2014年到2017年,我国纸质书的人均阅读量逐年增长D.2013年我国纸质书的人均阅读量比电子书的人均阅读量的1.8倍还多【分析】利用折线统计图结合相应数据,分别分析得出符合题意的答案.【解答】解:A、与2016年相比,2017年我国电子书人均阅读量有所降低,正确;B、2012年至2017年,我国纸质书的人均阅读量的中位数是4.615,错误;C、从2014年到2017年,我国纸质书的人均阅读量逐年增长,正确;D、2013年我国纸质书的人均阅读量比电子书的人均阅读量的1.8倍还多,正确;故选:B.11.(4分)如图1,一个扇形纸片的圆心角为90°,半径为6.如图2,将这张扇形纸片折叠,使点A与点O恰好重合,折痕为CD,图中阴影为重合部分,则阴影部分的面积为()A.6π﹣B.6π﹣9C.12π﹣D.【分析】连接OD,如图,利用折叠性质得由弧AD、线段AC和CD所围成的图形的面积等于阴影部分的面积,AC=OC,则OD=2OC=6,CD=3,从而得到∠CDO=30°,∠COD=60°,然后根据扇形面积公式,利用由弧AD、线段AC和CD所围成的图形的面积=S扇形AOD﹣S△COD,进行计算即可.【解答】解:连接OD,如图,∵扇形纸片折叠,使点A与点O恰好重合,折痕为CD,∴AC=OC,∴OD=2OC=6,∴CD==3,∴∠CDO=30°,∠COD=60°,∴由弧AD、线段AC和CD所围成的图形的面积=S扇形AOD﹣S△COD=﹣•3•3=6π﹣,∴阴影部分的面积为6π﹣.故选:A.12.(4分)若平面直角坐标系内的点M满足横、纵坐标都为整数,则把点M叫做“整点”.例如:P(1,0)、Q(2,﹣2)都是“整点”.抛物线y=mx2﹣4mx+4m﹣2(m>0)与x轴交于点A、B两点,若该抛物线在A、B之间的部分与线段AB所围成的区域(包括边界)恰有七个整点,则m的取值范围是()A.≤m<1B.<m≤1C.1<m≤2D.1<m<2【分析】画出图象,利用图象可得m的取值范围【解答】解:∵y=mx2﹣4mx+4m﹣2=m(x﹣2)2﹣2且m>0,∴该抛物线开口向上,顶点坐标为(2,﹣2),对称轴是直线x=2.由此可知点(2,0)、点(2,﹣1)、顶点(2,﹣2)符合题意.①当该抛物线经过点(1,﹣1)和(3,﹣1)时(如答案图1),这两个点符合题意.将(1,﹣1)代入y=mx2﹣4mx+4m﹣2得到﹣1=m﹣4m+4m﹣2.解得m=1.此时抛物线解析式为y=x2﹣4x+2.由y=0得x2﹣4x+2=0.解得x1=2﹣≈0.6,x2=2+≈3.4.∴x轴上的点(1,0)、(2,0)、(3,0)符合题意.则当m=1时,恰好有(1,0)、(2,0)、(3,0)、(1,﹣1)、(3,﹣1)、(2,﹣1)、(2,﹣2)这7个整点符合题意.∴m≤1.【注:m的值越大,抛物线的开口越小,m的值越小,抛物线的开口越大】答案图1(m=1时)答案图2(m=时)②当该抛物线经过点(0,0)和点(4,0)时(如答案图2),这两个点符合题意.此时x轴上的点(1,0)、(2,0)、(3,0)也符合题意.将(0,0)代入y=mx2﹣4mx+4m﹣2得到0=0﹣4m+0﹣2.解得m=.此时抛物线解析式为y=x2﹣2x.当x=1时,得y=×1﹣2×1=﹣<﹣1.∴点(1,﹣1)符合题意.当x=3时,得y=×9﹣2×3=﹣<﹣1.∴点(3,﹣1)符合题意.综上可知:当m=时,点(0,0)、(1,0)、(2,0)、(3,0)、(4,0)、(1,﹣1)、(3,﹣1)、(2,﹣2)、(2,﹣1)都符合题意,共有9个整点符合题意,∴m=不符合题.∴m>.综合①②可得:当<m≤1时,该函数的图象与x轴所围成的区域(含边界)内有七个整点,故选:B.二、填空题(本大题共6小题,每小题4分,共24分)13.(4分)分解因式:m2﹣4=(m+2)(m﹣2).【分析】本题刚好是两个数的平方差,所以利用平方差公式分解则可.平方差公式:a2﹣b2=(a+b)(a ﹣b).【解答】解:m2﹣4=(m+2)(m﹣2).故答案为:(m+2)(m﹣2).14.(4分)在不透明的盒子中装有5个黑色棋子和若干个白色做子,每个棋子除颜色外都相同,任意摸出一个棋子,摸到黑色棋子的概率是,则白色棋子的个数是15.【分析】黑色棋子除以相应概率算出棋子的总数,减去黑色棋子的个数即为白色棋子的个数;【解答】解:5÷﹣5=15.∴白色棋子有15个;故答案为:15.15.(4分)一个正多边形的每个内角等于108°,则它的边数是5.【分析】根据相邻的内角与外角互为邻补角求出每一个外角的度数为72°,再用外角和360°除以72°,计算即可得解.【解答】解:∵正多边形的每个内角等于108°,∴每一个外角的度数为180°﹣108°=72°,∴边数=360°÷72°=5,∴这个正多边形是正五边形.故答案为:5.16.(4分)若代数式的值是2,则x=6.【分析】根据解分式方程的步骤依次计算可得.【解答】解:=2,去分母得:x﹣2=2(x﹣4),x﹣2=2x﹣8,x=6,经检验:x=6是原方程的解.故答案为:6.17.(4分)A、B两地相距20km,甲乙两人沿同一条路线从A地到B地.甲先出发,匀速行驶,甲出发1小时后乙再出发,乙以2km/h的速度度匀速行驶1小时后提高速度并继续匀速行驶,结果比甲提前到达.甲、乙两人离开A地的距离y(km)与时间t(h)的关系如图所示,则甲出发小时后和乙相遇.【分析】由图象得出解析式后联立方程组解答即可.【解答】解:由图象可得:y甲=4t(0≤t≤5);y乙=;由方程组,解得t=.故答案为.18.(4分)如图,矩形EFGH的四个顶点分别在矩形ABCD的各条边上,AB=EF,FG=2,GC=3.有以下四个结论:①∠BGF=∠CHG;②△BFG≌△DHE;③tan∠BFG=;④矩形EFGH的面积是4.其中一定成立的是①②④.(把所有正确结论的序号填在横线上)【分析】根据矩形的性质和全等三角形的判定分析各小题即可;【解答】解:∵∠FGH=90°,∴∠BGF+∠CGH=90°.又∵∠CGH+∠CHG=90°,∴∠BGF=∠CHG,故①正确.同理可得∠DEH=∠CHG.∴∠BGF=∠DEH.又∵∠B=∠D=90°,FG=EH,∴△BFG≌△DHE,故②正确.同理可得△AFE≌△CHG.∴AF=CH.易得△BFG∽△CGH.设GH、EF为a,∴=.∴=.∴BF=.∴AF=AB﹣BF=a﹣.∴CH=AF=a﹣.在Rt△CGH中,∵CG2+CH2=GH2,∴32+(a﹣)2=a2.解得a=2.∴GH=2.∴BF=a﹣=.在Rt△BFG中,∵cos∠BFG==,∴∠BFG=30°.∴tan∠BFG=tan30°=,故③错误.矩形EFGH的面积=FG×GH=2×2=4,故④正确.故答案为:①②④三、解答题(本大题共9小题,共78分)19.(6分)计算:2﹣1+|﹣5|﹣sin30°+(π﹣1)0.【分析】先利用负指数,绝对值,特殊角的三角函数,零次幂化简,最后合并即可得出结论.【解答】解:2﹣1+|﹣5|﹣sin30°+(π﹣1)0.=+5﹣+1=620.(6分)解不等式组:【分析】分别求出不等式①②的解集,同大取大;同小取小;大小小大中间找;大大小小找不到求出不等式组解集.【解答】解:由①,得3x﹣2x<3﹣1.∴x<2.由②,得4x>3x﹣1.∴x>﹣1.∴不等式组的解集为﹣1<x<2.21.(6分)如图,在▱ABCD中,连接BD,E是DA延长线上的点,F是BC延长线上的点,且AE=CF,连接EF交BD于点O.求证:OB=OD.【分析】欲证明OB=OD,只要证明△EOD≌△FOB即可;【解答】证明:∵▱ABCD中,∴AD=BC,AD∥BC.∴∠ADB=∠CBD.又∵AE=CF,∴AE+AD=CF+BC.∴ED=FB.又∵∠EOD=∠FOB,∴△EOD≌△FOB.∴OB=OD.22.(8分)本学期学校开展以“感受中华传统美德”为主题的研学活动,组织150名学生参观历史博物馆和民俗展览馆,每一名学生只能参加其中一项活动,共支付票款2000元,票价信息如下:(1)请问参观历史博物馆和民俗展览馆的人数各是多少人?(2)若学生都去参观历史博物馆,则能节省票款多少元?【分析】(1)设参观历史博物馆的有x人,参观民俗展览馆的有y人,根据等量关系:①一共150名学生;②一共支付票款2000元,列出方程组求解即可;(2)原来的钱数﹣参观历史博物馆的钱数,列出算式计算可求能节省票款多少元.【解答】解:(1)设参观历史博物馆的有x人,参观民俗展览馆的有y人,依题意,得,解得.答:参观历史博物馆的有100人,则参观民俗展览馆的有50人.(2)2000﹣150×10=500(元).答:若学生都去参观历史博物馆,则能节省票款500元.23.(8分)如图AB是⊙O的直径,P A与⊙O相切于点A,BP与⊙O相交于点D,C为⊙O上的一点,分别连接CB、CD,∠BCD=60°.(1)求∠ABD的度数;(2)若AB=6,求PD的长度.【分析】(1)解法一:要的圆周角定理得:∠ADB=90°,由同弧所对的圆周角相等和直角三角形的性质可得结论;解法二:根据同弧所对的圆心角是圆周角的2倍可得∠BOD=120°,由同圆的半径相等和等腰三角形的性质可得结论;(2)如图1,根据切线的性质可得∠BAP=90°,根据直角三角形30°角的性质可计算AD的长,由勾股定理计算DB的长,由三角函数可得PB的长,从而得PD的长.【解答】解:(1)方法一:如图1,连接AD.∵BA是⊙O直径,∴∠BDA=90°.∵=,∴∠BAD=∠C=60°.∴∠ABD=90°﹣∠BAD=90°﹣60°=30°.方法二:如图2,连接DA、OD,则∠BOD=2∠C=2×60°=120°.∵OB=OD,∴∠OBD=∠ODB=(180°﹣120°)=30°.即∠ABD=30°.(2)如图1,∵AP是⊙O的切线,∴∠BAP=90°.在Rt△BAD中,∵∠ABD=30°,∴DA=BA=×6=3.∴BD=DA=3.在Rt△BAP中,∵cos∠ABD=,∴cos30°==.∴BP=4.∴PD=BP﹣BD=4﹣3=.24.(10分)某校开设了“3D”打印、数学史、诗歌欣赏、陶艺制作四门校本课程,为了解学生对这四门校本课程的喜爱情况,对学生进行了随机问卷调查(问卷调查表如图所示),将调查结果整理后绘制例图1、图2两幅均不完整的统计图表.请您根据图表中提供的信息回答下列问题:(1)统计表中的a=80,b=0.20;(2)“D”对应扇形的圆心角为36度;(3)根据调查结果,请您估计该校2000名学生中最喜欢“数学史”校本课程的人数;(4)小明和小亮参加校本课程学习,若每人从“A”、“B”、“C”三门校本课程中随机选取一门,请用画树状图或列表格的方法,求两人恰好选中同一门校本课程的概率.【分析】(1)根据题意列出算式,再求出即可;(2)根据题意列出算式,再求出即可;(3)根据题意列出算式,再求出即可;(4)先列出表格,再根据题意列出算式,再求出即可.【解答】解:(1)a=36÷0.45=80,b=16÷80=0.20,故答案为:80,0.20;(2)“D”对应扇形的圆心角的度数为:8÷80×360°=36°,故答案为:36;(3)估计该校2000名学生中最喜欢“数学史”校本课程的人数为:2000×0.25=500(人);(4)列表格如下:共有9种等可能的结果,其中两人恰好选中同一门校本课程的结果有3种,所以两人恰好选中同一门校本课程的概率为:=.25.(10分)如图,直线y=ax+2与x轴交于点A(1,0),与y轴交于点B(0,b).将线段AB先向右平移1个单位长度、再向上平移t(t>0)个单位长度,得到对应线段CD,反比例函数y=(x>0)的图象恰好经过C、D两点,连接AC、BD.(1)求a和b的值;(2)求反比例函数的表达式及四边形ABDC的面积;(3)点N在x轴正半轴上,点M是反比例函数y=(x>0)的图象上的一个点,若△CMN是以CM为直角边的等腰直角三角形时,求所有满足条件的点M的坐标.【分析】(1)利用坐标轴上的点的特点即可得出结论;(2)先表示出点C,D坐标,进而代入反比例函数解析式中求解得出k,再判断出BC⊥AD,最后用对角线积的一半即可求出四边形的面积;(3)分两种情况,构造全等的直角三角形即可得出结论.【解答】解:(1)将点A(1,0)代入y=ax+2,得0=a+2.∴a=﹣2.∴直线的解析式为y=﹣2x+2.将x=0代入上式,得y=2.∴b=2.(2)由(1)知,b=2,∴B(0,2),由平移可得:点C(2,t)、D(1,2+t).将点C(2,t)、D(1,2+t)分别代入y=,得∴.∴反比例函数的解析式为y=,点C(2,2)、点D(1,4).如图1,连接BC、AD.∵B(0,2)、C(2,2),∴BC∥x轴,BC=2.∵A(1,0)、D(1,4),∴AD⊥x轴,AD=4.∴BC⊥AD.∴S四边形ABDC=×BC×AD=×2×4=4.(3)①当∠NCM=90°、CM=CN时,如图2,过点C作直线l∥x轴,交y轴于点G.过点M作MF⊥直线l于点F,交x轴于点H.过点N作NE⊥直线l于点E.∵∠MCN=90°,∴∠MCF+∠NCE=90°.∵NE⊥直线l于点E,∴∠ENC+∠NCE=90°.∴∠MCF=∠ENC.又∵∠MFC=∠NEC=90°,CN=CM,∴△NEC≌△CFM(AAS).∴CF=EN=2,FM=CE.∴FG=CG+CF=2+2=4.∴x M=4.将x=4代入y=,得y=1.∴点M(4,1);②当∠NMC=90°、MC=MN时,如图3,过点C作直线l⊥y轴与点F,则CF=x C=2.过点M作MG⊥x轴于点G,MG交直线l与点E,则MG⊥直线l于点E,EG=y C=2.∵∠CMN=90°,∴∠CME+∠NMG=90°.∵ME⊥直线l于点E,∴∠ECM+∠CME=90°.∴∠NMG=∠ECM.又∵∠CEM=∠NGM=90°,CM=MN,∴△CEM≌△MGN(AAS).∴CE=MG,EM=NG.设CE=MG=n,则y M=n,x M=CF+CE=2+n.∴点M(2+n,n).将点M(2+n,n)代入y=,得n=.解得n1=﹣1,n2=﹣﹣1(因为点M在第一象限,所以n大于0,所以舍去).∴x M=2+n=+1.∴点M(+1,﹣1).综合①②可知:点M的坐标为(4,1)或(+1,﹣1).26.(12分)在△ABC中,AB=AC,∠BAC=120°,以CA为边在∠ACB的另一侧作∠ACM=∠ACB,点D为射线BC上任意一点,在射线CM上截取CE=BD,连接AD、DE、AE.(1)如图1,当点D落在线段BC的延长线上时,直接写出∠ADE的度数;(2)如图2,当点D落在线段BC(不含边界)上时,AC与DE交于点F,请问(1)中的结论是否仍成立?如果成立,请给出证明;如果不成立,请说明理由;(3)在(2)的条件下,若AB=6,求CF的最大值.【分析】(1)利用SAS定理证明△ABD≌△ACE,根据相似三角形的性质得到AD=AE,∠CAE=∠BAD,根据等腰三角形的性质、三角形内角和定理计算即可证明;(2)同(1)的证明方法相同;(3)证明△ADF∽△ACD,根据相似三角形的性质得到AF=,求出AD的最小值,得到AF的最小值,求出CF的最大值.【解答】解:(1)∠ADE=30°.理由如下:∵AB=AC,∠BAC=120°,∴∠ABC=∠ACB=30°,∵∠ACM=∠ACB,∴∠ACM=∠ABC,在△ABD和△ACE中,,∴△ABD≌△ACE,∴AD=AE,∠CAE=∠BAD,∴∠DAE=∠BAC=120°,∴∠ADE=30°;(2)(1)中的结论成立,证明:∵∠BAC=120°,AB=AC,∴∠B=∠ACB=30°.∵∠ACM=∠ACB,∴∠B=∠ACM=30°.在△ABD和△ACE中,,∴△ABD≌△ACE.∴AD=AE,∠BAD=∠CAE.∴∠CAE+∠DAC=∠BAD+∠DAC=∠BAC=120°.即∠DAE=120°.∵AD=AE,∴∠ADE=∠AED=30°;(3)∵AB=AC,AB=6,∴AC=6,∵∠ADE=∠ACB=30°且∠DAF=∠CAD,∴△ADF∽△ACD.∴=.∴AD2=AF•AC.∴AD2=6AF.∴AF=.∴当AD最短时,AF最短、CF最长.易得当AD⊥BC时,AF最短、CF最长,此时AD=AB=3.∴AF最短===.∴CF最长=AC﹣AF最短=6﹣=.27.(12分)如图1,抛物线y=ax2+bx+4过A(2,0)、B(4,0)两点,交y轴于点C,过点C作x轴的平行线与抛物线上的另一个交点为D,连接AC、BC.点P是该抛物线上一动点,设点P的横坐标为m (m>4).(1)求该抛物线的表达式和∠ACB的正切值;(2)如图2,若∠ACP=45°,求m的值;(3)如图3,过点A、P的直线与y轴于点N,过点P作PM⊥CD,垂足为M,直线MN与x轴交于点Q,试判断四边形ADMQ的形状,并说明理由.【分析】(1)由点A、B坐标利用待定系数法求解可得抛物线解析式为y=x2﹣3x+4,作BG⊥CA,交CA的延长线于点G,证△GAB∽△OAC得=,据此知BG=2AG.在Rt△ABG中根据BG2+AG2=AB2,可求得AG=.继而可得BG=,CG=AC+AG=,根据正切函数定义可得答案;(2)作BH⊥CD于点H,交CP于点K,连接AK,易得四边形OBHC是正方形,应用“全角夹半角”可得AK=OA+HK,设K(4,h),则BK=h,HK=HB﹣KB=4﹣h,AK=OA+HK=2+(4﹣h)=6﹣h.在Rt△ABK中,由勾股定理求得h=,据此求得点K(4,).待定系数法求出直线CK的解析式为y =﹣x+4.设点P的坐标为(x,y)知x是方程x2﹣3x+4=﹣x+4的一个解.解之求得x的值即可得出答案.(3)先求出点D坐标为(6,4),设P(m,m2﹣3m+4)知M(m,4),H(m,0).及PH=m2﹣3m+4),OH=m,AH=m﹣2,MH=4.①当4<m<6时,由△OAN∽△HAP知=.据此得ON=m﹣4.再证△ONQ∽△HMQ得=.据此求得OQ=m﹣4.从而得出AQ=DM=6﹣m.结合AQ∥DM可得答案.②当m>6时,同理可得.【解答】解:(1)将点A(2,0)和点B(4,0)分别代入y=ax2+bx+4,得,解得:.∴该抛物线的解析式为y=x2﹣3x+4.过点B作BG⊥CA,交CA的延长线于点G(如图1所示),则∠G=90°.∵∠COA=∠G=90°,∠CAO=∠BAG,∴△GAB∽△OAC.∴=═=2.∴BG=2AG.在Rt△ABG中,∵BG2+AG2=AB2,∴(2AG)2+AG2=22.解得:AG=.∴BG=,CG=AC+AG=2+=.在Rt△BCG中,tan∠ACB═=.(2)如图2,过点B作BH⊥CD于点H,交CP于点K,连接AK.易得四边形OBHC是正方形.应用“全角夹半角”可得AK=OA+HK.设K(4,h),则BK=h,HK=HB﹣KB=4﹣h,AK=OA+HK=2+(4﹣h)=6﹣h.在Rt△ABK中,由勾股定理,得AB2+BK2=AK2.∴22+h2=(6﹣h)2.解得h=.∴点K(4,).设直线CK的解析式为y=hx+4.将点K(4,)代入上式,得=4h+4.解得h=﹣.∴直线CK的解析式为y=﹣x+4.设点P的坐标为(x,y),则x是方程x2﹣3x+4=﹣x+4的一个解.将方程整理,得3x2﹣16x=0.解得x1=,x2=0(不合题意,舍去).将x1=代入y=﹣x+4,得y=.∴点P的坐标为(,),故点P的横坐标m的值为.(3)四边形ADMQ是平行四边形.理由如下:∵CD∥x轴,∴y C=y D=4.将y=4代入y=x2﹣3x+4,得4=x2﹣3x+4.解得x1=0,x2=6.∴点D(6,4).根据题意,得P(m,m2﹣3m+4),M(m,4),H(m,0).∴PH=m2﹣3m+4,OH=m,AH=m﹣2,MH=4.①当4<m<6时,DM=6﹣m,如图3,∵△OAN∽△HAP,∴=.∴=.∴ON===m﹣4.∵△ONQ∽△HMQ,∴=.∴=.∴=.∴OQ=m﹣4.∴AQ=OA﹣OQ=2﹣(m﹣4)=6﹣m.∴AQ=DM=6﹣m.又∵AQ∥DM,∴四边形ADMQ是平行四边形.②当m>6时,同理可得:四边形ADMQ是平行四边形.综上,四边形ADMQ是平行四边形.。
2018年山东省济南市中考数学试题及答案(真题卷)
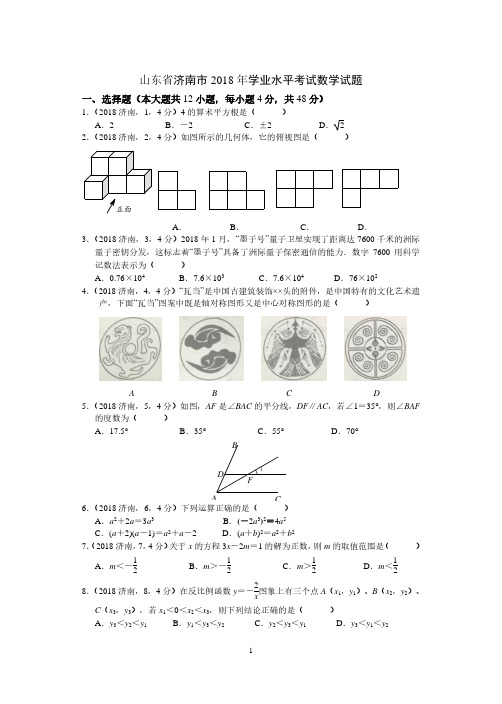
所围成的区域(包括边界)恰有七个整点,则 m 的取值范围是(
)
A.12≤m<1
B.12<m≤1
C.1<m≤2
D.1<m<2
二、填空题(本大题共 6 小题,每小题 4 分,共 24 分)
13.(2018 济南,13,4 分)分解因式:m2-4=____________; 14.(2018 济南,14,4 分)在不透明的盒子中装有 5 个黑色棋子和若于个白色做子,每个
B.2012 年至 2017 年,我国纸质书的人均阅读量的中位数是 4.57
C.从 2014 年到 2017 年,我国纸质书的人均阅读量逐年增长
D.2013 年我国纸质书的人均阅读量比电子书的人均阅读量的 1.8 倍还多
阅读量/本
6
5
4.77
4.39
4.56 4.58 4.65 4.66
4
3.22 3.26 3.21 3.12 3
)
A.m<-12
B.m>-12
C.m>12
D.m<12
【答案】B
8.(2018 济南,8,4 分)在反比例函数 y=-2x图象上有三个点 A(x1,y1)、B(x2,y2)、
C(x3,y3),若 x1<0<x2<x3,则下列结论正确的是(
)
A.y3<y2<y1
B.y1<y3<y2
棋子除颜色外都相同,任意摸出一个棋子,摸到黑包棋子的概率是14,则白色棋子的个
数是=____________; 15. (2018 济南,15,4 分)一个正多边形的每个内角等于 108°,则它的边数是=____________; 16.(2018 济南,16,4 分)若代数式xx- -24的值是 2,则 x=____________;
(完整版)2018年山东省济南市中考数学试卷(可编辑修改word版)

A . 12B . -12C .1 12D . - 1 122018 年ft 东省济南市中考数学试卷一、选择题(共 15 小题,每小题 3 分,满分 45 分) 1.-12 的绝对值是()2.如图,直线 a∥b,直线 c 与 a ,b 相交,∠1=65°,则∠2=()3.2018 年伦敦奥运会火炬传递路线全长约为 12800 公里,数字 12800 用科学记数法表示为( )4.下列事件中必然事件的是()A . 任意买一张电影票, 座位号是偶数A . 1.28× 103B . 12.8× 103C . 1.28× 104D . 0.128× 105A . 115°B . 65°C . 35°D . 25°B.正常情况下,将水加热到 100℃ 时水会沸腾C.三角形的内角和是360°D.打开电视机,正在播动画片5.下列各式计算正确的是()A.3x-2x=1 B.a2+a2=a4C.a5÷a5=a D.a3•a2=a56.下面四个立体图形中,主视图是三角形的是()A.B.C.D.7.化简5(2x-3)+4(3-2x)结果为()A.2x-3 B.2x+9 C.8x-3 D.18x-38.暑假即将来临,小明和小亮每人要从甲、乙、丙三个社区中随机选取一个社区参加综合实践活动,那么小明和小亮选到同一社区参加实践活动的概率为()A . 1 2B . 1 3C . 1 6D . 1 99. 如图,在 8×4 的矩形网格中,每格小正方形的边长都是 1,若△ABC 的三个顶点在图中相应的格点上,则 tan∠ACB的10. 下列命题是真命题的是()A. 对角线相等的四边形是矩形B. 一组邻边相等的四边形是菱形C. 四个角是直角的四边形是正方形D. 对角线相等的梯形是等腰梯形值为( ) A .B .C .1 12 D . 332 2A.2 +1 B.5C.1455D.52A.x=2 B.y=2 C.x=-1 D.y=-111.一次函数y=kx+b 的图象如图所示,则方程kx+b=0 的解为()12.已知⊙O1和⊙O2的半径是一元二次方程x2-5x+6=0 的两根,若圆心距O1O2=5,则⊙O1和⊙O2的位置关系是()13.如图,∠MON=90°,矩形ABCD 的顶点A、B 分别在边OM,ON 上,当B 在边ON 上运动时,A 随之在边OM 上运动,矩形ABCD 的形状保持不变,其中AB=2,BC=1,运动过程中,点D 到点O 的最大距离为()A.外离B.外切C.相交D.内切14.如图,矩形 BCDE 的各边分别平行于 x 轴或 y 轴,物体甲和物体乙分别由点 A(2,0)同时出发,沿矩形 BCDE 的边作环绕运动,物体甲按逆时针方向以 1 个单位/秒匀速运动,物体乙按顺时针方向以 2 个单位/秒匀速运动,则两个物体运动后的第 2018 次相遇地点的坐标是()A.(2,0)B.(-1,1)C.(-2,1)D.(-1,-1)15.如图,二次函数的图象经过(-2,-1),(1,1)两点,则下列关于此二次函数的说法正确的是()A. y 的最大值小于 0 B.当 x=0 时, y 的值大于 1C.当 x=-1 时, y 的值大于 1 D.当 x=-3 时, y 的值小于 0二、填空题(共6 小题,每小题 3 分,满分 18 分)16.分解因式:a2-1=.★★★★★17.计算:2sin30°-16=.18.不等式组2x−4<0x+1≥0的解集为.19.如图,在Rt△ABC中,∠C=90°,AC=4,将△ABC沿CB 向右平移得到△DEF,若平移距离为 2,则四边形 ABED 的面积等于.20.如图,在Rt△ABC中,∠B=90°,AB=6,BC=8,以其三边为直径向三角形外作三个半圆,矩形 EFGH 的各边分别与半圆相切且平行于 AB 或BC,则矩形 EFGH 的周长是.21.如图,济南建邦大桥有一段抛物线型的拱梁,抛物线的表达式为 y=ax2+bx.小强骑自行车从拱梁一端O 沿直线匀速穿过拱梁部分的桥面 OC,当小强骑自行车行驶 10 秒时和 26 秒时拱梁的高度相同,则小强骑自行车通过拱梁部分的桥面OC共需秒.三、解答题(共 7 小题,共 57 分,解答应写出文字说明,证明过程或演算步骤)22.(1)解不等式 3x-2≥4,并将解集在数轴上表示出来.(2)化简:a−1a−2÷a2−2a+12a−4.23.(1)如图 1,在▱ABCD 中,点 E,F 分别在 AB,CD 上,AE=CF.求证:DE=BF.(2)如图 2,在△ABC 中,AB=AC,∠A=40°,BD 是∠ABC 的平分线,求∠BDC 的度数.24.冬冬全家周末一起去济南ft区参加采摘节,他们采摘了油桃和樱桃两种水果,其中油桃比樱桃多摘了 5 斤,若采摘油桃和樱桃分别用了 80 元,且樱桃每斤价格是油桃每斤价格的 2 倍,问油桃和樱桃每斤各是多少元?25.济南以“泉水”而闻名,为保护泉水,造福子孙后代,济南市积极开展“节水保泉”活动,宁宁利用课余时间对某小区 300 户居民的用水情况进行了统计,发现5 月份各户居民的用水量比4 月份有所下降,宁宁将5 月份各户居民的节水量统计整理如下统计图表:节水量(米3) 1 1.5 2.5 3户数50 80 100 70(1)300 户居民 5 月份节水量的众数,中位数分别是多少米3?(2)扇形统计图中 2.5 米3对应扇形的圆心角为度;(3)该小区 300 户居民 5 月份平均每户节约用水多少米3?26.如图 1,在菱形 ABCD 中,AC=2,BD=23,AC,BD 相交于点 O.(1)求边 AB 的长;(2)如图 2,将一个足够大的直角三角板60°角的顶点放在菱形 ABCD 的顶点 A 处,绕点 A 左右旋转,其中三角板60°角的两边分别与边 BC,CD 相交于点 E,F,连接 EF 与AC 相交于点 G.①判断△AEF 是哪一种特殊三角形,并说明理由;②旋转过程中,当点 E 为边 BC 的四等分点时(BE>CE),求 CG 的长.27.如图,已知双曲线 y=kx经过点 D(6,1),点 C 是双曲线第三象限上的动点,过 C 作CA⊥x 轴,过 D 作DB⊥y 轴,垂足分别为 A,B,连接 AB,BC (1)求k 的值;(2)若△BCD的面积为 12,求直线 CD 的解析式;(3)判断 AB 与CD 的位置关系,并说明理由.28.如图 1,抛物线 y=ax2+bx+3 与x 轴相交于点 A(-3,0),B(-1,0),与 y 轴相交于点 C,⊙O1为△ABC的外接圆,交抛物线于另一点 D.(1)求抛物线的解析式;(2)求cos∠CAB的值和⊙O1的半径;(3)如图 2,抛物线的顶点为 P,连接 BP,CP,BD,M 为弦BD 中点,若点 N 在坐标平面内,满足△BMN∽△BPC,请直接写出所有符合条件的点 N 的坐标.。
2018年济南市中考数学试题及答案
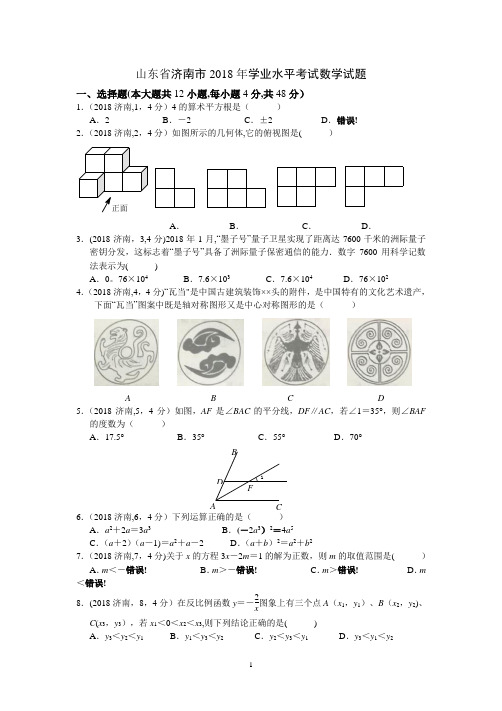
山东省济南市2018年学业水平考试数学试题一、选择题(本大题共12小题,每小题4分,共48分)1.(2018济南,1,4分)4的算术平方根是( )A .2B .-2C .±2D .错误! 2.(2018济南,2,4分)如图所示的几何体,它的俯视图是( )正面A .B .C .D .3.(2018济南,3,4分)2018年1月,“墨子号”量子卫星实现了距离达7600千米的洲际量子密钥分发,这标志着“墨子号”具备了洲际量子保密通信的能力.数字7600用科学记数法表示为( )A .0。
76×104B .7.6×103C .7.6×104D .76×102 4.(2018济南,4,4分)“瓦当"是中国古建筑装饰××头的附件,是中国特有的文化艺术遗产,下面“瓦当”图案中既是轴对称图形又是中心对称图形的是( )A B C D 5.(2018济南,5,4分)如图,AF 是∠BAC 的平分线,DF ∥AC ,若∠1=35°,则∠BAF 的度数为( ) A .17.5° B .35° C .55° D .70°6.(2018济南,6,4分)下列运算正确的是( ) A .a 2+2a =3a 3 B .(-2a 3)2=4a 5 C .(a +2)(a -1)=a 2+a -2 D .(a +b )2=a 2+b 2 7.(2018济南,7,4分)关于x 的方程3x -2m =1的解为正数,则m 的取值范围是( ) A .m <-错误! B .m >-错误! C .m >错误! D .m <错误!8.(2018济南,8,4分)在反比例函数y =-2x 图象上有三个点A (x 1,y 1)、B (x 2,y 2)、C (x 3,y 3),若x 1<0<x 2<x 3,则下列结论正确的是( )A .y 3<y 2<y 1B .y 1<y 3<y 2C .y 2<y 3<y 1D .y 3<y 1<y 21A B C DF9.(2018济南,9,4分)如图,在平面直角坐标系中,△ABC 的顶点都在方格线的格点上,将△ABC 绕点P 顺时针方向旋转90°,得到△A ′B ′C ′,则点P 的坐标为( ) A .(0,4) B .(1,1) C .(1,2) D .(2,1)xy–1–2–3–412341234567BCA A'C 'B'O10.(2018济南,10,4分)下面的统计图大致反应了我国2012年至2017年人均阅读量的情况.根据统计图提供的信息,下列推断不合理...的是( ) A .与2016年相比,2017年我国电子书人均阅读量有所降低 B .2012年至2017年,我国纸质书的人均阅读量的中位数是4.57C .从2014年到2017年,我国纸质书的人均阅读量逐年增长D .2013年我国纸质书的人均阅读量比电子书的人均阅读量的1.8倍还多11.(2018济南,11,4分)如图,一个扇形纸片的圆心角为90°,半径为6.如图2,将这张扇形纸片折叠,使点A 与点O 恰好重合,折痕为CD ,图中阴影为重合部分,则阴影部分的面积为( )A .6π-错误!错误!B .6π-9错误!C .12π-错误!错误!D .错误!AB CDO (A ) ABO阅读量/本年份电子书纸质书62345 4.394.774.564.584.65 4.662.352.483.22 3.26 3.213.1212.(2018济南,11,4分)若平面直角坐标系内的点M满足横、纵坐标都为整数,则把点M 叫做“整点".例如:P(1,0)、Q(2,-2)都是“整点".抛物线y=mx2-4mx+4m-2(m >0)与x轴交于点A、B两点,若该抛物线在A、B之间的部分与线段AB所围成的区域(包括边界)恰有七个整点,则m的取值范围是()A.错误!≤m<1 B.错误!<m≤1 C.1<m≤2D.1<m<2二、填空题(本大题共6小题,每小题4分,共24分)13.(2018济南,13,4分)分解因式:m2-4=____________;14.(2018济南,14,4分)在不透明的盒子中装有5个黑色棋子和若于个白色做子,每个棋子除颜色外都相同,任意摸出一个棋子,摸到黑包棋子的概率是错误!,则白色棋子的个数是=____________;15.(2018济南,15,4分)一个正多边形的每个内角等于108°,则它的边数是=____________; 16.(2018济南,16,4分)若代数式错误!的值是2,则x=____________;17.(2018济南,17,4分)A、B两地相距20km,甲乙两人沿同一条路线从A地到B地.甲先出发,匀速行驶,甲出发1小时后乙再出发,乙以2km/h的速度度匀速行驶1小时后提高速度并继续匀速行驶,结果比甲提前到达.甲、乙两人离开A地的距离s(km)与时间t(h)的关系如图所示,则甲出发____________小时后和乙相遇.18.(2018济南,18,4分)如图,矩形EFGH的四个顶点分别在矩形ABCD的各条边上,AB=EF,FG=2,GC=3.有以下四个结论:①∠BGF=∠CHG;②△BFG≌△DHE;③tan∠BFG=错误!;④矩形EFGH的面积是4错误!.其中一定成立的是____________.(把所有正确结论的序号填在横线上)三、解答题(本大题共9小题,共78分)19.(2018济南,19,6分)计算:2-1+│-5│-sin30°+(π-1)0.20.(2018济南,20,6分)解不等式组:错误!F21.(2018济南,21,6分)如图,在□ABCD中,连接BD,E是DA延长线上的点,F是BC延长线上的点,且AE =CF,连接EF交BD于点O.求证:OB=O D.22.(2018济南,22,8分)本学期学校开展以“感受中华传统买德”为主题的研学部动,组织150名学生多观历史好物馆和民俗晨览馆,每一名学生只能参加其中全顺活动,共支付票款2000元,票价信息如下:(1)请问参观历史博物馆和民俗展览馆的人数各是多少人?(2)若学生都去参观历史博物馆,则能节省票款多少元?23.(2018济南,23,8分)如图AB是⊙O的直径,P A与⊙O相切于点A,BP与⊙O相较于点D,C为⊙O上的一点,分别连接CB、CD,∠BCD=60°.(1)求∠ABD的度数;(2)若AB=6,求PD的长度.C24.(2018济南,24,10分)某校开设了“3D ”打印、数学史、诗歌欣赏、陶艺制作四门校本课程,为了解学生对这四门校本课程的喜爱情况,对学生进行了随机问卷调查(问卷调查表如图所示),将调查结果整理后绘制例图1 、图2两幅均不完整的统计图表. 请您根据图表中提供的信息回答下列问题: (1)统计表中的a =________,b =_______;(2)“D ”对应扇形的圆心角为_______度;(3)根据调查结果,请您估计该校2000名学生中最喜欢“数学史”校本课程的人数;(4)小明和小亮参加校本课程学习,若每人从“A "、“B ”、“C ”三门校本课程中随机选取一门,请用画树状图或列表格的方法,求两人恰好选中同一门校本课程的概率.25.(2018济南,25,10分)如图,直线y =ax +2与x 轴交于点A (1,0),与y 轴交于点B (0,b ).将线段AB 先向右平移1个单位长度、再向上平移t (t >0)个单位长度,得到对应线段CD ,反比例函数y =kx (x >0)的图象恰好经过C 、D 两点,连接AC 、B D . (1)求a 和b 的值;(2)求反比例函数的表达式及四边形ABDC 的面积;(3)点N 在x 轴正半轴上,点M 是反比例函数y =错误!(x >0)的图象上的一个点,若△CMN 是以CM 为直角边的等腰直角三角形时,求所有满足条件的点M 的坐标.第25题图 第25题备用图26.(2018济南,26,12分)在△ABC中,AB=AC,∠BAC=120°,以CA为边在∠ACB的另一侧作∠ACM=∠ACB,点D为射线BC上任意一点,在射线CM上截取CE=BD,连接AD、DE、AE.(1)如图1,当点D落在线段BC的延长线上时,直接写出∠ADE的度数;(2)如图2,当点D落在线段BC(不含边界)上时,AC与DE交于点F,请问(1)中的结论是否仍成立?如果成立,请给出证明;如果不成立,请说明理由;(3)在(2)的条件下,若AB=6,求CF的最大值.第26题图1 第26题图227.(2018济南,27,12分)如图1,抛物线y=ax2+bx+4过A(2,0)、B(4,0)两点,交y轴于点C,过点C作x 轴的平行线与不等式抛物线上的另一个交点为D,连接AC、B C.点P是该抛物线上一动点,设点P的横坐标为m(m>4).(1)求该抛物线的表达式和∠ACB的正切值;(2)如图2,若∠ACP =45°,求m 的值;(3)如图3,过点A 、P 的直线与y 轴于点N ,过点P 作PM ⊥CD ,垂足为M ,直线MN 与x 轴交于点Q ,试判断四边形ADMQ 的形状,并说明理由.第27题图1 第27题图2 第27题图3山东省济南市2018年学业水平考试数学试题一、选择题(本大题共12小题,每小题4分,共48分)1.(2018济南,1,4分)4的算术平方根是( )A .2B .-2C .±2D .错误! 【答案】A2.(2018济南,2,4分)如图所示的几何体,它的俯视图是( )正面A .B .C .D . 【答案】D 3.(2018济南,3,4分)2018年1月,“墨子号”量子卫星实现了距离达7600千米的洲际量子密钥分发,这标志着“墨子号”具备了洲际量子保密通信的能力.数字7600用科学记数法表示为( )A .0。
2018年山东省济南市中考数学试题及答案

山东省济南市2018年学业水平考试数学试题一、选择题(本大题共12小题,每小题4分,共48分)1.(2018济南,1,4分)4的算术平方根是( )A .2B .-2C .±2D . 2 2.(2018济南,2,4分)如图所示的几何体,它的俯视图是()正面A .B .C .D . 3.(2018济南,3,4分)2018年1月,“墨子号”量子卫星实现了距离达7600千米的洲际量子密钥分发,这标志着“墨子号”具备了洲际量子保密通信的能力.数字7600用科学记数法表示为( )A .0.76×104B .7.6×103C .7.6×104D .76×102 4.(2018济南,4,4分)“瓦当”是中国古建筑装饰××头的附件,是中国特有的文化艺术遗产,下面“瓦当”图案中既是轴对称图形又是中心对称图形的是( )A B C D 5.(2018济南,5,4分)如图,AF 是∠BAC 的平分线,DF ∥AC ,若∠1=35°,则∠BAF 的度数为( ) A .17.5° B .35° C .55° D .70°6.(2018济南,6,4分)下列运算正确的是( ) A .a 2+2a =3a 3 B .(-2a 3)2=4a 5 C .(a +2)(a -1)=a 2+a -2 D .(a +b )2=a 2+b 2 7.(2018济南,7,4分)关于x 的方程3x -2m =1的解为正数,则m 的取值范围是( ) A .m <-12 B .m >-12 C .m >12 D .m <128.(2018济南,8,4分)在反比例函数y =-2x 图象上有三个点A (x 1,y 1)、B (x 2,y 2)、C (x 3,y 3),若x 1<0<x 2<x 3,则下列结论正确的是( )A .y 3<y 2<y 1B .y 1<y 3<y 2C .y 2<y 3<y 1D .y 3<y 1<y 21A B C DF9.(2018济南,9,4分)如图,在平面直角坐标系中,△ABC 的顶点都在方格线的格点上,将△ABC 绕点P 顺时针方向旋转90°,得到△A ′B ′C ′,则点P 的坐标为( ) A .(0,4) B .(1,1) C .(1,2) D .(2,1)xy–1–2–3–412341234567BCA A'C 'B'O10.(2018济南,10,4分)下面的统计图大致反应了我国2012年至2017年人均阅读量的情况.根据统计图提供的信息,下列推断不合理...的是( ) A .与2016年相比,2017年我国电子书人均阅读量有所降低 B .2012年至2017年,我国纸质书的人均阅读量的中位数是4.57C .从2014年到2017年,我国纸质书的人均阅读量逐年增长D .2013年我国纸质书的人均阅读量比电子书的人均阅读量的1.8倍还多11.(2018济南,11,4分)如图,一个扇形纸片的圆心角为90°,半径为6.如图2,将这张扇形纸片折叠,使点A 与点O 恰好重合,折痕为CD ,图中阴影为重合部分,则阴影部分的面积为( ) A .6π-92 3 B .6π-9 3 C .12π-92 3 D .9π4AB CDO (A ) ABO阅读量/本年份电子书纸质书 4.394.774.564.584.65 4.662.352.483.22 3.26 3.213.1212.(2018济南,11,4分)若平面直角坐标系内的点M 满足横、纵坐标都为整数,则把点M 叫做“整点”.例如:P (1,0)、Q (2,-2)都是“整点”.抛物线y =mx 2-4mx +4m -2(m >0)与x 轴交于点A 、B 两点,若该抛物线在A 、B 之间的部分与线段AB 所围成的区域(包括边界)恰有七个整点,则m 的取值范围是( ) A .12≤m <1 B .12<m ≤1 C .1<m ≤2 D .1<m <2二、填空题(本大题共6小题,每小题4分,共24分)13.(2018济南,13,4分)分解因式:m 2-4=____________;14.(2018济南,14,4分)在不透明的盒子中装有5个黑色棋子和若于个白色做子,每个棋子除颜色外都相同,任意摸出一个棋子,摸到黑包棋子的概率是14,则白色棋子的个数是=____________; 15.(2018济南,15,4分)一个正多边形的每个内角等于108°,则它的边数是=____________; 16.(2018济南,16,4分)若代数式x -2x -4的值是2,则x =____________;17.(2018济南,17,4分)A 、B 两地相距20km ,甲乙两人沿同一条路线从A 地到B 地.甲先出发,匀速行驶,甲出发1小时后乙再出发,乙以2km/h 的速度度匀速行驶1小时后提高速度并继续匀速行驶,结果比甲提前到达.甲、乙两人离开A 地的距离s (km )与时间t (h )的关系如图所示,则甲出发____________小时后和乙相遇.18.(2018济南,18,4分)如图,矩形EFGH 的四个顶点分别在矩形ABCD 的各条边上,AB =EF ,FG =2,GC =3.有以下四个结论:①∠BGF =∠CHG ;②△BFG ≌△DHE ;③tan ∠BFG =12;④矩形EFGH 的面积是43.其中一定成立的是____________.(把所有正确结论的序号填在横线上)三、解答题(本大题共9小题,共78分)19.(2018济南,19,6分)计算:2-1+│-5│-sin30°+(π-1)0.BF解不等式组:⎩⎪⎨⎪⎧3x +1<2x +3 ①2x >3x -12 ②21.(2018济南,21,6分)如图,在□ABCD 中,连接BD ,E 是DA 延长线上的点,F 是BC 延长线上的点,且 AE =CF ,连接EF 交BD 于点O .求证:OB =O D .22.(2018济南,22,8分)本学期学校开展以“感受中华传统买德”为主题的研学部动,组织150名学生多观历史好物馆和民俗晨览馆,每一名学生只能参加其中全顺活动,共支付票款2000元,票价信息如下:(1)请问参观历史博物馆和民俗展览馆的人数各是多少人? (2)若学生都去参观历史博物馆,则能节省票款多少元?如图AB是⊙O的直径,P A与⊙O相切于点A,BP与⊙O相较于点D,C为⊙O上的一点,分别连接CB、CD,∠BCD=60°.(1)求∠ABD的度数;(2)若AB=6,求PD的长度.C24.(2018济南,24,10分)某校开设了“3D”打印、数学史、诗歌欣赏、陶艺制作四门校本课程,为了解学生对这四门校本课程的喜爱情况,对学生进行了随机问卷调查(问卷调查表如图所示),将调查结果整理后绘制例图1 、图2两幅均不完整的统计图表.请您根据图表中提供的信息回答下列问题:(1)统计表中的a=________,b=_______;(2)“D ”对应扇形的圆心角为_______度;(3)根据调查结果,请您估计该校2000名学生中最喜欢“数学史”校本课程的人数; (4)小明和小亮参加校本课程学习,若每人从“A ”、“B ”、“C ”三门校本课程中随机选取一门,请用画树状图或列表格的方法,求两人恰好选中同一门校本课程的概率. 25.(2018济南,25,10分)如图,直线y =ax +2与x 轴交于点A (1,0),与y 轴交于点B (0,b ).将线段AB 先向右平移1个单位长度、再向上平移t (t >0)个单位长度,得到对应线段CD ,反比例函数y =kx (x >0)的图象恰好经过C 、D 两点,连接AC 、B D . (1)求a 和b 的值;(2)求反比例函数的表达式及四边形ABDC 的面积;(3)点N 在x 轴正半轴上,点M 是反比例函数y =kx (x >0)的图象上的一个点,若△CMN是以CM 为直角边的等腰直角三角形时,求所有满足条件的点M 的坐标.第25题图 第25题备用图26.(2018济南,26,12分)在△ABC中,AB=AC,∠BAC=120°,以CA为边在∠ACB的另一侧作∠ACM=∠ACB,点D为射线BC上任意一点,在射线CM上截取CE=BD,连接AD、DE、AE.(1)如图1,当点D落在线段BC的延长线上时,直接写出∠ADE的度数;(2)如图2,当点D落在线段BC(不含边界)上时,AC与DE交于点F,请问(1)中的结论是否仍成立?如果成立,请给出证明;如果不成立,请说明理由;(3)在(2)的条件下,若AB=6,求CF的最大值.第26题图1 第26题图227.(2018济南,27,12分)如图1,抛物线y =ax 2+bx +4过A (2,0)、B (4,0)两点,交y 轴于点C ,过点C 作x 轴的平行线与不等式抛物线上的另一个交点为D ,连接AC 、B C .点P 是该抛物线上一动点,设点P 的横坐标为m (m >4).(1)求该抛物线的表达式和∠ACB 的正切值; (2)如图2,若∠ACP =45°,求m 的值;(3)如图3,过点A 、P 的直线与y 轴于点N ,过点P 作PM ⊥CD ,垂足为M ,直线MN 与x 轴交于点Q ,试判断四边形ADMQ 的形状,并说明理由.第27题图1 第27题图2 第27题图3山东省济南市2018年学业水平考试数学试题一、选择题(本大题共12小题,每小题4分,共48分)1.(2018济南,1,4分)4的算术平方根是( )A .2B .-2C .±2D . 2 【答案】A 2.(2018济南,2,4分)如图所示的几何体,它的俯视图是()正面A .B .C .D . 【答案】D 3.(2018济南,3,4分)2018年1月,“墨子号”量子卫星实现了距离达7600千米的洲际量子密钥分发,这标志着“墨子号”具备了洲际量子保密通信的能力.数字7600用科学记数法表示为( )A .0.76×104B .7.6×103C .7.6×104D .76×102 【答案】B 4.(2018济南,4,4分)“瓦当”是中国古建筑装饰××头的附件,是中国特有的文化艺术遗产,下面“瓦当”图案中既是轴对称图形又是中心对称图形的是( )A B C D 【答案】D 5.(2018济南,5,4分)如图,AF 是∠BAC 的平分线,DF ∥AC ,若∠1=35°,则∠BAF 的度数为( ) A .17.5° B .35° C .55° D .70°【答案】B 6.(2018济南,6,4分)下列运算正确的是( ) A .a 2+2a =3a 3 B .(-2a 3)2=4a 51ABCDFC .(a +2)(a -1)=a 2+a -2D .(a +b )2=a 2+b 2 【答案】C 7.(2018济南,7,4分)关于x 的方程3x -2m =1的解为正数,则m 的取值范围是( ) A .m <-12 B .m >-12 C .m >12 D .m <12【答案】B8.(2018济南,8,4分)在反比例函数y =-2x 图象上有三个点A (x 1,y 1)、B (x 2,y 2)、C (x 3,y 3),若x 1<0<x 2<x 3,则下列结论正确的是( )A .y 3<y 2<y 1B .y 1<y 3<y 2C .y 2<y 3<y 1D .y 3<y 1<y 2 【答案】C 9.(2018济南,9,4分)如图,在平面直角坐标系中,△ABC 的顶点都在方格线的格点上,将△ABC 绕点P 顺时针方向旋转90°,得到△A ′B ′C ′,则点P 的坐标为( ) A .(0,4) B .(1,1) C .(1,2) D .(2,1)【答案】C 10.(2018济南,10,4分)下面的统计图大致反应了我国2012年至2017年人均阅读量的情况.根据统计图提供的信息,下列推断不合理...的是( ) A .与2016年相比,2017年我国电子书人均阅读量有所降低 B .2012年至2017年,我国纸质书的人均阅读量的中位数是4.57C .从2014年到2017年,我国纸质书的人均阅读量逐年增长D .2013年我国纸质书的人均阅读量比电子书的人均阅读量的1.8倍还多【答案】B 11.(2018济南,11,4分)如图,一个扇形纸片的圆心角为90°,半径为6.如图2,将这张扇形纸片折叠,使点A 与点O 恰好重合,折痕为CD ,图中阴影为重合部分,则阴影部分的面积为( ) A .6π-92 3 B .6π-9 3 C .12π-92 3 D .9π4【答案】A12.(2018济南,11,4分)若平面直角坐标系内的点M 满足横、纵坐标都为整数,则把点M 叫做“整点”.例如:P (1,0)、Q (2,-2)都是“整点”.抛物线y =mx 2-4mx +4m -2(m >0)与x 轴交于点A 、B 两点,若该抛物线在A 、B 之间的部分与线段AB 所围成的区域(包括边界)恰有七个整点,则m 的取值范围是( ) A .12≤m <1 B .12<m ≤1 C .1<m ≤2 D .1<m <2【答案】B【解析】解:∵y =mx 2-4mx +4m -2=m (x -2)2-2且m >0,∴该抛物线开口向上,顶点坐标为(2,-2),对称轴是直线x =2.由此可知点(2,0)、点(2,-1)、顶点(2,-2)符合题意. 方法一:①当该抛物线经过点(1,-1)和(3,-1)时(如答案图1),这两个点符合题意. 将(1,-1)代入y =mx 2-4mx +4m -2得到-1=m -4m +4m -2.解得m =1. 此时抛物线解析式为y =x 2-4x +2.由y =0得x 2-4x +2=0.解得x 1=2-2≈0.6,x 2=2+2≈3.4.阅读量/本年份电子书纸质书O 62345 4.394.774.564.584.65 4.662.352.483.22 3.26 3.213.12AB CDO (A ) ABO∴x 轴上的点(1,0)、(2,0)、(3,0)符合题意.则当m =1时,恰好有 (1,0)、(2,0)、(3,0)、(1,-1)、(3,-1)、(2,-1)、(2,-2)这7个整点符合题意. ∴m ≤1.【注:m 的值越大,抛物线的开口越小,m 的值越小,抛物线的开口越大,】答案图1(m =1时) 答案图2( m =12时)②当该抛物线经过点(0,0)和点(4,0)时(如答案图2),这两个点符合题意. 此时x 轴上的点 (1,0)、(2,0)、(3,0)也符合题意.将(0,0)代入y =mx 2-4mx +4m -2得到0=0-4m +0-2.解得m =12.此时抛物线解析式为y =12x 2-2x .当x =1时,得y =12×1-2×1=-32<-1.∴点(1,-1)符合题意.当x =3时,得y =12×9-2×3=-32<-1.∴点(3,-1) 符合题意.综上可知:当m =12时,点(0,0)、(1,0)、(2,0)、(3,0)、(4,0)、(1,-1)、(3,-1)、(2,-2)、(2,-1)都符合题意,共有9个整点符合题意, ∴m =12不符合题.∴m >12.综合①②可得:当12<m ≤1时,该函数的图象与x 轴所围城的区域(含边界)内有七个整点,故答案选B .方法二:根据题目提供的选项,分别选取m =12,m =1,m =2,依次加以验证.①当m =12时(如答案图3),得y =12x 2-2x .由y =0得12x 2-2x =0.解得x 1=0,x 2=4.∴x 轴上的点(0,0)、(1,0)、(2,0)、(3,0)、(4,0)符合题意. 当x =1时,得y =12×1-2×1=-32<-1.∴点(1,-1)符合题意.当x =3时,得y =12×9-2×3=-32<-1.∴点(3,-1) 符合题意.综上可知:当m =12时,点(0,0)、(1,0)、(2,0)、(3,0)、(4,0)、(1,-1)、(3,-1)、(2,-2)、(2,-1)都符合题意,共有9个整点符合题意, ∴m =12不符合题.∴选项A 不正确.答案图3( m =12时) 答案图4(m =1时) 答案图5(m =2时)②当m =1时(如答案图4),得y =x 2-4x +2.由y =0得x 2-4x +2=0.解得x 1=2-2≈0.6,x 2=2+2≈3.4. ∴x 轴上的点(1,0)、(2,0)、(3,0)符合题意. 当x =1时,得y =1-4×1+2=-1.∴点(1,-1)符合题意. 当x =3时,得y =9-4×3+2=-1.∴点(3,-1) 符合题意.综上可知:当m =1时,点(1,0)、(2,0)、(3,0)、(1,-1)、(3,-1)、(2,-2) 、(2,-1)都符合题意,共有7个整点符合题意, ∴m =1符合题. ∴选项B 正确.③当m =2时(如答案图5),得y =2x 2-8x +6. 由y =0得2x 2-8x +6=0.解得x 1=1,x 2=3. ∴x 轴上的点(1,0)、(2,0)、(3,0)符合题意.综上可知:当m =2时,点(1,0)、(2,0)、(3,0)、(2,-2) 、(2,-1)都符合题意,共有5个整点符合题意, ∴m =2不符合题.二、填空题(本大题共6小题,每小题4分,共24分)13.(2018济南,13,4分)分解因式:m 2-4=____________; 【答案】(m +2)(m -2) 14.(2018济南,14,4分)在不透明的盒子中装有5个黑色棋子和若于个白色做子,每个棋子除颜色外都相同,任意摸出一个棋子,摸到黑包棋子的概率是14,则白色棋子的个数是=____________; 【答案】15 15.(2018济南,15,4分)一个正多边形的每个内角等于108°,则它的边数是=____________; 【答案】516.(2018济南,16,4分)若代数式x -2x -4的值是2,则x =____________;【答案】6 17.(2018济南,17,4分)A 、B 两地相距20km ,甲乙两人沿同一条路线从A 地到B 地.甲先出发,匀速行驶,甲出发1小时后乙再出发,乙以2km/h 的速度度匀速行驶1小时后提高速度并继续匀速行驶,结果比甲提前到达.甲、乙两人离开A 地的距离s (km )与时间t (h )的关系如图所示,则甲出发____________小时后和乙相遇.【答案】165.【解析】y 甲=4t (0≤t ≤4);y 乙=⎩⎨⎧2(t -1)(1≤t ≤2)9(t -2)t (2<t ≤4);由方程组⎩⎨⎧y =4t y =9(t -2)解得⎩⎨⎧t =165y =645. ∴答案为165.18.(2018济南,18,4分)如图,矩形EFGH 的四个顶点分别在矩形ABCD 的各条边上,AB =EF ,FG =2,GC =3.有以下四个结论:①∠BGF =∠CHG ;②△BFG ≌△DHE ;③tan ∠BFG =12;④矩形EFGH 的面积是43.其中一定成立的是____________.(把所有正确结论的序号填在横线上)BF【答案】①②④.【解析】设EH =AB =a ,则CD =GH =a . ∵∠FGH =90°,∴∠BGF +∠CGH =90°. 又∵∠CGH +∠CHG =90°,∴∠BGF =∠CHG …………………………………故①正确.同理可得∠DEH =∠CHG . ∴∠BGF =∠DEH . 又∵∠B =∠D =90°,FG =EH ,∴△BFG ≌△DHE …………………………………故②正确. 同理可得△AFE ≌△CHG .∴AF =CH .易得△BFG ∽△CGH .∴BF CG =FG GH .∴BF 3=2a .∴BF =6a .∴AF =AB -BF =a -6a .∴CH =AF =a -6a .在Rt △CGH 中,∵CG 2+CH 2=GH 2,∴32+( a -6a )2=a 2.解得a =2 3.∴GH =2 3.∴BF = a -6a = 3.在Rt △BFG 中,∵cos ∠BFG =BF FG =32,∴∠BFG =30°.∴tan ∠BFG =tan30°=33.…………………………………故③正确. 矩形EFGH 的面积=FG ×GH =2×23=43…………………………………故④正确.三、解答题(本大题共9小题,共78分)19.(2018济南,19,6分)计算:2-1+│-5│-sin30°+(π-1)0.解:2-1+│-5│-sin30°+(π-1)0.=12+5-12+1=620.(2018济南,20,6分)解不等式组:⎩⎪⎨⎪⎧3x +1<2x +3 ①2x >3x -12 ② 解:由① ,得3x -2x <3-1. ∴x <2. 由② ,得 4x >3x -1. ∴x >-1.∴不等式组的解集为-1<x <2.21.(2018济南,21,6分)如图,在□ABCD 中,连接BD ,E 是DA 延长线上的点,F 是BC 延长线上的点,且 AE =CF ,连接EF 交BD 于点O .求证:OB =O D .证明:∵□ABCD中,∴AD=BC,AD∥B C.∴∠ADB=∠CB D.又∵AE=CF,∴AE+AD=CF+B C.∴ED=F B.又∵∠EOD=∠FOB,∴△EOD≌△FO B.∴OB=O D.22.(2018济南,22,8分)本学期学校开展以“感受中华传统买德”为主题的研学部动,组织150名学生多观历史好物馆和民俗晨览馆,每一名学生只能参加其中全顺活动,共支付票款2000元,票价信息如下:(1)请问参观历史博物馆和民俗展览馆的人数各是多少人?(2)若学生都去参观历史博物馆,则能节省票款多少元?解:(1)设参观历史博物馆的有x人,则参观民俗展览馆的有(150-x)人,依题意,得10x+20(150-x)2000.10x+3000-20x=2000.-10x=-1000.∴x=100.∴150-x=50.答:参观历史博物馆的有100人,则参观民俗展览馆的有50人.(2)2000-150×10=500(元).答:若学生都去参观历史博物馆,则能节省票款500元.23.(2018济南,23,8分)如图AB是⊙O的直径,P A与⊙O相切于点A,BP与⊙O相较于点D,C为⊙O上的一点,分别连接CB、CD,∠BCD=60°.(1)求∠ABD的度数;(2)若AB=6,求PD的长度.C【解析】解:(1)方法一:连接AD (如答案图1所示). ∵BA 是⊙O 直径,∴∠BDA =90°.∵⌒BD =⌒BD ,∴∠BAD =∠C =60°.∴∠ABD =90°-∠BAD =90°-60°=30°.CC第23题答案图1 第23题答案图2方法二:连接DA 、OD (如答案图2所示),则∠BOD =2∠C =2×60°=120°. ∵OB =OD ,∴∠OBD =∠ODB =12(180°-120°)=30°.即∠ABD =30°.(2)∵AP 是⊙O 的切线,∴∠BAP =90°. 在Rt △BAD 中,∵∠ABD =30°, ∴DA =12BA =12×6=3.∴BD =3DA =33.在Rt △BAP 中,∵cos ∠ABD =AB PB ,∴cos30°=6PB =32.∴BP =43.∴PD =BP -BD =43-33=3.24.(2018济南,24,10分)某校开设了“3D ”打印、数学史、诗歌欣赏、陶艺制作四门校本课程,为了解学生对这四门校本课程的喜爱情况,对学生进行了随机问卷调查(问卷调查表如图所示),将调查结果整理后绘制例图1 、图2两幅均不完整的统计图表.请您根据图表中提供的信息回答下列问题:(1)统计表中的a =________,b =_______; (2)“D ”对应扇形的圆心角为_______度;(3)根据调查结果,请您估计该校2000名学生中最喜欢“数学史”校本课程的人数; (4)小明和小亮参加校本课程学习,若每人从“A ”、“B ”、“C ”三门校本课程中随机选取一门,请用画树状图或列表格的方法,求两人恰好选中同一门校本课程的概率. 解:(1)a =36÷0.45=80. b =16÷80=0.20.(2)“D ”对应扇形的圆心角的度数为:8÷80×360°=36°.(3)估计该校2000名学生中最喜欢“数学史”校本课程的人数为: 2000×0.25=500(人). (4)列表格如下:3种,所以两人恰好选中同一门校本课程的概率为:39=13.25.(2018济南,25,10分)如图,直线y =ax +2与x 轴交于点A (1,0),与y 轴交于点B (0,b ).将线段AB 先向右平移1个单位长度、再向上平移t (t >0)个单位长度,得到对应线段CD ,反比例函数y=kx (x >0)的图象恰好经过C 、D 两点,连接AC 、B D . (1)求a 和b 的值;(2)求反比例函数的表达式及四边形ABDC 的面积;(3)点N 在x 轴正半轴上,点M 是反比例函数y =kx (x >0)的图象上的一个点,若△CMN是以CM 为直角边的等腰直角三角形时,求所有满足条件的点M 的坐标.第25题图 第25题备用图【解析】解:(1)将点A (1,0)代入y =ax +2,得0=a +2.∴a =-2. ∴直线的解析式为y =-2x +2.将x =0代入上式,得y =2.∴b =2.∴点B (0,2). (2)由平移可得:点C (2,t )、D (1,2+t ).将点C (2,t )、D (1,2+t )分别代入y =kx,得 ⎩⎨⎧t =k22+t =k 1.解得⎩⎨⎧k =4t =2. ∴反比例函数的解析式为y =4x,点C (2,2)、点D (1,4).分别连接BC 、AD (如答案图1).∵B (0,2)、C (2,2),∴BC ∥x 轴,BC =2. ∵A (1,0)、D (1,4),∴AD ⊥x 轴,AD =4. ∴BC ⊥A D .∴S 四边形ABDC =12×BC ×AD =12×2×4=4.第25题答案图1(3)①当∠NCM =90°、CM =CN 时(如答案图2所示),过点C 作直线l ∥x 轴,交y 轴于点G .过点M 作MF ⊥直线l 于点F ,交x 轴于点H .过点N 作NE ⊥直线l 于点E . 设点N (m ,0)(其中m >0),则ON =m ,CE =2-m . ∵∠MCN =90°,∴∠MCF +∠NCE =90°. ∵NE ⊥直线l 于点E ,∴∠ENC +∠NCE =90°.∴∠MCF =∠EN C .又∵∠MFC =∠NEC =90°,CN =CM ,∴△NEC ≌△CFM . ∴CF =EN =2,FM =CE =2-m .∴FG =CG +CF =2+2=4.∴x M =4. 将x =4代入y =4x,得y =1.∴点M (4,1).l第25题答案图2 第25题答案图3 ②当∠NMC =90°、MC =MN 时(如答案图3所示),过点C 作直线l ⊥y 轴与点F ,则CF =x C =2.过点M 作MG ⊥x 轴于点G ,MG 交直线l 与点E ,则MG ⊥直线l 于点E ,EG =y C =2. ∵∠CMN =90°,∴∠CME +∠NMG =90°.∵ME ⊥直线l 于点E ,∴∠ECM +∠CME =90°.∴∠NMG =∠ECM .又∵∠CEM =∠NGM =90°,CM =MN ,∴△CEM ≌△MGN .∴CE =MG ,EM =NG .设CE =MG =a ,则y M =a ,x M =CF +CE =2+a .∴点M (2+a ,a ).将点M (2+a ,a ) 代入y =4x ,得a =42+a.解得a 1=5-1,a 2=-5-1.∴x M =2+a =5+1.∴点M (5+1,5-1).综合①②可知:点M 的坐标为(4,1)或(5+1,5-1). 26.(2018济南,26,12分)在△ABC 中,AB =AC ,∠BAC =120°,以CA 为边在∠ACB 的另一侧作∠ACM =∠ACB ,点D 为射线BC 上任意一点,在射线CM 上截取CE =BD ,连接AD 、DE 、AE . (1)如图1,当点D 落在线段BC 的延长线上时,直接写出∠ADE 的度数;(2)如图2,当点D 落在线段BC (不含边界)上时,AC 与DE 交于点F ,请问(1)中的结论是否仍成立?如果成立,请给出证明;如果不成立,请说明理由; (3)在(2)的条件下,若AB =6,求CF 的最大值.M第26题图1 第26题图2【解析】解:(1) ∠ADE =30°.(2) (1)中的结论是否还成立证明:连接AE (如答案图1所示).∵∠BAC =120°,AB =AC ,∴∠B =∠ACB =30°. 又∵∠ACM =∠ACB ,∴∠B =∠ACM =30°. 又∵CE =BD ,∴△ABD ≌△ACE .∴AD =AE ,∠1=∠2. ∴∠2+∠3=∠1+∠3=∠BAC =120°.即∠DAE =120°.又∵AD =AE ,∴∠ADE =∠AED =30°.答案图1 答案图2(3) ∵AB =AC ,AB =6,∴AC =6. ∵∠ADE =∠ACB =30°且∠DAF =∠CAD ,∴△ADF ∽△AC D.∴AD AC =AF AD .∴AD 2=AF ·A C .∴AD 2=6AF .∴AF =AD 26.∴当AD 最短时,AF 最短、CF 最长.易得当AD ⊥BC 时,AF 最短、CF 最长(如答案图2所示),此时AD =12AB =3.∴AF 最短=AD 26=326=32.∴CF 最长=AC - AF 最短=6-32=92.27.(2018济南,27,12分)如图1,抛物线y =ax 2+bx +4过A (2,0)、B (4,0)两点,交y 轴于点C ,过点C 作x 轴的平行线与不等式抛物线上的另一个交点为D ,连接AC 、B C .点P 是该抛物线上一动点,设点P 的横坐标为m (m >4).(1)求该抛物线的表达式和∠ACB 的正切值; (2)如图2,若∠ACP =45°,求m 的值;(3)如图3,过点A 、P 的直线与y 轴于点N ,过点P 作PM ⊥CD ,垂足为M ,直线MN 与x 轴交于点Q ,试判断四边形ADMQ 的形状,并说明理由.第27题图1 第27题图2 第27题图3【解析】 解:(1)将点A (2,0)和点B (4,0)分别代入y =ax 2+bx +4,得⎩⎨⎧0=4a +2x +40=16a +4b +4.解得⎩⎪⎨⎪⎧a =12b =-3.∴该抛物线的解析式为y =12x 2-3x +4.将x =0代入上式,得y =4.∴点C (0,4),OC =4.在Rt △AOC 中,AC =OA 2+OC 2=22+42=2 5.设直线AC 的解析式为y =kx +4,将点A (2,0)代入上式,得0=2k +4.解得k =-2. ∴直线AC 的解析式为y =-2x +4.同理可得直线BC 的解析式为y =-x +4. 求tan ∠ACB 方法一:过点B 作BG ⊥CA ,交CA 的延长线于点G (如答案图1所示),则∠G =90°.∵∠COA =∠G =90°,∠CAO =∠BAG ,∴△GAB ∽△OA C.∴BG AG =OC OA =42=2.∴BG =2AG . 在Rt △ABG 中,∵BG 2+AG 2=AB 2,∴(2AG )2+AG 2=22.AG =25 5.∴BG =455,CG =AC +AG =25+255=125 5.在Rt △BCG 中,tan ∠ACB =BG CQ =4551255=13.第27题答案图1 第27题答案图2求tan ∠ACB 方法二:过点A 作AE ⊥AC ,交BC 于点E (如答案图2所示),则k AE ·k AC =-1.∴-2k AE =-1.∴k AE =12.∴可设直线AE 的解析式为y =12x +m .将点A (2,0)代入上式,得0=12×2+m .解得m =-1.∴直线AE 的解析式为y =12x -1.由方程组⎩⎪⎨⎪⎧y =12x -1y =-x +4 解得⎩⎨⎧x =103y =23.∴点E (103,23). ∴AE =⎝⎛⎭⎫2-1032+⎝⎛⎭⎫0-232=235.在Rt △AEC 中,tan ∠ACB =AE AC =23525=13.求tan ∠ACB 方法三:过点A 作AF ⊥BC ,交BC 点E (如答案图3所示),则k AF ·k BC =-1. ∴-k AF =-1.∴k AF =1.∴可设直线AF 的解析式为y =x +n .将点A (2,0)代入上式,得0=2+n .解得n =-2.∴直线AF 的解析式为y =x -2.由方程组⎩⎨⎧y =x -2y =-x +4 解得⎩⎨⎧x =3y =1.∴点F (3,1).∴AF =(3-2)2+(1-0)2=2,CF =(3-0)2-(1-4)2=3 2.在Rt △AEC 中,tan ∠ACB =AF CF =232=13.第27题答案图3(2)方法一:利用“一线三等角”模型将线段AC 绕点A 沿顺时针方向旋转90°,得到线段AC ′,则 AC ′=AC ,∠C ′AC =90°,∠CC ′A =∠ACC ′=45°. ∴∠CAO +∠C ′AB =90°. 又∵∠OCA +∠CAO =90°, ∴∠OCA =∠C ′A B .过点C ′作C ′E ⊥x 轴于点E .则∠C ′EA =∠COA =90°. ∵∠C ′EA =∠COA =90°,∠OCA =∠C ′AB ,AC ′=AC ,∴△C ′EA ≌△AO C .∴C ′E =OA =2,AE =OC =4. ∴OE =OA +AE =2+4=6. ∴点C ′(6,2).设直线C ′C 的解析式为y =hx +4.将点C ′(6,2)代入上式,得2=6h +4.解得h =-13.∴直线C ′C 的解析式为y =-13x +4.∵∠ACP =45°,∠ACC ′=45°,∴点P 在直线C ′C 上.设点P 的坐标为(x ,y ),则x 是方程12x 2-3x +4=-13x +4的一个解.将方程整理,得3x 2-14x =0.解得x 1=163,x 2=0(不合题意,舍去).将x 1=163代入y =-13x +4,得y =209.∴点P 的坐标为(163,209).第27题答案图4 第27题答案图5(2)方法二:利用正方形中的“全角夹半角”模型.过点B 作BH ⊥CD 于点H ,交CP 于点K ,连接AK .易得四边形OBHC 是正方形. 应用“全角夹半角”可得AK =OA +HK .设K (4,h ),则BK =h ,HK =HB -KB =4-h ,AK =OA +HK =2+(4-h )=6-h .在Rt △ABK 中,由勾股定理,得AB 2+BK 2=AK 2.∴22+ h 2=(6-h )2.解得h =83.∴点K (4,83).设直线CK 的解析式为y =hx +4.将点K (4,83)代入上式,得83=4h +4.解得h =-13.∴直线CK 的解析式为y =-13x +4.设点P 的坐标为(x ,y ),则x 是方程12x 2-3x +4=-13x +4的一个解.将方程整理,得3x 2-14x =0.解得x 1=163,x 2=0(不合题意,舍去).将x 1=163代入y =-13x +4,得y =209.∴点P 的坐标为(163,209).(3)四边形ADMQ 是平行四边形.理由如下: ∵CD ∥x 轴,∴y C =y D =4.将y =4代入y =12x 2-3x +4,得 4=12x 2-3x +4.解得x 1=0,x 2=6.∴点D (6,4).根据题意,得P (m ,12m 2-3m +4),M (m ,4),H (m ,0).∴PH =12m 2-3m +4),OH =m ,AH =m -2,MH =4.①当4<m <6时(如答案图5所示),DM =6-m∵△OAN ∽△HAP ,∴ON PH =OA AH .∴ON 12m 2-3m +4=2m -2.∴ON =m 2-6m +8m -2=(m -4)(m -2)m -2=m -4.∵△ONQ ∽△HMP ,∴ON HM =OQ HQ .∴ON 4=OQm -OQ .∴m -44=OQm -OQ.∴OQ =m -4.∴AQ =OA -OQ =2-(m -4)=6-m .∴AQ = DM =6-m .又∵AQ ∥DM ,∴四边形ADMQ 是平行四边形.第27题答案图6 第27题答案图7②当m >6时(如答案图6所示),同理可得:四边形ADMQ 是平行四边形.综合①、②可知:四边形ADMQ是平行四边形.。
2018山东济南市中考数学试题[答案解析]
![2018山东济南市中考数学试题[答案解析]](https://img.taocdn.com/s3/m/a5749ff7aa00b52acfc7cae9.png)
山东省济南市2018年学业水平考试数学试题一、选择题(本大题共12小题,每小题4分,共48分)1.(2018济南,1,4分)4的算术平方根是()A.2 B.-2 C.±2 D. 2【答案】A2.(2018济南,2,4分)如图所示的几何体,它的俯视图是()A. B. C. D.【答案】D3.(2018济南,3,4分)2018年1月,“墨子号”量子卫星实现了距离达7600千米的洲际量子密钥分发,这标志着“墨子号”具备了洲际量子保密通信的能力.数字7600用科学记数法表示为()A.0.76×104 B.7.6×103 C.7.6×104 D.76×102【答案】B4.(2018济南,4,4分)“瓦当”是中国古建筑装饰××头的附件,是中国特有的文化艺术遗产,下面“瓦当”图案中既是轴对称图形又是中心对称图形的是()A B C D【答案】D5.(2018济南,5,4分)如图,AF是∠BAC的平分线,DF∥AC,若∠1=35°,则∠BAF的度数为()A.17.5° B.35° C.55° D.70°【答案】B6.(2018济南,6,4分)下列运算正确的是()A.a2+2a=3a3 B.(-2a3)2=4a51ABCDFC .(a +2)(a -1)=a 2+a -2D .(a +b )2=a 2+b 2【答案】C 7.(2018济南,7,4分)关于x 的方程3x -2m =1的解为正数,则m 的取值范围是( ) A .m <-12 B .m >-12 C .m >12 D .m <12【答案】B8.(2018济南,8,4分)在反比例函数y =-2x图象上有三个点A (x 1,y 1)、B (x 2,y 2)、C (x 3,y 3),若x 1<0<x 2<x 3,则下列结论正确的是( )A .y 3<y 2<y 1B .y 1<y 3<y 2C .y 2<y 3<y 1D .y 3<y 1<y 2【答案】C 9.(2018济南,9,4分)如图,在平面直角坐标系中,△ABC 的顶点都在方格线的格点上,将△ABC 绕点P 顺时针方向旋转90°,得到△A ′B ′C ′,则点P 的坐标为( ) A .(0,4) B .(1,1) C .(1,2) D .(2,1)【答案】C 10.(2018济南,10,4分)下面的统计图大致反应了我国2012年至2017年人均阅读量的情况.根据统计图提供的信息,下列推断不合理...的是( ) A .与2016年相比,2017年我国电子书人均阅读量有所降低 B .2012年至2017年,我国纸质书的人均阅读量的中位数是4.57C .从2014年到2017年,我国纸质书的人均阅读量逐年增长D .2013年我国纸质书的人均阅读量比电子书的人均阅读量的1.8倍还多【答案】B 11.(2018济南,11,4分)如图,一个扇形纸片的圆心角为90°,半径为6.如图2,将这张扇形纸片折叠,使点A 与点O 恰好重合,折痕为CD ,图中阴影为重合部分,则阴影部分的面积为( ) A .6π-92 3 B .6π-9 3 C .12π-92 3 D .9π4【答案】A12.(2018济南,11,4分)若平面直角坐标系内的点M 满足横、纵坐标都为整数,则把点M 叫做“整点”.例如:P (1,0)、Q (2,-2)都是“整点”.抛物线y =mx 2-4mx +4m -2(m >0)与x 轴交于点A 、B 两点,若该抛物线在A 、B 之间的部分与线段AB 所围成的区域(包括边界)恰有七个整点,则m 的取值范围是( ) A .12≤m <1 B .12<m ≤1 C .1<m ≤2 D .1<m <2【答案】B【解析】解:∵y =mx 2-4mx +4m -2=m (x -2)2-2且m >0,∴该抛物线开口向上,顶点坐标为(2,-2),对称轴是直线x =2.由此可知点(2,0)、点(2,-1)、顶点(2,-2)符合题意. 方法一:①当该抛物线经过点(1,-1)和(3,-1)时(如答案图1),这两个点符合题意.将(1,-1)代入y =mx 2-4mx +4m -2得到-1=m -4m +4m -2.解得m =1.此时抛物线解析式为y =x 2-4x +2.由y =0得x 2-4x +2=0.解得x 1=2-2≈0.6,x 2=2+2≈3.4.AB CDO (A ) ABO年份电子书纸质书62345∴x 轴上的点(1,0)、(2,0)、(3,0)符合题意.则当m =1时,恰好有 (1,0)、(2,0)、(3,0)、(1,-1)、(3,-1)、(2,-1)、(2,-2)这7个整点符合题意. ∴m ≤1.【注:m 的值越大,抛物线的开口越小,m 的值越小,抛物线的开口越大,】答案图1(m =1时) 答案图2( m =12时)②当该抛物线经过点(0,0)和点(4,0)时(如答案图2),这两个点符合题意. 此时x 轴上的点 (1,0)、(2,0)、(3,0)也符合题意.将(0,0)代入y =mx 2-4mx +4m -2得到0=0-4m +0-2.解得m =12.此时抛物线解析式为y =12x 2-2x .当x =1时,得y =12×1-2×1=-32<-1.∴点(1,-1)符合题意.当x =3时,得y =12×9-2×3=-32<-1.∴点(3,-1) 符合题意.综上可知:当m =12时,点(0,0)、(1,0)、(2,0)、(3,0)、(4,0)、(1,-1)、(3,-1)、(2,-2)、(2,-1)都符合题意,共有9个整点符合题意, ∴m =12不符合题.∴m >12.综合①②可得:当12<m ≤1时,该函数的图象与x 轴所围城的区域(含边界)内有七个整点,故答案选B .方法二:根据题目提供的选项,分别选取m =12,m =1,m =2,依次加以验证.①当m =12时(如答案图3),得y =12x 2-2x .由y =0得12x 2-2x =0.解得x 1=0,x 2=4.∴x 轴上的点(0,0)、(1,0)、(2,0)、(3,0)、(4,0)符合题意. 当x =1时,得y =12×1-2×1=-32<-1.∴点(1,-1)符合题意.当x =3时,得y =12×9-2×3=-32<-1.∴点(3,-1) 符合题意.综上可知:当m =12时,点(0,0)、(1,0)、(2,0)、(3,0)、(4,0)、(1,-1)、(3,-1)、(2,-2)、(2,-1)都符合题意,共有9个整点符合题意, ∴m =12不符合题.∴选项A 不正确.答案图3( m =12时) 答案图4(m =1时) 答案图5(m =2时)②当m =1时(如答案图4),得y =x 2-4x +2.由y =0得x 2-4x +2=0.解得x 1=2-2≈0.6,x 2=2+2≈3.4. ∴x 轴上的点(1,0)、(2,0)、(3,0)符合题意.当x =1时,得y =1-4×1+2=-1.∴点(1,-1)符合题意. 当x =3时,得y =9-4×3+2=-1.∴点(3,-1) 符合题意.综上可知:当m =1时,点(1,0)、(2,0)、(3,0)、(1,-1)、(3,-1)、(2,-2) 、(2,-1)都符合题意,共有7个整点符合题意, ∴m =1符合题. ∴选项B 正确.③当m =2时(如答案图5),得y =2x 2-8x +6.由y =0得2x 2-8x +6=0.解得x 1=1,x 2=3. ∴x 轴上的点(1,0)、(2,0)、(3,0)符合题意.综上可知:当m =2时,点(1,0)、(2,0)、(3,0)、(2,-2) 、(2,-1)都符合题意,共有5个整点符合题意, ∴m =2不符合题.二、填空题(本大题共6小题,每小题4分,共24分)13.(2018济南,13,4分)分解因式:m 2-4=____________; 【答案】(m +2)(m -2) 14.(2018济南,14,4分)在不透明的盒子中装有5个黑色棋子和若于个白色做子,每个棋子除颜色外都相同,任意摸出一个棋子,摸到黑包棋子的概率是14,则白色棋子的个数是=____________; 【答案】15 15.(2018济南,15,4分)一个正多边形的每个内角等于108°,则它的边数是=____________; 【答案】516.(2018济南,16,4分)若代数式x -2x -4的值是2,则x =____________; 【答案】6 17.(2018济南,17,4分)A 、B 两地相距20km ,甲乙两人沿同一条路线从A 地到B 地.甲先出发,匀速行驶,甲出发1小时后乙再出发,乙以2km/h 的速度度匀速行驶1小时后提高速度并继续匀速行驶,结果比甲提前到达.甲、乙两人离开A 地的距离s (km )与时间t (h )的关系如图所示,则甲出发____________小时后和乙相遇.【答案】165.【解析】y 甲=4t (0≤t ≤4);y 乙=⎩⎨⎧2(t -1)(1≤t ≤2)9(t -2)t (2<t ≤4);由方程组⎩⎨⎧y =4ty =9(t -2)解得⎩⎨⎧t =165y =645. ∴答案为165.18.(2018济南,18,4分)如图,矩形EFGH 的四个顶点分别在矩形ABCD 的各条边上,AB=EF ,FG =2,GC =3.有以下四个结论:①∠BGF =∠CHG ;②△BFG ≌△DHE ;③tan ∠BFG =12;④矩形EFGH 的面积是43.其中一定成立的是____________.(把所有正确结论的序号填在横线上)F【答案】①②④.【解析】设EH =AB =a ,则CD =GH =a . ∵∠FGH =90°,∴∠BGF +∠CGH =90°. 又∵∠CGH +∠CHG =90°,∴∠BGF =∠CHG …………………………………故①正确.同理可得∠DEH =∠CHG . ∴∠BGF =∠DEH .又∵∠B =∠D =90°,FG =EH ,∴△BFG ≌△DHE …………………………………故②正确. 同理可得△AFE ≌△CHG .∴AF =CH . 易得△BFG ∽△CGH .∴BF CG =FG GH .∴BF 3=2a .∴BF =6a.∴AF =AB -BF =a -6a.∴CH =AF =a -6a.在Rt △CGH 中,∵CG 2+CH 2=GH 2,∴32+( a -6a )2=a 2.解得a =2 3.∴GH =2 3.∴BF = a -6a= 3.在Rt △BFG 中,∵cos ∠BFG =BF FG =32,∴∠BFG =30°. ∴tan ∠BFG =tan30°=33.…………………………………故③正确. 矩形EFGH 的面积=FG ×GH =2×23=43…………………………………故④正确.三、解答题(本大题共9小题,共78分)19.(2018济南,19,6分)计算:2-1+│-5│-sin30°+(π-1)0.解:2-1+│-5│-sin30°+(π-1)0.=12+5-12+1=620.(2018济南,20,6分)解不等式组:⎩⎪⎨⎪⎧3x +1<2x +3 ①2x >3x -12 ② 解:由① ,得3x -2x <3-1. ∴x <2. 由② ,得 4x >3x -1. ∴x >-1.∴不等式组的解集为-1<x <2.21.(2018济南,21,6分)如图,在□ABCD 中,连接BD ,E 是DA 延长线上的点,F 是BC 延长线上的点,且 AE =CF ,连接EF 交BD 于点O .求证:OB =O D .证明:∵□ABCD中,∴AD=BC,AD∥B C.∴∠ADB=∠CB D.又∵AE=CF,∴AE+AD=CF+B C.∴ED=F B.又∵∠EOD=∠FOB,∴△EOD≌△FO B.∴OB=O D.22.(2018济南,22,8分)本学期学校开展以“感受中华传统买德”为主题的研学部动,组织150名学生多观历史好物馆和民俗晨览馆,每一名学生只能参加其中全顺活动,共支付票款2000元,票价信息如下:(1)请问参观历史博物馆和民俗展览馆的人数各是多少人?(2)若学生都去参观历史博物馆,则能节省票款多少元?解:(1)设参观历史博物馆的有x人,则参观民俗展览馆的有(150-x)人,依题意,得10x+20(150-x)2000.10x+3000-20x=2000.-10x=-1000.∴x=100.∴150-x=50.答:参观历史博物馆的有100人,则参观民俗展览馆的有50人.(2)2000-150×10=500(元).答:若学生都去参观历史博物馆,则能节省票款500元.23.(2018济南,23,8分)如图AB是⊙O的直径,PA与⊙O相切于点A,BP与⊙O相较于点D,C为⊙O上的一点,分别连接CB、CD,∠BCD=60°.(1)求∠ABD的度数;(2)若AB=6,求PD的长度.C【解析】解:(1)方法一:连接AD (如答案图1所示). ∵BA 是⊙O 直径,∴∠BDA =90°.∵⌒BD =⌒BD ,∴∠BAD =∠C =60°.∴∠ABD =90°-∠BAD =90°-60°=30°.CC第23题答案图1 第23题答案图2 方法二:连接DA 、OD (如答案图2所示),则∠BOD =2∠C =2×60°=120°. ∵OB =OD ,∴∠OBD =∠ODB =12(180°-120°)=30°.即∠ABD =30°.(2)∵AP 是⊙O 的切线,∴∠BAP =90°. 在Rt △BAD 中,∵∠ABD =30°,∴DA =12BA =12×6=3.∴BD =3DA =33.在Rt △BAP 中,∵cos ∠ABD =AB PB ,∴cos30°=6PB =32.∴BP =43.∴PD =BP -BD =43-33=3.24.(2018济南,24,10分)某校开设了“3D ”打印、数学史、诗歌欣赏、陶艺制作四门校本课程,为了解学生对这四门校本课程的喜爱情况,对学生进行了随机问卷调查(问卷调查表如图所示),将调查结果整理后绘制例图1 、图2两幅均不完整的统计图表.请您根据图表中提供的信息回答下列问题:(1)统计表中的a =________,b =_______; (2)“D ”对应扇形的圆心角为_______度;(3)根据调查结果,请您估计该校2000名学生中最喜欢“数学史”校本课程的人数; (4)小明和小亮参加校本课程学习,若每人从“A ”、“B ”、“C ”三门校本课程中随机选取一门,请用画树状图或列表格的方法,求两人恰好选中同一门校本课程的概率. 解:(1)a =36÷0.45=80. b =16÷80=0.20.(2)“D ”对应扇形的圆心角的度数为:8÷80×360°=36°.(3)估计该校2000名学生中最喜欢“数学史”校本课程的人数为: 2000×0.25=500(人). (4)列表格如下:3种,所以两人恰好选中同一门校本课程的概率为:39=13.25.(2018济南,25,10分)如图,直线y =ax +2与x 轴交于点A (1,0),与y 轴交于点B (0,b ).将线段AB 先向右平移1个单位长度、再向上平移t (t >0)个单位长度,得到对应线段CD ,反比例函数y=k x(x >0)的图象恰好经过C 、D 两点,连接AC 、B D . (1)求a 和b 的值;(2)求反比例函数的表达式及四边形ABDC 的面积;(3)点N 在x 轴正半轴上,点M 是反比例函数y =k x(x >0)的图象上的一个点,若△CMN 是以CM 为直角边的等腰直角三角形时,求所有满足条件的点M 的坐标.第25题图 第25题备用图【解析】解:(1)将点A (1,0)代入y =ax +2,得0=a +2.∴a =-2. ∴直线的解析式为y =-2x +2.将x =0代入上式,得y =2.∴b =2.∴点B (0,2). (2)由平移可得:点C (2,t )、D (1,2+t ).将点C (2,t )、D (1,2+t )分别代入y =kx ,得 ⎩⎨⎧t =k 22+t =k 1.解得⎩⎨⎧k =4t =2.∴反比例函数的解析式为y =4x,点C (2,2)、点D (1,4).分别连接BC 、AD (如答案图1).∵B (0,2)、C (2,2),∴BC ∥x 轴,BC =2. ∵A (1,0)、D (1,4),∴AD ⊥x 轴,AD =4. ∴BC ⊥A D .∴S 四边形ABDC =12×BC ×AD =12×2×4=4.第25题答案图1(3)①当∠NCM =90°、CM =CN 时(如答案图2所示),过点C 作直线l ∥x 轴,交y 轴于点G .过点M 作MF ⊥直线l 于点F ,交x 轴于点H .过点N 作NE ⊥直线l 于点E . 设点N (m ,0)(其中m >0),则ON =m ,CE =2-m . ∵∠MCN =90°,∴∠MCF +∠NCE =90°.∵NE ⊥直线l 于点E ,∴∠ENC +∠NCE =90°.∴∠MCF =∠EN C .又∵∠MFC =∠NEC =90°,CN =CM ,∴△NEC ≌△CFM . ∴CF =EN =2,FM =CE =2-m .∴FG =CG +CF =2+2=4.∴x M =4. 将x =4代入y =4x,得y =1.∴点M (4,1).l第25题答案图2 第25题答案图3 ②当∠NMC =90°、MC =MN 时(如答案图3所示),过点C 作直线l ⊥y 轴与点F ,则CF =x C =2.过点M 作MG ⊥x 轴于点G ,MG 交直线l 与点E ,则MG ⊥直线l 于点E ,EG =y C =2.∵∠CMN =90°,∴∠CME +∠NMG =90°.∵ME ⊥直线l 于点E ,∴∠ECM +∠CME =90°.∴∠NMG =∠ECM .又∵∠CEM =∠NGM =90°,CM =MN ,∴△CEM ≌△MGN .∴CE =MG ,EM =NG .设CE =MG =a ,则y M =a ,x M =CF +CE =2+a .∴点M (2+a ,a ).将点M (2+a ,a ) 代入y =4x ,得a =42+a.解得a 1=5-1,a 2=-5-1.∴x M=2+a=5+1.∴点M(5+1,5-1).综合①②可知:点M的坐标为(4,1)或(5+1,5-1).26.(2018济南,26,12分)在△ABC中,AB=AC,∠BAC=120°,以CA为边在∠ACB的另一侧作∠ACM=∠ACB,点D为射线BC上任意一点,在射线CM上截取CE=BD,连接AD、DE、AE.(1)如图1,当点D落在线段BC的延长线上时,直接写出∠ADE的度数;(2)如图2,当点D落在线段BC(不含边界)上时,AC与DE交于点F,请问(1)中的结论是否仍成立?如果成立,请给出证明;如果不成立,请说明理由;(3)在(2)的条件下,若AB=6,求CF的最大值.第26题图1 第26题图2【解析】解:(1) ∠ADE=30°.(2) (1)中的结论是否还成立证明:连接AE(如答案图1所示).∵∠BAC=120°,AB=AC,∴∠B=∠ACB=30°.又∵∠ACM=∠ACB,∴∠B=∠ACM=30°.又∵CE=BD,∴△ABD≌△ACE.∴AD=AE,∠1=∠2.∴∠2+∠3=∠1+∠3=∠BAC=120°.即∠DAE=120°.又∵AD =AE ,∴∠ADE =∠AED =30°.D答案图1 答案图2(3) ∵AB =AC ,AB =6,∴AC =6.∵∠ADE =∠ACB =30°且∠DAF =∠CAD ,∴△ADF ∽△AC D.∴AD AC =AF AD .∴AD 2=AF ·A C .∴AD 2=6AF .∴AF =AD 26.∴当AD 最短时,AF 最短、CF 最长.易得当AD ⊥BC 时,AF 最短、CF 最长(如答案图2所示),此时AD =12AB =3.∴AF 最短=AD 26=326=32. ∴CF 最长=AC - AF 最短=6-32=92.27.(2018济南,27,12分)如图1,抛物线y =ax 2+bx +4过A (2,0)、B (4,0)两点,交y 轴于点C ,过点C 作x 轴的平行线与不等式抛物线上的另一个交点为D ,连接AC 、B C .点P 是该抛物线上一动点,设点P 的横坐标为m (m >4).(1)求该抛物线的表达式和∠ACB 的正切值; (2)如图2,若∠ACP =45°,求m 的值;(3)如图3,过点A 、P 的直线与y 轴于点N ,过点P 作PM ⊥CD ,垂足为M ,直线MN 与x 轴交于点Q ,试判断四边形ADMQ 的形状,并说明理由.第27题图1 第27题图2 第27题图3【解析】解:(1)将点A (2,0)和点B (4,0)分别代入y =ax 2+bx +4,得⎩⎨⎧0=4a +2x +40=16a +4b +4.解得⎩⎪⎨⎪⎧a =12b =-3.∴该抛物线的解析式为y =12x 2-3x +4.将x =0代入上式,得y =4.∴点C (0,4),OC =4.在Rt △AOC 中,AC =OA 2+OC 2=22+42=2 5.设直线AC 的解析式为y =kx +4,将点A (2,0)代入上式,得0=2k +4.解得k =-2. ∴直线AC 的解析式为y =-2x +4.同理可得直线BC 的解析式为y =-x +4. 求tan ∠ACB 方法一:过点B 作BG ⊥CA ,交CA 的延长线于点G (如答案图1所示),则∠G =90°.∵∠COA =∠G =90°,∠CAO =∠BAG ,∴△GAB ∽△OA C.∴BG AG =OC OA =42=2.∴BG =2AG . 在Rt △ABG 中,∵BG 2+AG 2=AB 2,∴(2AG )2+AG 2=22.AG =25 5.∴BG =455,CG =AC +AG =25+255=125 5.在Rt △BCG 中,tan ∠ACB =BG CQ =4551255=13.第27题答案图1 第27题答案图2求tan ∠ACB 方法二:过点A 作AE ⊥AC ,交BC 于点E (如答案图2所示),则k AE ·k AC =-1.∴-2k AE =-1.∴k AE =12.∴可设直线AE 的解析式为y =12x +m .将点A (2,0)代入上式,得0=12×2+m .解得m =-1.∴直线AE 的解析式为y =12x -1.由方程组⎩⎪⎨⎪⎧y =12x -1y =-x +4解得⎩⎨⎧x =103y =23.∴点E (103,23).∴AE =⎝ ⎛⎭⎪⎫2-1032+⎝ ⎛⎭⎪⎫0-232=235. 在Rt △AEC 中,tan ∠ACB =AE AC =23525=13.求tan ∠ACB 方法三:过点A 作AF ⊥BC ,交BC 点E (如答案图3所示),则k AF ·k BC =-1. ∴-k AF =-1.∴k AF =1.∴可设直线AF 的解析式为y =x +n .将点A (2,0)代入上式,得0=2+n .解得n =-2.∴直线AF 的解析式为y =x -2.由方程组⎩⎨⎧y =x -2y =-x +4解得⎩⎨⎧x =3y =1.∴点F (3,1).∴AF =(3-2)2+(1-0)2=2,CF =(3-0)2-(1-4)2=3 2.在Rt △AEC 中,tan ∠ACB =AF CF =232=13.第27题答案图3(2)方法一:利用“一线三等角”模型将线段AC 绕点A 沿顺时针方向旋转90°,得到线段AC ′,则 AC ′=AC ,∠C ′AC =90°,∠CC ′A =∠ACC ′=45°. ∴∠CAO +∠C ′AB =90°. 又∵∠OCA +∠CAO =90°, ∴∠OCA =∠C ′A B .过点C ′作C ′E ⊥x 轴于点E .则∠C ′EA =∠COA =90°. ∵∠C ′EA =∠COA =90°,∠OCA =∠C ′AB ,AC ′=AC ,∴△C ′EA ≌△AO C .∴C ′E =OA =2,AE =OC =4.∴OE =OA +AE =2+4=6. ∴点C ′(6,2).设直线C ′C 的解析式为y =hx +4.将点C ′(6,2)代入上式,得2=6h +4.解得h =-13.∴直线C ′C 的解析式为y =-13x +4.∵∠ACP =45°,∠ACC ′=45°,∴点P 在直线C ′C 上.设点P 的坐标为(x ,y ),则x 是方程12x 2-3x +4=-13x +4的一个解.将方程整理,得3x 2-14x =0.解得x 1=163,x 2=0(不合题意,舍去).将x 1=163代入y =-13x +4,得y =209.∴点P 的坐标为(163,209).第27题答案图4 第27题答案图5(2)方法二:利用正方形中的“全角夹半角”模型.过点B 作BH ⊥CD 于点H ,交CP 于点K ,连接AK .易得四边形OBHC 是正方形. 应用“全角夹半角”可得AK =OA +HK .设K (4,h ),则BK =h ,HK =HB -KB =4-h ,AK =OA +HK =2+(4-h )=6-h .在Rt △ABK 中,由勾股定理,得AB 2+BK 2=AK 2.∴22+ h 2=(6-h )2.解得h =83.∴点K (4,83).设直线CK 的解析式为y =hx +4.将点K (4,83)代入上式,得83=4h +4.解得h =-13.∴直线CK 的解析式为y =-13x +4.设点P 的坐标为(x ,y ),则x 是方程12x 2-3x +4=-13x +4的一个解.将方程整理,得3x 2-14x =0.解得x 1=163,x 2=0(不合题意,舍去).将x 1=163代入y =-13x +4,得y =209.∴点P 的坐标为(163,209).(3)四边形ADMQ 是平行四边形.理由如下: ∵CD ∥x 轴,∴y C =y D =4.将y =4代入y =12x 2-3x +4,得 4=12x 2-3x +4.解得x 1=0,x 2=6.∴点D (6,4).根据题意,得P (m ,12m 2-3m +4),M (m ,4),H (m ,0).∴PH =12m 2-3m +4),OH =m ,AH =m -2,MH =4.①当4<m <6时(如答案图5所示),DM =6-m∵△OAN ∽△HAP ,∴ON PH =OA AH .∴ON 12m 2-3m +4=2m -2.∴ON =m 2-6m +8m -2=(m -4)(m -2)m -2=m -4.∵△ONQ ∽△HMP ,∴ON HM =OQ HQ .∴ON 4=OQm -OQ .∴m -44=OQm -OQ.∴OQ =m -4. ∴AQ =OA -OQ =2-(m -4)=6-m . ∴AQ = DM =6-m .又∵AQ ∥DM ,∴四边形ADMQ 是平行四边形.第27题答案图6 第27题答案图7②当m>6时(如答案图6所示),同理可得:四边形ADMQ是平行四边形.综合①、②可知:四边形ADMQ是平行四边形.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
山东省济南市2018年学业水平考试数学试题一、选择题(本大题共12小题,每小题4分,共48分)1.(2018济南,1,4分)4的算术平方根是( )A .2B .-2C .±2D . 2 2.(2018济南,2,4分)如图所示的几何体,它的俯视图是( )正面A .B .C .D . 3.(2018济南,3,4分)2018年1月,“墨子号”量子卫星实现了距离达7600千米的洲际量子密钥分发,这标志着“墨子号”具备了洲际量子保密通信的能力.数字7600用科学记数法表示为( )A .0.76×104B .7.6×103C .7.6×104D .76×102 4.(2018济南,4,4分)“瓦当”是中国古建筑装饰××头的附件,是中国特有的文化艺术遗产,下面“瓦当”图案中既是轴对称图形又是中心对称图形的是( )A B C D 5.(2018济南,5,4分)如图,AF 是∠BAC 的平分线,DF ∥AC ,若∠1=35°,则∠BAF 的度数为( ) A .17.5° B .35° C .55° D .70°6.(2018济南,6,4分)下列运算正确的是( ) A .a 2+2a =3a 3 B .(-2a 3)2=4a 5 C .(a +2)(a -1)=a 2+a -2 D .(a +b )2=a 2+b 2 7.(2018济南,7,4分)关于x 的方程3x -2m =1的解为正数,则m 的取值范围是( ) A .m <-12 B .m >-12 C .m >12 D .m <128.(2018济南,8,4分)在反比例函数y =-2x 图象上有三个点A (x 1,y 1)、B (x 2,y 2)、C (x 3,y 3),若x 1<0<x 2<x 3,则下列结论正确的是( )A .y 3<y 2<y 1B .y 1<y 3<y 2C .y 2<y 3<y 1D .y 3<y 1<y 21A B C DF9.(2018济南,9,4分)如图,在平面直角坐标系中,△ABC 的顶点都在方格线的格点上,将△ABC 绕点P 顺时针方向旋转90°,得到△A ′B ′C ′,则点P 的坐标为( ) A .(0,4) B .(1,1) C .(1,2) D .(2,1)xy–1–2–3–412341234567BCA A'C 'B'O10.(2018济南,10,4分)下面的统计图大致反应了我国2012年至2017年人均阅读量的情况.根据统计图提供的信息,下列推断不合理...的是( ) A .与2016年相比,2017年我国电子书人均阅读量有所降低 B .2012年至2017年,我国纸质书的人均阅读量的中位数是4.57C .从2014年到2017年,我国纸质书的人均阅读量逐年增长D .2013年我国纸质书的人均阅读量比电子书的人均阅读量的1.8倍还多11.(2018济南,11,4分)如图,一个扇形纸片的圆心角为90°,半径为6.如图2,将这张扇形纸片折叠,使点A 与点O 恰好重合,折痕为CD ,图中阴影为重合部分,则阴影部分的面积为( ) A .6π-92 3 B .6π-9 3 C .12π-92 3 D .9π4AB CDO (A ) ABO阅读量/本年份电子书纸质书62345 4.394.774.564.584.65 4.662.352.483.22 3.26 3.213.1212.(2018济南,11,4分)若平面直角坐标系内的点M 满足横、纵坐标都为整数,则把点M 叫做“整点”.例如:P (1,0)、Q (2,-2)都是“整点”.抛物线y =mx 2-4mx +4m -2(m >0)与x 轴交于点A 、B 两点,若该抛物线在A 、B 之间的部分与线段AB 所围成的区域(包括边界)恰有七个整点,则m 的取值范围是( ) A .12≤m <1 B .12<m ≤1 C .1<m ≤2 D .1<m <2二、填空题(本大题共6小题,每小题4分,共24分)13.(2018济南,13,4分)分解因式:m 2-4=____________;14.(2018济南,14,4分)在不透明的盒子中装有5个黑色棋子和若于个白色做子,每个棋子除颜色外都相同,任意摸出一个棋子,摸到黑包棋子的概率是14,则白色棋子的个数是=____________; 15.(2018济南,15,4分)一个正多边形的每个内角等于108°,则它的边数是=____________; 16.(2018济南,16,4分)若代数式x -2x -4的值是2,则x =____________;17.(2018济南,17,4分)A 、B 两地相距20km ,甲乙两人沿同一条路线从A 地到B 地.甲先出发,匀速行驶,甲出发1小时后乙再出发,乙以2km/h 的速度度匀速行驶1小时后提高速度并继续匀速行驶,结果比甲提前到达.甲、乙两人离开A 地的距离s (km )与时间t (h )的关系如图所示,则甲出发____________小时后和乙相遇.18.(2018济南,18,4分)如图,矩形EFGH 的四个顶点分别在矩形ABCD 的各条边上,AB =EF ,FG =2,GC =3.有以下四个结论:①∠BGF =∠CHG ;②△BFG ≌△DHE ;③tan ∠BFG =12;④矩形EFGH 的面积是43.其中一定成立的是____________.(把所有正确结论的序号填在横线上)三、解答题(本大题共9小题,共78分)19.(2018济南,19,6分)计算:2-1+│-5│-sin30°+(π-1)0.F解不等式组:⎩⎪⎨⎪⎧3x +1<2x +3 ①2x >3x -12 ②21.(2018济南,21,6分)如图,在□ABCD 中,连接BD ,E 是DA 延长线上的点,F 是BC 延长线上的点,且 AE =CF ,连接EF 交BD 于点O .求证:OB =O D .22.(2018济南,22,8分)本学期学校开展以“感受中华传统买德”为主题的研学部动,组织150名学生多观历史好物馆和民俗晨览馆,每一名学生只能参加其中全顺活动,共支付票款2000元,票价信息如下:(1)请问参观历史博物馆和民俗展览馆的人数各是多少人? (2)若学生都去参观历史博物馆,则能节省票款多少元?如图AB是⊙O的直径,P A与⊙O相切于点A,BP与⊙O相较于点D,C为⊙O上的一点,分别连接CB、CD,∠BCD=60°.(1)求∠ABD的度数;(2)若AB=6,求PD的长度.C24.(2018济南,24,10分)某校开设了“3D”打印、数学史、诗歌欣赏、陶艺制作四门校本课程,为了解学生对这四门校本课程的喜爱情况,对学生进行了随机问卷调查(问卷调查表如图所示),将调查结果整理后绘制例图1 、图2两幅均不完整的统计图表.请您根据图表中提供的信息回答下列问题:(1)统计表中的a=________,b=_______;(2)“D ”对应扇形的圆心角为_______度;(3)根据调查结果,请您估计该校2000名学生中最喜欢“数学史”校本课程的人数; (4)小明和小亮参加校本课程学习,若每人从“A ”、“B ”、“C ”三门校本课程中随机选取一门,请用画树状图或列表格的方法,求两人恰好选中同一门校本课程的概率. 25.(2018济南,25,10分)如图,直线y =ax +2与x 轴交于点A (1,0),与y 轴交于点B (0,b ).将线段AB 先向右平移1个单位长度、再向上平移t (t >0)个单位长度,得到对应线段CD ,反比例函数y =kx (x >0)的图象恰好经过C 、D 两点,连接AC 、B D . (1)求a 和b 的值;(2)求反比例函数的表达式及四边形ABDC 的面积;(3)点N 在x 轴正半轴上,点M 是反比例函数y =kx (x >0)的图象上的一个点,若△CMN是以CM 为直角边的等腰直角三角形时,求所有满足条件的点M 的坐标.第25题图 第25题备用图26.(2018济南,26,12分)在△ABC中,AB=AC,∠BAC=120°,以CA为边在∠ACB的另一侧作∠ACM=∠ACB,点D为射线BC上任意一点,在射线CM上截取CE=BD,连接AD、DE、AE.(1)如图1,当点D落在线段BC的延长线上时,直接写出∠ADE的度数;(2)如图2,当点D落在线段BC(不含边界)上时,AC与DE交于点F,请问(1)中的结论是否仍成立?如果成立,请给出证明;如果不成立,请说明理由;(3)在(2)的条件下,若AB=6,求CF的最大值.第26题图1 第26题图227.(2018济南,27,12分)如图1,抛物线y =ax 2+bx +4过A (2,0)、B (4,0)两点,交y 轴于点C ,过点C 作x 轴的平行线与不等式抛物线上的另一个交点为D ,连接AC 、B C .点P 是该抛物线上一动点,设点P 的横坐标为m (m >4).(1)求该抛物线的表达式和∠ACB 的正切值; (2)如图2,若∠ACP =45°,求m 的值;(3)如图3,过点A 、P 的直线与y 轴于点N ,过点P 作PM ⊥CD ,垂足为M ,直线MN 与x 轴交于点Q ,试判断四边形ADMQ 的形状,并说明理由.第27题图1 第27题图2 第27题图3山东省济南市2018年学业水平考试数学试题一、选择题(本大题共12小题,每小题4分,共48分)1.(2018济南,1,4分)4的算术平方根是( )A .2B .-2C .±2D . 2 【答案】A 2.(2018济南,2,4分)如图所示的几何体,它的俯视图是( )正面A .B .C .D . 【答案】D 3.(2018济南,3,4分)2018年1月,“墨子号”量子卫星实现了距离达7600千米的洲际量子密钥分发,这标志着“墨子号”具备了洲际量子保密通信的能力.数字7600用科学记数法表示为( )A .0.76×104B .7.6×103C .7.6×104D .76×102 【答案】B 4.(2018济南,4,4分)“瓦当”是中国古建筑装饰××头的附件,是中国特有的文化艺术遗产,下面“瓦当”图案中既是轴对称图形又是中心对称图形的是( )A B C D 【答案】D 5.(2018济南,5,4分)如图,AF 是∠BAC 的平分线,DF ∥AC ,若∠1=35°,则∠BAF 的度数为( ) A .17.5° B .35° C .55° D .70°【答案】B 6.(2018济南,6,4分)下列运算正确的是( ) A .a 2+2a =3a 3 B .(-2a 3)2=4a 51ABCDFC .(a +2)(a -1)=a 2+a -2D .(a +b )2=a 2+b 2 【答案】C 7.(2018济南,7,4分)关于x 的方程3x -2m =1的解为正数,则m 的取值范围是( ) A .m <-12 B .m >-12 C .m >12 D .m <12【答案】B8.(2018济南,8,4分)在反比例函数y =-2x 图象上有三个点A (x 1,y 1)、B (x 2,y 2)、C (x 3,y 3),若x 1<0<x 2<x 3,则下列结论正确的是( )A .y 3<y 2<y 1B .y 1<y 3<y 2C .y 2<y 3<y 1D .y 3<y 1<y 2 【答案】C 9.(2018济南,9,4分)如图,在平面直角坐标系中,△ABC 的顶点都在方格线的格点上,将△ABC 绕点P 顺时针方向旋转90°,得到△A ′B ′C ′,则点P 的坐标为( ) A .(0,4) B .(1,1) C .(1,2) D .(2,1)【答案】C 10.(2018济南,10,4分)下面的统计图大致反应了我国2012年至2017年人均阅读量的情况.根据统计图提供的信息,下列推断不合理...的是( ) A .与2016年相比,2017年我国电子书人均阅读量有所降低 B .2012年至2017年,我国纸质书的人均阅读量的中位数是4.57C .从2014年到2017年,我国纸质书的人均阅读量逐年增长D .2013年我国纸质书的人均阅读量比电子书的人均阅读量的1.8倍还多【答案】B 11.(2018济南,11,4分)如图,一个扇形纸片的圆心角为90°,半径为6.如图2,将这张扇形纸片折叠,使点A 与点O 恰好重合,折痕为CD ,图中阴影为重合部分,则阴影部分的面积为( ) A .6π-92 3 B .6π-9 3 C .12π-92 3 D .9π4【答案】A12.(2018济南,11,4分)若平面直角坐标系内的点M 满足横、纵坐标都为整数,则把点M 叫做“整点”.例如:P (1,0)、Q (2,-2)都是“整点”.抛物线y =mx 2-4mx +4m -2(m >0)与x 轴交于点A 、B 两点,若该抛物线在A 、B 之间的部分与线段AB 所围成的区域(包括边界)恰有七个整点,则m 的取值范围是( ) A .12≤m <1 B .12<m ≤1 C .1<m ≤2 D .1<m <2【答案】B【解析】解:∵y =mx 2-4mx +4m -2=m (x -2)2-2且m >0,∴该抛物线开口向上,顶点坐标为(2,-2),对称轴是直线x =2.由此可知点(2,0)、点(2,-1)、顶点(2,-2)符合题意. 方法一:①当该抛物线经过点(1,-1)和(3,-1)时(如答案图1),这两个点符合题意. 将(1,-1)代入y =mx 2-4mx +4m -2得到-1=m -4m +4m -2.解得m =1. 此时抛物线解析式为y =x 2-4x +2.由y =0得x 2-4x +2=0.解得x 1=2-2≈0.6,x 2=2+2≈3.4.阅读量/本年份电子书纸质书201720162015201420132012O 62345 4.394.774.564.584.65 4.662.352.483.22 3.26 3.213.12AB CDO (A ) ABO∴x 轴上的点(1,0)、(2,0)、(3,0)符合题意.则当m =1时,恰好有 (1,0)、(2,0)、(3,0)、(1,-1)、(3,-1)、(2,-1)、(2,-2)这7个整点符合题意. ∴m ≤1.【注:m 的值越大,抛物线的开口越小,m 的值越小,抛物线的开口越大,】答案图1(m =1时) 答案图2( m =12时)②当该抛物线经过点(0,0)和点(4,0)时(如答案图2),这两个点符合题意. 此时x 轴上的点 (1,0)、(2,0)、(3,0)也符合题意.将(0,0)代入y =mx 2-4mx +4m -2得到0=0-4m +0-2.解得m =12.此时抛物线解析式为y =12x 2-2x .当x =1时,得y =12×1-2×1=-32<-1.∴点(1,-1)符合题意.当x =3时,得y =12×9-2×3=-32<-1.∴点(3,-1) 符合题意.综上可知:当m =12时,点(0,0)、(1,0)、(2,0)、(3,0)、(4,0)、(1,-1)、(3,-1)、(2,-2)、(2,-1)都符合题意,共有9个整点符合题意, ∴m =12不符合题.∴m >12.综合①②可得:当12<m ≤1时,该函数的图象与x 轴所围城的区域(含边界)内有七个整点,故答案选B .方法二:根据题目提供的选项,分别选取m =12,m =1,m =2,依次加以验证.①当m =12时(如答案图3),得y =12x 2-2x .由y =0得12x 2-2x =0.解得x 1=0,x 2=4.∴x 轴上的点(0,0)、(1,0)、(2,0)、(3,0)、(4,0)符合题意. 当x =1时,得y =12×1-2×1=-32<-1.∴点(1,-1)符合题意.当x =3时,得y =12×9-2×3=-32<-1.∴点(3,-1) 符合题意.综上可知:当m =12时,点(0,0)、(1,0)、(2,0)、(3,0)、(4,0)、(1,-1)、(3,-1)、(2,-2)、(2,-1)都符合题意,共有9个整点符合题意, ∴m =12不符合题.∴选项A 不正确.答案图3( m =12时) 答案图4(m =1时) 答案图5(m =2时)②当m =1时(如答案图4),得y =x 2-4x +2.由y =0得x 2-4x +2=0.解得x 1=2-2≈0.6,x 2=2+2≈3.4. ∴x 轴上的点(1,0)、(2,0)、(3,0)符合题意. 当x =1时,得y =1-4×1+2=-1.∴点(1,-1)符合题意. 当x =3时,得y =9-4×3+2=-1.∴点(3,-1) 符合题意.综上可知:当m =1时,点(1,0)、(2,0)、(3,0)、(1,-1)、(3,-1)、(2,-2) 、(2,-1)都符合题意,共有7个整点符合题意, ∴m =1符合题. ∴选项B 正确.③当m =2时(如答案图5),得y =2x 2-8x +6. 由y =0得2x 2-8x +6=0.解得x 1=1,x 2=3. ∴x 轴上的点(1,0)、(2,0)、(3,0)符合题意.综上可知:当m =2时,点(1,0)、(2,0)、(3,0)、(2,-2) 、(2,-1)都符合题意,共有5个整点符合题意, ∴m =2不符合题.二、填空题(本大题共6小题,每小题4分,共24分)13.(2018济南,13,4分)分解因式:m 2-4=____________; 【答案】(m +2)(m -2) 14.(2018济南,14,4分)在不透明的盒子中装有5个黑色棋子和若于个白色做子,每个棋子除颜色外都相同,任意摸出一个棋子,摸到黑包棋子的概率是14,则白色棋子的个数是=____________; 【答案】15 15.(2018济南,15,4分)一个正多边形的每个内角等于108°,则它的边数是=____________; 【答案】516.(2018济南,16,4分)若代数式x -2x -4的值是2,则x =____________;【答案】6 17.(2018济南,17,4分)A 、B 两地相距20km ,甲乙两人沿同一条路线从A 地到B 地.甲先出发,匀速行驶,甲出发1小时后乙再出发,乙以2km/h 的速度度匀速行驶1小时后提高速度并继续匀速行驶,结果比甲提前到达.甲、乙两人离开A 地的距离s (km )与时间t (h )的关系如图所示,则甲出发____________小时后和乙相遇.【答案】165.【解析】y 甲=4t (0≤t ≤4);y 乙=⎩⎨⎧2(t -1)(1≤t ≤2)9(t -2)t (2<t ≤4);由方程组⎩⎨⎧y =4t y =9(t -2)解得⎩⎨⎧t =165y =645. ∴答案为165.18.(2018济南,18,4分)如图,矩形EFGH 的四个顶点分别在矩形ABCD 的各条边上,AB =EF ,FG =2,GC =3.有以下四个结论:①∠BGF =∠CHG ;②△BFG ≌△DHE ;③tan ∠BFG =12;④矩形EFGH 的面积是43.其中一定成立的是____________.(把所有正确结论的序号填在横线上)F【答案】①②④.【解析】设EH =AB =a ,则CD =GH =a . ∵∠FGH =90°,∴∠BGF +∠CGH =90°. 又∵∠CGH +∠CHG =90°,∴∠BGF =∠CHG …………………………………故①正确.同理可得∠DEH =∠CHG . ∴∠BGF =∠DEH . 又∵∠B =∠D =90°,FG =EH ,∴△BFG ≌△DHE …………………………………故②正确. 同理可得△AFE ≌△CHG .∴AF =CH . 易得△BFG ∽△CGH .∴BF CG =FG GH .∴BF 3=2a .∴BF =6a. ∴AF =AB -BF =a -6a .∴CH =AF =a -6a .在Rt △CGH 中,∵CG 2+CH 2=GH 2,∴32+( a -6a )2=a 2.解得a =2 3.∴GH =2 3.∴BF = a -6a = 3.在Rt △BFG 中,∵cos ∠BFG =BF FG =32,∴∠BFG =30°. ∴tan ∠BFG =tan30°=33.…………………………………故③正确. 矩形EFGH 的面积=FG ×GH =2×23=43…………………………………故④正确.三、解答题(本大题共9小题,共78分)19.(2018济南,19,6分)计算:2-1+│-5│-sin30°+(π-1)0.解:2-1+│-5│-sin30°+(π-1)0.=12+5-12+1=620.(2018济南,20,6分)解不等式组:⎩⎪⎨⎪⎧3x +1<2x +3 ①2x >3x -12 ② 解:由① ,得3x -2x <3-1. ∴x <2. 由② ,得 4x >3x -1. ∴x >-1.∴不等式组的解集为-1<x <2.21.(2018济南,21,6分)如图,在□ABCD 中,连接BD ,E 是DA 延长线上的点,F 是BC 延长线上的点,且 AE =CF ,连接EF 交BD 于点O .求证:OB =O D .证明:∵□ABCD中,∴AD=BC,AD∥B C.∴∠ADB=∠CB D.又∵AE=CF,∴AE+AD=CF+B C.∴ED=F B.又∵∠EOD=∠FOB,∴△EOD≌△FO B.∴OB=O D.22.(2018济南,22,8分)本学期学校开展以“感受中华传统买德”为主题的研学部动,组织150名学生多观历史好物馆和民俗晨览馆,每一名学生只能参加其中全顺活动,共支付票款2000元,票价信息如下:(1)请问参观历史博物馆和民俗展览馆的人数各是多少人?(2)若学生都去参观历史博物馆,则能节省票款多少元?解:(1)设参观历史博物馆的有x人,则参观民俗展览馆的有(150-x)人,依题意,得10x+20(150-x)2000.10x+3000-20x=2000.-10x=-1000.∴x=100.∴150-x=50.答:参观历史博物馆的有100人,则参观民俗展览馆的有50人.(2)2000-150×10=500(元).答:若学生都去参观历史博物馆,则能节省票款500元.23.(2018济南,23,8分)如图AB是⊙O的直径,P A与⊙O相切于点A,BP与⊙O相较于点D,C为⊙O上的一点,分别连接CB、CD,∠BCD=60°.(1)求∠ABD的度数;(2)若AB=6,求PD的长度.C【解析】解:(1)方法一:连接AD (如答案图1所示). ∵BA 是⊙O 直径,∴∠BDA =90°.∵⌒BD =⌒BD ,∴∠BAD =∠C =60°.∴∠ABD =90°-∠BAD =90°-60°=30°.CC第23题答案图1 第23题答案图2方法二:连接DA 、OD (如答案图2所示),则∠BOD =2∠C =2×60°=120°. ∵OB =OD ,∴∠OBD =∠ODB =12(180°-120°)=30°.即∠ABD =30°.(2)∵AP 是⊙O 的切线,∴∠BAP =90°. 在Rt △BAD 中,∵∠ABD =30°, ∴DA =12BA =12×6=3.∴BD =3DA =33.在Rt △BAP 中,∵cos ∠ABD =AB PB ,∴cos30°=6PB =32.∴BP =43.∴PD =BP -BD =43-33=3.24.(2018济南,24,10分)某校开设了“3D ”打印、数学史、诗歌欣赏、陶艺制作四门校本课程,为了解学生对这四门校本课程的喜爱情况,对学生进行了随机问卷调查(问卷调查表如图所示),将调查结果整理后绘制例图1 、图2两幅均不完整的统计图表.请您根据图表中提供的信息回答下列问题:(1)统计表中的a =________,b =_______; (2)“D ”对应扇形的圆心角为_______度;(3)根据调查结果,请您估计该校2000名学生中最喜欢“数学史”校本课程的人数; (4)小明和小亮参加校本课程学习,若每人从“A ”、“B ”、“C ”三门校本课程中随机选取一门,请用画树状图或列表格的方法,求两人恰好选中同一门校本课程的概率. 解:(1)a =36÷0.45=80. b =16÷80=0.20.(2)“D ”对应扇形的圆心角的度数为:8÷80×360°=36°.(3)估计该校2000名学生中最喜欢“数学史”校本课程的人数为: 2000×0.25=500(人). (4)列表格如下:3种,所以两人恰好选中同一门校本课程的概率为:39=13.25.(2018济南,25,10分)如图,直线y =ax +2与x 轴交于点A (1,0),与y 轴交于点B (0,b ).将线段AB 先向右平移1个单位长度、再向上平移t (t >0)个单位长度,得到对应线段CD ,反比例函数y=kx (x >0)的图象恰好经过C 、D 两点,连接AC 、B D . (1)求a 和b 的值;(2)求反比例函数的表达式及四边形ABDC 的面积;(3)点N 在x 轴正半轴上,点M 是反比例函数y =kx (x >0)的图象上的一个点,若△CMN是以CM 为直角边的等腰直角三角形时,求所有满足条件的点M 的坐标.第25题图 第25题备用图【解析】解:(1)将点A (1,0)代入y =ax +2,得0=a +2.∴a =-2. ∴直线的解析式为y =-2x +2.将x =0代入上式,得y =2.∴b =2.∴点B (0,2). (2)由平移可得:点C (2,t )、D (1,2+t ). 将点C (2,t )、D (1,2+t )分别代入y =kx,得⎩⎨⎧t =k 22+t =k 1.解得⎩⎨⎧k =4t =2. ∴反比例函数的解析式为y =4x ,点C (2,2)、点D (1,4).分别连接BC 、AD (如答案图1).∵B (0,2)、C (2,2),∴BC ∥x 轴,BC =2. ∵A (1,0)、D (1,4),∴AD ⊥x 轴,AD =4. ∴BC ⊥A D .∴S 四边形ABDC =12×BC ×AD =12×2×4=4.第25题答案图1(3)①当∠NCM =90°、CM =CN 时(如答案图2所示),过点C 作直线l ∥x 轴,交y 轴于点G .过点M 作MF ⊥直线l 于点F ,交x 轴于点H .过点N 作NE ⊥直线l 于点E . 设点N (m ,0)(其中m >0),则ON =m ,CE =2-m . ∵∠MCN =90°,∴∠MCF +∠NCE =90°. ∵NE ⊥直线l 于点E ,∴∠ENC +∠NCE =90°.∴∠MCF =∠EN C .又∵∠MFC =∠NEC =90°,CN =CM ,∴△NEC ≌△CFM . ∴CF =EN =2,FM =CE =2-m .∴FG =CG +CF =2+2=4.∴x M =4. 将x =4代入y =4x,得y =1.∴点M (4,1).l第25题答案图2 第25题答案图3 ②当∠NMC =90°、MC =MN 时(如答案图3所示),过点C 作直线l ⊥y 轴与点F ,则CF =x C =2.过点M 作MG ⊥x 轴于点G ,MG 交直线l 与点E ,则MG ⊥直线l 于点E ,EG =y C =2. ∵∠CMN =90°,∴∠CME +∠NMG =90°.∵ME ⊥直线l 于点E ,∴∠ECM +∠CME =90°.∴∠NMG =∠ECM .又∵∠CEM =∠NGM =90°,CM =MN ,∴△CEM ≌△MGN .∴CE =MG ,EM =NG .设CE =MG =a ,则y M =a ,x M =CF +CE =2+a .∴点M (2+a ,a ).将点M (2+a ,a ) 代入y =4x ,得a =42+a.解得a 1=5-1,a 2=-5-1.∴x M=2+a=5+1.∴点M(5+1,5-1).综合①②可知:点M的坐标为(4,1)或(5+1,5-1).26.(2018济南,26,12分)在△ABC中,AB=AC,∠BAC=120°,以CA为边在∠ACB的另一侧作∠ACM=∠ACB,点D为射线BC上任意一点,在射线CM上截取CE=BD,连接AD、DE、AE.(1)如图1,当点D落在线段BC的延长线上时,直接写出∠ADE的度数;(2)如图2,当点D落在线段BC(不含边界)上时,AC与DE交于点F,请问(1)中的结论是否仍成立?如果成立,请给出证明;如果不成立,请说明理由;(3)在(2)的条件下,若AB=6,求CF的最大值.第26题图1 第26题图2【解析】解:(1) ∠ADE=30°.(2) (1)中的结论是否还成立证明:连接AE(如答案图1所示).∵∠BAC=120°,AB=AC,∴∠B=∠ACB=30°.又∵∠ACM=∠ACB,∴∠B=∠ACM=30°.又∵CE=BD,∴△ABD≌△ACE.∴AD=AE,∠1=∠2.∴∠2+∠3=∠1+∠3=∠BAC=120°.即∠DAE=120°.又∵AD =AE ,∴∠ADE =∠AED =30°.答案图1 答案图2(3) ∵AB =AC ,AB =6,∴AC =6. ∵∠ADE =∠ACB =30°且∠DAF =∠CAD ,∴△ADF ∽△AC D.∴AD AC =AF AD .∴AD 2=AF ·A C .∴AD 2=6AF .∴AF =AD 26.∴当AD 最短时,AF 最短、CF 最长.易得当AD ⊥BC 时,AF 最短、CF 最长(如答案图2所示),此时AD =12AB =3.∴AF 最短=AD 26=326=32.∴CF 最长=AC - AF 最短=6-32=92.27.(2018济南,27,12分)如图1,抛物线y =ax 2+bx +4过A (2,0)、B (4,0)两点,交y 轴于点C ,过点C 作x 轴的平行线与不等式抛物线上的另一个交点为D ,连接AC 、B C .点P 是该抛物线上一动点,设点P 的横坐标为m (m >4).(1)求该抛物线的表达式和∠ACB 的正切值; (2)如图2,若∠ACP =45°,求m 的值;(3)如图3,过点A 、P 的直线与y 轴于点N ,过点P 作PM ⊥CD ,垂足为M ,直线MN 与x 轴交于点Q ,试判断四边形ADMQ 的形状,并说明理由.第27题图1 第27题图2 第27题图3【解析】 解:(1)将点A (2,0)和点B (4,0)分别代入y =ax 2+bx +4,得⎩⎨⎧0=4a +2x +40=16a +4b +4.解得⎩⎪⎨⎪⎧a =12b =-3.∴该抛物线的解析式为y =12x 2-3x +4.将x =0代入上式,得y =4.∴点C (0,4),OC =4.在Rt △AOC 中,AC =OA 2+OC 2=22+42=2 5.设直线AC 的解析式为y =kx +4,将点A (2,0)代入上式,得0=2k +4.解得k =-2. ∴直线AC 的解析式为y =-2x +4.同理可得直线BC 的解析式为y =-x +4. 求tan ∠ACB 方法一:过点B 作BG ⊥CA ,交CA 的延长线于点G (如答案图1所示),则∠G =90°.∵∠COA =∠G =90°,∠CAO =∠BAG ,∴△GAB ∽△OA C.∴BG AG =OC OA =42=2.∴BG =2AG . 在Rt △ABG 中,∵BG 2+AG 2=AB 2,∴(2AG )2+AG 2=22.AG =25 5.∴BG =455,CG =AC +AG =25+255=125 5.在Rt △BCG 中,tan ∠ACB =BG CQ =4551255=13.第27题答案图1 第27题答案图2求tan ∠ACB 方法二:过点A 作AE ⊥AC ,交BC 于点E (如答案图2所示),则k AE ·k AC =-1.∴-2k AE =-1.∴k AE =12.∴可设直线AE 的解析式为y =12x +m .将点A (2,0)代入上式,得0=12×2+m .解得m =-1.∴直线AE 的解析式为y =12x -1.由方程组⎩⎪⎨⎪⎧y =12x -1y =-x +4 解得⎩⎨⎧x =103y =23.∴点E (103,23). ∴AE =⎝⎛⎭⎫2-1032+⎝⎛⎭⎫0-232=235.在Rt △AEC 中,tan ∠ACB =AE AC =23525=13.求tan ∠ACB 方法三:过点A 作AF ⊥BC ,交BC 点E (如答案图3所示),则k AF ·k BC =-1. ∴-k AF =-1.∴k AF =1.∴可设直线AF 的解析式为y =x +n .将点A (2,0)代入上式,得0=2+n .解得n =-2.∴直线AF 的解析式为y =x -2.由方程组⎩⎨⎧y =x -2y =-x +4 解得⎩⎨⎧x =3y =1.∴点F (3,1).∴AF =(3-2)2+(1-0)2=2,CF =(3-0)2-(1-4)2=3 2.在Rt △AEC 中,tan ∠ACB =AF CF =232=13.第27题答案图3(2)方法一:利用“一线三等角”模型将线段AC 绕点A 沿顺时针方向旋转90°,得到线段AC ′,则 AC ′=AC ,∠C ′AC =90°,∠CC ′A =∠ACC ′=45°. ∴∠CAO +∠C ′AB =90°. 又∵∠OCA +∠CAO =90°, ∴∠OCA =∠C ′A B .过点C ′作C ′E ⊥x 轴于点E .则∠C ′EA =∠COA =90°. ∵∠C ′EA =∠COA =90°,∠OCA =∠C ′AB ,AC ′=AC ,∴△C ′EA ≌△AO C .∴C ′E =OA =2,AE =OC =4. ∴OE =OA +AE =2+4=6. ∴点C ′(6,2).设直线C ′C 的解析式为y =hx +4.将点C ′(6,2)代入上式,得2=6h +4.解得h =-13.∴直线C ′C 的解析式为y =-13x +4.∵∠ACP =45°,∠ACC ′=45°,∴点P 在直线C ′C 上.设点P 的坐标为(x ,y ),则x 是方程12x 2-3x +4=-13x +4的一个解.将方程整理,得3x 2-14x =0.解得x 1=163,x 2=0(不合题意,舍去).将x 1=163代入y =-13x +4,得y =209.∴点P 的坐标为(163,209).第27题答案图4 第27题答案图5(2)方法二:利用正方形中的“全角夹半角”模型.过点B 作BH ⊥CD 于点H ,交CP 于点K ,连接AK .易得四边形OBHC 是正方形. 应用“全角夹半角”可得AK =OA +HK .设K (4,h ),则BK =h ,HK =HB -KB =4-h ,AK =OA +HK =2+(4-h )=6-h .在Rt △ABK 中,由勾股定理,得AB 2+BK 2=AK 2.∴22+ h 2=(6-h )2.解得h =83.∴点K (4,83).设直线CK 的解析式为y =hx +4.将点K (4,83)代入上式,得83=4h +4.解得h =-13.∴直线CK 的解析式为y =-13x +4.设点P 的坐标为(x ,y ),则x 是方程12x 2-3x +4=-13x +4的一个解.将方程整理,得3x 2-14x =0.解得x 1=163,x 2=0(不合题意,舍去).将x 1=163代入y =-13x +4,得y =209.∴点P 的坐标为(163,209).(3)四边形ADMQ 是平行四边形.理由如下: ∵CD ∥x 轴,∴y C =y D =4.将y =4代入y =12x 2-3x +4,得 4=12x 2-3x +4.解得x 1=0,x 2=6.∴点D (6,4).根据题意,得P (m ,12m 2-3m +4),M (m ,4),H (m ,0).∴PH =12m 2-3m +4),OH =m ,AH =m -2,MH =4.①当4<m <6时(如答案图5所示),DM =6-m∵△OAN ∽△HAP ,∴ON PH =OA AH .∴ON 12m 2-3m +4=2m -2.∴ON =m 2-6m +8m -2=(m -4)(m -2)m -2=m -4.∵△ONQ ∽△HMP ,∴ON HM =OQ HQ .∴ON 4=OQm -OQ .∴m -44=OQm -OQ.∴OQ =m -4.∴AQ =OA -OQ =2-(m -4)=6-m .∴AQ = DM =6-m .又∵AQ ∥DM ,∴四边形ADMQ 是平行四边形.第27题答案图6 第27题答案图7②当m >6时(如答案图6所示),同理可得:四边形ADMQ 是平行四边形.综合①、②可知:四边形ADMQ是平行四边形.。
