河南省罗山县楠杆高级中学2021届高三上学期第七次周考数学(文)试题 Word版含答案
2021年高三上学期期中统考数学(文)试题 含答案

2021年高三上学期期中统考数学(文)试题含答案本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分. 共 4页.满分150分,考试时间120分钟. 考试结束,将试卷答题卡交上,试题不交回.第Ⅰ卷选择题(共60分)注意事项:1.答卷前,考生务必将自己的姓名、准考证号、座号涂写在答题卡上.2.选择题每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案,不能答在试题卷上.3.第Ⅱ卷试题解答要作在答题卡各题规定的矩形区域内,超出该区域的答案无效.一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合要求的.1.若,则=A. B. C. D.2.已知集合,,则A. B. C. D.3.已知向量, ,如果向量与垂直,则的值为A. B. C. D.4.函数的图像为5.如果若干个函数的图象经过平移后能够重合,则称这些函数为“同簇函数”.给出下列函数:①;②;③;④.其中“同簇函数”的是A.①②B.①④C.②③D.③④6.若数列的前项和,则数列的通项公式A. B. C. D.7.已知命题;命题,则下列命题中为真命题的是A. B. C. D.8.已知,满足约束条件,若的最小值为,则A. B. C. D.9.在中,角的对边分别为,且.则A.B.C.D.10.函数是上的奇函数,,则的解集是A . B. C. D.11.定义在上的偶函数满足且,则的值为A. B. C. D.12.设函数,若实数满足则A. B.C. D.第Ⅱ卷非选择题(共90分)二、填空题:本大题共4小题,每小题4分,共16分.把答案填在答题卡中相应题的横线上.13.已知一元二次不等式的解集为,则的解集为. ()14. .15.设正数满足, 则当 ______时, 取得最小值.16.在中,,,,则.三、解答题:本大题共6小题,共74分.把解答写在答题卡中.解答应写出文字说明,证明过程或演算步骤.17.(本小题满分12分)已知,.(Ⅰ)若,求的值;(Ⅱ)设,若,求的值.18.(本小题满分12分)已知函数和的图象关于轴对称,且.(Ⅰ)求函数的解析式;(Ⅱ)当时,解不等式.19. (本小题满分12分)设是首项为,公差为的等差数列,是其前项和.(Ⅰ) 若,求数列的通项公式;(Ⅱ) 记,,且成等比数列,证明:().20.(本小题满分12分)如图,游客在景点处下山至处有两条路径.一条是从沿直道步行到,另一条是先从沿索道乘缆车到,然后从沿直道步行到.现有甲、乙两位游客从处下山,甲沿匀速步行,速度为.在甲出发后,乙从乘缆车到,在处停留后,再从匀速步行到.假设缆车匀速直线运动的速度为,索道长为,经测量,,.(Ⅰ) 求山路的长;(Ⅱ) 假设乙先到,为使乙在处等待甲的时间不超过分钟,乙步行的速度应控制在什么范围内?21.(本小题满分12分)新晨投资公司拟投资开发某项新产品,市场评估能获得万元的投资收益.现公司准备制定一个对科研课题组的奖励方案:奖金(单位:万元)随投资收益(单位:万元)的增加而增加,且奖金不低于万元,同时不超过投资收益的.(Ⅰ)设奖励方案的函数模型为,试用数学语言表述公司对奖励方案的函数模型的基本要求.(Ⅱ)下面是公司预设的两个奖励方案的函数模型: C B A①;②试分别分析这两个函数模型是否符合公司要求.22.(本小题满分14分)设函数(Ⅰ)当时,求函数的最大值;(Ⅱ)令(),其图象上存在一点,使此处切线的斜率,求实数的取值范围;(Ⅲ)当,时,方程有唯一实数解,求的值.xx11文倾向数学参考答案及评分标准一、二、13. 14. 15. 16.三、17解: (Ⅰ)∵∴又∵,……3分 ∴ , ………………5分∴.…………………6分(Ⅱ)∵a 2b (2cos 2cos ,2sin 2sin )(2,0)αβαβ+=++= ∴即 …………………8分两边分别平方再相加得: ∴ ∴ ……10分∵且 ∴ …………………12分18.解:(Ⅰ)设函数图象上任意一点,由已知点关于轴对称点一定在函数图象上…………………2分代入,得 …………………4分(Ⅱ)由整理得不等式为等价……………………6分当,不等式为,解为………………7分当,整理为,解为……………………9分当,不等式整理为解为.……………………11分综上所述,当,解集为;当,解集为;当,解集为.…………12分19解(Ⅰ)因为是等差数列,由性质知,…………2分所以是方程的两个实数根,解得,………4分∴或即或.……………6分(Ⅱ)证明:由题意知∴∴ …………7分∵成等比数列,∴ ∴ …………8分∴ ∴ ∵ ∴ ∴…10分∴a n a n n na d n n na S n 222)1(2)1(=-+=-+= ∴左边= 右边=∴左边=右边∴()成立. ……………12分20解: (Ⅰ) ∵,∴∴, …………………2分∴[]6563sin cos cos sin sin sin sin =+=+=+-=C A C A C A C A B )()(π …………4分 根据得所以山路的长为米. …………………6分(Ⅱ)由正弦定理得() …………8分甲共用时间:,乙索道所用时间:,设乙的步行速度为 ,由题意得,………10分整理得∴为使乙在处等待甲的时间不超过分钟,乙步行的速度应控制在内. …………………12分21.解:(Ⅰ)由题意知,公司对奖励方案的函数模型的基本要求是:当时,①是增函数;②恒成立;③恒成立………3分(Ⅱ)①对于函数模型:当时,是增函数,则显然恒成立 ……4分而若使函数在上恒成立,整理即恒成立,而,∴不恒成立.故该函数模型不符合公司要求. ……7分②对于函数模型:当时,是增函数,则.∴恒成立. ………8分设,则. 当时,()24lg 12lg 1lg 10555e e e g x x --'=-≤=<,所以在上是减函数, ……10分从而.∴,即,∴恒成立.故该函数模型符合公司要求. ……12分22.解:(Ⅰ)依题意,的定义域为,当时,,……………………2分由 ,得,解得;由 ,得,解得或.,在单调递增,在单调递减;所以的极大值为,此即为最大值……………………4分(Ⅱ),则有在上有解, ∴≥, ………6分所以 当时,取得最小值……………8分(Ⅲ)因为方程有唯一实数解,所以有唯一实数解,……9分 设,则,,所以由得,由得,所以在上单调递增,在上单调递减, . ……………11分若有唯一实数解,则必有11111()ln 011111m g e m m m m m e-=+=⇒=⇒=+---- 所以当时,方程有唯一实数解. ………14分38104 94D8 铘31576 7B58 筘27026 6992 榒•[22646 5876 塶z25325 62ED 拭27919 6D0F 洏237742 936E 鍮24070 5E06 帆33277 81FD 臽h+。
2021年高三上学期周考(12.4)文数试题 含答案

2021年高三上学期周考(12.4)文数试题含答案一、选择题.1.下列直线中与直线平行的一条是()A. B.C. D.2.过点和的直线的斜率为1,则实数的值为()A.1 B.2 C.1或4 D.1或23.如果,那么直线不经过的象限是()A.第一象限 B.第二象限 C.第三象限 D.第四象限4.已知等边的两个顶点,且第三个顶点在第四象限,则边所在的直线方程是()A. B. C. D.5. 直线经过点,则倾斜角与直线的倾斜角互为补角的一条直线方程是()A. B. C. D.6. 点关于轴和轴的对称的点依次是()A. B. C. D.7.已知两平行直线间的距离为3,则()A.-12 B.48 C.36 D.-12或488. 过点,且与原点距离最大的直线方程是()A. B. C. D.9.已知与是直线(为常数)上两个不同的点,则关于和的方程组的解的情况是()A.无论如何,总是无解 B.无论如何,总有唯一解C.存在,使之恰有两解 D.存在,使之有无穷多解10. 设两圆都和两坐标轴相切,且都过点,则两圆心的距离()A.4 B. C.8 D.11.直线与圆相交于两点,若,则的取值范围是()A. B. C. D.12.若圆始终平分圆的周长,则满足的关系是()A .B .C .D .二、填空题13.已知直线与直线有相同的斜率,且,则实数的值是____________.14.已知直线与两坐标轴所围成的三角形的面积不大于1,则实数的取值范围是____________. 15.已知直线恒经过一个定点,则过这一定点和原点的直线方程是____________. 16.已知实数满足,则的最小值等于 ____________. 三、解答题17.求斜率为,且与坐标轴所围成的三角形的周长是12的直线方程. 18.过点的直线被两平行线与截得的线段长,求直线的方程.19.已知方程()()()222321620m m x m m y m m R --++-+-=∈. (1)求该方程表示一条直线的条件;(2)当为何实数时,方程表示的直线斜率不存在?求出这时的直线方程; (3)已知方程表示的直线在轴上的截距为-3,求实数的值; (4)若方程表示的直线的倾斜角是45°,求实数的值.20. 中,已知,角的平分线所在的直线方程是边上高线所在的直线方程是,试求顶点的坐标 21.已知以点为圆心的圆与轴交于点,与轴交于点,其中为坐标原点. (1)求证:的面积为定值;(2)设直线与圆交于点,若,求圆的方程.22.如图,在平面直角坐标系中,点,直线,设圆的半径为1,圆心在上. (1)若圆心也在直线上,过点作圆的切线,求切线的方程; (2)若圆上存在点,使,求圆心的横坐标的取值范围.参考答案一、选择题题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 D A B C C C D A B B C B二、填空题13. 14. 且 15. 16.三、解答题17.解:设所求直线的方程为,故所求的直线方程是,即.18.解:当直线的方程为时,可验证不符合题意,故设的方程为,由解得;由解得,因为,所以,整理得,解得或.19.解:(1)当的系数不同时为零时,方程表示一条直线,令,解得;令解得.所以方程表示一条直线的条件是且.(2)由(1)易知,当时,方程表示的直线的斜率不存在,此时的方程为,它表示一条垂直于轴的直线.(3)依题意,有,所以,所以或,由(1)知所求.(4)因为直线的倾斜角是45°,所以斜率为1,故由,解得或(舍去).所以直线的倾斜角为45°时,.20.解:依条件,由,解得.因为角的平分线所在的直线方程是,所以点关于的对称点,在边所在的直线上,边所在的直线方程为,整理得,又边上高线所在的直线方程是,所以边所在的直线的斜率为.边所在的直线的方程是,整理得,联立,与,解得.21.(1)因为,圆与轴交于点,与轴交于点,所以,是直角三角,又圆心,所以,的面积为为定值.(2)直线与圆交于点,且,所以,的中垂线是斜率,由,得,则即圆半径其长为.故圆的方程是.22.解:(1)由得圆心为,∵圆的半径为1,∴圆的方程为:,显然切线的斜率一定存在,设所求圆的切线方程为,即,∴,∴,∴,∴或者,∴所求圆的切线方程为:或者即或者.(2)解:∵圆的圆心在在直线上,所以,设圆心为,则圆的方程为:,又∵,∴设为,则整理得:设为圆,∴点应该既在圆上又在圆上,即圆和圆有交点,∴,由得,由得,终上所述,的取值范围为:.35542 8AD6 論/ 27590 6BC6 毆\37413 9225 鈥36966 9066 遦32948 80B4 肴 Dj€29653 73D5 珕"z。
河南省罗山县楠杆高级中学2021届高三上学期第三次周考数学(文)试题 Word版含答案

文科数学
命题人:时间:2020.8.22
一、选择题(本大题共12小题,每小题5分,共60分)
1. ()
A. B. C. D.
2.已知集合 或 , ,则()
A. B. C. ∅D.
3.已知 ,则 ( )
A. B. C. D.
4.“a=1”是“函数 在区间[1, +∞)上为增函数”的()
∴a ,
∴y=f(x)在点(1,f(1))处的切线斜率k=f′(1) ,
又f(1)=0
故y=f(x)在点(1,f(1))处的切线方程y 即x+8y﹣1=0,
(2)若a≤2,x>1时,f′(x) 0,
∴f(x)在(1,+∞)上单调递增,f(x)>f(1)=0,符合题意,
若a>2,方程x2+(2﹣2a)+1=0的△=4a2﹣8a>0,
A.充分不必要条件B.必要不充分条件
C.充要条件D.既不充分也不必要条件
5.已知P(sin40°,-cos140°)为锐角α终边上的点,则α=()
A. 40°B. 50°C. 70°D. 80°
6.若 ,则()
A. B.
C. D.
7.已知函数 ,把函数 的图象沿 轴向左平移 个单位,得到函数 的图象,下列关于函数 的说法正确的是()
∴x2+(2﹣2a)+1=0有两个不等的根,设两根分别为x1,x2,且x1<x2,
∵x1+x2=2a﹣2,x1•x2=1,
∴0<x1<1<x2,<0,f′(x)<0,f(x)单调递减,
当x∈(1,x2)时,x2+(2﹣2a)+1<0,f′(x)<0,f(x)单调递减,
2021年高三上学期数学周练试题(文科实验班1.17) 含答案
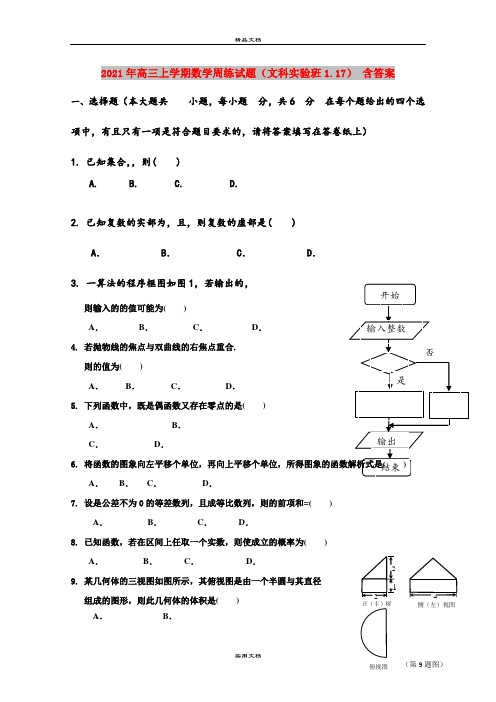
开始输入整数是否输出结束侧(左)视图4212正(主)视2021年高三上学期数学周练试题(文科实验班1.17) 含答案一、选择题(本大题共小题,每小题分,共6分在每个题给出的四个选项中,有且只有一项是符合题目要求的,请将答案填写在答卷纸上) 1. 已知集合,,则( )A. B. C. D.2. 已知复数的实部为,且,则复数的虚部是( ) A . B . C . D .3. 一算法的程序框图如图1,若输出的,则输入的的值可能为( )A .B .C .D . 4. 若抛物线的焦点与双曲线的右焦点重合, 则的值为( )A .B .C .D . 5. 下列函数中,既是偶函数又存在零点的是( ) A . B . C . D .6. 将函数的图象向左平移个单位,再向上平移个单位,所得图象的函数解析式是( )A .B .C .D .7. 设是公差不为0的等差数列,且成等比数列,则的前项和=( ) A . B . C .D .8. 已知函数,若在区间上任取一个实数,则使成立的概率为( ) A . B . C .D .9. 某几何体的三视图如图所示,其俯视图是由一个半圆与其直径 组成的图形,则此几何体的体积是( )A .B .C.D.10. 已知是内的一点,且,,若,和的面积分别为,则的最小值是( )A.B.C.D.11.如图,椭圆与双曲线有公共焦点、,它们在第一象限的交点为,且,,则椭圆与双曲线的离心率的倒数和为( )A.2B.C.D.12.已知函数, 则12340292015201520152015f f f f⎛⎫⎛⎫⎛⎫⎛⎫++++⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭的值为A.B.C.D.二、填空题:(本大题共4小题,每小题5分,满分20分)13.曲线在处的切线方程为_____________.14. 若满足且的最小值为,则的值为________.15. 已知三棱锥,,, 且,则三棱锥的外接球的表面积为________.16. .函数,,,,对任意的,总存在,使得成立,则的取值范围为.三、解答题(本大题共6小题,共70分)17.(本小题满分12分)设等差数列的前n项和为,数列的前n项和为满足(I)求数列的通项公式及数列的前n项和;(Ⅱ)是否存在非零实数,使得数列为等比数列?并说明理由18.(本小题满分12分)高三某班男同学有名,女同学有名,老师按照性别进行分层抽样组建了一个人的课外兴趣小组.(1)经过一个月的学习、讨论,这个兴趣小组决定选出两名同学做某项实验,方法是先从小组里选出一名同学做实验,该同学做完后,再从小组内剩下的同学中选一名同学做实验,求选出的两名同学中恰有一名女同学的概率;(2)试验结束后,第一次做试验的同学得到的试验数据为,第二次做试验的同学得到的试验数据为,请问哪位同学的实验更稳定?并说明理由.19.(本小题满分12分)如图,四棱锥,侧面是边长为的正三角形,且与底面垂直, 底面是的菱形,为的中点.(1) 在棱上是否存在一点,使得?若存在,指出点的位置并证明;若不存在,请说明理由; (2) 求点到平面的距离.20.(本小题满分12分) 已知圆:关于直线对称的圆为.(1)求圆的方程;(2)过点作直线与圆交于两点,是坐标原点.设,是否存在这样的直线,使得四边形的对角线相等?若存在,求出所有满足条件的直线的方程;若不存在,请说明理由.21.(本题满分12分) 设函数,.其中(1)设,求函数在上的值域;(2)证明:对任意正数,存在正数,使不等式成立.请考生从第(22)、(23)二题中任选一题作答。
2021年高三第7周综合练习卷数学文试题 含答案

2021年高三第7周综合练习卷数学文试题含答案一、选择题(本大题共10小题,每小题5分,满分50分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1、函数的定义域为()A. B. C. D.2、已知复数(其中,,是虚数单位),则的值为()A.B.C.D.3、如果函数的最小正周期为,则的值为()A.B.C.D.4、在中,,,,在上任取一点,使为钝角三角形的概率为()A.B.C.D.5、如图是一个空间几何体的三视图,则该几何体的侧面积为()A.B.图1 C.D.6、在平面直角坐标系中,若不等式组表示的平面区域的面积为,则实数的值为()A.B.C.D.7、已知幂函数在区间上单调递增,则实数的值为()A.B.C.或D.或8、已知两个非零向量与,定义,其中为与的夹角.若,,则的值为()A.B.C.D.9、已知函数,对于任意正数,是成立的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件10、已知圆,点是圆内一点,过点的圆的最短弦所在的直线为,直线的方程为,那么()A.,且与圆相离B.,且与圆相切C.,且与圆相交D.,且与圆相离二、填空题(本大题共5小题,考生作答4小题,每小题5分,满分20分.)(一)必做题(11~13题)11、若函数是偶函数,则实数的值为 . 12、已知集合,,若,则实数的取值范围为 .13、两千多年前,古希腊毕达哥拉斯学派的数学家曾经在沙滩上研究数学问题,他们在沙滩上画点或用小石子来表示数,按照点或小石子能排列的形状对数进行分类,如图中的实心点个数,,,,,被称为五角形数,其中第个五角形数记作,第个五角形数记作,第个五角形数记作,第个五角形数记作,,若按此规律继续下去,则 ,若,则 .(二)选做题(14、15题,考生只能从中选做一题)14、(几何证明选讲选做题)如图,圆的半径为,点是弦的中点,,弦过点,且,则的长为 . 15、(坐标系与参数方程选做题)在平面直角坐标系中,已知直线与曲线的参数方程分别为(为参数)和(为参数),若与相交于、两点,则 .三、解答题(本大题共2小题,共26分.解答应写出文字说明、证明过程或演算步骤.) 16、(本小题满分12分)已知函数. 求的值; 若,求的值.5 12 122 图217、(本小题满分14分)如图所示,在三棱锥中,,平面平面,于点,,,.求三棱锥的体积;证明:为直角三角形.图4高三文科数学综合练习卷(7)参考答案一、选择题(本大题共10小题,每小题5分,满分50分.在每小题给出的四个选项中,只有一项是符合题目要求的.)(一)必做题(11~13题)11、12、13、(二)选做题(14、15题,考生只能从中选做一题)14、15、三、解答题(本大题共2小题,共26分.解答应写出文字说明、证明过程或演算步骤.)16、(1)解:……………………………………………………1分 (3)分.…………………………………………………4分(2)解法1:因为……………………………………5分……………………………………6分.………………………………………7分所以,即.①因为,②由①、②解得.…………………………………………………………9分所以……………………………………………………11分.……………………………………………12分解法2:因为……………………………5分……………………………………………6分.…………………………………………7分所以…………………………………………………9分……………………………………………………10分……………………………………………………11分.…………………………………………………12分17、(1)证明:因为平面平面,平面平面,平面,,所以平面.………………………………………2分记边上的中点为,在△中,因为,所以.因为,,所以.……………………………………4分所以△的面积.……………………………………5分因为,所以三棱锥的体积.………7分(2)证法1:因为,所以△为直角三角形.因为,,所以.………9分连接,在△中,因为,,,所以.……10分由(1)知平面,又平面,所以.在△中,因为,,,所以.……………………………………12分在中,因为,,,所以.……………………………………………………………13分所以为直角三角形.…………………………………………………………14分证法2:连接,在△中,因为,,,所以.…………8分在△中,,,,所以,所以.……10分由(1)知平面,因为平面,所以.因为,所以平面.………………………………………………………………12分因为平面,所以.所以为直角三角形.……………………………………………………14分32248 7DF8 緸34396 865C 虜N22256 56F0 困28954 711A 焚32079 7D4F 絏27614 6BDE 毞20024 4E38 丸Rs26444 674C 杌21894 5586 喆。
河南省罗山县楠杆高中高三数学试题 doc

河南省罗山县楠杆高中高三数学试题(文科)第1-7章第Ⅰ卷 共 60分一.选择题(5×12=60分)1.设命题p :{x | |x |>1};命题q :{x | x 2+ 2x –3>0},则p ⌝是q ⌝的( ) A .充分不必要条件 B .必要不充分条件C .充要条件 D .即不充分也不必要条件 2.若0a >,0b >,则以下不等式中不.恒成立的是( )A 、11()()4a b a b ++≥B 、3322a b ab +≥C 、22222a b a b ++≥+D 3.函数()3sin(2)3f x x π=-的图象为C ,如下结论中错误..的是( ) A. 图象C 关于直线1112x π=对称B. 图象C 关于点203π(,)对称 C. 函数()f x 在区间51212ππ(-,)内是增函数 D. 由3sin 2y x =的图象向右平移3π个单位长度可以得到图象C4.在△ABC 中,角A 、B 、C 的对边分别为a 、b 、c ,若222()tan a c b B +-=,则角B 的值为( )A.6πB.3πC.6π或56πD.3π或23π5.将函数3log y x =的图像按向量a 平移后,得到函数32log 27x y +=的图像,则向量a =( )A. ()2,3 B. ()2,3- C ()2,3-- D. ()2,3-6.已知)(,n n n a a n a a -==+111,则数列{}n a 的通项公式=na ( )A. 12-nB. 11-+n n n )(C. 2n D. n7.设椭圆的两个焦点为F 1、F 2,如果过点F 1的直线被椭圆截得的最短线段MN 的长为532,且ΔMF 2N 的周长为20,则椭圆的离心率为 ( )A.522 B.517C.54D.538.已知数列4,,,121--a a 成等差数列, 4,,,1321--b b b 成等比数列,则212b a a -的值为( )A 、21 B 、—21 C 、21或—21 D 、41 9.在R 上定义运算).1(:y x y x -=⊗⊗若不等式1)()(<+⊗-a x a x 对任意实数x 成立,则( )A.11<<-aB.20<<aC.2321<<-a D.2123<<-a10.0)2(,0)(,0,),0)((=->'<∈≠f x f x R x x x f 且时当是奇函数,则不等式0)(>x f 的解集是( ) A .(—2,0) B .),2(+∞ C .),2()0,2(+∞- D .),2()2,(+∞--∞ 11.已知直线12:(3)(4)10,:2(3)230,l k x k y l k x y -+-+=--+=与平行,则k 得值是( )A. 1或3B.1或5C.3或5D.1或212.中心在原点,焦点在x 轴上的双曲线的实轴与虚轴相等,一个焦点到一条渐近线的距离为2,则双曲线方程为( )A .x 2-y 2=2 B .x 2-y 2=2 C . x 2-y 2=1 D .x 2-y 2=21第Ⅱ卷 共90分二.填空题(4×5=20)13.在锐角ABC ∆中,1,2,BC B A ==则cos AC A的值等于14.数列{a n }满足2112333 (32)n n na a a a -++++=,则n a =15.在平面直角坐标系xoy 中,已知△ABC 的顶点A (-4,0)和C(4,0),顶点B 在椭圆192522=+y x 上, 则=+BC A sin sin sin __ ____。
2021年高三上学期数学周练试卷(文科实验班12.29) 含答案

2021年高三上学期数学周练试卷(文科实验班12.29)含答案一、选择题(本大题共小题,每小题分,共5分在每个题给出的四个选项中,有且只有一项是符合题目要求的,请将答案填写在答卷纸上)1、过点(4,0)且斜率为的直线交圆于A,B两点,C为圆心,则的值为()A、6B、8C、D、42、已知数列{}为等差数列,是它的前n项和,若,,则=()A、32B、36C、40D、423、已知双曲线的一条渐近线方程是,则该双曲线的离心率等于()A、 B、C、 D、4、满足约束条件的目标函数的最大值是()A、-6B、e+1C、0D、e-15、设定义域为R的函数,则关于x的方程有5个不同的实数解,则=()A、B、C、2 D、16、点A是抛物线与双曲线的一条渐近线的交点(异于原点),若点A到抛物线的准线的距离为,则双曲线的离心率等于()A. B.2 C. D.47、已知符号函数,则函数的零点个数为()A.1 B.2 C.3 D.48、有下列命题:①在函数的图象中,相邻两个对称中心的距离为;②“且”是“”的必要不充分条件;③已知命题对任意的,都有,则“是:存在,使得”;④在中,若,则角等于或。
其中所有真命题的个数是()A.1 B.2 C.3 D.49.设集合,,函数若,且,则的取值范围是A.(]B. (]C. D .()10设集合A n ={x|(x -1)(x -n 2-4+ln n)<0},当n 取遍区间(1,3)内的一切实数,所有的集合A n 的并集是( )A .(1,13-ln 3)B .(1,6)C .(1,+∞)D .(1,2)二填空题(共6题,每题5分,共30分)11已知(1+x)+(1+x)2+…+(1+x)n =a 0+a 1x +a 2x 2+…+a n x n ,且a 1+a 2+…+a n -1=29-n ,则n =________12、早平面直角坐标系中中,直线是曲线的切线,则当时,实数的最小值是 -213、已知函数,。
2021年高三数学上学期周考(七)试题 理

2021年高三数学上学期周考(七)试题理本试卷共22小题,满分150分。
考试用时120分钟。
注意事项:1.答卷前,考生务必用黑色字迹的钢笔或签宇笔将自己的姓名和考生号、试室号、座位号填写在答题卡上。
用2B铅笔将试卷类型填涂在答题卡相应位置上。
将条形码横贴在答题卡右上角“条形码粘贴处”。
2.选择题每小题选出答案后,用2B铅笔把答题卡上对应题目选项的答案信息点涂黑;如需改动,用橡皮擦干净后,再选涂其他答案。
答案不能答在试卷上。
3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液。
不按以上要求作答的答案无效。
4.作答选做题时,请先用2B铅笔填涂选做题的题组号对应的信息点,再作答。
漏涂、错涂、多涂的,答案无效。
5.考生必须保持答题卡的整洁。
考试结束后,将试卷和答题卡一并交回。
一、选择题:本大题共10小题,每小题5分,满分50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 定义集合运算:.设,则集合的所有元素之和为()A.0;B.2;C.3;D.62. 复数等于()A.1+iB.-1+iC.1-iD.-1-i3. 把曲线y cos x+2y-1=0先沿x轴向右平移个单位,再沿y轴向下平移1个单位,得到的曲线方程是()A.(1-y)sin x+2y-3=0B.(y-1)sin x+2y-3=0C.(y+1)sin x+2y+1=0D.-(y+1)sin x+2y+1=04. 在区间上随机取一个数,的值介于0到之间的概率为()A. B. C. D.5. 等差数列的前n项和为,且 =6,=4,则公差d等于A.1 B C.- 2 D 36. 若a<0,>1,则 ( )A.a>1,b>0 B.a>1,b<0 C. 0<a<1, b>0 D. 0<a<1, b<07. 若且,则下列不等式恒成立的是()A. B. C. D.8.我省高中学校自实施素质教育以来,学生社团得到迅猛发展.某校高一新生中的五名同学打算参加“春晖文学社”、“舞者轮滑俱乐部”、“篮球之家”、“围棋苑”四个社团.若每个社团至少有一名同学参加,每名同学至少参加一个社团且只能参加一个社团,且同学甲不参加“围棋苑”,则不同的参加方法的种数为()A.72 B.108 C.180 D.2169. 若函数的零点与的零点之差的绝对值不超过0.25,则可以是A. B.C. D.10.在△中,=2,∠=120°,则以A,B为焦点且过点的双曲线的离心率为()A.B.C.D.二、填空题:本大题共6小题,考生作答5小题,每小题5分,满分25分.(一)必做题(11~13题)9. 若函数f(x)=a-x-a(a>0且a1)有两个零点,则实数a的取值范围是 .10. 设某几何体的三视图如下(尺寸的长度单位为m)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
楠杆高中2020-2021高三上学期周考试卷(七)
文科数学参考答案
1、选择题
BCACD CADDB AB
2、填空题
13. 14.100 15. 16. 或8
3、解答题
17解:(1)由已知得 ;
由 解得 ,所以
(2)由题意 ,解得
18.解:(1)由已知 ,∴ ,
所以当且仅当 时, 取得最大值 .
此时, 的面积
所以 的面积的最大值为
22.解:(1)由题知 的定义域为 .
又 ,则 .
又因为 ,所以切点为 .
所以 ,
解得 .
(2)当 时, .
当 时,不等式 恒成立
即不等式 , 恒成立.
设 , ,
则 .
因为 ,
所以 .
所以 在 上单调递减,
从而 .
要使原不等式恒成立,即 恒成立,
∴ , ,
∵ ,∴ 为单调递增函数.
(2)∵ ,∴ ,
而 为奇函数,∴ ,
∵ 为单调递增函数,∴ ,
∴ ,∴ ,∴ .
19解:1)因为 ,所以 ,又 ,
则 ,即 或 (舍).
所以 ,解得 ,
所以 .
(2)因为 ,所以 ,
所以 .
20.解f(x)= +cos 2x=sin 2x+cos 2x= sin .
故 .
即 的取值范围为 .
lg(x101+x102+…+x200)=.
15.,若 ,
且 , , 成等比数列,则 .
16.已知直线 与曲线 和曲线 均相切,
则 .
三、解答题(本大题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。)
17.(本小题10分)已知集合 ,集合
(1)求A∩B;
A. B. C. D.
12.已知函数 与 的图象上存在关于 轴对称的点,则实数 的取值范围是()
A. B. C. D.
二、填空题(本大题共4小题,每小题5分,共20分.将答案填在题后的横线上.)
13.若 ,则 .
14.已知数列{xn}满足:lgxn+1=1+lgxn(n∈N+),且x1+x2+…+x100=1,则
6.指数函数 ( ,且 )在 上是减函数,则函数 在其定义域上的单调性为()
A.单调递增
B.单调递减
C.在 上递增,在 上递减
D.在 上递减,在 上递增
7.把函数 图象上各点的横坐标缩短到原来的 倍(纵坐标不变),
再将图象向右平移 个单位,那么所得图象的一条对称轴方程为( )
A. B. C. D.
8.若 , , ,则有()
(1)函数f(x)的最小正周期T= =π,
令2kπ+ ≤2x+ ≤2kπ+ ,k∈Z,则2kπ+ ≤2x≤2kπ+ ,k∈Z,故kπ+ ≤x≤kπ+ ,k∈Z,
所以函数f(x)的单调递减区间为 (k∈Z).
(2)图象如下:
21.解:(1)由正弦定理及
得
所以
又因为 ,所以
(2)由余弦定理,得 ,即
因为 ,
(2)若集合 ,且 ,求实数 的取值范围.
18. (本小题满分12分)已知函数 为奇函数.
(1)判断 的单调性并证明;
(2)解不等式 .
19.(本小题满分12分)已知等比数列 的公比 ,其前 项和为 ,且 , 与 的等差中项为 .
(1)求数列 的通项公式;
(2)设 ,数列 的前 项和为 ,求 .
20.(本小题满分12分)已知函数 .
(1)求函数f(x)的最小正周期和单调递减区间;
(2)在所给坐标系中画出函数在区间 的图象(只列表作图不写过程).
21 .(本小题满分12分)在 中,角 对边分别为 ,已知
(1)求 的大小;
(2)若 ,求 面积的最大值.
22.(本小题满分12分)已知函数 , .
(1)若 的图像在 处的切线经过点 ,求 的值;
A. B. C. D.
9 .已知函数f(x)= 若|f(x)|≥ax,则a的取值范围是().
A.(-∞,0]B.(-∞,1]C.[-2,1]D.[-2,0]
10.已知函数 ,若函数 在 上存在零点,则实数 的取值范围是()
A. B. C. D.
11.在 中, 是线段 上靠近 的三等分点, 是线段 的中点, 与 交于 点若 ,则 的值分别为()
2.若命题 : ,则 为()
A. B.
C. D.
3.已知向量 , , ,则“ ”是“ ”的()
A.充要条件B.充分不必要条件
C.必要不充分条件D.既不充分也不必要条件
4.记等差数列 的前 项和为 ,已知 ,则 ()
A. B. C. D.
5.已知变量 , 满足约束条件 则 的最大值为()
A.2B.3C.4D.6
楠杆高中2020-2021高三上学期周考试卷(七)
文科数学
命题人:时间:2020.10.11
一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知集合A={x|lg(x-2)<1},集合B={x| -2x-3<0},则A∪B等于()
A.(2,12)B.(一l,12)C.(一l,3)D.(2,3)
