复化求积公式
合集下载
复化求积公式

h[ 2
f ( x0 )
n1
2
k 1
f ( xk )
f ( xn )]
复化梯形公式
Tn
h 2
[
f
(
x0
)
n1
2
k 1
f ( xk )
f ( xn )]
复化梯形公式
计算方法
2.复化辛浦生公式
计算方法
在每个小区间[xk1, xk ]上应用辛浦生公式得:
xk
xk 1
则
f
b
( x)dx h[ f 6
计算方法
在 每 个 小 区 间[ xk1, xk ]上 应 用 梯 形 公 式 得 :
xk xk 1
f ( x)dx
h 2
[
f
(
xk1
)
f ( xk )]
则
b
n
f (x)dx =
xk f (x)dx
a
k 1 xk1
n k 1
h[ f 2
(xk1)
f
(xk )]
计算方法
x0 x1 x2 x3
2
三、区间逐次分半求积法
计算方法
复化求积公式可有效提高计算精度,但对给定 的误差限,如何确定节点的个数,即[a,b]应多少等 份?由截断误差可以估计步长的取值情况,但需要 给出各阶导数的最大值,这往往是比较困难的,且 估计值往往偏大.
接下来,我们将考虑步长的更为实用的选取方 法.
计算方法
若用Tn及T2n分别表示将[a, b]n等分及2n等分的复化 梯形公式,则
f(x) 1 0.997 0.9896 0.976 0.95 0.936 0.908 0.877 0.841 3978 158 7267 8851 1556 8516 1925 4709
数值分析(18)复化求积法

1 2
h2
b
4
a
,
直到 T2n Tn 为止,将T2n作为积分的近似值。
数值分析
数值分析
下面推导由n到2n的复化梯形公式
给出误差限,将[a,b]n等分,步长hn
b
a n
,
用复化梯形公式:
在[xk , xk1 ]上,T1k
hn 2
(
f
( xk )
f ( xk1 ))
在[a, b]上,
T (hn ) Tn
理查逊外推算法流程 1,0
1,1 2,0
1,2 2,1 3,0
M
M
MO
1,n 2,n1 3,n2 L n1,0
数值分析
数值分析
二、龙贝格(Romberg)方法
龙贝格(Romberg)算法是将理查逊(Richardson)外推法应 用于数值积分,由低精度求积公式推出高精度求积公式的算法。
h
ba 2k
数值分析
数值分析
变步长复化梯形公式的递推公式: (由n到2n)
T2n
1 2 Tn
Hn 2
其中Tn
hn 2
(
f (a)
n1
f (b)) hn
k 1
f ( xk )
n1
H n
hn
k0
f
(
x
k
1
)
2
实际计算中的递推公式为
ba
T1
[ f (a) f (b)] 2
1
b a n1
ba
T2n 2 Tn
复 化 梯 形 公 式 的 截 断 误差 有 展 开 式
b a
f ( x)dx Tn
C2h2
chap4第2节 复化求积公式
Rn [ f ]
h (b a )
2
f ( ), (a , b)
12
如果记 M 2 max f ( x )
a xb
则有 Rn [ f ]
b
a
f ( x )dx Tn
( b a )h 12
2
M2
(b a ) 12n
2
3
M2
上式说明复化梯形公式是收敛的。
这时由
xk x k 1
得到
h h f f ( x )dx f ( xk 1 ) 4 f ( x 1 ) f ( xk ) k 2880 6 2 n
5
(4)
( k )
b
a
f ( x )dx
i 1
xk
f ( x )dx
x k 1
5 n h h (4) f ( k ) f ( x k 1 ) 4 f ( x 1 ) f ( x k ) 2880 k 1 k k 1 6 2
1
1 4 4 4 2 2 2 1 4 6 1 1 9 9
3.1230
4 )3
而梯形公式的结果为
1 x
0
1
4
2
dx
1 0 2
(
4
1 0 11
例 4.4 用复化梯形公式计算积分 I 0 e dx ,应将区间 [0,1]多少等分,才可以使其截断误差不超过 1 10 4
x
1
2
解:复化梯形公式的误差为
Rn [ f ] f ( x )dx Tn
a b
(b a ) 12n
数值分析63 复化求积公式龙贝格求积公式讲解

起来加以考虑 . 注意到每个子区间 [xk, xk+1]经过二分
只增加了一个分点
1 xk?1/ 2 ? 2 ( xk ? xk?1)
设hn=(b? a)/n, xk=a+kh n (k=0,1,? ,n),在[xk, xk+1] 上用梯形公式得
T1 ?
hn 2
?f
(
xk
)
?
f ? ( xk ? 1 )
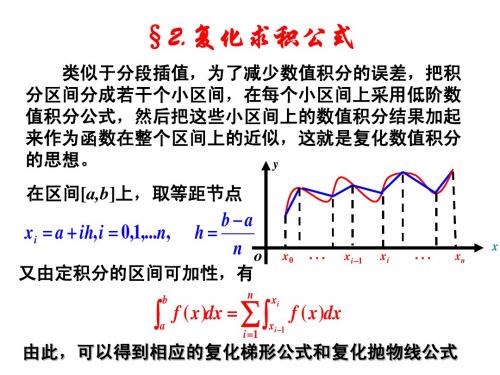
复化求积的基本想法 :
将积分区间 [a, b]n等分, 步长
h?
b
? n
a
,
分点为
xk=a+kh (k=0,1,…,n) , 则由定积分性质知
? ? ? I ?
b
n?1
f ( x )dx ?
xk?1 f ( x )d x
a
k ? 0 xk
每个子区间 上的积分
?xk?1 f ( x )dx xk
用低阶求积公式 , 然后把所有区间的 计算结果求和 ,
注2: 同样也可用 | S4m-S2m |<ε 来控制计算的精度 . 这就是下面要介绍的 龙贝格求 积公式 .
6.4 龙贝格求积公式
6.4.1 梯形公式的递推化
复化求积方法可提高求积精度,实际计算时若
精度不够可将步长逐次分半 . 设将区间 [a, b]分为n等
分,共有 n+1个分点,如果将求积区间再分一次,则 分点增至 2n+1个,我们将二分 前后两个积分值 联系
果T8=0.9456909 只有2位有效数字,而应用复化辛普 森公式计算的结果 S4= 0.9460832 却有6位有效数字 .
注:为了利用余项公式估计误差,要求 f(x)=sin x/x 的高阶导数,由于
只增加了一个分点
1 xk?1/ 2 ? 2 ( xk ? xk?1)
设hn=(b? a)/n, xk=a+kh n (k=0,1,? ,n),在[xk, xk+1] 上用梯形公式得
T1 ?
hn 2
?f
(
xk
)
?
f ? ( xk ? 1 )
复化求积的基本想法 :
将积分区间 [a, b]n等分, 步长
h?
b
? n
a
,
分点为
xk=a+kh (k=0,1,…,n) , 则由定积分性质知
? ? ? I ?
b
n?1
f ( x )dx ?
xk?1 f ( x )d x
a
k ? 0 xk
每个子区间 上的积分
?xk?1 f ( x )dx xk
用低阶求积公式 , 然后把所有区间的 计算结果求和 ,
注2: 同样也可用 | S4m-S2m |<ε 来控制计算的精度 . 这就是下面要介绍的 龙贝格求 积公式 .
6.4 龙贝格求积公式
6.4.1 梯形公式的递推化
复化求积方法可提高求积精度,实际计算时若
精度不够可将步长逐次分半 . 设将区间 [a, b]分为n等
分,共有 n+1个分点,如果将求积区间再分一次,则 分点增至 2n+1个,我们将二分 前后两个积分值 联系
果T8=0.9456909 只有2位有效数字,而应用复化辛普 森公式计算的结果 S4= 0.9460832 却有6位有效数字 .
注:为了利用余项公式估计误差,要求 f(x)=sin x/x 的高阶导数,由于
4-3复化求积公式

1 n1 min f ( x ) f ( k ) max f ( x ) a xb a xb n k 0
故存在 [a , b] 使
1 n1 f ( ) f ( k ) n k 0
所以复化梯形公式的积分余项为
h3 RTn I Tn nf ( ) 12 ba 2 h f ( ) 12 3 b a [a , b] f ( ) 2 12n
由此解得
n 6616.67
2
所以
n 79
即至少要把区间[1,2]分为79等份。
对本例题的进一步思考:h是否越小越好?
前面介绍的复化求积公式对提高精度是行之 有效的,但使用前必须给出合适的步长h。
h太小则计算量增加
误差有积累,更需计算稳定
h太大则精度不满足
(收敛性)
计算方案:事先估计法 变步长(事后估计) 自适应步长法
2.系数Ak >0,满足 Ak b a ,故方法是稳定的.
k 0
n
三、例题
x
0
f(x)
1 0.9973978
ቤተ መጻሕፍቲ ባይዱ
sin x 举例 对于函数 f ( x ) x , 1/8
试利用下表计算积分
I
1 sin
1/4
3/8 1/2 5/8 3/4 7/8
0.9896158
0.9767267 0.9588510 0.9361556 0.9088516 0.8771925
3*. 复化柯特斯公式 如果将每个小区间[xk,xk+1]四等分,内分点 依次记为 xk 1 , xk 1 , xk 3 ,
4 2 4
则相应地可得复化柯特斯公式。
数值计算方法 复化求积公式 - 复化求积公式

nn
(t
0 j0
j )dt
jk
柯
特点: 插值型的、节点等距
特 斯
存在问题: 节点较多时,高次插值的不稳定导致高阶N-
公
K
式
解决办法公:式的复不化稳求定积。
复化求积法:区间分成若干子区间,在每个子区间上用低 阶求积公式。
N=1时的牛-柯公式
1
梯 形 公 式 T b a f a f b
牛 顿 -
xk1 xk
f
( x )dx
h[ 2
f
(xk )
f
(
xk
1
)]
h3 12
f ''(k )
k [ xk , xk1]
求和可得
I
b
n1
f (x)dx
xk1 f ( x )dx
a
k0 xk
h 2
n1
[
k0
f
(
xk
)
f ( xk1)]
Rn ( f )
2
记
Tn
h 2
n1 k0
[
f
(
xk
)
f ( xk1)]
b
lim
n
T
n
a
f ( x)dx,
复 化
事实上
h n1
Tn
2
[
k0
f
(
xk
)
Hale Waihona Puke f ( xk1 )]梯 形 公
1 b a n1
ba n
2 n
f (xk )
k0
n
f ( xk ).
k 1
式 的 收
lim
第二节复化求积公式和龙贝格求积公式

Tn )
对于复化辛蒲生公式、柯特斯公式可以类似得到
I
S2n
1 42 1(S2n
Sn )
1 I C2n 43 1 (C2n Cn )
不足
收敛速度慢
应用步长逐次减半得到的复化梯形值、复化 辛蒲生值、复化柯特斯值与精确值的比较
I
T2n
1 4 1(T2n
Tn )
n1
Sn (
f
)
6
f
(a)
4
k0
f
(
x
k
1 2
)
2
k
1
f
( xk )
f
(b)
复化梯形公式(n
=
8),h
1 8
0.946083070367
T8 (
f
)
1
2
8
f
(0)
2
f
1 (
)
8
f
(
1 )
4
3 f( )
8
f
(1) 2
f (5) 8
f
(3) 4
f
(
7 8
)
f
(1)
0.945692
复化辛蒲生公式(n
=
4),h
1 4
S4 (
f
)
1 64
f
(0)
4
f (1) 8
f
(3) 8
f
(5) 8
数值分析6.3 复化求积公式、龙贝格求积公式讲解

精度不够可将步长逐次分半. 设将区间 [a, b]分为n等
分,共有n+1个分点,如果将求积区间再分一次,则
分点增至2n+1个,我们将二分前后两个积分值联系
起来加以考虑. 注意到每个子区间[xk, xk+1]经过二分
只增加了一个分点
x k 1/ 2
1 ( x k xk 1 ) 2
设hn=(ba)/n, xk=a+khn (k=0,1,,n),在[xk, xk+1]
I f ( x )dx
b a k 0 n 1 xk 1 xk
f ( x )dx
每个子区间[xk, xk+1]上的积分用梯形公式, 得
xk 1 xk
h f ( x )dx [ f ( xk ) f ( xk 1 )] 2
xk 1 xk
I
k 0
6.3 复化求积公式
从求积公式的余项的讨论中我们看到,被积函数
所用的插值多项式次数越高,对函数光滑性的要求也
越高.另一方面,插值节点的增多(n的增大),在使用
牛顿-柯特斯公式时将导致求积系数出现负数(当n≥8
时, 牛顿-柯特斯求积系数会出现负数),即牛顿-柯特
斯公式是不稳定的,不可能通过提高阶的方法来提高 求积精度.
b n 1 xk 1 xk a
I f ( x )dx
k 0
f ( x )dx
h n 1 I [ f ( xk ) 4 f ( xk 1/2 ) f ( xk 1 )] 6 k 0
n 1 n 1 h [ f (a ) 4 f ( xk 1/2 ) 2 f ( xk ) f ( b)] 6 k 0 k 1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
运算量基本 相同,都用
了9个点
= 3.138988494
S4
1 24
f
(0)
4
odd
f
( xk ) 2
even
f
( xk )
f
(1)
其中
xk
k 8
= 3.141592502
Q: 给定精度 ,如何取 n ? 例如:要求 | I Tn | ,如何判断 n = ?
例:分别用复化梯形和复化Simpson求积公式计算积分I
Sn
h [ 3
f
(a) 4
odd
k
f
(xk ) 2 f
even k
(xk )
f
(b)]
➢ 收敛速度与误差估计:
定义
若一个复化积分公式的误差满足
lim
h0
R[ f hp
]
C
且C
0,
则称该公式是 p 阶收敛的。
复化梯形公式:
R[ f ] h2 (b a) f '' ( ) h2 b f '' (x)dx /*中值定理*/
h2 (b a) 12
k 1
f (k )
n
/*中值定理*/
h2 (b a) f ( ), (a, b)
12
➢ 复化 Simpson 公式:
h
b
n
a
,
xk a k h
(k 0, ..., n)
xk1 xk
f ( x)dx
h
6
[f(xk来自)4f
(
xk
1 2
)
f ( xk1 )]
12
12 a
R[ f ] 1
h2
12
b a
f ''(x)dx 1 [ f '(b) 12
f '(a)]
2阶收敛
4阶收敛
6阶收敛
例1:计算
1
0
4 1 x2
dx 用8等分的梯形公式和4等分的Simpson公式计算
解:
1
7
T8
16
f
(0) 2
k 1
f
(xk ) f
(1)
其中
xk
k 8
§3 复合求积 /* Composite Quadrature */
高次插值有Runge 现象,故采用分段低次插值 分段低次合成的 Newton-Cotes 复合求积公式。
➢ 复合梯形公式: h b a ,
n
xk
akh
(k 0, ..., n)
在每个 [ xk1, xk ]上用梯形公式:
xk xk1
xk
xk
1 2
x k1
4
4
4
4
4
b
h
n1
n1
a
f
(x)dx
[ 6
f
(a) 4
k 0
f
(
xk
1 2
)
2
k 1
f
(xk )
f
(b)]
= Sn
R[
f
]
b
a
h 4
f
(4) ( )
180 2
注:为方便编程,可采用另一记法:令 n’ = 2n 为偶数,
这时
h b a h , n 2
xk
a k,h 有
1 sin x dx,
0x
要求误差不超过=1 106
2 解:利用max | f (k) (x) |
1
0 x 1
k 1
1.复化梯形公式
I C4 0.946083004
事后误差估 计式,可用 来判断迭代 是否停止。
§4 龙贝格积分 /* Romberg Integration */
f ( x)dx
xk
xk 2
1
[
f
(
xk
1
)
f (xk )],
k 1, ..., n
b f ( x)dx
a
nh k1 2 [ f ( xk1 )
f ( xk )]
h 2
f
(a)
2
n1 k 1
f (xk )
f (b)
= Tn
n
R[ f ]
n [ h3 k1 12
f (k )]
复化梯形公式算法简单,但精度较差,收敛速度(2阶收敛) 较慢,如何提高收敛速度?
4m
1
注:按上面规律,可以构造线性组合系数为
4m
, 1
4m
1
的新的积分公式,但当m>4时,前一个系数接近于1,后一个
系数接近于0,这样构造出的新公式与前一个公式结果差别不
大,反而增加计算量,因此实际上常做到Romberg公式为止。
