《理论力学》武清玺第五章_点的运动_习题全解
理论力学(武清玺,高教版)课后习题解答(6)

ac = aB + aCB + aCB
τ
n
(b)
作加速度矢量图,P2 为BC的瞬心,而 P2C = 9 r
∴ ω BC =
vc 3 1 ωo = rω o ⋅ = P2 C 2 9r 6
2
aCB = BC ⋅ ω BC = 3 3r ⋅ (
n
ωo
6
)2 =
3 2 rω o 12
n
将 (b) 式在BC方向线上投影: ac = a B cos 30o − aCB =
r 2 3 3 3 2 2 ωo ⋅ − rω o = rω o 3 2 12 12
8-23 解: (1) v A = OA ⋅ ω AB 杆的速度瞬心为 O, 所以 AB 的角速度为ω, 因此: v B = OB ⋅ ω = 200 × 2 = 400 mm/s ω vA
由于 aa = ae + ae + ar + ar + aC
n n
va
M
v r = rw2 = 100 × 6 = 600(mm/s)
ω2
r O
vr
ω1
α1
arτ arn
A O
τ
τ
a
n e
aC
M
ae = 3rα1 = 3 × 100 × 3 = 900mm/s ar = rα 2 = 100 × 4 = 400mm/s
y
vD D
Q v A cos ϕ = v B = OB ⋅ ω ∴ ω AD OB ⋅ w v OB ⋅ ω cos ϕ = A = = PA PA PA ⋅ cos ϕ
2 2
P
ωAD
《理论力学》武清玺第五章_点的运动_习题全解

第五章 点的运动 习题全解[习题5-1] 一点按2123+-=t t x 的规律沿直线动动(其中t 要s 计,x 以m 计).试求:(1)最初s 3内的位移;(2)改变动动方向的时刻和所在位置;(3)最初s 3内经过的路程;(4)s t 3=时的速度和加速度;(5)点在哪段时间作加速度,哪段时间作减速运动. 解:(1)求最初s 3内的位移.m x 220120)0(3=+⨯-= m x 723123)3(3-=+⨯-=)(927)0()3(m x x x -=--=-=∆ (动点的位移为9m,位移的方向为负x 方向). (2)求改变动动方向的时刻和所在位置. 改变方向时,动点的速度为零.即: 01232=-==t dtdxv , 亦即:当s t 2=时,动点改变运动方向.此时动点所在的位置为: )(1422122)2(3m x -=+⨯-= (3)求最初s 3内经过的路程.)(23716|)14(7||214|)3~2()2~0()3~0(m S S S =+=---+--=+= (4)求s t 3=时的速度和加速度1232-==t dt dx v )/(151233)3(2s m dt dx v =-⨯== t dtdv a 6== )/(1836)3(2s m a =⨯=(5)求动点在哪段时间作加速度,哪段时间作减速运动.若v 与a 同号,则动点作加速运动; 若v 与a 异号,则动点作减速运动.即: 同号时有:0)2)(2(18)4(18)6)(123(22>+-=-=-=t t t t t t t va0)2)(2(>+-t t t20<<t .即当s t 20<<时,动点作加速动动.Oxy图题25-异号时有:0)2)(2(<+-t t t2>t即当s t 2>时,动点作减速运动.[习题5-2] 已知图示机构中,l AB OA ==,a AC DM CM ===,求出t ωϕ=时,点M 的动动方程和轨迹方程。
理论力学课后答案第五章

第五章思考题5.1虚功原理中的“虚功”二字作何解释?用虚功原理理解平衡问题,有何优点和缺点?5.2 为什么在拉格朗日方程中,a θ不包含约束反作用力?又广义坐标与广义力的含义如何?我们根据什么关系由一个量的量纲定出另一个量的量纲?5.3广义动量a p 和广义速度a q &是不是只相差一个乘数m ?为什么a p 比aq &更富有意义? 5.4既然aq T &∂∂是广义动量,那么根据动量定理,⎪⎪⎭⎫ ⎝⎛∂∂αq T dt d &是否应等于广义力a θ?为什么在拉格朗日方程()14.3.5式中多出了a q T ∂∂项?你能说出它的物理意义和所代表的物理量吗?5.5为什么在拉格朗日方程只适用于完整系?如为不完整系,能否由式()13.3.5得出式()14.3.5?5.6平衡位置附近的小振动的性质,由什么来决定?为什么22s 个常数只有2s 个是独立的?5.7什么叫简正坐标?怎样去找?它的数目和力学体系的自由度之间有何关系又每一简正坐标将作怎样的运动?5.8多自由度力学体系如果还有阻尼力,那么它们在平衡位置附近的运动和无阻尼时有何不同?能否列出它们的微分方程?5.9 dL 和L d 有何区别?a q L ∂∂和aq L ∂∂有何区别? 5.10哈密顿正则方程能适用于不完整系吗?为什么?能适用于非保守系吗?为什么?5.11哈密顿函数在什么情况下是整数?在什么情况下是总能量?试祥加讨论,有无是总能量而不为常数的情况?5.12何谓泊松括号与泊松定理?泊松定理在实际上的功用如何?5.13哈密顿原理是用什么方法运动规律的?为什么变分符号δ可置于积分号内也可移到积分号外?又全变分符号∆能否这样?5.14正则变换的目的及功用何在?又正则变换的关键何在?5.15哈密顿-雅可比理论的目的何在?试简述次理论解题时所应用的步骤.5.16正则方程()15.5.5与()10.10.5及()11.10.5之间关系如何?我们能否用一正则变换由前者得出后者?5.17在研究机械运动的力学中,刘维定理能否发挥作用?何故?5.18分析力学学完后,请把本章中的方程和原理与牛顿运动定律相比较,并加以评价.第五章思考题解答5.1 答:作.用于质点上的力在任意虚位移中做的功即为虚功,而虚位移是假想的、符合约束的、无限小的.即时位置变更,故虚功也是假想的、符合约束的、无限小的.且与过程无关的功,它与真实的功完全是两回事.从∑⋅=ii i r F W ρρδδ可知:虚功与选用的坐标系无关,这正是虚功与过程无关的反映;虚功对各虚位移中的功是线性迭加,虚功对应于虚位移的一次变分.在虚功的计算中应注意:在任意虚过程中假定隔离保持不变,这是虚位移无限小性的结果.虚功原理给出受约束质点系的平衡条件,比静力学给出的刚体平衡条件有更普遍的意义;再者,考虑到非惯性系中惯性力的虚功,利用虚功原理还可解决动力学问题,这是刚体力学的平衡条件无法比拟的;另外,利用虚功原理解理想约束下的质点系的平衡问题时,由于约束反力自动消去,可简便地球的平衡条件;最后又有广义坐标和广义力的引入得到广义虚位移原理,使之在非纯力学体系也能应用,增加了其普适性及使用过程中的灵活性.由于虚功方程中不含约束反力.故不能求出约束反力,这是虚功原理的缺点.但利用虚功原理并不是不能求出约束反力,一般如下两种方法:当刚体受到的主动力为已知时,解除某约束或某一方向的约束代之以约束反力;再者,利用拉格朗日方程未定乘数法,景观比较麻烦,但能同时求出平衡条件和约束反力.5.2 答 因拉格朗日方程是从虚功原理推出的,而徐公原理只适用于具有理想约束的力学体系虚功方程中不含约束反力,故拉格朗日方程也只适用于具有理想约束下的力学体系,αθ不含约束力;再者拉格朗日方程是从力学体系动能改变的观点讨论体系的运动,而约束反作用力不能改变体系的动能,故αθ不含约束反作用力,最后,几何约束下的力学体系其广义坐标数等于体系的自由度数,而几何约束限制力学体系的自由运动,使其自由度减小,这表明约束反作用力不对应有独立的广义坐标,故αθ不含约束反作用力.这里讨论的是完整系的拉格朗日方程,对受有几何约束的力学体系既非完整系,则必须借助拉格朗日未定乘数法对拉格朗日方程进行修正.广义坐标市确定质点或质点系完整的独立坐标,它不一定是长度,可以是角度或其他物理量,如面积、体积、电极化强度、磁化强度等.显然广义坐标不一定是长度的量纲.在完整约束下,广义坐标数等于力学体系的自由度数;广义力明威力实际上不一定有力的量纲可以是力也可以是力矩或其他物理量,如压强、场强等等,广义力还可以理解为;若让广义力对应的广义坐标作单位值的改变,且其余广义坐标不变,则广义力的数值等于外力的功由W q r F s i ni i δδθδααα==⋅∑∑==11ρρ知,ααδθq 有功的量纲,据此关系已知其中一个量的量纲则可得到另一个量的量纲.若αq 是长度,则αθ一定是力,若αθ是力矩,则αq 一定是角度,若αq 是体积,则αθ一定是压强等.5.3 答 αp 与αq &不一定只相差一个常数m ,这要由问题的性质、坐标系的选取形式及广义坐标的选用而定。
理论力学第五章 点的运动

【例5.1】 已知点的运动方程为 x r cost y r sin t 其中:r、ω是常数。求动点的运动轨迹、速度与加速度。
目录
第五章 点的运动\描述点运动的直角坐标表示法
【解】 为求动点的运动轨迹,将运动方程平方后相加,消去t得 x2 y2 r 2
这说明动点的运动轨迹是以O为圆心、r为半径的一个圆。当 ωt=0时,x=r, y=0,动点位于x轴上,当ωt=π/2时,x=0, y=r,动点位 于y轴上。 y v 动点的速度在坐标轴上的投影为 M r v x r sin t t v y r cost x O 因此速度的大小为
z M k O r z
a
v x y
i
j y
上式表明,动点的加速度在各坐标轴上的投影分别等于动点相 应的位置坐标对时间t的二阶导数。 目录
第五章 点的运动\描述点运动的直角坐标表示法 加速度的大小及方向余弦为
2 2 2 d x d y d z 2 2 2 2 2 2 a ax a y az ( 2 ) ( 2 ) ( 2 ) dt dt dt ay ax az cosa , i cosa , j cosa , k a a a
x x(t ) y y (t )
当动点始终沿一直线运动时,如取该直线为坐标轴Ox,则动点 的运动方程为
x x(t )
目录
第五章 点的运动\描述点运动的直角坐标表示法
5.2.2 用直角坐标表示点的速度
如图所示,若以O点为坐标原点建立 Oxyz直角坐标系,则动点的位置矢量r 可表示为
第五章 点的运动\描述点运动的弧坐标表示法
dr τ ds 式中:—沿轨迹切向指向弧坐标正向的单位矢量。此外,
《理论力学》第五章 点的运动

动点的速度等于它的矢 径对于时间的一阶导数
r-动点 对于点O的
矢径或位置矢
矢径r的矢端线是 点的运动轨迹
单位
§5-2 点的运动的直角坐标表示法
点的运动方程
即 x xt y yt z zt
r xi y j zk
M v
HOHAI UNIVERSITY ENGINEERING MECHANICS
4. M点的加速度
I
a x r sin t
2
a y r 2 cos t
( a, x )
2
; ( a, y )
例1:图示机构中A、B两滑块可分别沿互相垂直的两 直槽滑动。已知BA=a,AM=b,=t+(, 为常 y 量),求点M的运动轨迹、速度和加速度。 M
HOHAI UNIVERSITY ENGINEERING MECHANICS
F2=(y、z)
y
HOHAI UNIVERSITY ENGINEERING MECHANICS
x
F1=(x、y)
z
例
一人在路灯下由灯柱起以匀速 u 沿直线背离灯
HOHAI UNIVERSITY ENGINEERING MECHANICS
点的直线运动
点的曲线运动
点的合成运动
刚体的平行移动 刚体的定轴转动 刚体的平面运动 刚体的定点运动 刚体的一般运动
刚体的基本 运动形式
刚体的运动
第五章
HOHAI UNIVERSITY ENGINEERING MECHANICS
点的运动
轨迹或路径:点在空间所占据的位置随时 间连续变化而形成的曲线 直线 轨 迹 曲线 矢量法
d v d( ve ) d v d e a e v dt ds dt dt
理论力学运动学习题及详解
n a BA
C为研究点
n aC aA aCA ae ar
O2
D
y
n ae a A aCA
AB 0
aA
A
C
aCA 0 n aA aCA ae
A
C
ar
n e
a
n BA
aA aBA
B
aB
r r
2
2 AB
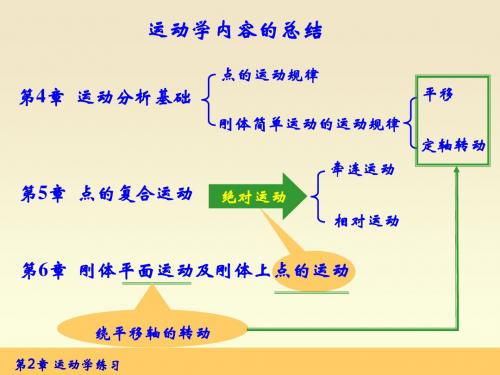
第2章 运动学练习
O2 D
A
vO 2 rω ωO 2ω r r
r
vA
r
O
O
vA 2 rωO 4 rω
第2章 运动学练习
.1已知 OA r , AB l 、 常数,轮滚动,求 vc、ac 。 (1)各连接点速度图
AB 0
vB v A r
对BC: BC
vc CvC ωBC
v R cos
=
v R cos
vO
R
Cv O θ
vO ω CvO v tg θ
v
第2章 运动学练习
课堂练习
2.已知尺寸, 、 r,求vC ?
A
AC
r Cv A
vC
C
B
r
vC AC CvC
AC
Cv
第2章 运动学练习
课堂练习
3.已知、 ,求 v A? r
a 常量, an 0
,点做何种运动( B)。
B.匀变速曲线运动 D.匀变速直线运动
(3)已知点的运动方程为 x 2t 2 4, y 3t 2 3 ,其轨迹方程为(
B)
理论力学(第7版)第五章 点的运动学

运 动 规 律
[例5-1 ] 已知点的运动方程为x=2sin 4t m,y=2cos 4t m, z=4t m。 求:点运动轨迹的曲率半径 。
解:
vx x 8 cos 4t , ax 32 sin 4t x
r r t
—以矢量表示的 点的运动方程
矢端曲线:动点M在运动过程中,矢 径r的末端绘出的一条连续曲线。 ——动点M的运动轨迹
3
二.点的速度
dr v r dt
方向:沿着矢径r的矢端曲线的切线 方向,且与此点的运动方向一致。
大小:速度矢的模,表明点运动的快慢。
三.加速度
dv d 2r a r 2 dt dt
dv v2 a a a n a a n n n dt
17
5-3 自然法 曲率(1 / ) :
定义——曲线切线的转角对弧长 一阶导数的绝对值。表示曲线的 弯曲程度。
d lim| | t 0 S dS 1
由于a , an均在密切面内,全加速a必在密切面内。 度
— 与 弧 坐 标 的 正 向 一 致 n — 指 向 曲 线 内 凹 一 侧 b — 与 , n 构 成 右 手 系
b n
[注]:自然坐标系是沿曲 13 线而变动的游动坐标系。
(动画自然坐标轴的几何性质)
曲线在P点的密切面形成
5-3 自然法
二.点的速度
当t 0时,r MM' S
v y y 8 sin 4t , a y 32 cos 4t y
v z z 4, a z 0 z
2 2 2 2 v v x v 2 v z 80 m s , a a x a 2 a z 32m s 2 y y
理论力学 第五章 点的运动学(合)

[讨论] (1) d v 与 d v 有何不同? 就直线和曲线分别说明。
dt dt
d v = a ——点的加速度矢。 dt
对直线、曲线都一样。
d v ——速度大小对时间的变化率 dt 在直线中为加速度大小: d v = a
dt
在曲线中为切向加速度大小: d v dt
=
at
36
第五章 点的运动学
(2)点作曲线运动, 画出下列情况下加速度的大致方向。 ① M1点作匀速运动; ② M2点作加速运动; ③ M3点作减速运动。
(2)速度
vx = x& = rω (1− cosωt)
vy = y& = rω sin ωt
v=
v
2 x
+
v
2 y
= rω
2
− 2 cosωt
=
2rω
sin
ωt
2
(3)切向、法向加速度
at = v&
= rω 2 cos ωt
2
an
=
rω 2
sin
ωt
2
思考:如何求点M的法向加速度?
30
第五章 点的运动学
dt dt
dt
dt
=
d2 x dt2 i
+ d2 y dt2
j
+
d2 dt
z
2
k
解析表达式: a = a x i + a y j + a z k
ax
=
d vx dt
=
d2 x d t2
=
v& x
=
&x&
ay
=
d vy dt
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第五章 点的运动 习题全解[习题5-1] 一点按2123+-=t t x 的规律沿直线动动(其中t 要s 计,x 以m 计).试求:(1)最初s 3内的位移;(2)改变动动方向的时刻和所在位置;(3)最初s 3内经过的路程;(4)s t 3=时的速度和加速度;(5)点在哪段时间作加速度,哪段时间作减速运动. 解:(1)求最初s 3内的位移.m x 220120)0(3=+⨯-= m x 723123)3(3-=+⨯-=)(927)0()3(m x x x -=--=-=∆ (动点的位移为9m,位移的方向为负x 方向). (2)求改变动动方向的时刻和所在位置. 改变方向时,动点的速度为零.即: 01232=-==t dtdxv , 亦即:当s t 2=时,动点改变运动方向.此时动点所在的位置为: )(1422122)2(3m x -=+⨯-= (3)求最初s 3内经过的路程.)(23716|)14(7||214|)3~2()2~0()3~0(m S S S =+=---+--=+= (4)求s t 3=时的速度和加速度1232-==t dt dx v )/(151233)3(2s m dt dx v =-⨯== t dtdv a 6== )/(1836)3(2s m a =⨯=(5)求动点在哪段时间作加速度,哪段时间作减速运动.若v 与a 同号,则动点作加速运动; 若v 与a 异号,则动点作减速运动.即: 同号时有:0)2)(2(18)4(18)6)(123(22>+-=-=-=t t t t t t t va0)2)(2(>+-t t t20<<t .即当s t 20<<时,动点作加速动动.Oxy图题25-异号时有:0)2)(2(<+-t t t2>t即当s t 2>时,动点作减速运动.[习题5-2] 已知图示机构中,l AB OA ==,a AC DM CM ===,求出t ωϕ=时,点M 的动动方程和轨迹方程。
解:设动点M 的坐标为),(y x M ,则由图中的几何关系可知,运动方程为: t l x ωcos =t a l t a t l y ωωωsin )2(sin 2sin -=-= 把上式两边分别平方后相加,得到轨迹方程:1)2(2222=-+a l y l x [习题5-3] 跨过滑轮C 的绳子一端挂有重物B,另一端A 被人拉着沿水平方向运动,其速度为s m v /10=,A 点到地面的距离保持常量m h 1=.滑轮离地面的高度m H 9=,其半径忽略不计.当运动开始时,重物在地面上0B 处,绳AC 段在铅直位置C A 0处.求重物B 上升的运动方程和速度方程,以及重物B 到达滑轮处所需的时间.解:从图中可知,绳子的原长约为16m.在任一瞬时,绳子的长度为:BC l t +⨯+22)1(8.即:16822≈++BC l t 22816t l BC +-=B 点的y 坐标,即重物B 上升的运动方程为:86464168822-+=++-=-=t t l y BC B重物B 上升的速度方程为:222646422)864(ttt t t dt d dt dy v B B +=+=-+==重物到达滑轮时,所走过的路程为8m,即:dt tt vdt dy 264+==C t t t d dt t t y ++=++=+=⎰⎰222264642)64(64当0=t 时,0=y ,8-=C ,故:8642-+=t y ,依题意:88642=-+t ,解得:s t 9.13=[习题5-4] 偏心轮半径为r ,转动轴到轮心的偏心距d OC =,坐标轴Ox 如图所示.求杆AB 的运动方程,已知t ωϕ=,ω为常量.解:AB 杆作竖向平动.A 点的运动代表AB 杆的运动.由图中的几何关系可知,A 点的坐标,即AB 杆的运动方程为:Adt r sin sin =ω t rdA ωsin sin =t d r r t rd A A ωω2222222sin 1sin 1sin 1cos -=-=-=t d r t d A r t d x A ωωω222sin cos cos cos -+=+=[习题5-5] 半圆形凸轮以匀速s mm v /10=沿水平方向向左运动,活塞杆AB 长l 沿铅直方向运动.挡运动开始时,活塞杆A 端在凸轮的最高点上.如凸轮的半径mm R 80=,求活塞B 的运动方程和速度方程.解:活塞杆AB 作竖向平动.以凸轮圆心为坐标原点,铅垂向上方向为x 轴的正向,则由图中的几何关系可知,任一时刻,B 点的坐标,即活塞B 的运动方程为:)(64)()(cos 22222cm t l vt R l Rvt R R l R l x B -+=-+=-⋅+=+=ϕ活塞B 的速度方程为:)/(646422122s cm ttt t dt dx v B B --=--==[习题5-6] 已知杆OA 与铅直线夹角6t πϕ=(ϕ以rad 计,t 以s 计),小环M 套在杆OA,CD上,如图所示.铰O 至水平杆CD 的距离mm h 400=.求小环M 的速度方程与加速度方程,并求s t 1=时小环M 的速度及加速度.解:以OA 铅垂时小环M 的位置为坐标原点,水平向右方向为x 轴的正向.任一瞬时, M 的坐标,即运动方程为: )(6tan 400tan mm th x M πϕ==小环M 的速度方程为:)/)(6(sec 32006)6(sec 400)6tan 400(22s mm tt t dt d dt dx v M M πππππ=⋅===)/(279)/)(6(sec 3200)1(2s mm s mm v M ==ππ 小环M 加速度方程为:6sec 3200)6sec 3200(22t dt d t dt d dt dv a M M ππππ===)/(6tan 6sec 920066tan 6sec 6sec 23200222s mm t t t t t ππππππππ⋅⋅=⋅⋅⋅=)/(1696tan 6sec 9200)1(222s mm a M =⋅⋅=πππ[习题5-7] 滑道连杆机构如图所示,曲柄OA 长r ,按规律t ωϕϕ+=0转动(ϕ以rad 计,t 以s 计),ω为一常量.求滑道上B 点的运动方程,速度方程及加速度方程.解:以O 为坐标原点,OB 方向为x 轴的正向,则B 点的坐标,即运动方程为: l t r x B ++=)cos(0ωϕ B 点的速度方程为: )sin()sin(])cos([000t r t r l t r dtddt dx v B B ωϕωωωϕωϕ+-=⋅+-=++==B 点的加速度方程为: )cos()]sin([020t r t r dtddt dv a B B ωϕωωϕω+-=+-==[习题5-8] 动点A 和B 在同一直角坐标系中的运动方程分别为22{t y t x A A ==, 422{ty t x B B ==其中,y x ,以mm 计, t 以s 计.试求:(1)两点的运动轨迹;(2)两点相遇的时刻;(3)两点相遇时刻它们各自的速度;(4)两点相遇时刻它们各自的加速度. 解: (1)求两点的运动轨迹A 点的运动轨迹:22A A x y = B 点的运动轨迹:22B B x y =(2)求两点相遇的时刻两点相遇时,它们的坐标相同.B A x x =, 2t t =, s t 1=.即当s t 1=时,两点相遇. (3)求两点相遇时刻它们各自的速度 1==dt dx v A xA , t dtdyv A yA 4==, 2161t v A += 两点相遇时,A 点的速度为:大小:)/(12.4161)1(s mm v A =+=.方向:"'050577514arctan arctan===xAyA vA v v θt dt dx v B xB 2==, 38t dtdyv B yA ==, 62644t t v A += 两点相遇时,B 点的速度为: 大小:)/(25.8644)1(s mm v B =+=.方向:"'050577528arctan arctan===xByB vB v v θ(4)求两点相遇时刻它们各自的加速度 0==dtdv a xAxA , )/(42s mm dt dv a yA yA == 2/4s mm a A = 两点相遇时,A 点的加速度为:大小:2/4)1(s mm a A =,方向:沿y 轴正向.2==dtdv a xBxB , 224t dt dv a yB yB == 45764t a B += 两点相遇时,B 点的加速度为:大小:)/(08.245764)1(2s mm a B =+=方向:"'0111485224arctan==aB θ [习题5-9] 点M 以匀速率u 在直管OA 内运动,直管OA 又按t ωϕ=规律绕O 转动.当0=t 时, M 在O 点,求其在任一瞬时的速度及加速度的大小.解: ut r =,t ωϕ=, 设任一瞬时,M 点的坐标为),(y x M ,则点M 的运动方程为:t ut r x ωϕcos cos ==, t ut r y ωϕsin sin ==速度方程为:t t u t u t ut t u t ut dtddt dx v x ωωωωωωωsin cos )sin (cos )cos (-=⋅-+===t t t u t t u t u v x ωωωωωωcos sin 2sin )(cos 222222⋅-+= t t u t u t ut t u t ut dtddt dy v y ωωωωωωωcos sin cos sin )sin (+=⋅⋅+===t t t u t t u t u v y ωωωωωωcos sin 2cos )(sin222222⋅++=2222)(t u u v v y x ω+=+任一瞬时,速度的大小为:22222)(1)(t u t u u v v v y x ωω+=+=+=加速度方程为:)sin cos (t t u t u dtddt dv a x x ωωω-==]cos sin [)sin (ωωωωωωω⋅⋅+⋅-⋅-⋅=t t u t u t ut t u t u ωωωωcos sin 22--=t t t u t t u t u a x ωωωωωωωcos sin 4cos )(sin 4322222222⋅++=)cos sin (t t u t u dtddtdv a y y ωωω+==ωωωωωωω⋅-⋅+⋅+⋅⋅=)sin (cos [cos t t u t u t ut t u t u ωωωωsin cos 22⋅-=t t t u t t u t u a y ωωωωωωωcos sin 4sin )(cos 4322222222⋅-+= 222222)(4t u u a a y x ωω+=+任一瞬时,速度的大小为:2222222)(4)(4t u t u u a a a y x ωωωω+=+=+=[习题5-10] 一圆板在Oxy 平面内运动.已知圆板中心C 的运动方程为2243t t x C +-=,223t t y C ++=(其中C C y x ,以m 计, t 以s 计).板上一点M 与C 的距离m l 4.0=,直线段CM 与x 轴的夹角22t =ϕ(ϕ以rad 计, t 以s 计),试求s t 1=时M 点的速度及加速度.解: 设M 点的坐标为M(x,y),则M 点的坐标,即运动方程为:)2cos(4.0243cos 22t t t l x x C ++-=+=ϕ )2sin(4.023sin 22t t t l y y C +++=+=ϕ速度方程:t t t t t t dtddt dx v x 4)2sin (4.044)]2cos(4.0243[222⋅-++-=++-==22sin 6.144t t t v x -+-=)/(46.1)14.31802sin(6.144)1(0s m v x -=⨯-+-=t t t t t t dtddt dy v y 42cos 4.022)]2sin(4.023[222⋅⋅++=+++==22cos 6.122t t t v y ++=)/(33.3)14.31802cos(6.122)1(0s m v y =⨯++=s t 1=时M 点的速度为:j i v 33.346.1+-= (s m /)加速度方程:]42cos 2[sin 6.14)2sin 6.144(222t t t t t t t dtddt dv a x x ⋅+-=-+-==2222cos 4.62sin 6.14t t t a x --=)/(215.5)14.31802cos(4.6)14.31802sin(6.14)1(00s m a x =⨯-⨯-=]4)2sin (2[cos 6.12)2cos 6.122(222t t t t t t t dtddtdv a y y ⋅-++=++==2222sin 4.62cos 6.12t t t a y -+=)/(484.4)14.31802sin(4.6)14.31802cos(6.12)1(00s m a y -=⨯-⨯+=s t 1=时M 点的加速度为:j i a 484.4215.5-=[习题5-11] 一段凹凸不平的路面可近似地用下列正弦曲线表示:20sin04.0xy π=,其中x,y均以m 计.设有一汽车沿x 方向的运动规律为t x 20=(x 以m 计,t 以s 计).问汽车经过该段路面时,在什么位置加速度的绝对值最大?最大的加速度值是多少? 解: 20202020cos 04.02020cos 04.0)20sin 04.0(⋅⋅⋅⋅=⋅⋅⋅===πππππt dt dx x x dt d dt dy v y )cos(04.0t v y ⋅=ππt t t dtddtdv a y y πππππππsin 04.0)sin (04.0)]cos(04.0[2-=⋅-=⋅==)/(20s m dtdxv x ==0==dtdv a xx t a a y ππsin 04.02-==当Λ,2,1,2)12(=-=n n t ππ,即s n t 212-=时, 加速度的绝对值最大, )/(04.0||22max s m a π=.此时汽车的位置在: ))(12(1021220m n n x -=-⨯=,)(04.02010sin 04.0m y =⨯=π [习题5-12] 一点作平面曲线运动,其速度方程为3=x v ,t v y ππ4sin 2=,其中y x v v ,以s m /计,t 以s 计.已知在初瞬时该点在坐标原点,求该点的运动方程和轨迹方程。
