第3章 复合运动—习题3-1
大学物理第三章部分课后习题答案

大学物理第三章部分课后习题答案3-1半径为R、质量为M的均匀薄圆盘上,挖去一个直径为R的圆孔,孔的中心在求所剩部分对通过原圆盘中心且与板面垂直的轴的转动惯量。
分析:用补偿法(负质量法)求解,由平行轴定理求其挖去部分的转动惯量,用原圆盘转动惯量减去挖去部分的转动惯量即得。
注意对同一轴而言。
解:没挖去前大圆对通过原圆盘中心且与板面垂直的轴的转动惯量为:1R处,2J11MR2①2由平行轴定理得被挖去部分对通过原圆盘中心且与板面垂直的轴的转动惯量为:1MRMR3J2Jcmd2()2()2MR2②2424232由①②式得所剩部分对通过原圆盘中心且与板面垂直的轴的转动惯量为:JJ1J213MR2323-2如题图3-2所示,一根均匀细铁丝,质量为M,长度为L,在其中点O处弯成120角,放在某Oy平面内,求铁丝对O某轴、Oy轴、Oz轴的转动惯量。
分析:取微元,由转动惯量的定义求积分可得解:(1)对某轴的转动惯量为:L20J某rdm(lin600)22M1dlML2L32(2)对y轴的转动惯量为:L1ML2M5Jy()2(lin300)2dlML20322L96(3)对Z轴的转动惯量为:1ML1Jz2()2ML2322122题图3-23-3电风扇开启电源后经过5达到额定转速,此时角速度为每秒5转,关闭电源后经过16风扇停止转动,已知风扇转动惯量为0.5kgm,且摩擦力矩Mf和电磁力矩M均为常量,求电机的电磁力矩M。
分析:Mf,M为常量,开启电源5内是匀加速转动,关闭电源16内是匀减速转动,可得相应加速度,由转动定律求得电磁力矩M。
解:由定轴转动定律得:MMfJ1,即52520.54.12Nm5163-4飞轮的质量为60kg,直径为0.5m,转速为1000r/min,现要求在5内使其制动,求制动力F,假定闸瓦与飞轮之间的摩擦系数0.4,飞轮的质量全部分布在轮的外周上,MJ1MfJ1J20.5尺寸如题图3-4所示。
分析:分别考虑两个研究对象:闸瓦和杆。
第3章 复合运动—习题
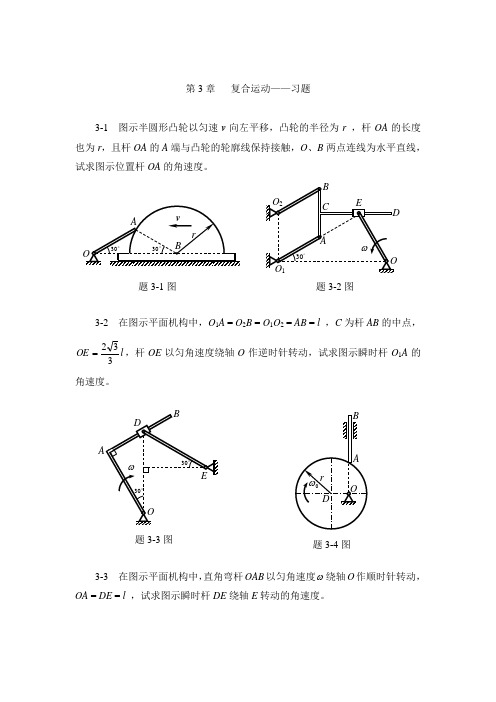
第3章 复合运动——习题3-1 图示半圆形凸轮以匀速v 向左平移,凸轮的半径为r ,杆OA 的长度也为r ,且杆OA 的A 端与凸轮的轮廓线保持接触,O 、B 两点连线为水平直线,试求图示位置杆OA 的角速度。
3-2 在图示平面机构中,O 1A = O 2B = O 1O 2 = AB = l ,C 为杆AB 的中点,l OE 332=,杆OE 以匀角速度绕轴O 作逆时针转动,试求图示瞬时杆O 1A 的角速度。
3-3 在图示平面机构中,直角弯杆OAB 以匀角速度ω绕轴O 作顺时针转动,OA = DE = l ,试求图示瞬时杆DE 绕轴E 转动的角速度。
题3-1图题3-3图题3-4图题3-2图3-4 在图示平面系统中,半径为r ,偏心距OD = r /2 的凸轮以匀角速度0ω绕轴O 作顺时针转动,轴O 在杆AB 的正下方,试求图示位置杆AB 运动的速度。
3-5 在图示平面系统中,长度为l = 2r 的杆OA 以匀角速度0ω绕轴O 作逆时针转动,通过杆A 端与半径为r 的圆盘B 的盘缘接触,从而带动圆盘B 在水平地面上作纯滚动,试求图示瞬时(杆OA 处于水平位置)圆盘B 的角速度。
3-6 在图示平面机构中,O 1A = O 2B = l ,AB = 2l ,杆O 1A 以匀角速度0ω绕轴O 1作逆时针转动。
在图示位置套筒D 恰好位于杆AB 的中点,试求该位置杆DE 沿水平滑道运动的速度。
题3-6图题3-7图题3-8图题3-5图3-7 图示系统处于铅垂平面内,倾角为30°的三角块在水平地面上以匀速度v 向左运动,以推动半径为r 的圆盘A 在铅垂墙面上运动。
试在以下两种情况下分别求圆盘的角速度:(1) 圆盘相对于墙面作纯滚动;(2) 圆盘相对于三角块作纯滚动。
3-8 在图示平面系统中,杆OD 以匀角速度0ω绕轴O 作逆时针转动,滑块B 以匀速0v 水平向右运动,AB = l ,试求图示位置杆AB 的角速度。
工程力学-复合运动

O1 e2
大小 vCD O1B·O1? vBr2?
O1 D
求出
O
E
vBe2
L
cos
O1
vCD
cos
L
O1
cos2
L
vCD
l cos2
2L
3l
8L
()
vBr 2
vCD
sin
l
4
()
8
例题
例 题 10
§3 复合运动
3.加速度分析 (1)对动点A、动系e1
aA
aA
0
aAn
ae1
ar1
22
例题
*
例 题 11
§3 复合运动
A
ω4 O
ω1
Ⅲ Ⅱ Ⅳ Ⅰ
ω1
ω423例题*例 题 11§3 复合运动
解:把动系固连于系杆OA上,则牵连角速度ωe就是待求
的角速度ω4 (设为),即ωe = ω4 ( )。
ω 3r= ω4
Ⅲ
已 知 齿 轮 Ⅰ 的 绝 对 角 速 度 ω1 () ,故如能求出它对于动系的
R A
Ш
E
h 60º
O1
图示机构,已知系杆OA=3R,AE=1.5R,系杆OA
的角速度ω0=常数,试求图示位置曲柄O1B的角速 度和角加速度。
29
例题
例 题 13(习题3.29)
§3 复合运动
解: 1.运动分析: 杆OA、O1B 定轴转动,
轮Ⅰ不动,
动系e1
r3
r2
R
R
r1 O
ІІ
A
Ш
轮Ⅱ,Ⅲ和套筒E一般平面运动。
根据轮与杆的接触特点选择适当的动点动系
《运动分析》第三章课后练习

3-1填空题:1.速度瞬心是两刚体上瞬时速度相等的重合点。
2.若瞬心的绝对速度为零,则该瞬心称为绝对瞬心;若瞬心的绝对速度不为零,则该瞬心称为相对瞬心。
3.当两个构件组成移动副时,其瞬心位于垂直于导路方向的无穷远处。
当两构件组成高副时,两个高副元素作纯滚动,则其瞬心就在接触点处;若两个高副元素间有相对滑动时,则其瞬心在过接触点两高副元素的公法线上。
4.当求机构的不互相直接联接各构件间的瞬心时,可应用三心定理来求。
5.3个彼此作平面平行运动的构件间共有 3 个速度瞬心,这几个瞬心必定位于一条直线上。
6.机构瞬心的数目K与机构的构件数N的关系是K=N(N-1)/2 。
7.铰链四杆机构共有6个速度瞬心,其中3个是绝对瞬心。
8.速度比例尺μν表示图上每单位长度所代表的速度大小,单位为:(m/s)/mm 。
加速度比例尺μa表示图上每单位长度所代表的加速度大小,单位为(m/s2)/mm。
9.速度影像的相似原理只能应用于构件,而不能应用于整个机构。
10.在摆动导杆机构中,当导杆和滑块的相对运动为平动,牵连运动为转动时(以上两空格填转动或平动),两构件的重合点之间将有哥氏加速度。
哥氏加速度的大小为2×相对速度×牵连角速度;方向为相对速度沿牵连角速度的方向转过90°之后的方向。
P直接标注在图上)。
3-2试求出图示各机构在图示位置时全部瞬心的位置(用符号ij3-3 在图a 所示的四杆机构中,l AB =60mm,l CD =90mm ,l AD =l BC =120mm ,ω2=10rad/s ,试用瞬心法求:1)当φ=165°时,点C 的速度v C ;2)当φ=165°时,构件3的BC 线上速度最小的一点E 的位置及速度的大小;3)当v C =0时,φ角之值(有两个解); 解:1)以选定的比例尺μl 作机构运动简图(图b )。
2)求v C ,定出瞬心P 13的位置(图b ) v C =ω33413P P μl=34132313Bl l v P P P P μμg g g=1060583833⨯⨯⨯⨯≈2.4×174=418(mm/s) 3)定出构件3的BC 线上 速度最小的点E 的位置:E 点位置如图所示。
人教版高中物理-有答案-人教版物理选修3-1第三章专题复习1:带电粒子在复合场中的运动

人教版物理选修3-1第三章专题复习1:带电粒子在复合场中的运动一、多选题。
1. 如图所示,某空间存在正交的匀强磁场和匀强电场,电场方向水平向右,磁场方向垂直于纸面(未画出),一带电微粒刚好能沿直线斜向上运动,下列说法正确的是()A.磁场方向一定垂直于纸面向里B.微粒一定带负电C.微粒的电势能一定增加D.微粒的机械能一定增加2. 如图所示,一个带负电的油滴以水平向右的速度v进入一个方向垂直纸面向外的匀强磁场B后,保持原速度做匀速直线运动.如果使匀强磁场发生变化,则下列判断中正确的是()A.磁场B减小,油滴动能增加B.磁场B增大,油滴机械能不变C.使磁场方向反向,油滴动能减小D.使磁场方向反向后再减小,油滴重力势能减小3. 一质量为m、电荷量为−q的圆环,套在与水平面成θ角的足够长的粗糙细杆上,圆环的直径略大于杆的直径,细杆处于磁感应强度为B的匀强磁场中,磁场方向水平且垂直于杆.现给圆环—沿杆向上的初速度v0(取初速度v0的方向为正方向),以后的运动过程中圆环运动的速度图像可能是()A. B.C. D.二、选择题。
如图所示,两个倾角分别为30∘和60∘的光滑斜面同定于水平面上,并处于方向垂直纸面向里、磁感应强度为B的匀强磁场中.两个质量均为m、带电荷量均为+q的小滑块甲和乙分别从两个斜面顶端由静止释放,运动一段时间后,两小滑块都将飞离斜面,在此过程中()A.甲滑块飞离斜面瞬间的速度比乙滑块飞离斜面瞬间的速度大B.甲滑块在斜面上运动的时间比乙滑块在斜面上运动的时间短C.甲滑块在斜面上运动的位移与乙滑块在斜面上运动的位移大小相同D.两滑块飞离斜面时,下滑的高度相等绝缘光滑斜面与水平面成α角,一质量为m、电荷量为−q的小球从斜面上高ℎ处,以初速度为v0、方向与斜面底边MN平行射入,如图所示,整个装置处在磁感应强度大小为B的匀强磁场中,磁场方向平行于斜面向上.已知斜面足够大,小球能够沿斜面到达底边MN.则下列判断正确的是()A.小球在斜面上做非匀变速曲线运动B.小球到达底边MN的时间t=√2ℎg sin2αcosαC.匀强磁场磁感应强度的取值范围为B≤mgqv0D.匀强磁场磁感应强度的取值范围为B≥mg cosαqv0三、解答题。
物理学简明教程(马文蔚等著)第三章课后练习题答案详解

物理学简明教程(马文蔚等著)第三章课后练习题答案详解物理学简明教程(马文蔚等著)第三章课后练习题答案详解3 -1有两个力作用在一个有固定转轴的刚体上:(1) 这两个力都平行于轴作用时,它们对轴的合力矩一定是零;(2) 这两个力都垂直于轴作用时,它们对轴的合力矩可能是零;(3) 当这两个力的合力为零时,它们对轴的合力矩也一定是零;(4) 当这两个力对轴的合力矩为零时,它们的合力也一定是零.对上述说法下述判断正确的是( )(A) 只有(1)是正确的(B)(1)、(2)正确,(3)、(4)错误(C) (1)、(2)、(3)都正确,(4)错误 (D)(1)、(2)、(3)、(4)都正确分析与解力对轴之力矩通常有三种情况:其中两种情况下力矩为零:一是力的作用线通过转轴,二是力平行于转轴(例如门的重力并不能使门转).不满足上述情况下的作用力(含题述作用力垂直于转轴的情况)对轴之矩不为零,但同时有两个力作用时,只要满足两力矩大小相等,方向相反,两力矩对同一轴的合外力矩也可以为零,由以上规则可知(1)(2)说法是正确.对于(3)(4)两种说法,如作用于刚体上的两个力为共点力,当合力为零时,它们对同一轴的合外力矩也一定为零,反之亦然.但如这两个力为非共点力,则以上结论不成立,故(3)(4)说法不完全正确.综上所述,应选(B).3-2关于力矩有以下几种说法:(1) 对某个定轴转动刚体而言,内力矩不会改变刚体的角加速度;(2) 一对作用力和反作用力对同一轴的力矩之和必为零;(3) 质量相等,形状和大小不同的两个刚体,在相同力矩的作用下,它们的运动状态一定相同.对上述说法下述判断正确的是( )(A) 只有(2)是正确的 (B) (1)、(2)是正确的(C)(2)、(3)是正确的 (D) (1)、(2)、(3)都是正确的分析与解刚体中相邻质元之间的一对内力属于作用力与反作用力,且作用点相同,故对同一轴的力矩之和必为零,因此可推知刚体中所有内力矩之和为零,因而不会影响刚体的角加速度或角动量等,故(1)(2)说法正确.对说法(3)来说,题述情况中两个刚体对同一轴的转动惯量因形状、大小不同有可能不同,因而在相同力矩作用下,产生的角加速度不一定相同,因而运动状态未必相同,由此可见应选(B).3-3均匀细棒OA可绕通过其一端O而与棒垂直的水平固定光滑轴转动,如图所示,今使棒从水平位置由静止开始自由下落,在棒摆到竖直位置的过程中,下述说法正确的是( )(A) 角速度从小到大,角加速度不变(B) 角速度从小到大,角加速度从小到大(C) 角速度从小到大,角加速度从大到小(D) 角速度不变,角加速度为零分析与解如图所示,在棒下落过程中,重力对轴之矩是变化的,其大小与棒和水平面的夹角有关.当棒处于水平位置,重力矩最大,当棒处于竖直位置时,重力矩为零.因此在棒在下落过程中重力矩由大到小,由转动定律知,棒的角加速亦由大到小,而棒的角速度却由小到大(由机械能守恒亦可判断角速度变化情况),应选(C).3 -4 一汽车发动机曲轴的转速在12 s 内由1.2×103 r·min-1均匀的增加到2.7×103 r·min-1.(1) 求曲轴转动的角加速度;(2) 在此时间内,曲轴转了多少转?分析这是刚体的运动学问题.刚体定轴转动的运动学规律与质点的运动学规律有类似的关系,本题为匀变速转动.解 (1) 由于角速度ω=2π n (n 为单位时间内的转数),根据角加速度的定义tωαd d =,在匀变速转动中角加速度为()200s rad 1.13π2-?=-=-=tn n t ωωα (2) 发动机曲轴转过的角度为()0020π221n n t ωωt αt ωθ-=-=+= 在12 s 内曲轴转过的圈数为3902π20=+==t n n θN 圈3 -5 一飞轮由一直径为30㎝,厚度为2.0㎝的圆盘和两个直径为10㎝,长为8.0㎝的共轴圆柱体组成,设飞轮的密度为7.8×103 kg·m -3,求飞轮对轴的转动惯量.分析根据转动惯量的可叠加性,飞轮对轴的转动惯量可视为圆盘与两圆柱体对同轴的转动惯量之和;而匀质圆盘、圆柱体对轴的转动惯量的计算可查书中公式,或根据转动惯量的定义,用简单的积分计算得到.解根据转动惯量的叠加性,由匀质圆盘、圆柱体对轴的转动惯量公式可得2424122221121m kg 136.021π161 2212212?=??? ??+=??+??? ???=+=ad ld ρd m d m J J J3 -6 一燃气轮机在试车时,燃气作用在涡轮上的力矩为2.03×03N·m ,涡轮的转动惯量为25.0kg·m 2 .当轮的转速由2.80×103 r·min -1 增大到1.12×104 r·min -1时,所经历的时间t 为多少?分析由于作用在飞轮上的力矩是恒力矩,因此,根据转动定律可知,飞轮的角加速度是一恒量;又由匀变速转动中角加速度与时间的关系,可解出飞轮所经历的时间.该题还可应用角动量定理直接求解.解1 在匀变速转动中,角加速度t ωωα0-=,由转动定律αJ M =,可得飞轮所经历的时间()s 8.10200=-=-=n n M J πJ M ωωt 解2 飞轮在恒外力矩作用下,根据角动量定理,有()00d ωωJ t M t-=? 则()s 8.10π200=-=-=n n MJ J M ωωt3-7 电风扇接通电源后一般经5s 后到达额定转速10min r 300-?=n ,而关闭电源后经16 s 后风扇停止转动,已知电风扇的转动惯量为2m kg 5.0?,设启动时电磁力矩M 和转动时的阻力矩f M 均为常数,求启动时的电磁力矩M .分析由题意知M 和f M 均为常数,故启动时电风扇在M 和f M 共同作用下,作匀加速转动,直至到达额定转速,关闭电源后,电风扇仅在f M 的作用下作匀减速转动.运用匀变速转动的运动学规律和转动定律既可求解.解设启动时和关闭电源后,电风扇转动时的角加速度分别为1α和2α,则启动过程αJ M M =-f110t αω=关闭电源后2f αJ M =-0220=+t αω 联解以上各式并将60200n πω=以及0n 、1t 、2t 、J 值代入,得 m N 12.4?=M3 -8 一质量为m′、半径为R 的均匀圆盘,通过其中心且与盘面垂直的水平轴以角速度ω转动,若在某时刻,一质量为m 的小碎块从盘边缘裂开,且恰好沿垂直方向上抛,问它可能达到的高度是多少?破裂后圆盘的角动量为多大?分析盘边缘裂开时,小碎块以原有的切向速度作上抛运动,由质点运动学规律可求得上抛的最大高度.此外,在碎块与盘分离的过程中,满足角动量守恒条件,由角动量守恒定律可计算破裂后盘的角动量.解 (1) 碎块抛出时的初速度为R ω=0v由于碎块竖直上抛运动,它所能到达的高度为g R ωg h 222220==v(2) 圆盘在裂开的过程中,其角动量守恒,故有L L L '-=0 式中ωR m L 221'=为圆盘未碎时的角动量;ωmR L 2='为碎块被视为质点时,碎块对轴的角动量;L 为破裂后盘的角动量.则ωR m m L 221??-'=3-9 一位溜冰者伸开双臂来以1.01s r -?绕身体中心轴转动,此时的转动惯量为1.33 2m kg ?,她收起双臂来增加转速,如收起双臂后的转动惯量变为0.48 2m kg ?.求(1)她收起双臂后的转速;(2)她收起双臂前后绕身体中心轴的转动动能各为多少?分析各种物体(含刚体和变形体)在运动过程中,只要对空间某定点或定轴的外力矩之和为零,则物体对同一点或轴的角动量就守恒,在本题中当溜冰者绕身体中心轴转动时,人体重力和地面支持力均与该轴重合,故无外力矩作用,满足角动量守恒.此时改变身体形状(即改变对轴的转动惯量)就可改变转速,这是在体育运动中经常要利用的物理规律.解(1)由分析知,有ωωJ J =00则 1-00s r 77.2?==ωωJJ (2)收起双臂前 J 26.2212001k ==ωJ E收起双臂后 J 72.6212k2==ωJ E此时由于人体内力做功,有 1k 2k E E >的上端点,开始时棒自由悬挂.以100 N 的力打击它的下端点,打击时间为0.02 s .(1) 若打击前棒是静止的,求打击时其角动量的变化;(2) 棒的最大偏转角.分析该题属于常见的刚体转动问题,可分为两个过程来讨论:(1) 瞬间的打击过程.在瞬间外力的打击下,棒受到外力矩的角冲量,根据角动量定理,棒的角动量将发生变化,则获得一定的角速度.(2) 棒的转动过程.由于棒和地球所组成的系统,除重力(保守内力)外无其他外力做功,因此系统的机械能守恒,根据机械能守恒定律,可求得棒的偏转角度.解 (1) 由刚体的角动量定理得120s m kg 0.2d -??====?t ΔFl t M ωJ L Δ(2) 取棒和地球为一系统,并选O 处为重力势能零点.在转动过程中,系统的机械能守恒,即()θmgl ωJ cos 1212120-= 由式(1)、(2)可得棒的偏转角度为8388Δ31arccos o 222'=-=gl m t F θ棒的一端的水平轴转动.如将此棒放在水平位置,然后任其落下,求:(1) 当棒转过60°时的角加速度和角速度;(2) 下落到竖直位置时的动能;(3) 下落到竖直位置时的角速度.分析转动定律M =Jα是一瞬时关系式,为求棒在不同位置的角加速度,只需确定棒所在位置的力矩就可求得.由于重力矩()θl mg θM cos 2=是变力矩,角加速度也是变化的,因此,在求角速度时,就必须根据角加速度用积分的方法来计算(也可根据转动中的动能定理,通过计算变力矩的功来求).至于棒下落到竖直位置时的动能和角速度,可采用系统的机械能守恒定律来解,这是因为棒与地球所组成的系统中,只有重力作功(转轴处的支持力不作功),因此,系统的机械能守恒.解 (1) 棒绕端点的转动惯量231ml J=由转动定律M =Jα可得棒在θ 位置时的角加速度为()l θg J θM α2cos 3==当θ =60°时,棒转动的角加速度2s 418-=.α 由于θωωt ωαd d d d ==,根据初始条件对式(1)积分,有=o 6000d d θαωωω 则角速度为1600s 98.7sin 3o-==l θg ω(2) 根据机械能守恒,棒下落至竖直位置时的动能为J 98.021==mgl E K (3) 由于该动能也就是转动动能,即221ωJ E K =,所以,棒落至竖直位置时的角速度为1s 57.832-==='lg J E ωK。
人教版高中物理选修3-1专题三 带电粒子在复合场中的运动课后练习.docx

高中物理学习材料桑水制作专题三 带电粒子在复合场中的运动课后练习1.图中为一“速度选择器”装置示意图。
a 、b 为水平放置的平行金属板,一束具有各种不同速率的电子沿水平方向经小孔O 进入a 、b 两板之间。
为了选取具有某种特定速率的电子,可在a 、b 间加上电压,并沿垂直于纸面的方向加一匀强磁场,使所选电子能够沿水平直线OO'运动由O'射出,电子重力不计,可能达到上述目的的办法是 A .使a 板电势低于b 板,磁场方向垂直纸面向里 B .使a 板电势高于b 板,磁场方向垂直纸面向里 C .使a 板电势高于b 板,磁场方向垂直纸面向外 D .使a 板电势低于b 板,磁场方向垂直纸面向外2.如图所示,从S 处发出的热电子经加速电压U 加速后垂直进入相互垂直的匀强电场和匀强磁场中,发现电子流向上极板偏转。
设两极板间电场强度为E ,磁感应强度为B 。
欲使电子沿直线从电场和磁场区域通过,只采取下列措施,其中可行的是 A .适当增大电场强度E B .适当增大磁感应强度BC .适当增大加速电场极板之间的距离D .适当减小加速电压U3.1930年,劳伦斯制成了世界上第一台回旋加速器,工作原理示意图如图所示.关于回旋加速器,下列说法正确的是( ) A .粒子从电场中获得能量B .交流电的周期随粒子速度的增大而增大C .要使粒子获得的最大动能增大,可以增大D 形盒的半径OabO'D .不改变交流电的频率和磁感应强度B ,加速质子的回旋加速器也可以用来加速α粒子 4.如图所示是电磁流量计的示意图。
圆管由非磁性材料制成,空间有匀强磁场。
当管中的导电液体流过磁场区域时,测出管壁上MN 两点的电动势E ,就可以知道管中液体的流量Q ——单位时间内流过管道横截面的液体的体积。
已知管的直径为d ,磁感应强度为B ,则关于Q 的表达式正确的是A .B E d Q ⋅⋅=π B .BE d Q 4⋅⋅=πC .B E d Q 42⋅=πD .BE d Q 2⋅=π5.环形对撞机是研究高能离子的重要装置,如图正、负离子由静止经过电压为U 的直线加速器加速后,沿圆环切线方向注入对撞机的真空环状空腔内,空腔内存在着与圆环平面垂直的匀强磁场,磁感应强度大小为B.(两种带电粒子将被局限在环状空腔内,沿相反方向做半径相等的匀强圆周运动,从而在碰撞区迎面相撞.)为维持带电粒子在环状空腔中的匀速圆周运动,下列说法正确是 ( )A .对于给定的加速电压,带电粒子的比荷q /m 越大,磁感应强度B 越大 B .对于给定的加速电压,带电粒子的比荷q /m 越大,磁感应强度B 越小C .对于给定的带电粒子,加速电压U 越大,粒子运动的周期越小D .对于给定的带电粒子,不管加速电压U 多大,粒子运动的周期都不变6.如图所示,一个质量为m ,电荷量为-q ,不计重力的带电粒子从x 轴上的P (a ,0)点以速度v ,沿与x 正方向成60°的方向射入第一象限内的匀强磁场中,并恰好垂直于y 轴射出第一象限。
理论力学(刘又文 彭献)答案第3章

h
ω α
O
图 3.3
x
对时间 t 求导, 答: 速度计算对, 加速度计算不对, 因只将 ϕ 而没有把 sec 2 ϕ
对 t 求导。正确答案是:
a=
dv + 2tanϕ ⋅ ϕ 2 ) + 2hϕ sec 2 ϕ ⋅ tanϕ ⋅ ϕ = hsec 2ϕ ( ϕ = h sec2 ϕ ⋅ ϕ dt
A
vA
C
vC
dv A = 0; dt
an
aC
ρ
B
vB aB
图 3.2
71
n 法向加速度大小, a A =
v A2
ρ
= 25 m/s 2 。对吗?
答: a τA = 0 不对, 因为 v A = 5 m/s 是瞬时值, 而 aτ = 这个变量对 t 求导,所以只有知道 s=f(t)才能求 aτ 。
n = aA
8.如图 3.7a、b 所示速度矢量图对吗?
A
A
vr
va ve v
vr
M B
ω
O
C
ve
va
(a)
图 3.7
(b)
答:不对。图 a 中 va 方向错误,图 b 中 ve 方向错误。正确答案如图 c、d 所 示。
A
vr
ve vr va O
C
ve
va
(c)
(d)
四、科氏加速度: aC = 2ω × vr 注:全国自然科学名词审定委员会 1993 年公布的《力学名词》中改用“科 氏加速度” 。
dv d 2 s 是对弧坐标 s=f(t) = dt dt 2
v2 A
ρ
n 是对的,因 a A 仅与速度的瞬时值及该点的曲率半径有关。
