第二章财务管理的基本概念第一节货币时间价值
中级会计基础精讲班:财务管理-第2章-财务管理基础

基础精讲班中级财务管理2019年全国会计专业技术中级资格考试主讲老师:孙孝群第二章财务管理基础第二章财务管理基础章节概述第二章财务管理基础近3年考试来看,分值为6-7分。
但本章是后面学习的基础,例如,第一节货币时间价值影响到第六章投资管理,甚至可以说第六章投资管理是货币时间价值的应用;第三节成本性态分析是我们学习第八章成本管理的基础。
第二节风险与收益,理解起来有难度,过于理论的内容不建议同学们思考,主要是记住结论,应对考试,因为该部分内容涉及一些数学原理。
第二章财务管理基础第一节货币时间价值第一节货币时间价值本节教材大标题并不能体现出内在逻辑关系。
其实本节主要讲了三大类问题,一是货币时间价值的概念,二是货币时间价值的计算,三是货币时间价值的应用,利率的计算,其中货币时间价值的计算是重点,包含了复利终值和现值的计算(单笔收付),年金终值和现值的计算(多笔等额收付)。
总结如下,本节讲了:第一节货币时间价值第一节货币时间价值【知识点:货币时间价值的概念】一、货币时间价值含义货币时间价值是指在没有风险和没有通货膨胀的情况下,货币经历一定时间的投资和再投资所增加的价值,也称为资金的时间价值。
二、货币时间价值两种表示方法1.绝对数:A企业经过一年的经营,增值1000万元。
(不常用)第一节货币时间价值2.相对数(习惯使用)第一节货币时间价值(二)复利现值【例题】某人为了5年后能从银行取出100元,在复利年利率2%的情况下,求当前应存入金额。
没有现值系数的情况下应当如何算?第一节货币时间价值有现值系数的情况下如何算?【知识点:普通年金终值和现值】一、普通年金终值1.普通年金终值系数通过一到例题感知普通年金终值的推导。
【例】孙老师是位热心于公众事业的人,自2019年12月底开始,他每年都要向一位失学儿童捐款1000元,帮助这位失学儿童从小学一年级就读完九年义务教育。
假设每年定期存款利率都是2%,则小王9年的捐款在2021年年底相当于多少钱?19年底的1000元按复利终值算,产生2期利息,即n-1期的利息。
2020中级会计 财管 第二章 财务管理基础
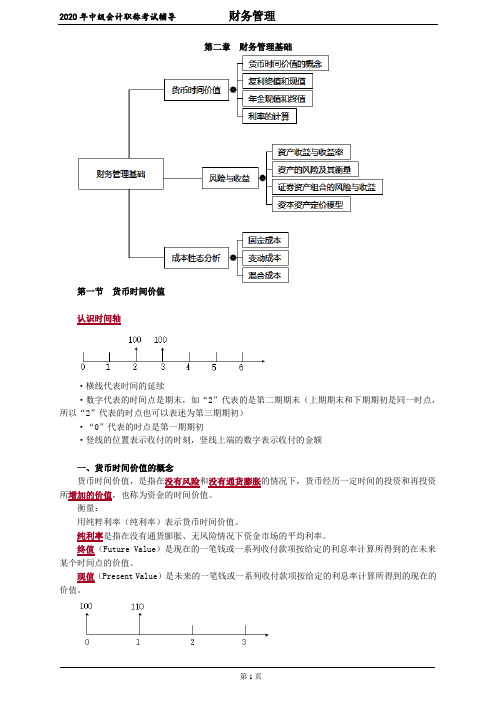
第二章财务管理基础第一节货币时间价值认识时间轴·横线代表时间的延续·数字代表的时间点是期末,如“2”代表的是第二期期末(上期期末和下期期初是同一时点,所以“2”代表的时点也可以表述为第三期期初)·“0”代表的时点是第一期期初·竖线的位置表示收付的时刻,竖线上端的数字表示收付的金额一、货币时间价值的概念货币时间价值,是指在没有风险和没有通货膨胀的情况下,货币经历一定时间的投资和再投资所增加的价值,也称为资金的时间价值。
衡量:用纯粹利率(纯利率)表示货币时间价值。
纯利率是指在没有通货膨胀、无风险情况下资金市场的平均利率。
终值(Future Value)是现在的一笔钱或一系列收付款项按给定的利息率计算所得到的在未来某个时间点的价值。
现值(Present Value)是未来的一笔钱或一系列收付款项按给定的利息率计算所得到的现在的价值。
单利是指按照固定的本金计算利息的一种计息方式。
按照单利计算的方法,只有本金在贷款期限中获得利息,不管时间多长,所生利息均不加入本金重复计算利息。
复利是指不仅对本金计算利息,还对利息计算利息的一种计息方式。
二、复利终值和现值计算(一)复利终值计算【例题·计算分析题】若将1 000元以3%的利率存入银行,则3年后的本利和是多少?F=P×(1+i)n其中:(1+i)n为复利终值系数,用(F/P,i,n)表示。
F=P×(F/P,i,n)『正确答案』F=P×(F/P,i,n)=1 000×(F/P,3%,3)=1 000×1.0927=1 092.7(元)(二)复利现值计算由F=P×(1+i)n得:=F×(1+i)-n=F×(P/F,i,n)其中:(P/F,i,n)为复利现值系数,与复利终值系数互为倒数。
【例题·计算分析题】假设甲存入银行一笔钱,以3%的利率计息,想在3年后得到1 000元,则现在需存入银行多少钱? 已知:(P/F,3%,3)=0.9151『正确答案』P=F×(P/F,i,n)=1 000×(P/F,3%,3)=1 000×0.9151=915.1(元)三、年金终值和现值年金,是指间隔相等的系列等额收付款项。
中级会计师-财务管理-基础练习题-第二章财务管理基础-第一节货币时间价值

中级会计师-财务管理-基础练习题-第二章财务管理基础-第一节货币时间价值[单选题]1.某公司向银行借入20000元,借款期为9年,每年的还本付息额为(江南博哥)4000元,则借款利率为()。
[已知:(P/A,12%,9)=5.3282,(P/A,14%,9)=4.9464]A.13.06%B.13.72%C.15.36%D.16.5%正确答案:B参考解析:本题的考点是利用插值法求利息率。
据题意:20000=4000×(P/A,i,9),解得:(P/A,i,9)=5故选项B正确,选项A、C、D不正确。
[单选题]4.某公司拟于5年后一次还清所欠债务100000元,假定银行利息率为10%,5年期,利率为10%的普通年金终值系数为6.1051;5年期,利率为10%的普通年金现值系数为3.7908,则应从现在起每年年末等额存入银行的偿债基金为()元。
A.16379.75B.26379.66C.379080D.610510正确答案:A参考解析:本题属于已知终值求年金,故答案为:A=F/(F/A,10%,5)=100000/6.1051=16379.75(元)。
故选项A正确,选项B、C、D不正确。
[单选题]5.下列各项中,关于货币时间价值的说法不正确的是()。
A.用相对数表示的货币时间价值也称为纯粹利率B.没有通货膨胀时,短期国库券的利率可以视为纯利率C.货币的时间价值用增加的价值占投入货币的百分数来表示D.货币时间价值是指在没有风险的情况下货币经历一定时间的投资和再投资所增加的价值正确答案:D参考解析:货币时间价值,是指在没有风险和没有通货膨胀的情况下,货币经历一定时间的投资和再投资所增加的价值,也称为资金的时间价值。
故选项D错误。
在实务中,人们习惯使用相对数字表示货币的时间价值,即用增加的价值占投入货币的百分数来表示(选项C正确)。
用相对数表示的货币时间价值也称为纯粹利率(简称纯利率)(选项A正确)。
第二章财务管理之时间价值和风险价值

递延年金现值的计算
例15 某企业向银行借入一笔款项,银行贷款
的年利息率为8%,银行规定前10年不用还本 付息,但从第11年至第20年每年年末偿还本息 1000元,问这笔款项的现值应为多少?
思路一
P=A*[(P/A,i,n+m)- (P/A,i,m)]
A = 150× ( A/F , 8% , 3 ) =150/3.2462=46.21万元
(三)普通年金现值的计算
P A(1 i)1 A(1 i)2 A(1 i)(n1) A(1 i)n 1 (1 i)n
P A i
P A(P / A,i, n)
举例:普通年金现值计算
例9:某企业未来5年每年年末等额从银 行取1万元,为职工发奖金,年利率3%, 现在应该存入多少金额以保证未来5年每 年末从银行等额提出1万元?
=1000*1.08*14.487
=15 645
例13 某企业租用一设备,在10年中每年年 初要支付租金5 000元,年利息率为8%, 问这些租金的现值是多少?
思路一
P=A*[(F/A,i,n-1)+1] =1000* [(F/A,8%,9)+1 ] =1000*(6.247+1) =36 235元
风险是“一定时期内”的风险。
与风险相联系的另一个概念是不确定性。严格说 来,风险和不确定性有区别。
风险可能给投资人带来超出预期的收益,也可能 带来超出预期的损失。
财务管理中的风险按形成的原因一般可分为经营 风险和财务风险两大类。
二、风险程度的衡量——概率分析法
确定概率分布 计算期望值 计算标准离差
25
第二章 财务管理基础(中级财务管理知识点与实例)

第二章财务管理基础考情分析:重点章节,以客观题和计算分析题形式考查。
分值6-8分。
第一节货币时间价值一、货币时间价值的概念货币时间价值是指:在没有风险和通货膨胀的情况下,货币经历一定时间的投资和再投资所增加的价值。
二、复利终值和现值复利是指:一次收付款项、多次收付款项但每次金额不相等。
(一)复利终值F=P×(F/P,i,n)【例】某人将100万元存入银行,年利率4%,半年计息一次,按照复利计算,求5年后的本利和。
答案:F=P×(F/P,2%,10)=100×(F/P,2%,10)=100×1.2190=121.90【例】某项目的建设工期为3年。
其中,第一年贷款400万元,第二年贷款500万元,第三年贷款300万元,贷款均为年初发放,年利率为12%。
若采用复利法计算建设期间的贷款利息,则第三年末贷款的本利和为()万元。
A.1525.17B.1361.76C.1489.17D.1625.17答案:A。
400×(F/P,12%,3)+500×(F/P,12%,2)+300×(F/P,12%,1)=1 525.17。
(二)复利现值P=F×(P/F,i,n)【例】某人拟在5年后获得本利和100万元。
假设存款年利率为4%,按照复利计息,他现在应存入多少元?答案:P=F×(P/F,4%,5)=100×(P/F,4%,5)=100×0.8219=82.19【例】随着折现率的提高,未来某一款项的现值将逐渐增加。
()答案:×。
在折现期间不变的情况下,折现率越高,折现系数越小,现值越小。
结论:(1)复利终值与复利现值互为逆运算;(2)复利终值系数(1+i)n与复利现值系数1/(1+i)n互为倒数(即复利终值系数×复利现值系数=1)。
【例】某人拟购置房产,开发商提出两个方案:方案一是现在一次性支付80万元;方案二是5年后支付100万元。
财务管理-第二章--财务管理的价值观念

复利终值公式:FV=PV(1+i)n
其中 FV ―复利终值; PV―复利现值; i―利息率; n―计息期数; (1+i)n为复利终值系数,记为FVIFi,n或(F/P,i,n)
FV=PV ·FVIFi,n
某企业为开发新产品,向银行借款100 万元,年利率为10%。借款期限为5年,问 5年后一次归还银行的本利和是多少?
FA=A·FVIFA8%,5 =A(F/A,8%,5) =100×5.8666=586.66(元)
拟在5年后还清100000元债务,从现在起每年等额存入银 行一笔款项。假设银行存款利率为10%,每年需要存入多少元?
已知:5年后的终值10万元,求A? F=A(F/A,i,n) A=F / (F/A,i,n)
2000 2000 2000 2000 2000
0
1
2
3
4
5 年末
这是期限为5年每年收入2000元的普通年金的现金流
0
1
2
3
4
5 年初
3000 3000 3000 3000 3000 这是期限为5年每年支付为3000元的预付年金的现金流
年金案例
• 学生贷款偿还 • 汽车贷款偿还 • 保险金 • 抵押贷款偿还 • 养老储蓄
•关系:利率一年内复利多次时,实际利率大于名义 利率, 假设r—名义利率;M—每年复利次数;i—实
际利率
•第一年末 F=P×(1+r/M)M
•
I=P ×(1+r/M)M-P=P[(1+r/M)M-1]
•
i= I/P=(1+r/M)M –1
•接上题:
• F=P×(1+r/M)M = 100(F/P,5%,4)
第二章财务管理基础知识

第一子模块 货币时间价值与风险教学目的及要求:本节学习难度大,计算方法问题是基础,学习时要认真理解资金时间价值、 理解相关的例题。
教学重点:复利终值、复利现值、普通年金、教学难点:普通年金教学时数:2课时教学方法:讲授法 练习法教学内容:第一节 资金时间价值I ……利率,通常指每年利息与本金之比;L ……利息;S ……本金与利息之和,又称本利和或终值;T ……时间,通常以年为单位。
1.单利利息的计算例1某企业有一张带息期票,面额为1 200元,票面利率为3%,出票日期6月15日,8月14日到期(共60天),则到期利息为:I =1200×3%×36060=6(元) 在计算利息时,除非特别指明,给出的利率是指年利率。
对于不足1年的利息,以1年等于360天来折算。
一、资金时间价值的概念资金时间价值也称货币时间价值,是指货币经历一定时间的投资和再投资所增加的价值。
按照马克思主义观点,货币是价值的表现形式,但货币本身并不能增值。
只有当投资者将货币投入生产领域才是资本,才能带来价值的增值。
企业资金循环和周转的起点是投入货币资金。
从量的规定性来看,货币的时间价值是在没有风险和没有通货膨胀条件下的社会平均资金利润率。
二、资金时间价值的计算终值又称将来值,是现在一定量现金在未来某一时点上的价值,俗称本利和。
现值又称本金,是指未来某一时点上的一定量现金折算到现在的价值。
终值与现值的计算与利息计算有关,在实际工作中有两种方式计息,即单利和复利。
终值与现值的计算与利息计算有关,在实际工作中有两种方式计息,即单利和复利(一)单利的计算单利是计算利息的一种方法。
按照这种方法,只要本金在贷款期限中获得利息,不管时间多长,所生利息均不加入本金重复计算利息。
在单利计算中,经常使用以下符号:P ……本金,又称期初金额或现值;2.单利终值的计算假设例1中带息期票到期,出票人应付的本利和即票据终值为:S =1 200×(1+3%×36060)=1 206(元) 例2假定工商银行的一年期定期存款利率为 6%,某公司现在将本金1 000万元存入银行,采用单利计息,则第一、第二、第三年末的终值(本利和)分别为: S 1=1 000×(1+6%×1)=1 060(万元)S 2=1 000×(1+6%×2)=1 120(万元)S 3=1 000×(l +6%×3)=1 180(万元)即每期得到的利息不参与以后各期计息。
财务管理的基本原理

答案:(1)125.97万元;(2)126.53万元;(3) 根据(2)不能满足;(4)25.05万元
34
小结
重点:现值、终值、年金的 概念理解和计算
难点:递延年金的计算
35
第二节 风险报酬
36
一、风险报酬的概念
(一)风险的含义 事物的未来结果分类 确定型 → 唯一结果、必然发生 风险型 → 多种可能结果、知道发生的概率 不确定型 →多种可能结果、不知道发生的概率 在财务管理的实践中,
P A
i
0
1234
AA AA
A(1+i)0 A(1+i)-1
A(1+i)-2
A(1+i)-3
P
A1
(1 i
i)n
(1
i)
预付年金现值
P
1 (1 i)(n1)
A
i
A
P
A1
(1
i) i
(
n 1)
1
(1)假设每年复利一次,则2007年1月1日该笔存款 的终值是多少?
(2)假设每半年复利一次,则2007年1月1日该笔存 款的终值是多少?
(3)假设该公司希望2007年1月1日该笔存款的终值 达到130万元,按照每半年复利一次,试问目前的利率能 否满足该公司的要求? (4)计算该公司今后5年内每年末平均可提取的现金数。
指各期期初等额的收付款项。 (1)预付年金终值的计算
公式:F=A(1+i)+A(1+i)2+……+A(1+i)n F=A(F/A,i,n)(1+i)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一节 货币的时间价值
一、利率 :货币的价格
1、单利与复利
表:年利率为10%的100元投资经过不同时间段的终值
单利
复利
年份 初始价值+利息
终值 初始价值+利息
终值
1 100+10
=110 100 +10
=110
2 110+10
=120 110+11
=121
3 120+10
字。 对于每季度计复利一次,其第三年末的终值为: FV3=100×(1+0.08/4)4×3 =126.53元 每年计复利一次的终值为: FV3=100×(1+0.08)3 =125.97元
连续复利终值计算
无限次计复利(连续复利计算continuously compounded rate)Βιβλιοθήκη 复利终值与计算利息次数关系
与之相比,每年、每半年、每季度和每月计算复利一次 条件下,年末终值分别为125.97、126.53、126.82、 127.12。因此,对于给定的利率,按连续复利所计算出 的第n年末的终值大于其他方式计算出的相应终值。随着 等式FVn=PV(1+r/m)m n中m的增大,终值增加的速度 递减,直到最终达到连续复利方式下所得到的终值水平。
利息的利息,亦即前期产生的利息也会产生利息,这就是复利。 第三年末,该储户将有: FV3=100×(1+0.08)3 =125.97元
二、复利终值:FVn=A(1+i)n
复利终值系数FVIFi,n= (1+i)n 或者写为F/V,i,n
学习用终值复利系数表 例:某企业有1200万元,拟投入一个报酬率为8%的
200 2090+10 =2100 17,264,116,042+1,726,411,604=18,990,527,646
215 2240+10 =2250 72,116,497,132+7,211,649,731=79,328,146,845
如果有人在清朝鸦片战争前40年(1800年)按10%利率投资100元,那他将留给子孙近 190亿元。
FV1/2 = 100×(1+0.08/2)=104.00元 到第一年年末,它将为:
FV1=100×(1+0.08/2)2 =108.16元 与之相比,如果每年仅支付一次利息,则终值为108元。0。
16元的差异归因于一个事实:前6个月中最后一个月的月 末所得的4。00元在后6个月中也获得了利息。一年中利息 支付的次数越多,则该年末的终值也会越大。
投资项目,经过多少年该向投资额能增加一倍? 例:某企业有1200万元,希望在19年后该资金增长
到原来的3倍,选择投资项目最低可接受的项目报酬率 为多少?
二、复利终值:FVn=A(1+i)n
例题答案: 2400=1200(1+8%)n ,2= (1+8%)n n=9 查复利终值系数表 F/A,8%,n=2 3600=1200(1+i %)19 ,3= (1+i)19 i=6%
不同利率、期数与复利终值图
(时间越长,FV越大;利率越高,FV越大)
FV
r=15%
r=10%
r=5%
时间
2、一年计利息多次
假设储户的银行帐户中有100元,年利率为8%,利息每半 年支付一次。计算其年末的终值?
在前六个月(前半年)中,收益率是4%(年利率为8%的 一半),于是在6个月末的终值是:
三、复利现值: PVn= A/(1+i)n
若银行一年期存款利率为8%,为了能在一年后购买价值为700元的商 品,你今天需要在银行里存多少钱?
如果A1表示你希望在一年后收到的货币数量,PV表示现在的存款数量, 且k为年利率,我们有如下等式:
A1 = PV(1+k) 在本例中,有700=PV(1+8%),解出PV=700/1.08=648.15元 即你今天存入648.15元,则在一年后可得到700元。换一种表达方式
2、一年计利息多次
假设每年支付利息m次,第n年末终值的一般计算公式如下: FVn=PV(1+r/m)m n 每季计复利一次 举个例子,假设上面的例子中,利息每
季度支付一次,试计算其第一年末的终值?它将是: FV1=100×(1+0.08/4)4 =108.24元 很明显,该数据大于每一年或每半年计复利一次所得的数
当m趋于无穷大时,表达式(1+r/m)m n将趋近于ern ,其中e约为
2.71828,其定义为:
1
e = lim(1+ )m
m→∞
m
若以利率r连续计算复利,PV0的初始投资在第n年末的终值计算公式为:
FVn=PV0 ern
对于前面的例子而言,若无限次计算复利,第三年末的终值为:
FV3 = 100×e0。08×3 =100×2.718280。08×3 =127.12
=130 121+12.1
=133.1
4 130+10
=140 133.1+13.3
=146.4
10 190+10
=200 236+24
=259
20 290+10
=300 612+61
=673
50 590+10
=600 10,672+1,067
=11,739
100 1090+10
=1100 1,252,783+125,278 =1,378,061
货币的时间价值:利率、时间因素影响
1776年1.8美元的2001年所值
年息率
(复息算) 2001年值 上升倍数
2%
$162
90倍
4%
$14,586
8,103倍
6%
$1,312,949 729,416倍
8%
$118,187,944 65,659,969倍
225年前的1.8美元的今天所值,以年利率8%(8厘) 复利计算,是1.18多亿,上升幅度了6500多万倍!
二、复利终值:FVn=A(1+i)n
1、一年计利息一次
假设一个人在银行帐户中存款100元,若利率为8%,每年计复利一次, 那 么 第 一 年 末 这 100 元 将 值 多 少 钱 ? 即 求 出 100 元 年 末 的 终 值 (terminal value)(或未来值)
FV1=100×(1+0.08)=108元 如果该储户第二年继续把钱存在银行,这108元到第二年末,其终值为: FV2=100×(1+0.08)2 =116.64元 其中8元是初始的100元得到的利息,0.64元是第一年末得到的8元的
