最新初中数学方程与不等式之不等式与不等式组知识点
中考数学复习专题三-不等式和不等式组(解析版)

中考专题复习知识点1、不等式的解:能使不等式成立的未知数的值叫做不等式的解。
知识点2、不等式的解集:一个含有未知数的不等式的解的全体叫做这个不等式的解集。
知识点3、不等式的解集在数轴上的表示: (1)x >a :数轴上表示a 的点画成空心圆圈,表示a 的点的右边部分来表示;(2)x <a :数轴上表示a 的点画成空心圆圈,表示a 的点的左边部分来表示;(3)x ≥a :数轴上表示a 的点画成实心圆点,表示a 的点及表示a 的点的右边部分来表示;(4)x ≤a :数轴上表示a 的点画成实心圆点,表示a 的点及表示a 的点的左边部分来表示。
在数轴上表示大于3的数的点应该是数3所对应点的右边。
画图时要注意方向(向右)和端点(不包括数3,在对应点画空心圆圈)。
如图所示:同样,如果某个不等式的解集为x ≤-2, 那么它表示x 取-2左边的点 画实心圆点。
如图所示:总结:在数轴上表示不等式解集的要点: 小于向左画,大于向右画;无等号画空心圆圈,有等号画圆点。
知识点4、不等式的性质:(1)不等式的两边都加上(或减去)同一个数或同一个整式,不等号的方向不变;(2)不等式的两边都乘以(或除以)同一个正数,不等号的方向不变;(3)不等式的两边都乘以(或除以)同一个负数,不等号的方向改变。
知识点5、一元一次不等式:只含有一个未知数,并且未知数的最高次数是1,系数不等于0的不等式,叫做一元一次不等式。
知识点6、解一元一次不等式的一般步骤:(1)去分母;(2)去括号;(3)移项;(4)合并同类项;(5)未知数的系数化为1。
通过这些步骤可以把一元一次不等式转化为x >a (x ≥a )或x <a (x ≤a )的形式。
知识点7、一元一次不等式组:由几个含有同一个未知数的一次不等式组成的不等式组叫做一元一次不等式组。
知识点8、知识点9、解不等式组:求不等式组解集的过程叫做解不等式组。
知识点10、解一元一次不等式组的一般步骤:先分别解不等式组中的各个不等式,然后再求出这几个不等式解集的公共部分。
初中数学方程与不等式知识点整理

初中数学方程与不等式知识点整理方程与不等式是初中数学中的重要内容,它们在解决实际问题、建立数学模型和推断问题解的存在性和唯一性等方面发挥着重要的作用。
本文将对初中数学中关于方程与不等式的知识点进行整理和总结,以帮助同学们更好地掌握和应用这一知识。
1. 方程的定义及基本概念方程是含有一个或多个未知数的等式。
常见的方程类型有一元一次方程、二元一次方程和二次方程等。
解一个方程的过程就是求满足方程的未知数的值,这些值称为方程的解。
两个方程称为互为等价方程,当且仅当它们有相同的解。
2. 一元一次方程一元一次方程是形如ax + b = 0的方程,其中a和b是已知数,x是未知数。
解一元一次方程的步骤如下:(1) 移项:将方程中的项整理到等式的同一侧;(2) 合并同类项:将方程中的同类项合并;(3) 用反运算消元:利用加减乘除的性质,将方程中的项消去;(4) 化简方程:将方程化简成形如x = c的等式。
3. 二元一次方程二元一次方程是形如ax + by = c的方程,其中a、b和c是已知数,x和y是未知数。
解二元一次方程的方法有图解法和代入法。
图解法是将方程转化为直线,通过画出这条直线来求解方程。
代入法是利用特定的值代入方程,求解得出满足方程的未知数的值。
4. 二次方程二次方程是形如ax² + bx + c = 0的方程,其中a、b和c是已知数,x是未知数。
解二次方程的一般步骤如下:(1) 化简方程:将方程化简成形如px² + q = 0的等式;(2) 变形:利用配方法或其他方法将方程转化为完全平方;(3) 求根公式:利用求根公式求出方程的解;(4) 检验解的合法性:将得到的解带入原方程,检验是否满足方程。
5. 不等式的定义及基本概念不等式是比较两个数大小关系的数学语句。
常见的不等式类型有一元一次不等式、一元二次不等式和绝对值不等式等。
解一个不等式的过程是求满足不等式的数的范围,这个范围称为不等式的解集。
方程与不等式知识点

方程与不等式知识点一、方程的概念与性质方程是将含有未知数的等式称为方程。
一般形式为:P(x)=0,其中P(x)为多项式函数,x为未知数。
方程的次数是多项式中各项次数的最大值。
方程的性质有以下几个方面:1.方程的根:方程P(x)=0的解称为方程的根。
方程的根可以是实数也可以是复数。
2.方程的根与系数的关系:设方程P(x)=0的根为a,则P(a)=0,反之,如果P(a)=0,那么a就是方程P(x)=0的根。
3.方程的解的性质:若a是方程P(x)=0的根,则(x-a)是P(x)的一个因式。
4.方程的根的个数:n次方程P(x)=0的解的个数至多为n个。
二、方程的解法1.一次方程的解法:设方程a1x+a0=0,其中a1≠0,则方程的解为x=-a0/a12.二次方程的解法:设方程ax^2 + bx + c = 0,其中a ≠ 0,则方程的解公式为x = (-b ± √(b^2 - 4ac))/(2a)。
3.高次方程的解法:对于高次方程,一般采用因式分解、配方法、卡尔丹法等方法求解。
三、不等式的概念与性质不等式是使用不等号连接的数学关系,在不等式中,未知数的取值满足特定的条件。
常见的不等式有大于等于(≥)、小于等于(≤)、大于(>)、小于(<)等。
不等式的性质有以下几个方面:1.不等式的解集:满足不等式所有条件的数值的集合称为不等式的解集。
2.在不等关系中,可以在两边同加或者同减一个数,可以在两边同乘或者同除正数,但是如果两边同乘或者同除负数的话,应该将不等号翻转。
3.对于不等式组的解集,满足所有不等式的解的交集称为不等式组的解集。
四、不等式的解法1.一次不等式的解法:将不等式变形,找到未知数的取值范围,得到的范围即是不等式的解。
2.二次不等式的解法:将二次不等式化为零,找到对应的方程,并求出方程的解,然后根据二次不等式表示的形式将解的范围确定下来。
3.绝对值不等式的解法:对于绝对值不等式,根据绝对值的性质,将不等式分成正负两种情况进行求解。
不等式与方程根知识点总结

不等式与方程根知识点总结一、不等式的基本概念1.1 不等式的定义不等式是一种比较两个数大小关系的数学表达式,它由不等号(>、<、≥、≤)连接的两个表达式组成。
例如,3x+5>7就是一个不等式,其中3x+5和7分别是两个表达式,>是不等号。
1.2 不等式的性质不等式有一些基本的性质,包括传递性、反对称性和加减乘除性。
传递性指的是如果a>b且b>c,则a>c;反对称性指的是如果a>b且b>a,则a=b;加减乘除性指的是如果a>b,则a+c>b+c,a-c>b-c,a×c>b×c,a/c>b/c(其中c>0)。
1.3 不等式的解法解不等式的方法分为图解法和代数法两种。
图解法是通过将不等式转化成图形的方式来求解,代数法是通过代数运算来求解。
对于一元一次不等式,通常使用图解法来求解。
1.4 不等式的应用不等式在实际问题中有着广泛的应用,例如在经济学、管理学和自然科学等领域。
例如,利润不等式可以用来描述一个企业的盈利状况,生态平衡不等式可以用来描述生态系统的稳定性。
二、方程的基本概念2.1 方程的定义方程是一个等式,它表示两个表达式相等。
例如,3x+5=7就是一个方程,其中3x+5和7是两个表达式,=是等号。
2.2 方程的性质方程有一些基本的性质,包括等价性、对称性和变换性。
等价性指的是如果a=b,则b=a;对称性指的是如果a=b且b=c,则a=c;变换性指的是如果a=b且c=d,则a+c=b+d。
2.3 方程的解法解方程的方法分为试解法、代数法和图解法三种。
试解法是通过试验一些数值来求解,代数法是通过代数运算来求解,图解法是通过将等式转化成图形的方式来求解。
2.4 方程的应用方程在实际问题中也有着广泛的应用,例如在物理学、工程学和金融学等领域。
例如,牛顿第二定律可以用方程的形式来表示,弹性力学中的胡克定律也可以用方程的形式来表示。
方程组与不等式组知识点总结

方程组与不等式组知识点总结一、方程组。
1. 二元一次方程组。
- 定义。
- 含有两个未知数,并且含有未知数的项的次数都是1的整式方程叫做二元一次方程。
把两个含有相同未知数的二元一次方程(或者一个二元一次方程,一个一元一次方程)联立起来,组成的方程组叫做二元一次方程组。
例如x + y=5 2x - y = 1。
- 解法。
- 代入消元法。
- 步骤:从方程组中选一个系数比较简单的方程,将这个方程中的一个未知数用含另一个未知数的代数式表示出来,如对于方程组y = 2x - 3 3x+2y = 8,由第一个方程y = 2x - 3,将y代入第二个方程得3x+2(2x - 3)=8,然后解这个一元一次方程求出x的值,再把x的值代入y = 2x - 3求出y的值。
- 加减消元法。
- 步骤:当方程组中两个方程的同一未知数的系数相等或互为相反数时,把这两个方程的两边分别相减或相加,消去这个未知数,得到一个一元一次方程。
例如对于方程组3x+2y = 11 5x - 2y = 13,将两个方程相加得(3x + 2y)+(5x - 2y)=11 + 13,即8x=24,解得x = 3,再把x = 3代入3x+2y = 11求出y的值。
2. 三元一次方程组。
- 定义。
- 含有三个未知数,并且含有未知数的项的次数都是1的整式方程组成的方程组叫做三元一次方程组。
例如x + y+z = 6 2x - y+z = 3 3x + 2y - z=4。
- 解法。
- 思路是通过消元将三元一次方程组转化为二元一次方程组,再转化为一元一次方程求解。
例如先消去z,可以将第一个方程x + y+z = 6与第三个方程3x + 2y - z = 4相加得到4x+3y = 10,再将第一个方程x + y+z = 6与第二个方程2x - y+z = 3相减得到-x + 2y=3,这样就得到了一个二元一次方程组4x + 3y=10 -x+2y = 3,然后用二元一次方程组的解法求解。
人教版九年级数学第二单元《方程(组)与不等式(组)》中考知识点梳理
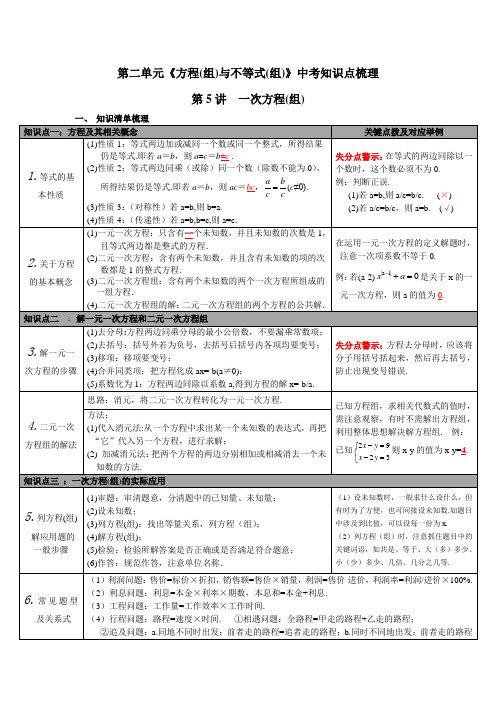
第二单元《方程(组)与不等式(组)》中考知识点梳理第5讲一次方程(组)第6讲一元二次方程第7讲分式方程三、知识清单梳理第8讲一元一次不等式(组)知识点一:不等式及其基本性质关键点拨及对应举例1.不等式的相关概念(1)不等式:用不等号(>,≥,<,≤或≠)表示不等关系的式子.(2)不等式的解:使不等式成立的未知数的值.(3)不等式的解集:使不等式成立的未知数的取值范围.例:“a与b的差不大于1”用不等式表示为a-b≤1.2.不等式的基本性质性质1:若a>b,则a±c>b±c;性质2:若a>b,c>0,则ac>bc,ac>bc;性质3:若a>b,c<0,则ac<bc,ac<bc.牢记不等式性质3,注意变号.如:在不等式-2x>4中,若将不等式两边同时除以-2,可得x<2.知识点二:一元一次不等式3.定义用不等号连接,含有一个未知数,并且含有未知数项的次数都是1的,左右两边为整式的式子叫做一元一次不等式. 例:若230mmx++>是关于x的一元一次不等式,则m的值为-1.4.解法(1)步骤:去分母;去括号;移项;合并同类项;系数化为1.失分点警示系数化为1时,注意系数的正负性,若系数是负数,则不等式改变方向.(2)解集在数轴上表示:x≥a x>a x≤a x<a知识点三:一元一次不等式组的定义及其解法5.定义由几个含有同一个未知数的一元一次不等式合在一起,就组成一个一元一次不等式组.(1)在表示解集时“≥”,“≤”表示含有,要用实心圆点表示;“<”,“>”表示不包含要用空心圆点表示.(2)已知不等式(组)的解集情况,求字母系数时,一般先视字母系数为常数,再逆用不等式(组)解集的定义,反推出含字母的方程,最后求出字母的值.如:已知不等式(a-1)x<1-a 的解集是x>-1,则a的取值范围是a<1.6.解法先分别求出各个不等式的解集,再求出各个解集的公共部分7.不等式组解集的类型假设a<b解集数轴表示口诀x ax b≥⎧⎨≥⎩x≥b大大取大x ax b≤⎧⎨≤⎩x≤a小小取小x ax b≥⎧⎨≤⎩a≤x≤b大小,小大中间找x ax b≤⎧⎨≥⎩无解大大,小小取不了知识点四:列不等式解决简单的实际问题8.列不等式解应用题(1)一般步骤:审题;设未知数;找出不等式关系;列不等式;解不等式;验检是否有意义.(2)应用不等式解决问题的情况:a.关键词:含有“至少(≥)”、“最多(≤)”、“不低于(≥)”、“不高于(≤)”、“不大(小)于”、“超过(>)”、“不足(<)”等;注意:列不等式解决实际问题中,设未知数时,不应带“至少”、“最多”等字眼,与方程中设未知数一致.。
人教版初中数学不等式与不等式组基础知识点归纳总结

人教版初中数学不等式与不等式组基础知识点归纳总结单选题1、不等式组{3(x −1)>x −72x +2⩾3x的解集是( ) A .﹣2<x≤2B .x <﹣2C .x≥2D .无解答案:A解析:分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集.解不等式3(x ﹣1)>x ﹣7,得:x >﹣2,解不等式2x+2≥3x ,得:x≤2,则不等式组的解集为﹣2<x≤2,故选:A .小提示:本题考查了解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.2、下列说法中错误的是( )A .不等式x +2≤3的整数解有无数个B .不等式x +4<5的解集是x <1C .不等式x <3的正整数解有限个D .0是不等式2x <−1的解答案:D解析:逐一对选项进行分析即可.A. 不等式x +2≤3的解集为x ≤1 ,所以整数解有无数个,故正确;B. 不等式x +4<5的解集是x <1,故正确;C. 不等式x <3的正整数解为1,2,是有限个,故正确;D. 0不是不等式2x <−1的解,故错误;故选:D .小提示:本题主要考查不等式的解集及解的个数,会解不等式是解题的关键.3、“x 的2倍与3的和是非负数”列成不等式为( )A .2x +3≥0B .2x +3>0C .2x +3≤0D .2x +3<0答案:A解析:非负数就是大于或等于零的数,再根据x 的2倍与3的和是非负数列出不等式即可.解:“x 的2倍与3的和是非负数”列成不等式为:2x +3≥0,故选:A.小提示:本题考查的是列不等式,掌握“非负数是正数或零,用不等式表示就是大于或等于零”是解题的关键.4、关于x 的方程4x-2m+1=5x-8的解是负数,则m 的取值范围是( )A .m>92B .m<0C .m<92D .m>0 答案:A解析:解:方程4x -2m +1=5x -8的解为x =9-2m .由题意得:9-2m <0,则m >92.故选A .5、下列式子:①3>0;②4x +5>0;③x <3;④x 2+x ;⑤x ≠﹣4;⑥x +2>x +1,其中不等式有( )个A .3B .4C .5D .6答案:C解析:根据不等式定义可得答案.①3>0;②4x +5>0;③x <3;⑤x ≠﹣4;⑥x +2>x +1是不等式,共5个,故选C .小提示:本题考查不等式的定义,熟练掌握不等式的定义是解题的关键.6、关于x 的一元一次方程4x-m+1=3x-1的解是负数,则m 的取值范围是( ).A .m=2B .m >2C .m <2D .m≤2答案:C解析:∵方程x ﹣m +2=0的解是负数,∴x =m ﹣2<0,解得:m <2,故选C .7、下列某不等式组的解集在数轴上表示如图所示,则该不等式组是( )A .{x −1<3x +1<3B .{x −1<3x +1>3C .{x −1>3x +1>3D .{x −1>3x +1<3答案:B分析:先根据在数轴上表示不等式解集的方法得出该不等式组的解集,再找出符合条件的不等式组即可.详解:A、此不等式组的解集为x<2,不符合题意;B、此不等式组的解集为2<x<4,符合题意;C、此不等式组的解集为x>4,不符合题意;D、此不等式组的无解,不符合题意;故选B.点睛:本题考查的是在数轴上表示不等式的解集,解答此类题目时一定要注意实心与空心圆点的区别,即一般在数轴上只标出原点和界点即可.定边界点时要注意,点是实心还是空心,若边界点含于解集为实心点,不含于解集即为空心点.8、不等式3x−1>x+1的解集在数轴上表示为( )A.B.C.D.答案:C解析:试题解析:由3x﹣1>x+1,可得2x>2,解得x>1,所以一元一次不等式3x﹣1>x+1的解在数轴上表示为:故选C.点睛:首先根据解一元一次不等式的方法,求出不等式3x﹣1>x+1的解集,然后根据在数轴上表示不等式的解集的方法,把不等式3x﹣1>x+1的解集在数轴上表示出来即可.9、用不等式表示:x 减去2的差的绝对值不大于32_________________. 答案:|x −2|≤32解析:根据题意以及不等式的定义列不等式.解:x 减2的绝对值不大于32,列式:|x −2|≤32.故答案是:|x −2|≤32. 小提示:本题考查列不等式,解题的关键是根据不等式的定义,找到题目中的不等关系进行列式.10、一次测验共出5道题,做对一题得一分,已知26人的平均分不少于4.8分,最低的得3分,至少有3人得4分,则得5分的有______ 人.答案:22解析:解:设得5分的人数为x 人,得3分的人数为y 人.则可得{x +y +3=265x +3y +12>26×4.8,解得:x >21.9. ∵一共26人,最低的得3分,至少有3人得4分,∴得5分最多22人,即x ≤22.∴21.9<x ≤22且x 为整数,所以x =22.故得5分的人数应为22人.故答案为22.点睛:此题考查不等式组的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程组,再求解.解题过程中一定要符合题目的意思,以事实为依据.11、已知不等式组{x >1x <a −1无解,则a 的取值范围为__.答案:a⩽2解析:求出不等式组中每个不等式的解集,根据已知即可得出关于a的不等式,即可得出答案.解:∵不等式组{x>1x<a−1无解,∴a−1⩽1,解得:a⩽2,所以答案是:a⩽2.小提示:本题考查了一元一次不等式组的应用,解此题的关键是能得出关于a的不等式,题目比较好,难度适中.12、不等式组{2x−1<3−12x−1≤0的整数解的和为________.答案:-2解析:先根据一元一次不等式组解出x的取值,根据x是整数解得出x的可能取值,再相加.解:{2x−1<3①−12x−1≤0②,解不等式①得,x<2;解不等式②得,x≥-2,∴不等式组的解集是:-2≤x<2,∴不等式组的整数解是:-2,-1,0,1,∴整数解的和为-2-1+0+1=-2,所以答案是:-2.小提示:本题考查了解一元一次不等式组,不等式组的整数解的应用,解题的关键是能根据不等式的解集求出不等式组的解集.13、已知关于x的不等式3x-5k>-7的解集是x>1,则k的值为________.答案:2解析:试题分析:不等式可变形为:3x>5k-7,x>5k−7,3∵关于x的不等式3x-5k>-7的解集是x>1,∴5k−7=1,3解得:k=2.故答案为2.点睛:本题考查了不等式的解集,利用不等式的解集得出关于k的方程是解题关键.解答题14、在平面直角坐标系中,若P、Q两点的坐标分别为P(x1,y1)和Q(x2,y2),则定|x1−x2|和|y1−y2|中较小的一个(若它们相等,则任取其中一个)为P、Q两点的“直角距离小分量”,记为d min(P,Q).例如:P(−2,3),Q(0,2),因为x1=−2,x2=0,|x1−x2|=|−2−0|=2;y1=3,y2=2,|y1−y2|=|3−2|=1,而|3−2|<|−2−0|,所以d min(P,Q)=|3−2|=1.(1)请直接写出A(3,−2)和B(−1,1)的直角距离小分量d min(A,B)=_________;(2)点D是坐标轴上的一点,它与点C(3,−1)的直角距离小分量d min(C,D)=2,求出点D的坐标;(3)若点M(m+1,2m−2)满足以下条件:a)点M在第一象限;b)点M与点N(5,0)的直角距离小分量d min(M,N)<2c)∠MON>45°,O为坐标原点.请写出满足条件的整点(横纵坐标都为整数的点)M的坐标_______.答案:(1)3;(2)D(0,1)或D(0,−3);(3)M(5,6)或(6,8)解析:(1)根据新概念求得即可;(2)分两种情况,根据“直角距离小分量”的定义得出即可;(3)根据题意得出{m+1>02m−2>0,解出m的取值范围,再由∠MON>45°可推导出K OM =2m−2m+1>1,解出m的取值范围,根据横纵坐标都为整数的点取m的值即可.解:(1)∵A(3,−2),B(−1,1),∴|3+1|=4>|−2−1|=3,∴d min(A,B)=3;故答案为3;(2)∵点D是坐标轴上的一点,若D在x轴上,设D(a,0),由于|0+1|=1<2与题意矛盾,故点D是在y轴上的一点,设D(0,b),|0−3|=3>2,∴|b+1|=2,解得:b=1或−3,∴D(0,1)或D(0,−3);(3)由题意得:{m+1>02m−2>0,解得m>1,|m+1−5|=|m−4|,|2m−2−0|=2|m−1|,∴(m−4)2−[2(m−1)]2=−3m2+12,当1<m<2时,d min(M,N)=2|m−1|<2,解得:0<m<2,当m≥2时,d min(M,N)=|m−4|<2,解得:2<m<6,∴m的取值范围是:0<m<2或2<m<6,∵∠MON>45°恰好为l OM的倾斜角,∴K OM>1,K OM=2m−2m+1>1,解得:m<−1或m>3综上:m的取值范围是:3<m<6,∵横纵坐标都为整数,∴m=4和5,∴M(5,6)或(6,8),所以答案是:M(5,6)或(6,8).小提示:本题考查了坐标与图形的性质,解一元一次不等式组,解题的关键是根据新概念列出不等式组.15、求不等式2x+13≤3x−25+1的非负整数解.答案:不等式的非负整数解为0、1、2、3、4.解析:去分母,去括号,移项,合并同类项,即可得出不等式的解集.去分母得:5(2x +1)≤3(3x -2)+15,去括号得:10x +5≤9x -6+15,移项得:10x -9x ≤-5-6+15,合并同类项得x ≤4,∴不等式的非负整数解为0、1、2、3、4.小提示:考查了不等式的性质和解一元一次不等式,主要考查学生运用不等式的性质解一元一次不等式的能力.。
中考数学常见易错知识点汇总(方程组与不等式组)

中考数学常见易错知识点汇总(方程组与不
等式组)
方程(组)与不等式(组)
易错点1:各种方程(组)的解法要熟练掌握,方程(组)无解的意义是找不到等式成立的条件。
易错点2:运用等式性质时,两边同除以一个数必须要注意不能为0 的情况,还要关注解方程与方程组的基本思想。
(消元降次)主要陷阱是消除了一个带X 公因式要回头检验!
易错点3:运用不等式的性质3时,容易忘记改不改变符号的方向而导致结果出错。
易错点4:关于一元二次方程的取值范围的题目易忽视二次项系数不为0导致出错。
易错点5:关于一元一次不等式组有解无解的条件易忽视相等的情况。
易错点6:解分式方程时首要步骤去分母,分数相相当于括
号,易忘记根检验,导致运算结果出错。
易错点7:不等式(组)的解得问题要先确定解集,确定解集的方法运用数轴。
易错点8:利用函数图象求不等式的解集和方程的解。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
最新初中数学方程与不等式之不等式与不等式组知识点一、选择题1.a 的一半与b 的差是负数,用不等式表示为( )A .102a b -< B .102a b -≤ C .()102a b -< D .102a b -< 【答案】D【解析】【分析】列代数式表示a 的一半与b 的差,是负数即小于0. 【详解】 解:根据题意得102a b -< 故选D .【点睛】 本题考查了列不等式,首先要列出表示题中数量关系的代数式,再由不等关系列不等式.2.如果不等式(2)25a x a ->-的解集是4x <,则不等式251a y ->的解集是( ).A .52y < B .25y < C .52y > D .25y > 【答案】B【解析】【分析】 根据不等式的性质得出20a -<,2542a a -=-,解得32a =,则2a=3,再解不等式251a y ->即可.【详解】解:∵不等式(a-2)x >2a-5的解集是x <4,∴20a -<, ∴2542a a -=-, 解得32a =, ∴2a=3, ∴不等式2a-5y >1整理为351y ->, 解得:25y <.故选:B .【点睛】本题考查了含字母系数的不等式的解法,有一定难度,注意不等式两边同乘以(或除以)同一个负数,不等号的方向改变.3.不等式的解集在数轴上表示正确的是( )A .B .C .D .【答案】C【解析】【分析】 先解不等式,根据解集确定数轴的正确表示方法.【详解】解:不等式2x+1>-3,移项,得2x >-1-3,合并,得2x >-4,化系数为1,得x >-2.故选C .【点睛】本题考查解一元一次不等式,注意不等式的性质的应用.4.若不等式24x <的解都能使关于x 的一次不等式2(1)x x a ++<成立,则a 的取值范围是( )A .8a ≥B .8a ≤C .8a >D .8a <【答案】A【解析】【分析】先求出不等式24x <的解集,再求出不等式2(1)x x a ++<的解集,即可得出关于a 的不等式并求解即可.【详解】解:由24x <可得:x <2;由2(1)x x a ++<可得:x <23a -; 由题意得:23a -≥2,解得:a≥8; 故答案为A .【点睛】本题主要对解一元一次不等式组、不等式的解集等知识,根据题意得到关于a 的不等式是解答本题的关键.5.若某人要完成2.1千米的路程,并要在18分钟内到达,已知他每分钟走90米,若跑步每分钟可跑210米,问这人完成这段路程,至少要跑多少分钟?设要跑x 分钟,则列出的不等式为( )A .21090(18)2100x x +-≥B .90210(18)2100x x +-≤C .21090(18) 2.1x x +-≤D .21090(18) 2.1x x +->【答案】A【解析】设至少要跑x 分钟,根据“18分钟走的路程≥2100米”可得不等式:210x+90(18–x )≥2100,故选A .6.若关于x 的不等式(-1) 1m x m <-的解集为1x >,则m 的取值范围是( ) A .1m >B .1m <C .1m ≠D .1m =【答案】B【解析】【分析】根据不等式的基本性质3,两边都除以m-1后得到x >1,可知m-1<0,解之可得.【详解】∵不等式(m-1)x <m-1的解集为x >1,∴m-1<0,即m <1,故选:B .【点睛】此题考查不等式的解集,熟练掌握不等式的基本性质是解题的关键.7.解不等式组3422133x x x -≥⎧⎪⎨+>-⎪⎩①②时,不等式①②的解集在同一条数轴上表示正确的是( )A .B .C.D.【答案】D【解析】【分析】先求出不等式组中各个不等式的解集,再利用数轴确定不等式组的解集.【详解】x≤-,解不等式①得:1x<,解不等式②得:5将两不等式解集表示在数轴上如下:故选:D.【点睛】本题考查了解一元一次不等式组,在数轴上表示不等式的解集解不等式组时要注意解集的确定原则:同大取大,同小取小,大小小大取中间,大大小小无解了.x-≥0的解集在数轴上表示正确的是()8.不等式26A.B. C.D.【答案】B【解析】【分析】先求解出不等式的解集,再表示在数轴上【详解】解不等式:2x-6≥02x≥6x≥3数轴上表示为:故选:B【点睛】本题考查不等式的求解,需要注意,若不等式两边同时乘除负数,则不等号需要变号9.已知三个实数a,b,c满足a﹣2b+c<0,a+2b+c=0,则()A.b>0,b2﹣ac≤0B.b<0,b2﹣ac≤0C.b>0,b2﹣ac≥0D.b<0,b2﹣ac≥0【答案】C【分析】根据a ﹣2b +c <0,a +2b +c =0,可以得到b 与a 、c 的关系,从而可以判断b 的正负和b 2﹣ac 的正负情况.【详解】∵a ﹣2b +c <0,a +2b +c =0,∴a +c =﹣2b ,∴a ﹣2b +c =(a +c )﹣2b =﹣4b <0,∴b >0,∴b 2﹣ac =222222a c a ac c ac +++⎛⎫-= ⎪⎝⎭=2222042a ac c a c -+-⎛⎫= ⎪⎝⎭…, 即b >0,b 2﹣ac ≥0,故选:C .【点睛】此题考查不等式的性质以及因式分解的应用,解题的关键是明确题意,判断出b 和b 2-ac 的正负情况.10.某种商品的进价为800元,出售时标价为1200元,后来由于该商品积压,商店准备打折销售,但要保证利润率不低于5%,则至多可打( )A .6折B .7折C .8折D .9折 【答案】B【解析】【详解】设可打x 折,则有1200×10x -800≥800×5%, 解得x≥7.即最多打7折.故选B .【点睛】本题考查的是一元一次不等式的应用,解此类题目时注意利润和折数,计算折数时注意要除以10.解答本题的关键是读懂题意,求出打折之后的利润,根据利润率不低于5%,列不等式求解.11.某商品进价为800元,出售时标价为1200元,后来商店准备打折出售,但要保持利润率不低于20%,则最多打( )折.A .6折B .7折C .8折D .9折【答案】C【解析】设打了x 折,用售价×折扣﹣进价得出利润,根据利润率不低于20%,列不等式求解.【详解】解:设打了x 折,由题意得,1200×0.1x ﹣800≥800×20%,解得:x≥8.答:至多打8折.故选:C【点睛】本题考查一元一次不等式的应用,正确理解利润率的含义,理解利润=进价×利润率,是解题的关键.12.如果,0a b c ><,那么下列不等式成立的是( )A .a c b +>B .a c b c +>-C .11ac bc ->-D .()()11a c b c -<- 【答案】D【解析】【分析】根据不等式的性质即可求出答案.【详解】解:∵0c <,∴11c -<-,∵a b >,∴()()11a c b c -<-,故选:D .【点睛】本题考查不等式的性质,解题的关键是熟练运用不等式的性质,本题属于中等题型.13.已知4<m <5,则关于x 的不等式组0420x m x -<⎧⎨-<⎩的整数解共有( ) A .1个B .2个C .3个D .4个 【答案】B【解析】【分析】先求解不等式组得到关于m 的不等式解集,再根据m 的取值范围即可判定整数解.【详解】不等式组0420x m x -<⎧⎨-<⎩①②由①得x <m ;由②得x >2;∵m 的取值范围是4<m <5,∴不等式组0420x m x -<⎧⎨-<⎩的整数解有:3,4两个. 故选B .【点睛】本题考查了一元一次不等式组的整数解,用到的知识点是一元一次不等式组的解法,m 的取值范围是本题的关键.14.已知实数(0)a a >,b ,c 满足0a b c ++<,20a b +=,则下列判断正确的是( ).A .c a <,24b ac >B .c a <,24b ac <C .c a >,24b ac >D .c a >,24b ac <【答案】A【解析】【分析】由20a b +=,可得2,b a =- 代入0a b c ++<可得答案,再由2b a =-得到224,b a =利用已证明的基本不等式c a <,利用不等式的基本性质可得答案.【详解】解:20,a b +=Q 2,b a ∴=- 224,b a =0,a b c ++Q <20,a a c ∴-+<,c a ∴<0,a Q > 40,a ∴>244,a ac ∴>24.b ac ∴>故选A .【点睛】本题考查的是不等式的基本性质,掌握不等式的基本性质是解题关键.15.如图,不等式组315215x x --⎧⎨-<⎩…的解集在数轴上表示为( ) A . B .C .D .【答案】C【解析】【分析】 根据解一元一次不等式组的步骤:先解第一个不等式,再解第二个不等式,然后在数轴上表示出两个解集找公共部分即可.【详解】由题意可知:不等式组315215x x ①②--⎧⎨-<⎩…,不等式①的解集为2x ≥-,不等式②的解集为3x <,不等式组的解集为23x -≤<,在数轴上表示应为. 故选C .【点睛】本题主要考查了一元一次不等式组的解法,熟知和掌握不等式组解法的步骤和在数轴上表示解集是解题关键.16.不等式组213312x x +⎧⎨+≥-⎩<的解集在数轴上表示正确的是( ) A .B .C .D .【答案】A【解析】【分析】先求出不等式组的解集,再在数轴上表示出来即可.【详解】 213312x x +⎧⎨+≥-⎩<①② ∵解不等式①得:x <1,解不等式②得:x≥-1,∴不等式组的解集为-1≤x <1, 在数轴上表示为:,故选A .本题考查了解一元一次不等式组和在数轴上表示不等式组的解集,能根据不等式的解集求出不等式组的解集是解此题的关键.17.已知不等式组2010x x -⎧⎨+≥⎩<,其解集在数轴上表示正确的是( ) A .B .C .D .【答案】D【解析】【分析】分别解不等式组中的每一个不等式,确定出各不等式解集的公共部分,进而在数轴上表示出来即可.【详解】2010x x -⎧⎨+≥⎩<①②, 解①得:x<2,解②得:x≥-1,故不等式组的解集为:-1≤x<2,故解集在数轴上表示为:.故选D.【点睛】本题考查了解一元一次不等式组,正确掌握解题方法以及解集的确定方法“同大取大,同小取小,大小小大中间找,大大小小无解了”是解题的关键.18.已知点P (1﹣a ,2a+6)在第四象限,则a 的取值范围是( )A .a <﹣3B .﹣3<a <1C .a >﹣3D .a >1【答案】A【解析】根据第四象限的点的横坐标是正数,纵坐标是负数列出不等式组求解即可.【详解】解:∵点P(1﹣a,2a+6)在第四象限,∴10 260aa->⎧⎨+<⎩解得a<﹣3.故选A.【点睛】本题考查了点的坐标,一元一次不等式组的解法,求不等式组解集的口诀:同大取大,同小取小,大小小大中间找,大大小小找不到(无解).19.不等式组10235xx+≤⎧⎨+<⎩的解集在数轴上表示为()A.B.C.D.【答案】C【解析】【分析】先分别解不等式,得到不等式组的解集,再在数轴上表示解集.【详解】因为,不等式组10235xx+≤⎧⎨+<⎩的解集是:x≤-1,所以,不等式组的解集在数轴上表示为故选C【点睛】本题考核知识点:解不等式组.解题关键点:解不等式.20.若关于x的分式方程11144axx x-+=--有整数解,其中a为整数,且关于x的不等式组2(1)43,50x xx a+≤+⎧⎨-<⎩有且只有3个整数解,则满足条件的所有a的和为()A .8B .9C .10D .12【答案】C【解析】【分析】 分别解分式方程和不等式组,根据题目要求分别求出a 的取值范围,再综合分析即可得出a 的值,最后求和即可.【详解】 解:解分式方程11144ax x x -+=--, 得4x 1a=-. 又∵4x ≠,解得0a ≠.又∵方程有整数解,∴11a -=±,2±,4±,解得:2,3a =,1-,5,3-.解不等式组2(1)43,50x x x a +≤+⎧⎨-<⎩, 得,25a x -<…. 又不等式组有且只有3个整数解,可求得:05a <≤.综上所述,a 的值为2,3,5,其和为10.故选:C .【点睛】本题主要考查分式方程与不等式组的综合运用,掌握解分式方程的方法,会求不等式组的整数解是解此题的关键.。
