弹性波动方程数值解的有限元并行算法
弹性力学的有限元求法
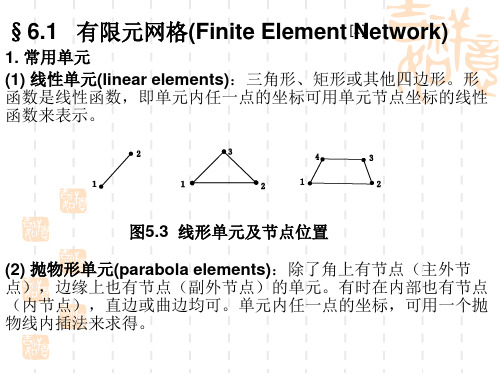
形态函数的几何意义
1 Ni 2A (ai bi x ci y)
1x y
Ni
11 2A
xj
yj
1 xm ym
Ni
SPJM SMIJ
Nj
SPMI SIJM
Nm
SPIJ SIJM
任意一点P的形态函数Ni是点P与结点I的对边所构 成的三角形面积与整个单元面积之比。
2.3单元载荷移置
有限元法的求解对象是单元的组合体，待求解 的未知变量都定义在单元的结点上，因此作用 在弹性体上的外力，需要移置到相应的单元结 点上成为结点载荷。
)T {P}
( xp, yp)
由于虚位移是任意的，
{R}e ([N ]
)T {P}
( xp, yp)
(2-16)
例2.3、在均质，等厚的三角形单元ijm的一点p （0.25a, 0.5a）上作用有集中载荷Px, Py。
Rxi Ni
Ryi
0
Rxj Ryj
Nj 0
Rxm
N
a1 a4
a2 a5
x x
a3 a6
y y
(2-6)
将3个结点上的坐标和位移分量代入公式（2-6） 就可以将六个待定系数用结点坐标和位移分量 表示出来。首先计算位移分量u的系数，
ui a1 a2 xi a3 yi u j a1 a2 x j a3 y j um a1 a2 xm a3 ym
图5.4 抛物线形单元及节点位置
2. 单元划分要注意的几个问题 (1) 相邻两个单元的节点要与节点重合（外节点与外节点、内节点 与内节点），不能与无节点边重合。
( ,)
(2) 单元不必是相同尺寸，应力有突变的地方，单元划分应较小。 (3) 任何一个单元必须只能在一种材料区，即它不能跨越两种材料
弹性波正演模型的快速有限元算法
弹性波正演模型的快速有限元算法
钱勇先
【期刊名称】《石油地球物理勘探》
【年(卷),期】1990(000)003
【摘要】用有限元法做弹性波正演模型计算已进入实用阶段,但有限元法所要求的大存储量和计算速度慢的缺点依然存在。
本文在深入分析有限元算法的基础上,注意到刚度矩阵,耦合矩阵在特殊单元中的对称性、耦合矩阵具有的转置性及某些特殊特征,采用正方形单元并将与节点相乘的元素归并到时间离散中运算,使计算速度提高一倍,使整体矩阵的存放量减少一半。
文中最后给出了一个计算实例,证实该快速算法的正确性。
【总页数】8页(P260-266,378)
【作者】钱勇先
【作者单位】江汉石油学院物探系
【正文语种】中文
【中图分类】TE13
【相关文献】
1.弹性波动方程数值解的有限元并行算法 [J], 王月英;孙成禹
2.一种基于矢量有限元与多层快速多极子技术的电磁散射快速并行算法 [J], 袁军;刘其中;郭景丽
3.基于能量最小化原理的弹性波CT成像频域有限元反演算法 [J], 薛龙;刘天云;张建民
4.拟地震法电磁波场有限元法正演模型 [J], 沈飚;何继善
5.基于能量最小化原理的弹性波CT成像频域有限元反演算法 [J], 薛龙;刘天云;张建民;
因版权原因，仅展示原文概要，查看原文内容请购买。
第八章 弹性连续体振动的有限元解
205第八章 弹性连续体振动的有限元解上一章讨论的弹性连续体振动问题都只是在简单的特殊边界情况下才能得到精确解，而对于复杂弹性连续体的振动，通常无法得到精确解。
因此，只能采用近似解，近似解方法很多，其要旨在于将无限自由度系统（连续体）变换成为有限多自由度系统（离散系统）来处理。
下面仅介绍现代工程中常用的有限元分析法（简称有限元）。
有限元的基本思想是将一个复杂结构（连续系统）看成是有限个基本元素（单元）在有限个结点彼此相联结的组合结构。
每个单元都是一个弹性体。
有限元法通常是采用位移法，即以结点处的位移作为基本未知量，单元的位移是用结点位移的插值函数表示，单元以至整个结构的一切参数包括位移、应变、应力等都通过结点位移表示出来。
从振动问题来看，最后是将一个连续体的振动问题变成了一个以有限个结点位移为广义坐标的多自由度系统的振动问题。
由于平面刚架所采用的单元综合有受轴向力杆及横向弯曲的两种作用，因此本节着重通过平面刚架（杆系结构）的振动为例来阐明有限元的基本概念与分析步骤。
有限单元法分析过程基本上可分为结构离散化、单元分析、整体分析三个步骤。
一. 结构的离散化如图8-1所示平面刚架，它由三根杆件组成，杆件之间通过刚结点2、3相互连接，若在某些结点上受有作用在刚架平面内的激扰力，这就是一个平面刚架的振动问题。
结构的离散化就是将结构分成若干个单元。
在此例中，取三个杆各为一个单元。
共分成三个单元，在图中分别以①、②、③标明各单元的标号。
各单元之间以及它们与基础的联结点称为结点。
结点编号分别为1、2、3、4。
结点1、4是杆件和基础固定联结的结点，它们不能运动，称为固定结点。
2、3点是杆件间的联结点，是可以运动的，称为可动结点。
可动结点的数目乘以每个结点的基本未知量的数目就是整个结构的自由度数。
对于工程结构来说，结构划分的单元愈多，则结构的自由度数愈多，计算工作量就愈大，但计算结果愈有可能趋于精确解，因此在结构离散化过程中，划分单元的多少，应综合考虑精确度与计算工作量的因素。
第二章 弹性力学问题有限元方法的一般原理和表达格式
第二章 弹性力学问题有限元方法的一般原理和表达格式 2.1 引言本章将讨论通过弹性力学变分原理建立弹性力学问题有限元法列式的基本步骤。
最小位能原理的未知场变量是位移，以结点位移为基本未知量，并以最小位能为基础建立的有限单元位移元。
它是有限元方法中应用最普遍的单元。
对于一个力学或物理问题，在建立其数学模型以后，用有限元方法对它进行分析的首要步骤是选择单元形式。
平面问题三结点三角形单元是有限元方法最早采用，而且至今仍经常采用的单元形式。
我们将以此作为典型，讨论如何应用广义坐标建立单元位移模式与位移插值函数，以及如何根据最小位能原理建立有限元求解方程的原理、方法与步骤，并进而导出弹性力学问题有限元方法的一般列式。
2.2 弹性力学平面问题的有限元列式2.2.1 单元位移模式及插值函数典型的三结点三角形单元结点编码为i,j,m 。
每个结点有两个位移分量，如图2.2所示。
每个结点的位移可用位移矢量i α表示，即⎥⎦⎤⎢⎣⎡=i i i v u α ),,(m j i每个单元有6个结点位移分量（称为6个自由度），于是单元结点的位移向量可表示为[]Tm m j j i im j i e v u v u v u =⎥⎥⎦⎤⎢⎢⎣⎡=ααααe α为单元结点位移列阵。
1．单元的位移模式和广义坐标在有限元方法中单元的位移模式，是指在单元内位移的插值函数，其一般形式采用多项式作为近似函数，因为多项式运算简单，并且随着项数的增多，可以逼近任何一段光滑的函数曲线。
假设3结点三角形单元位移模式选取一次多项式y x u 321βββ++=y x v 654βββ++= （2.2.1）它的矩阵形式是φβ=u （2.2.2）其中⎥⎦⎤⎢⎣⎡=v u u ，⎥⎦⎤⎢⎣⎡=ϕϕφ00 []y x 1=ϕ[]T 654321βββββββ=由于三个结点也在单元内，满足位移模式，于是得i i i y x u 321βββ++=j j j y x u 321βββ++= （2.2.3） m m m y x u 321βββ++=上式是关于321,,βββ的线性方程组。
2 弹性力学与有限元法
•剪应力
图1
2013-7-21
8
Institute of Mechanical Engineering and Automation
[ 应力的概念 ]
•正应力 为了表明这个正应力的作用面和作用方向，加上一个 角码，例如，正应力σx是作用在垂直于x轴的面上同时也 沿着x轴方向作用的。 •剪应力 加上两个角码，前一个角码表明作用面垂直于哪一个坐 标轴，后一个角码表明作用方向沿着哪一个坐标轴。例如， 剪应力τxy是作用在垂直于x轴的面上而沿着y轴方向作用的。
[ 几何方程、刚体位移 ]
•求剪应变 xy ，也就是线素AB与AD之间的直角的改变 •x向线素AB的转角 a y向线素AD的转角 b
y
u u dy y
C'
v
v dy y
D" b D '
D C
•A点在y方向的位移分量 为v； •B点在y方向的位移分量：
v
u
A
A'
a
dy
B'
v v dx x
连续性假设
2013-7-21
完全弹性假设 均匀性和各向同性假设 小变形、小转动假设 自然状态假设（无初始应力）
4
Institute of Mechanical Engineering and Automation
基本定律
牛顿定律
动量平衡原理
⇨ 平衡(运动)微分方程
⇨ 应力张量的对称性
u dx x
u
A'
a
A dx 0
2013-7-21
B
u u dx x
B"
x
图2
弹性体力学数值模拟算法
弹性体力学数值模拟算法弹性体力学数值模拟算法是一种用于模拟弹性材料力学行为的数值计算方法。
该算法可以通过计算机模拟得出弹性体的应力分布、变形情况以及其他相关参数，为工程设计、科学研究以及现实世界中的弹性材料应用提供了有力支持。
一、弹性体力学概述弹性体力学是研究物体由于外力而发生形变时的力学行为，主要关注物体的应力、应变以及相应的力学性质。
弹性体力学数值模拟算法正是基于这些力学特性进行计算。
在弹性体力学中，弹性模量、剪切模量以及泊松比等参数是十分关键的。
弹性体力学数值模拟算法通过考虑这些参数，结合物体的几何形状以及外力条件，利用计算方法来模拟物体的力学行为。
二、有限元法数值模拟算法有限元法是弹性体力学数值模拟算法中常用的一种方法。
该方法将弹性体划分为许多小的有限单元，在每个单元内进行数学计算，再通过组合这些小单元的结果，得出整个弹性体的力学行为。
具体而言，有限元法首先进行网格划分，将弹性体分割成许多小单元，然后在每个单元内利用数学公式推导出该单元的力学行为。
这些小单元之间通过边界条件相互连接，构成整个体系。
最后，通过求解线性方程组，得到弹性体的应力分布和变形情况。
有限元法数值模拟算法的优点是适用于各种复杂形状的弹性体，并且精度较高。
然而，该方法在处理大规模模拟问题时，计算量较大，需要较高的计算资源。
三、有限差分法数值模拟算法有限差分法是另一种常用的弹性体力学数值模拟算法。
该方法将弹性体通过网格划分为一系列小的节点，在每个节点处利用差分近似推导出该节点的力学行为。
有限差分法通过离散化的方式，将偏微分方程转化为差分方程，再通过求解这些差分方程得到相应的力学参数。
这个过程类似于对输出信号进行采样，将连续的物理问题离散化为一个个节点上的差分问题。
有限差分法数值模拟算法的优点是计算较为简单，容易实现。
但是对于复杂形状的物体，可能需要更多的节点和更小的步长来保证计算精度。
四、其他数值模拟算法除了有限元法和有限差分法，还有其他一些弹性体力学数值模拟算法，如边界元法、网格无关法等。
有限元与数值方法-讲稿6-7 弹性力学有限元的一般原理与格式
1 1 x1 y1 u1 u 1 x y 2 2 2 2 1 x y u 3 3 3 3
1 x1 y 1 x2 1 x3 y1 y2 y3
0 N1
N2 0
e B
0 N2
N3 0
B2
B3
Bi
N i x 0 N i y
0 N i y N i x
则单元内应变可表示为：
B1 1e B2 2e B3 3e
有限元与数值方法第6讲
授课教师：刘书田
Tel：84706149； Email：stliu@ 教室：综合教学楼 351
时间：2013年4月19日：8：00—10：50
1
第二篇：弹性力学有限元的基本理论和格式
2.1 弹性力学有限元的一般格式 平面问题的有限元格式 弹性力学有限元的一般格式和求解步骤 有限元解的性质和收敛准则 2.2 单元与插值函数的构造 2.3 等参元与数值积分 等参元与数值积分 典型的等参单元 2.4 有限元法应用中的实际考虑 建立有限元模型： 计算结果的性质和处理 子结构法 对称性和周期性的利用 非协调元与分片实验
18
单元应力矩阵
应力：
x y D D B e xy
S e
[ S ] [ D][B]
称为单元应力矩阵
19
单元应变能和外力势能的矩阵表达
应变能 U为： y
ui i b j 0 bm 0 u j 0 c j 0 cm j c j b j cm bm u m m
弹性力学及有限元
热传导案例
总结词
热传导是有限元分析中用于模拟物体内部热量传递规律的应用之一。
详细描述
在电子、机械、化工和材料等领域，热传导分析用于研究材料的热性能、热应力和热变形等。通过有 限元方法，可以模拟物体内部的热量传递过程，预测温度分布和热应力分布，优化材料和系统的热设 计。
06
结论展望
结论
01
02
有限元分析
有限元分析是一种数值分析方法，通过将复杂的物体或系统离散 化为有限个小的单元（或称为元素），并分析这些单元的应力、 应变和位移，从而对整个物体或系统的行为进行预测和分析。
主题的重要性
工程应用
弹性力学和有限元分析在工程领域中具有广泛的应用，如结 构分析、机械设计、航空航天、土木工程等。通过这些方法 ，工程师可以更准确地预测和分析结构的性能，优化设计， 提高安全性。
03
04
研究意义
弹性力学及有限元分析在工程 领域具有广泛应用，为复杂结 构的分析提供了有效方法。
主要成果
本文系统地介绍了弹性力学的 基本原理和有限元分析的方法 ，并通过实例验证了其有效性 。
研究限制
由于时间和资源的限制，本研 究未能涵盖所有相关领域，未 来研究可进一步拓展。
对实践的指导意义
本文为实际工程中的结构分析 提供了理论依据和实践指导， 有助于提高结构的安全性和稳 定性。
优势
有限元方法具有广泛的适用性，可以用于求解各种复杂的物理问题；能够处理 复杂的几何形状和边界条件；可以通过增加单元数目来提高解的精度；可以方 便地处理非线性问题和材料非均质性问题等。
局限性
有限元方法需要较大的计算资源和时间，尤其对于大规模问题；对于某些特殊 问题（如高速冲击、爆炸等），需要采用特殊处理方法；对于多物理场耦合问 题，需要采用多场耦合有限元方法等。
弹性力学与有限元完整版
x
y
•应力分量：
x、 y、 z、 xy、 yz、 zx
{
}
z xy
yz
zx
3 一点应变分量
①微分单元体的变形：
微分单元体棱边的伸长和缩短；正应变 棱边之间夹角的变化；剪应变
正应变分量 3个：
x、 y、 z
剪应变分量 3个：
xy、yz、 zx
第一篇 弹性力学
第一章 弹性力学基本方程
1.1 绪论 1.2 弹性力学的基本假定 1.3 几个基本概念 1.4 弹性力学基本方程
第二章 弹性力学平面问题
2.1 平面应力问题 2.2 平面应变问题 2.3 平面问题的基本方程
第三章 弹性力学问题求解方法简述
第一章 弹性力学基本方程
1.1 绪论 1.2 弹性力学的基本假定 1.3 几个基本概念 1.4 弹性力学基本方程
平面应力问题讨论的弹性 体为薄板。薄壁厚度远小于 结构另外两个方向的尺度。 薄板的中面为平面，其所受 外力，包括体力均平行于中 面O-xy面内，并沿厚度方向 z不变。而且薄板的两个表 面不受外力作用。
平面应力问题 ①几何特征
薄壁厚度为h远小于结构另外两个方向的尺寸 等厚度 中心层平直
②受力特征
•平面应力与平面应变问题的： 平衡方程、几何方程相同。
但物理方程不同。 从空间问题推得。
• ① 平面应力的物理关系
① 平面应力的物理关系
D
1 μ 0
E
[D]
1 μ2
μ
0
1 0
0 1 μ
2
• ② 平面应变的物理关系
z yz = zx 0
② 平面应变的物理关系
弹性力学平面问题的有限元法
软件应用有限元法需要掌握相关软件的使用方法和操作技巧，同时需要具备一定的弹性力学和有限元法的基本理论知识。
常见的有限元分析软件包括ANSYS、ABAQUS、SolidWorks等，这些软件提供了丰富的单元库、材料库和边界条件库，用户可以通过软件的前处理、求解和后处理等步骤进行弹性力学问题的求解。
有限元法的软件应用
弹性力学平面问题的单元分析
将所有单元的刚度矩阵组合起来，形成整体的平衡方程。
整体平衡方程
将边界条件转化为等效的力或位移，并加入到整体平衡方程中。
边界条件处理
采用适当的数值方法求解整体平衡方程，得到各节点的位移和应力。
求解方法
弹性力学平面问题的整体分析
04
CHAPTER
有限元法的实现与软件应用
有限元法的编程实现是利用计算机编程语言（如Python、C等）将有限元法的理论计算过程转化为计算机程序的过程。
有限元法具有灵活性和通用性，可以处理各种复杂的几何形状和边界条件，能够得到较为精确的数值解。此外，有限元法还具有可扩展性和可移植性，能够方便地应用于其他领域的问题求解。
优点
有限元法的计算量较大，对于大规模的问题求解可能会耗费较长时间和计算资源。此外，有限元法的求解精度和稳定性也受到离散化的影响，需要合理选择单元类型和划分网格。
详细描述
应用实例二：建筑结构的稳定性分析
总结词
机械零件的强度分析是有限元法的又一应用领域，通过对零件进行应力、应变分析，可以优化零件的设计和提高其可靠性。
详细描述
在机械零件的强度分析中，有限元法被广泛应用于模拟和分析零件在不同工况下的应力、应变分布。通过对零件进行离散化处理，可以精确地模拟其工作状态，并计算出各部分的应力、应变等受力情况。这种方法能够发现潜在的应力集中区域和薄弱环节，为零件的设计优化和可靠性提高提供指导。同时，有限元分析还可以用于评估不同工艺参数对零件性能的影响，为生产过程中的工艺控制提供依据。
第十九章section5弹性理论与有限元解法
§5 弹性理论与有限元解法有限元法用来解弹性体的小变形问题是很有效的.这是由于变形能与外力势能或总势能可以表示为形式划一的二次泛函.由于弹性力学问题提法,特别是边界条件的复杂性,要使有限元解法灵活运用,还需要对各种问题作些分析与讨论.因此本节除了介绍各类问题与§1中B 、D 等有关的基本关系式外，还着重分析边界条件在有关变分问题中所起的作用，并讨论各类变分问题与微分方程定解问题的等价性。
一、 三维的弹性问题本节在直角坐标系(x ,y ,z )中讨论弹性体内部受力与形变的情况.为了简化论述,假设弹性体是单连通、均匀并各向同性的,必要时还用通常的矢量记号以突出其力学意义.[应力与平衡方程] 弹性体在外力、温差等作用下，各部分之间将产生内力，表示内力的大小是作用面上受力的强度或单位面积所受的力,即所谓应力.对弹性体内的一点P ,可在其邻近作一微元六面体，其棱边平行于坐标轴。
六面体的六个面中有三个面其外法线方向分别与x 轴、y 轴或z 轴同向（其余三个则与坐标轴反向）,可分别称为x ,y ,z 坐标面(或第1,2,3坐标面).设321,,σσσ分别表示作用于x ,y ,z 坐标面的应力,并记i σ的三个分量为321,,i i i σσσ(对其余三个面的应力取号相反.例如,图19.18上所示的分量全是正的),这九个分量ij σ(i ,j =1,2,3) 构成一个张量,称为应力张量.从图可看出,分量ii σ表示第i 坐标面上的正应力(受拉取正,受压为负);而分量ij σ则表示沿第i 坐标面剪应力的二分量(使扭角变成锐角的为正).由微元六面体力矩的平衡可得剪应力互等定律,即ij σ =ji σ (j i ≠)因此应力张量是对称的,其分量只有六个是独立的.在有限元解法中,一般是把这六个分量按如下次序排成列矢量,并记作τσσσσσσσ),,,,,(}{123123332211=设过点P 作一任意的斜面,其法线n 的方向余弦为(321,,n n n ),则利用与三坐标面围成的四面体的平衡条件可得作用于该斜面的应力n σ的三个分量∑=++=31332211i j j j iij n n n n σσσσ(j =1,2,3)于是n σ在方向余弦为(321,,m m m )的直线上的投影,即其分量为∑==31,j i j i ij nm m n σσ这表明,一个点的应力状态完全由该点的六个应力分量{σ}所决定.例如,作用于上述斜面的正应力为∑==31,j i j i ij nn n n σσ而沿该斜面的剪应力方向取n n ⨯⨯n σ,大小等于∑∑∑===-=-=313131,2222)()(j i j i j i ij iij nnn n n n n σσσστ反过来,对于0=n τ的斜面称为P 点的应力主面,相应的法线称为P 点的应力主轴,而其正应力nn σ称为P 点的主应力.可以证明,在弹性体内任意一点,一定存在三个互相正交的主应力,而且其中最大(小)的一个就是该点的极大(小)正应力.三个正应力之和332211σσσΘ++= 称为体积应力,它在坐标变换下是个不变量,因而等于三个主应力之和.设τ),,(}{321f f f f ==f ,表示作用于P 点的体力(单位体积的外力),对体积元素作积分或均值分析都可以推出力的平衡方程0321=+∂∂+∂∂+∂∂i ii i f zy x σσσ (i =1,2,3) (26) [应变与几何方程] 弹性体内任一点P (x ,y ,z )在小变形后移到),,(z y x P ''''其位移函数为τ),,(w v u =u式中z z w y y v x x u -'=-'=-'=,,它们是(x ,y ,z )的微量函数,假定有一微小线段PN =dr 其方向余弦为(321,,n n n ),经过小变形变为r d N P '='',则沿该方向的正应变n ε定义为单位伸长,即drdr r d n -'=ε从变形前后的r d '与dr 关于位移的表达式不难得出1}])1([])1([])1({[1232123212321-+++++++++++=n w w n w n v n n v v n u n u n u n z y x z y x z y x n ε展开右端的根式并略去高阶无穷小量(即位移导数的高次项),就得到)()()(211332232221y x x z z y z y x n u v n n w u n n v w n n w n v n u n ++++++++=ε设另一线段PM 的方向余弦为(321,,m m m ),变形前的夹角θ=∠MPN ,则33221131cos m n m n m n m n i i i ++==∑=θ (27)设变形后的夹角θ'='''∠N P M (图19.19),则∑=''='31cos i i i m n θ根据变形前后两线段大小、方向的变化,不难得出))(())(()(2cos )1(cos 31132332332211x x z y z y x m n w u m n m n v w m n m n w m n v m n u m n +++++++++--='θεεθ))((1221y x u v m n m n +++ (28)对照(27),(28)可知,只要在P 点给定如下六个导数值:yx x z xy x y x u v w u v w wv u +==+==+==⎪⎩⎪⎨⎧===211213313223332211εεεεεεεεε (29)就可以完全确定P 点邻近的变形状态.ii ε表示沿第i 坐标轴的正应变,ij ε表示经过小变形第i ,j 坐标方向之间的直角改变量即所谓剪应变(12ε如图19.20所示,变形后成锐角为正,成钝角为负).这六个量称为应变分量,记作τεεεεεεε),,,,,(}{123123332211=同样可以证明,在弹性体内任意一点,一定存在互相正交的应变主轴,变形后三轴交角仍然保持直角,即剪应变为零;三主轴的正应变称为主应变,而且其中最大(小)的一个就是该点的极大(小)的正应变.三个正应变之和332211εεε++=e称为体积应变,也是个不变量,而且表示微元中每单位体积的改变量.对于各向同性体来说,应力主轴与应变主轴的方向还是一致的.§1中所述的变形能密度}{}{21}{}{21d εσσεττ==V正是把坐标系变换到共同的主轴方向并应用虎克定律而推导出来的.关系式(29)称为几何方程,其矩阵形式为)92(000000000}{123123332211'≡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂=⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=u B w v u xy x z y z z y xεεεεεεε[物理方程与弹性系数] 对杆件作简单拉、压的小变形实验证明,单独的轴向(取为x 轴)力不会引起剪应变,其正压力x σ与正应变x ε之间具有如下的线性关系x x E εσ=或1111εσE =如果考虑到沿x 方向的伸长还伴有侧向收缩,则产生沿y ,z 方向的正应变x z y νεεε-==或113322νεεε-==这就是虎克定律,式中系数E ,v 分别称为弹性模数和泊松比.从胡克定律就可以推导出应变与应力之间的一般关系式,即所谓物理方程)30(1)1(2)]([11)1(2)]([11)1(2)]([1121212221133333131313311222223232333221111⎪⎪⎪⎩⎪⎪⎪⎨⎧=+=+-==+=+-==+=+-=σσεσσνσεσσεσσνσεσσεσσνσεGE v E G E v E G E v E式中)1(2v E G +=称为剪切弹性模数. 从(30)求逆得出应力与应变之间的关系式)(),3,2,1(2j i G i G e ijij ii ii ≠==+=εσελσ或写成矩阵形式:)31(}{}{000000000000000000200020002}{εελλλλλλλλλσD G G G G G G≡⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡+++=式中)21)(1(v v Ev -+=λ与G 称为拉梅系数,e 就是体积应变.它与体积应力Θ成正比:ΘE v e 21-= 或 e vE 21-=Θ式中比例常数vE21-称为体积弹性模数.[边界条件] 弹性体Ω的边界Ω'承受面力τ),,(}{321q q q q ==q有三种方式:固定支承,荷载支承和弹性支承.假定Ω'接受这三种支承的部分分别记作2,ΩΩ''1和3Ω',则其边界条件可表示为 1° 几何约束条件: 在1Ω'上给定位移,即w w v v u u ===',,1Ω2° 面力平衡条件: 在2Ω'上给定荷载即面力q ,(321,,n n n )表示2Ω'上任一面积元素的外法线方向余弦.由于应力要与面力平衡,从(27)可得其条件为)3,2,1(∑312=='=j q n i ji ijσΩ3° 耦合平衡条件: 在3Ω'上弹性体与另一弹性结构耦合,这些耦合边界上的位移既不受约束也不完全自由,而是接受与其位移偏差(相对于某一给定的位移值w v u ,,)成正比的弹性反力.每单位面积上它的三个分量可表示为)3,2,1(][)]()()([321321=+++-=-+-+--j q w c v c u c w w c v v c u u c jj j j j j j这里弹性支承系数矩阵C =(ji c )是正定的,而w c v c u c q j j j j 321++=可看作给定的面力.同样,这反力应由3Ω'上的应力来平衡.于是其条件可写成)3,2,1()(-∑313213=+++='=j q w c v c u c n i jj j j i ijσΩ[外力势能及其计算公式] 弹性体内及其边界上,凡给定的外力因变形而作功的部分都要累加起来,再补上负号可看作弹性体相对于外力系统的势能,即所谓外力势能-F (u ).例如在弹性体内部除体力f 外,也可能有部分施加集中的面力、线力和点力，这些力与该部分的位移的内积就是它们所作的功，因此都要算进去。
第2讲、有限元与弹性力学的基本原理
Fn σ＝ S
例如图示， > 0 ，σ
（ 1）
其中，F 沿作用力截面的法线方向。 。
二、线应变（相对伸长或压缩） 绝对伸长（或压缩）与原长之比称为相对伸长（或 压缩）。公式： ∆l
ε=
当
ε ε > 0 时，为拉伸形变； < 0 时，为压缩形变，因而，
b − b0 ∆b = b0 b0
有限元分析的基本原理
有限元与弹性力学的基本原理
之所以介绍弹性力学的有限元法的主要是:它概念浅 显，易于掌握，既可以从直观的物理模型来理解，也可 以按严格的数学逻辑来研究; 不仅能成功地分析具有复 杂边界条件、非线性、非均质材料、动力学等难题，而 且还可以推广到解答数学方程的其它边值问题，如热传 导、电磁场、流体力学等问题。
梁的弯曲
中性层：一根杆中处于中间的既不拉伸又不压缩的层， 如图中的 CC' 层。 对于纯梁弯曲形变有：
1 12τ ρ= = R Ybh3
其中：R 和 ρ 分别为中性层的半径和曲率；h 和b 分 别为梁的高度和宽度，τ为梁仅受的靠端部的力偶。
杆的扭曲
产生扭转的力偶
τ
和实心圆柱扭转角 ϕ 的关系：
τ=
三维问题的弹性力学基本方程
平衡方程 几何方程(应变-位移关系) 物理方程（应力-应变关系） 力的边界条件 几何边界条件 弹性体的应变能和余能
平面(二维)平衡方程
平面问题的静力学平衡,设微小正六面体,在X,Y方向的尺寸dx,dy,Z方向的尺 寸取一个单位长度.
∑ MC = 0
两个对面存在微小差量,通过中心点C,平行与Z轴的直线为轴,列出平衡方程 ∑ M c = 0
l0
（ 2）
求解弹性波动方程
求解弹性波动方程弹性波动方程是波动力学中的重要概念，描述了固体、液体等弹性体中的波动传播情况。
求解弹性波动方程可以帮助我们更好地了解地震、地质勘探、材料力学等领域中的问题。
本文将从弹性波动方程的概念、求解方法及应用方面进行探讨。
一、弹性波动方程的概念弹性波动是指在弹性介质中，由于外力的作用导致的能量传递方式，其传播速度与介质的物理性质有关。
弹性波动方程则是描述弹性波传播过程的数学模型，通常也称为弹性振动方程。
弹性波动方程通常包含两个基本变量：质点的位移和质点的速度。
在三维坐标系中，弹性波动方程可以写成如下形式：ρ∂²u/∂t² = ∂iτij/∂xj其中，ρ为介质密度，u为波动的位移，τij为应力张量，xj表示坐标轴方向，i、j为坐标轴的编号。
二、求解弹性波动方程的方法求解弹性波动方程可以采用有限元法、有限差分法、声波分解法等多种方法。
其中，有限元法和有限差分法是比较常用的求解方法。
1. 有限元法有限元法是一种比较通用的求解偏微分方程的方法，其主要思想是将求解区域离散化成若干个单元，然后对每个单元内的位移和应力进行求解。
最后将所有单元的解合并起来，就可以得到整个区域内的位移和应力分布情况。
2. 有限差分法有限差分法是一种利用差分近似方法来求解微分方程的数值方法。
其思想是将求解区域划分为网格，然后在每个网格节点处用差分公式来逼近微分方程的解。
最后通过数值计算来得到整个区域内的解。
三、弹性波动方程的应用弹性波动方程在地质勘探、地震学、材料力学等领域中有广泛的应用。
1. 地质勘探地质勘探中需要了解地下结构，以便确定油气、煤炭等矿产资源的位置和规模。
在勘探中，我们可以通过广播一定频率的声波，然后通过测量接收到的反射波、折射波等来推导地下结构的性质。
弹性波动方程能够有效地描述声波在地下结构中的传播情况，从而帮助勘探人员更准确地掌握地下资源的分布情况。
2. 地震学地震学是研究地震、地震波等现象的学科，也是弹性波动方程的重要应用领域。
波动方程有限元—差分法数值解
波动方程有限元—差分法数值解有限元差分法是新兴的数值解法，可以用于计算复杂的波动方程。
本文研究了有限元差分法在解决波动方程的数值方面的应用，主要从以下几方面来探讨。
首先，介绍了波动方程的定义及其特性，简要介绍了波动方程模型的建立和求解，以及有限元差分法在求解波动方程中的应用。
其次，提出了三种典型的有限元差分法求解波动方程的算法：时间歉分差分法、时间步长变化差分法和双时间空间差分法。
之后给出了三种算法的实现过程，通过计算了实例，验证了有限元差分法的有效性。
最后，归纳总结了有限元差分法的特点和优点，指出除了有限元差分法外，还可以使用基于全时空的解析方法求解波动方程的有效性。
波动方程是用于描述物理系统的变化的常微分方程，例如用于描述热传导问题的拉普拉斯方程，用于描述电磁学场的马尔科夫方程，以及用于描述流体动力学问题的贝尔加拉里散度方程等。
由于波动方程的解一般是复杂的，有限元差分法可以利用有限个均匀分布的有限元素网格来模拟波动方程，然后采用差分法进行数值求解。
有限元差分法的使用可以使波动方程的解变得更加精确，同时由于其求解的过程是近似的，因此也可以节省计算时间，节约资源。
此外，有限元差分法还可以应用于并行计算，以提高计算速度。
由于近年来随着计算机性能的不断提高，有限元差分法在解决波动方程的数值解中逐渐被认可，逐渐被广泛应用。
综上所述，有限元差分法是一种新兴的数值解法，能够比较有效地求解复杂的波动方程，有助于深入研究物理系统的变化，在实际应用中有重要的意义。
因此，有关有限元差分法在波动方程求解中的应用，以及这种求解方法的特点和优点，应予以深入研究，以挖掘这种数值方法的潜力，为解决实际物理问题提供有效的数值支持。
北航有限元第3讲 弹性问题有限元方法(1)
要求单元的外力功，关键是求出单元上的体积力和面 积力等效作用到节点上的力的大小。
北京航空航天大学
Step 3. 单元集成——应变能
单元等效节点力列阵：
Pe 1 Pe = e P2
北京航空航天大学
构造单元位移函数： u ( x) = a0 + a1 x
利用节点条件： u ( xi ) = a0 + a1 xi = ui
u ( x j ) = a0 + a1 x j = u j
北京航空航天大学
1 ∫Ω σ ijδε ij dV = ∫Ω σ ij ⋅ 2 δ ui, j + δ u j ,i dV = ∫ σ ijδ ui , j dV = ∫ (σ ijδ ui ), j dV − ∫ σ ij , jδ ui dV
Ω Ω Ω
分部积分 高斯定理
= ∫ σ ijδ ui l j dA − ∫ σ ij , jδ ui dV
体积力 分布面力 集中力
外力载荷
北京航空航天大学
3.3 简单杆系问题的有限元求解过程
F
北京航空航天大学
Step 1: 几何离散——自然离散为2个杆单元 Setp 2: 单元特征分析
构造单元位移函数 应变的表达 应力的表达 单元的应变能 单元的外力功
北京航空航天大学
Step 3: 单元集成—系统的总势能 Step 4: 变分处理—线性方程组 Step 5: 处理位移边界条件并求解 Step 6: 计算每个单元的应变及应力
北京航空航天大学
∆ V= – W
弹性势能
弹性势能—弹性体变形后，产生弹性内力， 弹性势能—弹性体变形后，产生弹性内力，这 种力也具有对外作功的能力，称为弹性势能， 种力也具有对外作功的能力，称为弹性势能， 或弹性应变能。 或弹性应变能。
波动方程有限元解有关理论
1.1控制方程在经典的线弹性理论当中，线弹性均匀介质的运动方程为⋅⋅=+∂∂i i jij u f x ρρσ (3,2,1=i ) (1-1)其中，应力张量ij σ和应变张量kl ε满足Hooke 定律，即满足本构方程:kl ijkl ij c εσ= (1-2)应变张量kl ε可通过位移矢量i u 确定，从而给出几何方程:)(21,,k l l k kl u u +=ε (k,l=1,2,3) (1-3)各向同性线弹性材料的弹性特征可以用下列材料常数进行描述:弹性模量E,剪切 模量μ、泊松比v 、体积模量K 和Lame 常数λ等。
这些常数中任意两个独立，而其它 几个常数能够用它们间接进行表示。
在各向异性的情形下，则需要采用21个相互独立 的弹性常数ijkl C ，进行表示。
介质表面S 上的边界条件为u i i S x t x u t x u ∈=),,(),( (1-4)σσS x t x p n t x i j ij ∈=),,(),( (1-5)由方程(2-1)-(2-3)这三个线弹性动力学的控制方程所描述的线弹性动力问题的初始 条件为V x x u t x u i i ∈=),(),(00 (1-6)V x x v t x u i i ∈=⋅),(),(00 (1-7)其中，)(x u i ，)(0x v i ，),(t x u i 和),(t x p i 是已知量。
由弹性动力学问题解的唯一性定理可知:若弹性体(体积为Y ，表面为S)的解能 满足方程(1-1)-式(1-7)，则其位移场、应力场和应变场的解答是唯一的。
将三个控制方程合并，可以得到用位移表示的运动方程:⋅⋅=+i i lj k ijkl u f u c ρρ, (3,2,1=i ) (1-8)方程(1-8)所示的就是著名的Navie-Cauchy 运动方程。
而在各向同性线弹性的情形 下，则有)(jk il jl ik kl ij ijkl c δδδδμδλδ++= (1-9)因此，各向同性材料的本构关系也为表示为⎩⎨⎧=≠=+=)(,1)(,0,2j i j i ij ij kk ij ij δμεελδσ (1-10)1.2有限元方程现在我们考虑一个任意形状的封闭区域，并将其用一定形式的网格划分为相应的有 限单元，各单元的单元矩阵可由如下所示的虚功方程求得。
弹性力学与有限元法分析及实例讲解
弹性力学与有限元法分析弹性力学是固体力学的一个重要分支，是研究弹性固体在受外力作用、温度改变、边界约束或其他外界因素作用下而发生的应力、形变和位移状态的科学。
有限单元法是力学、数学、物理学、计算方法、计算机技术等多种学科综合发展和结合的产物，是随着计算机技术的广泛应用而迅速发展起来的一种数值分析方法。
有限元法的基本思想就是化整为零，分散分析，再集零为整。
即用结构力学方法求解弹性力学问题，实质是将复杂的连续体划分为有限多个简单的单元体，单元体之间仅仅通过结点相连，实现化无限自由度问题为有限稀有度问题，将连续场函数的（偏）微分方程的求解问题转化为有限个参数的代数方程组的求解问题。
有限元方法经过近半个世纪的发展，目前已经成为各种工程问题特别是结构分析问题的标准分析方法，而有限元软件也已成为现代结构设计中不可缺少的工具。
有限元软件是有限元理论通向实际工程应用的桥梁，它的应用极大地提高了力学学科解决自然科学和工程实际问题的能力，进一步促进了有限元方法的发展。
ANSYS 软件是融结构、流体、电场、磁场、声场分析于一体的大型通用有限元分析软件，广泛用于机械制造、石油化工、航空航天、汽车交通、土木工程、造船、水利等一般工业及科学研究。
ANSYS 软件的组成：（一）前处理模块该模块为用户提供了一个强大的实体建模及网格划分工具，可以方便的构造有限元模型，软件提高了100种以上的单元类型，用来模拟工程中的各种结构和材料。
包括：1.实体建模：参数化建模，布尔运算及体素库，拖拉、旋转、拷贝、蒙皮、倒角等。
2.自动网格划分，自动进行单元形态、求解精度检查及修正。
3.在集合模型上加载：点加载、分布载荷、体载荷、函数载荷。
4.可扩展的标准梁截面形状库。
（二）分析计算模块该模块包括结构分析（可进行线性分析、非线性分析和高度非线性分析）、流体动力学分析、电磁场分析、声场分析、压电分析以及多物理场的耦合分析，可模拟多种物理介质的相互作用，具有灵敏度分析及优化分析能力。
弹性力学有限元分析法3
2013-7-12
13
在离散体中任取一个单元，三个节点按逆时针方向顺序编 号为i，j，m。节点坐标分别表示为（xi，yi），（xj，yj）， （xm，ym）。
2013-7-12
14
对于弹性力学平面问题，一个三角形单元上的每 个节点应有2个位移分量，则三角形单元共有6个自 由度： ui , vi , u j , v j , um , vm 。 三角形单元的节点位移矢量是：
(4) 4 4 (4) 5 5
60 52 52 45 u 0.07504 0.08442 0.07941in 15 15
2013-7-12 32
3.2 一维三节点单元
• 一维三节点单元 用二次函数代替线性 函数要求使用三个节 点来定义一个单元,这 是因为至少要有三个 点才能确定一个二次 函数.第三个点可以取 在单元的中点.
(3) 3 3 (3) 4 4
10 8 85 T 34 20 25.6 C 5 5
对于这个例子，注意
S3(2)
和
S3(3)
的区别。
2013-7-12
30
• 假设承受的是轴向负荷 , 应用线性单元, 柱体的 垂直位移由下式确定.
B
A
2013-7-12
31
（a）应用总体坐标Y，点A的位移由单元（1）表示：
X X j
X Xi l
X X j
X j Xi l
1
2.形函数的和为1。
X Xi si s j 1 X j Xi X j Xi
2013-7-12 27
Xj X
3. 形函数对于x导数的和为0
d Xj X d X Xi 1 1 ( ) ( ) 0 dX X j X i dX X j X i X j Xi X j Xi
波动方程求解方法
常用的波动方程求解方法主要有以下几种:有限差分法、有限元法和伪谱法、积分方程法等。
1、有限差分方法由于适应性强，计算快速，因此是最先发展起来而且使用范围最广的数值方法，有限差分方法最大的弱点之一就是会产生数值频散。
有限差分法采用差分算式近似逼近偏导数运算，从而使波动方程的偏导数运算问题转化成差分代数问题，最后通过求解差分代数方程组得到近似解结果。
有限差分法的差分算式本身就是一种局部点运算，不需要考虑原函数中所求点值在邻域范围上的函数的变化情况，而只需要用到所求点值附近点上的值，所以能够很好的适用于复杂情况, 但是难保模拟精度。
有限差分方法有较高的空间域分辨率，而在频率域上分辨率反而会极低，稳定性同时还受到网格间距和时间步长的影响。
同时，虽然有限差分法还伴随有数值频散的问题，但是计算速度较快。
有限差分法目前主要有以下三大类:规则网格方程、弹性方程和交错网格方程。
有限差分法的具体操作可以分为两个部分:(1)用差分代替微分方程中的微分，将连续变化的变量离散化，从而得到差分方程组的数学形式:(2)求解差分方程组。
在第一步中，通过网格剖分法，将函数定义域分成大量相邻而不重合的子区域。
通常采用的是规则的剖分方式，最常用的是正方形网格。
这样可以便于计算机自动实现和减少计算的复杂性。
网格线划分的交点称为节点。
若与某个节点P 相邻的节点都是定义在场域内的节点，则P 点称为正则节点;反之，若节点P 有处在定义域外的相邻节点，则P 点称为非正则节点。
在第二步中，数值求解的关键就是要应用适当的计算方法，求得特定问题在 所有这些节点上的离散近似值。
目前最常用的两种有限差分方法包括:基于位移 波动方程的二阶中心差分法和基于一阶速度-应力波动方程的高阶交错网格法， 前者算法简单，易于实现，但差分精度具有局限性，最后得到的是节点上z x ,分量的位移离散近似值，后者算法稍复杂，但可以提高差分精度，最终得到的是节点上的位移速度离散近似值。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
e M
和
w
e M
分别为 x
和z
方向的位移函数;
u
e M
为 ueM 对时间的二阶导数; i 为局部有限元插值函
数。
得到整体有限元运动方程为
M Ui + K 1 U i + L1 Wi = 0;
MW i + K 2 Wi + L 2 Ui = 0.
( 2)
其中
K1 =
v
2 P
K
1e MN
+
v
2 S
KM2eN
区域 的整体 参数 矩阵
MiM N
,
K
1i MN
,
K
2i MN
,
L
1i MN
和
L
2i MN
,
p
R=
R
i MN
.
i= 1
式中, i 为 CPU 序号( 0
K 2, L 1 和 L 2。
( 4) i < p ); R 代表 M , K1,
求解空间的分配 情况是将原串行算法中一个
CPU 上的空间量和计算量分担到 p 个 CPU 上, 如图
自 1976 年哥伦比亚大学研究人员首次将有限 元法引入到地震波研究领域以来, 许多学者就该方 法做了大量研究, 先后对比了模拟弹性波传播的有 限差分法和有限元法的精度[ 1] , 研究了地震波在不 同介质中的传播性质, 以及处理三维弹性波动方程 的思路; 研究了三角形有限单元、正方形有限单元、 不规则四边形有限单元以及矩形和三角形的混合有 限单元[ 2] 下地震波数值模拟, 以及地震波模拟的低 阶和高阶有限元法[ 3] 。有限元法有其独特的优势: 能够模拟任意不规则的地质体, 不受边界几何条件 的限制; 能够简单地处理自由边界条件; 可以方便地
大空间量和运算量的需求。此算法具有理论上的正确性和实践上的可行性。
关键词: 有限元; 并行算法; 弹性波动方程; 数值模拟; 块 三对角矩阵
中图分类号: P 315. 31
文献标识码: A
Finite element parallel algorithm for numerical solution of elastic wave equation
1 所示。
图 1 整体有限元分到 p 个 CPU 上的分配情况
2. 2 线性方程组并行求解 线性方程求解是正演模拟中重要部分, 也是耗
时最多的部分。在时间上需要递推求解运动方程, 采 用传统的串行算法, 巨大的内存量使得巨型方程组 的求解速度极慢。以 159 159 的剖分为例, 节点数 为 160 160 个, 每一节点有两个位移分量 u 和 w , 每一个总体参数矩阵行数为 51 200, 带宽为 323, 采 用带状存储, 共需要内存约 80 MB。此外, 若根据需 要细分网格, 减小时间上的递推步长, 则需要更多的 内存量和运算时间, 这是单 CPU 串行算法的局限。
WANG Yue- ying , SUN Cheng- yu
( Faculty of Geo-Resource and I nf or mation in China University of Petroleum , Dongying 257061, Shandong Pr ovince, China)
模拟任意震源; 能适应变速不均匀介质情况等优点。 然而有限元法也有其巨大的局限性, 需要巨大的空 间量和计算量, 而计算机的空间和运算能力是有限 的, 外加地震波方程较其他领域的控制方程复杂, 所 以, 有限元不能满足在实际生产中的要求。随着计 算机硬件的发展, 高性价比微机群的出现和基于消 息传递的并行平台的不断完善, 为有限单元法在地 震波场正演模拟中的发展提供了新的空间。有限元 法的 化整为零、集零为整 的基本思想[ 4] 与并行处 理技术的基本原则 分而治之 基本 一致[ 5] 。笔者 采用多 CPU 的并行处理方法, 以有效满足有限元法
各研究所和高等院校。在新的计算环境下继续研究
有限元法, 增强了有限元法在实际资料处理中的可
行性。采用并行求解, 把求解区域分到多个 CPU 上, 既克服了单 CPU 的物理限制, 又提高了运算速度。
并行求解的思路可以从两个方面并行, 一方面是有
限元参数矩阵的并行计算; 另一方面是线性方程组
的并行求解。
每一 有 限单 元应 满足 文献 [ 6] 中式 ( 18) , 化 简 式
( 18) , 得
MeMN
u
e M
+
(
v
2 P
K
1e MN
+
v
2 S
K
2e MN
)
u
e M
+
(
v
2 P
L
1e MN
-
2v
2 S
L
1e MN
+
v
2 S
L
2e MN
)
w
e M
=
0;
MeMN
w
e M
+
(
v
2 P
KM2eN
+
v
2 S
K
1e MN
)
w
e M
+
(
v
2 P
L
2e MN
-
2v
2 S
L
2e MN
+
v
2 S
L
1e MN
)
u
e M
=
0.
( 1) 其中
MeMN =
m
ndx dz ,
K
1e MN
=
m
x
n
x
d
x
d
z
,
A
A
K
2e MN
=
A
m
z
zndxdz ,
L
1e MN
=
A
m
z
n
x
d
x
dz
,
L
2e MN
=
A
m
x
n
z
d
x
d
z
.
式中,
u
,
K2 =
v
2 P
K
2e MN
+
v
2 S
KM1eN
,
L1 =
v
2 P
LM1eN
ห้องสมุดไป่ตู้
-
2v
2 S
L M1 eN
+
v
2 S
LM2eN
,
L2 =
v
2 P
LM2eN
-
2v
2 S
L M2 eN
+
v
2 S
LM1eN
.
U 和 W 分别为 x 和 z 方向上的位移矢量。通常将式
( 2) 统一为一个运动方程式为
MVi + K Vi = 0.
( 3)
式中, M 为系统质量矩阵; K 为系统刚度矩阵; V 为
节点位移矢量; V 为 V 对时间的二阶导数。
采用有限差分法来求解运动方程( 3) , 将最终化
为求解线性方程问题。
2 有限元并行求解
基于单 CPU 的串行算法的物理限制, 难以满足 有限元法高内存量和大运算量的要求, 制约了有限 元法的进一步发展。计算机硬软件技术的发展, 高性 价比微机群逐步代替了昂贵的工作站、巨型机进入
3 实现方案
采用多 CPU 的有限元并行算法求解弹性波动
方程, 有效地克服了传统的基于单一 CUP 的串行算 法的不足, 具体实现思路如下:
( 1) 把求解空 间离散为一系列有限单元, 并对
节点标号。
( 2) 根据 求解空 间确 定 CPU 的个 数 p ( p = 2q ) , 将求解空间等分到各个 CPU 上, 以确保生成的
王月英, 孙成禹
( 中国石油大学 地球资源与信息学院, 山东 东营 257061)
摘要: 在求解弹 性波动方程中, 有限元法的高 内存量和巨大运算 量的需求在基于单 CP U 串行算法中 一直难于满足,
制约其 优势的发挥。根据有限元法的 化整为零、集零 为整 的 基本思 想与并行 处理技 术的 分 而治之 的 原则基 本
收稿日期: 2006- 03- 09 作者简介: 王月英( 1977- ) , 女( 汉族) , 山东沾化人, 博士研究生, 主要从事地震波理论与方法研究。
28
中国石油大学学报( 自然科学版)
2006 年 10 月
的高内存量和巨大运算量的需求。
1 弹性波动方程数值解有限元算法
以二维问题为例, 根据变分原理和虚功原理, 在 无外力作用的情况下处于运动平衡状态的弹性体,
2006 年 第 30 卷 第 5期
中国石油大学学报( 自然科学版) Jour nal of China U niv ersity of Petroleum
文章编号: 1673- 5005( 2006) 05- 0027- 04
V ol. 30 No. 5 Oct. 2006
弹性波动方程数值解的有限元并行算法
一致, 采用基于多 CP U 的并行算法, 从有限 元参数矩阵计算和线 性方程组求解两个 方面入手, 把求解区域分到多 个
CPU 上并行计算参数矩阵, 对线性方程组采用循环块三 对角线方 程组进 行并行 求解。对比 了不同 大小空 间和不 同
CPU 个数下的加速比, 证实了多 CPU 的并行算法 能够克服基于单 CP U 串行算法的 物理限制, 满足了有 限元法的 巨
线性方程组并行求解方法分为直接法和迭代法
两类。线性方程组并行直接解法的优点是算法稳定