清华大学研究生课程《钢筋混凝土有限元》

合集下载

钢筋混凝土有限元模型1

清华大学研究生课程——《钢筋混凝土有限元》
清华大学研究生课程——《钢筋混凝土有限元》
清华大学研究生课程——《钢筋混凝土有限元》
局部坐标系下的刚度矩阵
2k x ' 0 2k y ' sym kx ' 0 2k x ' 0 ' 0 2 ' k k y y [K '] = l 0 − 2k x ' 0 2k x ' 6 − kx ' − ky ' 0 − 2k y ' 0 2k y ' 0 − 2k ' 0 0 0 2k x ' kx ' kx ' x − 2k y ' 0 − ky ' 0 0 2k y ' ky ' 0
0 Ni
Nj 0
0 Nj
Nm 0
ui v i 0 u j Nm v j u m vm
[ε ] = [B][δ ]
bi 1 0 2∆ c i 0 ci bi bj 0 cj 0 cj bj bm 0 cm
钢筋与混凝土的粘结滑移本构
[K ] = [T ]T [K '][T ]
清华大学研究生课程——《钢筋混凝土有限元》
清华大学研究生课程——《钢筋混凝土有限元》
清华大学研究生课程——《钢筋混凝土有限元》
局部粘结滑移关系
!
反复荷载下的粘结滑移关系
滕智明模型
Nilson Houde & Mirza
fc ' 415
形函数矩阵
[∆w'] =
u1 ' v ' 1 u ' 1 x' 1 x' 1 x' 1 x' 2 0 −( + ) 0 ( + ) 0 ( − ) 0 v ' − ( 2 − l ) 2 2 l 2 l 2 l 1 x' 1 x' 1 x' 1 x' 0 −( − ) 0 −( + ) 0 ( + ) 0 ( − ) u 3 ' 2 l 2 l 2 l 2 l v ' 3 u ' 4 v4 ' ∆u ' = [N '][δ '] = ∆v '

混凝土的开裂有限元分析-XinzhengLu

2 (1 + ν ) K III E
!
求θ 使得(σθ)max
清华大学研究生课程——《钢筋混凝土有限元》
清华大学研究生课程——《钢筋混凝土有限元》
清华大学研究生课程——《钢筋混凝土有限元》
计算方法
∂σ θ =0 ∂θ r = r0

裂缝扩展判断标准
∂ 2σ θ ∂θ 2 <0 r =r0
受弯破坏
!
裂缝使得混凝土的抗弯刚度损失超过1/3 斜裂缝是构件破坏的重要原因裂面抗剪贡献占整个构件承载力的30%以上
!
受剪受扭破坏
! !
!
局部承压破坏、受拉破坏都和裂缝行为关系密切
清华大学研究生课程——《钢筋混凝土有限元》
清华大学研究生课程——《钢筋混凝土有限元》
清华大学研究生课程——《钢筋混凝土有限元》
K I cos
θ0
2
(3 cos θ 0 − 1) − K II sin
θ0
2
K θ > K IC
!
(9 cos θ 0 + 5) > 0
清华大学研究生课程——《钢筋混凝土有限元》
清华大学研究生课程——《钢筋混凝土有限元》
清华大学研究生课程——《钢筋混凝土有限元》
有限元法求KI, KII
u= 1 4G 1 4G r [K I f1 (θ ) + K II g1 (θ )] 2π r [K I f 2 (θ ) + K II g 2 (θ )] 2π
! ! !
最大周向应力理论
σr =
σθ = τ rθ =
裂缝扩展单位长度时所需要的能量 G 弹性情况下，能量判据可以与应力强度因子判据互换

混凝土的单轴应力应变关系和双轴强度准则试题混凝土的组成应力应变关系

举例
清华大学研究生课程——《钢筋混凝土有限元》
清华大学研究生课程——《钢筋混凝土有限元》
混凝土双轴实验
清华大学研究生课程——《钢筋混凝土有限元》
混凝土破坏照片
清华大学研究生课程——《钢筋混凝土有限元》
双轴压缩应力应变关系
清华大学研究生课程——《钢筋混凝土有限元》
双轴拉伸应力应变关系
清华大学研究生课程——《钢筋混凝土有限元》
混凝土的拉伸实验
难题
夹具：胶粘、预埋钢筋脆性破坏：高刚度试验机破坏观测：灌注墨水
清华大学研究生课程——《钢筋混凝土有限元》
混凝土受拉应力应变关系
早期对混凝土的认识：脆性材料、受拉不存在下降段
精细试验发现混凝土受拉也存在一个下降段现在一般认为混凝土、岩石等属于半脆性材料
（quasi-brittle）混凝土受拉更容易受到偶然因素的影响，比受
压更加不稳定
清华大学研究生课程——《钢筋混凝土有限元》
拉伸试验机
清华大学研究生课程——《钢筋混凝土有限元》
混凝土受拉曲线的表示方法
基于裂缝宽度的表示方法
优点：与标距无关，与构件尺寸关系不大缺点：裂缝宽度观测非常困难，而且是构件
清华大学研究生课程——《钢筋混凝土有限元》
混凝土的单轴应力应变关系和双轴强度准则
江见鲸陆新征清华大学土木系
2005
清华大学研究生课程——《钢筋混凝土有限元》
混凝土的组成
混凝土：
微观层次：水泥凝胶、氢氧化钙结晶、未水化的水泥颗粒、空隙、毛细管、孔隙水、气泡……
细观层次：水泥浆、粗骨料宏观层次：均匀材料
拉压应力应变关系
清华大学研究生课程——《钢筋混凝土有限元》

混凝土的开裂有限元分析

裂纹尖端应力场

应力强度因子

弹性理论得到的裂纹尖端应力
σx = σy = τ xy =
KI 2πr K II
θ θ 3θ cos (1 − sin sin ) 2 2 2
θ θ 3θ cos (1 + sin sin ) 2 2 2 2πr θ θ 3θ cos (sin cos ) 2 2 2
清华大学研究生课程——《钢筋混凝土有限元》
开裂单元
多裂缝模型

当主应力方向和裂缝方向差距较大时，由于裂面剪力锁死往往导致出现错误结果多裂缝模型认为当主应力方向和裂缝方向夹角超过一定范围θ后，原有的裂缝闭合，重新在新的主应力方向生成新的裂缝 θ ＝30度（6裂缝模型）45度（4裂缝模型）
清华大学研究生课程——《钢筋混凝土有限元》
清华大学研究生课程——《钢筋混凝土有限元》
清华大学研究生课程——《钢筋混凝土有限元》
固定裂缝模型与转动裂缝模型

固定裂缝模型

分布裂缝模型中，一般认为，当单元内部的最大拉应力达到开裂应力时，混凝土即开裂混凝土开裂后，改变混凝土材料为各向异性材料，主应力和主应变方向可能不再一致。同时，初始裂缝方向和主应力方向也不再一致，裂缝表面将出现剪应力
分离裂缝模型的具体步骤

开裂标准和裂缝发展方向
主拉应力虚拟裂缝模型断裂力学方法
开裂标准和裂缝发展方向裂缝发展与模型网格调整裂面行为
清华大学研究生课程——《钢筋混凝土有限元》
清华大学研究生课程——《钢筋混凝土有限元》

实际裂缝
虚拟裂缝
清华大学研究生课程——《钢筋混凝土有限元》

钢筋混凝土受弯构件的有限元分析

Ｚｈｅｎｇｚｈｏｕ４５００５３，Ｃｈｉｎａ）
Ａｂｓｔｒａｃｔ：Ａｓｔｈｅｆｉｎｉｔｅｅｌｅｍｅｎｔａｎａｌｙｓｉｓｓｏｆｔｗａｒｅ，ａｎｓｙｓｃａｎｂｅｗｉｄｅｌｙｕｓｅｄｉｎｅｎｇｉｎｅｅｒｉｎｇｆｉｅｌｄｓ，ｔｈｒｏｕｇｈｒｅａｓｏｎａｂｌｅｍｏｄｅｌａｎｄｐａｒａｍｅｔｅｒｓｅｔｔｉｎｇｓ，ｗｅｃａｎｇｅｔｉｍｐｏｒｔａｎｔｒｅｆｅｒｅｎｃｅｆｏｒｓｔｒｕｃｔｕｒａｌｄｅｓｉｇｎ．Ｋｅｙｗｏｒｄｓ：ｆｉｎｉｔｅｅｌｅｍｅｎｔａｎａｌｙｓｉｓ；ｓｔｒｕｃｔｕｒａｌｄｅｓｉｇｎ；ＡＮＳＹＳ
程设计中。ＡＮＳＹＳ作为强大的有限元分析软件自然
土应力一应变的对应关系。现有混凝土本构关系一般都是基于连续介质力学的本构理论，结合混凝土的力学特性，确定本构关系中的材料参数。混凝土的本
ｉｈｕｉ
（ＺｈｅｎｇｚｈｏｕＳｃｉｅｎｃｅＲｅｓｅａｒｃｈ＆ｄｅｓｉｇｎＩｎｓｔｉｔｕｔｅＳｔａｔｅＡｄｍｉｎｉｓｔｒａｔｉｏｎｏｆＧｒａｉｎＲｅｓｅｒｖｅ，

非线性弹性三维本构关系

( ) e~c′ =
C1γ
2 1
+ C2γ 1
e~c ；
( ) eu′
=
C1γ
2 1
+
C2γ 1
e~u
其中C1 和C2 是输入参数。通常 C1 = 1.4 ， C2 = −0.4 。用σ~c′ ，σ~u′ ， e~c′ 和e~u′ 代替没有撇号的参数，就确定多轴状态下的等效单轴应力应变关系。
清华大学研究生课程——《钢筋混凝土有限元》
清华大学研究生课程——《钢筋混凝土有限元》
增量模型
! 增量形式的切线模量
Et
=
dσ dε
Saenz’s Model
σ
=
1+
E0 Ec
E 0ε
−
2
ε ε0
+
ε ε0
2
Et
=
1
+
E0
1
−
ε ε0
2
E0 Es
−
2
ε ε0
+
ε ε0
2
2
清华大学研究生课程——《钢筋混凝土有限元》
Bathe 模型(ADINA源程序)
受压应力水平较高时
D
=
(1
+ν
1
)(1
−
2ν
)
×
(1−ν )E1 νE12
(1−ν )E2
νE13
νE23
(1−ν )E3
0 0 0
0.5(1− 2ν )E12
0 0 0 0
0.5(1− 2ν )E13
0
0
0
0
0
0.5(1
−
2ν

非线性方程组的解法

评述
! 概念简单，对于比例加载的全量模型尤其适用
! 当出现卸载或往复荷载时可能不适合
清华大学研究生课程——《钢筋混凝土有限元》
等刚度法
[δ1] = [K0 ]−1[P]
[ ] [ ] δ → Pinternal11源自[ ] [ ] [ ] ∆P1
=
P
−
P internal 1
[∆δ 2 ] = [K0 ]−1[∆P1]
σy σt
dσt1
εt dεt εt3
εt2
ε εt1
清华大学研究生课程——《钢筋混凝土有限元》
应力更新隐式算法
! Backward Euler 算法
(输入
σ
n−1 ij
,
ε
p ij
n−1
,
∆ε
n ij
)
首先计算弹性应力增量:σ
t ij
=
σ
n−1 ij
+
De,ijkl
∆ε
n kl
判断是否屈服:
f
p A
清华大学研究生课程——《钢筋混凝土有限元》
割线刚度法
[δ1] = [K0 ]−1[P] [δ1] → [K1] [δ 2 ] = [K1]−1[P]
……
[δ n ] = [Kn−1]−1[P]
清华大学研究生课程——《钢筋混凝土有限元》
评述
! 理论上收敛速度最快 ! 每次迭代都要形成刚度矩阵 ! 当接近屈服时，或者出现软化时，切线
整体刚度矩阵
! 已知 t F , tδ , ∆F
{ } { } ! 求
δ t+∆t = tδ + [K]−1{∆F}
[K] = ∑[Ke ]

混凝土有限元分析

混凝土有限元分析廖奕全（06级防灾减灾工程及防护工程，06114249）摘要：用传统的理论解析方法分析钢筋混凝土结构，只能解决一些非常简单的构件或结构的非线性问题，对大量的钢筋混凝土结构的非线性分析问题只能用数值方法解决，因此，有限元方法作为一个强有力的数值分析工具，在钢筋混凝土结构的非线性分析中得到了广泛地应用。

随着有限元理论和计算机技术的进步，钢筋混凝土非线性有限元分析方法也得以迅速的发展并发挥出巨大的作用。

关键词：钢筋混凝土有限元分析有限元模型钢筋混凝土结构是土木工程中应用最广泛的一种建筑结构。

相比其它材料结构，钢筋混凝土结构有以下特点：①造价低，往往是建筑结构的首选材料；②易于浇注成各种形状，满足建筑功能及各种工艺的要求；⑧充分发挥钢筋和混凝土的作用，结构受力合理：④材料的重度与强度之比不大；⑤材料性能复杂，一般的计算模型难与实际结构的受力情况相符。

正因为钢筋混凝土材料的这些优缺点，长期以来，钢筋混凝土在工程中的应用如此广泛；为了满足工程需要所建立的反映混凝土材料性能的计算模型也不断完善。

然而，混凝土是一种由水泥、水、砂、石及各种掺合料、外加剂混合而成的成分复杂、性能多样的材料。

到目前为止，还没有一种公认的、能全面反映混凝土的力学行为和性质的计算模型或本构关系。

因此，对钢筋混凝土的力学性能研究还需要学术界和工程人员继续努力。

长期以来，人们用线弹性理论来分析钢筋混凝土结构的受力和变形，以极限状态的设计方法来确定构件的承载能力。

这种设计方法在一定程度上能满足工程的要求。

随着国民经济的发展，越来越多大型、复杂的钢筋混凝土结构需要修建，而且对设计周期和工程质量也提出了更高的要求。

这样一来，常规的线弹性理论分析方法用于钢筋混凝土结构和构件的设计就力不从心。

设计人员常有“算不清楚”以及“到底会不会倒”的困惑。

为此，钢筋混凝土非线性有限元分析方法开始受到重视。

同时，随着有限元理论和计算机技术的进步，钢筋混凝土非线性有限元分析方法也得以迅速的发展并发挥出巨大的作用。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

τ ( kgf/cm 2 ) = 100 × 10 2 S (cm) − 58.5 × 10 6 S 2 + 8.53 × 10 9 S 3
!
τ (kgf/cm 2 ) = (54 × 103 S (cm) − 25.7 × 10 6 S 2 + 5.98 × 109 S 3 − 0.558 × 1012 S 4 )
清华大学研究生课程——《钢筋混凝土有限元》
清华大学研究生课程——《钢筋混凝土有限元》
单根钢筋的刚度矩阵
cosθ sin θ [K ] = EA l cos θ
2
几何变形相似
Ub U2 = b1 l2 Ub = Vb = U 2 b1 l2 V2 b1 l2
清华大学研究生课程——《钢筋混凝土有限元》
清华大学研究生课程——《钢筋混凝土有限元》
钢筋单元
! ! ! !
钢筋与混凝土的界面单元形式
!
弹簧单元
[∆w'] =
[K ] =
− cosθ sin θ
常用单元桁架单元梁单元二维或三维
弹簧单元
!
Spring, link Goodman
∆u ' − cosθ = ∆v ' sin θ
[ε ] = [B ] = ∂[N ] ∂{x}
B 几何矩阵
ui v 0 i u j cm v j bm u m v m
1 xi 1 ∆ = 1 xj 2 1 xm
yi yj ym
u N i = v 0
钢筋与混凝土的粘结滑移本构
[K ] = [T ]T [K '][T ]
清华大学研究生课程——《钢筋混凝土有限元》
清华大学研究生课程——《钢筋混凝土有限元》
清华大学研究生课程——《钢筋混凝土有限元》
局部粘结滑移关系
!
反复荷载下的粘结滑移关系
滕智明模型
Nilson Houde & Mirza
fc ' 415
sin θ − cos θ cos θ sin θ
sin θ − cosθ
T
cosθ sin θ
!
滑移单元
!
ui sin θ vi cosθ u j v j
sin θ − cosθ cosθ sin θ sin θ cosθ
清华大学研究生课程——《钢筋混凝土有限元》
清华大学研究生课程——《钢筋混凝土有限元》
高斯积分
[K ] = ∫−1 ∫−1 [B ] [D ][B ] J tdξdη = ∑∑ wi ([B ] [D ][B ] J t ) i
1 1 T T i =1 j =1 n n
其他常用单元
! !
参阅教学网页上相关程序
!
滕智明
τ (MPa ) = (61.5S (mm) − 693S 2 + 3.14 × 10 3 S 3 − 0.478 ×10 4 S 4 ) f ts c / d F ( x)
清华大学研究生课程——《钢筋混凝土有限元》
清华大学研究生课程——《钢筋混凝土有限元》
清华大学研究生课程——《钢筋混凝土有限元》
[J ] = 1
x1 − (1 − η ) (1 − η ) (1 + η ) − (1 + η ) x2 4 − (1 − ξ ) (1 − ξ ) (1 + ξ ) − (1 + ξ ) x3 x4
y1 y2 y3 y4
清华大学研究生课程——《钢筋混凝土有限元》
雅可比矩阵
∂N i ∂N i ∂x ∂N i ∂y = + ∂ξ ∂x ∂ξ ∂y ∂ξ
∂N i ∂x ∂ξ ∂ξ = ∂N i ∂x ∂η ∂η
∂N i ∂N i ∂x ∂N i ∂y = + ∂η ∂x ∂η ∂y ∂η
v = ∑ N i vi
形函数矩阵
[∆w'] =
u1 ' v ' 1 u ' 1 x' 1 x' 1 x' 1 x' 2 0 −( + ) 0 ( + ) 0 ( − ) 0 v ' − ( 2 − l ) 2 2 l 2 l 2 l 1 x' 1 x' 1 x' 1 x' 0 −( − ) 0 −( + ) 0 ( + ) 0 ( − ) u 3 ' 2 l 2 l 2 l 2 l v ' 3 u ' 4 v4 ' ∆u ' = [N '][δ '] = ∆v '
i =1
N1 =
1 (1 − ξ )(1 − η ) 4 1 N 2 = (1 + ξ )(1 − η ) 4 1 N 3 = (1 + ξ )(1 + η ) 4 1 N 4 = (1 − ξ )(1 + η ) 4
∂y ∂N i ∂N i x ∂ξ ∂x ∂N = [J ] ∂∂ N ∂y i i ∂ y ∂y ∂η
! ! !
n 1
高斯点 0.0
权因子 2 .0
平面8节点等参元空间8节点等参元
2 ± 1/ 3 1.0 3 ± 0.7745967 0.555556 0.0 0.888889
planarFEM.pdf 3D_Solid_src.pdf source_planefem.zip
清华大学研究生课程——《钢筋混凝土有限元》
!
!
常用的钢筋混凝土有限元组合方式：
! ! !
!
将钢筋与混凝土分别作为不同单元来处理一般将混凝土简化为实体单元，钢筋简化为梁单元或桁架单元钢筋与混凝土之间的滑移可以通过在钢筋与混凝土之间添加相应的界面单元加以模拟
清华大学研究生课程——《钢筋混凝土有限元》
清华大学研究生课程——《钢筋混凝土有限元》
清华大学研究生课程——《钢筋混凝土有限元》
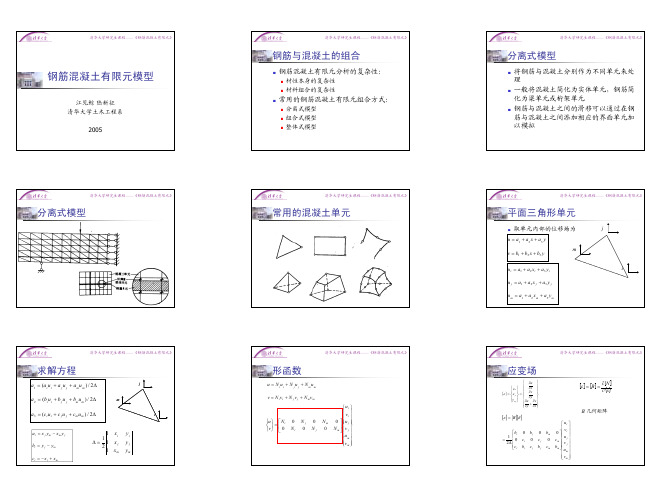
分离式模型
常用的混凝土单元
平面三角形单元
!
取单元内部的位移场为
m
j
u = a1 + a 2 x + a 3 y v = b1 + b2 x + b3 y
u i = a1 + a 2 x i + a 3 y i
i
u j = a1 + a 2 x j + a3 y j u m = a1 + a 2 x m + a 3 y m
清华大学研究生课程——《钢筋混凝土有限元》
清华大学研究生课程——《钢筋混凝土有限元》
清华大学研究生课程——《钢筋混凝土有限元》
局部坐标系下的刚度矩阵
2k x ' 0 2k y ' sym kx ' 0 2k x ' 0 ' 0 2 ' k k y y [K '] = l 0 − 2k x ' 0 2k x ' 6 − kx ' 39; 0 2k y ' 0 − 2k ' 0 0 0 2k x ' kx ' kx ' x − 2k y ' 0 − ky ' 0 0 2k y ' ky ' 0
! !
最早由Goodman提出作为岩石力学中的节理单元单元宽度为零，不影响网格划分与混凝土单元位移插值函数一样
1 [(u 3 '−u 2 ') + (u 4 '−u1 ')] 2 1 [(v3 '−v 2 ') + (v4 '−v1 ')] 2
1 [(u3 '−u 2 ') + (u 4 '−u1 ')] l 1 [(v3 '−v 2 ') + (v 4 '−v1 ')] l
=
清华大学研究生课程——《钢筋混凝土有限元》
清华大学研究生课程——《钢筋混凝土有限元》
清华大学研究生课程——《钢筋混凝土有限元》
单元刚度矩阵
[D ] =
1 ν 0 E ν 1 0 1 −ν 1−ν 0 0 2
三角形单元程序
!
等参单元
! !
PlanarFEM
清华大学研究生课程——《钢筋混凝土有限元》
清华大学研究生课程——《钢筋混凝土有限元》
清华大学研究生课程——《钢筋混凝土有限元》
钢筋与混凝土的组合
分离式模型
!
钢筋混凝土有限元模型
江见鲸陆新征清华大学土木工程系 2005
!
钢筋混凝土有限元分析的复杂性：
! !
材性本身的复杂性材料组合的复杂性分离式模型组合式模型整体式模型
整体坐标系局部坐标系
[K ] = [B ]T [D ][B ]t∆
参考网页上的教学程序planarFEM.pdf
清华大学研究生课程——《钢筋混凝土有限元》
清华大学研究生课程——《钢筋混凝土有限元》
清华大学研究生课程——《钢筋混凝土有限元》
母单元插值函数
u = ∑ N i ui
i =1 4 4
单元内应变场
ai = x j y m − xm y j bi = y j − y m ci = − x j + x m
m i j
形函数