专题十-与几何图形有关的探究题
中考数学几何模型专题专题十—经典模型
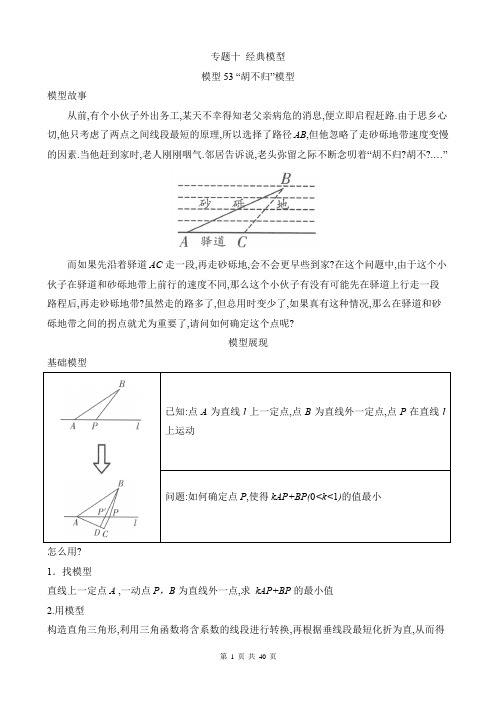
专题十经典模型模型53 “胡不归”模型模型故事从前,有个小伙子外出务工,某天不幸得知老父亲病危的消息,便立即启程赶路.由于思乡心切,他只考虑了两点之间线段最短的原理,所以选择了路径AB,但他忽略了走砂砾地带速度变慢的因素.当他赶到家时,老人刚刚咽气.邻居告诉说,老头弥留之际不断念叨着“胡不归?胡不?.…”而如果先沿着驿道AC走一段,再走砂砾地,会不会更早些到家?在这个问题中,由于这个小伙子在驿道和砂砾地带上前行的速度不同,那么这个小伙子有没有可能先在驿道上行走一段路程后,再走砂砾地带?虽然走的路多了,但总用时变少了,如果真有这种情况,那么在驿道和砂砾地带之间的拐点就尤为重要了,请问如何确定这个点呢?模型展现基础模型怎么用?1．找模型直线上一定点A ,一动点P，B为直线外一点,求kAP+BP的最小值2.用模型构造直角三角形,利用三角函数将含系数的线段进行转换,再根据垂线段最短化折为直,从而得到线段和最小值,最后运用锐角三角函数求解即可 模型分析如图,求这类带有系数的折线最值问题,通常我们都是将折线转化成为线段,再利用两点之间线段最短或垂线段最短求解，该模型就是利用了垂线段最短的性质,具体解题步骤如下: 一找:找带有系数k 的线段kAP ;二构:在点B 异侧,构造以线段AP 为斜边的直角三角形; ①以定点A 为顶点作①CAP ,使得sin ①P AC =h ; ①过动点P 作垂线构造Rt ①P AC ; 三转化:化折为直,将kAP 转化为PC ;四求解:使得hAP +BP =PC +BP ,利用“垂线段最短”转化为求BD 的长度.拓展延伸熟记特殊角的锐角三角函数值，kAP +BP 中系数k 发生变化时,所构造的直角三角形也会发生变化,同学们需要牢记特殊角度的正弦值：01sin 30 =2，0sin 60，0sin 45 =2，03sin 375，04sin 53 5例1如图， 在①ABC 中，AC =6，①A =30°，点D 是AB 边上一动点，（点拨：两定点A 、C ，动点D ，含特殊角30°）则12AD CD 的最小值为_________（点拨：线段数量关系的最小值,考虑“胡不归”）考什么?直角三角形的性质,30°,60°角的锐角三角函数值,垂线段最短.思路点拨哪条线段带有系数,就以它为斜边构造直角三角形,使得其中一锐角的正弦值恰好与系数相等.例2如图, 在平行四边形ABCD中,①DAB=45°，（点拨：特殊角）AB=6，BC=2，P为CD边上的一动点，则22PB PD（点拨：线段数量关系出现，且0＜k＜1，模型出现）的最小值为_____________考什么?平行四边形的性质,直角三角形的性质,45°角的锐角三角函数值,垂线段最短。
【中考数学专题】10 与翻折或轴对称作图有关的几何证明题解析-
专题十：与翻折或轴对称作图有关的几何证明题解析专题导例如图，M、N是正方形ABCD的边CD上的两个动点，满足AM＝BN，连接AC交BN于点E，连接DE交AM于点F，连接CF，若正方形的边长为6，则线段CF的最小值是．【分析】：先判断出Rt△ADM≌Rt△BCN（HL），得出∠DAM＝∠CBN，进而判断出△DCE≌△BCE （SAS），得出∠CDE＝∠CBE，即可判断出∠AFD＝90°，根据直角三角形斜边上的中线等于斜边的一半可得OF＝AD＝3，利用勾股定理列式求出OC，然后根据三角形的三边关系可知当O、F、C 三点共线时，CF的长度最小．方法剖析轴对称的性质（1）对应线段相等，对应角相等；对称点的连线被对称轴垂直平分；（2）轴对称图形变换的特征是不改变图形的形状和大小，只改变图形的位置，新旧图形具有对称性；（3）轴对称的两个图形，它们对应线段或延长线相交，交点在对称轴上.轴对称（折叠）的思考层次全等变换：对应边相等，对应角相等；对称轴性质：对应点所连线段被对称轴（折痕）垂直平分，对称轴（折痕）上的点到对应点的距离相等；指出：（1）在翻折下，前后的图形关于折痕成轴对称，注意前后的图形成镜面对称，即前后的图形的左右位置互换；（2）翻折或对称中建构勾股方程来求取线段长及对最值类问题进行探究；（3）轴对称常见的结构，折叠会产生垂直平分，等腰三形.导例答案：解：如图，在正方形ABC D中，AD＝BC＝CD，∠ADC＝∠BCD，∠DCE＝∠BCE，在Rt△ADM和Rt△BCN中，，∴Rt△ADM≌Rt△BCN（HL），∴∠DAM＝∠CBN，在△DCE和△BCE中，，∴△DCE≌△BCE（SAS），∴∠CDE＝∠CBE∴∠DAM＝∠CDE，∵∠ADF+∠CDE＝∠ADC＝90°，∴∠DAM+∠ADF＝90°，∴∠AFD＝180°﹣90°＝90°，取AD的中点O，连接OF、OC，则OF＝DO ＝AD＝3，在Rt△OD C中，OC ＝＝3根据三角形的三边关系，OF+CF＞OC，∴当O、F、C三点共线时，CF的长度最小，最小值＝OC﹣OF＝3﹣3．故答案为：3﹣3．典型例题类型一：利用已知直线作对称图形进行证明例1、在等边△AB C中，点D在BC边上，点E在AC的延长线上，DE＝DA（如图1）．（1）求证：∠BAD＝∠EDC；（2）点E关于直线BC的对称点为M，连接DM，AM．①依题意将图2补全；②证明：在点D运动的过程中，始终有DA＝AM．【分析】（1）先判断出∠BAD+∠CAD＝60°，进而得出∠BAD+∠E＝60°，即可得出结论；（2）①由对称性即可补全图形；②由对称性判断出DM＝DE，∠MDC＝∠EDC，再用三角形的外角的性质，判断出∠ADC＝∠B+∠BAD＝∠B+∠MDC，进而判断出△ADM是等边三角形，即可得出结论．类型二：对已知图形进行翻折进行证明例2．如图，矩形ABC D中，AB＝4，AD＝3，把矩形沿直线AC折叠，使点B落在点E处，AE交CD于点F，连接DE．（1）求证：△DEC≌△EDA；（2）求DF的值；（3）在线段AB上找一点P，连结FP使FP⊥AC，连结PC，试判定四边形APCF的形状，并说明理由，直接写出此时线段PF的大小．【分析】（1）根据矩形的性质、轴对称的性质可得到AD＝EC，AE＝DC，即可证到△DEC≌△EDA （SSS）；（2）易证AF＝CF，设DF＝x，则有AF＝4﹣x，然后在Rt△ADF中运用勾股定理就可求出DF的长．（3）根据三角形的内角和定理求得∠APF＝∠AFP根据等角对等边得出AF＝AP进而得出FC＝AP，从而证得四边形APCF是平行四边形，又因为FP⊥AC证得四边形APCF为菱形，然后根据菱形的面积S菱形＝PF•AC＝AP•AD，即可求得．专项突破1.如图，在Rt△AB C中，∠C＝90°，点D、E分别是BC、AB上一个动点，连接DE．将点B沿直线DE折叠，点B的对应点为F，若AC＝3，BC＝4，当点F落在AC的三等分点上时，BD的长为．2．如图，正方形ABC D中，点E是BC延长线上一点，连接DE，过点B作BF⊥DE于点F，连接F C．（1）求证：∠FBC＝∠CDF；（2）作点C关于直线DE的对称点G，连接CG，FG，猜想线段DF，BF，CG之间的数量关系，并证明你的结论．3.已知矩形ABCD，其中AD＞AB，依题意先画出图形，然后解答问题．（1）F为DC边上一点，把△ADF沿AF折叠，使点D恰好落在BC上的点E处．在图1中先画出点E，再画出点F，若AB＝8，AD＝10，直接写出EF的长为；（2）把△ADC沿对角线AC折叠，点D落在点E处，在图2先画出点E，AE交CB于点F，连接BE．求证：△BEF是等腰三角形．4.如图，Rt△AB C中，∠ACB=90°，AC=BC，点D为AB边上的一个动点（不与点A，B及A B中点重合），连接CD，点A关于直线CD的对称点为点E，直线BE，CD交于点F．（1）如图1，当∠ACD=15°时，根据题意将图形补充完整，并直接写出∠BFC的度数；（2）如图2，当45°＜∠ACD＜90°时，用等式表示线段AC，EF，BF之间的数量关系，并加以证明．5．在Rt△AB C中，∠ACB＝90°，CA＝C B．点D为线段BC上一个动点（点D不与点B，C重合），连接AD，点E在射线AB上，连接DE，使得DE＝D A．作点E关于直线BC的对称点F，连接BF，DF．（1）依题意补全图形；（2）求证：∠CAD＝∠BDF；（3）用等式表示线段AB，BD，BF之间的数量关系，并证明．6．如图①，在等腰三角形AB C中，AB＝AC＝8，BC＝14．如图②，在底边BC上取一点D，连结AD，使得∠DAC＝∠AC D．如图③，将△ACD沿着AD所在直线折叠，使得点C落在点E处，连结BE，得到四边形ABE D．则BE的长是．7．在等边三角形ABC外侧作射线AP，∠BAP=α，点B关于射线AP的对称点为点D，连接CD交AP于点E.（1）依据题意补全图形；（2）当α=20°时，∠ADC= ；∠AEC= ；（3）连接BE，求证：∠AEC=∠BEC；（4）当0°<α<60°时，用等式表示线段AE，CD，DE之间的数量关系，并证明．8.在等边△ABC外侧作直线AP，点B关于直线AP的对称点为D，连结BD，CD，其中CD交直线AP与点E．（1）如图1，若∠P AB＝30°，则∠ACE＝；（2）如图2，若60°＜∠P AB＜120°，请补全图形，判断由线段AB，CE，ED可以构成一个含有多少度角的三角形，并说明理由．9．如图1，将一张矩形纸片ABCD沿着对角线BD向上折叠，顶点C落到点E处，BE交AD于点F.(1)求证：△BDF是等腰三角形；(2)如图2，过点D作DG∥BE，交BC于点G，连结FG交BD于点O.①判断四边形BFDG的形状，并说明理由；②若AB＝6，AD＝8，求FG的长．10.【问题情境】如图①，在Rt△AB C中，∠ACB＝90°，AC＝BC，点D为A B中点，连结CD，点E为CB上一点，过点E且垂直于DE的直线交AC于点F．易知：BE＝CF．（不需要证明）【探索发现】如图②，在Rt△AB C中，∠ACB＝90°，AC＝BC，点D为A B中点，连结CD，点E为CB的延长线上一点，过点E且垂直于DE的直线交AC的延长线于点F．【问题情境】中的结论还成立吗？请说明理由．【类比迁移】如图③，在等边△AB C中，AB＝4，点D是A B中点，点E是射线AC上一点（不与点A、C重合），将射线DE绕点D逆时针旋转60°交BC于点F．当CF＝2CE时，CE＝．11．在△AB C中，∠ACB＝90°，AC＜BC，点D在AC的延长线上，点E在BC边上，且BE＝AD，（1）如图1，连接AE，DE，当∠AEB＝110°时，求∠DAE的度数；（2）在图2中，点D是AC延长线上的一个动点，点E在BC边上（不与点C重合），且BE＝AD，连接AE，DE，将线段AE绕点E顺时针旋转90°得到线段EF，连接BF，DE．①依题意补全图形；②求证：BF＝DE．专题十：与翻折或轴对称作图有关的几何证明题解析例1．解：（1）∵△ABC是等边三角形，∴∠BAC＝∠ACB＝60°，∴∠BAD+∠CAD＝60°，∵DE＝DA，∴∠CAD＝∠E，∴∠BAD+∠E＝60°，∵∠EDC+∠E＝∠ACB＝60°，∴∠BAD＝∠EDC；（2）①补全图形如图2所示；②∵△ABC是等边三角形，∴∠B＝60°，由对称性得，∠EDC＝∠MDC，由（1）知，∠EDC＝∠BAD，∴∠MDC＝∠BAD，∵∠ADC＝∠B+∠BAD＝∠B+∠MD C．∴∠ADM＝∠B＝60°，由对称性得，DM＝DE，∵DE＝DA，∴DA＝DM，∴△ADM是等边三角形，∴DA＝DM，即：在点D运动的过程中，始终有DA＝AM．例2．（1）证明：∵四边形ABCD是矩形，∴AD＝BC，AB＝CD，AB∥CD，∴∠ACD＝∠CAB，∵△AEC由△ABC翻折得到，∴AB＝AE，BC＝EC，∠CAE＝∠CAB，∴AD＝CE，DC＝EA，∠ACD＝∠CAE，在△ADE与△CE D中，，∴△DEC≌△EDA（SSS）；（2）解：如图1，∵∠ACD＝∠CAE，∴AF＝CF，设DF＝x，则AF＝CF＝4﹣x，在RT△ADF中，AD2+DF2＝AF2，即32+x2＝（4﹣x）2，解得；x＝，即DF＝．（3）解：四边形APCF为菱形，设AC、FP相较于点O∵FP⊥AC∴∠AOF＝∠AOP又∵∠CAE＝∠CAB，∴∠APF＝∠AFP∴AF＝AP∴FC＝AP又∵AB∥CD∴四边形APCF是平行四边形又∵FP⊥AC∴四边形APCF为菱形，在矩形ABC D中，AB＝4，AD＝3，∴AC＝5，∵S菱形＝PF•AC＝AP•AD，∵AP＝AF＝4﹣＝∴PF＝＝．专项突破1.解：∵折叠∴BD＝DF，∵点F落在AC的三等分点上∴CF＝1或CF＝2，若CF＝1时，在Rt△CDF中，DF2＝CD2+CF2，∴BD2＝（4﹣BD）2+1∴BD＝当CF＝2时，在Rt△CDF中，DF2＝CD2+CF2，∴BD2＝（4﹣BD）2+4∴BD＝故答案为：或2．解：（1）∵ABCD为正方形，∴∠DCE＝90°．∴∠CDF+∠E＝90°，又∵BF⊥DE，∴∠FBC+∠E＝90°，∴∠FBC＝∠CDF（2）如图所示：在线段FB上截取FM，使得FM＝F D．∵∠BDC＝∠MDF＝45°，∴∠BDM＝∠CDF，∵＝＝，∴△BDM∽△CDF，∴＝＝，∠DBM＝∠DCF，∴BM＝CF，∴∠CFE＝∠FCD+∠CDF＝∠DBM+∠BDM＝∠DMF＝45°，∴∠EFG＝∠EFC＝45°，∴∠CFG＝90°，∵CF＝FG，∴CG＝CF，∴BM＝CG，∴BF＝BM+FM＝CG+DF．补充方法：连接GM，证明四边形BMGC是平行四边形即可．3.解：（1）如图1，在BC上截取AE＝AD得点E，作AF垂直DE交CD于点F（或作∠AED的平分线AF交CD于点F，或作EF垂直AE交CD于点F等等），∵四边形ABCD是矩形，∴AB＝CD＝8，AD＝BC＝10，∠B＝∠C＝90°，在Rt△ABE中，BE＝＝6，∴EC＝10﹣6＝4，设EF＝DF＝x，在Rt△EF C中，则有x2＝（8﹣x）2+42，解得x＝5，∴EF＝5．故答案为：5；（2）证明：如图2，作DH垂直AC于点H，延长DH至点E，使HE＝DH．方法1：∵△ADC≌△AEC，∴AD＝AE＝BC，AB＝DC＝EC，在△ABE与△CE B中，，∴△ABE≌△CEB（SSS），∴∠AEB＝∠CBE，∴BF＝EF，∴△BEF是等腰三角形．方法2：∵△ADC≌△AEC，∴AD＝AE＝BC，∠DAC＝∠EAC，又∴AD∥BC，∴∠DAC＝∠ACB，∴∠EAC＝∠ACB，∴F A＝FC，∴FE＝FB，∴△BEF是等腰三角形．4.（1）如图1中，连接E C．∵A，E关于CD对称，∴∠DCA=∠DCE=15°，CA=CE=C B．∵∠ACB=90°，∴∠ECB=60°，∴△ECB是等边三角形，∴∠CEB=60°，∵∠CEB=∠BFC+∠DCE，∴∠BFC=60°-15°=45°．（2）结论：EF2+BF2=2AC2．理由：如图2，连接CE，AF，延长AC交FE的延长线于点G．∵A，E关于CD对称，∴AC=CE，AF=EF，又∵CF=CF，∴△ACF≌△ECF（SSS），∴∠CAF=∠1，∵AC=BC，∴BC=CE，∴∠1=∠2，∴∠CAF=∠2，∵∠ACB=90°，∴∠G+∠2=90°，∴∠CAF+∠G=90°，∴∠AFG=90°，在Rt△AF B中，AB2=AF2+BF2，在Rt△AB C中，AB2=AC2+BC2=2AC2，∴BF2+AF2=2AC2，∴BF2+EF2=2AC2．5．（1）如图所示：（2）∵∠ACB＝90°，CA＝CB，∴∠BAC＝∠CBA＝45°，∴∠CAD+∠DAB＝45°，∵DA＝DE，∴∠DAE＝∠DEB，∵∠DBA是△DBE的一个外角，∴∠EDB+∠DEB＝∠DBA＝45°，∴∠EDB＝∠CAD，∵点E关于直线BC的对称点F，∴∠EDB＝∠FDB，∴∠CAD＝∠FDB；（3）线段AB，BD，BF之间的数量关系是AB﹣BF=√2BD，证明：过点D作AC的平行线交AB于M点，∴∠C＝∠MDB＝90°，∠CAB＝∠DMB＝45°，∴∠DMB＝∠DBM，∴DM＝DB，∴MB=√2BD，∵点E关于直线BC的对称点F，∴DE＝DF，∵AD＝DE，∴AD＝DF，∵AC∥MD，∴∠CAD＝∠ADM，∵∠CAD＝∠FDB，∴∠ADM＝∠FDB，∴△ADM≌△FDB（SAS），∴AM＝BF，∴AB﹣BF＝AB﹣AM＝MB，又∵MB=√2BD，∴AB﹣BF=√2B D．6.解：∵AB＝AC，∴∠ABC＝∠C，∵∠DAC＝∠ACD，∴∠DAC＝∠ABC，∵∠C＝∠C，∴△CAD∽△CBA，∴＝，∴＝，∴CD＝，BD＝BC﹣CD＝，∵∠DAM＝∠DAC＝∠DBA，∠ADM＝∠ADB，∴△ADM∽△BDA，∴＝，即＝，∴DM＝，MB＝BD﹣DM＝，∵∠ABM＝∠C＝∠MED，∴A、B、E、D四点共圆，∴∠ADB＝∠BEM，∠EBM＝∠EAD＝∠ABD，∴△ABD∽△MBE，∴＝，∴BE ＝＝＝．故答案为：．7．（1）如图；EDP（2）40°；60 °；（3）证明：∵点B关于射线AP的对称点为点D，∴△BAE≌△DAE．∴∠BAE=∠DAE=α．∵AD=AB=AC，∴∠ADC=()1806022α︒-︒+=60°－α．∴∠AEC=60°．∵∠ACB=60°，∠ACD=∠ADC=60°－α，∴∠BCE=α．∵∠ABC=60°，∠ABE=∠ADC=60°－α，∴∠BEC=60°．（4）证明：法一：在CD上截取AF=AE．F EDAB C P∵∠AEF =60°，∴△AEF 是等边三角形．∴∠AFC =∠AED =120°．∵∠ACD =∠ADC =60°－α，∴△ADE ≌△ACF ．∴DE =CF ．∴CD =2DE +EF ．∵AE =EF ，∴CD =2DE +AE ．法二：在CD 上截取BG =BE ．GEDAB C P∵∠BEC =60°，∴△BEG 是等边三角形．∴∠BGC =∠AED =120°．∵∠BCE =∠DAE =α，∴△BCG ≌△DAE ．∴AE =CG ．∵EG =BE =DE ，∴CD =2DE +CG ．∴CD =2DE +AE ．8.解：（1）连接AD ，如图1．∵点D 与点B 关于直线AP 对称，∴AD ＝AB ，∠DAP ＝∠BAP ＝30°，∵AB ＝AC ，∠BAC ＝60°，∴AD ＝AC ，∠DAC ＝120°，∴2∠ACE +60°+60°＝180°，∴∠ACE ＝30°，故答案为：30°；（3）线段AB ，CE ，ED 可以构成一个含有60°角的三角形．证明：连接AD ，EB ，如图2．∵点D 与点B 关于直线AP 对称，∴AD ＝AB ，DE ＝BE ，∴∠EDA ＝∠EBA ，∵AB ＝AC ，AB ＝AD ，∴AD ＝AC ，∴∠ADE ＝∠ACE ，∴∠ABE ＝∠ACE ．设AC ，BE 交于点F ，又∵∠AFB ＝∠CFE ，∴∠BAC ＝∠BEC ＝60°，∴线段AB ，CE ，ED 可以构成一个含有60°角的三角形．9．(1)根据折叠，∠DBC ＝∠DBE ，又AD ∥BC ，∴∠DBC ＝∠ADB ，∴∠DBE ＝∠ADB ，∴DF ＝BF ，∴△BDF 是等腰三角形(2)①菱形，理由：∵四边形ABCD 是矩形，∴AD ∥BC ，∴FD ∥BG ，又∵FD ∥BG ，∴四边形BFDG 是平行四边形，∵DF ＝BF ，∴四边形BFDG 是菱形②∵AB ＝6，AD ＝8，∴BD ＝10.∴OB ＝12BD ＝5.设DF ＝BF ＝x ，∴AF ＝AD －DF ＝8－x .∴在Rt △ABF 中，AB 2＋AF 2＝BF 2，即62＋(8－x )2＝x 2，解得x ＝254，即BF ＝254，∴FO ＝BF 2－OB 2＝（254）2－52＝154，∴FG ＝2FO ＝152 10.解：【问题情境】证明：∵在Rt △AB C 中，∠ACB ＝90°，AC ＝BC ，点D 为A B 中点， ∴CD ⊥AB ，CD ＝BD ＝AD ＝AB ，∠BCD ＝∠B ＝45°，∴∠BDC ＝90°，∵∠EDF ＝90°，∴∠CDF＝∠BDE，在△BDE与△CDF中，，∴△BDE≌△CDF（ASA），∴BE＝CF；【探索发现】成立，理由：∵在Rt△AB C中，D为A B中点，∴CD＝BD，又∵AC＝BC，∴DC⊥AB，∴∠DBC＝∠DCB＝45°，∵DE⊥DF，∴∠EDF＝90°，∴∠EDB+∠BDF＝∠CDF+∠BDF＝90°，∴∠CDF＝∠BDE，∴∠ADF＝∠CDE，∴AF＝CE，∴CF＝BE；【类比迁移】∵△ABC是等边三角形，∴∠A＝∠B＝60°，∵∠FDE＝60°，∴∠BDF＝120°﹣∠ADE，∠AED＝120°﹣∠ADE，∴∠BDF＝∠AED，∴△ADE∽△BDF，∴，∵点D为A B中点，AB＝4，∴AD＝BD＝2，AC＝BC＝4，∵CF＝2CE，∴设CE＝x，则CF＝2x，当点E在线段AC上时，∴AE＝4﹣x，BF＝4﹣2x，∴＝，解得：x＝3﹣，x＝3+（不合题意，舍去），∴CE＝3﹣，如图④，当点E在AC的延长线上时，∵AE＝4+x，BF＝4﹣2x，∴＝，解得：x＝﹣1+，（负值舍去），∴CE＝﹣1+．综上所述，CE＝3﹣或﹣1+，故答案为：3﹣或﹣1+．11.解：（1）∵∠AEB＝110°，∠ACB＝90°，∴∠DAE＝∠AEB﹣∠ACB＝20°；（2）①补全图形，如图所示．②证明：由题意可知∠AEF＝90°，EF＝AE．∵∠ACB＝90°，∴∠AEC+∠BEF＝∠AEC+∠DAE＝90°．∴∠BEF＝∠DAE．∵在△EBF和△ADE中，，∴△EBF≌△ADE（SAS）．∴DE＝BF．。
浙教版四年级数学几何图形探索题
浙教版四年级数学几何图形探索题在数学课程中，学习几何图形是一个重要的内容。
通过几何图形的学习，我们可以培养学生的观察力、逻辑思维和空间想象能力。
本文将针对浙教版四年级数学课本中的几何图形探索题进行分析和解答。
1.正方形与长方形的探究在四年级的数学课本中，我们首先学习了正方形和长方形这两种常见的几何图形。
请考虑以下问题：问题一：能否找到一种方法，将一个正方形切割成两个相等的长方形？为什么？答案：不能。
由于正方形的四条边相等，因此无法找到一条切割线，使得切割后的两个图形完全相等。
一个直观的推理是，如果切割一次，会产生一个长方形和一个不完整的长方形，无法满足两个图形完全相等的条件。
问题二：能否找到一种方法，将一个长方形切割成两个相等的正方形？为什么？答案：可以。
将长方形切割成两个相等的正方形是可能的。
我们可以在长方形的一条边上找到一个中点，然后从该点处作垂直于该边的切割线，将长方形分割成两个相等的正方形。
2.三角形的探究在数学课本中，我们还学习了三角形这一几何图形。
请思考以下问题：问题一：三角形的内角和是多少度？答案：三角形的内角和是180度。
这是由于三角形的三个内角相加等于一条直线上的直角，而一条直线上的角度为180度。
问题二：如何判断一个角是否是直角？答案：一个角是直角的判断方法是判断这个角的度数是否等于90度。
我们可以使用量角器或直尺等工具进行测量，也可以将该角与已知的直角进行比较。
3.圆形的探究圆形是数学中的一个重要几何图形。
请思考以下问题：问题一：如何计算圆的面积？答案：圆的面积可以用公式A = πr²来计算，其中A表示面积，π表示圆周率，r表示半径。
半径是从圆心到圆的任何一点的距离。
通过将圆的半径代入公式中，我们可以计算出圆的面积。
问题二：如何计算圆的周长？答案：圆的周长可以用公式C = 2πr来计算，其中C表示周长，π表示圆周率，r表示半径。
通过将圆的半径代入公式中，我们可以计算出圆的周长。
初中数学(几何探究型问题)题库及答案
初中数学（几何探究型问题）题库及答案1．（2019•北京）在△ABC中，D，E分别是△ABC两边的中点，如果DE上的所有点都在△ABC的内部或边上，则称DE为△ABC的中内弧．例如，图1中DE 是△ABC的一条中内弧．（1）如图2，在Rt△ABC中，AB=AC=D，E分别是AB，AC的中点，画出△ABC的最长的中内弧DE，并直接写出此时DE的长；（2）在平面直角坐标系中，已知点A（0，2），B（0，0），C（4t，0）（t>0），在△ABC中，D，E分别是AB，AC的中点．①若t12=，求△ABC的中内弧DE所在圆的圆心P的纵坐标的取值范围；②若在△ABC中存在一条中内弧DE，使得DE所在圆的圆心P在△ABC的内部或边上，直接写出t的取值范围．【解析】（1）如图2，以DE为直径的半圆弧DE，就是△ABC的最长的中内弧DE，连接DE.∵∠A=90°，AB=AC=D，E分别是AB，AC的中点.∴BC sin AC B ===4，DE 12=BC 12=⨯4=2.∴弧12DE =⨯2π=π． （2）如图3，由垂径定理可知，圆心一定在线段DE 的垂直平分线上，连接DE ，作DE 垂直平分线FP ，作EG ⊥AC 交FP 于G .①当t 12=时，C （2，0），∴D （0，1），E （1，1），F （12，1）.设P （12，m ）由三角形中内弧定义可知，圆心线段DE 上方射线FP 上均可，∴m ≥1.∵OA =OC ，∠AOC =90°. ∴∠ACO =45°. ∵DE ∥OC .∴∠AED =∠ACO =45°.作EG ⊥AC 交直线FP 于G ，FG =EF 12=. 根据三角形中内弧的定义可知，圆心在点G 的下方（含点G ）直线FP 上时也符合要求. ∴m 12≤.综上所述，m 12≤或m ≥1． ②如图4，设圆心P 在AC 上.∵P 在DE 中垂线上.∴P 为AE 中点，作PM ⊥OC 于M ，则PM 32=. ∴P （t ，32）. ∵DE ∥BC .∴∠ADE =∠AOB =90°.∴AE === ∵PD =PE . ∴∠AED =∠PDE .∵∠AED +∠DAE =∠PDE +∠ADP =90°. ∴∠DAE =∠ADP . ∴AP =PD =PE 12=AE .由三角形中内弧定义知，PD ≤PM .∴12AE 32≤，AE ≤3≤3，解得：t ≤ ∵t >0. ∴0<t≤【名师点睛】此题是一道圆的综合题，考查了圆的性质，弧长计算，直角三角形性质等，给出了“三角形中内弧”新定义，要求学生能够正确理解新概念，并应用新概念解题．2．（2019•天津）在平面直角坐标系中，O为原点，点A（6，0），点B在y轴的正半轴上，∠ABO=30°．矩形CODE的顶点D，E，C分别在OA，AB，OB上，OD=2．（Ⅰ）如图①，求点E的坐标；（Ⅱ）将矩形CODE沿x轴向右平移，得到矩形C′O′D′E′，点C，O，D，E 的对应点分别为C′，O′，D′，E′．设OO′=t，矩形C′O′D′E′与△ABO重叠部分的面积为S．①如图②，当矩形C′O′D′E′与△ABO重叠部分为五边形时，C′E′，E′D′分别与AB相交于点M，F，试用含有t的式子表示S，并直接写出t的取值范围；S t的取值范围（直接写出结果即可）．【解析】（Ⅰ）∵点A（6，0）.∴OA=6.∵OD=2.∴AD=OA-OD=6-2=4.∵四边形CODE是矩形.∴DE∥OC.∴∠AED=∠ABO=30°.在Rt△AED中，AE=2AD=8，ED===∵OD =2.∴点E 的坐标为（2，．（Ⅱ）①由平移的性质得：O ′D ′=2，E ′D ME ′=OO ′=t ，D ′E ′∥O ′C ′∥OB . ∴∠E ′FM =∠ABO =30°.∴在Rt △MFE ′中，MF =2ME ′=2t ，FE ′===.∴S △MFE ′12=ME ′·FE ′12=⨯t 22=.∵S 矩形C ′O ′D ′E ′=O ′D ′·E ′D =∴S =S 矩形C ′O ′D ′E ′-S △MFE ′.∴S 2=-t 2，其中t 的取值范围是：0<t <2；②当S =O 'A =OA -OO '=6-t .∵∠AO 'F =90°，∠AFO '=∠ABO =30°.∴O 'F ='A =6-t ）.∴S 12=（6-t ）（6-t ）=解得：t =6，或t =6.∴t =6S 时，如图④所示：O 'A =6-t ，D 'A =6-t -2=4-t .∴O 'G =6-t ），D 'F =4-t ）.∴S 12=6-t ）4-t ） 解得：t 52=.S t 的取值范围为52≤t ≤6．【名师点睛】本题是四边形综合题目，考查了矩形的性质、坐标与图形性质、勾股定理、平移的性质、直角三角形的性质、梯形面积公式等知识；本题综合性强，有一定难度，熟练掌握含30°角的直角三角形的性质时是解题的关键． 3．（2019•陕西）问题提出：（1）如图1，已知△ABC ，试确定一点D ，使得以A ，B ，C ，D 为顶点的四边形为平行四边形，请画出这个平行四边形； 问题探究：（2）如图2，在矩形ABCD 中，AB =4，BC =10，若要在该矩形中作出一个面积最大的△BPC ，且使∠BPC =90°，求满足条件的点P 到点A 的距离； 问题解决：（3）如图3，有一座塔A ，按规定，要以塔A 为对称中心，建一个面积尽可能大的形状为平行四边形的景区BCDE ．根据实际情况，要求顶点B 是定点，点B到塔A的距离为50米，∠CBE=120°，那么，是否可以建一个满足要求的面积最大的平行四边形景区BCDE？若可以，求出满足要求的平行四边形BCDE的最大面积；若不可以，请说明理由．（塔A的占地面积忽略不计）【解析】（1）如图记为点D所在的位置．（2）如图.∵AB=4，BC=10，∴取BC的中点O，则OB>AB．∴以点O为圆心，OB长为半径作⊙O，⊙O一定于AD相交于P1，P2两点.连接BP1，P1C，P1O，∵∠BPC=90°，点P不能再矩形外.∴△BPC的顶点P1或P2位置时，△BPC的面积最大.作P1E⊥BC，垂足为E，则OE=3.∴AP1=BE=OB-OE=5-3=2.由对称性得AP2=8．（3）可以，如图所示，连接BD.∵A为BCDE的对称中心，BA=50，∠CBE=120°.∴BD=100，∠BED=60°.作△BDE的外接圆⊙O，则点E在优弧BD上，取BED的中点E′，连接E′B，E′D.则E′B=E′D，且∠BE′D=60°，∴△BE′D为正三角形．连接E′O并延长，经过点A至C′，使E′A=AC′，连接BC′，DC′.∵E′A⊥BD.∴四边形E′D为菱形，且∠C′BE′=120°.作EF⊥BD，垂足为F，连接EO，则EF≤EO+OA-E′O+OA=E′A.∴S△BDE12=·BD·EF12≤·BD·E′A=S△E′BD.∴S平行四边形BCDE≤S平行四边形BC′DE′=2S△E′BD=1002·m2）.所以符合要求的BCDE的最大面积为2．【名师点睛】本题属于四边形综合题，考查了平行四边形的判定和性质，圆周角定理，三角形的面积等知识，解题的关键是理解题意，学会添加常用辅助线，属于中考压轴题．4．（2019•海南）如图，在边长为1的正方形ABCD中，E是边CD的中点，点P 是边AD上一点（与点A、D不重合），射线PE与BC的延长线交于点Q．（1）求证：△PDE≌△QCE；（2）过点E作EF∥BC交PB于点F，连结AF，当PB=PQ时.①求证：四边形AFEP是平行四边形；②请判断四边形AFEP是否为菱形，并说明理由．【解析】（1）∵四边形ABCD是正方形.∴∠D=∠ECQ=90°.∵E是CD的中点.∴DE=CE.又∵∠DEP=∠CEQ.∴△PDE≌△QCE．（2）①∵PB=PQ.∴∠PBQ=∠Q.∵AD∥BC.∴∠APB=∠PBQ=∠Q=∠EPD.∵△PDE≌△QCE.∴PE=QE.∵EF∥BQ.∴PF=BF.∴在Rt△P AB中，AF=PF=BF.∴∠APF=∠P AF.∴∠P AF=∠EPD.∴PE∥AF.∵EF∥BQ∥AD.∴四边形AFEP是平行四边形；②四边形AFEP不是菱形，理由如下：设PD=x，则AP=1-x.由（1）可得△PDE≌△QCE.∴CQ=PD=x.∴BQ=BC+CQ=1+x.∵点E、F分别是PQ、PB的中点.∴EF是△PBQ的中位线.∴EF12=BQ12x+=.由①知AP=EF，即1-x12x+ =.解得x1 3 =.∴PD13=，AP23=.在Rt△PDE中，DE1 2 =.∴PE==∴AP≠PE.∴四边形AFEP不是菱形．【名师点睛】本题是四边形的综合问题，解题的关键是掌握正方形的性质、全等三角形的判定与性质、直角三角形的性质、平行四边形与菱形的判定、性质等知识点．5．（2019•江西）在图1，2，3中，已知ABCD，∠ABC=120°，点E为线段BC 上的动点，连接AE，以AE为边向上作菱形AEFG，且∠EAG=120°．（1）如图1，当点E与点B重合时，∠CEF=__________°；（2）如图2，连接AF．①填空：∠F AD__________∠EAB（填“>”“<”“=”）；②求证：点F在∠ABC的平分线上．（3）如图3，连接EG，DG，并延长DG交BA的延长线于点H，当四边形AEGH是平行四边形时，求BC的值．AB【解析】（1）∵四边形AEFG是菱形.∴∠AEF=180°-∠EAG=60°.∴∠CEF=∠AEC-∠AEF=60°.故答案为：60°．（2）①∵四边形ABCD是平行四边形.∴∠DAB=180°-∠ABC=60°.∵四边形AEFG是菱形，∠EAG=120°.∴∠F AE=60°.∴∠F AD=∠EAB.故答案为：=．②如图，作FM⊥BC于M，FN⊥BA交BA的延长线于N.则∠FNB=∠FMB=90°.∴∠NFM=60°，又∠AFE=60°.∴∠AFN=∠EFM.∵EF=EA，∠F AE=60°.∴△AEF为等边三角形.∴F A=FE.在△AFN和△EFM中，AFN EFMFNA FME FA FE∠=∠⎧⎪∠=∠⎨⎪=⎩.∴△AFN≌△EFM（AAS）∴FN=FM，又FM⊥BC，FN⊥BA.∴点F在∠ABC的平分线上．（3）如图.∵四边形AEFG是菱形，∠EAG=120°.∴∠AGF=60°.∴∠FGE=∠AGE=30°.∵四边形AEGH为平行四边形.∴GE∥AH.∴∠GAH=∠AGE=30°，∠H=∠FGE=30°.∴∠GAN=90°，又∠AGE=30°.∴GN=2AN.∵∠DAB=60°，∠H=30°.∴∠ADH=30°.∴AD=AH=GE.∵四边形ABCD为平行四边形.∴BC=AD.∴BC=GE.∵四边形ABEH为平行四边形，∠HAE=∠EAB=30°.∴平行四边形ABEN为菱形.∴AB=AN=NE.∴GE=3AB.∴BCAB3．【名师点睛】本题考查的是相似三角形的判定和性质、全等三角形的判定和性质、菱形的性质、平行四边形的性质，掌握全等三角形的判定定理和性质定理、菱形的性质、直角三角形的性质是解题的关键．6．（2019•宁夏）如图，在△ABC中，∠A=90°，AB=3，AC=4，点M，Q分别是边AB，BC上的动点（点M不与A，B重合），且MQ⊥BC，过点M作BC的平行线MN，交AC于点N，连接NQ，设BQ为x．（1）试说明不论x为何值时，总有△QBM∽△ABC；（2）是否存在一点Q，使得四边形BMNQ为平行四边形，试说明理由；（3）当x为何值时，四边形BMNQ的面积最大，并求出最大值．【解析】（1）∵MQ⊥BC.∴∠MQB=90°.∴∠MQB=∠CAB，又∠QBM=∠ABC.∴△QBM∽△ABC．（2）当BQ=MN时，四边形BMNQ为平行四边形.∵MN∥BQ，BQ=MN.∴四边形BMNQ为平行四边形．（3）∵∠A=90°，AB=3，AC=4.∴BC==5.∵△QBM∽△ABC.∴QB QM BMAB AC BC==，即345x QM BM==.解得，QM43=x，BM53=x.∵MN∥BC.∴MN AMBC AB=，即53353xMN-=.解得，MN=525 9 -x.则四边形BMNQ的面积12=⨯（5259-x+x）43⨯x3227=-（x4532-）27532+.∴当x4532=时，四边形BMNQ的面积最大，最大值为7532．【名师点睛】本题考查的是相似三角形的判定和性质、平行四边形的判定、二次函数的性质，掌握相似三角形的判定定理、二次函数的性质是解题的关键．7．（2019•安徽）如图，Rt△ABC中，∠ACB=90°，AC=BC，P为△ABC内部一点，且∠APB=∠BPC=135°．（1）求证：△P AB∽△PBC；（2）求证：P A=2PC；（3）若点P到三角形的边AB，BC，CA的距离分别为h1，h2，h3，求证h12=h2·h3．【解析】（1）∵∠ACB=90°，AB=BC.∴∠ABC=45°=∠PBA+∠PBC.又∠APB=135°.∴∠P AB+∠PBA=45°.∴∠PBC=∠P AB.又∵∠APB=∠BPC=135°.（2）∵△P AB ∽△PBC .∴PA PB ABPB PC BC==. 在Rt △ABC 中，AB =AC .∴ABBC= ∴PB PA ==，. ∴P A =2PC ．（3）如图，过点P 作PD ⊥BC ，PE ⊥AC 交BC 、AC 于点D ，E .∴PF =h 1，PD =h 2，PE =h 3. ∵∠CPB +∠APB =135°+135°=270°. ∴∠APC =90°. ∴∠EAP +∠ACP =90°.又∵∠ACB =∠ACP +∠PCD =90°. ∴∠EAP =∠PCD . ∴Rt △AEP ∽Rt △CDP .∴2PE APDP PC==，即322h h =. ∴h 3=2h 2.∴12h ABh BC ==.∴12h .∴2212222322h h h h h h ==⋅=．即：h 12=h 2·h 3．【名师点睛】此题主要考查了相似三角形的判定和性质，等腰直角三角形的性质，判断出∠EAP =∠PCD 是解本题的关键．8．（2019•重庆A 卷）如图，在平行四边形ABCD 中，点E 在边BC 上，连结AE ，EM ⊥AE ，垂足为E ，交CD 于点M ，AF ⊥BC ，垂足为F ，BH ⊥AE ，垂足为H ，交AF 于点N ，点P 是AD 上一点，连接CP ．（1）若DP =2AP =4，CP =CD =5，求△ACD 的面积． （2）若AE =BN ，AN =CE ，求证：AD=+2CE ．【解析】（1）作CG ⊥AD 于G ，如图1所示：设PG =x ，则DG =4-x .在Rt △PGC 中，GC 2=CP 2-PG 2=17-x 2.在Rt△DGC中，GC2=CD2-GD2=52-（4-x）2=9+8x-x2.∴17-x2=9+8x-x2.解得：x=1，即PG=1.∴GC=4.∵DP=2AP=4.∴AD=6.∴S△ACD12=⨯AD×CG12=⨯6×4=12．（2）连接NE，如图2所示：∵AH⊥AE，AF⊥BC，AE⊥EM.∴∠AEB+∠NBF=∠AEB+∠EAF=∠AEB+∠MEC=90°.∴∠NBF=∠EAF=∠MEC.在△NBF和△EAF中，NBF EAFBFN EFA AE BN∠=∠⎧⎪∠=∠⎨⎪=⎩.∴△NBF≌△EAF.∴BF=AF，NF=EF.∴∠ABC=45°，∠ENF=45°，FC=AF=BF.∴∠ANE=∠BCD=135°，AD=BC=2AF.在△ANE和△ECM中，MEC EAF AN ECANE ECM ∠=∠⎧⎪=⎨⎪∠=∠⎩.∴△ANE≌△ECM.∴CM=NE.又∵NF2=NE2=MC.∴AF2=MC+EC.∴AD=+2EC．【名师点睛】本题考查了平行四边形的性质、全等三角形的判定与性质、勾股定理、三角形面积公式等知识；熟练掌握平行四边形的性质，证明三角形全等是解题的关键．。
中考数学压轴题专题十动态几何问题
中考数学压轴题专题十动态几何问题试题特点用运动的观点来探究几何图形变化规律的问题称为动态几何问题，此类问题的显著特点是图形中的某个元素（如点、线段、三角形等）或整个图形按照某种规律运动，图形的各个元素在运动变化过程中互相依存、和谐统一，体现了数学中“变”与“不变”、“一般”与“特殊”的辩证思想．其主要类型有：1．点的运动（单点运动、多点运动）；2．线段（直线）的运动；3．图形的运动（三角形运动、四边形运动、圆运动等）．方式趋势动态几何题已成为中考试题的一大热点题型．在近几年各地的中考试卷中，以动点问题、平面图形的平移、翻折、旋转、剪拼问题等为代表的动态几何题频频出现在填空、选择、解答等各种题型中，总体呈现源于教材、高于教材，入口宽、难易适度、梯度分明，考查同学们对图形的直觉能力以及从变化中看到不变实质的数学洞察力．热点解析一、点的运动【题1】（2011盐城）如图1，已知一次函数y＝－x＋7与正比例函数y＝43x的图象交于点A，且与x轴交于点B．(1)求点A和点B的坐标；(2)过点A作AC⊥y轴于点C，过点B作直线l∥y轴，动点P从点O出发，以每秒1个单位长的速度，沿O－C－A的路线向点A运动；同时直线l从点B出发，以相同速度向左平移，在平移过程中，直线l交x轴于点R，交线段BA或线段AO于点Q．当点P到达点A时，点P和直线l都停止运动．在运动过程中，设动点P运动的时间为t秒．①当t为何值时，以A、P、R为顶点的三角形的面积为8?②是否存在以A、P、Q为顶点的三角形是等腰三角形？若存在，求t的值；若不存在，请说明理由．【思路】(1)联立方程y＝－x＋7和y＝43x即可求出点A的坐标，令－x＋7＝0即可得点B的坐标．(2)①只要把三角形的面积用t表示，求出即可．应注意分P在OC上运动和P在CA上运动两种情况．（D只要把有关线段用t表示，找出满足AP＝AQ，AP＝PQ，AQ＝PQ的条件时t的值即可，应注意分别讨论P在OC上运动（此时直线∠与AB相交）和P在CA上运动（此时直线∠与AO相交）时AP＝AQ，AP＝PQ，AQ＝PQ的条件．【失分点】以A、P、Q为顶点的三角形是等腰三角形有多种可能，容易考虑不周．【反思】涉及的主要知识点有：一次函数的图象和性质，解二元一次方程组，勾股定理，锐角三角函数，解一元二次方程，等腰三角形的判定．【牛刀小试】1．（2010湖北咸宁）如图6，直角梯形ABCD中，AB∥DC，∠DAB＝90°，AD＝2DC＝4，AB＝6．动点M以每秒1个单位长的速度，从点A沿线段AB向点B运动；同时点P以相同的速度，从点C沿折线C－D－A向点A运动，当点M到达点B 时，两点同时停止运动．过点M作直线∠∥AD，与线段CD的交点为E，与折线A－C －B的交点为Q．点M运动的时间为t（秒）．(1)当t＝时，求线段QM的长．(2)当0<t<2时，如果以C，P，Q为顶点的三角形为直角三角形，求t的值．(3)当t>2时，连接PQ交线段AC于点R，请探究CQRQ是否为定值．若是，试求这个定值；若不是，请说明理由．2．（2010湖南娄底）如图7，在梯形ABCD中，AB∥CD，AB＝2，DC＝10，AD＝BC＝5，点M，N分别在边AD，BC上运动，并保持MN∥AB，ME⊥DC，NF⊥DC，垂足分别为E，F．(1)求梯形ABCD的面积．(2)探究一：四边形MNFE的面积有无最大值？若有，请求出这个最大值；若无，请说明理由．(3)探究二：四边形MNFF能否为正方形？若能，请求出正方形的面积；若不能，请说明理由．3．(2010广西钦州)如图8，将OA＝6，AB＝4的矩形OABC放置在平面直角坐标系中，动点M，N以每秒1个单位的速度分别从点A，C同时出发，其中点M沿AO向终点0运动，点N沿CB向终点B运动，当两个动点运动了ts时，过点N作NP⊥BC，交OB 于点P，连接MP．(1)点B的坐标为_______；用含￡的式子表示点P的坐标为_______．(2)记△OMP的面积为S，求S与t的函数关系式(0<t<6)．并求t为何值时，S有最大值．(3)试探究：当S有最大值时，在y轴上是否存在点T，使直线MT把△ONC分割成三角形和四边形两部分，且三角形的面积是△ONC面积的13？若存在，求出点T的坐标；若不存在，请说明理由．二、线的运动【题2】（2010云南昭通）如图，已知直线l的解析式为y＝－x＋6，它与x轴，y 轴分别相交于A，B两点．平行于直线l的直线n从原点出发，沿x轴正方向以每秒1个单位长度的速度运动，运动时间为t秒，运动过程中始终保持n∥l．直线n与x轴，y轴分别相交于C，D两点．线段CD的中点为P，以P为圆心，以CD为直径在CD上方作半圆，半圆面积为S．当直线n与直线l重合时，运动结束．(1)求A，B两点的坐标．(2)求S与t的函数关系式及自变量t的取值范围．(3)直线n在运动过程中，①当t为何值时，半圆与直线l相切？②是否存在这样的T值，使得半圆面积S＝12S梯形ABCD？若存在，求出t值；若不存在，说明理由。
2019年浙江省中考数学真题分类汇编 专题10 图形的性质之解答题(解析版)
专题10 图形的性质之解答题参考答案与试题解析一．解答题（共23小题）1．（2019•舟山）如图，在矩形ABCD中，点E，F在对角线BD．请添加一个条件，使得结论“AE＝CF”成立，并加以证明．【答案】解：添加的条件是BE＝DF（答案不唯一）．证明：∵四边形ABCD是矩形，∴AB∥CD，AB＝CD，∴∠ABD＝∠BDC，又∵BE＝DF（添加），∴△ABE≌△CDF（SAS），∴AE＝CF．【点睛】本题考查矩形的性质、全等三角形的判定和性质等知识，解题的关键是熟练掌握全等三角形的判定方法，属于中考常考题型．2．（2019•温州）如图，在△ABC中，AD是BC边上的中线，E是AB边上一点，过点C作CF∥AB交ED 的延长线于点F．（1）求证：△BDE≌△CDF．（2）当AD⊥BC，AE＝1，CF＝2时，求AC的长．【答案】（1）证明：∵CF∥AB，∴∠B＝∠FCD，∠BED＝∠F，∵AD是BC边上的中线，∴BD＝CD，∴△BDE≌△CDF（AAS）；（2）解：∵△BDE≌△CDF，∴BE＝CF＝2，∴AB＝AE+BE＝1+2＝3，∵AD⊥BC，BD＝CD，∴AC＝AB＝3．【点睛】本题考查了全等三角形的判定和性质，平行线的性质，熟练掌握全等三角形的判定和性质是解题的关键．3．（2019•杭州）如图，在△ABC中，AC＜AB＜BC．（1）已知线段AB的垂直平分线与BC边交于点P，连接AP，求证：∠APC＝2∠B．（2）以点B为圆心，线段AB的长为半径画弧，与BC边交于点Q，连接AQ．若∠AQC＝3∠B，求∠B 的度数．【答案】解：（1）证明：∵线段AB的垂直平分线与BC边交于点P，∴P A＝PB，∴∠B＝∠BAP，∵∠APC＝∠B+∠BAP，∴∠APC＝2∠B；（2）根据题意可知BA＝BQ，∴∠BAQ＝∠BQA，∵∠AQC＝3∠B，∠AQC＝∠B+∠BAQ，∴∠BQA＝2∠B，∵∠BAQ+∠BQA+∠B＝180°，∴5∠B＝180°，∴∠B＝36°．【点睛】本题主要考查了等腰三角形的性质、垂直平分线的性质以及三角形的外角性质，难度适中．4．（2019•衢州）已知：如图，在菱形ABCD中，点E，F分别在边BC，CD上，且BE＝DF，连结AE，AF．求证：AE＝AF．【答案】证明：∵四边形ABCD是菱形，∴AB＝AD，∠B＝∠D，∵BE＝DF，∴△ABE≌△ADF（SAS），∴AE＝CF．【点睛】此题考查菱形的性质，关键是根据菱形的性质和全等三角形的判定和性质解答．5．（2019•湖州）如图，已知在△ABC中，D，E，F分别是AB，BC，AC的中点，连结DF，EF，BF．（1）求证：四边形BEFD是平行四边形；（2）若∠AFB＝90°，AB＝6，求四边形BEFD的周长．【答案】（1）证明：∵D，E，F分别是AB，BC，AC的中点，∴DF∥BC，EF∥AB，∴DF∥BE，EF∥BD，∴四边形BEFD是平行四边形；（2）解：∵∠AFB＝90°，D是AB的中点，AB＝6，∴DF＝DB＝DA AB＝3，∵四边形BEFD是平行四边形，∴四边形BEFD是菱形，∵DB＝3，∴四边形BEFD的周长为12．【点睛】本题考查了平行四边形的性质和判定，菱形的判定和性质，三角形的中位线的性质，熟练掌握平行四边形的性质是解题的关键．6．（2019•杭州）如图，已知正方形ABCD的边长为1，正方形CEFG的面积为S1，点E在DC边上，点G 在BC的延长线上，设以线段AD和DE为邻边的矩形的面积为S2，且S1＝S2．（1）求线段CE的长；（2）若点H为BC边的中点，连接HD，求证：HD＝HG．【答案】解：（1）设正方形CEFG的边长为a，∵正方形ABCD的边长为1，∴DE＝1﹣a，∵S1＝S2，∴a2＝1×（1﹣a），解得，（舍去），，即线段CE的长是；（2）证明：∵点H为BC边的中点，BC＝1，∴CH＝0.5，∴DH，∵CH＝0.5，CG，∴HG，∴HD＝HG．【点睛】本题考查正方形的性质、矩形的性质，解答本题的关键是明确题意，利用数形结合的思想解答．7．（2019•宁波）如图，矩形EFGH的顶点E，G分别在菱形ABCD的边AD，BC上，顶点F，H在菱形ABCD 的对角线BD上．（1）求证：BG＝DE；（2）若E为AD中点，FH＝2，求菱形ABCD的周长．【答案】解：（1）∵四边形EFGH是矩形，∴EH＝FG，EH∥FG，∴∠GFH＝∠EHF，∵∠BFG＝180°﹣∠GFH，∠DHE＝180°﹣∠EHF，∴∠BFG＝∠DHE，∵四边形ABCD是菱形，∴AD∥BC，∴∠GBF＝∠EDH，∴△BGF≌△DEH（AAS），∴BG＝DE；（2）连接EG，∵四边形ABCD是菱形，∴AD＝BC，AD∥BC，∵E为AD中点，∴AE＝ED，∵BG＝DE，∴AE＝BG，AE∥BG，∴四边形ABGE是平行四边形，∴AB＝EG，∵EG＝FH＝2，∴AB＝2，∴菱形ABCD的周长＝8．【点睛】本题考查了菱形的性质，矩形的性质，全等三角形的判定和性质，正确的识别作图是解题的关键．8．（2019•舟山）在6×6的方格纸中，点A，B，C都在格点上，按要求画图：（1）在图1中找一个格点D，使以点A，B，C，D为顶点的四边形是平行四边形．（2）在图2中仅用无刻度的直尺，把线段AB三等分（保留画图痕迹，不写画法）．【答案】解：（1）由勾股定理得：CD＝AB＝CD'，BD＝AC＝BD''，AD'＝BC＝AD''；画出图形如图1所示；（2）如图2所示．【点睛】本题考查了平行四边形的判定与性质、勾股定理、平行线分线段成比例定理；熟练掌握勾股定理好平行线分线段成比例定理是解题的关键．9．（2019•温州）如图，在7×5的方格纸ABCD中，请按要求画图，且所画格点三角形与格点四边形的顶点均不与点A，B，C，D重合．（1）在图1中画一个格点△EFG，使点E，F，G分别落在边AB，BC，CD上，且∠EFG＝90°．（2）在图2中画一个格点四边形MNPQ，使点M，N，P，Q分别落在边AB，BC，CD，DA上，且MP ＝NQ．【答案】解：（1）满足条件的△EFG，如图1，2所示．（2）满足条件的四边形MNPQ如图所示．【点睛】本题考查作图﹣应用与设计，勾股定理，全等三角形的判定和性质等知识，解题的关键是学会利用数形结合的思想解决问题，属于中考常考题型．10．（2019•衢州）如图，在4×4的方格子中，△ABC的三个顶点都在格点上．（1）在图1中画出线段CD，使CD⊥CB，其中D是格点．（2）在图2中画出平行四边形ABEC，其中E是格点．【答案】解：（1）线段CD即为所求．（2）平行四边形ABEC即为所求．【点睛】本题考查作图﹣应用与设计，平行四边形的判定等知识，解题的关键是学会利用数形结合的思想解决问题，属于中考常考题型．11．（2019•金华）如图，在7×6的方格中，△ABC的顶点均在格点上．试按要求画出线段EF（E，F均为格点），各画出一条即可．【答案】解：如图：从图中可得到AC边的中点在格点上设为E，过E作AB的平行线即可在格点上找到F，则EG平分BC；EC，EF，FC，借助勾股定理确定F点，则EF⊥AC；借助圆规作AB的垂直平分线即可；【点睛】本题考查三角形作图；在格点中利用勾股定理，三角形的性质作平行、垂直、中点是解题的关键．12．（2019•绍兴）有一块形状如图的五边形余料ABCDE，AB＝AE＝6，BC＝5，∠A＝∠B＝90°，∠C＝135°，∠E＞90°，要在这块余料中截取一块矩形材料，其中一条边在AE上，并使所截矩形材料的面积尽可能大．（1）若所截矩形材料的一条边是BC或AE，求矩形材料的面积．（2）能否截出比（1）中更大面积的矩形材料？如果能，求出这些矩形材料面积的最大值；如果不能，说明理由．【答案】解：（1）①若所截矩形材料的一条边是BC，如图1所示：过点C作CF⊥AE于F，S1＝AB•BC＝6×5＝30；②若所截矩形材料的一条边是AE，如图2所示：过点E作EF∥AB交CD于F，FG⊥AB于G，过点C作CH⊥FG于H，则四边形AEFG为矩形，四边形BCHG为矩形，∵∠C＝135°，∴∠FCH＝45°，∴△CHF为等腰直角三角形，∴AE＝FG＝6，HG＝BC＝5，BG＝CH＝FH，∴BG＝CH＝FH＝FG﹣HG＝6﹣5＝1，∴AG＝AB﹣BG＝6﹣1＝5，∴S2＝AE•AG＝6×5＝30；（2）能；理由如下：在CD上取点F，过点F作FM⊥AB于M，FN⊥AE于N，过点C作CG⊥FM于G，则四边形ANFM为矩形，四边形BCGM为矩形，∵∠C＝135°，∴∠FCG＝45°，∴△CGF为等腰直角三角形，∴MG＝BC＝5，BM＝CG，FG＝DG，设AM＝x，则BM＝6﹣x，∴FM＝GM+FG＝GM+CG＝BC+BM＝11﹣x，∴S＝AM×FM＝x（11﹣x）＝﹣x2+11x＝﹣（x﹣5.5）2+30.25，∴当x＝5.5时，S的最大值为30.25．【点睛】本题考查了矩形的性质、等腰直角三角形的判定与性质、矩形面积公式以及二次函数的应用等知识；熟练掌握矩形的性质，证明三角形是等腰直角三角形是解题的关键．13．（2019•宁波）定义：有两个相邻内角互余的四边形称为邻余四边形，这两个角的夹边称为邻余线．（1）如图1，在△ABC中，AB＝AC，AD是△ABC的角平分线，E，F分别是BD，AD上的点．求证：四边形ABEF是邻余四边形．（2）如图2，在5×4的方格纸中，A，B在格点上，请画出一个符合条件的邻余四边形ABEF，使AB 是邻余线，E，F在格点上．（3）如图3，在（1）的条件下，取EF中点M，连结DM并延长交AB于点Q，延长EF交AC于点N．若N为AC的中点，DE＝2BE，QB＝3，求邻余线AB的长．【答案】解：（1）∵AB＝AC，AD是△ABC的角平分线，∴AD⊥BC，∴∠ADB＝90°，∴∠DAB+∠DBA＝90°，∠F AB与∠EBA互余，∴四边形ABEF是邻余四边形；（2）如图所示（答案不唯一），四边形AFEB为所求；（3）∵AB＝AC，AD是△ABC的角平分线，∴BD＝CD，∵DE＝2BE，∴BD＝CD＝3BE，∴CE＝CD+DE＝5BE，∵∠EDF＝90°，点M是EF的中点，∴DM＝ME，∴∠MDE＝∠MED，∵AB＝AC，∴∠B＝∠C，∴△DBQ∽△ECN，∴，∵QB＝3，∴NC＝5，∵AN＝CN，∴AC＝2CN＝10，∴AB＝AC＝10．【点睛】本题为四边形综合题，涉及到直角三角形中线定理、三角形相似等知识点，这种新定义类题目，通常按照题设顺序逐次求解，较为容易．14．（2019•台州）我们知道，各个角都相等，各条边都相等的多边形叫做正多边形．对一个各条边都相等的凸多边形（边数大于3），可以由若干条对角线相等判定它是正多边形．例如，各条边都相等的凸四边形，若两条对角线相等，则这个四边形是正方形．（1）已知凸五边形ABCDE的各条边都相等．①如图1，若AC＝AD＝BE＝BD＝CE，求证：五边形ABCDE是正五边形；②如图2，若AC＝BE＝CE，请判断五边形ABCDE是不是正五边形，并说明理由：（2）判断下列命题的真假．（在括号内填写“真”或“假”）如图3，已知凸六边形ABCDEF的各条边都相等．①若AC＝CE＝EA，则六边形ABCDEF是正六边形；（假）②若AD＝BE＝CF，则六边形ABCDEF是正六边形．（假）【答案】（1）①证明：∵凸五边形ABCDE的各条边都相等，∴AB＝BC＝CD＝DE＝EA，在△ABC、△BCD、△CDE、△DEA、EAB中，，∴△ABC≌△BCD≌△CDE≌△DEA≌EAB（SSS），∴∠ABC＝∠BCD＝∠CDE＝∠DEA＝∠EAB，∴五边形ABCDE是正五边形；②解：若AC＝BE＝CE，五边形ABCDE是正五边形，理由如下：在△ABE、△BCA和△DEC中，，∴△ABE≌△BCA≌△DEC（SSS），∴∠BAE＝∠CBA＝∠EDC，∠AEB＝∠ABE＝∠BAC＝∠BCA＝∠DCE＝∠DEC，在△ACE和△BEC中，，∴△ACE≌△BEC（SSS），∴∠ACE＝∠CEB，∠CEA＝∠CAE＝∠EBC＝∠ECB，∵四边形ABCE内角和为360°，∴∠ABC+∠ECB＝180°，∴AB∥CE，∴∠ABE＝∠BEC，∠BAC＝∠ACE，∴∠CAE＝∠CEA＝2∠ABE，∴∠BAE＝3∠ABE，同理：∠CBA＝∠D＝∠AED＝∠BCD＝3∠ABE＝∠BAE，∴五边形ABCDE是正五边形；（2）解：①若AC＝CE＝EA，如图3所示：则六边形ABCDEF是正六边形；假命题；理由如下：∵凸六边形ABCDEF的各条边都相等，∴AB＝BC＝CD＝DE＝EF＝F A，在△AEF、△CAB和△ECD中，，∴△AEF≌△CAB≌△ECD（SSS），如果△AEF、△CAB、△ECD都为相同的等腰直角三角形，则∠F＝∠D＝∠B＝90°，而正六边形的各个内角都为120°，∴六边形ABCDEF不是正六边形；故答案为：假；②若AD＝BE＝CF，则六边形ABCDEF是正六边形；假命题；理由如下：如图4所示：连接AE、AC、CE、BF，在△BFE和△FBC中，，∴△BFE≌△FBC（SSS），∴∠BFE＝∠FBC，∵AB＝AF，∴∠AFB＝∠ABF，∴∠AFE＝∠ABC，在△F AE和△BCA中，，∴△F AE≌△BCA（SAS），∴AE＝CA，同理：AE＝CE，∴AE＝CA＝CE，由①得：△AEF、△CAB、△ECD都为相同的等腰直角三角形，则∠F＝∠D＝∠B＝90°，而正六边形的各个内角都为120°，∴六边形ABCDEF不是正六边形；故答案为：假．【点睛】本题是四边形综合题目，考查了正多边形的判定、全等三角形的判定与性质、等腰三角形的性质、三角形内角和定理等知识；本题综合性强，有一定难度，证明三角形全等是解题的关键．15．（2019•嘉兴）小波在复习时，遇到一个课本上的问题，温故后进行了操作、推理与拓展．（1）温故：如图1，在△ABC中，AD⊥BC于点D，正方形PQMN的边QM在BC上，顶点P，N分别在AB，AC上，若BC＝6，AD＝4，求正方形PQMN的边长．（2）操作：能画出这类正方形吗？小波按数学家波利亚在《怎样解题》中的方法进行操作：如图2，任意画△ABC，在AB上任取一点P'，画正方形P'Q'M'N'，使Q'，M'在BC边上，N'在△ABC内，连结BN'并延长交AC于点N，画NM⊥BC于点M，NP⊥NM交AB于点P，PQ⊥BC于点Q，得到四边形PPQMN．小波把线段BN称为“波利亚线”．（3）推理：证明图2中的四边形PQMN是正方形．（4）拓展：在（2）的条件下，在射线BN上截取NE＝NM，连结EQ，EM（如图3）．当tan∠NBM 时，猜想∠QEM的度数，并尝试证明．请帮助小波解决“温故”、“推理”、“拓展”中的问题．【答案】（1）解：如图1中，∵PN∥BC，∴△APN∽△ABC，∴，即，解得PN．（2）能画出这样的正方形，如图2中，正方形PNMQ即为所求．（3）证明：如图2中，由画图可知：∠QMN＝∠PQM＝∠NPQ＝∠BM′N′＝90°，∴四边形PNMQ是矩形，MN∥M′N′，∴△BN′M′∽△BNM，∴，同理可得：，∴，∵M′N′＝P′N′，∴MN＝PN，∴四边形PQMN是正方形．（4）解：如图3中，结论：∠QEM＝90°．理由：由tan∠NBM，可以假设MN＝3k，BM＝4k，则BN＝5k，BQ＝k，BE＝2k，∴，，∴，∵∠QBE＝∠EBM，∴△BQE∽△BEM，∴∠BEQ＝∠BME，∵NE＝NM，∴∠NEM＝∠NME，∵∠BME+∠EMN＝90°，∴∠BEQ+∠NEM＝90°，∴∠QEM＝90°．【点睛】本题属于四边形综合题，考查了正方形的性质和判定，相似三角形的判定和性质等知识，解题的关键是理解题意，灵活运用所学知识解决问题，属于中考压轴题．16．（2019•舟山）小波在复习时，遇到一个课本上的问题，温故后进行了操作、推理与拓展．（1）温故：如图1，在△ABC中，AD⊥BC于点D，正方形PQMN的边QM在BC上，顶点P，N分别在AB，AC上，若BC＝a，AD＝h，求正方形PQMN的边长（用a，h表示）．（2）操作：如何画出这个正方形PQMN呢？如图2，小波画出了图1的△ABC，然后按数学家波利亚在《怎样解题》中的方法进行操作：先在AB上任取一点P'，画正方形P'Q'M'N'，使点Q'，M'在BC边上，点N'在△ABC内，然后连结BN'，并延长交AC于点N，画NM⊥BC于点M，NP⊥NM交AB于点P，PQ⊥BC于点Q，得到四边形PQMN．（3）推理：证明图2中的四边形PQMN是正方形．（4）拓展：小波把图2中的线段BN称为“波利亚线”，在该线上截取NE＝NM，连结EQ，EM（如图3），当∠QEM＝90°时，求“波利亚线”BN的长（用a，h表示）．请帮助小波解决“温故”、“推理”、“拓展”中的问题．【答案】（1）解：如图1中，∵PN∥BC，∴△APN∽△ABC，∴，即，解得PN（2）能画出这样的正方形，如图2中，正方形PNMQ即为所求．（3）证明：如图2中，由画图可知：∠QMN＝∠PQM＝∠NPQ＝∠BM′N′＝90°，∴四边形PNMQ是矩形，MN∥M′N′，∴△BN′M′∽△BNM，∴，同理可得：∴，∵M′N′＝P′N′，∴MN＝PN，∴四边形PQMN是正方形（4）如图，过点N作ND⊥ME于点D∵MN＝EN，ND⊥ME，∴∠NEM＝∠MNE，ED＝DM∵∠BMN＝∠QEM＝90°∴∠EQM+∠EMQ＝90°，∠EMQ+∠EMN＝90°∴∠EMN＝∠EQM，且MN＝QN，∠QEM＝∠NDM＝90°∴△QEM≌△MDN（AAS）∴EQ＝DM EM，∵∠BMN＝∠QEM＝90°∴∠BEQ+∠NEM＝90°，∠BME+∠NME＝90°∴∠BEQ＝∠BME，且∠MBE＝∠MBE∴△BEQ∽△BME∴，∴BM＝2BE，BE＝2BQ∴BM＝4BQ∴QM＝3BQ＝MN，BN＝5BQ∴∴BN MN（）【点睛】本题属于四边形综合题，考查了正方形的性质和判定，相似三角形的判定和性质等知识，解题的关键是理解题意，灵活运用所学知识解决问题，属于中考压轴题．17．（2019•衢州）如图，在等腰△ABC中，AB＝AC，以AC为直径作⊙O交BC于点D，过点D作DE⊥AB，垂足为E．（1）求证：DE是⊙O的切线．（2）若DE，∠C＝30°，求的长．【答案】（1）证明：连接OD；∵OD＝OC，∴∠C＝∠ODC，∵AB＝AC，∴∠B＝∠C，∴∠B＝∠ODC，∴OD∥AB，∴∠ODE＝∠DEB；∵DE⊥AB，∴∠DEB＝90°，∴∠ODE＝90°，即DE⊥OD，∴DE是⊙O的切线．（2）解：连接AD，∵AC是直径，∴∠ADC＝90°，∵AB＝AC，∴∠B＝∠C＝30°，BD＝CD，∴∠OAD＝60°，∵OA＝OD，∴△AOD是等边三角形，∴∠AOD＝60°，∵DE，∠B＝30°，∠BED＝90°，∴CD＝BD＝2DE＝2，∴OD＝AD＝tan30°•CD22，∴的长为：．【点睛】本题考查了切线的判定．要证某线是圆的切线，已知此线过圆上某点，连接圆心与这点（即为半径），再证垂直即可．18．（2019•金华）如图，在▱OABC中，以O为圆心，OA为半径的圆与BC相切于点B，与OC相交于点D．（1）求的度数．（2）如图，点E在⊙O上，连结CE与⊙O交于点F，若EF＝AB，求∠OCE的度数．【答案】解：（1）连接OB，∵BC是圆的切线，∴OB⊥BC，∵四边形OABC是平行四边形，∴OA∥BC，∴OB⊥OA，∴△AOB是等腰直角三角形，∴∠ABO＝45°，∴的度数为45°；（2）连接OE，过点O作OH⊥EC于点H，设EH＝t，∵OH⊥EC，∴EF＝2HE＝2t，∵四边形OABC是平行四边形，∴AB＝CO＝EF＝2t，∵△AOB是等腰直角三角形，∴OA t，则HO t，∵OC＝2OH，∴∠OCE＝30°．【点睛】本题主要利用了切线和平行四边形的性质，其中（2），要利用（1）中△AOB是等腰直角三角形结论．19．（2019•温州）如图，在△ABC中，∠BAC＝90°，点E在BC边上，且CA＝CE，过A，C，E三点的⊙O交AB于另一点F，作直径AD，连结DE并延长交AB于点G，连结CD，CF．（1）求证：四边形DCFG是平行四边形．（2）当BE＝4，CD AB时，求⊙O的直径长．【答案】（1）证明：连接AE，∵∠BAC＝90°，∴CF是⊙O的直径，∵AC＝EC，∴CF⊥AE，∵AD是⊙O的直径，∴∠AED＝90°，即GD⊥AE，∴CF∥DG，∵AD是⊙O的直径，∴∠ACD＝90°，∴∠ACD+∠BAC＝180°，∴AB∥CD，∴四边形DCFG是平行四边形；（2）解：由CD AB，设CD＝3x，AB＝8x，∴CD＝FG＝3x，∵∠AOF＝∠COD，∴AF＝CD＝3x，∴BG＝8x﹣3x﹣3x＝2x，∵GE∥CF，∴，∵BE＝4，∴AC＝CE＝6，∴BC＝6+4＝10，∴AB8＝8x，∴x＝1，在Rt△ACF中，AF＝10，AC＝6，∴CF3，即⊙O的直径长为3．【点睛】本题考查了三角形的外接圆与外心，平行四边形的判定和性质，勾股定理，圆周角定理，熟练掌握平行四边形的判定定理是解题的关键．20．（2019•绍兴）在屏幕上有如下内容：如图，△ABC内接于⊙O，直径AB的长为2，过点C的切线交AB的延长线于点D．张老师要求添加条件后，编制一道题目，并解答．（1）在屏幕内容中添加条件∠D＝30°，求AD的长．请你解答．（2）以下是小明、小聪的对话：小明：我加的条件是BD＝1，就可以求出AD的长小聪：你这样太简单了，我加的是∠A＝30°，连结OC，就可以证明△ACB与△DCO全等．参考此对话，在屏幕内容中添加条件，编制一道题目（可以添线添字母），并解答．【答案】解：（1）连接OC，如图，∵CD为切线，∴OC⊥CD，∴∠OCD＝90°，∵∠D＝30°，∴OD＝2OC＝2，∴AD＝AO+OD＝1+2＝3；（2）添加∠DCB＝30°，求AC的长，解：∵AB为直径，∴∠ACB＝90°，∵∠ACO+∠OCB＝90°，∠OCB+∠DCB＝90°，∴∠ACO＝∠DCB，∵∠ACO＝∠A，∴∠A＝∠DCB＝30°，在Rt△ACB中，BC AB＝1，∴AC BC．【点睛】本题考查了切线的性质：圆的切线垂直于经过切点的半径．若出现圆的切线，必连过切点的半径，构造定理图，得出垂直关系．也考查了圆周角定理．21．（2019•杭州）如图，已知锐角三角形ABC内接于圆O，OD⊥BC于点D，连接OA．（1）若∠BAC＝60°，①求证：OD OA．②当OA＝1时，求△ABC面积的最大值．（2）点E在线段OA上，OE＝OD，连接DE，设∠ABC＝m∠OED，∠ACB＝n∠OED（m，n是正数），若∠ABC＜∠ACB，求证：m﹣n+2＝0．【答案】解：（1）①连接OB、OC，则∠BOD BOC＝∠BAC＝60°，∴∠OBC＝30°，∴OD OB OA；②∵BC长度为定值，∴△ABC面积的最大值，要求BC边上的高最大，当AD过点O时，AD最大，即：AD＝AO+OD，△ABC面积的最大值BC×AD2OB sin60°；（2）如图2，连接OC，设：∠OED＝x，则∠ABC＝mx，∠ACB＝nx，则∠BAC＝180°﹣∠ABC﹣∠ACB＝180°﹣mx﹣nx∠BOC＝∠DOC，∵∠AOC＝2∠ABC＝2mx，∴∠AOD＝∠COD+∠AOC＝180°﹣mx﹣nx+2mx＝180°+mx﹣nx，∵OE＝OD，∴∠AOD＝180°﹣2x，即：180°+mx﹣nx＝180°﹣2x，化简得：m﹣n+2＝0．【点睛】本题为圆的综合运用题，涉及到解直角三角形、三角形内角和公式，其中（2），∠AOD＝∠COD+∠AOC是本题容易忽视的地方，本题难度适中．22．（2019•宁波）如图1，⊙O经过等边△ABC的顶点A，C（圆心O在△ABC内），分别与AB，CB的延长线交于点D，E，连结DE，BF⊥EC交AE于点F．（1）求证：BD＝BE．（2）当AF：EF＝3：2，AC＝6时，求AE的长．（3）设x，tan∠DAE＝y．①求y关于x的函数表达式；②如图2，连结OF，OB，若△AEC的面积是△OFB面积的10倍，求y的值．【答案】证明：（1）∵△ABC是等边三角形，∴∠BAC＝∠C＝60°，∵∠DEB＝∠BAC＝60°，∠D＝∠C＝60°，∴∠DEB＝∠D，∴BD＝BE；（2）如图1，过点A作AG⊥BC于点G，∵△ABC是等边三角形，AC＝6，∴BG，∴在Rt△ABG中，AG BG＝3，∵BF⊥EC，∴BF∥AG，∴，∵AF：EF＝3：2，∴BE BG＝2，∴EG＝BE+BG＝3+2＝5，在Rt△AEG中，AE；（3）①如图1，过点E作EH⊥AD于点H，∵∠EBD＝∠ABC＝60°，∴在Rt△BEH中，，∴EH，BH，∵，∴BG＝xBE，∴AB＝BC＝2BG＝2xBE，∴AH＝AB+BH＝2xBE BE＝（2x）BE，∴在Rt△AHE中，tan∠EAD，∴y；②如图2，过点O作OM⊥BC于点M，设BE＝a，∵，∴CG＝BG＝xBE＝ax，∴EC＝CG+BG+BE＝a+2ax，∴EM EC a+ax，∴BM＝EM﹣BE＝ax a，∵BF∥AG，∴△EBF∽△EGA，∴，∵AG，∴BF，∴△OFB的面积，∴△AEC的面积，∵△AEC的面积是△OFB的面积的10倍，∴，∴2x2﹣7x+6＝0，解得：，∴，【点睛】此题是圆的综合题，关键是根据等边三角形的性质、勾股定理和相似三角形的判定和性质解答．23．（2019•湖州）已知在平面直角坐标系xOy中，直线l1分别交x轴和y轴于点A（﹣3，0），B（0，3）．（1）如图1，已知⊙P经过点O，且与直线l1相切于点B，求⊙P的直径长；（2）如图2，已知直线l2：y＝3x﹣3分别交x轴和y轴于点C和点D，点Q是直线l2上的一个动点，以Q为圆心，2为半径画圆．①当点Q与点C重合时，求证：直线l1与⊙Q相切；②设⊙Q与直线l1相交于M，N两点，连结QM，QN．问：是否存在这样的点Q，使得△QMN是等腰直角三角形，若存在，求出点Q的坐标；若不存在，请说明理由．【答案】解：（1）如图1，连接BC，∵∠BOC＝90°，∴点P在BC上，∵⊙P与直线l1相切于点B，∴∠ABC＝90°，而OA＝OB，∴△ABC为等腰直角三角形，则⊙P的直径长＝BC＝AB＝3；（2）过点作CM⊥AB，由直线l2：y＝3x﹣3得：点C（1，0），则CM＝AC sin45°＝42圆的半径，故点M是圆与直线l1的切点，即：直线l1与⊙Q相切；（3）如图3，①当点M、N在两条直线交点的下方时，由题意得：MQ＝NQ，∠MQN＝90°，设点Q的坐标为（m，3m﹣3），则点N（m，m+3），则NQ＝m+3﹣3m+3＝2，解得：m＝3；②当点M、N在两条直线交点的上方时，同理可得：m＝3；故点P的坐标为（3，6﹣3）或（3，6+3）．【点睛】本题为圆的综合运用题，涉及到一次函数、圆的切线性质等知识点，其中（2），关键要确定圆的位置，分类求解，避免遗漏.。
九年级中考数学复习专题十 几何动态探究题
专题十几何动态探究题1. 如图，在菱形ABCD中，∠ABC＝120°，点E，F分别是边AB，BC上的动点，在运动过程中，始终保持AE＝BF，若AB＝2，则EF的取值范围为________．第1题图2.如图，在三角形纸片ABC中，点D是BC边上一点，连接AD，把△ABD沿着AD翻折，得到△AED，DE与AC交于点G，连接BE交AD于点F，若DG＝GE，AF＝3，BF＝2，△ADG的面积为2，则点F到BC的距离为________．第2题图3. 如图，在Rt△ABC中，AB＝AC＝4 cm，∠BAC＝90°，O为边BC上一点，OA＝OB＝OC，点M、N分别在边AB、AC上运动，且始终保持AN＝BM.在运动过程中，四边形AMON的面积为________cm2.第3题图4. 如图，在正方形ABCD中，AB＝4，O是BC边的中点，点E是正方形内一动点，OE＝2，连接DE，将线段DE绕点D逆时针旋转90°得DF，连接AE、CF.则线段OF长的最小值为________．第4题图5. 如图，在△ABC中，AB＞AC，∠B＝45°，AC＝5，BC＝42，则AB的长为________；若E是AB边上一点，将△BEC沿EC所在直线翻折得到△DEC，DC交AB于点F，当DE∥AC时，tan∠BCD的值为________．第5题图6.如图，在Rt△ABC中，∠ACB＝90°，AC＝BC＝4 cm，将△ABC绕点A顺时针旋转30°得到△AB′C′，直线BB′、CC′交于点D，则CD的长为________cm.第6题图7. 如图，四边形ABCD是正方形，且AB＝2，将正方形ABCD绕点A顺时针旋转后得到正方形AEFG，在旋转过程中，当点A、G、C三点共线时，则点F到BC的距离为________．第7题图8.如图，在边长为2的菱形ABCD中，∠A＝60°，M是AD边的中点，N是AB边上一个动点，将△AMN沿MN所在直线翻折得到△A′MN，连接A′C，则A′C长度的最小值是________．第8题图9. 如图，在边长为4的正方形ABCD中，将△ABD沿射线BD平移，得到△EGF，连接EC，GC.则EC＋GC的最小值为________．第9题图10. 如图，在菱形ABCD 中，tan A ＝43，M ，N 分别在边AD ，BC 上，将四边形AMNB 沿MN 翻折，使AB 的对应线段EF 经过顶点D ，当EF ⊥AD 时，BN CN的值为________．第10题图11.如图，在△ABC 中，已知AD 是BC 边上的中线，∠ADC ＝60°，BC ＝3AD.将△ABD 沿直线AD 翻折，点B 落在平面上的点B ′处，连接AB ′交BC 于点E ，那么CE ∶BE 的值为________．第11题图12.如图，在平行四边形ABCD 中，AB ＝2，∠ABC ＝45°，点E 为射线AD 上一动点，连接BE ，将BE 绕点B 逆时针旋转60°得到BF ，连接AF ，则AF 的最小值是________．第12题图13. 如图，在矩形ABCD 中，AB ＝3，BC ＝4，点M 为AD 的中点，点N 为AB 上一点，连接MN ，CN ，将△AMN 沿直线MN 折叠后，点A 恰好落在CN 上的点P 处，则CN 的长为________．第13题图14. 如图，在▱ABCD 中，AB ＝3，BC ＝5，AC ⊥AB ，△ACD 沿AC 的方向以每秒1个单位的速度平移得到△EFG (点E 在线段AC 上，运动到点C 停止运动，且不与点A 重合)，同时，点H 从点C 出发以相同的速度沿CB 方向移动，当△EFG 停止平移时，点H 也停止移动，连接EH ，GH ，当EH ⊥GH 时，AE BH的值为________．第14题图15.如图，在正方形ABCD中，E是线段CD上一点，连接AE，将△ADE沿AE翻折至△AEF，连接BF并延长BF交AE延长线于点P，当PF＝22BF时，DECD＝________．第15题图16. 如图，在边长为6的菱形ABCD中，AC为其对角线，∠ABC＝60°，点M、N分别是边BC、CD上的动点，且MB＝NC.连接AM、AN、MN，MN交AC于点P，则点P到直线CD的距离的最大值为________．第16题图17. 如图，在边长为6的等边△ABC中，点D在边AC上，AD＝1，线段PQ在边AB上运动，PQ＝1，则四边形PCDQ面积的最大值为________；四边形PCDQ周长的最小值为________．第17题图18.如图，在矩形ABCD中，AB＝9，BC＝12，F是边AD上一点，连接BF，将△ABF沿BF折叠使点A落在G点，连接AG并延长交CD于点E，连接GD.若△DEG是以DG为腰的等腰三角形，则AF的长为________．第18题图19. 如图，Rt△ABC中，∠ACB＝90°，AC＝BC＝8，F为AC中点，D是线段AB上一动点，连接CD，将线段CD绕点C沿逆时针方向旋转90°得到线段CE，连接EF，则点D在运动过程中，EF的最大值为________，最小值为________．第19题图20. 如图①，把一张正方形纸片对折得到长方形ABCD，再沿∠ADC的平分线DE折叠，如图②，点C落在点C′处，最后按图③所示方式折叠，使点A落在DE的中点A′处，折痕是FG.若原正方形．．．．纸片的边长为6 cm，则FG＝________ cm.第20题图21. 如图，在△ABC中，AC＝BC＝4，∠ACB＝120°，CD⊥AB，点P是直线CD上一点，连接P A，将线段P A绕点P逆时针旋转120°得到P A′，点M、N分别是线段AC、P A′的中点，连接MN，则线段MN的最小值为________．第21题图22. 如图，在矩形ABCD中，AB＝6，BC＝8，点E是AB边上一点，且AE＝4，点F是BC边上的任意一点，把△BEF沿EF翻折，点B的对应点为点G，连接AG、CG，则四边形AGCD面积的最小值为________，此时BF的长为________．第22题图专题十几何动态探究题1. 3≤EF≤2【解析】如解图，连接BD，过点D作DH⊥AB，垂足为点H，∵四边形ABCD为菱形，∠ABC＝120°，∴∠A＝∠DBA＝∠C＝60°，AB＝BD＝BC，∵AE＝BF，∴BE＝CF，∴△DBE≌△DCF(SAS)．∴DE＝DF，∠BDE＝∠CDF，∵∠EDF＝∠EDB＋∠BDF＝∠CDF＋∠BDF＝60°，∴△DEF 是等边三角形，∴EF＝DE，当点E与点H重合时，DE的值最小，此时DE＝AD·sin A＝3，当点E与点A (或点B )重合时，DE 的长最大，此时DE ＝2，∴EF 的取值范围为3≤EF ≤2. 第1题解图 2. 255 【解析】∵DG ＝GE ，∴S △ADG ＝S △AEG ＝2，∴S △ADE ＝4，由翻折的性质得△ADB ≌△ADE ，BE ⊥AD ，∴S △ABD ＝S △ADE ＝4，∠BFD ＝90°，∴12(AF ＋DF )·BF ＝4，即12(3＋DF )×2＝4，∴DF ＝1，∴DB ＝BF 2＋DF 2＝22＋12＝5，设点F 到BD 的距离为h ，则有12BD ·h ＝12BF ·DF ，即12×5·h ＝12×2×1，∴h ＝255.3. 4 【解析】∵AC ＝AB ，∠BAC ＝90°，∴∠B ＝∠C ＝45°，∵OA ＝OB ＝OC ，∴∠BAO ＝∠CAO ＝45°，∠AOB ＝∠AOC ＝90°，∴∠B ＝∠BAO ＝∠CAO ，在△AON 和△BOM 中，⎩⎪⎨⎪⎧OA ＝OB ∠CAO ＝∠B AN ＝BM，∴△AON ≌△BOM (SAS)，∴S △AON ＝S △BOM ，∴S △AON ＋S △AOM ＝S △BOM ＋S △AOM ，即S 四边形AMON ＝S △AOB ，∴S 四边形AMON ＝12S △ABC ＝12×12×4×4＝4 cm 2.4. 210－2 【解析】如解图，连接DO ，将线段DO 绕点D 逆时针旋转90°得到DM ，连接FM ，OM ，∵ ∠EDF ＝ ∠ODM ＝90°，∴ ∠EDO ＝∠FDM ，在△EDO 与△FDM 中，⎩⎪⎨⎪⎧DE ＝DF ∠EDO ＝∠FDM DO ＝DM，∴ △EDO ≌△FDM (SAS) ，∴ FM ＝OE ＝2，∵在正方形ABCD 中，AB ＝4，O 是BC 边的中点，∴ OC ＝2，∴OD ＝42＋22＝2 5 ，∴OM ＝2OD ＝210，∵OF ≥OM －MF ，∴OF ≥210－2 ，∴线段OF 长的最小值为210－2.第4题解图5. 7；34 【解析】如解图，过点A 作AM ⊥BC 于点M .在Rt △ABM 中，∵∠AMB ＝90°，∠B ＝45°，∴BM ＝AM ，AB ＝2AM ，设AM ＝BM ＝x ，在Rt △AMC 中，∵AC 2＝AM 2＋CM 2，∴52＝x 2＋(42－x )2，解得x＝722或22(舍)，∴AB ＝2x ＝7.过点F 作FN ⊥BC 于点N .∵DE ∥AC ，∴∠ACF ＝∠D ＝∠B ，∵∠CAF ＝∠CAB ，∴△ACF ∽△ABC ，∴AC AB ＝AF AC ，∴AC 2＝AF ·AB ，∴AF ＝257，∴BF ＝AB －AF ＝7－257＝247，∴BN ＝FN ＝1227，∴CN ＝BC －BN ＝42－1227＝1627，∴tan ∠BCD ＝FN CN ＝12271627＝34.第5题解图6. 2 6 cm 【解析】如解图，过点C 作CE ⊥BD 交DB 的延长线于点E ，由旋转的性质得∠B ′AB ＝∠C ′AC＝30°，AB ′＝AB ，AC ′＝AC ，∴∠B ′BA ＝∠C ′CA ＝12×(180°－30°)＝75°，∵∠ACB ＝90°，AC ＝BC ＝4cm ，∴∠ABC ＝∠BAC ＝45°，∠DCB ＝90°－∠C ′CA ＝15°，∴∠CDE ＝180°－∠B ′BA －∠ABC －∠DCB ＝180°－75°－45°－15°＝45°，∴∠DCE ＝∠CDE ＝45°，DE ＝CE ，∴∠BCE ＝∠DCE －∠DCB ＝45°－15°＝30°，在Rt △BCE 中，BC ＝4 cm ，∠BCE ＝30°，∴BE ＝12BC ＝2 cm ，∴CE ＝BC 2－BE 2＝42－22＝2 3 cm ，∴CD ＝CE cos45°＝2322＝2 6 cm.第6题解图7. 2－2或2＋2 【解析】由旋转的性质可知AG ＝FG ＝AB ＝2，AF ＝2AG ＝2.分两种情况讨论：①如解图①，当点G 在线段AC 上时，连接AC ，BF ，可知点B 在线段AF 上，即点F 到BC 的距离为BF 的长，∴BF ＝AF －AB ＝2－2；②如解图②，当点G 在CA 的延长线上时，连接AC ，AF ，此时点F 在BA 的延长线上，即点F 到BC 的距离为BF 的长，∴BF ＝AB ＋AF ＝2＋ 2.综上所述，点F 到BC 的距离为2－2或2＋ 2.图①图②第7题解图8. 7－1 【解析】如解图①，以点M 为圆心，AM 长为半径作圆，过点M 作MH ⊥CD 交CD 的延长线于点H ，连接MC ，∵菱形ABCD 的边长为2，∠DAB ＝60°，M 是AD 的中点，∴MA ＝MA ′＝MD ＝12AD ＝1，∴点A ′在⊙M 上运动，由解图①得，只有当A ′运动到与点M 、C 三点共线时，A ′C 的长度最小，∵CH ∥AB ，∴∠MDH ＝∠DAB ＝60°，在Rt △MDH 中，DH ＝MD ·cos ∠MDH ＝12，MH ＝MD ·sin ∠MDH ＝32，在Rt △MHC 中，HC ＝DH ＋DC ＝12＋2＝52，由勾股定理得MC ＝HC 2＋MH 2＝7，此时A ′C ＝MC －MA ′＝7－1，即A ′C 长度的最小值为7－1.第8题解图①【一题多解】如解图②，连接MC ，过点M 作MH ⊥CD 交CD 的延长线于点H ，由题意可知，MA ＝MA ′＝12AD ，在△ MA ′C 中，由三角形三边关系可知，一定存在MA ′＋A ′C ≥MC ，∴当点M 、A ′、C 三点共线时，A ′C 的长度最小，此时A ′C ＝MC －MA ′，其余解法同上．第8题解图②9. 45 【解析】如解图，连接AE 并延长，作点D 关于AE 的对称点H ，连接EH ，ED ，过点H 作HM ⊥CD ，与CD 的延长线交于点M ，则DE ＝EH ，∵△ABD 沿射线BD 平移得△EGF ，∴AE ∥BD ，AB ＝EG ，AB ∥EG ，∵AB ∥CD ，AB ＝CD ＝4，∴EG ∥CD ，EG ＝CD ＝4，∴四边形CDEG 是平行四边形，∴CG ＝DE ＝EH ，∴当点C ，E ，H 三点共线时，EC ＋GC 取得最小值，最小值为CH 的长．∵AE ∥BD ，AB ∥CD ，∴四边形ABDM 为平行四边形，∴DM ＝AB ＝4，∠DAM ＝45°，∴∠ADH ＝45°，∴∠MDH ＝45°，∴DM ＝HM ＝4，∴CH ＝CM 2＋HM 2＝（4＋4）2＋42＝45，∴EC ＋GC 的最小值为4 5.第9题解图10. 27 【解析】如解图，延长NF 与DC 交于点H .由折叠的性质得∠E ＝∠A ，∠EFN ＝∠B ，EM ＝AM ，EF ＝AB .∵EF ⊥AD ，∴∠MDE ＝90°.在Rt △MDE 中，tan E ＝DM DE ＝tan A ＝43，设DM ＝4k ，则DE ＝3k ，EM＝5k .∴AM ＝5k ，AD ＝9k .∵四边形ABCD 是菱形，∴AB ＝CD ＝BC ＝AD ＝9k ，∠C ＝∠A ，AB ∥CD ，AD ∥BC .∴∠A ＋∠ADC ＝180°，∠A ＋∠B ＝180°.∵∠ADF ＝90°，∴∠A ＋∠FDH ＝90°.∵∠DFH ＋∠EFN ＝180°，∠A ＋∠B ＝180°，∠EFN ＝∠B ，∴∠A ＝∠DFH .∴∠DFH ＋∠FDH ＝90°.∴∠DHF ＝90°.∵EF ＝AB ＝9k ，DE ＝3k ，∴DF ＝6k .在Rt △DHF 中，tan ∠DFH ＝tan A ＝43，易得sin ∠DFH ＝45，∴DH ＝DF ·sin ∠DFH ＝245k .∴HC ＝9k －245k ＝215k .在Rt △CHN 中，tan C ＝ tan A ＝43，易得cos C ＝35.∴NC ＝HC cos C ＝7k .∴BN ＝9k －7k ＝2k .∴BN CN ＝2k 7k ＝27.第10题解图11. 37 【解析】如解图，过点A 作AF ⊥BC 于点F ，过点B ′作B ′G ⊥BC 于点G ，∵∠ADC ＝60°，∴∠ADB ＝120°，由折叠的性质得，∠ADB ′＝120°，∠CDB ′＝60°，B ′D ＝BD ，∵BC ＝3AD ，AD 是BC 边上的中线，∴设AD ＝m ，则BC ＝3m ，BD ＝B ′D ＝32m ，在Rt △ADF 中，DF ＝AD ·cos60°＝12m ，AF ＝AD ·sin60°＝32m ，∴BF ＝BD ＋DF ＝2m ，CF ＝BC －BF ＝m ，在Rt △B ′DG 中，DG ＝B ′D ·cos60°＝34m ，B ′G ＝B ′D ·sin60°＝334m ，∴FG ＝DG －DF ＝14m ，∵AF ⊥BC ，B ′G ⊥BC ，∴AF ∥B ′G ，∴△AFE ∽△B ′GE ∴FE GE ＝AF B ′G ＝32m334m＝23，∵FE ＋GE ＝FG ＝14m ，∴FE ＝110m ，∴BE ＝BF ＋FE ＝2110m ，CE ＝CF －FE ＝910m ，∴CE BE ＝910m 2110m ＝37.第11题解图12. 6＋22 【解析】如解图，以AB 为边向下作等边△ABK ，连接EK ，在EK 上取一点T ，连接AT ，使得TA ＝TK .由旋转的性质得BE ＝BF ，∠EBF ＝60°，∵△ABK 为等边三角形，∴BK ＝BA ，∠EBF ＝∠ABK ＝60°，∴∠ABF ＝∠KBE ，∴△ABF ≌△KBE (SAS)，∴AF ＝EK ，根据垂线段最短可知，当KE ⊥AD 时，KE 的值最小，即AF 最小．∵四边形ABCD 是平行四边形，∴AD ∥BC ，∴∠BAD ＝180°－∠ABC ＝135°，∵∠BAK ＝60°，∴∠EAK ＝75°，∵∠AEK ＝90°，∴∠AKE ＝15°，∵TA ＝TK ，∴∠TAK ＝∠AKT ＝15°，∴∠ATE ＝∠TAK ＋∠AKT ＝30°，设AE ＝a ，则AT ＝TK ＝2a ，ET ＝3a ，在Rt △AEK 中，AE 2＋EK 2＝AK 2，∴a 2＋(2a ＋3a )2＝22，∴a ＝6－22，∴EK ＝2a ＋3a ＝6＋22，∴AF 的最小值为6＋22.第12题解图13. 133 【解析】如解图，连接CM ，在矩形ABCD 中，AB ＝3，BC ＝4，∴AD ＝BC ＝4，CD ＝AB ＝3，∠D ＝90°，由折叠的性质得，AM ＝PM ，∠MPN ＝∠A ＝90°，∠AMN ＝∠PMN ，∴∠CPM ＝90°，∵点M 为AD 的中点，∴AM ＝DM ＝12AD ＝2，∴PM ＝AM ＝DM ＝2，在Rt △CPM 与Rt △CDM 中，⎩⎪⎨⎪⎧PM ＝DM CM ＝CM，∴Rt △CPM ≌Rt △CDM (HL)，∴CP ＝CD ＝3，∠CMP ＝∠CMD ，∴∠NMC ＝∠NMP ＋∠CMP ＝12(∠AMP ＋∠DMP )＝90°，∴CM ＝DM 2＋CD 2＝22＋32＝13，∵∠CPM ＝∠CMN ＝90°，∠MCP ＝∠NCM ，∴△CMP ∽△CNM ，∴CM CN ＝CP CM ，即13CN ＝313，∴CN ＝133.第13题解图14. 37 【解析】如解图，过点E 作EM ⊥BC 的于点M ，过点G 作GN ⊥BC 交BC 的延长线于点N ，∴四边形EMNG 是矩形，∴EG ＝MN ＝5，EM ＝GN ，∵∠BAC ＝∠EMH ＝90°，∠ACB ＝∠MCE ，∴△ABC ∽△MEC ，∴AB ME ＝BC EC ＝AC MC ，∵AB ＝3，BC ＝5，在Rt △ABC 中，由勾股定理得AC ＝4，设运动时间为t (0＜t ≤4)，则AE ＝CH ＝t ，CE ＝4－t ，∴3ME ＝54－t ＝4MC ，∴EM ＝12－3t 5，CM ＝16－4t 5，∴HN ＝5－MH ＝5－(CM －CH )＝5－(16－4t 5－t )＝9＋9t 5.∵EH ⊥GH ，∴∠EHG ＝90°，∴∠EHM ＋∠GHN ＝90°，又∵EM ⊥BC ，∴∠EHM ＋∠MEH ＝90°，∴∠GHN ＝∠MEH ，又∵∠EMH ＝∠HNG ＝90°，∴△EMH ∽△HNG ，∴EM HN ＝MH NG ，即12－3t 59＋9t 5＝16－4t5－t 12－3t 5，整理得2t 2－3t ＝0，解得t ＝32或t ＝0(舍去)，即AE ＝32，BH ＝5－CH ＝5－32＝72，∴AE BH ＝3272＝37.第14题解图15. 2－1 【解析】如解图，过点A 作AM ⊥BP 于点M ，过点E 作EN ⊥BP 于点N .∵四边形ABCD 是正方形，∴AD ＝AB ，∠BAD ＝90°，由翻折的性质得AD ＝AF ，∠DAE ＝∠EAF ，∴AB ＝AF ，∵AM ⊥BF ，∴BM ＝FM ，∠BAM ＝∠FAM ，∴∠PAM ＝∠PAF ＋∠FAM ＝12∠BAD ＝45°，∵∠AMP ＝90°，∴∠P ＝∠PAM＝45°，∴AM ＝MP ，设BF ＝2a ，则BM ＝MF ＝a ，PF ＝22BF ＝2a ，∴AM ＝PM ＝FM ＋PF ＝a ＋2a ，∵∠AMF ＝∠AFE ＝∠ENF ＝90°，∴∠AFM ＋∠EFN ＝90°，∠EFN ＋∠FEN ＝90°，∴∠AFM ＝∠FEN ，∴△AMF ∽△FNE ，∴AM FM ＝FN EN ＝a ＋2aa ＝1＋2，设EN ＝PN ＝x ，则FN ＝(1＋2)x ，∴(1＋2)x ＋x ＝2a ，∴x ＝(2－1)a ，∴EN ＝(2－1)a ，∴EF AF ＝EN FM ＝（2－1）a a＝2－1，∵CD ＝AD ＝AF ，DE ＝EF ，∴DE CD ＝EFAF ＝2－1.第15题解图16. 334 【解析】如解图，过点P 作PE ⊥CD 于点E .∵∠ABC ＝60°，AB ＝BC ，∴△ABC 为等边三角形，∠ACB ＝∠ACD ＝60°，在△ABM 和△ACN 中，⎩⎪⎨⎪⎧AB ＝AC ∠ABM ＝∠ACN ，BM ＝CN∴△ABM ≌△ACN (SAS)，∴AM ＝AN ，∠BAM ＝∠CAN ，∴∠MAN ＝∠BAM ＋∠MAC ＝60°，∴△AMN 为等边三角形，∵∠B ＝∠ACB ＝∠AMP ＝60°，∴∠BAM ＋∠BMA ＝∠BMA ＋∠CMP ＝180°－60°＝120°，∴∠BAM ＝∠CMP ，∠BMA ＝∠CPM ，∴△BAM ∽△CMP ，∴BA BM ＝CM CP ，设BA 长为a ，BM 长为x ，则CM ＝a －x ，∴a x ＝a －xCP ，∴a ·CP ＝x (a －x )＝－x 2＋ax ＝－(x －a 2)＋a 24，∴CP ＝－1a (x －a 2)＋a 4，∴当x ＝a 2时，CP 最长，即当AM ⊥BC 时，△AMN 边长最小，此时CP 最长，满足条件，∵AB ＝AC ，AM ⊥BC ，∴BM ＝MC ＝3，∠CMP ＝30°，∠CPM ＝90°，∴PC ＝12MC ＝32，在Rt △PCE 中，∵∠ACD ＝60°，∴PE ＝PC ·sin60°＝334.第16题解图17. 3134；6＋39 【解析】设AQ ＝x ，则S 四边形PCDQ ＝S △ABC －S △ADQ －S △BCP ＝34×62－12·x ·32×1－12×(6－x －1)×32×6＝332＋534x ，∵x 的最大值为6－1＝5，∴当x ＝5时，S 四边形PCDQ 最大，最大值为332＋534×5＝3134；如解图，作点D 关于AB 的对称点D ′，连接D ′Q ，以D ′Q 、PQ 为边作平行四边形PQD ′M ，则DQ ＝D ′Q ＝MP ，∴C 四边形PCDQ ＝PM ＋PC ＋PQ ＋DC ，DD ′＝2AD ·sin60°＝3，D ′M ＝PQ ＝1，过点C 作CH ⊥AB ，交AB 于点H ，交D ′M 的延长线于点N ，则∠N ＝90°，CH ＝BC ·sin60°＝33，NH ＝12DD ′＝32，∴MN ＝AH －D ′M －AD ·cos60°＝AC ·cos60°－1－12＝3－1－12＝32，CN ＝NH ＋CH ＝32＋33＝732，当点M ，P ，C 在同一直线上时，MP ＋CP 的最小值等于CM 的长，即DQ ＋CP 的最小值等于CM 的长，此时，Rt △MNC 中，CM ＝MN 2＋CN 2＝（32）2＋（732）2＝39，又∵PQ ＝1，CD ＝6－1＝5，∴四边形PCDQ 周长的最小值为CM ＋PQ ＋CD ＝6＋39.第17题解图18. 27－952或92 【解析】分两种情况讨论，如解图①，当GD ＝GE 时，过点G 作GM ⊥AD 于点M ，GN ⊥CD 于点N .设AF ＝x .∵四边形ABCD 是矩形，∴AD ＝BC ＝12，∠BAF ＝∠ADE ＝90°，由翻折的性质得AF ＝FG ，BF ⊥AG ，∴∠DAE ＋∠BAE ＝90°，∠ABF ＋∠BAE ＝90°，∴∠ABF ＝∠DAE ，∴△BAF ∽△ADE ，∴AB DA ＝AF DE ，即912＝x DE ，∴DE ＝43x ，∵GM ⊥AD ，GN ⊥CD ，∴∠GMD ＝∠GND ＝∠MDN ＝90°，∴四边形GMDN 是矩形，∴GM ＝DN ＝EN ＝23x ，∵GD ＝GE ，∴∠GDE ＝∠GED ，∵∠GDA ＋∠GDE ＝90°，∠GAD ＋∠GED ＝90°，∴∠GDA ＝∠GAD ，∴GA ＝GD ＝GE ，∵GM ⊥AD ，∴AM ＝MD ＝6，在Rt △FGM 中，由勾股定理得x 2＝(6－x )2＋(23x )2，解得x ＝27－952或27＋952(舍)，∴AF ＝27－952；如解图②，当DG ＝DE 时，由翻折的性质得，BA ＝BG ，∴∠BAG ＝∠BGA ，∵DG ＝DE ，∴∠DGE ＝∠DEG ，∵AB ∥CD ，∴∠BAE ＝∠DEG ，∴∠AGB ＝∠DGE ，∴B ，G ，D 三点共线，∵BD ＝AB 2＋AD 2＝92＋122＝15，BG ＝BA ＝9，∴DG ＝DE ＝6，由①知，△BAF ∽△ADE ，∴AF DE ＝AB DA ，即AF 6＝912，∴AF ＝92.综上所述，AF 的值为27－952或92.图①图②第18题解图19. 45；22 【解析】如解图，取BC 的中点G ，连接DG ，由旋转的性质得DC ＝EC ，∠DCE ＝90°，∵∠ACB ＝90°，AC ＝BC ＝8，F 为AC 中点，∴CG ＝CF ，∠DCG ＋∠ACD ＝∠ECF ＋∠ACD ＝90°，∴∠DCG ＝∠ECF ，∴△DCG ≌△ECF (SAS)，∴DG ＝EF .分两种情况讨论：如解图①，当GD ⊥AB 时，DG 最短，此时△BDG 是等腰直角三角形，∴DG ＝BG ·sin45°＝4×22＝22，∴EF 的最小值为22；当点D 与点B 重合时，DG ＝BG ＝4；如解图②，当点D 与点A 重合时，DG ＝CG 2＋AC 2＝42＋82＝45＞4，∴EF 的最大值为45，最小值为2 2.图①图②第19题解图20. 10 【解析】如解图，过点A ′作A ′H ⊥AD 于点H ，延长FA ′与BE 的延长线交于点J ，过点F 作FI ⊥BE 于点I ，∵A ′是DE 的中点，∴A ′H 是△DC ′E 的中位线，∴A ′H ＝12C ′E ＝12×3＝32 cm ，由折叠性质知∠A ′DH ＝45°，∴DH ＝A ′H ＝32 cm ，设AF ＝x cm ，则FH ＝6－x －32＝(92－x ) cm ，由折叠的性质得A ′F ＝AF＝x cm ，在Rt △A ′HF 中，由勾股定理得A ′F 2－FH 2＝A ′H 2，即x 2－(92－x )2＝(32)2，解得x ＝52，∴A ′F ＝AF ＝52 cm ，FH ＝92－52＝2 cm ，∴EI ＝FC ′＝FH ＋DH －C ′D ＝2＋32－3＝12 cm ，∵A ′是DE 的中点，易证△A ′DF ≌△A ′EJ ，∴EJ ＝DF ＝2＋32＝72 cm ，A ′F ＝A ′J ＝52 cm ，∴FJ ＝5 cm ，由折叠的性质得∠AFG ＝∠JFG ，∵AD ∥BJ ，∴∠JGF ＝∠AFG ＝∠JFG ，∴JG ＝JF ＝5 cm ，∴GI ＝JG －JE －EI ＝5－72－12＝1 cm ，在Rt △FGI 中，FI ＝3 cm ，∴FG ＝32＋12＝10 cm.第20题解图21. 5217 【解析】如解图，点P 在直线CD 上运动时，当MN 垂直于点N 的运动轨迹(直线)时，MN 最短，当点P 和C 重合时，N 1 是CB 的中点，当PA ′和直线CD 重合时，N 2 是PA ′的中点，∵AC ＝CB ＝4，∠ACB ＝120°，CD ⊥AB ，∴CD ＝2，AD ＝23，∴AB ＝2AD ＝43，∵M 、N 1分别是AC 、BC 中点，∴MN 1∥AB ，MN 1＝12AB ＝23，DE ＝1，∵PA ′是PA 绕点P 逆时针旋转120°得到的，当PA ′和直线CD 重合时，PA ′＝PA ，∠APA ′＝120°，∴∠APD ＝60°，∴AP ＝AD sin60°＝2332＝4，DP ＝AP ·cos60°＝4×12＝2，∵N 2是PA ′的中点，∴PN 2＝2，EN 2＝2＋2＋1＝5，∵MN 1∥AB ，CD ⊥AB ，MN 1⊥CD ，在△MEN 2和△N 1EN 2中，⎩⎪⎨⎪⎧ME ＝N 1E ∠MEN 2＝∠N 1EN 2EN 2＝EN 2，∴△MEN 2≌△N 1EN 2(SAS)，∴N 2M ＝N 2N 1，在Rt △MN 2E 中，N 2M ＝ME 2＋EN 22＝（3）2＋52＝27，∴S △MN 1N 2＝12MN 1·EN 2＝12×23×5＝53，又∵S △MN 1N 2＝12N 1N 2·MN ，∴12×27×MN ＝53，∴MN ＝5217.第21题解图22. 30；6 【解析】如解图①，连接AC ，分别过点E ，G 作AC 的垂线，垂足为M ，N ，易证△AEM ∽△ACB ，∴AE AC ＝EM CB ，∵AB ＝6，BC ＝8，∴AC ＝AB 2＋BC 2＝10，∴410＝EM 8，∴EM ＝165.∵△BEF 沿EF 翻折后点B 的对应点为点G ，∴GE ＝BE ＝2，∴点G 在以点E 为圆心，2为半径的⊙E (在矩形ABCD 内的部分)上．连接EN ，则EG ＋GN ≥EN ≥EM ，∴GN ≥EM －EG ＝165－2＝65.∵S 四边形AGCD ＝S △ACD ＋S △AGC ＝12AD ·CD ＋12AC ·GN ＝24＋5GN ，如解图②，当点G 在EM 上，即点N 与点M 重合，此时GN 取得最小值65，S 四边形AGCD 取得最小值为24＋5GN ＝24＋5×65＝30；如解图②，过点F 作FH ⊥AC 于点H ，∵EM ⊥FG ，EM ⊥AC ，∴四边形FGMH 是矩形，∴FH ＝GM ＝65，∵∠FCH ＝∠ACB ，∠CHF ＝∠CBA ＝90°，∴△CHF ∽△CBA ，∴CF CA ＝FH AB ，即CF 10＝656，∴CF ＝2，∴BF ＝BC －CF ＝8－2＝6.图①图②第22题解图。
七年级数学几何图形探索题目
七年级数学几何图形探索题目【正文开始】在七年级的数学学习中，几何图形是一个重要的内容。
通过探索几何图形，不仅可以提高学生的观察和思维能力，还可以培养他们的逻辑思维和问题解决能力。
下面，我们将一起来解答一些关于七年级数学几何图形的探索题目。
1. 问题一：给定一个直角三角形，已知斜边的长度为10cm，其中一个直角边的长度为6cm，求另一个直角边的长度。
解析：根据勾股定理，直角三角形中的斜边的平方等于两个直角边的平方和。
设另一个直角边的长度为x，则有：x² + 6² = 10²x² + 36 = 100x² = 64x = 8所以，另一个直角边的长度为8cm。
2. 问题二：画一个正方形ABCD，边长为5cm。
在边AB上找一点E，使得AE的长度为3cm。
连接DE，求角ADE的度数。
解析：正方形的每个内角都是90度，所以角ADE是一个直角。
根据正方形的性质，AE和DE相等，且均等于半边长。
因此，AE = DE = 2.5cm。
3. 问题三：在一个等边三角形ABC中，点D是AB边上的一点，角ACD的度数为30度。
连接DC和BC，求角BDC的度数。
解析：由等边三角形的性质可知，三个内角均为60度。
角ACD为30度，所以角BCD为60度。
因此，角BDC的度数为60度。
4. 问题四：画一个矩形EFGH，已知EF的长度为4cm，EH的长度为3cm。
连接FG和GH，求角GHE的度数。
解析：我们先计算矩形的两个对角线的长度。
根据勾股定理，对角线的长度为：FG = √(EF² + (2*EH)²) = √(4² + (2*3)²) = √(16 + 36) = √52 = 2√13 cm GH = √(((2*EF)²) + EH²) = √(((2*4)²) + 3²) = √(64+9) = √73 cm根据余弦定理，角GHE的度数可以通过以下公式求解：cos GHE = (FG² + GH² - FH²) / (2 * FG * GH)cos GHE = ((2√13)² + (√73)² - 3²) / (2 * 2√13 * √73)cos GHE = (52 + 73 - 9) / (4√13 * √73)cos GHE = 116 / (4√949)cos GHE = 29 / √949通过查表或计算器，我们可以得到cos GHE的值为 0.993536。
2019年(四川版)高考数学分项汇编 专题10 立体几何(含解析)理
第十章 立体几何一．基础题组1.【2007四川，理4】如图，ABCD -A 1B 1C 1D 1为正方体，下面结论错误．．的是( )（A ）BD ∥平面CB 1D 1 （B ）AC 1⊥BD（C ）AC 1⊥平面CB 1D 1 （D ）异面直线AD 与CB 1所成角为60°2.【2007四川，理14】如图，在正三棱柱ABC -A 1B 1C 1中，侧棱长为2，底面三角形的边长为1，则BC 1与侧面ACC 1A 1所成的角是 .BB 13.【2008四川，理9】设直线l ⊂平面α，过平面α外一点A 与,l α都成030角的直线有且只有：( ) （Ａ）１条 （Ｂ）２条 （Ｃ）３条 （Ｄ）４条【点评】：此题重点考察线线角，线面角的关系，以及空间想象能力，图形的对称性；【突破】：数形结合，利用圆锥的母线与底面所成的交角不变画图，重视空间想象能力和图形的对称性； 4.【2010四川，理15】如图，二面角l αβ--的大小是60°，线段AB α⊂.B l ∈，AB 与l 所成的角为30°.则AB 与平面β所成的角的正弦值是 .【答案】4【命题意图】本题考查立体几何中的二面角、线面角的求法.关键是利用三垂线定理及其逆定理把要求的角作出来.α∙AB∙βDB 1B5.【2011四川，理3】1l ，2l ，3l 是空间三条不同的直线，则下列命题正确的是（ ） (A )12l l ⊥，23l l ⊥13l l ⇒ （B ）12l l ⊥，23l l ⇒13l l ⊥(C )233l l l ⇒ 1l ，2l ，3l 共面（D ）1l ，2l ，3l 共点⇒1l ，2l ，3l 共面6.【2011四川，理15】如图，半径为R 的球O 中有一内接圆柱.当圆柱的侧面积最大时，球的表面积与该圆柱的侧面积之差是 .7.【2012四川，理6】下列命题正确的是（ ）A 、若两条直线和同一个平面所成的角相等，则这两条直线平行B 、若一个平面内有三个点到另一个平面的距离相等，则这两个平面平行C 、若一条直线平行于两个相交平面，则这条直线与这两个平面的交线平行D 、若两个平面都垂直于第三个平面，则这两个平面平行8. 【2012四川，理14】如图，在正方体1111ABCD A B C D 中，M 、N 分别是棱CD 、1CC 的中点，则异面直线1A M 与DN 所成角的大小是____________。
几何图形的识别-解析题(70道)
几何图形的识别-解析题(70道)题目1：等边三角形的性质是什么？{content}题目2：如何计算一个圆的面积？{content}题目3：一个矩形的长是10cm，宽是5cm，求矩形的面积。
{content}题目4：解释什么是相似三角形。
{content}题目5：一个正方形的对角线长度是多少？{content}题目6：如何求一个圆锥的体积？{content}题目7：解释什么是直角梯形。
{content}题目8：一个球的半径是5cm，求球的体积。
{content}题目9：一个三角形的两边长度分别是3cm和4cm，第三边的长度是多少？{content}题目10：如何计算一个立方体的表面积？{content}题目11：一个圆柱的底面半径是7cm，高是10cm，求圆柱的体积。
{content}题目12：解释什么是椭圆。
{content}题目13：一个扇形的圆心角是90度，半径是10cm，求扇形的面积。
{content}题目14：一个圆台的上底半径是5cm，下底半径是10cm，高是6cm，求圆台的体积。
{content}题目15：如何计算一个圆形的周长？{content}题目16：一个梯形的上底是4cm，下底是10cm，高是5cm，求梯形的面积。
{content}题目17：解释什么是菱形。
{content}题目18：一个立方体的边长是3cm，求立方体的体积。
{content}题目19：一个圆柱的底面半径是3cm，高是8cm，求圆柱的表面积。
{content}题目20：如何计算一个球体的表面积？{content}题目21：一个圆锥的底面半径是4cm，高是9cm，求圆锥的体积。
{content}题目22：一个三角形的三个角分别是30度，60度和90度，这个三角形是什么类型的三角形？{content}题目23：一个圆台的上下底半径分别是5cm和10cm，高是8cm，求圆台的侧面积。
{content}题目24：如何计算一个圆形的直径？{content}题目25：一个正六边形的边长是6cm，求正六边形的面积。
中考数学专题复习_几何探究题
专题复习几何探究问题一、结论探究【例1】如图①，已知△ABC是等腰直角三角形，∠BAC=900，点D是BC中点，作正方形DEFG，使点A、C分别在DG和DE上，连接AE、BG（1）试猜想线段BG和AE的数量关系，请直接写出你得到的结论（2）将正方形DEFG绕点D逆时针旋转一定角度后（旋转角大于00，小于或等于3600），如图②，通过观察和测量等方法判断（1）中的结论是否仍然成立如果成立，请予以证明；如果不成立，请说明理由。
（3）若BC=DE=2，在（2）的旋转过程中，当AE为最大值时，求AF的值。
'变式练习：已知正方形ABCD中，E为对角线BD上一点，过E点作EF⊥BD交BC于F，连接DF，G为DF中点，连接EG，CG．（1）直接写出线段EG与CG的数量关系；（2）将图1中△BEF绕B点逆时针旋转45º，如图2所示，取DF中点G，连接EG，CG．你在（1）中得到的结论是否发生变化写出你的猜想并加以证明．（3）将图1中△BEF绕B点旋转任意角度，如图3所示，再连接相应的线段，问（1）中的结论是否仍然成立（不要求证明）| A D]G图1FA[EG图2、AE图3DFEC BAB'C'二、条件探究【例2】已知两个全等的直角三角形纸片ABC 、DEF ，如图（1）放置，点B 、D 重合，点F 在BC 上，AB 与EF 交于点G ，∠C=∠EFB=900，∠E=∠ABC=300，AB=DE=4 （1）求证：△EGB 是等腰三角形（2）若纸片DEF 不动，问△ABC 绕点F 旋转最小 度时，四边形ACDE 成为以ED 为底的梯形（如图（2）），求此梯形的高。
,【例3】如图，Rt △AB C 是由Rt △ABC 绕点A 顺时针旋转得到的，连结CC 交斜边于点E ，CC 的延长线交BB 于点F ． |（1）证明：△ACE ∽△FBE ；（2）设∠ABC =α，∠CAC =β，试探索α、β满足什么关系时，△ACE 与△FBE 是全等三角形，并说明理由．；E图1A:CD图2三、类比探究 【例4】（1）操作发现：如图，矩形ABCD 中，E 是AD 的中点，将△ABE 沿BE 折叠后得到△GBE ，且点G 在举行ABCD 内部．小明将BG 延长交DC 于点F ，认为GF =DF ，你同意吗说明理由． （2）问题解决：保持（1）中的条件不变，若DC =2DF ，求ABAD的值； /（3）类比探求：保持（1）中条件不变，若DC =nDF ，求ABAD的值．【例5】如果一条直线把一个平面图形的面积分成相等的两部分，我们把这条直线称为这个平面图形的一条面积等分线．如，平行四边形的一条对线所在的直线就是平行四边形的一条面积等分线．（1）三角形的中线、高线、角平分线分别所在的直线一定是三角形的面积等分线的有________；（（2）如图1，梯形ABCD 中，AB ∥DC ，如果延长DC 到E ，使CE ＝AB ，连接AE ，那么有S 梯形ABCD＝S △ABE ．请你给出这个结论成立的理由，并过点A 作出梯形ABCD 的面积等分线（不写作法，保留作图痕迹）；（3）如图，四边形ABCD 中，AB 与CD 不平行，S △ADC ＞S △ABC ，过点A 能否作出四边形ABCD 的面积等分线若能，请画出面积等分线，并给出证明；若不能，说明理由．AB。
中考数学重难点题型：12道几何探究题解析
中考数学重难点题型---12道几何探究题解析考点1 三角形几何探究1．如果三角形的两个内角α与β满足2α＋β＝90°，那么我们称这样的三角形为“准互余三角形”．(1)若△ABC 是“准互余三角形”，∠C ＞90°，∠A ＝60°，则∠B ＝15°；(2)如图1，在Rt △ABC 中，∠ACB ＝90°，AC ＝4，BC ＝5.若AD 是∠BAC 的平分线，不难证明△ABD 是“准互余三角形”．试问在边BC 上是否存在点E(异于点D)，使得△ABE 也是“准互余三角形”？若存在，请求出BE 的长；若不存在，请说明理由．(3)如图2，在四边形ABCD 中，AB ＝7，CD ＝12，BD ⊥CD ，∠ABD ＝2∠BCD ，且△ABC 是“准互余三角形”，求对角线AC 的长．解：(1)∵△ABC 是“准互余三角形”，∠C ＞90°，∠A ＝60°，∴2∠B ＋∠A ＝90°，解得∠B ＝15°. (2)如答图1，在Rt △ABC 中，∵∠B ＋∠BAC ＝90°，∠BAC ＝2∠BAD ，∴∠B ＋2∠BAD ＝90°， ∴△ABD 是“准互余三角形”． ∵△ABE 也是“准互余三角形”， ∴只有2∠B ＋∠BAE ＝90°.∵∠B ＋∠BAE ＋∠EAC ＝90°，∴∠CAE ＝∠B. ∵∠C ＝∠C ＝90°，∴△CAE ∽△CBA ，∴CA 2＝CE·CB， ∴CE ＝165，∴BE ＝5－165＝95.(3)如答图2，将△BCD沿BC翻折得到△BCF，∴CF＝CD＝12，∠BCF＝∠BCD，∠CBF＝∠CBD.∵∠ABD＝2∠BCD，∠BCD＋∠CBD＝90°，∴∠ABD＋∠DBC＋∠CBF＝180°，∴点A，B，F共线，∴∠A＋∠ACF＝90°，∴2∠ACB＋∠CAB≠90°，∴只有2∠BAC＋∠ACB＝90°，∴∠FCB＝∠FAC.∵∠F＝∠F，∴△FCB∽△FAC，∴CF2＝FB·FA，设FB＝x，则有x(x＋7)＝122，∴x＝9或x＝－16(舍去)，∴AF＝7＋9＝16，在Rt△ACF中，AC＝AF2＋CF2＝162＋122＝20.2．将一副三角尺按图1摆放，等腰直角三角尺的直角边DF恰好垂直平分AB，与AC相交于点G，BC＝2 3 cm.(1)求GC的长；(2)如图2，将△DEF绕点D顺时针旋转，使直角边DF经过点C，另一直角边DE与AC相交于点H，分别过H，C作AB的垂线，垂足分别为M，N，通过观察，猜想MD与ND的数量关系，并验证你的猜想．(3)在(2)的条件下，将△DEF沿DB方向平移得到△D′E′F′，当D′E′恰好经过(1)中的点G时，请直接写出DD′的长度．解：(1)在Rt△ABC中，∵BC＝23，∠B＝60°，∴AC＝BC·tan60°＝6，AB＝2BC＝43，在Rt△ADG中，AG＝ADcos30°＝4，∴CG＝AC－AG＝6－4＝2.(2)结论：DM＋DN＝2 3.理由：∵HM⊥AB，CN⊥AB，∴∠AMH＝∠DMH＝∠CNB＝∠CND＝90°.∵∠A＋∠B＝90°，∠B＋∠BCN＝90°，∴∠A＝∠BCN，∴△AHM∽△CBN，∴AMCN＝HMBN①，同理可证：△DHM∽△CDN，∴DNMH＝CNDM②由①②可得AM·BN＝DN·DM，∴DMAM＝BNDN，∴DM＋AMAM＝BN＋DNDN，∴ADAM＝BDDN.∵AD＝BD，∴AM＝DN，∴DM＋DN＝AM＋DM＝AD＝2 3.第2题答图(3)如答图，作GK∥DE交AB于K.在△AGK中，AG＝GK＝4，∠A＝∠GKD＝30°，作GH⊥AB于H.则AH＝AG·cos30°＝23，可得AK＝2AH＝43，此时K与B重合．∴DD′＝DB＝2 3.考点2四边形几何探究3．我们定义：有一组邻角相等且对角线相等的凸四边形叫做邻对等四边形．概念理解(1)我们所学过的特殊四边形中的邻对等四边形是矩形或正方形； 性质探究(2)如图1，在邻对等四边形ABCD 中，∠ABC ＝∠DCB ，AC ＝DB ，AB>CD ，求证：∠BAC 与∠CDB 互补；拓展应用(3)如图2，在四边形ABCD 中，∠BCD ＝2∠B ，AC ＝BC ＝5，AB ＝6，CD ＝4.在BC 的延长线上是否存在一点E ，使得四边形ABED 为邻对等四边形？如果存在，求出DE 的长；如果不存在，说明理由．(1)解：矩形或正方形．(2)证明：如答图1，延长CD 至E ，使CE ＝BA ，连接BE.在△ABC 和△ECB 中，⎩⎨⎧AB ＝EC ，∠ABC ＝∠ECB ，BC ＝CB ，∴△ABC ≌△ECB(SAS)， ∴BE ＝CA ，∠BAC ＝∠E.∵AC ＝DB ，∴BD ＝BE ，∴∠BDE ＝∠E ，∴∠CDB ＋∠BDE ＝∠CDB ＋∠E ＝∠BAC ＋∠CDB ＝180°，即∠BAC 与∠CDB 互补．(3)解：存在这样一点E ，使得四边形ABED 为邻对等四边形，如答图2，在BC 的延长线上取一点E ，使得CE ＝CD ＝4，连接DE ，AE ，BD ，则四边形ABED 为邻对等四边形．理由如下：∵CE ＝CD ，∴∠CDE ＝∠CED. ∵∠BCD ＝2∠ABC ，∴∠ABC ＝∠DEB ，∴∠ACE ＝∠BCD.在△ACE 和△BCD 中，⎩⎨⎧AC ＝BC ，∠ACE ＝∠BCD ，CE ＝CD ，∴△ACE ≌△BCD(SAS)，∴BD ＝AE ，四边形ABED 为邻对等四边形． ∵∠CBA ＝∠CAB ＝∠CDE ＝∠CED ， ∴△ABC ∽△DEC ， ∴AB BC ＝65＝DE CE ＝DE 4，∴DE ＝245.4．将矩形ABCD 绕点A 顺时针旋转α(0°＜α＜360°)，得到矩形AEFG.(1)如图，当点E 在BD 上时．求证：FD ＝CD ；(2)当α为何值时，GC ＝GB ？画出图形，并说明理由．解：(1)由旋转可得，AE ＝AB ，∠AEF ＝∠ABC ＝∠DAB ＝90°，EF ＝BC ＝AD ，∴∠AEB ＝∠ABE. ∵∠ABE ＋∠EDA ＝90°＝∠AEB ＋∠DEF ， ∴∠EDA ＝∠DEF.∵DE ＝ED ，∴△AED ≌△FDE(SAS)， ∴DF ＝AE ，∵AE ＝AB ＝CD ，∴CD ＝DF.(2)当GB ＝GC 时，点G 在BC 的垂直平分线上，分两种情况讨论： ①当点G 在AD 右侧时，如答图1，取BC 的中点H ，连接GH 交AD 于M ， ∵GC ＝GB ，∴GH ⊥BC ，∴四边形ABHM 是矩形， ∴AM ＝BH ＝12AD ＝12AG ，∴GM 垂直平分AD ，∴GD ＝GA ＝DA ， ∴△ADG 是等边三角形，∴∠DAG ＝60°， ∴旋转角α＝60°；②当点G 在AD 左侧时，如答图2，同理可得△ADG 是等边三角形，∴∠DAG ＝60°， ∴旋转角α＝360°－60°＝300°. 综上，α为60°或300°时，GC ＝GB.5．如图1，边长为4的正方形ABCD 中，点E 在AB 边上(不与点A ，B 重合)，点F 在BC 边上(不与点B ，C 重合)．第一次操作：将线段EF 绕点F 顺时针旋转，当点E 落在正方形上时，记为点G ； 第二次操作：将线段FG 绕点G 顺时针旋转，当点F 落在正方形上时，记为点H ； 依此操作下去…(1)图2中的△EFD 是经过两次操作后得到的，其形状为等边三角形，求此时线段EF 的长； (2)若经过三次操作可得到四边形EFGH.①请判断四边形EFGH 的形状为正方形，此时AE 与BF 的数量关系是AE ＝BF ；②以①中的结论为前提，设AE 的长为x ，四边形EFGH 的面积为y ，求y 与x 的函数关系式及面积y 的取值范围．解：(1)如题图2，由旋转性质可知EF ＝DF ＝DE ，则△DEF 为等边三角形． 在Rt △ADE 和Rt △CDF 中，⎩⎨⎧AD ＝CD ，DE ＝DF ，∴Rt △ADE ≌Rt △CDF(HL)．∴AE ＝CF. 设AE ＝CF ＝x ，则BE ＝BF ＝4－x ∴△BEF 为等腰直角三角形．∴DE ＝DF ＝EF ＝2(4－x)．在Rt △ADE 中，由勾股定理得AE 2＋AD 2＝DE 2，即x 2＋42＝[2(4－x)]2， 解得x 1＝8－43，x 2＝8＋43(舍去)． ∴EF ＝2(4－x)＝46－4 2.△DEF 的形状为等边三角形，EF 的长为46－4 2.第5题答图(2)①四边形EFGH 的形状为正方形，此时AE ＝BF.理由如下：依题意画出图形，如答图所示，连接EG ，FH ，作HN ⊥BC 于N ，GM ⊥AB 于M. 由旋转性质可知，EF ＝FG ＝GH ＝HE ， ∴四边形EFGH 是菱形， 由△EGM ≌△FHN ，可知EG ＝FH ，∴四边形EFGH 的形状为正方形，∴∠HEF ＝90°. ∵∠1＋∠2＝90°，∠2＋∠3＝90°，∴∠1＝∠3. ∵∠3＋∠4＝90°，∠2＋∠3＝90°，∴∠2＝∠4.在△AEH 和△BFE 中，⎩⎨⎧∠1＝∠3，EH ＝EF ，∠2＝∠4，∴△AEH ≌△BFE(ASA)，∴AE ＝BF.②利用①中结论，易证△AEH ，△BFE ，△CGF ，△DHG 均为全等三角形， ∴BF ＝CG ＝DH ＝AE ＝x ，AH ＝BE ＝CF ＝DG ＝4－x.∴y ＝S 正方形ABCD －4S △AEH ＝4×4－4×12·x·(4－x)＝2x 2－8x ＋16，∴y ＝2x 2－8x ＋16(0＜x ＜4)．∵y ＝2x 2－8x ＋16＝2(x －2)2＋8，∴当x ＝2时，y 取得最小值8；当x ＝0或4时，y ＝16.∴y的取值范围为8≤y＜16.6．提出问题如图，已知在矩形ABCD中，AB＝2，BC＝3，点P是线段AD边上的一动点(不与端点A，D重合)，连接PC，过点P作PE⊥PC交AB于点E，在点P的运动过程中，图中各角和线段之间是否存在某种关系和规律？特殊求解当点E为AB的中点，且AP>AE时，求证：PE＝PC.深入探究当点P在AD上运动时，对应的点E也随之在AB上运动，求整个运动过程中BE的取值范围．解：特殊求解∵PE⊥PC，∴∠APE＋∠DPC＝90°.∵∠D＝90°，∴∠DPC＋∠DCP＝90°.∴∠APE＝∠DCP.∵∠A＝∠D＝90°，∴△APE∽△DCP，∴APDC＝AEDP.设AP＝x，则有DP＝3－x.而AE＝BE＝1，∴x(3－x)＝2×1，解得x1＝2，x2＝1.∵AP>AE，∴AP＝2，AE＝PD＝1，∴△APE≌△DCP，∴PE＝PC.深入探究设AP＝x，AE＝y，由AP·DP＝AE·DC，可得x(3－x)＝2y.∴y＝12x(3－x)＝－12x2＋32x＝－12(x－32)2＋98.∴在0<x<3范围内，当x ＝32时，y 最大＝98.∵当AE ＝y 取得最大值时，BE 取得最小值为2－98＝78，∴BE 的取值范围为78≤BE<2.7．已知Rt △OAB ，∠OAB ＝90°，∠ABO ＝30°，斜边OB ＝4，将Rt △OAB 绕点O 顺时针旋转60°，如图1，连接BC.(1)填空：∠OBC ＝60°；(2)如图1，连接AC ，作OP ⊥AC ，垂足为P ，求OP 的长度；(3)如图2，点M ，N 同时从点O 出发，在△OCB 边上运动，M 沿O→C→B 路径匀速运动，N 沿O→B→C 路径匀速运动，当两点相遇时运动停止，已知点M 的运动速度为1.5单位/秒，点N 的运动速度为1单位/秒，设运动时间为x 秒，△OMN 的面积为y ，求当x 为何值时y 取得最大值．最大值为多少？解：(1)由旋转性质可知OB ＝OC ，∠BOC ＝60°， ∴△OBC 是等边三角形，∴∠OBC ＝60°.第7题答图1(2)如答图1中， ∵OB ＝4，∠ABO ＝30°， ∴OA ＝12OB ＝2，AB ＝3OA ＝23，∴S △AOC ＝12·OA·AB＝12×2×23＝2 3.∵△BOC 是等边三角形，∴∠OBC ＝60°，∠ABC ＝∠ABO ＋∠OBC ＝90°， ∴AC ＝AB 2＋BC 2＝2r(32＋42)＝27，∴OP ＝2S △AOC AC ＝4327＝2217.第7题答图2(3)①当0＜x≤83时，M 在OC 上运动，N 在OB 上运动，此时过点N 作NE ⊥OC 且交OC 于点E.如答图2，则NE ＝ON·sin60°＝32x ，∴S △OMN ＝12·OM·NE＝12×1.5x×32x ，∴y ＝338x 2，∴当x ＝83时，y 有最大值，最大值为833.第7题答图3②当83＜x≤4时，M 在BC 上运动，N 在OB 上运动．如答图3，作MH ⊥OB 于H.则BM ＝8－1.5x ，MH ＝BM·sin60°＝32(8－1.5x)，∴y ＝12×ON×MH＝－338x 2＋23x.当x ＝83时，y 取得最大值，最大值为833.第7题答图4③当4＜x≤4.8时，M，N都在BC上运动，作OG⊥BC于G.如答图4，MN＝12－2.5x，OG＝AB＝23，∴y＝12·MN·OG＝123－532x，当x＝4时，y有最大值，最大值为2 3.综上所述，y有最大值，最大值为83 3.8．在菱形ABCD中，∠ABC＝60°，点P是射线BD上一动点，以AP为边向右侧作等边△APE，点E 的位置随着点P的位置变化而变化．(1)如图1，当点E在菱形ABCD内部或边上时，连接CE，BP与CE的数量关系是PB＝EC，CE与AD 的位置关系是CE⊥AD；(2)当点E在菱形ABCD外部时，(1)中的结论是否还成立？若成立，请予以证明；若不成立，请说明理由(选择图2，图3中的一种情况予以证明或说理)；(3)如图4，当点P在线段BD的延长线上时，连接BE.若AB＝23，BE＝219，求四边形ADPE的面积．解：(1)结论：PB＝EC，CE⊥AD.理由：如答图1中，连接AC.∵四边形ABCD是菱形，∠ABC＝60°，∴△ABC，△ACD都是等边三角形，∠ABD＝∠CBD＝30°.∵△APE是等边三角形，∴AB＝AC，AP＝AE，∠BAC＝∠PAE＝60°，∴△BAP≌△CAE，∴BP＝CE，∠ABP＝∠ACE＝30°，延长CE交AD于H，∵∠CAH＝60°，∴∠CAH＋∠ACH＝90°，∴∠AHC＝90°，即CE⊥AD.第8题答图2(2)结论仍然成立．理由：如答图2，连接AC交BD于O，设CE交AD于H.∵四边形ABCD是菱形，∠ABC＝60°，∴△ABC，△ACD都是等边三角形，∠ABD＝∠CBD＝30°.∵△APE是等边三角形，∴AB＝AC，AP＝AE，∠BAC＝∠PAE＝60°，∴△BAP≌△CAE，∴BP＝CE，∠ABP＝∠ACE＝30°，∵∠CAH＝60°，∴∠CAH＋∠ACH＝90°，∴∠AHC＝90°，即CE⊥AD.(3)如答图3，连接AC 交BD 于点O ，连接CE 交AD 于点H ， 由(2)可知EC ⊥AD ，CE ＝BP ， 在菱形ABCD 中，AD ∥BC ， ∴EC ⊥BC.∵BC ＝AB ＝23，BE ＝219， ∴在Rt △BCE 中，EC ＝2r(192－2r(3)2)＝8，∴BP ＝CE ＝8.∵AC 与BD 是菱形的对角线， ∴∠ABD ＝12∠ABC ＝30°，AC ⊥BD ，∴BD ＝2BO ＝2AB·cos30°＝6，∴OA ＝12AB ＝3，DP ＝BP －BD ＝8－6＝2，∴OP ＝OD ＋DP ＝5，在Rt △AOP 中，AP ＝AO 2＋OP 2＝27， ∴S 四边形ADPE ＝S △ADP ＋S △AEP ＝12DP·AO＋34·AP 2＝12×2×3＋34×(27)2＝8 3.考点3 三角形、四边形混合几何探究9．我们把两条中线互相垂直的三角形称为“中垂三角形”，例如图1，图2，图3中，AF ，BE 是△ABC 的中线，AF ⊥BE ，垂足为P ，像△ABC 这样的三角形均称为“中垂三角形”，设BC ＝a ，AC ＝b ，AB ＝c.特例探索(1)如图1，当∠ABE ＝45°，c ＝22时，a ＝____25____，b ＝____25____. 如图2，当∠ABE ＝30°，c ＝4时，a ＝____213____，b ＝____27____. 归纳证明(2)请你观察(1)中的计算结果，猜想a 2，b 2，c 2三者之间的关系，用等式表示出来，并利用图3证明你发现的关系式．拓展应用(3)如图4，在□ABCD中，点E，F，G分别是AD，BC，CD的中点，BE⊥EG，AD＝25，AB＝3，求AF的长．解：(1)∵AF⊥BE，∠ABE＝45°，∴AP＝BP＝22AB＝2.∵AF，BE是△ABC的中线，∴EF∥AB，EF＝12AB＝2，∴∠PFE＝∠PEF＝45°，∴PE＝PF＝1.在Rt△FPB和Rt△PEA中，AE＝BF＝12＋22＝5，∴AC＝BC＝25，∴a＝b＝2 5.如答图1，连接EF.同理可得EF＝12×4＝2.∵EF∥AB，∴△PEF∽△PBA，∴PFAP＝PEPB＝EFAB＝12.在Rt△ABP中，AB＝4，∠ABP＝30°，∴AP＝2，PB＝23，∴PF＝1，PE＝ 3.在Rt△APE和Rt△BPF中，AE＝7，BF＝13，∴a＝213，b＝27.(2)猜想：a2＋b2＝5c2，证明如下：如答图2，连接EF.设∠ABP＝α，∴AP＝csinα，PB＝ccosα，由(1)同理可得PF＝12PA＝csinα2，PE＝12PB＝ccosα2， ∴AE 2＝AP 2＋PE 2＝c 2sin 2α＋c 2cos 2α4，BF 2＝PB 2＋PF 2＝c 2cos 2α＋c 2sin 2α4，∴(b 2)2＝c 2sin 2α＋c 2cos 2α4，(a 2)2＝c 2sin 2α4＋c 2cos 2α，∴a 24＋b 24＝c 2sin 2α4＋c 2cos 2α＋c 2sin 2α＋c 2cos 2α4， ∴a 2＋b 2＝5c 2.(3)如答图3，连接AC ，EF 交于点H ，AC 与BE 交于点Q ，设BE 与AF 的交点为P. ∵点E ，G 分别是AD ，CD 的中点，∴EG ∥AC. ∵BE ⊥EG ，∴BE ⊥AC.∵四边形ABCD 是平行四边形，∴AD ∥BC ，AD ＝BC ＝25，∴∠EAH ＝∠FCH. ∵E ，F 分别是AD ，BC 的中点， ∴AE ＝12AD ，BF ＝12BC ，∴AE ＝BF ＝CF ＝12AD ＝ 5.∵AE ∥BF ，∴四边形ABFE 是平行四边形， ∴EF ＝AB ＝3，AP ＝PF.在△AEH 和△CFH 中，⎩⎨⎧∠EAH ＝∠FCH ，∠AHE ＝∠FHC ，AE ＝CF ，∴△AEH ≌△CFH ，∴EH ＝FH ，∴EP ，AH 分别是△AFE 的中线，由(2)的结论得AF 2＋EF 2＝5AE 2，或连接F 与AB 的中点M ，证MF 垂直BP ，构造出“中垂三角形”，由AB ＝3，BC ＝12AD ＝5及(2)中的结论，直接可求AF.10．我们定义：如图1，在△ABC 中，把AB 绕点A 顺时针旋转α(0°＜α＜180°)得到AB′，把AC 绕点A 逆时针旋转β得到AC′，连接B′C′.当α＋β＝180°时，我们称△AB′C′是△ABC 的“旋补三角形”，△AB′C′边B′C′上的中线AD 叫做△ABC 的“旋补中线”，点A 叫做“旋补中心”．特例感知(1)在图2，图3中，△AB′C′是△ABC 的“旋补三角形”，AD 是△ABC 的“旋补中线”． ①如图2，当△ABC 为等边三角形时，AD 与BC 的数量关系为AD ＝12BC ；②如图3，当∠BAC ＝90°，BC ＝8时，则AD 长为4. 猜想论证(2)在图1中，当△ABC 为任意三角形时，猜想AD 与BC 的数量关系，并给予证明． 拓展应用(3)如图4，在四边形ABCD ，∠C ＝90°，∠D ＝150°，BC ＝12，CD ＝23，DA ＝6.在四边形内部是否存在点P ，使△PDC 是△PAB 的“旋补三角形”？若存在，给予证明，并求△PAB 的“旋补中线”长；若不存在，说明理由．图1 图2 图3 图4解：(1)①∵△ABC 是等边三角形，∴AB ＝BC ＝AC ＝AB′＝AC′.∵DB′＝DC′， ∴AD ⊥B′C′.∵∠BAC ＝60°，∠BAC ＋∠B′AC′＝180°， ∴∠B′AC′＝120°，∴∠B′＝∠C′＝30°， ∴AD ＝12AB′＝12BC.②∵∠BAC ＝90°，∠BAC ＋∠B′AC′＝180°，∴∠B′AC′＝∠BAC＝90°.∵AB＝AB′，AC＝AC′，∴△BAC≌△B′AC′，∴BC＝B′C′.∵B′D＝DC′，∴AD＝12B′C′＝12BC＝4.(2)结论：AD＝12 BC.证明如下：如答图1，延长AD到M，使得AD＝DM，连接B′M，C′M.∵B′D＝DC′，AD＝DM，∴四边形AC′MB′是平行四边形，∴AC′＝B′M＝AC.第10题答图1∵∠BAC＋∠B′AC′＝180°，∠B′AC′＋∠AB′M＝180°，∴∠BAC＝∠MB′A.∵AB＝AB′，∴△BAC≌△AB′M，∴BC＝AM，∴AD＝12 BC.(3)存在．理由：如答图2，延长AD交BC的延长线于M，作BE⊥AD于E，作线段BC的垂直平分线交BE于P，交BC于F，连接PA，PD，PC，作△PCD的中线PN，第10题答图2连接DF交PC于O.∵∠ADC＝150°，∴∠MDC＝30°.在Rt△DCM中，CD＝23，∠DCM＝90°，∠MDC＝30°，∴CM＝2，DM＝4，∠M＝60°.在Rt△BEM中，∠BEM＝90°，BM＝14，∠MBE＝30°，∴EM＝12BM＝7，∴DE＝EM－DM＝3.∵AD＝6，∴AE＝DE.∵BE⊥AD，∴PA＝PD，PB＝PC.在Rt△CDF中，CD＝23，CF＝6，∴tan∠CDF＝3，∴∠CDF＝60°＝∠CPF，易证△FCP≌△CFD，∴CD＝PF.∵CD∥PF.∴四边形CDPF是矩形，∴∠CDP＝90°，∴∠ADP＝∠ADC－∠CDP＝60°，∴△ADP是等边三角形，∴∠ADP＝60°.∵∠BPF＝∠CPF＝60°，∴∠BPC＝120°，∴∠APD＋∠BPC＝180°，∴△PDC是△PAB的“旋补三角形”．在Rt△PDN中，∠PDN＝90°，PD＝AD＝6，DN＝3，∴PN＝DN2＋PD2＝r(32＋62)＝39.考点4 多边形几何探究11．【图形定义】如图，将正n边形绕点A顺时针旋转60°后，发现旋转前后两图形有另一交点O，连接AO，我们称AO为“叠弦”；再将“叠弦”AO所在的直线绕点A逆时针旋转60°后，交旋转前的图形于点P，连接PO，我们称∠OAB为“叠弦角”，△AOP为“叠弦三角形”；【探究证明】(1)请在图1和图2中选择其中一个证明：“叠弦三角形”(△AOP)是等边三角形．(2)如图2，求证：∠OAB＝∠OAE′；【归纳猜想】(3)图1、图2中的“叠弦角”的度数分别为15°，24°；(4)图n中，“叠弦三角形”是等边三角形(填“是”或“不是”)；(5)图n中，“叠弦角”的度数为60°－180°n.(用含n的式子表示)解：(1)∵四边形ABCD是正方形，由旋转知，AD＝AD′，∠D＝∠D′＝90°，∠DAD′＝∠OAP＝60°，∴∠DAP＝∠D′AO，∴△APD≌△AOD′(ASA)，∴AP＝AO.∵∠OAP＝60°，∴△AOP是等边三角形；第11题答图(2)如答图，作AM⊥DE于M，作AN⊥CB于N.∵五边形ABCDE是正五边形，由旋转知，AE＝AE′，∠E＝∠E′＝108°，∠EAE′＝∠OAP＝60°，∴∠EAP＝∠E′AO.在Rt△AEM和Rt△ABN中，∠AEM＝∠ABN＝72°，AE＝AB，∴Rt△AEM≌Rt△ABN (AAS)，∴∠EAM ＝∠BAN ，AM ＝AN.在Rt △APM 和Rt △AON 中，AP ＝AO ，AM ＝AN ， ∴Rt △APM ≌Rt △AON (HL)， ∴∠PAM ＝∠OAN ，∴∠PAE ＝∠OAB, ∴∠OAE′＝∠OAB.(3)由(1)知，△APD ≌△AOD′， ∴∠DAP ＝∠D′AO.在Rt △AD′O 和Rt △ABO 中，⎩⎨⎧AD′＝AB ，AO ＝AO ，∴Rt △AD′O≌Rt △ABO(HL)， ∴∠D′AO＝∠BAO.由旋转得，∠DAD′＝60°.∵∠DAB ＝90°， ∴∠D′AB＝∠DAB －∠DAD′＝30°， ∴∠D′AO＝12∠D′AB＝15°，∵题图2的多边形是正五边形， ∴∠EAB ＝5－2×180°5＝108°，∴∠E′AB＝∠EAB －∠EAE′＝108°－60°＝48°， ∴同理可得，∠E′AO＝12∠E′AB＝24°.(4)是(5)同(3)的方法得，∠OAB ＝[(n －2)×180°÷n－60°]÷2＝60°－180°n.考点5 圆形几何探究12．如图，在半径为3 cm 的⊙O 中，A ，B ，C 三点在圆上，∠BAC ＝75°.点P 从点B 开始以π5cm/s 的速度在劣弧BC 上运动，且运动时间为t s ，∠AOB ＝90°，∠BOP ＝n°.(1)求n与t之间的函数关系式，并求t的取值范围；(2)试探究：当点P运动多少秒时，①在BP，PC，CA，AB四条线段中有两条相互平行？②以P，B，A，C四点中的三点为顶点的三角形是等腰三角形？解：(1)∵∠BOP＝n°，∴π5t＝3πn180，n＝12t.当n＝150时，150＝12t，t＝12.5.∴t的取值范围为0≤t≤12.5.(2)①∠BOP＝n°，n＝12t.如答图1，当BP∥AC时，t＝5.理由：∵∠PBA＝180°－75°＝105°，∠OBA＝45°，∴∠OBP＝60°.∵OB＝OP，∴∠BOP＝60°，∴60＝12t，t＝5.如答图2，当PC∥AB时，t＝10.理由：易得∠PBA＝∠BAC＝75°，∴∠PBO＝∠BPO＝30°，∴∠BOP＝120°，∴120＝12t，t＝10.综上所述，当点P的运动时间为5 s时，BP∥AC.当点P的运动时间为10 s时，PC∥AB.②在△ABP中，以AB为腰时(如答图3)，∠BPA＝∠BAP＝45°，∠BOP＝90°，∴t＝7.5. 以AB为底边时(如答图4)，∠BPA＝45°，∠BAP＝67.5°，∠BOP＝2×67.5°＝135°，∴t＝11.25.如答图5，在△APC中，易得∠AOC＝120°，∴∠APC＝60°，△APC是等边三角形．∴∠AOP＝120°，∴∠BOP＝30°，t＝2.5.如答图6，在△BPC中，∠BPC＝105°，只有BP＝PC这种情况．此时点P是弧BC的中心，∴∠BOP＝75°，t＝6.25.综上所述，当点P的运动时间为7.5 s或11.25 s时，△ABP为等腰三角形；当点P的运动时间为2.5 s时，△APC为等边三角形；当点P的运动时间为6.25 s时，△BPC为等腰三角形．。
中考针对性训练——几何探究压轴题(有答案详解)
针对性训练-----几何探究题1.如图1,在正方形ABCD 内有一点P 满足AP=AB ，PB=PC ，连结AC 、PD. （1）求证:△APB ≌△DPC ；（2）求证:∠PAC=21∠BAP ；（3）若将原题中的正方形ABCD 变为等腰梯形ABCD(如图2),AD ∥BC,且BA=AD=DC,形内一点P 仍满足AP=AB ，PB=PC,试问(2)中结论还成立吗若成立请给予证明;若不成立,请说明理由.ABDCP图PCDAB图2．如图1，在ABC △中，ACB ∠为锐角，点D 为射线BC 上一点，联结AD ，以AD 为一边且在AD 的右侧作正方形ADEF ． （1）如果AB AC =，90BAC =o∠，①当点D 在线段BC 上时（与点B 不重合），如图2，线段CF BD 、所在直线的位置关系为 __________ ，线段CF BD 、的数量关系为 ；②当点D 在线段BC 的延长线上时，如图3，①中的结论是否仍然成立，并说明理由；（2）如果AB AC ≠，BAC ∠是锐角，点D 在线段BC 上，当ACB ∠满足什么条件时，CF BC ⊥（点C F 、不重合），并说明理由．(3）若AC=42，BC=3，在（2）的条件下，设正方形ADEF 的边DE 与线段CF 相交于点P ，求线段CP 长的最大值。
图1E图2EC图3BDCE图2BAEBD图13.如图1，在正方形ABCD 中，E 是AB 上一点，F 是AD 延长线上一点，且DF ＝BE ． （1）求证：CE ＝CF ；（2）在图1中，若G 在AD 上，且∠GCE ＝45°，则GE ＝BE ＋GD 成立吗为什么 （3）运用（1）（2）解答中所积累的经验和知识， 完成下题：如图2，在直角梯形ABCD 中，AD ∥BC （BC ＞AD ），∠B ＝90°，AB ＝BC ＝12，E 是AB 上一点，且∠DCE ＝45°，BE ＝4，求DE 的长．4．如图，在Rt △ABC 中，∠A ＝90º，AB ＝6，AC ＝8，D ，E 分别是边AB ，AC 的中点，点P从点D 出发沿DE 方向运动，过点P 作PQ ⊥BC 于Q ，过点Q 作QR ∥BA 交AC 于R ，当点Q 与点C 重合时，点P 停止运动．设BQ ＝x ，QR ＝y ．（1）求点D 到BC 的距离DH 的长；（2）求y 关于x 的函数关系式（不要求写出自变量的取值范围）；（3）是否存在点P ，使△PQR 为等腰三角形若存在，请求出所有满足要求的x 的值；若不存在，请说明理由．A BCD ER PH QBHQABCD E R PHQABCDE M N图18ABCDEM N 图19图17N M EDCBA5．如图17，点A 是△ABC 和△ADE 的公共顶点，∠BAC ＋∠DAE ＝180°，AB ＝k ·AE ，AC ＝k ·AD ，点M 是DE 的中点，直线AM 交直线BC 于点N ．⑴探究∠ANB 与∠BAE 的关系，并加以证明．说明：如果你经过反复探索没解决问题，可以从下面①②中选取一个作为已知条件，再完成你的证明，选取①比选原题少得2分，选取②比选原题少得5分．① 如图18，k ＝1；②如图19，AB ＝AC ．⑵若△ADE 绕点A 旋转，其他条件不变，则在旋转的过程中⑴的结论是否发生变化如果没有发生变化，请写出一个可以推广的命题；如果有变化，请画出变化后的一个图形，并直接写出变化后∠ANB 与∠BAE 的关系．6.已知，CD 是经过BCA ∠顶点C 的一条直线，CA CB =．E F ，分别是直线CD 上两点，且BEC CFA α∠=∠=∠．（1）若直线CD 经过BCA ∠的内部，且E F ，在射线CD 上，请解决下面两个问题： ①如图9-1，若90BCA ∠=o，90α∠=o，则BE CF ；EFAF -（填“>”，“<”或“=”）；②如图9-2，若0180BCA <∠<oo，请添加一个关于α∠与BCA ∠关系的条件 ，使①中的两个结论仍然成立，并证明两个结论成立．（2）如图9-3，若直线CD 经过BCA ∠的外部，BCA α∠=∠，请提出EF BE AF ，，三条线段数量关系的合理猜想（不要求证明）．ABCE FDDABCE F ADFC EB图9-1图9-2图9-37．在等边ABC ∆的两边AB 、AC 所在直线上分别有两点M 、N ，D 为ABC V 外一点，且︒=∠60MDN ,︒=∠120BDC ,BD=DC. 探究：当M 、N 分别在直线AB 、AC 上移动时，BM 、NC 、MN 之间的数量关系及AMN ∆的周长Q 与等边ABC ∆的周长L 的关系．图1 图2 图3（I ）如图1，当点M 、N 边AB 、AC 上，且DM=DN 时，BM 、NC 、MN 之间的数量关系是 ； 此时=LQ； （II ）如图2，点M 、N 边AB 、AC 上，且当DM ≠DN 时，猜想（I ）问的两个结论还成立吗写出你的猜想并加以证明；（III ） 如图3，当M 、N 分别在边AB 、CA 的延长线上时，若AN=x ，则Q= （用x 、L 表示）．GDE FA参考答案1. (1)略（2）略（3）设︒=∠︒=∠y BAP x PAC ,，︒-=∠=∠)60(x DCA CAD 则 ︒=∠y PDCx y x X -+=+6060型得，由得x y 2=即BAP PAC ∠=∠212．（1）①垂直，相等；……………1分②当点D 在BC 的延长线上时①的结论仍成立．………………2分 由正方形ADEF 得 AD ＝AF ，∠DAF ＝90º．∵∠BAC ＝90º，∴∠DAF ＝∠BAC ， ∴∠DAB ＝∠FAC ， 又AB ＝AC ，∴△DAB ≌△FAC ， ∴CF ＝BD ， ∠ACF ＝∠ABD ． ∵∠BAC ＝90º， AB ＝AC ， ∴∠ABC ＝45º，∴∠ACF ＝45º，∴∠BCF ＝∠ACB +∠ACF ＝90º． 即 CF ⊥BD .…………5分（2）当∠ACB ＝45º时，CF ⊥BD （如图）． …………6分 理由：过点A 作AG ⊥AC 交CB 或CB 的延长线于点G ，则∠GAC ＝90º， ∵∠ACB ＝45°,∠AGC ＝90°—∠ACB ＝45°， ∴∠ACB ＝∠AGC ，∴AC ＝AG ，∵点D 在线段BC 上，∴点D 在线段GC 上，由（1）①可知CF ⊥BD . …7分BA G DE图1（3）如图：作AQBC 于Q ∵∠ACB=45° AC=42 ∴CQ=AQ=4 ∵∠PCD=∠ADP=90°∴∠ADQ+∠CDP=∠CDP+∠CPD=90° ∴△ADQ ∽△DPC ∴DQ PC =AQCD设CD 为x （0＜x ＜3）则DQ=CQ －CD=4－x 则x PC -4=4x∴PC=41(－x 2+4x)=－41(x －2)2+1≥1 当x=2时，PC 最长，此时PC=13.（1）证明：如图1，在正方形ABCD 中，∵BC ＝CD ，∠B ＝∠CDF ，BE ＝DF ， ∴△CBE ≌△CDF ． ∴CE ＝CF ．…….3分 （2）GE ＝BE ＋GD 成立．理由是： ∵△CBE ≌△CDF ， ∴∠BCE ＝∠DCF ． ∴∠BCE ＋∠ECD ＝∠DCF ＋∠ECD即∠ECF ＝∠BCD ＝90°， 又∠GCE ＝45°， ∴∠GCF ＝∠GCE ＝45°．∵CE ＝CF ，∠GCE ＝∠GCF ，GC ＝GC ， ∴△ECG ≌△FCG ． ……..4分∴GE ＝GF ∴GE ＝DF ＋GD ＝BE ＋GD ．…..5分（3）解：过C 作CG ⊥AD ，交AD 延长线于G ． 在直角梯形ABCD 中，∵AD ∥BC ∴∠A ＝∠B ＝90°．又∠CGA ＝90°，AB ＝BC ， ∴四边形ABCG 为正方形． ………6分∴AG ＝BC ＝12． 已知∠DCE ＝45°，根据（1）（2）可知，ED ＝BE ＋DG ．.. 7分设DE ＝x ，则DG ＝x －4， ∴AD ＝AG －DG=12－（x －4）=16－x ．在Rt △AED 中， ∵222AE AD DE +=，即()222816+-=x x ．解这个方程，得：x ＝10． ∴DE ＝10．BA EG4.（1）Q Rt A ∠=∠，6AB =，8AC =，10BC ∴=． Q 点D 为AB 中点，132BD AB ∴==．90DHB A ∠=∠=o Q ，B B ∠=∠． BHD BAC ∴△∽△， DH BD AC BC ∴=，3128105BD DH AC BC ∴==⨯=g ．---------------2分（2）QR AB Q ∥，90QRC A ∴∠=∠=o． C C ∠=∠Q ，RQC ABC ∴△∽△，RQ QC AB BC ∴=，10610y x -∴=，即y 关于x 的函数关系式为：365y x =-+． -------5分 （3）存在，分三种情况：①当PQ PR =时，过点P 作PM QR ⊥于M ，则QM RM =．1290∠+∠=o Q ，290C ∠+∠=o ，1C ∴∠=∠．84cos 1cos 105C ∴∠===，45QM QP ∴=， 1364251255x ⎛⎫-+ ⎪⎝⎭∴=，185x ∴=． --------8分 ②当PQ RQ =时，312655x -+=， 6x ∴=． -------10分 ③当PR QR =时，则R 为PQ 中垂线上的点，于是点R 为EC 的中点，11224CR CE AC ∴===．tan QR BA C CR CA ==Q ，366528x -+∴=，152x ∴=． -----13分综上所述，当x 为185或6或152时，PQR △为等腰三角形． -----14分5．（1）∠ANB +∠BAE =180º．……1分证明：（法一）如图1，延长AN 到F ，使MF =AM ，连接DF 、EF . ………………2分 ∵点M 是DE 的中点，∴DM =ME ， ∴四边形ADFE 是平行四边形 ，……………3分 ∴AD ∥EF ，AD =EF ， ∴∠DAE +∠AEF =180º， ∵∠BAC +∠DAE =180º， ∴∠BAC =∠AEF ，………4分 ∵AB =kAE ，AC =kAD ，A BCD ERPH QM2 1 BHQAB CDE R PH QM ADNEBCF图1∴AD AC AE AB =， ∴EFACAE AB =……6分 ∴△ABC ∽△EAF ∴∠B =∠EAF …………8分∵∠ANB +∠B +∠BAF =180º ∴∠ANB +∠EAF +∠BAF =180º 即∠ANB +∠BAE =180º，…………10分（法二）如图2，延长DA 到F ，使AF =AD ，连接EF .………2分∵∠BAC +∠DAE =180º，∠DAE +∠EAF =180º，∴∠BAC =∠EAF ，………………3分 ∵AB =kAE ，AC =kAD ，∴AD AC AE AB=， ∴AFAC AE AB =，………4分 ∴△ABC ∽△AEF ，………5分∴∠B =∠AEF ，………6分 ∵点M 是DE 的中点，∴DM =ME ，又∵AF =AD ， ∴AM 是△DEF 的中位线， ∴AM ∥EF ，……7分 ∴∠NAE =∠AEF ，∴∠B =∠NAE ，……8分 ∵∠ANB +∠B +∠BAN =180º， ∴∠ANB +∠NAE +∠BAN =180º， 即∠ANB +∠BAE =180º．………10分(2)变化．如图3（仅供参考），∠ANB =∠BAE ．……12分 选取（ⅰ），如图4.证明：延长AM 到F ，使MF =AM ，连接DF 、EF . ∵点M 是DE 的中点，∴DM =ME∴四边形ADFE 是平行四边形，…………4分 ∴AD ∥FE ，AD =EF ， ∴∠DAE +∠AEF =180º， ∵∠BAC +∠DAE =180º， ∴∠BAC =∠DAE ， ………6分 ∵AB =kAE ，AC =kAD ，1=k ， ∴AB =AE ，AC =AD ，∴AC =EF ，……7分 ∴△ABC ≌△EAF ， ∴∠B =∠EAF ， …8分 ∵∠ANB +∠B +∠BAF =180º， ∴∠ANB +∠EAF +∠BAF =180º， 即∠ANB +∠BAE =180º．……10分M ADNEBCFK H图2F图4图3ABCDEM N选取（ⅱ），如图5. 证明：∵AB =AC ，∴∠B =21（180º-∠BAC ），…………3分 ∵∠BAC +∠DAE =180º， ∴∠DAE =180º-∠BAC ， ∴∠B =21∠DAE ， ∵AB =kAE ，AC =kAD ， ∴AE =AD ， ∵AM 是△ADE 的中线，AB =AC ， ∴∠EAM =21∠DAE ， ∴∠B =∠EAM ，………4分 ∵∠ANB +∠B +∠BAM =180º， ∴∠ANB +∠EAM +∠BAM =180º， 即∠ANB +∠BAE =180º．…5分6.（1）①=；=； 2分 ②所填的条件是：180BCA α∠+∠=o． 4分证明：在BCE △中，180180CBE BCE BEC α∠+∠=-∠=-∠oo ．180BCA α∠=-∠o Q ，CBE BCE BCA ∴∠+∠=∠．又ACF BCE BCA ∠+∠=∠Q ，CBE ACF ∴∠=∠．又BC CA =Q ，BEC CFA ∠=∠， ()BCE CAF AAS ∴△≌△．BE CF ∴=，CE AF =． 又EF CF CE =-Q ，EF BE AF ∴=-． 7分（2）EF BE AF =+．7.（I ）如图1， BM 、NC 、MN 之间的数量关系 BM+NC=MN ．此时32=L Q ． （II ）猜想：结论仍然成立．证明：如图，延长AC 至E ，使CE=BM ，连接DE ．ΘCD BD =,且ο120=∠BDC ．∴ο30=∠=∠DCB DBC ．ABC DMN 图5E又ABC ∆是等边三角形，∴90MBD NCD ∠=∠=o．在MBD ∆与ECD ∆中：⎪⎩⎪⎨⎧=∠=∠=DC BD ECD MBD CEBM ∴≅∆MBD ECD ∆(SAS) ． ∴DM=DE, CDE BDM ∠=∠∴ο60=∠-∠=∠MDN BDC EDN 在MDN ∆与EDN ∆中：⎪⎩⎪⎨⎧=∠=∠=DN DN EDN MDN DE DM ∴≅∆MDN EDN ∆(SAS) ∴MN=NE=NC+BM AMN ∆的周长Q=AM+AN+MN=AB+AC =2AB而等边ABC ∆的周长L=3AB ∴3232==AB AB L Q . （III ）如图3，当M 、N 分别在AB 、CA 的延长线上时，若AN=x ，则Q=2x +L 32（用x 、L 表示）．8.如图24－1，正方形ABCD 和正方形QMNP ， M 是正方形ABCD 的对称中心，MN 交AB 于F ，QM 交AD 于E ．（1）猜想：ME 与MF 的数量关系（2）如图24－2，若将原题中的“正方形”改为“菱形”，且∠M =∠B ，其它条件不变，探索线段ME 与线段MF 的数量关系，并加以证明．（3）如图24－3，若将原题中的“正方形”改为“矩形”，且AB:BC=1:2，其它条件不变，QP N FE D CBMA24--3DEQ ANF B MCD 24--2EQPNAFMBCF EQMDNP B A C探索线段ME 与线段MF 的数量关系，并说明理由．（4）如图24－4，若将原题中的“正方形”改为平行四边形，且∠M =∠B ，AB:BC = m ，其它条件不变，求出ME ：MF 的值。
中考数学总复习课件： 二轮专题复习 与几何图形有关的探究题 (共38张PPT)
(3)当△ADE 是等腰三角形时，求 AE 的长． 【思路引导】分三种情况进行讨论： ①当 AD＝DE 时， 如图甲， 由(1)可知， 此时△ABD≌△DCE， 则 AB＝CD； 1 ②当 AE＝ED 时，如图乙，易得 ED＝2EC； ③当 AD＝AE 时，∠AED＝∠EDA＝30°，∠EAD＝120°， 此时点 D 与点 B 重合，不符合题意，此情况不存在．
(2)设BD＝x，AE＝y，求y关于x的函数解析式，并写出自变量x的取值范围；
【思路引导】如图，作高AF，根据含30 °角的直角三角形的性质求AF的长 ，根据勾股定理求BF的长，则可得BC的长，根据(1)中的相似三角形列比例式
可得函数解析式，并确定自变量的取值范围．
解：如图，∵AB＝AC＝2，∠BAC＝120°，过点 A 作 AF⊥BC 于点 F， 1 ∴∠AFB＝90°.∵AB＝2，∠ABF＝30°，∴AF＝2AB＝1.∴BF＝ 3. ∴BC＝2BF＝2 3，则 DC＝2 3－x，EC＝2－y.∵△ABD∽△DCE， AB DC 2 2 3－x 12 ∴BD＝ CE .∴x＝ ，化简，得 y＝2x － 3x＋2(0＜x＜2 3)． 2－y
解：当 AD＝DE 时，如图甲，由(1)可知，此时△ABD≌△DCE， 12 则 AB＝CD，即 2＝2 3－x，x＝2 3－2，代入 y＝2x － 3x＋2， 解得 y＝4－2 3，即 AE＝4－2 3； 当 AE＝ED 时，如图乙，则∠EAD＝∠EDA＝30°， ∠AED＝120°，∴∠DEC＝60°，∠EDC＝90°，
专题十 与几何图形有关的探究题
数学
本题型基本上是每年中考的必考题，且多以几何压轴题的形式出现，常把圆、 四边形与三角函数的知识结合起来考查，综合程度较高，所以难度较大．预 计2018年仍会考查与几何图形有关的探究题．
中考复习-几何探究题(含答案)
几何探究题1题（1）如图1，图2，图3，在ABC △中，分别以AB AC ，为边，向ABC △外作正三角形，正四边形，正五边形,BE CD ，相交于点O ．①如图1,求证：ABE ADC △≌△；②探究：如图1，BOC ∠= ；如图2,BOC ∠=; 如图3，BOC ∠= ．（2)如图4,已知：AB AD ，是以AB 为边向ABC △外所作正n 边形的一组邻边；AC AE ，是以AC 为边向ABC △外所作正n 边形的一组邻边．BE CD ，的延长相交于点O ．①猜想：如图4，BOC ∠= （用含n 的式子表示）；②根据图4证明你的猜想．2题.请阅读下列材料: 问题：如图1，在菱形ABCD 和菱形BEFG 中,点A B E ，，在同一条直线上，P 是线段()()a a b a b +-的中点，连结PG PC ，．若60ABC BEF ∠=∠=，探究PG 与PC 的位置关系及PGPC的值． 小聪同学的思路是:延长GP 交DC 于点H ,构造全等三角形，经过推理使问题得到解决．问题：(1）写出上面问题中线段PG 与PC 的位置关系及PGPC的值； （2）将图1中的菱形BEFG 绕点B 顺时针旋转，使菱形BEFG 的对角线BF 恰好与菱形ABCD 的边AB 在同一条直线上,原问题中的其他条件不变（如图2）．你在（1）中得到的两个结论是否发生变化?写出你的猜想并加以证明．（3）若图1中2(090)ABC BEF ∠=∠=<<αα，将菱形BEFG 绕点B 顺时针旋转任意角度，原问题中的其他条件不变，请你直接写出PGPC的值（用含α的式子表示）． D A BE F C P G 图1 D C G PA B F图23题。
如图，等腰梯形ABCD 中，AB =4,CD =9，∠C =60°，动点P 从点C 出发沿CD 方向向点D 运动，动点Q 同时以相同速度从点D 出发沿DA 方向向终点A 运动,其中一个动点到达端点时，另一个动点也随之停止运动. （1)求AD 的长；（2）设CP =x ，问当x 为何值时△PD Q 的面积达到最大，并求出最大值；（3）探究:在BC 边上是否存在点M 使得四边形PD Q M 是菱形?若存在，请找出点M ，并求出BM 的长；不存在,请说明理由.4题已知矩形ABCD 和点P ，当点P 在BC 上任一位置（如图（1）所示）时，易证得结论：2222PA PC PB PD +=+，请你探究：当点P 分别在图（2)、图（3）中的位置时，2222PA PB PC PD 、、和又有怎样的数量关系？请你写出对上述两种情况的探究结论，并利用图（2）证明你的结论．答:对图（2)的探究结论为____________________________________． 对图(3）的探究结论为_____________________________________． 证明：如图（2)（第25题图） （备用图）5题如图,以矩形OABC的顶点O为原点，OA所在的直线为x轴，OC所在的直线为y轴,建立平面直角坐标系．已知OA＝3,OC＝2，点E是AB的中点，在OA上取一点D，将△BDA沿BD翻折，使点A落在BC边上的点F处．（1）直接写出点E、F的坐标;（2)设顶点为F的抛物线交y轴正半轴．．．于点P，且以点E、F、P为顶点的三角形是等腰三角形,求该抛物线的解析式；（3）在x轴、y轴上是否分别存在点M、N，使得四边形MNFE的周长最小?如果存在,求出周长的最小值;如果不存在,请说明理由．6题如图1，四边形ABCD是正方形，G是CD边上的一个动点(点G与C、D不重合），以CG为一边在正方形ABCD外作正方形CEFG，连结BG，DE．我们探究下列图中线段BG、线段DE的长度关系及所在直线的位置关系：(1）①猜想如图1中线段BG、线段DE的长度关系及所在直线的位置关系；②将图1中的正方形CEFG绕着点C按顺时针（或逆时针)方向旋转任意角度α，得到如图2、如图3情形．请你通过观察、测量等方法判断①中得到的结论是否仍然成立,并选取图2证明你的判断．(2）将原题中正方形改为矩形（如图4—6），且AB=a,BC=b，CE=ka，CG=kb（a≠b，k>0)，第（1)题①中得到的结论哪些成立，哪些不成立？若成立，以图5为例简要说明理由．（3）在第（2)题图5中,连结DG、BE，且a=3，b=2，k=12,求22BE DG+的值．7题正方形ABCD中,点O是对角线AC的中点，P是对角线AC上一动点，过点P作PF⊥CD于点F。
中考数学专题巩固：几何图形探究题(含解析)
几何图形探究题1．(1)问题发现如图①，在Rt △ABC 中，∠BAC ＝90°，AB ＝2，AC ＝4，点D 为BC 的中点，过点D 作射线DE ⊥DF ，分别交AB ，AC 于点E ，F ，当DE ⊥AB ，DF ⊥AC 时，DEDF ＝________； (2)类比探究若∠EDF 绕着点D 旋转到图②的位置，(1)中其他条件不变，DEDF ＝________；若改变点D 的位置，当CD BD ＝a b 时，求DEDF 的值，请就图③的情形写出解答过程；图① 图②第1题图(3)问题解决如图③，AB ＝2，AC ＝4，连接EF ，当CD ＝____时，△DEF 为等腰直角三角形；当CD ＝____时，△DEF 与△ABC 相似．图③ 第1题图解：(1)2；【解法提示】∵DE ⊥AB ，DF ⊥AC ，∠BAC ＝90°，∴DF ∥AE ，DE ∥AC ，∴△BED∽△BAC，△CDF∽△CBA，∴DEAC＝BDBC，DFAB＝CDBC，∵点D为BC的中点，AB＝2，AC＝4，∴DE4＝12，DF2＝12，∴DE＝2，DF＝1，∴DEDF＝2.(2)2；【解法提示】如解图①，过点D作DM⊥AB于点M，作DN⊥AC于点N，∵∠A＝∠DMA＝∠DNA＝90°，∴∠MDN＝90°，∵∠MDE＋∠EDN＝∠NDF ＋∠EDN，∴∠MDE＝∠NDF，又∵∠DME＝∠DNF，∴△DEM∽△DFN，∴DEDF＝DMDN，由(1)可得DMDN＝2，∴DEDF＝2.第1题解图①如解图②，过点D作DG⊥AB于点G，作DH⊥AC于点H，∴∠GDH＝90°，∴∠EDG＋∠GDF＝∠FDH＋∠GDF＝90°，∴∠EDG＝∠FDH，又∵∠DGE＝∠DHF＝90°，第1题解图②∴△DGE∽△DHF，∴DEDF＝DGDH，∵∠BAC＝90°，∴DG ∥AC ，DH ∥AB ，∴△BDG ∽△BCA ，△CDH ∽△CBA ， ∴DG AC ＝BD BC ，CD BC ＝DH AB ， ∵CD BD ＝a b ，∴BD BC ＝BD BD ＋CD ＝b a ＋b ，CD BC ＝CD BD ＋CD ＝a a ＋b ，∴DG 4＝b a ＋b ，DH 2＝aa ＋b ，∴DE DF ＝DG DH ＝2ba ； (3)453；855或 5.【解法提示】∵∠EDF ＝90°，∴当△DEF 为等腰直角三角形时，DE ＝DF ，由(2)中的结论可知，DE DF ＝2ba ＝1，∴a ＝2b ，∴BC ＝3b ，在Rt △ABC 中，∵AB ＝2，AC ＝4，由勾股定理得BC ＝22＋42＝25，∴CD ＝23BC ＝453.∵∠EDF ＝∠A ＝90°，∴△DEF 与△ABC 相似有两种情况：①当△DEF ∽△ABC 时，DE AB ＝DF AC ，即DE DF ＝AB AC ＝12，∴2b a ＝12，∴a ＝4b ，∴CD ＝45BC ＝855；②当△DEF ∽△ACB 时，DE AC ＝DF AB ，即DE DF ＝AC AB ＝2，∴2b a ＝2，∴a ＝b ，∴CD ＝12BC＝ 5.综上所述，当CD ＝855或5时，△DEF 与△ABC 相似．2．在数学兴趣小组活动中，小亮进行数学探究活动．△ABC 是边长为2的等边三角形，E 是AC 上一点，小亮以BE 为边向BE 的右侧作等边三角形BEF ，连接CF .(1)如图①，当点E 在线段AC 上时，EF 、BC 相交于点D ，小亮发现有两个三角形全等，请你找出来，并证明；(2)当点E 在线段AC 上运动时，点F 也随着运动，若四边形ABFC 的面积为734，求AE的长；(3)如图②，当点E在AC的延长线上运动时，CF、BE相交于点D，请你探求△ECD的面积S1与△DBF的面积S2之间的数量关系，并说明理由；(4)如图②，当△ECD的面积S1＝36时，求AE的长．图①图②第2题图解：(1)△ABE≌△CBF.理由如下：∵△ABC与△EBF都是等边三角形，∴AB＝CB，BE＝BF，∠ABC＝∠EBF＝60°，∴∠CBF＝∠ABE＝60°－∠CBE，∴△ABE≌△CBF(SAS)；(2)由(1)知点E在运动过程中始终有△ABE≌△CBF.∵S四边形BECF＝S△BCF＋S△BCE，∴S四边形BECF＝S△ABC，∵△ABC是边长为2的等边三角形，∴S△ABC＝34×22＝3，∴S四边形BECF＝3，又∵S四边形ABFC ＝734，∴S △ABE ＝S 四边形ABFC －S 四边形BECF ＝334， 在△ABE 中，∵∠A ＝60°，∴AB 边上的高为AE ·sin60°，则S △ABE ＝12AB ·AE ·sin60°＝12×2×32AE ＝334，∴AE ＝32； (3)S 2－S 1＝ 3.理由如下：∵△ABC 与△EBF 都是等边三角形，∴AB ＝CB ，BE ＝BF ，∠ABC ＝∠EBF ＝60°，∴∠CBF ＝∠ABE ＝60°＋∠CBE ，∴△ABE ≌△CBF ， ∴S △ABE ＝S △CBF ，∴S △FDB ＝S △ECD ＋S △ABC ， ∴S △FDB －S △ECD ＝S △ABC ＝3，即S 2－S 1＝3； (4)由(3)知S 2－S 1＝3，即S △FDB －S △ECD ＝3， 由S △ECD ＝36得S △BDF ＝736，∵△ABE ≌△CBF ， ∴AE ＝CF ，∠BAE ＝∠BCF ＝60°，又∵∠BAE ＝∠ABC ＝60°，得∠ABC ＝∠BCF ，∴CF ∥AB ，则在△BDF 中，DF 边上的高是AC ·sin60°＝3，∴12DF ×3＝736，解得DF ＝73，设CE ＝x ，则2＋x ＝CD ＋DF ＝CD ＋73， ∴CD ＝x －13，在△ABE 中，由CD ∥AB 得，CD AB ＝CE AE ，即x －132＝xx ＋2，化简得3x2－x－2＝0，∴x＝1或x＝－23(舍)，即CE＝1，∴AE＝3.3．如图①，在菱形ABCD中，∠ABC＝60°，若点E在AB的延长线上，EF∥AD，EF＝BE，点P是DE的中点，连接FP并延长交AD于点G，连接FB.(1)过D点作DH⊥AB，垂足为点H，若DH＝23，BE＝14AB，求DG的长；(2)连接CP，求证：CP⊥FP；(3)如图②，若点E在CB的延长线上运动，点F在AB的延长线上运动，且BE＝BF，连接DE，点P为DE的中点，连接FP，CP，那么第(2)问的结论成立吗？若成立，求出PFCP的值；若不成立，请说明理由．图①图②第3题图(1)解：∵四边形ABCD为菱形，∠ABC＝60°，∴DA∥BC，CD＝CB，∠CDG＝∠CBA＝60°，∴∠DAH＝∠ABC＝60°，∵DH⊥AB，∴∠DHA＝90°，在Rt△ADH中，sin∠DAH＝DH AD，∴AD＝DHsin∠DAH＝2332＝4，又∵AB＝AD，∴BE＝14AB＝14×4＝1，∵EF∥AD，∴∠PDG＝∠PEF，∵P为DE的中点，∴PD＝PE，又∵∠DPG＝∠EPF，∴△PDG≌△PEF(ASA)，∴DG＝EF，又∵EF＝BE，∴DG＝EF＝1；(2)证明：如解图①，连接CG，CF，第3题解图①由(1)知△PDG≌△PEF，∴PG＝PF，∵EF∥AD，AD∥BC，∴EF ∥BC ，∴∠FEB ＝∠CBA ＝60°， ∵EF ＝BE ，∴△BEF 为等边三角形， ∴BF ＝EF ＝BE ，∠EBF ＝60°， ∵DG ＝EF ，∠ABC ＝60°，∴BF ＝DG ，∠CBF ＝∠ABC ＝∠CDG ＝60°， 在△CDG 与△CBF 中，⎩⎨⎧CD ＝CB∠CDG ＝∠CBF DG ＝BF， ∴△CDG ≌△CBF (SAS)， ∴CG ＝CF ， ∵PG ＝PF ， ∴CP ⊥FP ；(3)解：CP ⊥FP 仍成立．如解图②，过D 作EF 的平行线，交FP 的延长线于点G ，连接CG ，CF ，第3题解图②易证△PEF ≌△PDG ，∴DG ＝EF ＝BF ， ∵DG ∥EF ， ∴∠GDP ＝∠FEP ， ∵DA ∥BC ， ∴∠ADP ＝∠PEC ，∴∠GDP －∠ADP ＝∠FEP －∠PEC ， ∴∠GDA ＝∠BEF ＝60°，∴∠CDG ＝∠ADC ＋∠GDA ＝120°， ∵∠CBF ＝180°－∠ABC ＝120°， 在△CDG 和△CBF 中，⎩⎨⎧CD ＝CB∠CDG ＝∠CBF ，DG ＝BF∴△CDG ≌△CBF (SAS)， ∴CG ＝CF ，∠DCG ＝∠FCB ， ∵PG ＝PF ，∴CP ⊥PF ，∠GCP ＝∠FCP ， ∵∠DCB ＝180°－∠ABC ＝120°， ∴∠DCG ＋∠GCE ＝120°， ∴∠FCE ＋∠GCE ＝120°， 即∠GCF ＝120°，∴∠FCP＝12∠GCF＝60°，在Rt△CPF中，tan∠FCP＝tan60°＝PFCP＝ 3.∴PFCP＝ 3.4．已知点O是△ABC内任意一点，连接OA并延长到点E，使得AE＝OA，以OB，OC为邻边作▱OBFC，连接OF，与BC交于点H，再连接EF.(1)如图①，若△ABC为等边三角形，求证：①EF⊥BC；②EF＝3BC；(2)如图②，若△ABC为等腰直角三角形(BC为斜边)，猜想(1)中的两个结论是否成立？若成立，直接写出结论即可；若不成立，请说明理由；(3)如图③，若△ABC是等腰三角形，且AB＝AC＝kBC，求EF与BC之间的数量关系．图①图②图③第4题图(1)证明：①如解图①，连接AH，∵四边形OBFC 是平行四边形， ∴BH ＝HC ＝12BC ，OH ＝HF ， ∵△ABC 是等边三角形， ∴AB ＝BC ，AH ⊥BC ， 又∵OA ＝AE ，OH ＝HF ， ∴AH 是△OEF 的中位线， ∴AH ＝12EF ，AH ∥EF ， ∴EF ⊥BC ；②由①得AH ⊥BC ，AH ＝12EF ， ∵在Rt △ABH 中，AH 2＝AB 2－BH 2， ∴AH ＝BC 2－（12BC ）2＝32BC ，∴32BC ＝12EF ， ∴EF ＝3BC ；(2)解：EF ⊥BC 仍然成立，EF ＝BC ； 【解法提示】如解图②，连接AH ，∵四边形OBFC是平行四边形，∴BH＝HC＝12BC，OH＝HF，又∵△ABC是以BC为斜边的等腰直角三角形，∴AH⊥BC，AH＝BH＝12BC，又∵OA＝AE，OH＝HF，∴AH是△OEF的中位线，∴AH＝12EF，AH∥EF，∴EF⊥BC，EF＝2AH＝BC，∴(1)中的结论①EF⊥BC仍成立，但结论②不成立，EF 与BC的关系应为EF＝BC；(3)解：如解图③，连接AH，第4题解图③∵四边形OBFC是平行四边形，∴BH＝HC＝12BC，OH＝HF，又∵△ABC是等腰三角形，AB＝kBC，∴AH ⊥BC ，在Rt △ABH 中，AH 2＝AB 2－BH 2＝(kBC )2－(12BC )2＝(k 2－14)BC 2， ∴AH ＝4k 2－12BC ，又∵OA ＝AE ，OH ＝HF ， ∴AH 是△OEF 的中位线， ∴AH ＝12EF ， ∴4k 2－12BC ＝12EF ， ∴EF ＝4k 2－1 BC .5．如图①，在△ABC 中，∠ABC ＝45°，AH ⊥BC 于点H ，点D 在AH 上，且DH ＝CH ，连接BD . (1)求证：BD ＝AC ；(2)将△BHD 绕点H 旋转，得到△EHF (点B ，D 分别与点E ，F 对应)，连接AE .①如图②，当点F 落在AC 上(F 不与C 重合)时，若BC ＝4，tan C ＝3，求AE 的长；②如图③，△EHF 是由△BHD 绕点H 逆时针旋转30°得到的，设射线CF 与AE 相交于点G ，连接GH .试探究线段GH 与EF 之间满足的等量关系，并说明理由．图① 图② 图③第5题图(1)证明：∵∠ABC ＝45°，AH ⊥BC ， ∴△ABH 是等腰直角三角形， ∴BH ＝AH ，在△BHD 和△AHC 中，⎩⎨⎧BH ＝AH∠BHD ＝∠AHC DH ＝CH， ∴△BHD ≌△AHC (SAS)， ∴BD ＝AC ；(2)解：①如解图①，过点H 作HM ⊥AE 交AE 于点M ，第5题解图①在Rt △AHC 中，tan C ＝3， ∴AHHC ＝3， ∴BH ＝AH ＝3CH ， 又∵BC ＝4，∴BC ＝BH ＋HC ＝4CH ＝4，∴CH＝1，BH＝3，由旋转的性质可以得到，HE＝BH＝3，HF＝DH＝HC＝1，∠EHF＝∠AHB＝∠AHC＝90°，∴∠EHA＝∠FHC，∴∠EAH＝∠C＝∠AEH，∴AM＝EM，∴tan∠EAH＝tan C＝3，设AM＝x，则HM＝AM·tan∠EAH＝3x，在Rt△AHM中，由AH2＝AM2＋HM2，得32＝x2＋(3x)2，∴x＝310 10，∴AE＝2AM＝2x＝310 5；②EF＝2GH.理由：设AH交CG于点N，如解图②，由旋转的性质可得，HE＝HB＝HA，HF＝HD＝HC，∵旋转角度为30°，∴∠FHD＝∠BHE＝30°，∴∠EHA＝∠FHC＝120°，第5题解图②∴∠FCH＝∠GAH＝30°，又∵∠ANG＝∠HNC，∴△ANG∽△CNH，∴∠AGN＝∠CHN＝90°，GN AN＝HN CN，又∵∠GNH＝∠ANC，∴△GNH∽△ANC，∴GHAC＝GNAN＝12，∵由(1)可知，△BHD≌△AHC. ∴△EHF≌△AHC，∴EF＝AC，∴EFGH＝ACGH＝2，∴EF＝2GH.6．我们定义：如图①，在△ABC中，把AB绕点A顺时针旋转α(0°＜α＜180°)得到AB′，把AC绕点A逆时针旋转β得到AC′，连接B′C′.当α＋β＝180°时，我们称△AB′C′是△ABC的“旋补三角形”，△AB′C′边B′C′上的中线AD叫做△ABC的“旋补中线”，点A叫做“旋补中心”．特例感知(1)在图②，图③中，△AB′C′是△ABC的“旋补三角形”，AD是△ABC的“旋补中线”．①如图②，当△ABC为等边三角形时，AD与BC的数量关系为AD＝____BC；②如图③，当∠BAC＝90°，BC＝8时，则AD长为________；猜想论证(2)在图①中，当△ABC为任意三角形时，猜想AD与BC的数量关系，并给予证明；拓展应用(3)如图④，在四边形ABCD中，∠C＝90°，∠D＝150°，BC＝12，CD＝23，DA＝6.在四边形内部是否存在点P，使△PDC是△P AB的“旋补三角形”？若存在，给予证明，并求△P AB的“旋补中线”长；若不存在，说明理由．图①图②图③图④第6题图解：(1)①12；② 4；【解法提示】①由旋转可得到AB＝AB′＝AC＝AC′，∵∠BAC＝60°，∴∠B′AC′＝120°，∴∠AB′C′＝30°，又∵AD为B′C′上的中线，∴AD⊥B′C′，∴AD＝12AB′＝12AB＝12BC；②由“旋补三角形”定义可得：∠B′AC′＝90°，易证△AB′C′≌△ABC，∴B′C′＝BC，∵点D为B′C′的中点，∴AD＝12BC＝4.(2)AD＝12BC.证明：如解图①，延长AD至E，使DE＝AD.第6题解图①∵AD是△ABC的“旋补中线”，∴B′D＝C′D.∴四边形AB′EC′是平行四边形，∴EC′∥B′A，EC′＝B′A，∴∠AC′E＋∠B′AC′＝180°.由定义可知∠B′AC′＋∠BAC＝180°，B′A＝BA，AC＝AC′，∴∠AC′E＝∠BAC，EC′＝BA，∴△AC′E≌△CAB，∴AE＝BC，∵AD＝12AE，∴AD＝12BC；(3)存在；证明：如解图②，作PE垂直平分BC，且使PE＝CD，连接P A，PB，PC，PD，可得PC＝PB，∵∠DCE＝∠CEP＝90°，∴PE∥CD；∴四边形PECD为矩形；∴PE＝CD＝23，PD＝CE＝AD＝6，∠PDC＝90°；∴tan∠PCE＝PECE＝33，∴∠PCE＝∠PBE＝30°，即∠BPC＝120°，又由∠ADC＝150°，可得∠ADP＝60°，∴△P AD为等边三角形，第6题解图②∴PD＝P A，∠APD＝60°.∵∠BPC＋∠DP A＝120°＋60°＝180°，∴△PCD是△P AB的“旋补三角形”；取CD的中点M，连接PM，可得DM ＝3，PD ＝6.由勾股定理得PM ＝DM 2＋PD 2＝（3）2＋62＝39， ∴△P AB 的“旋补中线”长为39.7．如图，在△ABC 中，矩形EFGH 的一边EF 在AB 上，顶点G 、H 分别在BC 、AC 上，CD 是边AB 上的高，CD 交GH 于点I ，若CI ＝4，HI ＝3，AD ＝92，矩形DFGI 恰好为正方形．(1)求正方形DFGI 的边长；(2)如图，延长AB 至P ，使得AC ＝CP ，将矩形EFGH 沿BP 的方向向右平移，当点G 刚好落在CP 上时，试判断移动后的矩形与△CBP 重叠部分的形状是三角形还是四边形，为什么？第7题图解：(1)∵四边形EFGH 为矩形， ∴HG ∥EF ，∴HI AD ＝CI CD ，即392＝4CD ，解得CD ＝6，∴ID ＝CD －CI ＝2，即正方形DFGI 的边长为2； (2)移动后的矩形与△CBP 重叠部分的形状是三角形． 理由如下：如解图，设在移动过程中，当点G 刚好落在CP 上时，矩形EFGH 移动到矩形E ′F ′G ′H ′，∵AC ＝PC ，CD ⊥AB ， ∴∠A ＝∠P ，AD ＝PD ， 在△AEH 和△PF ′G ′中，∵⎩⎨⎧∠A ＝∠P∠AEH ＝∠PF ′G ′EH ＝F ′G ′，第7题解图∴△AEH ≌△PF ′G ′(AAS)， ∴AE ＝PF ′， ∵AD ＝PD ，∴AD －AE ＝PD －PF ′， 即DE ＝DF ′＝3， ∵HG ∥AB ， ∴△CHG ∽△CAB ， ∴HG AB ＝CI CD ，即3＋2AB ＝44＋2，解得AB ＝152， ∴DB ＝AB －AD ＝3，∴DB＝DF′，即点F′与点B重合，也就是说在移动过程中，当点G刚好落在CP上时，矩形EFGH的F点刚好运动到点B，∴移动后的矩形与△CBP重叠部分的形状是三角形．8．如图①，在▱ABCD中，DH⊥AB于点H，CD的垂直平分线交CD于点E，交AB于点F，AB＝6，DH＝4，BF∶F A＝1∶5.(1)如图②，作FG⊥AD于点G，交DH于点M，将△DGM沿DC方向平移，得到△CG′M′，连接M′B.①求四边形BHMM′的面积；②直线EF上有一动点N，求△DNM周长的最小值．(2)如图③，延长CB交EF于点Q，过点Q作QK∥AB，过CD边上的动点P作PK∥EF，并与QK交于点K，将△PKQ沿直线PQ翻折，使点K的对应点K′恰好落在直线AB上，求线段CP的长．图①图②图③备用图第8题图解：(1)①在▱ABCD中，AB＝6，∵直线EF垂直平分CD，∴EF⊥CD，∵CD∥AB，∴EF⊥BH，又∵DH⊥AB，∴四边形EFHD为矩形，∴DE＝FH＝3，又∵BF∶F A＝1∶5，∴AH＝2，第8题解图①∵Rt△AHD∽Rt△MHF，∴HMFH＝AHDH，即HM3＝24，∴HM＝1.5，根据平移的性质，MM'＝CD＝6，如解图①，连接BM，∴四边形BHMM′的面积为12×(6＋4)×1.5＝7.5；②如解图②，连接CM交直线EF于点N，连接DN，第8题解图②∵直线EF垂直平分CD，∴CN＝DN，∵MH＝1.5，∴DM＝2.5，在Rt△CDM中，MC2＝DC2＋DM2，∴MC2＝62＋(2.5)2，解得MC＝6.5，∴MN＋DN＝MN＋CN＝MC，∴△DNM周长的最小值为DM＋MC＝9；(2)∵BF∥CE，∴QFQF＋4＝BFCE＝13，∴QF＝2，∴PK＝PK′＝6，如解图③，过点K′作E′F′∥EF，分别交CD于点E'，交QK于点F'，第8题解图③当点P在线段CE上时，在Rt△PK′E′中，PE′2＝PK′2－E′K′2，∴PE′＝25，∵Rt△PE′K′∽Rt△K′F′Q，∴PE′K′F′＝E′K′QF′，即252＝4QF′，解得QF′＝45 5，第8题解图④∴PE＝PE′－EE′＝25－455＝655，∴CP＝15－655，同理可得，如解图④，当点P在线段DE上时，CP′＝15＋655，综上所述，CP的长为15－655或15＋655.9．问题发现(1)如图①，在△OAB和△OCD中，OA＝OB，OC＝OD，∠AOB＝∠COD ＝40°，连接AC，BD交于点M.填空：①ACBD的值为________；②∠AMB的度数为________．类比探究(2)如图②，在△OAB和△OCD中，∠AOB＝∠COD＝90°，∠OAB＝∠OCD＝30°，连接AC交BD的延长线于点M.请判断ACBD的值及∠AMB的度数，并说明理由；拓展延伸(3)在(2)的条件下，将△OCD绕点O在平面内旋转，AC，BD所在直线交于点M.若OD＝1，OB＝7，请直接写出当点C与点M重合时AC的长．图①图②备用图第9题图解：(1)①1；②40°；(2)ACBD＝3，∠AMB＝90°；理由如下：∵∠AOB＝∠COD＝90°，∠OAB＝∠OCD＝30°，∴CODO＝AOBO＝3，∠COD＋∠AOD＝∠AOB＋∠AOD，即∠AOC＝∠BOD，∴△AOC∽△BOD，∴ACBD＝CODO＝3，∠CAO＝∠DBO.∵∠AOB＝90°，∴∠DBO＋∠ABD＋∠BAO＝90°.∴∠CAO＋∠ABD＋∠BAO＝90°，∴∠AMB＝90°；(3)①点C与点M重合时，如解图①，同理得：△AOC∽△BOD，∴∠AMB＝90°，设BD＝x，则AC＝3x，Rt△COD中，∠OCD＝30°，OD＝1，∴CD＝2，BC＝x－2，Rt△AOB中，∠OAB＝30°，OB＝7，∴AB＝2OB＝27，在Rt△AMB中，由勾股定理得：AC2＋BC2＝AB2，(3x)2＋(x－2)2＝(27)2，解得x1＝3，x2＝－2(舍去)，∴AC＝33；②点C与点M重合时，如解图②，同理可得：∠AMB＝90°，ACBD＝3，设BD＝x，则AC＝3x，在Rt△AMB中，由勾股定理得：AC2＋BC2＝AB2，(3x)2＋(x＋2)2＝(27)2解得x1＝－3(舍去)，x2＝2，∴AC＝23，综上所述，AC的长为33或2 3.图①图②第9题解图10．如图，已知△BAD和△BCE均为等腰直角三角形，∠BAD＝∠BCE＝90°，点M为DE的中点，过点E作EN∥AD交AM的延长线于点N.(1)当A，B，C三点在同一条直线上时(如图①)，直接写出线段AD与NE的数量关系为________．(2)将图①中的△BCE绕点B旋转，当A，B，E三点在同一直线上时(如图②)，判断△ACN是什么特殊三角形并说明理由．(3)将图①中△BCE绕点B旋转到图③位置，此时A，B，M三点在同一直线上．求证：若AC＝32，AD＝1，则四边形ACEN的面积为21 2.图①图②图③第10题图(1)解：AD＝NE.【解法提示】∵EN∥AD，∴∠MAD＝∠MNE，∠ADM＝∠NEM.∵点M为DE的中点，∴DM＝EM.∴△ADM≌△NEM(AAS)．∴AD＝NE；(2)解：△ACN为等腰直角三角形．理由如下：∵△BAD和△BCE均为等腰直角三角形，∴AB＝AD，CB＝CE，∠CBE＝∠CEB＝45°.∵AD∥NE，∴∠DAE＋∠NEA＝180°.∵∠DAE＝90°，∴∠NEA＝90°.∴∠NEC＝135°.∵A，B，E三点在同一条直线上，∴∠ABC＝180°－∠CBE＝135°.∴∠ABC＝∠NEC.∵△ADM≌△NEM，∴AD＝NE.∵AD＝AB，∴AB＝NE，∴△ABC≌△NEC.∴AC＝NC，∠ACB＝∠NCE.∴∠ACN＝∠BCE＝90°.∴△ACN为等腰直角三角形；(3)证明：如解图，连接CM.第10题解图∵AD∥NE，M为DE的中点，∴易得△ADM≌△NEM，∴AD＝NE.∵AD＝AB，∴AB＝NE，∵AD∥NE，∴AN⊥NE，在四边形BCEN中，∵∠BCE＝∠BNE＝90°，∴∠NBC＋∠NEC＝360°－180°＝180°，∵∠NBC＋∠ABC＝180°，∴∠ABC＝∠NEC，∴△ABC≌△NEC.∴AC＝NC，∠ACB＝∠NCE.∴∠ACN＝∠BCE＝90°.∴△ACN为等腰直角三角形，由(1)可知，△AMD≌△NME，∴AM＝MN，AD＝NE＝1，∴CM⊥AN，AM＝CM＝MN，∵AC＝32，∴AM＝CM＝MN＝3，∴S四边形ACEN ＝S△AMC＋S直角梯形MNEC＝12×3×3＋12×(3＋1)×3＝212.31。
几何形状探索小学数学专项练习题及
几何形状探索小学数学专项练习题及解析几何形状是小学数学中的一个重要内容，通过探索和解决几何形状的问题，可以培养学生的观察能力、空间想象力以及逻辑思维能力。
本文将介绍一些小学数学中的几何形状专项练习题，并给出相应的解析。
一、直线、线段和射线1. 练习题：A. 请画出两个相交但不重合的直线。
B. 请画出一个线段和一个射线。
2. 解析：A. 直线是由无数个点组成的，可以延伸到无穷远。
两条直线可以相交，但要求它们不重合，即没有公共的点。
B. 线段是由两个端点确定的，它有起点和终点，并且长度有限。
射线有一个起点，并且延伸到无穷远。
可以通过在一条直线上选择一个起点和一个方向来确定一条射线。
二、三角形1. 练习题：A. 请画出一个等边三角形。
B. 请画出一个直角三角形。
2. 解析：A. 等边三角形的三条边长度相等，三个角也相等，每个角都是60°。
B. 直角三角形是指其中一个角是90°的三角形。
可以通过画一个直角和两条与直角相交的线段来构造直角三角形。
三、四边形1. 练习题：A. 请画出一个正方形。
B. 请画出一个平行四边形。
2. 解析：A. 正方形是一种特殊的长方形，它的四条边长度相等且四个角都是90°。
B. 平行四边形是指两组对边分别平行的四边形。
可以通过画两条平行线段，再分别在这两条平行线段上选择两个点，然后连接这四个点来构造平行四边形。
四、圆形1. 练习题：A. 请画出一个圆形。
B. 请画出一个半径为5cm的圆。
2. 解析：A. 圆形是平面上所有到一个固定点距离相等的点的集合。
可以通过用指定的半径和一个点为圆心画弧线来构造一个圆。
B. 半径是指圆心到圆上任意一点的距离，可以通过指定一个半径长度和一个点为圆心来画一个半径为5cm的圆。
通过以上练习题和解析，我们可以帮助小学生巩固对几何形状的认知和理解能力。
同时，这些练习题也可以帮助他们发展观察能力、培养空间想象力，并提高解决问题的能力。
(中考压轴题)几何图形探究学习型问题合题及解析
几何图形探究学习型问题类型一线段问题1.我们定义：如图①，在△ABC 中，把AB 绕点A 顺时针旋转α≤(0°＜α＜180°)得到AB′，把AC 绕点A 逆时针旋转β得到AC′，连接B′C′.当α＋β＝180°时，我们称△AB′C′是△ABC 的“旋补三角形”．△AB′C′边B′C′ 上的中线AD 叫做△ABC 的“旋补中线”，点A 叫做“旋补中心”．特例感知(1)在图②，图③中，△AB′C′是△ABC 的“旋补三角形”，AD 是△ABC 的“旋补中线”．①如图②，当△ABC 为等边三角形时，AD 与BC 的数量关系为AD＝BC ；②如图③，当∠BAC＝90°，BC＝8 时，则AD 长为．猜想论证(2)在图①中，当△ABC 为任意三角形时，猜想AD 与BC 的数量关系，并给予证明．拓展应用(3)如图④，在四边形ABCD 中，∠C＝90°，∠D＝150°，BC＝12，CD＝2 3，DA＝6.在四边形内部是否存在点P，使△PDC 是△PAB 的“旋补三角形”？若存在，给予证明，并求△PAB 的“旋补中线”长；若不存在，请说明理由．第1 题图第1 题图④2.(1)操作发现：如图①，D 是等边△ABC 边BA 上一动点(点D 与点B 不重合)，连接DC，以DC 为边在BC 上方作等边△DCF，连接AF.直接写出线段AF 与BD 之间的数量关系；(2)类比猜想：如图②，当△ABC 为以BC 为斜边的等腰直角三角形，D 是边BA 上一动点(点D 与点B 不重合)，连接DC，以DC 为斜边在BC 上方作等腰直角△FDC，连接AF.请直接写出AF 与BD 的数量关系；(3)深入探究：①如图③，当△ABC 为以BC 为底边的等腰三角形，D是边BA 上一动点(点D 与点B 不重合)，连接DC，以DC 为底边在BC 上方作等腰△FDC，∠BCA＝∠DCF，且∠BAC＝α，连接AF.线段AF 与BD 之间有怎样的数量关系？证明你发现的结论；②如图④，当△ABC 为任意三角形，D 是边BA 上一动点(点D 与点B 不重合)，连接DC，以DC 为边在BC 上方作△FDC∽△ABC 结论．B C，且AC＝k，连接AF.线段AF 与BD 之间有怎样的数量关系？直接写出你发现的第2 题图3.我们把两条中线互相垂直的三角形称为“称为中垂三角形”，例如图①，图②，图③中，AF，BE 是△ABC 的中线，AF⊥BE，垂足为P，像△ABC 这样的三角形均称为“中垂三角形”，设BC＝a，AC＝b，AB＝c.特例探索(1)如图1，当∠ABE＝45°，c＝2 2时，a＝，b＝．如图②，当∠ABE＝30°，c＝4 时，a＝，b＝．归纳证明(2)请你观察(1)中的计算结果，猜想a2，b2，c2 三者之间的关系，用等式表示出来，并利用图③证明你发现的关系式．拓展应用(3)如图④，在平行四边形ABCD 中，点E、F、G 分别是AD，BC，CD 的中点，BE⊥EG，AD＝2 5，AB＝3，求AF 的长．第3 题图4.类比等腰三角形的定义，我们定义：有一组邻边相等的凸四边形叫做“等邻边四边形”．(1)概念理解：如图①，在四边形ABCD 中，添加一个条件使得四边形ABCD 是“等邻边四边形”．请写出你添加的一个条件．(2)问题探究：①小红猜想：对角线互相平分的“等邻边四边形”是菱形，她的猜想正确吗？请说明理由．②如图②，小红画了一个Rt△ABC，其中∠ABC＝90°，AB＝2，BC＝1，并将Rt△ABC 沿∠ABC 的平分线BB′方向平移得到△A′B′C′，连结AA′，BC′，小红要使平移后的四边形ABC′A′是“等邻边四边形”，应平移多少距离(即线段BB′的长)?(3)拓展应用：如图③，“等邻边四边形”ABCD 中，AB＝AD，∠BAD＋∠BCD＝90°，AC，BD 为对角线，AC＝2AB，试探究BC，CD，BD 的数量关系．第4 题图类型二面积问题1.我们可以定义：有一组邻边相等的凸四边形叫做“等邻边四边形”．问题探究(1)如图①，已知矩形ABCD 中，AB>BC，试在矩形ABC D 上确定一点P，使△BCP 为等腰三角形．(2)如图②，在菱形ABCD 中，∠ABC＝120°，AB＝4，点M、N 分别在AD、CD 上(不含端点)，若∠MBN ＝60°，判断四边形DMBN 是否一定为“等邻边四边形”？如果是“等邻边四边形”，说明理由并求出其周长最小值；如果不是，请说明理由．尝试应用(3)现有一个平行四边形材料ABCD，工作人员需要将其制作成一个“等邻边四边形”面板．如图③，在▱ABCD 中，AB＝17，BC＝7，tan B＝4，点E 在BC 上，且BE＝4，在▱ABCD 内或者边上，确定一点F，使四边形ABEF 为面积最大的“等邻边四边形”，若能实现，求出最大面积，若不能实现，试说明理由．第1 题图2.问题提出：菱形的面积不仅可以用底乘以高来求，而且可以用对角线乘积的一半．那么我们日常生活中常见的风筝的形状即“筝形”是不是也可以用这种方法求面积呢？问题探究：如图①，四边形ABCD 是我们常见的风筝的图案，其中对角线BD 长为20 cm，AC 长为40 cm，AC 垂直平分BD，垂足为E，求筝形ABCD 的面积．111 1解：由已知：S 四边形ABCD＝S△ABD＋S△CBD＝2BD·AE＋2·BD×CE＝2BD·(AE＋CE)＝2BD·AC.我们发现这个结论对于筝形依然成立．图①图②图③第2 题图类比总结：满足什么条件的图形可以通过这种方法求面积呢？让我们先研究下面图形的面积．如图②，四边形ABCD 的对角线AC、BD 互相垂直，其中对角线BD 长为20 cm，AC 长为15 cm，垂足为E，求四边形ABCD 的面积．(请写出求解过程)研究到这里，我们可以得出一个结论：结论1：对角线互相垂直的四边形的面积等于．拓展提高：通过结论1 的研究对于普通的对角线不垂直的四边形的面积的求解能不能有什么启示呢？下面让我们一起来研究．如图③，四边形ABCD 的对角线BD 长为20 cm，点A 到BD 的距离与点C 到BD 的距离之和为15 cm，求四边形ABCD 的面积．(请写出求解过程)结论2：任意四边形的面积等于．问题应用：(1)如图④，矩形ABCD 中，AD＝6 cm，AB＝4 cm，EF∥AD，点G、H 分别是AD、BC 上任一点，求四边形EGFH 的面积．(2)如图⑤，四边形ABCD 放在了一组等距平行线中，已知BD＝6 cm，四边形ABCD 的面积为24 cm2，求两条平行线间的距离．第2 题图④第2 题图⑤3.定义：我们把三角形被一边中线分成的两个三角形叫做“友好三角形”．性质：如果两个三角形是“友好三角形”，那么这两个三角形的面积相等．理解：如图①，在△ABC 中，CD 是AB 边上的中线，那么△ACD 和△BCD 是“友好三角形”，并且S△ACD ＝S△BCD.应用：如图②，在矩形ABCD 中，AB＝4，BC＝6，点E 在AD 上，点F 在BC 上，AE＝BF，AF 与BE 交于点O.(1)求证：△AOB 和△AOE 是“友好三角形”；(2)连接OD，若△AOE 和△DOE 是“友好三角形”，求四边形CDOF 的面积．探究：在△ABC 中，∠A＝30°，AB＝4，点D 在线段AB 上，连接CD，△ACD 和△BCD 是“友好三角形”，1将△ACD 沿CD 所在直线翻折，得到△A′CD，若△A′CD 与△ABC 重合部分的面积等于△ABC 面积的4，请直接写出△ABC 的面积．第3 题图4.探索发现：(1)如图①，在△ABC 中，AD 是BC 边上的中线，若△ABC 的面积为S，则△ACD 的面积为．(2)在图②中，E 、F 分别是▱ABCD 的边AB、BC 的中点，若▱ABCD 的面积为S，求四边形BEDF 的面积，并说明理由．(3)在图③中，E、F 分别是▱ABCD 的边AB、BC 上的点，且AE 1AB，BF 1BC，若▱ABCD 的面积为＝3 ＝3S，则四边形BEDF 的面积为．解决问题：(4)如图④中，矩形ABCD 中，AB＝nBC(n 为常数，且n＞0)．E 是AB 边上的一个动点，F 是BC 边上的1一个动点．若在两点运动的过程中，四边形BEDF 的面积始终等于矩形面积的2，请探究线段AE、BF 应满足怎样的数量关系，并说明理由．第4 题图3 类型三角度问题(拓展)1.问题探究(1)如图①，AB 是⊙O 的弦，直线l 与⊙O 相交于M、N 两点，M1、M2是直线l 上异于点M、N 的两个点，则∠AMB、∠AM1B、∠AM2B 的大小关系是；第1 题图(2)如图②，AB 是⊙O 的弦，直线l 与⊙O 相切于点M，点M1是直线l 上异于点M 的任意一点，请在图②中画出图形，试判断∠AMB、∠AM1B 的大小关系，并说明理由；问题解决(3)如图③是某游乐场的平面示意图，场所保卫人员想在线段OQ 上找一点M 安装监控装置，用来监控OP 边上的AB 段，已知当∠AMB 最大时，可以让监控效果达到最佳．若∠POQ＝60°，OA＝400 m，AB ＝200 m，问在线段OQ 上是否存在一点M，使得∠AMB 最大？若存在，请求出此时∠AMB 的度数和OM 的长；若不存在，请说明理由．2. (1)如图①，已知 E 是矩形 ABCD 的边 AB 上一点，EF ⊥DE 交 BC 于点 F ，证明：△ADE ∽△BEF ；(2)这个相似的基本图形像字母 K ，可以称为“K ”型相似，但更因为图形的结构特征是一条线上有 3 个垂直关系，也常被称为“一线三垂直”，那普通的 3 个等角又会怎样呢？变式一：如图②，已知等边△ABC ，点 D 、E 分别为 BC ，AC 上的点，∠ADE ＝60°. ①图②中有相似三角形吗？请说明理由．②如图③，若将∠ADE 在△ABC 的内部(∠ADE 两边不与 BC 重合)绕点 D 逆时针旋转一定的角度，还有相似三角形吗？．(若有请写出相似三角形，没有则填“无”)变式二：如图④，隐藏变式一图形中的线段 AE ，在得到的新图形中，①如果∠B ＝∠C ＝∠ADE ＝50°，图中有相似三角形吗？请说明理由； ②如图⑤，若∠B ＝∠C ＝∠ADE ＝α，α 为任意角度，还有相似三角形吗？ ；(若有请写出相似三角形，没有则填“无”)变式三：如图⑥，已知，相邻两条平行直线间的距离相等，若等腰直角△ABC 的三个顶点分别在这三条平行直线上，则 cos α 的值是．(直接写出结果)图①第 2 题图图②图③ 第 2 题图 图④图⑤ 第 2 题图 图⑥3.【定义】若一个四边形恰好关于其中一条对角线所在的直线对称，则我们将这个四边形叫做镜面四边形．【理解】(1)下列说法是否正确．(对的打“√”，错的打“”)①平行四边形是一个镜面四边形．( )②镜面四边形的面积等于对角线积的一半．( )(2)如图①，请你在4×4 的网格(每个小正方形的边长为1)中画出一个镜面四边形，使它的顶点在格点上，且有一边长为5；【应用】(3)如图②，已知镜面四边形ABCD，∠BAD＝60°，∠ABC＝90°，AB≠BC，P 是AD 上一点，AE 丄BP 于点E，在BP 的延长线上取一点F，使EF＝BE，连接AF，作∠FAD 的平分线AG 交BF 于点G，CM 丄BF 于点M，连接CG.①求∠EAG 的度数；②比较BM 与EG 的大小，并说明理由；③若以线段CB、CG、AG 为边构成的三角形是直角三角形，求cos∠CBM 的值(直接写出答案)．第3 题图第 1 题图④2 几何图形探究学习型问题类型一 线段问题1. 我们定义：如图①，在△ABC 中，把 AB 绕点 A 顺时针旋转 α≤(0°＜α＜180°)得到 AB ′，把 AC 绕点 A 逆时针旋转 β 得到 AC ′，连接 B ′C ′.当 α＋β＝180°时，我们称△AB ′C ′是△ABC 的“旋补三角形”．△AB ′C ′边 B ′C ′ 上的中线 AD 叫做△ABC 的“旋补中线”，点 A 叫做“旋补中心”．特例感知(1)在图②，图③中，△AB ′C ′是△ABC 的“旋补三角形”，AD 是△ABC 的“旋补中线”． ①如图②，当△ABC 为等边三角形时，AD 与 BC 的数量关系为 AD ＝ BC ；②如图③，当∠BAC ＝90°，BC ＝8 时，则 AD 长为．猜想论证(2)在图①中，当△ABC 为任意三角形时，猜想 AD 与 BC 的数量关系，并给予证明． 拓展应用(3)如图④，在四边形 ABCD 中，∠C ＝90°，∠D ＝150°，BC ＝12，CD ＝2 3，DA ＝6.在四边形内部是否存在点 P ，使△PDC 是△PAB 的“旋补三角形”？若存在，给予证明，并求△PAB 的“旋补中线”长；若不存在，请说明理由． 1解 ：(1)① 2；② 4；【解法提示】①由旋转可得到 AB ＝AB ′＝AC ＝AC ′，∵∠BAC ＝60°，∴∠B ′AC ′＝120°，即∠AB ′ C ′＝∠AC ′B ′＝30°， 又∵AD 为 B ′C ′上的中线，∴ AD1 1 1＝2AB ′＝2AB ＝2BC ；②由“旋补三角形”定义可得：∠B ′AC ′＝90°， ∴△AB ′C ′≌△ABC ，∴B ′C ′＝BC ， ∴AD ＝1BC ＝4.(2)猜想：AD 1BC .＝2第 1 题图第 1 题解图①第 1 题解图③2 2 证明：如解图①，延长 AD 至 E ，使 DE ＝AD ，连接 B ′E ，C ′E . ∵AD 是△ABC 的“旋补中线”， ∴B ′D ＝C ′D .∴四边形 AB ′EC ′是平行四边形， ∴EC ′∥B ′A ，EC ′＝B ′A ， ∴∠AC ′E ＋∠B ′AC ′＝180°.由定义可知∠B ′AC ′＋∠BAC ＝180°，B ′A ＝BA ，AC ＝AC ′， ∴∠AC ′E ＝∠BAC ，EC ′＝BA ， ∴△AC ′E ≌△CAB (SAS)， ∴AE ＝BC ， ∵AD ＝1AE ， ∴AD ＝1BC ；【一题多解】①证明：如解图②，延长 B ′A 至 F ，使 AF ＝B ′A ，连接 C ′F ， ∴∠B ′AC ′＋∠C ′AF ＝180°.由定义可知∠B ′AC ′＋ ∠BAC ＝180°，B ′A ＝BA ，AC ＝AC ′， ∴∠CAB ＝∠C ′AF ，AB ＝AF ， ∴△ABC ≌△AFC ′(SAS)， ∴BC ＝FC ′，∵B ′D ＝C ′D ，B ′A ＝AF ，∴在△B ′C ′F 中，AD 1FC ′，＝2∴AD 1BC .＝2②证明：如解图③，将△AB ′C ′绕点 A 顺时针旋转∠C ′AC 的度数，得到△AEC ，此时 AC ′与 AC 重合，D 的对应点为 D ′，连接 AD ′.由定义可知∠B ′AC ′＋∠BAC ＝180°. 由旋转得∠B ′AC ′＝∠EAC ， ∴∠BAC ＋∠EAC ＝180°， ∴E ，A ，B 三点在同一直线上， ∵AB ＝AB ′＝AE ，ED ′＝D ′C ， ∴AD ′是△EBC 的中位线，第 1 题解图②2∴AD ′＝1BC ， 1 即 AD ＝2BC . (3)存在；证明：如解图④，在四边形 ABCD 中选一点 P ，作 PE 垂直平分 BC ，且使 PE ＝CD ， 连接 PA 、PB 、PC 、PD ，可 得 PC ＝PB ，PE ∥CD, ∠DCE ＝90°. ∴四边形 PECD 为矩形；∴PE ＝CD ＝2 3，PD ＝CE ＝AD ＝6，∠PDC ＝90°；∴tan ∠PCE ＝PE ＝ 3CE 3 ， ∴∠PCE ＝∠PBE ＝30°，即∠BPC ＝120°； 又由∠ADC ＝150°，可得∠ADP ＝60°， ∴△PAD 为等边三角形， ∴PD ＝PA ，∠APD ＝60°；∵∠BPC ＋∠DPA ＝120°＋60°＝180°， ∴△PCD 是△PAB 的“旋补三角形”； 如解图⑤，取 CD 的中点 M ，连接 PM ， 可 得 DM ＝ 3，PD ＝6.由勾股定理得 PM ＝ DM 2＋PD 2＝ （ 3）2＋62＝ 39.2. (1)操作发现：如图①，D 是等边△ABC 边 BA 上一动点(点 D 与点 B 不重合)，连接 DC ，以 DC 为边在 BC 上方作等边△DCF ，连接 AF .直接写出线段 AF 与 BD 之间的数量关系；(2)类比猜想：如图②，当△ABC 为以 BC 为斜边的等腰直角三角形，D 是边 BA 上一动点(点 D 与点 B 不重合)，连接 DC ，以 DC 为斜边在 BC 上方作等腰直角△FDC ，连接 AF .请直接写出 AF 与 BD 的数量关系； (3)深入探究：①如图③，当△ABC 为以 BC 为底边的等腰三角形，D 是边 BA 上一动点(点 D 与点 B 不重合)，连接 DC ， 以 DC 为底边在 BC 上方作等腰△FDC ，∠BCA ＝∠DCF ，且∠BAC ＝α，连接 AF .线段 AF 与 BD 之间有怎样的数量关系？证明你发现的结论；②如图④，当△ABC 为任意三角形，D 是边 BA 上一动点(点 D 与点 B 不重合)，连接 DC ，以 DC 为边在BC 上方作△FDC ∽△ABCB C ，且AC＝k ，连接 AF .线段 AF 与 BD 之间有怎样的数量关系？直接写出你发现的第 1 题解图④第 1 题解图⑤结论．解：(1)BD ＝AF;【解法提示】∵△ABC 、△DCF 都为等边三角形， ∴FC ＝DC ，AC ＝BC ，∠FCA ＋∠ACD ＝∠BCD ＋∠ACD ＝60°， ∴∠FCA ＝∠DCB ， 在△FCA 和△DCB 中，⎧CF ＝CD⎨∠FCA ＝∠DCB ， ⎩CA ＝CB∴△FCA ≌△DCB ， ∴BD ＝AF . (2)BD ＝ 2AF;【解法提示】∵△ABC 、△DCF 都是等腰直角三角形，∴F C ＝ A C 2 CD∴ F C ，CB ＝ 2 ，A C CD ＝CB ，∵∠F CA ＋∠ACD ＝∠BCD ＋∠ACD ＝45°， ∴∠FCA ＝∠DCB ， ∴△FCA ∽△DCB ， ∴A F AC 2 BD ＝CB ＝ 2 ，∴BD ＝ 2AF ；(3) B D 1 ①AF ＝2sin 2α；第 2 题图2 2AF理由：∵△ABC 为以 BC 为底边的等腰三角形，△FDC 为以 DC 为底边的等腰三角形，∠BCA ＝∠DCF ， ∴△ABC ∽△FDC ， ∴BC C D AC ＝CF ，∵∠ACF ＋∠ACD ＝∠BCD ＋∠ACD ， ∴∠ACF ＝∠BCD ， ∴△BCD ∽△ACF ， ∴BD BC AF ＝AC ，如解图，过点 A 作 AP ⊥BC 于点 P ， B C 2 CP 1 1 则AC ＝ AC ＝2sin 2∠BAC ＝2sin 2α， ∴BD 1 AF ＝2sin 2α； ②BD ＝k . 【解法提示】∵△FDC ∽△ABC ， ∴CF C DCA ＝CB ，∠FCA ＋∠ACD ＝∠BCD ＋∠ACD ， ∴∠FCA ＝∠DCB ， ∴△FCA ∽△DCB ， ∴BD BC AF ＝AC ＝k .3. 我们把两条中线互相垂直的三角形称为“称为中垂三角形”，例如图①，图②，图③中，AF ，BE 是△ABC 的中线，AF ⊥BE ，垂足为 P ，像△ABC 这样的三角形均称为“中垂三角形”，设 BC ＝a ，AC ＝b ，AB ＝c . 特例探索(1)如图 1，当∠ABE ＝45°，c ＝2 2时，a ＝ ，b ＝． 如图②，当∠ABE ＝30°，c ＝4 时，a ＝ ，b＝． 归纳证明(2)请你观察(1)中的计算结果，猜想 a 2，b 2，c 2 三者之间的关系，用等式表示出来，并利用图③证明你发现的关系式． 拓展应用(3)如图④，在平行四边形 ABCD 中，点 E 、F 、G 分别是 AD ，BC ，CD 的中点，BE ⊥EG ，AD ＝2 5， AB ＝3，求 AF 的长．第 2 题解图解：(1)2 5、2 5、2 13、2 7；；[解法提示]∵AF ⊥BE ，∠ABE ＝45°，∴AP ＝BP ＝ 2＝2，2 AB ∵AF ，BE 是△ABC 的中线，∴EF ∥AB ，EF 1AB ＝ 2，＝2 ∴∠PFE ＝∠PEF ＝45°， ∴PE ＝PF ＝1，在 Rt △FPB 和 Rt △PEA 中，AE ＝ BF ＝ 12＋22＝ 5，∴AC ＝BC ＝2 5， ∴a ＝b ＝2 5， 如解图①，连接 EF ， 1 同理可得：EF ＝2×4＝2， ∵EF ∥AB ， ∴△PEF ～△PBA ， ∴PF PE EF 1 AP ＝PB ＝AB ＝2，在 Rt △ABP 中， AB ＝4，∠ABP ＝30°， ∴AP ＝2，PB ＝2 3， ∴PF ＝1，PE ＝ 3， 在 Rt △APE 和 Rt △BPF 中， AE ＝ 7，BF ＝ 13，第 3 题图∴a ＝2 13，b ＝2 7，故答案为：2 5、2 5，2 13，2 7； (2)猜想：a 2＋b 2＝5c 2， 如解图②，连接 EF ， 设∠ABP ＝α，∴AP ＝c sin α，PB ＝c cos α， 1c sin α1 c cos α由(1)同理可得，PF ＝2PA ＝ 2 ，PE ＝2PB ＝ 2 ，22222c 2cos 2α22 2 2 2c 2sin 2αAE ＝AP ＋PE ＝c sin α＋ 4 ，BF ＝PB ＋PF ＝c cos α＋ 4 ， b 2 2 2 c 2cos 2α a 2c 2sin 2α 2 2∴(2) ＝c sin α＋4 ，(2) ＝ 4 ＋c cos α，a 2b 2c 2sin 2α 2 22 2c 2cos 2α∴ 4 ＋ 4 ＝ 4 ＋c cos α＋c sin α＋ 4 ，∴a 2＋b 2＝5c 2 ；(3)如解图③，连接 AC ，EF 交于点 H ，AC 与 BE 交于点 Q ，设 BE 与 AF 交于点 P ， ∵点 E 、G 分别是 AD ，CD 的中点， ∴EG ∥AC ， ∵BE ⊥EG ， ∴BE ⊥AC ，∵四边形 ABCD 是平行四边形， ∴AD ∥BC ，AD ＝BC ＝2 5， ∴∠EAH ＝∠FCH ，∵E ，F 分别是 AD ，BC 的中点， ∴AE ＝1 AD ，BF1BC ，2∴AE ＝BF ＝CF ＝21AD ＝ 5，＝2 ∵AE ∥BF ，∴四边形 ABFE 是平行四边形， ∴EF ＝AB ＝3，AP ＝PF ， 在△AEH 和△CFH 中，⎧∠EAH ＝∠FCH ⎨∠AHE ＝∠FHC ， ⎩AE ＝CF∴△AEH≌△CFH，∴EH＝FH，∴EP，AH 分别是△AFE 的中线且BE⊥AC，由(2)的结论得：AF2＋EF2＝5AE2，∴AF2＝5( 5)2－32＝16，∴AF＝4.4.类比等腰三角形的定义，我们定义：有一组邻边相等的凸四边形叫做“等邻边四边形”．(1)概念理解：如图①，在四边形ABCD 中，添加一个条件使得四边形ABCD 是“等邻边四边形”．请写出你添加的一个条件．(2)问题探究：①小红猜想：对角线互相平分的“等邻边四边形”是菱形，她的猜想正确吗？请说明理由．②如图②，小红画了一个Rt△ABC，其中∠ABC＝90°，AB＝2，BC＝1，并将Rt△ABC 沿∠ABC 的平分线BB′方向平移得到△A′B′C′，连结AA′，BC′，小红要使平移后的四边形ABC′A′是“等邻边四边形”，应平移多少距离(即线段BB′的长)?(3)拓展应用：如图③，“等邻边四边形”ABCD 中，AB＝AD，∠BAD＋∠BCD＝90°，AC，BD 为对角线，AC＝2AB，试探究BC，CD，BD 的数量关系．第3 题解图第4 题图－1－ 714－ 22 2 解：(1)AB ＝BC 或 BC ＝CD 或 CD ＝AD 或 AD ＝AB (任写一个即可)； (2)①正确，理由为：∵四边形的对角线互相平分，∴这个四边形是平行四边形， ∵四边形是“等邻边四边形”，∴这个四边形有一组邻边相等， ∴这个“等邻边四边形”是菱形； ②∵∠ABC ＝90°，AB ＝2，BC ＝1， ∴AC ＝ 5，∵将 Rt △ABC 平移得到△A ′B ′C ′，∴BB ′＝AA ′，A ′B ′∥AB ，A ′B ′＝AB ＝2，B ′C ′＝BC ＝1，A ′C ′＝AC ＝ 5， (I)当 AA ′＝AB 时，BB ′＝AA ′＝AB ＝2； (II)当 AA ′＝A ′C ′时，BB ′＝AA ′＝A ′C ′＝ 5； (III)当 A ′C ′＝BC ′＝ 5时，如解图①，延长 C ′B ′交 AB 于点 D ，则 C ′B ′⊥AB ， ∵BB ′平分∠ABC ， ∴∠ABB ′＝1 ∠ABC ＝45°， ∴∠BB ′D ＝1∠ABC ＝45° ∴B ′D ＝BD ， 设 B ′D ＝BD ＝x ， 则 C ′D ＝x ＋1，BB ′＝ 2x ，∵在 Rt △BC ′D 中，(BD )2＋(C ′D )2＝(BC ′ )2 ∴x 2＋(x ＋1)2＝( 5)2，解得：x 1＝1，x 2＝－2(不合题意，舍去)， ∴BB ′＝ 2x ＝ 2，(Ⅳ)当 BC ′＝AB ＝2 时，如解图②，与(Ⅲ)方法一同理可得：BD 2＋(C ′D )2＝(BC ′)2， 设 B ′D ＝BD ＝x ， 则 x 2＋(x ＋1)2＝22，7＋－1 解得：x 1＝ ∴BB ′＝ 2x ＝ 2，x 2＝ 2 ；2 (不合题意，舍去)，4－22综上所述，当平移距离为2，或5或2或时，平移后的四边形ABCD 是“等邻边四边形”．(3)BC，CD，BD 的数量关系为：BC2＋CD2＝2BD2，如解图③，∵AB＝AD，∴将△ADC 绕点A 旋转得到AD、AB 重合，得到△ABF，连接CF，∴△ABF≌△ADC，∴∠ABF＝∠ADC，∠BAF＝∠DAC，AF＝AC，FB＝CD，∴∠BAD＝∠CAF A C A D1，，AF＝AB＝∴△ACF∽△ABD，∴C F ACBD＝AB＝2，∴CF＝2BD，∵∠BAD＋∠ADC＋∠BCD＋∠ABC＝360°，∴∠ABC＋∠ADC＝360°－(∠BAD＋∠BCD)＝360°－90°＝270°，∴∠ABC＋∠ABF＝270°，∴∠CBF＝90°，∴BC2＋FB2＝CF2＝( 2BD)2＝2BD2，∴BC2＋CD2＝2BD2.第4 题解图类型二 面积问题1. 我们可以定义：有一组邻边相等的凸四边形叫做“等邻边四边形”． 问题探究(1)如图①，已知矩形 ABCD 中，AB >BC ，试在矩形 ABC D 上确定一点 P ，使△BCP 为等腰三角形． (2)如图②，在菱形 ABCD 中，∠ABC ＝120°，AB ＝4，点 M 、N 分别在 AD 、CD 上(不含端点)，若∠MBN ＝60°，判断四边形 DMBN 是否一定为“等邻边四边形”？如果是“等邻边四边形”，说明理由并求出其周长最小值；如果不是，请说明理由．尝试应用(3)现有一个平行四边形材料 ABCD ，工作人员需要将其制作成一个“等邻边四边形”面板．如图③，在 ▱ABCD 中，AB＝ 17，BC ＝7，tan B ＝4，点 E 在BC 上，且 BE ＝4，在▱ABCD 内或者边上，确定一点 F ， 使四边形 ABEF 为面积最大的“等邻边四边形”，若能实现，求出最大面积，若不能实现，试说明理由．解：(1)如解图①，点 P 1、P 2、P 3 即为所求作的点． (2)四边形 DMBN 是“等邻边四边形”，理由如下： 如解图②，连接 BD ，∵四边形 ABCD 是菱形，∠ABC ＝120°，∴∠C ＝60°，∠MDB ＝∠DBC∴∠MDB ＝∠C ， ∵BC ＝CD ，∴△BCD 是等边三角形， ∴BC ＝BD ，1 ＝2∠ABC ＝60°， ∵∠MBN ＝∠MBD ＋∠DBN ＝60°， ∠DBC ＝∠NBC ＋∠DBN ＝60°， ∴∠MBD ＝∠NBC ， ∴△BDM ≌△BCN (ASA)，第 1 题图第 1 题解图①3 2 ∴BM ＝BN ，DM ＝CN∴四边形 DMBN 是“等邻边四边形”． ∵四边形 ABCD 是菱形，AB ＝4， ∴AB ＝BC ＝CD ＝AD ＝4，∴四边形 DMBN 的周长为 BM ＋DM ＋DN ＋BN ＝BM ＋CN ＋DN ＋BN ＝2BN ＋CD ＝2BN ＋4， ∴要求四边形 DMBN 周长的最小值，即求 BN 的最小值， 当 BN ⊥CD 时线段 BN 最短， 在 Rt △BCN 中，∠C ＝60°，BC ＝4；∴BN ＝BC ·sin60°＝4× ＝2 3，∴四边形 DMBN 周长的最小值为 2×2 3＋4＝4 3＋4. (3)如解图③，连接 AE ，过点 A 作 AH ⊥BC 于点 H ， ∵tan B ＝4，∴可设 AH ＝4x ，BH ＝x ， 在 Rt △ABH 中，AH 2＋BH 2＝AB 2 ， ∴(4x )2＋x 2＝( 17)2，解得 x ＝1，∴AH ＝4，BH ＝1， S 1 1 △ABE ＝2BE ·AH ＝2×4×4＝8； 分三种情况讨论：(i)如解图③，当 AB ＝AF 时，四边形 ABEF 是“等邻边四边形”，︵此时点 F 在以 A 为圆心，AB 为半径的MN (不含端点 M ，M 在 BC 上，N 在 AD 上)上， 要使四边形 ABEF 面积最大，则点 F 在边 AD 上， ∵AF ＝AB ＝ 17，AD ∥BC ， ∴S11△AEF ＝2AF ·AH ＝2× 17×4＝2 17， ∴S 四 边 形 ABEF ＝S △ABE ＋S △AEF ＝8＋2 17；(ii)如解图④，当 EB ＝EF 时，四边形 ABEF 是“等邻边四边形”，︵此时点 F 在以 E 为圆心，EB 为半径的MN (不含端点 M ，M 在 AE 上，N 在 CD 上)上， 要使四边形 ABEF 面积最大，则点 F 在平行四边形内，且 EF ⊥AE ， ∵BE ＝4，BH ＝1，第 1 题解图②第 3 题解图③∴HE ＝3，在 Rt △AHE 中 ，AE ＝ AH 2＋HE 2＝ 42＋32＝5，∵EF ＝BE ＝4，∴S 11 △AEF ＝2AE ·EF ＝2×5×4＝10， ∴S 四边形 ABEF ＝S △ABE ＋S △AEF ＝8＋10＝18；(iii)如解图⑤，当 AF ＝EF 时，四边形 ABEF 是“等邻边四边形”，作 AE 的垂直平分线 MN ，可得此时点 F 在线段 MN (不含端点 M ，M 在 AE 上，N 在 AD 上)上， 要使四边形 ABEF 面积最大，则点 F 在边 AD 上， 过点 E 作 EP ⊥AD 于 P ，则 EP ＝AH ＝4，AP ＝HE ＝3， 设 AF ＝EF ＝y ，∴PF ＝y －3， ∵PF 2＋EP 2＝EF 2， ∴(y －3)2＋42＝y 2，25 解得 y ＝ 6 ，∴S 1 1 2525 △AEF ＝2AF ·EP ＝2× 6 ×4＝ 3 ，∴S ＝S ＋S ＝825 49 四边形 ABEF △ABE △AEF ＋ 3 ＝ 3 . 49 ∵8＋2 17< 3 <18，∴当 EB ＝EF ，点 F 在平行四边形内，且 EF ⊥AE 时，所得“等邻边四边形”ABEF 的面积最大，最大面积是 18. 2. 问题提出：菱形的面积不仅可以用底乘以高来求，而且可以用对角线乘积的一半．那么我们日常生活中常见的风筝的形状即“筝形”是不是也可以用这种方法求面积呢？ 问题探究：如图①，四边形 ABCD 是我们常见的风筝的图案，其中对角线 BD 长为 20 cm ，AC 长为 40 cm ，AC 垂直平分 BD ，垂足为 E ，求筝形 ABCD 的面积．1 1 1 1解：由已知：S 四边形 ABCD ＝S △ABD ＋S △CBD ＝2BD ·AE ＋2·BD ×CE ＝2BD ·(AE ＋CE )＝2BD ·AC .我们发现这个结 论对于筝形依然成立．第 3 题解图④第 1 题解图⑤类比总结：满足什么条件的图形可以通过这种方法求面积呢？让我们先研究下面图形的面积．如图②，四边形 ABCD 的对角线 AC 、BD 互相垂直，其中对角线 BD 长为 20 cm ，AC 长为 15 cm ，垂足为 E ，求四边形 ABCD 的面积．(请写出求解过程) 研究到这里，我们可以得出一个结论： 结论 1：对角线互相垂直的四边形的面积等于．拓展提高：通过结论 1 的研究对于普通的对角线不垂直的四边形的面积的求解能不能有什么启示呢？下面让我们一起来研究．如图③，四边形 ABCD 的对角线 BD 长为 20 cm ，点 A 到 BD 的距离与点 C 到 BD 的距离之和为 15 cm ， 求四边形 ABCD 的面积．(请写出求解过程) 结论 2：任意四边形的面积等于．问题应用：(1)如图④，矩形 ABCD 中，AD ＝6 cm ，AB ＝4 cm ，EF ∥ AD ，点 G 、H 分别是 AD 、BC 上任一点，求四边形 EGFH 的面积．(2)如图⑤，四边形 ABCD 放在了一组等距平行线中，已知 BD ＝6 cm ，四边形 ABCD 的面积为 24 cm 2， 求两条平行线间的距离．解：结论 1：两对角线乘积的一半．图①图②第 2 题图图③第 2 题图④第 2 题图⑤2 ＋2 ＝2 ＝ 2 ＝21 1 1 11 【解法提示】S 四边形 ABCD ＝S △ABD ＋S △CBD ＝2×BD ×AE ＋2×BD ×CE ＝2×BD ×(AE ＋CE )＝2×BD ×AC ＝2×20×15 ＝150 cm 2.结论 2：一条对角线和另一条对角线的两个端点的距离之和的积的一半．【解法提示】如解图①，连接 BD ，过点 A 作 AN ⊥BD 于点 N ，过点 C 作 CM ⊥BD 于点 M ，S ＝S ＋S 1 BD ×AN ＋1 BD ×CM 1 BD ×(AN ＋CM )1×20 cm×15 cm ＝150 cm 2，四边形 ABCD △ABD △CBD ＝2 2＝2 ＝2(1)如解图②，过点 H 作 HM ⊥EF 于点 M ，过点 G 作 GN ⊥EF 于点 N ， ∵四边形 ABCD 是矩形，∴AD ∥BC ，AD ＝BC ，AB ＝DC ，∠A ＝∠B ＝90°， ∵EF ∥AD ，∴四边形 AEFD 是平行四边形，EF ∥BC ， ∴EF ＝AD ＝6 cm ， ∵HM ⊥EF ，∴∠AEF ＝∠HMF ＝90°， ∴AE ∥HM ，∵AH ∥EM ，∠A ＝90°， ∴四边形 AEMH 是矩形， ∴AE ＝HM ， 同理 BE ＝GN ，∴HM ＋GN ＝AB ＝4 cm ，∴S 四边形 EGFH ＝S 1 △HEF ＋S △GEF ＝2EF ·HM 1EF ·GN 1EF ·(HM ＋GN ) 1EF ·AB 1×6×4＝12 cm 2；(2)如解图③，过点 A 作 AM ⊥BD 于点 M ，过点 C 作 CN ⊥BD 于点 N ，S ＝S ＋S 1 BD ×AM ＋1 BD ×CN 1BD ×(AM ＋CN )，四边形 ABCD △ABD △CBD ＝2 2 ＝2 即1×6 cm×(AM ＋CN )＝24 cm 2，第 2 题解图① 第 2 题解图②第 2 题解图③解得 AM ＋CN ＝8 cm ，即 3CN ＋CN ＝8 cm ，解得 CN ＝2 cm ， 即两条平行线间的距离为 2 cm.3. 定义：我们把三角形被一边中线分成的两个三角形叫做“友好三角形”．性质：如果两个三角形是“友好三角形”，那么这两个三角形的面积相等．理解：如图①，在△ABC 中，CD 是 AB 边上的中线，那么△ACD 和△BCD 是“友好三角形”，并且 S △ACD ＝S △BCD .应用：如图②，在矩形 ABCD 中，AB ＝4，BC ＝6，点 E 在 AD 上，点 F 在 BC 上，AE ＝BF ，AF 与 BE 交于点 O .(1)求证：△AOB 和△AOE 是“友好三角形”；(2)连接 OD ，若△AOE 和△DOE 是“友好三角形”，求四边形 CDOF 的面积．探究：在△ABC 中，∠A ＝30°，AB ＝4，点 D 在线段 AB 上，连接 CD ，△ACD 和△BCD 是“友好三角形”， 1 将△ACD 沿 CD 所在直线翻折，得到△A ′CD ，若△A ′CD 与△ABC 重合部分的面积等于△ABC 面积的4， 请直接写出△ABC 的面积．(1)证明：如解图①连接 EF ，∵四边形 ABCD 是矩形， ∴AD `BC ， ∵AE ＝BF ，∴四边形 ABFE 是平行四边形， ∴OE ＝OB ，∴△AOE 和△AOB 是友好三角形． (2)解：∵△AOE 和△DOE 是友好三角形，∴S ＝S ，AE ＝ED 1AD ＝3，△AOE △DOE ＝2 ∵△AOB 与△AOE 是友好三角形， ∴S △AOB ＝S △AOE ， ∵△AOE ≌△FOB ，第 3 题图 第 3 题解图①2 2 2 2∴S △AOE ＝S △FOB ，∴S △AOD ＝S △ABF ，∴S ＝S－2S＝4×6－1＝12. 四边形 CDOF探究：矩形 ABCD△ABF2×2×4×3解：△ABC 的面积为 2 或 2 3.； [解法提示]分为两种情况：①如解图②， ∵S △ACD ＝S △BCD ， ∴AD ＝BD ＝1AB ，∵△ACD 沿 CD 所在直线翻折．得到△A ′CD ，∴AD ＝A ′D 1 AB1×4＝2，＝2 ＝2∵△A ′CD 与△ABC 重合部分的面积等于△ABC 1面积的4，∴S1 1 1 1△DOC ＝4S △ABC ＝2S △BDC ＝2S △ADC ＝2S △A ′DC ， ∴DO ＝OB ，A ′O ＝CO ， ∴四边形 A ′DCB 是平行四边形， ∴BC ＝A ′D ＝2，过 B 作 BM ⊥AC 于点 M ， ∵AB ＝4，∠BAC ＝30°， ∴BM ＝1 AB ＝2＝BC ，即点 C 和点 M 重合， ∴∠ACB ＝90°，由勾股定理得：AC ＝ 42－22＝2 3，∴△ABC 的面积是1×BC ×AC 1 ＝2×2×2 3＝2 3；②如解图③， ∵S △ACD ＝S △BCD . ∴AD ＝BD ＝1 AB ，∵△ACD 沿 CD 所在直线翻折． 得到△A ′CD ，∴AD ＝A ′D 1 AB1×4＝2，＝2 ＝2第 3 题解图②第 3 题解图③第 4 题图2∵△A ′CD 与△ABC 重合部分的面积等于△ABC 1面积的4，∴S1 1 1 1△DOC ＝4S △ABC ＝2S △BDC ＝2S △ADC ＝2S △A ′DC ， ∴DO ＝OA ′，BO ＝CO ， ∴四边形 A ′BDC 是平行四边形， ∴A ′C ＝BD ＝2，过 C 作 CQ ⊥A ′D 于点 Q ， ∵A ′C ＝2，∠DA ′C ＝∠BAC ＝30°， ∴CQ ＝1A ′C ＝1，∴S ＝2S＝2S ＝ 1 ＝ 1＝2；△ABC△ADC△A ′DC 2×2×A ′D ×CQ 2×2×2×1综上所述，△ABC 的面积是 2 或 2 3. 4. 探索发现：(1)如图①，在△ABC 中，AD 是 BC 边上的中线，若△ABC 的面积为 S ，则△ACD 的面积为．(2)在图②中，E 、F 分别是▱ABCD 的边 AB 、BC 的中点，若▱ABCD 的面积为 S ，求四边形 BEDF 的面积，并说明理由．(3)在图③中，E 、F 分别是▱ABCD 的边 AB 、BC 上的点，且 AE 1AB ，BF 1BC ，若▱ABCD 的面积为S ，则四边形 BEDF 的面积为．解决问题：＝3 ＝3(4)如图④中，矩形 ABCD 中，AB ＝nBC (n 为常数，且 n ＞0)．E 是 AB 边上的一个动点，F 是 BC 边上的 1一个动点．若在两点运动的过程中，四边形 BEDF 的面积始终等于矩形面积的2，请探究线段 AE 、BF 应 满足怎样的数量关系，并说明理由．S解：(1)2；【解法提示】∵AD 为三角形 ABC 的底边中线， ∴DC 为 BC 的一半，2由题图可知△ABC 与△ADC 同高， 又知△ABC 面积为 S ， ∴三角形 ADC 1面积为2S ；(2)如解图①，连接 BD ，∵E ，F 分别为边 AB ，BC 的中点，∴同理(1)可知△BED 面积为△ABD 面积的一半，△BDF 面积为△BDC 面积的一半， 又∵▱ABCD 面积为 S ， ∴四边形 BEDF S面积为2；(3)S ；[解法提示]如解图②，连接 BD ，∵AE ＝1 AB ，BF 1BC ，3 ＝3∴计算同理于(2)， ∵▱ABCD 的面积为 S ，∴四边形 BEDF 1为2S .(4)如解图③，连接 BD ，由题意四边形 BEDF 的面积始终等于矩形面积的一半，第 4 题解图1 1即 AB ·BC ＝2(2BE ·AD ＋2BF ·AB )，∵AB ＝nBC ，∴AB ·BC ＝ 1 11BF ·AB )＝1 ＋BF ·AB ，∴BC ＝ 2(2BE ·n AB ＋2 1 ＋BF ，BE ·n ABBE ·n ∴1AB ＝1EB ＋BF ， n n∴AE ＝nBF .3 类型三角度问题(拓展)1.问题探究(1)如图①，AB 是⊙O 的弦，直线l 与⊙O 相交于M、N 两点，M1、M2是直线l 上异于点M、N 的两个点，则∠AMB、∠AM1B、∠AM2B 的大小关系是；第1 题图(2)如图②，AB 是⊙O 的弦，直线l 与⊙O 相切于点M，点M1是直线l 上异于点M 的任意一点，请在图②中画出图形，试判断∠AMB、∠AM1B 的大小关系，并说明理由；问题解决(3)如图③是某游乐场的平面示意图，场所保卫人员想在线段OQ 上找一点M 安装监控装置，用来监控OP 边上的AB 段，已知当∠AMB 最大时，可以让监控效果达到最佳．若∠POQ＝60°，OA＝400 m，AB ＝200 m，问在线段OQ 上是否存在一点M，使得∠AMB 最大？若存在，请求出此时∠AMB 的度数和OM 的长；若不存在，请说明理由．解：(1)∠AM1B＞∠AMB＞∠AM2B.【解法提示】如解图①，记AM2与⊙O 交于点F，连接BF，延长BM1与⊙O 交于点E，连接AE，可得∠AM1B 是△AEM1的一个外角，则∠AM1B>∠AEM1，∵∠AEM1和∠AMB 是同弧所对的圆周角，∴∠AEM1＝∠AMB，∴∠AM1B>∠AMB；同理，可得∠AFB>∠AM2B, ∠AMB＝∠AFB，∴∠AMB>∠AM2B，∴∠AM1B>∠AMB>∠AM2B.(2)∠A MB＞∠AM1B.理由如下：如解图②，在直线l 任取一点M1(不与点M 重合)，连接AM1交⊙O 于点N，连接BM1、BN，则∠AMB ＝∠ANB＞∠AM1B，∴∠AMB＞∠AM1B.第1 题解图。
中考数学专题突破-几何探究题
中考数学总复习专题十与几何图形有关的探究题试题新人教版【含解析】
专题十与几何图形相关的研究题图形变化问题【例 1】( 2016·沈阳 ) 在△ ABC中， AB＝ 6， AC＝ BC＝ 5，将△ ABC 绕点 A 按顺时针方向旋转，获得△ ADE，旋转角为α (0°＜α ＜180° )，点B的对应点为点D，点 C 的对应点为点 E，连结 BD， BE.(1)如图，当α＝ 60°时，延长 BE交 AD于点 F.①求证：△ ABD 是等边三角形；②求证： BF⊥AD， AF＝ DF；③请直接写出BE的长；(2)在旋转过程中，过点 D作 DG垂直于直线 AB，垂足为点 G，连结 CE，当∠ DAG＝∠ACB，且线段 DG与线段 AE无公共点时，请直接写出 BE＋ CE的值．剖析： (1) ①由旋转性质知 AB＝ AD，∠ BAD＝ 60°即可得证；②由 BA＝ BD，EA＝ ED依据垂直均分线的性质即可得证；③分别求出BF，EF的长即可得答案；(2) 由等量代换可证∠BAE＝∠ BAC，依据三线合一可得 CE⊥ AB，进而可得 CE＝ 2CH＝ 8， BE＝ 5，即可得答案．解： (1) ①∵△ ABC 绕点 A 顺时针方向旋转 60°获得△ ADE，∴ AB＝ AD，∠ BAD＝ 60°，∴△ ABD是等边三角形②由①得△ ABD 是等边三角形，∴ AB＝ BD，∵△ ABC绕点 A 顺时针方向旋转 60°获得△ADE，∴ AC＝ AE， BC＝ DE，又∵ AC＝ BC，∴ EA＝ ED，∴点 B， E 在 AD的垂直均分线上，∴ BE是 AD的垂直均分线，∵点 F 在 BE的延长线上，∴ BF⊥AD， AF＝DF③由②知 BF⊥AD， AF＝ DF，∴ AF＝DF＝ 3，∵ AE＝ AC＝ 5，∴ EF＝4，∵在等边三角形ABD3＝ 3 3，∴BE＝BF－EF＝ 3 3－4中， BF＝ AB·sin∠ BAF＝6×2(2)如图，∵∠ DAG＝∠ ACB，∠ DAE＝∠ BAC，∴∠ ACB＋∠ BAC＋∠ AB C＝∠ DAG＋∠ DAE ＋∠ ABC＝ 180°，又∵∠ DAG＋∠ DAE＋∠ BAE＝ 180°，∴∠ BAE＝∠ ABC，∵ AC＝ BC＝AE，∴11∠BAC＝∠ ABC，∴∠ BAE＝∠ BAC，∴ AB⊥ CE，且CH＝HE＝2CE，∵ AC＝ BC，∴ AH＝ BH＝2AB＝3，则 CE＝ 2CH＝ 8， BE＝ AE＝5，∴ BE＋ CE＝ 13几何图形中的动点问题【例 2】( 2016·达州 ) △ABC中，∠ BAC＝ 90°， AB＝ AC，点 D为直线 BC上一动点 ( 点D 不与 B， C重合 ) ，以 AD为边在 AD右边作正方形 ADEF，连结 CF.1(1)察看猜想如图 1，当点 D在线段 BC上时，① BC与 CF 的地点关系为 __垂直 __；② BC， CD， CF 之间的数目关系为 __BC＝ CD＋ CF__；(2)数学思虑如图 2，当点 D 在线段 CB的延长线上时，结论①，②能否仍旧建立？若建立，请赐予证明；若不建立，请你写出正确结论再赐予证明．(3)拓展延长如图 3，当点 D 在线段 BC的延长线上时，延长 BA交 CF于点 G，连结 GE.若已知 AB＝22，1CD＝ BC，恳求出GE的长．4剖析： (2) 依据正方形的性质获得∠BAC＝∠DAF＝90°，推出△ DAB≌△ FAC，依据全等三角形的性质以及等腰直角三角形的角的性质可获得结论；(3) 过 A 作 AH⊥BC于点 H，过 E 作 EM⊥BD 于点 M， EN⊥ CF 于点 N，先求出 AH， DH，证△ ADH≌△ DEM( AAS) 获得 EM＝DH， DM ＝AH，由等量代换获得 CN＝ EM，EN＝ CM，依据等腰直角三角形的性质获得 CG＝ BC＝4，依据勾股定理即可获得结论．解：(2)CF ⊥BC 建立；BC＝CD＋CF不建立，CD＝CF＋BC.证明：∵正方形ADEF，∴AD＝AF，∵∠BAC＝∠DAF＝90°，∴∠BAD＝∠CAF，可证△DAB≌△FAC( SAS) ，∴∠ABD＝∠ACF，∵∠BAC＝90°，AB＝ AC，∴∠ ACB＝∠ ABC＝ 45° . ∴∠ ABD＝180°－ 45°＝ 135°，∴∠ BCF ＝∠ ACF－∠ ACB ＝ 135°－ 45°＝ 90°，∴ CF⊥BC.∵ CD＝DB＋ BC， DB＝ CF，∴ CD＝ CF＋ BC(3) 过 A 作 AH⊥BC 于点 H，过 E 作 EM⊥BD 于点 M，EN⊥ CF 于点 N，∵∠ BAC＝ 90°， AB111＝AC，∴ BC＝ 2AB＝ 4，AH＝2BC＝ 2，∴CD＝4BC＝1，CH＝2BC＝ 2，∴ DH＝ 3，由 (2) 证得 BC⊥CF，CF＝ BD＝ 5，∵四边形 ADEF是正方形，∴ AD＝ DE，∠ ADE＝ 90°，∵ BC⊥ CF， EM⊥ BD， EN⊥ CF，∴四边形 CMEN是矩形，∴ NE＝ CM， EM＝ CN，∵∠ AHD＝∠ ADC＝∠ EMD＝ 90°，∴∠ ADH ＋∠ EDM＝∠EDM＋∠ DEM＝ 90°，∴∠ ADH＝∠ DEM，可证△ ADH≌△ DEM(AAS) ，∴ EM＝DH＝ 3，DM＝ AH＝ 2，∴CN＝ EM＝3， EN＝ CM＝ 3，∵∠ ABC＝ 45°，∴∠ BGC＝ 45°，∴△ BCG是等腰直角三角形，∴ CG＝BC＝ 4，∴ GN＝ 1，∴ EG＝22GN＋ EN＝ 10几何图形中的动线问题【例 3】( 2016·广东 ) 如图， BD是正方形ABCD的对角线， BC＝ 2，边 BC在其所在的直线上平移，将经过平移获得的线段记为 PQ，连结 PA，QD，并过点 Q作 QO⊥ BD，垂足为 O，连结 OA， OP.(1)请直接写出线段 BC在平移过程中，四边形 APQD是什么四边形？(2)请判断 OA，OP之间的数目关系和地点关系，并加以证明；(3)在平移变换过程中，设 y＝S△OPB， BP＝x(0 ≤ x≤ 2) ，求 y 与 x 之间的函数关系式，并求出 y 的最大值．剖析： (2) 证△ AOB≌△ POQ，可得 AO与 OP的数目与地点关系； (3) 依据等腰直角三角形2的性质可得 OE 的长，依据三角形的面积公式可得二次函数， 依据二次函数的性质可得答案．解： (1) 四边形 APQD 为平行四边形(2)OA ＝ OP ， OA ⊥ OP.证明：∵四边形 ABCD 是正方形，∴ AB ＝ BC ＝ PQ ，∠ ABO ＝∠ OBQ＝ 45 °，∵ OQ ⊥ BD ，∴∠ PQO ＝ 45°，∴∠ ABO ＝∠ OBQ ＝∠ PQO ＝ 45 °，∴ OB ＝ OQ ，可证 △AOB ≌△ POQ( ) ，∴ OA ＝OP ，∠ AOB ＝∠ POQ ，∴∠ AOP ＝∠ BOQ ＝ 90°，∴ OA ⊥ OPSASx ＋ 2(3) 过点 O 作 OE ⊥BC 于点 E. ①如图1，当 P 点在 B 点右边时，则 BQ ＝x ＋ 2， OE ＝ 2 ，1 x ＋2 121∴y ＝ 2×2 ·x ，即 y ＝4(x ＋ 1) － 4，又∵ 0≤x ≤2，∴当 x ＝ 2 时， y 有最大值为2；②如2－ x 1 2－ x1 2图 2，当 P 点在 B 点左边时，则 BQ ＝ 2－x ，OE ＝ 2 ，∴ y ＝ 2×2 ·x ，即 y ＝－ 4(x － 1)1 1＋ ，又∵ 0≤x ≤2，∴当 x ＝ 1 时， y 有最大值为. 综上所述，平移过程中△ OPB 的面积的最44大值为 21． ( 导学号 59042307)( 2016· 福州 ) 如图，矩形 ABCD 中， AB ＝ 4， AD ＝ 3， M 是边 CD 上一点，将△ ADM 沿直线 AM 对折，获得△ ANM.(1) 当 AN 均分∠ MAB 时，求 DM 的长；(2) 连结 BN ，当 DM ＝ 1 时，求△ ABN 的面积；(3) 当射线 BN 交线段 CD 于点 F 时，求 DF 的最大值．解： (1) 由折叠知△ ANM ≌△ ADM ，∴∠ MAN ＝∠ DAM ，∵ AN 均分∠ MAB ，∴∠ MAN ＝∠ NAB ，∴∠ DAM ＝∠ MAN ＝∠ NAB ，∵四边形 ABCD 是矩形，∴∠ DAB ＝90°，∴∠ DAM ＝ 30°，∴ DM＝AD · tan ∠ DAM ＝3× tan 30°＝ 3× 3＝ 33(2) 如图 1，延长 MN 交 AB 延长线于点 Q ，∵四边形 ABCD 是矩形，∴ AB ∥ DC ，∴∠ DMA＝∠ MAQ ，由折叠知△ ANM ≌△ ADM ， ∴∠ DMA ＝∠ AMQ ，AN ＝ AD ＝ 3，MN ＝ MD ＝ 1，∴∠ MAQ ＝∠ AMQ ，∴MQ ＝ AQ ，设 NQ ＝ x ，则 AQ ＝MQ ＝ 1＋x ，∵∠ ANM ＝ 90°，∴∠ ANQ ＝ 90°，在 Rt △ ANQ 中，由勾股定理得2 2 2 2 2 2AQ ＝ AN ＋NQ ，∴ (x ＋1) ＝ 3 ＋ x ，解得 x ＝4，∴ NQ ＝4， AQ ＝5，∵ AB ＝4，4 4 1 4 1 24 AQ ＝ 5，∴ S △ NAB ＝ 5S △NAQ ＝ 5× 2AN ·NQ ＝ 5×2×3×4＝ 5(3) 如图 2，过点 A 作 AH ⊥BF 于点 H ，∵四边形 ABCD 是矩形，∴ AB ∥ DC ，∴∠ HBA ＝∠ BFC ，∵∠ AHB ＝∠ BCF ＝ 90°，∴△ ABH ∽△ BFC ，∴ BH CFN ， H＝ ，∵ AH ≤ AN ＝3， AB ＝ 4，∴当点 AH BC3重合 ( 即 AH ＝AN)时， AH 最大， BH 最小， CF 最小， DF 最大，此时点 M ， F 重合， B ， N ， M 三点共线，如图 3，由折叠知 AD ＝ AH ，∵ AD ＝ BC ，∴ AH ＝ BC ，可证△ ABH ≌△ BFC( AAS )，∴ CF＝BH ，由勾股定理得 BH ＝ 2 2 2 27，∴ CF ＝ 7，∴ DF 的最大值＝ DC －CF＝ AB － AH ＝ 4 － 3 ＝ 4－ 72．( 导学号 59042308 )( 2016· 黑龙江 ) 如图，在平面直角坐标系中， 四边形 OABC 的极点 O 是坐标原点， 点 A 在第一象限， 点 C 在第四象限， 点 B 在 x 轴的正半轴上， ∠ OAB ＝90°且 OA ＝ AB ， OB ， OC 的长分别是一元二次方程 x 2－ 11x ＋ 30＝0 的两个根 (OB ＞ OC)．(1) 求点 A 和点 B 的坐标；(2) 点 P 是线段 OB 上的一个动点 ( 点 P 不与点 O ，B 重合 ) ，过点 P 的直线 l 与 y 轴平行，直线 l 交边 OA 或边 AB 于点 Q ，交边 OC 或边 BC 于点 R. 设点 P 的横坐标为 t ，线段 QR 的长度为 m ，已知 t ＝ 4 时，直线 l 恰巧过点 C ，当 0＜ t ＜ 3 时，求 m 对于 t 的函数关系式；(3) 当 m ＝ 3.5 时，请直接写出点 P 的坐标．解： (1) ∵方程 x 2－11x ＋ 30＝ 0 的解为 x 1＝ 5， x 2＝6，∴ OB ＝ 6， OC ＝5，∴ B 点坐标为(6 ， 0) ，作 AM ⊥x 轴于点 M ，∵∠ OAB ＝ 90°且 OA ＝ AB ，∴△ AOB 为等腰直角三角形，∴ OM1 ＝BM ＝ AM ＝ 2OB ＝ 3，∴ A 点坐标为 (3 ，3)(2) 作 CN ⊥ x 轴于点 N ，∵ t ＝4 时，直线 l 恰巧过点 C ，∴ ON ＝ 4，在 Rt △ OCN 中， CN ＝2 2 2 23 OC － ON ＝ 5 －4 ＝ 3，∴ C 点坐标为 (4 ，－ 3) ，可求直线 OC 的分析式为 y ＝－ 4x ，直线3 3 7 OA 的分析式为 y ＝ x ，∵ P(t ，0)(0 ＜ t ＜3) ，∴ Q(t ，t) ，R(t ，－ 4t) ，∴ QR ＝t － ( － 4t) ＝ 47 t ，即 m ＝4t(0 ＜ t ＜ 3)3 (3) 可求直线 AB 的分析式为 y ＝－ x ＋ 6，直线 BC 的分析式为 y ＝ x －9，当 0＜ t ＜ 3 时，277m ＝ 4t ，若 m ＝ 3.5 ，则 4t ＝ 3.5 ，解得 t ＝ 2，此时 P 点坐标为 (2 ， 0) ；当 3≤t ＜ 4 时， Q(t ，3 3 1 1－t ＋ 6) ，R(t ，－ t) ，∴ m ＝－ t ＋6－ ( － t) ＝－t ＋6，若 m ＝ 3.5 ，则－t ＋ 6＝3.5 ，解444433得 t ＝ 10( 不合题意舍去 ) ；当 4≤t ＜ 6 时， Q(t ，－ t ＋6) ，R(t ， t － 9) ，∴ m ＝－ t＋6－ (22552323t － 9) ＝－ 2t ＋ 15，若 m ＝ 3.5 ，则－ 2t ＋ 15＝ 3.5 ，解得 t ＝ 5 ，此时 P 点坐标为 ( 5 ，0) ．综 上所述，知足条件的P 点坐标为 (2 ， 0) 或(23， 0)543．( 导学号 59042309)( 2016·扬州 ) 已知正方形 ABCD的边长为 4，一个以点 A 为极点的 45°角绕点 A 旋转，角的两边分别与边 BC，DC的延长线交于点 E，F，连结 EF. 设 CE＝ a，CF＝ b.(1)如图 1，当∠ EAF 被对角线 AC均分时，求 a， b 的值；(2)当△ AEF 是直角三角形时，求 a， b 的值；(3)如图 3，研究∠ EAF 绕点 A 旋转的过程中 a， b 知足的关系式，并说明原因．解： (1) ∵四边形 ABCD是正方形，∴∠ BCD＝ 90°，∵ AC是正方形 ABCD的对角线，∴∠ACB＝∠ ACD＝ 45°，∴∠ ACF＝∠ ACE，∵∠ EAF 被对角线 AC 均分，∴∠ CAF＝∠ CAE，可证△ ACF≌△ ACE( ASA)，∴ AF＝CE，CF＝CE，∵ CE＝ a， CF＝ b，∴ a＝ b，∵ AF＝ CE，∴∠ AEF ＝∠ AFE，∵∠ EAF＝ 45°，∴∠ AEF＝∠ AFE＝ 67.5 °，∵ CE＝ CF，∠ ECF＝90°，∴∠ CEF ＝∠ CFE＝ 45°，∴∠ AEC＝∠ AFC＝ 22.5 °，∵∠ CAF＝∠ CAE＝ 22.5 °，∴∠ CAE＝∠ CEA，∴CE＝ AC＝4 2，即 a＝ b＝4 2(2)当△ AEF 是直角三角形时，①若∠ AEF＝ 90°，∵∠EAF＝ 45°，∴∠ AFE＝ 45°，∴△ AEF是等腰直角三角形， AE＝ EF，∵∠ AEB＋∠ BEF＝90°，∠ AEB＋∠ BAE＝90°，∴∠ BEF＝∠ BAE，可证△ ABE≌△ ECF(AAS) ，∴ AB＝EC， BE＝CF，即 a＝ AB＝ 4， b＝ BE＝BC＋ CE＝8；②若∠ AFE＝90°，同①的方法知CF＝ 4， CE＝ 8，∴a＝ 8， b＝ 4(3)ab ＝ 32. 原因：如图，∵ AC是正方形ABCD的对角线，∠ EAF＝45°，∴∠ ACD＝45°，∠ACF＝135°，∠ ACE＝135°，又∵∠ ACD＝∠ CAF＋∠ AFC，∠ EAF＝∠ EAC＋∠ FAC，∴∠ AFCAC CF22＝∠ EAC，又∵∠ ACF＝∠ ACE＝135°，∴△ ACF∽△ ECA，∴EC＝AC，∴ EC× CF＝ AC＝ 2AB＝32，∴ ab＝ 321． ( 导学号59042310)( 2016·随州 ) 喜好思虑的小茜在研究两条直线的地点关系查阅资料时，发现了“中垂三角形”，即两条中线相互垂直的三角形称为“中垂三角形”．如图1，图 2，图 3 中， AM，BN是△ ABC的中线， AM⊥BN于点 P，像△ ABC这样的三角形均为“中垂三角形”．设BC＝ a， AC＝b， AB＝ c.【特例研究】(1) 如图 1，当tan∠ PAB＝ 1， c＝4 2时， a＝ __4 5__， b＝ __4 5__；如图 2，当∠ PAB＝ 30°， c＝ 2 时， a＝ __ 7__， b＝__ 13__；5【概括证明】(2)请你察看 (1) 中的计算结果，猜想 a2，b2， c2三者之间的关系，用等式表示出来，并利用图 3 证明你的结论．【拓展证明】(3)如图 4， ?ABCD中， E， F 分别是 AD， BC 的三均分点，且 AD＝ 3AE，BC＝ 3BF，连结AF， BE， CE，且 BE⊥CE于点 E， AF 与 BE 订交点 G， AD＝35， AB＝ 3，求 AF 的长．解： (2)a 2＋ b2＝ 5c2.证明：连结MN.∵AM， BN是中线，1∴ MN∥AB， MN＝2AB，∴△ MPN∽△ APB，MPPN1∴＝＝，AP PB2设 MP＝ x， NP＝y，则 AP＝ 2x， BP＝ 2y ，2222222∴ a＝ BC＝4BM＝ 4(MP＋ BP ) ＝4x ＋ 16y，22222＝ 4y2＋ 16x2b ＝ AC＝ 4AN＝ 4(PN＋AP )，222222c ＝ AB＝ AP＋ BP＝ 4x＋ 4y，∴a2＋ b2＝20x 2＋ 20y 2＝5(4x 2＋ 4y2) ＝ 5c2(3)由 AAS可证△AGE≌△FGB，∴BG＝FG，取 AB中点 H，连结 FH 并延长交 DA的延长线于点 P，同理可证△ APH≌△ BFH，∴ AP＝BF， PE＝CF＝ 2BF，即 PE∥CF， PE＝ CF，∴四边形 CEPF是平行四边形，∴FP∥ CE，∵BE⊥CE，∴ FP⊥ BE，即 FH⊥BG，∴△ ABF是中垂三角形，由 (2) 可知 AB2＋ AF2＝5BF2，1∵AB＝3， BF＝ AD＝ 5，3∴9＋ AF2＝5×( 5) 2，∴ AF＝ 42． ( 导学号 59042311)( 2016·河南 )(1) 发现：如图 1，点 A 为线段 BC外一动点，且BC＝a， AB＝ b.填空：当点 A 位于 __CB的延长线上 __时，线段 AC 的长获得最大值，且最大值为 __a＋b__． ( 用含 a， b 的式子表示 )(2)应用：如图 2，点 A 为线段 BC外一动点，且 BC＝ 3， AB＝ 1，分别以 AB，AC为边，作等边三角形 ABD和等边三角形 ACE，连结 CD， BE.①请找出图中与BE相等的线段，并说明原因；②直接写出线段BE长的最大值．(3)拓展：如图 3，在平面直角坐标系中，点 A 的坐标为 (2 ， 0) ，点 B 的坐标为 (5 ，0) ，点 P 为线段 AB 外一动点，且 PA＝2， PM＝PB，∠ BPM＝90°，请直接写出线段 AM长的最大值及此时点 P 的坐标．6解： (2) ①CD＝ BE，原因：∵△＝∠CAE＝60 °，∴ ∠BAD＋△CAD≌△ EAB( SAS)，∴ CD＝BE ABD 与△ ACE是等边三角形，∴AD＝ AB，AC＝ AE，∠BAD ∠BAC＝∠CAE ＋∠BAC，即∠CAD＝∠EAB，可证②∵线段 BE 长的最大值＝线段 CD长的最大值，由 (1) 知，当线段 CD的长获得最大值时，点D 在 CB的延长线上，∴最大值为 BD＋ BC＝ AB＋ BC＝ 4(3)如图 1，连结 BM，将△ APM绕着点 P 顺时针旋转 90°获得△ PBN，连结 AN，则△ APN是等腰直角三角形，∴ PN＝ PA＝2， BN＝ AM，∵ A 的坐标为 (2 ， 0) ，点 B 的坐标为 (5 ， 0) ，∴OA＝ 2， OB＝ 5，∴ AB＝ 3，∴线段 AM长的最大值＝线段 BN长的最大值，∴当点 N 在线段 BA的延长线上时，线段 BN获得最大值，最大值＝ AB＋ AN，∵ AN＝2AP＝2 2，∴最大值为 2 2＋ 3. 如图 2，过 P 作 PE⊥x轴于 E，∵△ APN是等腰直角三角形，1∴PE＝ AE＝2AN＝2，∴ OE＝OA－ AE＝ 2－2，∴ P(2 －2，2)3． ( 导学号59042312)( 2016·葫芦岛 ) 如图①，在△ ABC 中，∠ BAC＝90°， AB＝ AC，点 E 在 AC上 ( 且不与点 A，C 重合 ) ，在△ ABC 的外面作△ CED，使∠ CED＝ 90°， DE＝CE，连结 AD，分别以 AB， AD为邻边作平行四边形 ABFD，连结 AF.(1)请直接写出线段 AF，AE的数目关系 __AF＝ 2AE__；(2)将△ CED绕点 C 逆时针旋转，当点 E 在线段 BC上时，如图②，连结 AE，请判断线段AF， AE的数目关系，并证明你的结论；(3) 在图②的基础上，将△ CED 绕点 C 持续逆时针旋转，请判断 (2) 问中的结论能否发生变化？若不变，联合图③写出证明过程；若变化，请说明原因．7解： (2)AF ＝ 2AE.原因：连结 EF，DF 交 BC于点 K. ∵四边形 ABFD是平行四边形，∴ AB∥DF，∴∠ DKE＝∠ ABC＝ 45°，∴∠ EKF＝ 180°－∠ DKE＝ 135°，∵∠ ADE＝ 180°－∠ EDC＝180°－ 45°＝ 135°，∴∠ EKF＝∠ ADE，∵∠ DKC＝∠ C，∴ DK＝ DC，∵ DF＝ AB＝ AC，∴ KF ＝AD，可证△ EKF≌△ EDA( SAS) ，∴ EF＝ EA，∠ KEF＝∠ AED，∴∠ FEA＝∠ BED＝ 90°，∴△ AEF是等腰直角三角形，∴ AF＝ 2AE(3)结论不变， AF＝ 2AE.原因：连结 EF，延长 FD 交 AC于点 K. ∵∠ EDF＝ 180°－∠ KDC－∠EDC＝ 135°－∠ KDC，∠ ACE＝ (90 °－∠ KDC)＋∠ DCE＝ 135°－∠ KDC，∴∠ EDF＝∠ ACE，∵DF＝AB， AB＝ AC，∴ DF＝ AC，可证△ EDF≌△ ECA( SAS) ，∴ EF＝ EA，∠ FED＝∠ AEC，∴∠FEA＝∠ DEC＝ 90°，∴△ AEF是等腰直角三角形，∴ AF＝2AE8。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
专题十与几何图形有关的探究题图形变化问题【例1】(2016·沈阳)在△ABC中，AB＝6，AC＝BC＝5，将△ABC绕点A按顺时针方向旋转，得到△ADE，旋转角为α(0°＜α＜180°)，点B的对应点为点D，点C的对应点为点E，连接BD，BE.(1)如图，当α＝60°时，延长BE交AD于点F.①求证：△ABD是等边三角形；②求证：BF⊥AD，AF＝DF；③请直接写出BE的长；(2)在旋转过程中，过点D作DG垂直于直线AB，垂足为点G，连接CE，当∠DAG＝∠ACB，且线段DG与线段AE无公共点时，请直接写出BE＋CE的值．分析：(1)①由旋转性质知AB ＝AD ，∠BAD ＝60°即可得证；②由BA ＝BD ，EA ＝ED 根据垂直平分线的性质即可得证；③分别求出BF ，EF 的长即可得答案；(2)由等量代换可证∠BAE ＝∠BAC ，根据三线合一可得CE ⊥AB ，从而可得CE ＝2CH ＝8，BE ＝5，即可得答案．解：(1)①∵△ABC 绕点A 顺时针方向旋转60°得到△ADE ，∴AB ＝AD ，∠BAD ＝60°，∴△ABD 是等边三角形②由①得△ABD 是等边三角形，∴AB ＝BD ，∵△ABC 绕点A 顺时针方向旋转60°得到△ADE ，∴AC ＝AE ，BC ＝DE ，又∵AC ＝BC ，∴EA ＝ED ，∴点B ，E 在AD 的垂直平分线上，∴BE 是AD 的垂直平分线，∵点F 在BE 的延长线上，∴BF ⊥AD ，AF ＝DF③由②知BF ⊥AD ，AF ＝DF ，∴AF ＝DF ＝3，∵AE ＝AC ＝5，∴EF ＝4，∵在等边三角形ABD 中，BF ＝AB ·sin ∠BAF ＝6×32＝33，∴BE ＝BF －EF ＝33－4 (2)如图，∵∠DAG ＝∠ACB ，∠DAE ＝∠BAC ，∴∠ACB ＋∠BAC ＋∠ABC ＝∠DAG＋∠DAE ＋∠ABC ＝180°，又∵∠DAG ＋∠DAE ＋∠BAE ＝180°，∴∠BAE ＝∠ABC ，∵AC ＝BC ＝AE ，∴∠BAC ＝∠ABC ，∴∠BAE ＝∠BAC ，∴AB ⊥CE ，且CH ＝HE ＝12CE ，∵AC ＝BC ，∴AH ＝BH ＝12AB ＝3，则CE ＝2CH ＝8，BE ＝AE ＝5，∴BE ＋CE ＝13几何图形中的动点问题【例2】(2016·达州)△ABC 中，∠BAC ＝90°，AB ＝AC ，点D 为直线BC 上一动点(点D 不与B ，C 重合)，以AD 为边在AD 右侧作正方形ADEF ，连接CF.(1)观察猜想如图1，当点D 在线段BC 上时，①BC 与CF 的位置关系为__垂直__；②BC ，CD ，CF 之间的数量关系为__BC ＝CD ＋CF__；(2)数学思考如图2，当点D 在线段CB 的延长线上时，结论①，②是否仍然成立？若成立，请给予证明；若不成立，请你写出正确结论再给予证明．(3)拓展延伸如图3，当点D 在线段BC 的延长线上时，延长BA 交CF 于点G ，连接GE.若已知AB＝22，CD ＝14BC ，请求出GE 的长．分析：(2)根据正方形的性质得到∠BAC ＝∠DAF ＝90°，推出△DAB ≌△FAC ，根据全等三角形的性质以及等腰直角三角形的角的性质可得到结论；(3)过A 作AH ⊥BC 于点H ，过E 作EM ⊥BD 于点M ，EN ⊥CF 于点N ，先求出AH ，DH ，证△ADH ≌△DEM(AAS )得到EM ＝DH ，DM ＝AH ，由等量代换得到CN ＝EM ，EN ＝CM ，根据等腰直角三角形的性质得到CG ＝BC ＝4，根据勾股定理即可得到结论．解：(2)CF ⊥BC 成立；BC ＝CD ＋CF 不成立，CD ＝CF ＋BC.证明：∵正方形ADEF ，∴AD ＝AF ，∵∠BAC ＝∠DAF ＝90°，∴∠BAD ＝∠CAF ，可证△DAB ≌△FAC(SAS )，∴∠ABD ＝∠ACF ，∵∠BAC ＝90°，AB ＝AC ，∴∠ACB ＝∠ABC ＝45°.∴∠ABD ＝180°－45°＝135°，∴∠BCF ＝∠ACF －∠ACB ＝135°－45°＝90°，∴CF ⊥BC.∵CD ＝DB ＋BC ，DB ＝CF ，∴CD ＝CF ＋BC(3)过A 作AH ⊥BC 于点H ，过E 作EM ⊥BD 于点M ，EN ⊥CF 于点N ，∵∠BAC ＝90°，AB ＝AC ，∴BC ＝2AB ＝4，AH ＝12BC ＝2，∴CD ＝14BC ＝1，CH ＝12BC ＝2，∴DH ＝3，由(2)证得BC ⊥CF ，CF ＝BD ＝5，∵四边形ADEF 是正方形，∴AD ＝DE ，∠ADE ＝90°，∵BC ⊥CF ，EM ⊥BD ，EN ⊥CF ，∴四边形CMEN 是矩形，∴NE ＝CM ，EM ＝CN ，∵∠AHD ＝∠ADC ＝∠EMD ＝90°，∴∠ADH ＋∠EDM ＝∠EDM ＋∠DEM ＝90°，∴∠ADH ＝∠DEM ，可证△ADH ≌△DEM(AAS )，∴EM ＝DH ＝3，DM ＝AH ＝2，∴CN ＝EM ＝3，EN ＝CM ＝3，∵∠ABC ＝45°，∴∠BGC ＝45°，∴△BCG 是等腰直角三角形，∴CG ＝BC ＝4，∴GN ＝1，∴EG ＝GN 2＋EN 2＝10几何图形中的动线问题【例3】 (2016·广东)如图，BD 是正方形ABCD 的对角线，BC ＝2，边BC 在其所在的直线上平移，将通过平移得到的线段记为PQ ，连接PA ，QD ，并过点Q 作QO ⊥BD ，垂足为O ，连接OA ，OP.(1)请直接写出线段BC 在平移过程中，四边形APQD 是什么四边形？(2)请判断OA ，OP 之间的数量关系和位置关系，并加以证明；(3)在平移变换过程中，设y ＝S △OPB ，BP ＝x(0≤x ≤2)，求y 与x 之间的函数关系式，并求出y 的最大值．分析：(2)证△AOB ≌△POQ ，可得AO 与OP 的数量与位置关系；(3)根据等腰直角三角形的性质可得OE 的长，根据三角形的面积公式可得二次函数，根据二次函数的性质可得答案．解：(1)四边形APQD 为平行四边形(2)OA ＝OP ，OA ⊥OP.证明：∵四边形ABCD 是正方形，∴AB ＝BC ＝PQ ，∠ABO ＝∠OBQ ＝45°，∵OQ ⊥BD ，∴∠PQO ＝45°，∴∠ABO ＝∠OBQ ＝∠PQO ＝45°，∴OB ＝OQ ，可证△AOB ≌△POQ(SAS )，∴OA ＝OP ，∠AOB ＝∠POQ ，∴∠AOP ＝∠BOQ ＝90°，∴OA ⊥OP(3)过点O 作OE ⊥BC 于点E.①如图1，当P 点在B 点右侧时，则BQ ＝x ＋2，OE ＝x ＋22，∴y ＝12×x ＋22·x ，即y ＝14(x ＋1)2－14，又∵0≤x ≤2，∴当x ＝2时，y 有最大值为2；②如图2，当P 点在B 点左侧时，则BQ ＝2－x ，OE ＝2－x 2，∴y ＝12×2－x 2·x ，即y ＝－14(x －1)2＋14，又∵0≤x ≤2，∴当x ＝1时，y 有最大值为14.综上所述，平移过程中△OPB 的面积的最大值为21．(导学号)(2016·福州)如图，矩形ABCD中，AB＝4，AD＝3，M是边CD上一点，将△ADM沿直线AM对折，得到△ANM.(1)当AN平分∠MAB时，求DM的长；(2)连接BN，当DM＝1时，求△ABN的面积；(3)当射线BN交线段CD于点F时，求DF的最大值．解：(1)由折叠知△ANM ≌△ADM ，∴∠MAN ＝∠DAM ，∵AN 平分∠MAB ，∴∠MAN＝∠NAB ，∴∠DAM ＝∠MAN ＝∠NAB ，∵四边形ABCD 是矩形，∴∠DAB ＝90°，∴∠DAM ＝30°，∴DM ＝AD ·tan ∠DAM ＝3×tan 30°＝3×33＝ 3 (2)如图1，延长MN 交AB 延长线于点Q ，∵四边形ABCD 是矩形，∴AB ∥DC ，∴∠DMA ＝∠MAQ ，由折叠知△ANM ≌△ADM ，∴∠DMA ＝∠AMQ ，AN ＝AD ＝3，MN ＝MD ＝1，∴∠MAQ ＝∠AMQ ，∴MQ ＝AQ ，设NQ ＝x ，则AQ ＝MQ ＝1＋x ，∵∠ANM ＝90°，∴∠ANQ ＝90°，在Rt △ANQ 中，由勾股定理得AQ 2＝AN 2＋NQ 2，∴(x ＋1)2＝32＋x 2，解得x ＝4，∴NQ ＝4，AQ ＝5，∵AB ＝4，AQ ＝5，∴S △NAB ＝45S △NAQ ＝45×12AN·NQ ＝45×12×3×4＝245(3)如图2，过点A 作AH ⊥BF 于点H ，∵四边形ABCD 是矩形，∴AB ∥DC ，∴∠HBA＝∠BFC ，∵∠AHB ＝∠BCF ＝90°，∴△ABH ∽△BFC ，∴BH AH ＝CF BC，∵AH ≤AN ＝3，AB ＝4，∴当点N ，H 重合(即AH ＝AN)时，AH 最大，BH 最小，CF 最小，DF 最大，此时点M ，F 重合，B ，N ，M 三点共线，如图3，由折叠知AD ＝AH ，∵AD ＝BC ，∴AH ＝BC ，可证△ABH ≌△BFC(AAS )，∴CF ＝BH ，由勾股定理得BH ＝AB 2－AH 2＝42－32＝7，∴CF ＝7，∴DF 的最大值＝DC －CF ＝4－72．(导学号)(2016·黑龙江)如图，在平面直角坐标系中，四边形OABC的顶点O是坐标原点，点A在第一象限，点C在第四象限，点B在x轴的正半轴上，∠OAB＝90°且OA＝AB，OB，OC的长分别是一元二次方程x2－11x＋30＝0的两个根(OB＞OC)．(1)求点A和点B的坐标；(2)点P是线段OB上的一个动点(点P不与点O，B重合)，过点P的直线l与y轴平行，直线l交边OA或边AB于点Q，交边OC或边BC于点R.设点P的横坐标为t，线段QR的长度为m，已知t＝4时，直线l恰好过点C，当0＜t＜3时，求m关于t的函数关系式；(3)当m＝3.5时，请直接写出点P的坐标．解：(1)∵方程x 2－11x ＋30＝0的解为x 1＝5，x 2＝6，∴OB ＝6，OC ＝5，∴B 点坐标为(6，0)，作AM ⊥x 轴于点M ，∵∠OAB ＝90°且OA ＝AB ，∴△AOB 为等腰直角三角形，∴OM ＝BM ＝AM ＝12OB ＝3，∴A 点坐标为(3，3) (2)作CN ⊥x 轴于点N ，∵t ＝4时，直线l 恰好过点C ，∴ON ＝4，在Rt △OCN 中，CN ＝OC 2－ON 2＝52－42＝3，∴C 点坐标为(4，－3)，可求直线OC 的解析式为y ＝－34x ，直线OA 的解析式为y ＝x ，∵P(t ，0)(0＜t ＜3)，∴Q(t ，t)，R(t ，－34t)，∴QR ＝t －(－34t)＝74t ，即m ＝74t(0＜t ＜3) (3)可求直线AB 的解析式为y ＝－x ＋6，直线BC 的解析式为y ＝32x －9，当0＜t ＜3时，m ＝74t ，若m ＝3.5，则74t ＝3.5，解得t ＝2，此时P 点坐标为(2，0)；当3≤t ＜4时，Q(t ，－t ＋6)，R(t ，－34t)，∴m ＝－t ＋6－(－34t)＝－14t ＋6，若m ＝3.5，则－14t ＋6＝3.5，解得t ＝10(不合题意舍去)；当4≤t ＜6时，Q(t ，－t ＋6)，R(t ，32t －9)，∴m ＝－t ＋6－(32t －9)＝－52t ＋15，若m ＝3.5，则－52t ＋15＝3.5，解得t ＝235，此时P 点坐标为(235，0)．综上所述，满足条件的P 点坐标为(2，0)或(235，0)3．(导学号 )(2016·扬州)已知正方形ABCD 的边长为4，一个以点A 为顶点的45°角绕点A 旋转，角的两边分别与边BC ，DC 的延长线交于点E ，F ，连接EF.设CE ＝a ，CF ＝b.(1)如图1，当∠EAF 被对角线AC 平分时，求a ，b 的值；(2)当△AEF 是直角三角形时，求a ，b 的值；(3)如图3，探索∠EAF 绕点A 旋转的过程中a ，b 满足的关系式，并说明理由．解：(1)∵四边形ABCD 是正方形，∴∠BCD ＝90°，∵AC 是正方形ABCD 的对角线，∴∠ACB ＝∠ACD ＝45°，∴∠ACF ＝∠ACE ，∵∠EAF 被对角线AC 平分，∴∠CAF ＝∠CAE ，可证△ACF ≌△ACE(ASA )，∴AF ＝CE ，CF ＝CE ，∵CE ＝a ，CF ＝b ，∴a ＝b ，∵AF ＝CE ，∴∠AEF ＝∠AFE ，∵∠EAF ＝45°，∴∠AEF ＝∠AFE ＝67.5°，∵CE ＝CF ，∠ECF ＝90°，∴∠CEF ＝∠CFE ＝45°，∴∠AEC ＝∠AFC ＝22.5°，∵∠CAF ＝∠CAE ＝22.5°，∴∠CAE ＝∠CEA ，∴CE ＝AC ＝42，即a ＝b ＝4 2(2)当△AEF 是直角三角形时，①若∠AEF ＝90°，∵∠EAF ＝45°，∴∠AFE ＝45°，∴△AEF 是等腰直角三角形，AE ＝EF ，∵∠AEB ＋∠BEF ＝90°，∠AEB ＋∠BAE ＝90°，∴∠BEF ＝∠BAE ，可证△ABE ≌△ECF(AAS )，∴AB ＝EC ，BE ＝CF ，即a ＝AB ＝4，b ＝BE ＝BC ＋CE ＝8；②若∠AFE ＝90°，同①的方法知CF ＝4，CE ＝8，∴a ＝8，b ＝4(3)ab ＝32.理由：如图，∵AC 是正方形ABCD 的对角线，∠EAF ＝45°，∴∠ACD ＝45°，∠ACF ＝135°，∠ACE ＝135°，又∵∠ACD ＝∠CAF ＋∠AFC ，∠EAF ＝∠EAC ＋∠FAC ，∴∠AFC ＝∠EAC ，又∵∠ACF ＝∠ACE ＝135°，∴△ACF ∽△ECA ，∴AC EC ＝CF AC，∴EC×CF＝AC2＝2AB2＝32，∴ab＝321．(导学号)(2016·随州)爱好思考的小茜在探究两条直线的位置关系查阅资料时，发现了“中垂三角形”，即两条中线互相垂直的三角形称为“中垂三角形”．如图1，图2，图3中，AM，BN是△ABC的中线，AM⊥BN于点P，像△ABC这样的三角形均为“中垂三角形”．设BC＝a，AC＝b，AB＝c.【特例探究】(1)如图1，当tan∠PAB＝1，c＝42时，a＝，b＝；如图2，当∠PAB＝30°，c＝2时，a＝，b＝；【归纳证明】(2)请你观察(1)中的计算结果，猜想a2，b2，c2三者之间的关系，用等式表示出来，并利用图3证明你的结论．【拓展证明】(3)如图4，▱ABCD中，E，F分别是AD，BC的三等分点，且AD＝3AE，BC＝3BF，连接AF，BE，CE，且BE⊥CE于点E，AF与BE相交点G，AD＝35，AB＝3，求AF 的长．解：(2)a 2＋b 2＝5c 2.证明：连接MN.∵AM ，BN 是中线，∴MN ∥AB ，MN ＝12AB ，∴△MPN ∽△APB ， ∴MP AP ＝PN PB ＝12， 设MP ＝x ，NP ＝y ，则AP ＝2x ，BP ＝2y ，∴a 2＝BC 2＝4BM 2＝4(MP 2＋BP 2)＝4x 2＋16y 2，b 2＝AC 2＝4AN 2＝4(PN 2＋AP 2)＝4y 2＋16x 2，c 2＝AB 2＝AP 2＋BP 2＝4x 2＋4y 2，∴a 2＋b 2＝20x 2＋20y 2＝5(4x 2＋4y 2)＝5c 2(3)由AAS 可证△AGE ≌△FGB ，∴BG ＝FG ，取AB 中点H ，连接FH 并延长交DA 的延长线于点P ，同理可证△APH ≌△BFH ， ∴AP ＝BF ，PE ＝CF ＝2BF ，即PE ∥CF ，PE ＝CF ，∴四边形CEPF 是平行四边形，∴FP ∥CE ，∵BE ⊥CE ，∴FP ⊥BE ，即FH ⊥BG ，∴△ABF 是中垂三角形，由(2)可知AB 2＋AF 2＝5BF 2，∵AB ＝3，BF ＝13AD ＝5， ∴9＋AF 2＝5×(5)2，∴AF ＝42．(导学号 )(2016·河南)(1)发现：如图1，点A 为线段BC 外一动点，且BC ＝a ，AB ＝b.填空：当点A 位于__CB 的延长线上__时，线段AC 的长取得最大值，且最大值为__a ＋b__．(用含a ，b 的式子表示)(2)应用：如图2，点A 为线段BC 外一动点，且BC ＝3，AB ＝1，分别以AB ，AC 为边，作等边三角形ABD 和等边三角形ACE ，连接CD ，BE.①请找出图中与BE 相等的线段，并说明理由；②直接写出线段BE 长的最大值．(3)拓展：如图3，在平面直角坐标系中，点A 的坐标为(2，0)，点B 的坐标为(5，0)，点P 为线段AB 外一动点，且PA ＝2，PM ＝PB ，∠BPM ＝90°，请直接写出线段AM 长的最大值及此时点P 的坐标．解：(2)①CD ＝BE ，理由：∵△ABD 与△ACE 是等边三角形，∴AD ＝AB ，AC ＝AE ，∠BAD ＝∠CAE ＝60°，∴∠BAD ＋∠BAC ＝∠CAE ＋∠BAC ，即∠CAD ＝∠EAB ，可证△CAD ≌△EAB(SAS )，∴CD ＝BE②∵线段BE 长的最大值＝线段CD 长的最大值，由(1)知，当线段CD 的长取得最大值时，点D 在CB 的延长线上，∴最大值为BD ＋BC ＝AB ＋BC ＝4(3)如图1，连接BM ，将△APM 绕着点P 顺时针旋转90°得到△PBN ，连接AN ，则△APN 是等腰直角三角形，∴PN ＝PA ＝2，BN ＝AM ，∵A 的坐标为(2，0)，点B 的坐标为(5，0)，∴OA ＝2，OB ＝5，∴AB ＝3，∴线段AM 长的最大值＝线段BN 长的最大值，∴当点N 在线段BA 的延长线上时，线段BN 取得最大值，最大值＝AB ＋AN ，∵AN ＝2AP ＝22，∴最大值为22＋3.如图2，过P 作PE ⊥x 轴于E ，∵△APN 是等腰直角三角形，∴PE ＝AE ＝12AN ＝2，∴OE ＝OA －AE ＝2－2，∴P(2－2，2)3．(导学号 )(2016·葫芦岛)如图①，在△ABC 中，∠BAC ＝90°，AB ＝AC ，点E 在AC 上(且不与点A ，C 重合)，在△ABC 的外部作△CED ，使∠CED ＝90°，DE ＝CE ，连接AD ，分别以AB ，AD 为邻边作平行四边形ABFD ，连接AF.(1)请直接写出线段AF，AE的数量关系；(2)将△CED绕点C逆时针旋转，当点E在线段BC上时，如图②，连接AE，请判断线段AF，AE的数量关系，并证明你的结论；(3)在图②的基础上，将△CED绕点C继续逆时针旋转，请判断(2)问中的结论是否发生变化？若不变，结合图③写出证明过程；若变化，请说明理由．解：(2)AF＝2AE.理由：连接EF，DF交BC于点K.∵四边形ABFD是平行四边形，∴AB∥DF，∴∠DKE＝∠ABC＝45°，∴∠EKF＝180°－∠DKE＝135°，∵∠ADE＝180°－∠EDC＝180°－45°＝135°，∴∠EKF＝∠ADE，∵∠DKC＝∠C，∴DK＝DC，∵DF＝AB＝AC，∴KF＝AD，可证△EKF≌△EDA(SAS)，∴EF＝EA，∠KEF＝∠AED，∴∠FEA＝∠BED＝90°，∴△AEF是等腰直角三角形，∴AF＝2AE(3)结论不变，AF＝2AE.理由：连接EF，延长FD交AC于点K.∵∠EDF＝180°－∠KDC －∠EDC＝135°－∠KDC，∠ACE＝(90°－∠KDC)＋∠DCE＝135°－∠KDC，∴∠EDF ＝∠ACE，∵DF＝AB，AB＝AC，∴DF＝AC，可证△EDF≌△ECA(SAS)，∴EF＝EA，∠FED＝∠AEC，∴∠FEA＝∠DEC＝90°，∴△AEF是等腰直角三角形，∴AF＝2AE。