(完整版)牛头刨床运动分析实例
例： 如图所示为一牛头刨床的机构运动简图。
设已知各构件尺寸为：1125mm l =，3600mm l =，4150mm l =，原动件1的方位角1=0~360θ︒︒和等角速度1=1rad/s w 。
试用矩阵法求该机构中各从动件的方位角、角速度和角加速度以及E 点的位移、速度和家速度的运动线图。
解：先建立一直角坐标系，并标出各杆矢量及方位角。
其中共有四个未知量3θ、4θ、3s 及E s 。
为求解需建立两个封闭矢量方程，为此需利用两个封闭图形ABCA 及CDEGC ，由此可得，613346,'E l l s l l l s +=+=+(1-1)写成投影方程为： 331133611334433446cos cos sin sin cos cos 0sin sin 'E s l s l l l l s l l l θθθθθθθθ==++-=+= (1-2)解上面方程组，即可求得3θ、4θ、3s 及E s 四个位置参数，其中23θθ=。
将上列各式对时间取一次、二次导数，并写成矩阵形式，即可得以下速度和加速度方程式。
速度方程式：3331133331131334443344cos sin 00sin sin cos 00cos 0sin sin 1000cos cos 0E s l s s l w w l l w l l v θθθθθθθθθθ⎡⎤--⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥---⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦ (1-3)机构从动件的位置参数矩阵：33333333443344cos sin 00sin cos 000sin sin 10cos cos 0s s l l l l θθθθθθθθ-⎡⎤⎢⎥⎢⎥⎢⎥---⎢⎥⎣⎦机构从动件的的速度列阵：334E s w w v ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦机构原动件的位置参数矩阵：1111sin cos 00l l θθ-⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦1w ：机构原动件的角速度加速度方程式：333333333344433443333333333333333344433344cos sin 00sin cos 000sin sin 10cos cos 0sin sin cos 00cos cos sin 000cos cos 00sin sin E s s s l l l l w s s w w s s w l w l w l w l w θθθθαθθαθθαθθθθθθθθθθ⎡⎤-⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥---⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦----=-----11131113144cos sin 000E l w s l w w w w v θθ⎡⎤⎡⎤-⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥+⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎢⎥⎣⎦(1-4)机构从动件的位置参数矩阵求导：33333333333333333444333444sin sin cos 00cos cos sin 000cos cos 00sin sin 0w s s w w s s w l w l w l w l w θθθθθθθθθθ⎡⎤---⎢⎥⎢⎥-⎢⎥⎢⎥--⎢⎥--⎢⎥⎣⎦机构从动件的的加速度列阵：334E s ααα⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦机构原动件的位置参数矩阵求导：111111cossinl wl wθθ-⎡⎤⎢⎥-⎢⎥⎢⎥⎢⎥⎣⎦主程序（matlab）：%牛头刨床运动分析主程序s;%x(1)——代表3θ；%x(2)——代表构件3的转角3θ；%x(3）——代表构件4的转角4s;%x(4)——代表E点的线位移El；%x(5)——代表1l;%x(6)——代表3l;%x(7)——代表4l;%x(8)——代表6l;%x(9）——代表'6w。
%x(10)——代表构件1的转角1x=[ 0.302 65*pi/180 169*pi/180 0.1 0.125 0.6 0.15 0.275 0.575 0];%赋初值dr=pi/180;%度转化为弧度dth=10*dr;w1=1;%每10度计算一个点for i=1:37y=ntpc(x); %调用从动件位置方程求解函数ntpc(自编)s3=y(1);theta3=y(2);theta4=y(3);se=y(4); %得到位置参数。
%将各位置参数用向量储存，便于后面绘图，角度用度表示ss3(i)=y(1);th1(i)=x(10)/dr;th3(i)=y(2)/dr;th4(i)=y(3)/dr;sse(i)=y(4);%进行速度分析A=[cos(theta3) -s3*sin(theta3) 0 0;sin(theta3) s3*cos(theta3) 0 0;0 -x(6)*sin(theta3) -x(7)*sin(theta4) -1;0 x(6)*cos(theta3) x(7)*cos(theta4) 0];%A机构从动件的位置参数矩阵B=[-x(5)*sin(x(10));x(5)*cos(x(10));0;0];%B机构原动件的位置参数列阵yy=w1*inv(A)*B;%公式1-3求解，yy表示机构从动件速度列阵，inv(A)是A的逆阵vs3=yy(1);w3=yy(2);w4=yy(3);vse=yy(4);%将各速度参数以向量的方式表示，以便后面绘图dvs3(i)=yy(1);dw3(i)=yy(2);dw4(i)=yy(3);dvse(i)=yy(4);%dA为从动件位置参数矩阵对时间一次求导%进行角速度分析dA=[-w3*sin(theta3) -vs3*sin(theta3)-s3*w3*cos(theta3) 0 0;w3*cos(theta3) vs3*cos(theta3)-s3*w3*sin(theta3) 0 0;0 -x(6)*w3*cos(theta3) -x(7)*w4*cos(theta4) 0;0 -x(6)*w3*sin(theta3) -x(7)*w4*sin(theta4) 0];%dB就是原动件位置参数列阵对时间一次求导dB=[-x(5)*w1*cos(x(10));-x(5)*w1*sin(x(10));0;0];KK=-dA*yy+w1*dB; %KK为公式1-4右端ya=inv(A)*KK;%公式1-4求解，ya为从动件加速度列阵%将各加速度以向量表示as3(i)=ya(1);atheta3(i)=ya(2);atheta4(i)=ya(3);ase(i)=ya(4);x(10)=x(10)+dth; %计算下一个点x(1)=s3;x(2)=theta3;x(3)=theta4;x(4)=se;end%绘制运动参数曲线subplot(2,2,1); % 选择第1个子窗口plot(th1,th3,th1,th4,th1,sse*1e3);%绘制位置线图subplot(2,2,2);plot(th1,dw3,th1,dw4,th1,dvse);%绘制速度线图subplot(2,2,3);plot(th1,atheta3,th1,atheta4,th1,ase); %绘制加速度线图%这个函数是关于牛头刨床位置方程求解，可得：s3,theta3,theta4,sE四个运动变量。
子程序：function y=ntpc(x)s;%x(1)——代表3θ；%x(2)——代表构件3的转角3θ；%x(3）——代表构件4的转角4s;%x(4)——代表E点的线位移El；%x(5)——代表1l;%x(6)——代表3l;%x(7)——代表4l;%x(8)——代表6l;%x(9）——代表'6w。
%x(10)——代表构件1的转角1%先赋初值；这些初值来自于主程序。
s3=x(1);theta3=x(2);theta4=x(3);se=x(4);epsilon=1e-6;%设置求解精度为10-6%用矩阵的形式表示位置方程组（4x1的矩阵）f=[s3*cos(theta3)-x(5)*cos(x(10));s3*sin(theta3)-x(5)*sin(x(10))-x(8);x(6)*cos(theta3)+x(7)*cos(theta4)-se; x(6)*sin(theta3)+x(7)*sin(theta4)-x(9)];%用牛顿-辛普森法求解while norm(f)>epsilon%J位置方程组的雅可比矩阵，即从动件位置参数矩阵J=[cos(theta3) -s3*sin(theta3) 0 0;sin(theta3) s3*cos(theta3) 0 0;0 -x(6)*sin(theta3) -x(7)*sin(theta4) -1;0 x(6)*cos(theta3) x(7)*cos(theta4) 0];dth=inv(J)*(-1.0*f); %计算增量，进行迭代，inv(J) 为J的逆阵s3=s3+dth(1);theta3=theta3+dth(2);theta4=theta4+dth(3);se=se+dth(4);f=[s3*cos(theta3)-x(5)*cos(x(10));s3*sin(theta3)-x(5)*sin(x(10))-x(8);x(6)*cos(theta3)+x(7)*cos(theta4)-se; x(6)*sin(theta3)+x(7)*sin(theta4)-x(9)]; norm(f);%若未达精度，会继续迭代。
end%输出4个参数y(1)=s3;y(2)=theta3;y(3)=theta4;y(4)=se;。
牛头刨床工作原理
牛头刨床的组成
原动部分：电动机； 传动部分：带轮机构，齿轮机构，曲轴连杆机构， 棘轮机构，螺旋机构； 执行部分：滑枕 ，工作台； 控制部分：离合手柄，变速控制手柄。
滑枕运动路线图
电动机→变速机构→摇杆机构→滑枕往复运动
牛头刨床摆动导杆机构运动简图及 自由度计算。
F 3n 2PL PH
档位 1 2 3 4 5 6
大斜 15.13 85.27 齿轮 转速 （r/mi n)
61.1
42.63 30.01 17.15
斜齿轮转速数据
快进电机参数：型号：Y801L2-4B5。功率： 0.55KW,转速：1390r/min。蜗杆头数： Z1=2，右旋。蜗轮齿数Z2=35，右旋。模 数m=2.5mm。
牛头刨床V带传动运动简图
工作台横向进给运动路线图
电动机→变速机构→棘轮进给机构→ 工作台横向进给运动。
V带传动特点分析
当量摩擦因数较大，V带传动产生的最大摩擦力 大约是平带的3倍，允许包角小，传动比较大，中 心距较小，预紧力较小；传动效率85%～95%， 带速范围20 ～ 30m/s，传递功率可达700KW， 只适合开口传动。
牛头刨床解析牛头刨床工作时装有刀架的滑枕3由床身内部的摆杆带动沿床身顶部的导轨作直线往复运动使刀具实现切削过程的主运动通过调整变速手柄5可以改变滑枕的运动速度行程长度则可通过滑枕行程调节柄6调节
牛头刨床机械系统及工 作原理PPT汇总
装备1011第6组： 王平
牛头刨床外形图及基本参数
牛头刨床主要由床身、滑枕、 刀架、工作台、横梁等组成， 如图所示。因其滑枕和刀架形 似牛头而得名。
圆锥齿轮数据
编号 14 15 16 17 18
齿数
机械基础实训2牛头刨床的设计(样本)解析
《机械基础》综合实训班级姓名学号题号组员课题二牛头刨床执行机构分析与设计设计要求与设计数据1)电动机轴与曲柄轴2平行，刨刀刀刃E点与铰链点C的垂直距离为50mm，使用寿命10年，每日一班制工作，载荷有轻微冲击。
2)为了提高工作效率，在空回程时刨刀快速退回，即要有急回运动，行程速比系数在1.4左右。
为了提高刨刀的使用寿命和工件的表面加工质量，在工作行程时，刨刀要速度平稳，切削阶段刨刀应近似匀速运动。
允许曲柄2转速偏差为±5％。
要求导杆机构的最大压力角应为最小值；3)凸轮机构的最大压力角应在许用值[α]之内，摆动从动件9的升、回程运动规律均为等加速等减速运动。
4)执行构件的传动效率按0.95计算，系统有过载保护。
按小批量生产规模设计。
5)曲柄转速在60r/min，刨刀的行程H在300mm左右为好，具体数据见下表。
(从教材第12页表中选取)[任务实施]（以教材第12页表中题号1的数据为例。
）任务一 平面机构的结构分析图4-2所示为牛头刨床的结构图，已知滑枕6的导轨高l h =1000mm ，大齿轮2的中心高l h1=540mm ，滑块销3的回转半径r x =240mm 。
绘制主体运动机构的运动简图，并通过自由度的计算，判断其运动的确定性。
解：1、机构分析。
牛头刨床主体运动机构由齿轮传动机构、导杆机构、凸轮机构、棘轮机构等组成，机构示意图如图4-17（a ）所示。
图4-17（a ） 牛头刨床主体运动机构示意图2、为了简单地说明问题，下面仅取导杆机构和凸轮机构这部分进行运动简图绘制和自由度计算。
1）确定运动副类型。
原动件曲柄与凸轮都固结在大齿轮2上，用轴通过轴承与机架7铰接成转动副O 2 ；凸轮2与滚子之间形成高副G 1，滑块3通过销子与大齿轮铰接成转动副A ；滑块3与导杆4用导轨联接为面接触成移动副Y 1；导杆分别与连杆5和机架铰接成转动副B 和O 4；连杆5与滑枕6铰接成转动副C ；滑枕6与机架1用导轨联接以面接触成移动副Y 2 。
牛头刨床运动分析
连杆机构运动分析机构运动分析的解析法有多种，其中比较常用的有矢量方程解析法、矩阵法和复数矢量法等。
用解析法作机构运动分析时，首先建立机构的位置方程，然后将其对时间求一次、二次导数，可以得到机构的速度方程和加速度方程，完成运动分析。
例3-1 图示为一牛头刨床的结构简图。
设已知各构件的尺寸为：，，，，。
并知原动件1 的方位角和等角速度。
求导杆3 的方位角，角速度及角加速度3ε和刨头5上点E 的位移，速度和加速度。
解：该牛头刨床为一个六杆机构。
先建立一直角坐标系如图，并标出各杆矢及各杆矢的方位角。
其中共有四个未知量、、、。
为求解需建立两个封闭矢量方程，为此需利用两个封闭图ABCA 及CDEGC 。
（1）求导杆3 的角位移，角速度和角加速度，由封闭形ABCA 可得写成复数形式为313126θθπi i ie s e l e l =+ （a ）展开得解上述两式可得因式中分子分母均为正，故知在第一象限。
式（a ）对时间t 求导，注意为变量，有33133311θθθωωi i i e dtds ie s ie l += （b ） 展开后可得m/srad/s （逆时针方向）再将式（b ）对时间t 求导，则有 3333133232233332112θθθθθωωεωi i i i i ie dt dse dts d es ies e l ++-=- （c ）展开后可求得1471.0/]2)s i n ([333132113=--=s dtds l ωθθωε rad/s 2 (逆时针方向)m/s 2其方向与相反。
（2）求刨头上点E 的位移，速度和加速度。
由封闭形CDEGC 可得写成复数形式为 E ii i s el el e l +=+2'64343πθθ （d ）展开得解之得由机构简图知在第二象限，故=175.3266º,而m式（d ）对时间t 求导可得dtds ie l ie l Ei i =+434433θθωω （e ） 解之得rad/s (逆时针方向)m/s其方向与相反。
牛头刨床机构方案分析
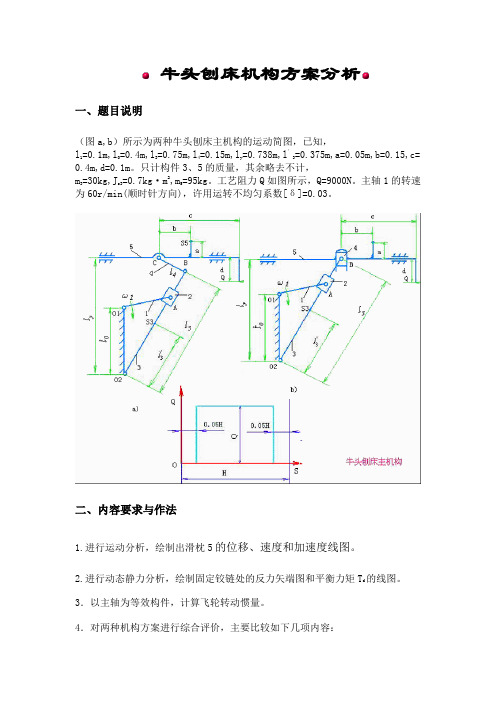
牛头刨床机构方案分析一、题目说明（图a,b）所示为两种牛头刨床主机构的运动简图，已知，l1=0.1m,l0=0.4m,l3=0.75m,l4=0.15m,l y=0.738m,l′3=0.375m,a=0.05m,b=0.15,c= 0.4m,d=0.1m。
只计构件3、5的质量，其余略去不计，m3=30kg,J s3=0.7kg·m2,m5=95kg。
工艺阻力Q如图所示，Q=9000N。
主轴1的转速为60r/min(顺时针方向)，许用运转不均匀系数[δ]=0.03。
二、内容要求与作法1.进行运动分析，绘制出滑枕5的位移、速度和加速度线图。
2.进行动态静力分析，绘制固定铰链处的反力矢端图和平衡力矩T d的线图。
3．以主轴为等效构件，计算飞轮转动惯量。
4．对两种机构方案进行综合评价，主要比较如下几项内容：工作行程中滑枕 5 的速度均匀程度。
固定铰链处的反力大小及方向变化。
平衡力矩平均值及波动情况。
飞轮转动惯量大小。
上机前认真读懂所用子程序，自编主程序，初始位置取滑枕 5 的左极限位置。
主程序中打开一数据文件“DGRAPS”，写入需要显示图形的数据。
三、课程设计说明书内容上机结束后，每位学生整理出课程设计说明书一份，其内容应包括：1.机构简图和已知条件。
2.滑枕初始位置及行程H的确定方法。
3.杆组的拆分方法及所调用的杆组子程序中虚参与实参对照表。
4.飞轮转动惯量的计算方法。
5.自编程序中主要标识符说明。
6.自编程序及计算结果清单。
7.各种线图：①滑枕的位移、速度和加速度线图，②平衡力矩线图③固定铰链处反力矢端图④等效转动惯量，等效阻力矩，等效构件角速度线图。
8.对两种方案的比较，评价。
9.以一个位置为例，用图解法做机构的运动分析，与解析法计算结果比较误差。
10．主要收获与建议。
指导教师参考上述内容提出具体要求，学生按照指导教师的要求书写并制订成册。
牛头刨床的连杆机构运动分析
牛头刨床的连杆机构运动分析0 前言机构运动分析的任务是对于结构型式及尺寸参数已定的具体机构，按主动件的位置、速度和加速度来确定从动件或从动件上指定点的位置、速度和加速度。
许多机械的运动学特性和运动参数直接关系到机械工艺动作的质量，运动参数又是机械动力学分析的依据，所以机构的运动分析是机械设计过程中必不可少的重要环节。
以计算机为手段的解析方法，由于解算速度快，精确度高，程序有一定的通用性，已成为机构运动分析的主要方法。
连杆机构作为在机械制造特别是在加工机械制造中主要用作传动的机构型式，同其他型式机构特别是凸轮机构相比具有很多优点。
连杆机构采用低副连接，结构简单，易于加工、安装并能保证精度要求。
连杆机构可以将主动件的运动通过连杆传递到与执行机构或辅助机构直接或间接相连的从动件，实现间歇运动，满足给定的运动要求，完成机器的工艺操作。
牛头刨床是一种利用工作台的横向运动和纵向往复运动来去除材料的一种切削加工机床。
工作台的纵向往复运动是机床的主运动，实现工件的切削。
工作台的横向运动即是进给运动，实现对切削精度的控制。
本文中只分析纵向运动的运动特性。
牛头刨床有很多机构组成，其中实现刨头切削运动的六连杆机构是一个关键机构。
刨床工作时，通过六杆机构驱动刨刀作往复移动。
刨刀右行时，当刨刀处于工作行程时;要求刨刀的速度较低且平稳，以减小原动机的容量和提高切削质量。
当刨刀处于返回行程时，刨刀不工作，称为空行程，此时要求刨刀的速度较高以提高生产率。
由此可见，牛头刨床的纵向运动特性对机床的性能有决定性的影响。
1 牛头刨床的六连杆机构牛头刨床有很多机构组成，其中实现刨头切削运动的六杆机构是一个关键机构。
图1所示的为一牛头刨床的六连杆机构。
杆1为原动件，刨刀装在C点上。
假设已知各构件的尺寸如表1所示，原动件1以等角速度ω1=1rad/s沿着逆时针方向回转，要求分析各从动件的角位移、角速度和角加速度以及刨刀C点的位移、速度和加速度的变化情况。
牛头刨床分析报告
2、各齿轮参数
齿顶高系数ha* 模数 压力角 齿顶高系数 2.5 20 Z3 2.5 Z4 Z5 Z6 36 Z7 42 顶隙系数c* 顶隙系数 0.625 Z8 48 Z9 71
齿轮 Z1 Z2
齿数 24 36 30 48 25
4、变速箱各档齿轮啮合
档位 齿轮传动示意图 啮合关系线图 传动比
nⅢ
四、牛头刨床连杆机构分析
1、牛头刨床连杆机构运动简图
自由度计算
F = 3 n − 2 PL − PH
F=自由度 F= n=活动构件数 (n=N-1，N=构件数） PL=低副数 PH=高副数
2牛头刨床主机构工作原理
• 牛头刨床是刨削类机床中应用较广的一种，工作时滑枕带 着刨刀，作直线住复运动，因滑枕前端的刀架形似牛头而 得名。它适合刨削中、小型零件。滑枕的移动速度是不均 匀的。滑枕的返回行程速度大于工作行程速度。由于采用 单刃刨刀加工，且在滑枕回程时不切削，牛头刨床的生产 率较低。普通牛头刨床由滑枕带着刨刀作水平直线住复运 动，刀架可在垂直面内回转一个角度，并可手动进给，工 作台带着工件作间歇的横向或垂直进给运动，常用于加工 平面、沟槽和燕尾面等。 • 牛头刨床的主运动 主运动为：电动机→变速机构（带传动机构、 主运动 齿轮传动机构）→摇杆机构→滑枕往复运动→刨刀工作； • 牛头刨床的进给运动 进给运动为：电动机→变速机构（带传动机构、 进给运动 齿轮机构）→棘轮进给机构→工作台横向进给运动（螺旋 机构）。
三、牛头刨床工作台快速进给机 构传动简图
工作台快速进给机构传动分析
• 啮合关系线图
1—2=3—4=5—6=8
传动比计算
i=z2z4z6/z1z3z5=35×17× × × 23/2×34×23=8.75 × × 螺杆转向分析
牛头刨床机械原理分析
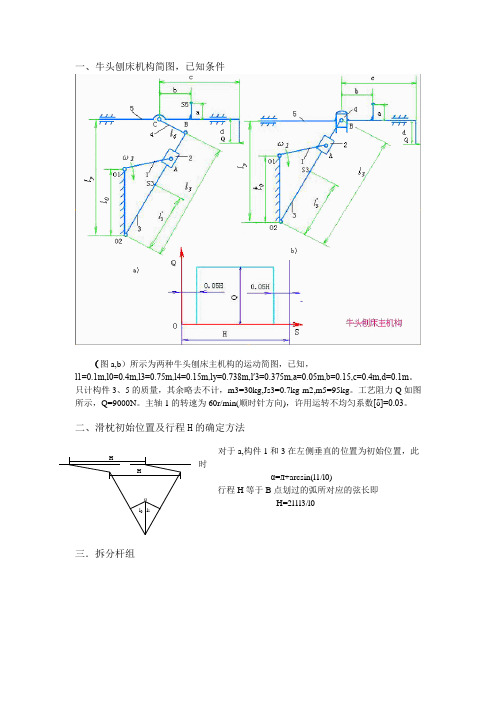
α l 1 l 0 H H 一、牛头刨床机构简图，已知条件（图a,b ）所示为两种牛头刨床主机构的运动简图，已知，l1=0.1m,l0=0.4m,l3=0.75m,l4=0.15m,ly=0.738m,l′3=0.375m,a=0.05m,b=0.15,c=0.4m,d=0.1m 。
只计构件3、5的质量，其余略去不计，m3=30kg,Js3=0.7kg·m2,m5=95kg 。
工艺阻力Q 如图所示，Q=9000N 。
主轴1的转速为60r/min(顺时针方向)，许用运转不均匀系数[δ]=0.03。
二、滑枕初始位置及行程H 的确定方法对于a,构件1和3在左侧垂直的位置为初始位置，此时 α=л+arcsin(l1/l0)行程H 等于B 点划过的弧所对应的弦长即H=2l1l3/l0三．拆分杆组四. 所调用的杆组子程序中虚参与实参对照表,源程序及运行结果4.1 a的运动分析。
源程序#include "graphics.h"/*图形库*/#include "subk.c"/*运动分析子程序*/#include "draw.c"/*绘图子程序*/main(){static double p[20][2],vp[20][2],ap[20][2],del;/*定义位置速度加速度数组和角度间隔*/ static double t[10],w[10],e[10],pdraw[370],vpdraw[370],apdraw[370];/*定义角度角速度角加速度数组和位置速度加速度方向*/static int ic;double r13,r24,r45,r27,r58;double r2,vr2,ar2;int i;double pi,dr;FILE*fp;char *m[]={"p","vp","ap"};/*定义指针*/r13=0.1;r24=0.75;r45=0.15;r27=0.375;r58=0.15;/*给长度付值*/del=15;/*给角度间隔付值*/t[6]=0.0;w[6]=0.0;e[6]=0.0;/*确定初始点*/pi=4.0*atan(1.0); /*求л*/dr=pi/180.0; /*求弧度*/w[1]=-2*pi;e[1]=0.0;p[1][1]=0.0;p[1][2]=0.0;p[2][1]=0.0;p[2][2]=-0.4;p[6][1]=0.0;p[6][2]=0.338; /*赋定铰链值*/printf(" \n The Kinematic Parameters of Point 6\n");printf("No THETA1 S6 V6 A6\n");printf(" deg m m/s m/s/s\n");/*在屏幕上写表头*/if((fp=fopen("zouye's k result","w"))==NULL){printf(" Can't open this file.\n");exit(0);}/*建立并打开文件zouye's k result*/ fprintf(fp," \n The Kinematic Parameters of Point 6\n");fprintf(fp,"No THETA1 S6 V6 A6\n"); fprintf(fp," deg m m/s m/s/s");/*在文件zouye's k result中写表头*/ ic=(int)(360.0/del);for(i=0;i<=ic;i++) /*建立循环，调用运动分析子程序*/ { t[1]=(i)*del*dr-asin(0.25);bark(1,3,0,1,r13,0.0,0.0,t,w,e,p,vp,ap);rprk(1,2,3,3,2,0.0,&r2, &vr2, &ar2, t,w,e,p,vp,ap);bark(2,4,0,3,r24,0.0, 0.0,t,w,e,p,vp,ap);rrpk(0,4,6,5,4,5,6,r45 ,&r2,&vr2,&ar2,t,w,e,p,vp,ap);/*r2,vr2,ar2在子程序中已定义为指针变量，所以其前面要加&符号*/ printf("\n%2d %12.3f%12.3f%12.3f%12.3f",i+1,t[1]/dr,p[5][1],vp[5][1],ap[5][1]);/*把运算结果写屏幕上*/fprintf(fp,"\n%2d %12.3f%12.3f%12.3f%12.3f",i+1,t[1]/dr,p[5][1],vp[5][1],ap[5][1]);/*把运算结果写在文件中*/pdraw[i]=p[5][1];vpdraw[i]=vp[5][1];apdraw[i]=ap[5][1];/*将运算结果传给pdraw[i] 、vpdraw[i] 、apdraw[i]以备绘图使用*/ if((i%16)==0){getch();} /*屏幕满16行停顿*/}fclose(fp); /*关闭文件zouye's k result*/getch();draw1(del,pdraw,vpdraw,apdraw,ic); /*调用绘图程序*/}运行结果The Kinematic Parameters of Point 6No. THETA1 S6 V6 A6deg m m/s m/s/s1 -14.478 0.038 0.000 -7.5532 0.522 0.032 0.282 -6.0023 15.522 0.015 0.502 -4.5794 30.522 -0.009 0.667 -3.3965 45.522 -0.040 0.788 -2.4336 60.522 -0.074 0.872 -1.6147 75.522 -0.112 0.923 -0.8498 90.522 -0.151 0.943 -0.0679 105.522 -0.190 0.928 0.77610 120.522 -0.228 0.877 1.68911 135.522 -0.263 0.787 2.66212 150.522 -0.293 0.654 3.68413 165.522 -0.316 0.479 4.76714 180.522 -0.332 0.256 5.96715 195.522 -0.337 -0.021 7.35416 210.522 -0.329 -0.359 8.84517 225.522 -0.306 -0.752 9.85018 240.522 -0.266 -1.155 9.06619 255.522 -0.211 -1.466 5.34720 270.522 -0.147 -1.570 -0.47421 285.522 -0.084 -1.434 -5.76222 300.522 -0.030 -1.123 -8.77723 315.522 0.009 -0.734 -9.57724 330.522 0.031 -0.345 -8.92425 345.522 0.038 -0.000 -7.5534.2 a的动态静力学分析源程序#include"graphics.h" /*图形库*/#include"subk.c" /*运动分析子程序*/#include"subf.c" /*动态静力分析子程序*/#include"draw.c" /*绘图子程序*/main(){static double p[20][2],vp[20][2],ap[20][2],del;static double t[10],w[10],e[10],tbdraw[370],tb1draw[370];static double fr[20][2],fe[20][2],fk[20][2],pk[20][2];static int ic;double sita1[370],fr1draw[370],sita2[370],fr2draw[370],sita3[370],fr3draw[370];double r13,r24,r29,r45,r49,r57,r58,r411;double r2,vr2,ar2,tb,we4;int i;double pi,dr,gam7,gam8,fr1,bt1,fr2,bt2,fr3,bt3,we1,we2,we3,we5,tb1;FILE *fp;sm[1]=0.0;sm[2]=0.0;sm[3]=30.0;sm[4]=0.0;sm[5]=95.0;sj[1]=0.0;sj[2]=0.0;sj[3]=0.7;sj[4]=0.0;sj[5]=0.0;r13=0.1;r24=0.75;r45=0.15;r29=0.375,r57=0.158;r58=0.412,r49=r45/2;gam7=0.24;gam8=-0.32;w[1]=-6.3;e[1]=0.0;del=15.0;t[5]=0.0; /*赋值*/pi=4.0*atan(1.0); /*求л*/dr=pi/180.0; /*求弧度*/t[5]=t[5]*dr; /*变角度为弧度*/p[2][1]=0.00;p[2][2]=-0.40;p[8][1]=0.0;p[8][2]=0.338; /*赋定铰链值*/printf("\n The Kineto-static Analysis of a Six-bar Linkase\n");printf("NO THETA1 FR1 BT1 FR2 BT2 TB TB1\n");printf(" (deg.) (N) (deg.) (N) (deg.) (N.M) (N.M)\n");/*在屏幕上写表头*/if((fp=fopen("zouye's f result","w"))==NULL){printf("Can't open this file.\n");exit(0);} /*建立并打开文件zouye's f result*/ fprintf(fp,"\n The Kineto-static Analysis of a Six-bar Linkase\n");fprintf(fp,"NO THETA1 FR1 BT1 FR2 BT2 TB TB1\n");fprintf(fp," (deg.) (N) (deg.) (N) (deg.) (N.M) (N.M)\n");/*在文件中写表头*/ic=(int)(360.0/del);for(i=0;i<=ic;i++) /*建立循环，调用运动分析子程序*/{t[1]=(double)(i)*del*dr+3.4;bark(1,3,0,1,r13,0.0,0.0,t,w,e,p,vp,ap);rprk(1,2,3,3,2,0.0,&r2,&vr2,&ar2,t,w,e,p,vp,ap);bark(3,0,3,3,0.0,0.0,0.0,t,w,e,p,vp,ap);bark(2,0,4,2,0.0,r24,0.0,t,w,e,p,vp,ap);bark(2,0,9,2,0.0,r29,0.0,t,w,e,p,vp,ap);rrpk(1,4,6,5,4,5,6,r45,&r2,&vr2,&ar2,t,w,e,p,vp,ap);bark(4,0,11,4,0.0,r411,0.0,t,w,e,p,vp,ap);bark(5,0,7,5,0.0,r57,gam7,t,w,e,p,vp,ap);bark(4,0,5,4,0.0,r45,0.0,t,w,e,p,vp,ap);bark(5,0,8,5,0.0,r58,gam8,t,w,e,p,vp,ap);rrpf(4,6,5,11,7,0,8,8,4,5,p,vp,ap,t,w,e,fr,fk,pk);rprf(2,3,9,3,4,0,0,2,3,p,vp,ap,t,w,e,fr,fk,pk);barf(1,1,3,1,p,ap,e,fr,&tb);/*r2,vr2,ar2,tb在子程序中已定义为指针变量，所以前面要加&符号*/ fr1=sqrt(fr[1][1]*fr[1][1]+fr[1][2]*fr[1][2]);bt1=atan2(fr[1][2],fr[1][1]);fr2=sqrt(fr[2][1]*fr[2][1]+fr[2][2]*fr[2][2]);bt2=atan2(fr[2][2],fr[2][1]);fr3=sqrt(fr[3][1]*fr[3][1]+fr[3][2]*fr[3][2]);bt3=atan2(fr[3][2],fr[3][1]);/*求合力的大小和方向*/we1=-(ap[1][1]*vp[1][1]+(ap[1][2]+9.81)*vp[1][2])*sm[1]-e[1]*w[1]*sj[1];we2=-ap[9][1]*vp[9][1]*sm[2]+fe[9][1]*vp[9][1];we3=-(ap[3][1]*vp[3][1]+(ap[3][2]+9.81)*vp[3][2])*sm[3]-e[3]*w[3]*sj[3];we4=-(ap[11][1]*vp[11][1]+(ap[11][2]+9.81)*vp[11][2])*sm[4]-e[4]*w[4]*sj[4];extf(p,vp,ap,t,w,e,8,fe);we5=-ap[7][1]*vp[7][1]*sm[5]+fe[8][1]*vp[7][1];tb1=-(we1+we2+we3+we4+we5)/w[1];/*用简易方法求平衡力偶*/printf("%3d%6.0f%11.3f%11.3f%11.3f%11.3f%11.3f%11.3f\n",i,t[1]/dr,fr1,bt1/dr,fr2,bt2/dr,tb,tb1 );/*把运动结果写屏幕上*/fprintf(fp,"%3d%6.0f%11.3f%11.3f%11.3f%11.3f%11.3f%11.3f\n",i,t[1]/dr,fr1,bt1/dr,fr2,bt2/dr,tb ,tb1); /*把运动结果写入文件中*/tbdraw[i]=tb;tb1draw[i]=tb1;fr1draw[i]=fr1;fr2draw[i]=fr2;fr3draw[i]=fr3;sita1[i]=bt1;sita2[i]=bt2;sita3[i]=bt3;/*把运算结果传给tbdraw[i] tb1draw[i] fr1draw[i] fr2draw[i] fr3draw[i]以备绘图使用*/ if(i%16==0)getch(); /*屏幕满16行停顿*/}fclose(fp); /*关闭文件zouye's f result*/getch();draw2(del,tbdraw,tb1draw,ic);draw3(del,sita1,fr1draw,sita2,fr2draw,sita3,fr3draw,ic);}extf(p,vp,ap,t,w,e,nexf,fe)double p[20][2],vp[20][2],ap[20][2],t[10],w[10],e[10],fe[10][2];int nexf;{fe[nexf][2]=0.0;if(vp[nexf][1]>0){if(p[nexf][1]<0.72&&p[nexf][1]>0.38)fe[nexf][1]=-9000.0;else fe[nexf][1]=0.0;}else{fe[nexf][1]=0.0;}}The Kineto-static Analysis of a Six-bar LinkaseNO THETA1 FR1 BT1 FR2 BT2 TB TB1 (deg.) (N) (deg.) (N) (deg.) (N.M) (N.M)0 195 355.282 67.989 18.632 -165.523 -28.442 -28.4421 210 1923.754 23.436 924.150 -152.846 21.344 21.3442 225 2166.498 21.500 1124.030 -155.945 85.714 85.7143 240 2104.241 19.591 1153.267 -160.299 135.860 135.8604 255 1493.323 20.672 830.703 -166.272 121.017 121.0175 270 438.405 70.608 87.693 -173.789 14.416 14.4166 285 1392.150 158.254 760.026 -2.611 -111.834 -111.8347 300 2237.518 161.116 1214.604 -11.494 -147.706 -147.7068 315 2306.569 159.114 1189.988 -19.540 -94.948 -94.9489 330 1972.225 156.805 947.071 -25.768 -24.032 -24.03210 345 1580.374 155.081 693.725 -29.381 26.695 26.69511 360 1250.442 154.093 493.780 -29.921 54.252 54.25212 375 14248.360 -11.867 6232.520 152.281 -639.605 -639.60513 390 13939.753 -10.053 5580.259 158.149 -893.387 -893.38714 405 13734.891 -7.761 5076.677 166.790 -1090.629 -1090.62915 420 13601.753 -5.127 4765.469 177.276 -1232.061 -1232.06116 435 13529.369 -2.270 4660.370 -171.892 -1318.662 -1318.66217 450 13527.866 0.703 4734.618 -162.283 -1352.621 -1352.62118 465 13625.388 3.691 4942.696 -154.888 -1336.983 -1336.98319 480 13862.436 6.591 5254.181 -149.980 -1274.005 -1274.00520 495 14284.767 9.293 5671.992 -147.349 -1162.759 -1162.75921 510 14935.884 11.674 6229.899 -146.549 -996.859 -996.85922 525 931.348 27.133 330.571 -147.622 -62.714 -62.71423 540 1223.460 26.116 483.274 -148.826 -54.228 -54.22824 555 1570.895 24.954 687.806 -150.565 -27.678 -27.678五、飞轮转动惯量计算1、飞轮转动惯量的计算方法1）计算等效驱动力矩Td；2）计算间隔i-1，i内的盈亏功；3）计算个离散点处的盈亏功Ei；4）挑选处Emax和Emin，最大盈亏功为Emax-Emin；5）计算飞轮转动惯量Jf。
牛头刨床机构运动分析
高等机构学题目: 牛头刨床机构运动分析院系名称：机械与动力学院专业班级：机械工程学生姓名：学号：学生姓名：学号：学生姓名：学号：指导教师：2015年12 月17日目录一问题描述................................................................................................................................ - 1 -二运动分析................................................................................................................................ - 1 -2.1矢量法构建机构独立位置方程 ............................................................................. - 1 -2.2机构速度分析 ............................................................................................................. - 2 -2.3机构加速度分析......................................................................................................... - 2 -2.4机构运动线图绘制.................................................................................................... - 3 -三总结......................................................................................................................................... - 4 -附录一：Matlab程序............................................................................................................... - 4 -牛头刨床机构运动分析一 问题描述如图1-1所示的牛头刨床机构中，800h mm =，1360h mm =，2120h mm =，200AB l mm =，960CD l mm =，160DE l mm =。
机械原理牛头刨床课程设计----运动分析
机械原理牛头刨床课程设计----运动分析第一篇：机械原理牛头刨床课程设计----运动分析3的角位移l1=120;l6=240;x=-pi/6:2*pi/36:11*pi/6;y=atan((l6+l1*sin(x))./(l1*cos(x)));fori=14:1:31 y(i)=pi+y(i);end >> plot(x*180/pi,y*180/pi) E的位移 l1=120;l6=240;x=-pi/6:2*pi/36:11*pi/6;y=atan((l6+l1*sin(x))./(l1*cos(x)));for i=14:1:31 y(i)=pi+y(i);end l=466.507;l3=500;l4=97.929;a=pi-asin((l-l3*sin(y))./l4);b=l3*cos(y)+l4*cos(a);plot(x*180/pi,b) 4的角位移l1=120;l6=240;x=-pi/6:2*pi/36:11*pi/6;y=atan((l6+l1*sin(x))./(l1*cos(x)));for i=14:1:31 y(i)=pi+y(i);end l=466.507;l3=500;l4=97.929;a=pi-asin((l-l3*sin(y))./l4);>> plot(x*180/pi,a*180/pi)3的角速度l1=120;l6=240;x1=-pi/6:2*pi/36:11/6*pi;y1=l1*2*pi*(l1+l6*sin(x1))./(l6*l6+l1*l1+2*l6 *l1*sin(x1));plot(x1*180/pi,y)4的角速度l1=120;l6=240;>> x=-pi/6:2*pi/36:11*pi/6;>> y=atan((l6+l1*sin(x))./(l1*cos(x)));>> for i=14:1:31 y(i)=pi+y(i);end >> l=466.507;l3=500;l4=97.929;>> a=pi-asin((l-l3*sin(y))./l4);>>y1=l1*2*pi*(l1+l6*sin(x))./(l6*l6+l1*l1+2*l6*l1*sin(x));>>y4=(y1.*l3.*cos(y))./(l4.*cos(a));>> plot(x*180/pi,y4)E的速度l1=120;l6=240;x=-pi/6:2*pi/36:11*pi/6;y=atan((l6+l1*sin(x))./(l1*cos(x)));fori=14:1:31 y(i)=pi+y(i);end l=466.507;l3=500;l4=97.929;a=pi-asin((l-l3*sin(y))./l4);y1=l1*2*pi*(l1+l6*sin(x))./(l6*l6+l1*l1+2*l6*l1*sin(x ));>> v=-(y1.*l3.*sin(y+a))./cos(a);>> plot(x*180/pi,v)3的角加速度l1=120;l6=240;x=-pi/6:2*pi/36:11*pi/6;y3=(l6.*l6-l1.*l1).*l6.*l1.*2.*2.*pi.*pi.*cos(x)./((l6.*l6+l1.*l1+2.*l6.*l1.*sin(x)).* (l6.*l6+l1.*l1+2.*l6.*l1.*sin(x)));>>plot(x*180/pi,y3)4的角加速度>> l1=120;l6=240;x=-pi/6:2*pi/36:11*pi/6;y=atan((l6+l1*sin(x))./(l1*cos(x)));fori=14:1:31 y(i)=pi+y(i);end l=466.507;l3=500;l4=97.929;a=pi-asin((l-l3*sin(y))./l4);y1=l1*2*pi*(l1+l6*sin(x))./(l6*l6+l1*l1+2*l6*l1*sin(x ));y4=-(y1.*l3.*cos(y))./(l4.*cos(a));>> y3=(l6.*l6-l1.*l1).*l6.*l1.*2.*2.*pi.*pi.*cos(x)./((l6.*l6+l1.*l1+2.*l6.*l1.*sin(x)).* (l6.*l6+l1.*l1+2.*l6.*l1.*sin(x)));a4=((y3.*l3.*cos(y)-y1.*y1.*l3.*sin(y)).*l4.*cos(a)+y1.*l3.*l4.*cos(y).*sin(a).*y4)./((l4.*c os(a)).*(l4.*cos(a)));>> plot(x*180/pi,a4)E的加速度l1=120;l6=240;x=-pi/6:2*pi/36:11*pi/6;y=atan((l6+l1*sin(x))./(l1*cos(x)));fori=14:1:31 y(i)=pi+y(i);end l=466.507;l3=500;l4=97.929;a=asin((l-l3*sin(y))./l4);y1=l1*2*pi*(l1+l6*sin(x))./(l6*l6+l1*l1+2*l6*l1*sin(x ));y4=-(y1.*l3.*cos(y))./(l4.*cos(a));y3=(l6.*l6-l1.*l1).*l6.*l1.*2.*2.*pi.*pi.*cos(x)./((l6.*l6+l1.*l1+2.*l6.*l1.*sin(x)).* (l6.*l6+l1.*l1+2.*l6.*l1.*sin(x)));>> e=-((y3.*l3.*sin(y-a)+y1.*l3.*cos(y+a).*(y1+y4)).*cos(a)+y1.*l3.*sin(y+a).*sin(a).*y4). /(cos(a).*cos(a));>> plot(x*180/pi,e)第二篇：机械原理课程设计牛头刨床机械原理课程设计——牛头刨床设计说明书（3）待续2.6．滑块6的位移，速度，加速度随转角变化曲线§其位移，速度，加速度随转角变化曲线如图所示：三．设计方案和分析§3.1方案一3.1.1方案一的设计图3.1.2方案一的运动分析及评价（1）运动是否具有确定的运动该机构中构件n=5。
牛头刨床导杆机构运动分析方案四
牛头刨床导杆机构运动分析一、设计任务及要求:(1)已知：牛头刨床的导杆机构的曲柄每分钟转速n2，各构件尺寸及重心位置，且报头导路x-x位于导杆端点B所作圆弧的平分线上。
数据如下表所示：1、用c语言编写计算程序,对机构进行动态分析和动态显示。
2、上机调试程序并打印结果。
3、画出导杆4的角位移，角速度，角加速度的曲线。
4、编写设计计算说明书。
二、数学模型的建立如图三个向量组成封闭图形，于是有0321=+-Z Z Z按复数式可以写成a （cos α+isin α）-b(cos β+isin β)+d(cos θ3+isin θ3)=0 （1）由于θ3=90º，上式可化简为a （cos α+isin α）-b(cos β+isin β)+id=0 （2）根据（2）式中实部、虚部分别相等得acos α-bcos β=0 (3)asin α-bsin β+d=0 (4)(3)(4)联立解得 β=arctanacosaasinad + (5)b= 2adsina d a 22++ (6) 将（2）对时间求一阶导数得 ω2=β’=baω1cos(α-β) (7) υc =b ’=-a ω1sin(α-β) (8)将（2）对时间求二阶导数得 ε3=β’=b1[a ε1cos(α-β)- a ω21sin(α-β)-2υc ω2] （9) a c =b ”=-a ε1sin(α-β)-a ω21cos(α-β)+b ω22 (10)a c 即滑块沿杆方向的加速度，通常曲柄可近似看作均角速转动，则ε1=0。
三、程序框图四、程序清单及运行结果：#include<graphics.h>#include<math.h>#include<conio.h>#include<stdio.h>#define PI 3.1415926#define M PI/180#define C 2*PI*70/60#define l1 95#define l2 400#define l4 800#define l5 (0.32*l4)#define l7 l4-Ys6void dtmn();void pist(float x0,float y0,float l,float h, float theta);void slide(float x0,float y0,float x1,float h);void pirot(float x0,float y0,float l);void sgd();void cur();/****************************主函数****************************/ main(){int Q2,i=0,j=0,Q_2[72];float Q4,Q41,Q411,w3,a3,Q5,Q51;float Q511,sA,sA1,sA11,Se,w4,Ve,Se1,a4,Se11;float S_e[72],S_e1[72],S_e11[72],Q_511[72];FILE *fl;","w"))==NULL){printf("mydata.txt cannot open!\n");exit(0);}/*int gd=DETECT,gm;initgraph(&gd,&gm,"c:\\turboc2");cleardevice();*/clrscr();printf(" zhuanjiao weiyi sudu jiaojiasudu jiasudu \n");for(Q2=0;Q2<=360;Q2+=5){i++;if(i%12==0){getch();printf(" zhuanjiao weiyi sudu jiaojiasudu jiasudu \n");}if(Q2>=0&&Q2<90||Q2>270&&Q2<=360){Q4=atan((l2+l1*sin(Q2*M))/(l1*cos(Q2*M)));Q4/=M;}else if(Q2==90||Q2==270){Q4=90;}else if(Q2>90&&Q2<180){Q4=PI-atan((l2+l1*sin(Q2*M))/(-l1*cos(Q2*M)));Q4/=M;}else if(Q2>=180&&Q2<270){Q4=PI-atan((l2+l1*sin(Q2*M))/(-l1*cos(Q2*M)));Q4/=M;}if(Q4==90) sA=l2+l1;else if(Q4==270) sA=l2-l1;elsesA=l1*cos(Q2*M)/cos(Q4*M);sA1=-l1*C*sin((Q2-Q4)*M);Q41=-l1*C*cos((Q2-Q4)*M)/sA;w3=Q41;Q411=(C*C*l1*sin((Q4-Q2)*M)-w3*sA1)/sA;a3=Q411;if(((l7-l4*sin(Q4*M))/l5)>=0&&((l7-l4*sin(Q4*M))/l5)<=1)Q5=180-asin(l7-(l4*sin(Q4*M))/l5)/M;else if(((l7-l4*sin(Q4*M))/l5)>=-1&&((l7-l4*sin(Q4*M))/l5)<=0)Q5=180+asin((l7-l4*sin(Q4*M))/l5)/M;Se=l4*cos(Q4*M)+l5*cos(Q5*M);Q51=-w3*l4*cos(Q4*M)/(l5*cos(Q5*M));w4=Q51;Se1=-w3*l4*sin((Q4-Q5)*M)/cos(Q5*M);Q511=(Q41*Q41*l4*sin(Q4*M)+Q51*Q51*l5*sin(Q5*M)-Q411*l4*cos(Q4* M))/(l5*cos(Q5*M));Se11=-(a3*l4*sin((Q4-Q5)*M)+w3*w3*l4*cos((Q4-Q5)*M)-w4*w4*l5)/cos( Q5*M);S_e[j]=Se;S_e1[j]=Se1;Q_511[j]=Q511;S_e11[j]=Se11;Q_2[j]=Q2;printf("%7d % % % %\n",Q_2[j],S_e[j],S_e1[j],Q_511[j],S_e11[j]);fprintf(fl,"%7d % % % %\n",Q_2[j],S_e[j],S_e1[j],Q_511[j],S_e11[j]);}j++;fclose(fl);cur();dtmn();sgd();}/**********************sudu,jiasudu,weiyi,quxiantuhanshu*************************/void cur(){/*float w1=2*PI,L1=110,L4=135,L61=490,L3=540,L6=380; */float Q4,Q2,sA,w3,sA1,sA11,Se,Se1,Se11,a3,a4,Q411,Q5,Q51,w4;int gd=DETECT, gmode,i;initgraph(&gd,&gmode,"c:\\turboc2");clrscr();for(Q2=0;Q2<=2*PI;Q2+=1.0*PI/1000){if(Q2>=0&&Q2<PI/2||Q2>PI*1.5&&Q2<=2*PI)Q4=atan((l2+l1*sin(Q2))/(l1*cos(Q2)));else if(Q2==PI/2.0||Q2==1.5*PI)Q4=PI/2;else if(Q2>PI/2&&Q2<PI)Q4=PI-atan((l2+l1*sin(Q2))/(-l1*cos(Q2)));elseQ4=PI-atan((l2+l1*sin(Q2))/(-l1*cos(Q2)));if(Q2!=PI/2&&Q2!=1.5*PI)sA=l1*cos(Q2)/cos(Q4);else if(Q2==PI/2)sA=l1+l2;elsesA=l2-l1;/* sA1=-l1*w1*sin(Q2-Q4); */w3=l1*C*cos(Q2-Q4)/sA;Q411=(C*C*l1*sin(Q4-Q2)-2*w3*sA)/sA;a3=Q411;if(((l7-l4*sin(Q4))/l5)>=0&&((l7-l4*sin(Q4))/l5)<=1)Q5=PI-asin((l7-l4*sin(Q4))/l5);else if(((l7-l4*sin(Q4))/l5)>=-1&&((l7-l4*sin(Q4))/l5)<0)Q5=PI+asin((l7-l4*sin(Q4))/l5);Se=l4*cos(Q4)+l5*cos(Q5);Q51=-w3*l4*cos(Q4)/(l5*cos(Q5));w4=Q51;Se1=-w3*l4*sin(Q4-Q5)/cos(Q5);/*Q511=(Q41*Q41*l4*sin(Q4)+Q51*Q51*l5*sin(Q5)-Q411*Q411*l4*cos(Q4 ))/(l5*cos(Q5));*/Se11=-(a3*l4*sin(Q4-Q5)+w3*w3*l4*cos(Q4-Q5)-w4*w4*l5)/cos(Q5);line(100,200,500,200);setcolor(5);line(492,201,500,200);line(492,199,500,200);line(100,10,100,350);setcolor(5);line(99,18,100,10);line(101,18,100,10);putpixel(100+Q2*180/PI,200-Se/5,1); /*绘制位移曲线*/putpixel(100+Q2*180/PI,200-Se1/100,2); /*绘制速度曲线*/putpixel(100+Q2*180/PI,200-Se11/100,4);} /*绘制加速度曲线*/ setcolor(10);settextjustify(CENTER_TEXT,0);outtextxy(300,300,"RED___JIASUDU");outtextxy(300,330,"GREEN___SUDU");outtextxy(300,360,"BLUE___WEIYI");/* outtextxy(300,50,"SUDU JIASUDU WEIYI GUAN XI QU XIAN TU");*/outtextxy(300,50,"SUDU JIASUDU WEIYI GUAN XI QU XIAN TU");getch();closegraph();}/***************************运动模拟图函数*******************/void dtmn(){int gd=DETECT,gmode,n;initgraph(&gd,&gmode,"c:\\turboc2");cleardevice();do{setbkcolor(0);sgd();}while(!kbhit());getch();}/****************************导轨函数*********************/ void slide(float x0,float y0,float x1,float h){float xr;int i,n;xr=x0+x1;line(x0,y0,xr,y0);n=x1/h;for(i=0;i<=n;i++){moveto(x0+i*h,y0+h);lineto(x0+(i+1)*h,y0);}}/************************摇块函数*************************/ void pist(float x0,float y0,float l,float h,float theta){float x,y;x=x0-cos(theta)*l/2+h/2*sin(theta);y=y0+l/2*sin(theta)+h/2*cos(theta);moveto(x,y);linerel(l*cos(theta),-l*sin(theta)); /***绘制轮廓线******/linerel(-h*sin(theta),-h*cos(theta));linerel(-l*cos(theta),l*sin(theta));lineto(x,y);}/*************************支点函数*********************/void pirot(float x0,float y0,float l){/*float PI=3.1415926;*/float x,y;int i,n;int h=4;setcolor(4);circle(x0,y0,3);setcolor(9);x=x0-l/2;y=y0+sin(PI/3)*l;moveto(x0,y0);lineto(x,y);linerel(18,0);lineto(x0,y0);n=l/4;for(i=0;i<=n;i++){moveto(x+i*h,y+h);lineto(x+(i+1)*h,y);}}/************************连杆,摇块,导轨函数***************/ void sgd(){int i;int x04,y04,x02,y02;int l02a=l1/2;int l04b=l4/2;float xa,ya,xb,yb,xc,yc,l;float lbc=l5/2;float ss,theta;for(i=0;i<64;i++) /*****动态模拟******/;/*坐标计算*/x04=400; x02=400;y04=400; y02=225;xa=x02+l02a*cos(ss);ya=y02+l02a*sin(ss);l=sqrt((xa-x04)*(xa-x04)+(ya-y04)*(ya-y04));xb=x04+(xa-x04)*l04b/l;yb=y04+(ya-y04)*l04b/l;yc=135;xc=xb-sqrt(lbc*lbc-(yb-yc)*(yb-yc));theta=-atan((ya-y04)/(xa-x04));setcolor(4);cleardevice();circle(xb,yb,3);circle(xa,ya,3);circle(xc,yc,3);setcolor(8);line(50,135,500,135);rectangle(xc+7,yc+6,xc-7,yc-6); /*绘制滑块C*/line(x02,y02,xa,ya);line(xc,yc,xb,yb);line(xb,yb,x04,y04);setcolor(7);pirot(x02,y02,16); /*绘制支点X04,X02*/ pirot(x04,y04,16);pist(xa,ya,20,10,theta); /*绘制滑块A*/slide(60,135,100,10);slide(500,135,570,10);setcolor(8);settextstyle(3,0,2);outtextxy(200,30,"DAOGAN YUNDONG MONI");outtextxy(200,440,"PRESS ANY KEY TO RETURN");outtextxy(200,420,"PRESS BREAK TO STOP");delay(2000);}}运行结果：zhuanjiao weiyi sudu jiaojiasudu jiasudu90 -256.000 1125.473 -6.185 0.004270 -256.000 -1125.473 -6.185 0.005曲线图象及导杆图形五、课程设计总结：通过一周的课程设计，我更加了解了机械原理课程设计的各方面内容；进一步掌握了机构分析的基本知识，熟悉了机械设计的一般方法。