《物理光学与应用光学》习题及选解
物理光学与应用光学石顺祥课后问题详解

《物理光学与应用光学》习题及选解第一章习题1-1. 一个线偏振光在玻璃中传播时,表示为:i E ))65.0(10cos(10152t cz-⨯⨯=π,试求该光的频率、波长,玻璃的折射率。
1-2. 已知单色平面光波的频率为z H 1014=ν,在z = 0 平面上相位线性增加的情况如图所示。
求f x , f y , f z 。
1-3. 试确定下列各组光波表示式所代表的偏振态: (1))sin(0kz t E E x -=ω,)cos(0kz t E E y -=ω; (2) )cos(0kz t E E x -=ω,)4cos(0πω+-=kz t E E y ;(3) )sin(0kz t E E x -=ω,)sin(0kz t E E y --=ω。
1-4. 在椭圆偏振光中,设椭圆的长轴与x 轴的夹角为α,椭圆的长、短轴各为2a 1、2a 2,E x 、E y 的相位差为ϕ。
求证:ϕαcos 22tan 220000y x y x E E E E -=。
1-5.已知冕牌玻璃对0.3988μm 波长光的折射率为n = 1.52546,11m 1026.1/--⨯-=μλd dn ,求光在该玻璃中的相速和群速。
1-6. 试计算下面两种色散规律的群速度(表示式中的v 表示是相速度):(1)电离层中的电磁波,222λb c v +=,其中c 是真空中的光速,λ是介质中的电磁波波长,b 是常数。
(2)充满色散介质()(ωεε=,)(ωμμ=)的直波导管中的电磁波,222/a c c v p -=εμωω,其中c 真空中的光速,a 是与波导管截面有关的常数。
1-7. 求从折射率n = 1.52的玻璃平板反射和折射的光的偏振度。
入射光是自然光,入射角分别为︒0,︒20,︒45,0456'︒,︒90。
1-8. 若入射光是线偏振的,在全反射的情况下,入射角应为多大方能使在入射面振动和垂直入射面振动的两反射光间的相位差为极大?这个极大值等于多少?1-9. 电矢量振动方向与入射面成45°的线偏振光,入射到两种透明介质的分界面上,若入射角︒=501θ,n 1 = 1,n 2 = 1.5,则反射光的光矢量与入射面成多大的角度?若︒=601θ时,该角度又为多1-2题用图大?1-10. 若要使光经红宝石(n = 1.76)表面反射后成为完全偏振光,入射角应等于多少?求在此入射角的情况下,折射光的偏振度P t 。
物理光学与应用光学习题及选解
2 2
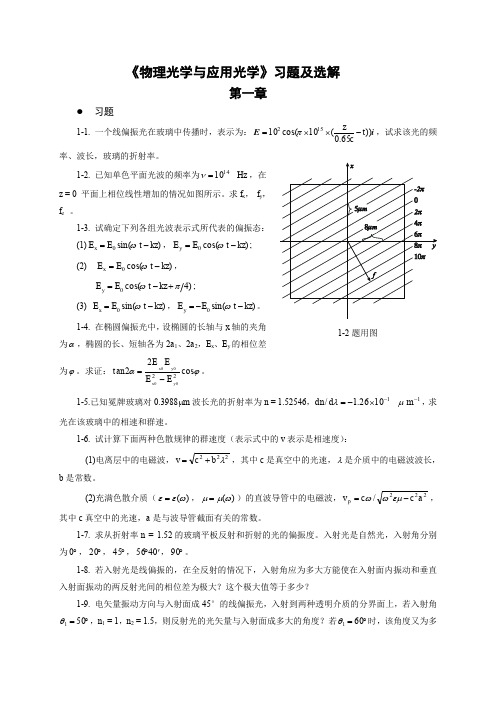
1-12. 一束自然光从空气垂直入射到玻璃表面,试计算玻璃表面的反射率 R0 = ?此反射率 R0 与 反射光波长是否有关?为什么?若光束以 45°角入射,其反射率 R45 = ?由此说明反射率与哪些因 素有关(设玻璃折射率为 1.52)? 1-13. 如图所示,当光从空气斜入射到平行平面玻璃片上时,从上、下表面反射的光 R1 和 R2 之 间相位关系如何?它们之间是否有附加的“半波程差”?对入射角大于和小于布儒斯特角的两种情 况分别进行讨论。
部分习题解答
a2 a1 2a a 2 tan 所以: tan2 2 1 22 2 1 tan 1 ( a 2 ) 2 a1 a 2 a1 2
a 1-4. 证:由图可以看出: tan 2 , a1
2E x0 E y 0 c o s E2 E2 x0 y0
在 (E 2 E2 ) sin 2 2E x 0 E y 0 cos2 cos 0 时,即交叉项系数为零时,这时的 E x ' 、 E y ' 轴即 x0 y0 为椭圆的长轴和短轴。 由 (E 2 E2 ) sin 2 2E x 0 E y 0 cos2 cos 0 x0 y0
sin 2 1 cos2 2 cos2 1 sin 2 2 2 sin 1 cos 2 cos1 sin 2 sin 2 (1 2 )
(sin1 cos 2 cos1 sin 2 ) 2 4 sin 1 cos 2 cos1 sin 2 sin 2 (1 2 ) sin 2 (1 2 ) sin 21 sin 2 2 sin 2 (1 2 )
物理光学与应用光学习题解第八章

第八章习题8-1. 身高为1.8m的人站在照相机前3.6m处拍照,若拟拍成100mm高的像,照相机镜头的焦距为多少?8-2. 单透镜成像时,若共轭距为250mm,求下列情况下透镜的焦距:(1) 实物,β=-4;(2) 实物,β=-1/4;(3) 虚物,β=-4。
8-3. 设一个光学系统处于空气中,β=-10,由物面到像面的距离为7200mm,物镜两焦点距离为1140mm,求透镜的焦距。
8-4. 一个薄透镜对某物体成实像,放大率为-1,今以另一个薄透镜紧贴在第一透镜上,则见像向透镜方向移动勒20mm,放大率为原来的3/4倍,求两块透镜的焦距。
8-5. 一透镜对无穷远处和物方焦点前5m的物体成像,二像的轴向间距为3mm,求透镜的焦距。
8-6. 位于光学系统前的一个20mm高的物体被成-12mm的倒立实像,当物体向系统方向移动100mm时,其像位于无穷远,求系统焦距。
8-7. 一薄透镜f1’=100mm和另一薄透镜f2’=50mm组合,组合焦距仍为100mm,求二者的相对位置和组合的主点位置。
8-8. 用焦距同为60mm的两个薄透镜组成目镜,两者间距为40mm,求目镜的焦距和主点位置。
8-9. 一薄透镜系统由6D和-8D的两个薄透镜组成,两者间距为30mm,求组合系统的光焦度和主点位置。
若把两透镜顺序颠倒,再求其光焦度和主点位置。
8-10. 一个球形透镜,直径为40mm,折射率为1.5,求其焦距和主点位置。
8-11. 已知透镜r1=-200mm,r2=-300mm,d=50mm,n=1.5,求其焦距和主点位置。
8-12. 有一双薄透镜系统,f1’=100mm,f2’=-50mm,要求总长度为系统焦距的0.7倍,求二透镜的间距和系统焦距。
8-13. 由两个相同的双凸厚透镜位于同一直线上,相距26mm,构成透镜的两个球面的半径分别为60mm和40mm,厚度为20mm,折射率为1.5163,求透镜组的焦距和基点的位置。
物理光学与应用光学第二版课件及课后习题答案63页PPT

37、我们唯一不会改正的缺点是软弱。——拉罗什福科
xiexie! 38、我这个人走得很慢,但是我从不后退。——亚伯拉罕·林肯
39、勿问成功的秘诀为何,且尽全力做你应该做的事吧。——美华纳
40、学而不思则罔,思而不学则殆。——孔子
物理光学与应用光学第 二版课件及课后习题答
案
6、纪律是自由的第一条件。——黑格 尔 7、纪律是集体的面貌,集体的声音, 集体的 动作, 集体的 表情, 集体的 信念。 ——马 卡连柯
8、我们现在必须完全保持党的纪律, 否则一 切都会 陷入污 泥中。 ——马 克思 9、学校没有纪律便如磨坊没有水。— —夸美 纽斯
10、一个人应该:活泼而守纪律,天 真而不 幼稚, 勇敢而 鲁莽, 倔强而 有原则 ,热情 而不冲 动,乐 观而不源自盲目。 ——马 克思谢谢!
36、自己的鞋子,自己知道紧在哪里。——西班牙
物理光学与应用光学习题解

第七章●习题7-1. 有一玻璃球,折射率为3,今有一光线射到球面上,入射角为60°,求反射光线和折射光线的夹角。
7-2. 水槽有水20cm深,槽底有一个点光源,水的折射率为1.33,水面上浮一不透明的纸片,使人从水面上任意角度观察不到光,则这一纸片的最小面积是多少?7-3. 空气中的玻璃棒,n’=1.5163,左端为一半球形,r=-20mm。
轴上有一点光源,L =-60mm。
求U=-2°的像点的位置。
7-4. 简化眼把人眼的成像归结为只有一个曲率半径为5.7mm,介质折射率为1.333的单球面折射,求这种简化眼的焦点的位置和光焦度。
7-5. 有一玻璃球,折射率为n=1.5,半径为R,放在空气中。
(1)物在无穷远时,经过球成像在何处?(2) 物在球前2R处时像在何处?像的大小如何?7-6. 一个半径为100mm的玻璃球,折射率为1.53。
球内有两个气泡,看来一个恰好在球心,另一个在球的表面和球心之间,求两个气泡的实际位置。
7-7. 一个玻璃球直径为60mm,折射率为1.5,一束平行光入射在玻璃球上,其会聚点应该在什么位置?7-8. 一球面反射镜,r=-100mm,求β=0,-0.1,-1,5,10情况下的物距和像距。
7-9. 一球面镜对其前面200mm处的物体成一缩小一倍的虚像,求该球面镜的曲率半径。
7-10. 垂直下望池塘水底的物时,若其视见深度为1m,求实际水深,已知水的折射率为4/3。
7-11. 有一等边折射率三棱镜,其折射率为1.65,求光线经该棱镜的两个折射面折射后产生最小偏向角时的入射角和最小偏向角。
●部分习题解答7-2. 解:水中的光源发出的光波在水——空气界面将发生折射,由于光波从光密介质传播到光疏介质,在界面将发生全反射,这时只有光波在界面的入射角小于水——空气界面的全反射的临界角,光线才有可能进入空气,因此界面的透光区域为一个以光源在界面上的垂7-2题用图直投影点为心的圆面,如右图,该圆面的面积即为所求纸片的最小面积。
大学_物理光学与应用光学第二版(石顺祥著)课后答案下载

物理光学与应用光学第二版(石顺祥著)课后答案下载物理光学与应用光学第二版(石顺祥著)课后答案下载《学习指导书》可以作为工科高等院校光电信息类、光学工程类学科及电子科学与技术、光信息科学与技术、光电子技术等专业的“物理光学与应用光学”、“物理光学”、“光学”等课程的教学参考书,也可以作为其它专业学习的'参考书,亦可作为相关专业考研的参考书。
物理光学与应用光学第二版(石顺祥著):内容简介点击此处下载物理光学与应用光学第二版(石顺祥著)物理光学与应用光学第二版(石顺祥著):目录第1章光在各向同性介质中的传播特性1.1 基本要求1.2 基本概念和公式1.3 典型例题1.4 习题选解第2章光的干涉2.1 基本要求2.2 基本概念和公式2.3 典型例题2.4 习题全解第3章光的衍射3.1 基本要求3.2 基本概念和公式3.3 典型例题3.4 习题选解第4章光在各向异性介质中的传播特性 4.1 基本要求4.2 基本概念和公式4.3 典型例题4.4 习题全解第5章晶体的感应双折射5.1 基本要求5.2 基本概念和公式5.3 典型例题5.4 习题全解第6章光的吸收、色散和散射6.1 基本要求6.2 基本概念和公式6.3 典型例题6.4 习题全解第7章几何光学基础7.1 基本要求7.2 基本概念和公式7.3 典型例题7.4 习题选解第8章理想光学系统8.1 基本要求8.2 基本概念和公式8.3 典型例题8.4 习题选解第9章光学系统像差基础和光路计算 9.1 基本要求9.2 基本概念和公式9.3 典型例题9.4 习题选解第10章光学仪器的基本原理10.1 基本要求10.2 基本概念和公式 10.3 典型例题10.4 习题选解。
物理光学与应用光学习题解第三章

第三章习题3-1. 由氩离子激光器发出波长λ= 488 nm 的蓝色平面光,垂直照射在一不透明屏的水平矩形孔上,此矩形孔尺寸为0.75 mm ×0.25 mm 。
在位于矩形孔附近正透镜〔f = 2.5 m 〕焦平面处的屏上观察衍射图样。
试描绘出所形成的中央最大值。
3-2. 由于衍射效应的限制,人眼能分辨某汽车两前灯时,人离汽车的最远距离l = ?〔假定两车灯相距1.22 m 。
〕3-3. 一准直的单色光束〔λ= 600 nm 〕垂直入射在直径为1.2 cm 、焦距为50 cm 的汇聚透镜上,试计算在该透镜焦平面上的衍射图样中心亮斑的角宽度和线宽度。
3-4. 〔1〕显微镜用紫外光〔λ= 275 nm 〕照明比用可见光〔λ= 550 nm 〕照明的分辨本领约大多少倍?〔2〕它的物镜在空气中的数值孔径为0.9,用用紫外光照明时能分辨的两条线之间的距离是多少?〔3〕用油浸系统〔n = 1.6〕时,这最小距离又是多少?3-5. 一照相物镜的相对孔径为1:3.5,用λ= 546 nm 的汞绿光照明。
问用分辨本领为500线 / mm 的底片来记录物镜的像是否合适?3-6. 用波长λ= 0.63m μ的激光粗测一单缝的缝宽。
若观察屏上衍射条纹左右两个第五级极小的间距是6.3cm ,屏和缝之间的距离是5m ,求缝宽。
3-7. 今测得一细丝的夫琅和费零级衍射条纹的宽度为 1 cm ,已知入射光波长为0.63m μ,透镜焦距为50 cm ,求细丝的直径。
3-8. 考察缝宽b = 8.8×10-3 cm ,双缝间隔d = 7.0×10-2 cm 、波长为0.6328m μ时的双缝衍射,在中央极大值两侧的两个衍射极小值间,将出现多少个干涉极小值?若屏离开双缝457.2 cm ,计算条纹宽度。
3-9.在双缝夫琅和费衍射实验中,所用波长λ= 632.8nm ,透镜焦距f = 50 cm ,观察到两相邻亮条纹之间的距离e = 1.5 mm ,并且第4级亮纹缺级。
物理光学与应用光学考题

中北大学《物理光学与应用光学》考试重点班级:10050141姓名:X X学号:10050141XY1、在双轴晶体中,为什么不能采用。
光与e光的称呼来区分两个正交线偏正光?(P213)当波矢k沿着除两个光轴和三个主轴方向传播时,过折射率椭球中心且垂直于k的平面与折射率椭球的截线均为椭圆,这些椭圆不具有对称性,相应的两个线偏振光的折射率都与k的方向有关,这两个光均为非常光。
故在双轴晶体中,不能采用o光与e光的称呼来区分两个正交线偏正光。
2、渥拉斯顿棱镜的工作原理:(@u2aicsin[(〃。
-代)tan。
],角随入射光波长分离的不同稍有变化);格兰-汤普森棱镜的工作原理:(格兰••汤普森棱镜利用全反射原理工作的,存在着入射光束锥角限制)。
(P223)3、简述折射率椭球的两个重要性质?折射率椭球方程是?(P206)折射率椭球的两个重要性质:①与波法线k相应的两个特许折射率於和分别等于这个椭圆的两个主轴的半轴长。
②与波法线k相应的两个特许偏振光D的振动方向/和d",分别平行于G和几。
T折射率椭球方程:工+工+工=1% W 珥4、什么是“片堆”?简述利用“片堆”产生线偏振光的工作过程?(P36)片堆是由一组平行平面玻璃片叠加在一起构成的,将一些玻璃放在圆筒内,使其表面法线与圆筒轴构成布儒斯特角。
工作过程:当自然光沿圆筒轴以布備斯特角入射并通过片堆时,因透过片堆的折射光连续不断地以相同的状态入射和折射,每通过一次界面,都从折射光中反射部分垂直纸面分量, 最后使通过片堆的透射光接近为一个平行入射面振动的线偏振光。
cD = s Q n2E L5、晶体光学的两个基本方程:(彳r),物理意义:(决定了在晶体中传播的单1—亠2色平面光波电磁波的结构,给出了沿某个k (s)方向传播的光波D (E)与晶体特性n (山)的关系)。
(P197 & P198)6、散射:光束通过不均匀介质所产生的的偏离原来传播方向像四周散射的现彖叫做光的散射;根据散射光波矢k和波长变化与否可分为两种:散射光波矢k变化,但波长不变的散射有(瑞利散射、米氏散射、分子散射);散射光波矢k和波长均变化的散射有(喇曼散射、布里渊散射);光的方向相对于入射光改变而波长也改变的散射有(喇曼散射、布里渊散射)(P286)7、什么是基模高斯光束(pl2) ?基模高斯光束的特性有哪些(pl3) ?什么是消失波?消失波具有哪些特点(p39) ?解:高斯光束:由激光器产生的激光既不是均匀平面光波,也不是均匀球面波,而是振幅和等相位面都在变化的高斯球面光波,简称高斯光束。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《物理光学与应用光学》习题及选解第一章习题1-1. 一个线偏振光在玻璃中传播时,表示为:i E ))65.0(10cos(10152t cz-⨯⨯=π,试求该光的频率、波长,玻璃的折射率。
1-2. 已知单色平面光波的频率为z H 1014=ν,在z = 0 平面上相位线性增加的情况如图所示。
求f x , f y , f z 。
1-3. 试确定下列各组光波表示式所代表的偏振态: (1))sin(0kz t E E x -=ω,)cos(0kz t E E y -=ω; (2) )cos(0kz t E E x -=ω,)4cos(0πω+-=kz t E E y ;(3) )sin(0kz t E E x -=ω,)sin(0kz t E E y --=ω。
1-4. 在椭圆偏振光中,设椭圆的长轴与x 轴的夹角为α,椭圆的长、短轴各为2a 1、2a 2,E x 、E y 的相位差为ϕ。
求证:ϕαcos 22tan 220000y x y x E E E E -=。
1-5.已知冕牌玻璃对0.3988μm 波长光的折射率为n = 1.52546,11m 1026.1/--⨯-=μλd dn ,求光在该玻璃中的相速和群速。
1-6. 试计算下面两种色散规律的群速度(表示式中的v 表示是相速度):(1)电离层中的电磁波,222λb c v +=,其中c 是真空中的光速,λ是介质中的电磁波波长,b 是常数。
(2)充满色散介质()(ωεε=,)(ωμμ=)的直波导管中的电磁波,222/a c c v p -=εμωω,其中c 真空中的光速,a 是与波导管截面有关的常数。
1-7. 求从折射率n = 1.52的玻璃平板反射和折射的光的偏振度。
入射光是自然光,入射角分别为︒0,︒20,︒45,0456'︒,︒90。
1-8. 若入射光是线偏振的,在全反射的情况下,入射角应为多大方能使在入射面内振动和垂直入射面振动的两反射光间的相位差为极大?这个极大值等于多少?1-9. 电矢量振动方向与入射面成45°的线偏振光,入射到两种透明介质的分界面上,若入射角︒=501θ,n 1 = 1,n 2 = 1.5,则反射光的光矢量与入射面成多大的角度?若︒=601θ时,该角度又为多1-2题用图大?1-10. 若要使光经红宝石(n = 1.76)表面反射后成为完全偏振光,入射角应等于多少?求在此入射角的情况下,折射光的偏振度P t 。
1-11. 如图所示,光线穿过平行平板,由n 1进入n 2的界面振幅反射系数为r ,透射系数为t ,下表面的振幅反射系数为r',透射系数为t'。
试证明:相应于平行和垂直于图面振动的光分量有:①'⊥⊥-=r r ,②'////r r -=,③1'2=+⋅⊥⊥⊥r t t ,④1'////2//=⋅+t t r ,⑤=⋅+'1////r r '////t t ⋅。
1-12. 一束自然光从空气垂直入射到玻璃表面,试计算玻璃表面的反射率R 0 = ?此反射率R 0与反射光波长是否有关?为什么?若光束以45°角入射,其反射率R 45 = ?由此说明反射率与哪些因素有关(设玻璃折射率为1.52)?1-13. 如图所示,当光从空气斜入射到平行平面玻璃片上时,从上、下表面反射的光R 1和R 2之间相位关系如何?它们之间是否有附加的“半波程差”?对入射角大于和小于布儒斯特角的两种情况分别进行讨论。
1-14. 如图所示的一根圆柱形光纤,纤芯折射率为n 1,包层折射率为n 2,且n 1 > n 2,(1)证明入射光的最大孔径角2u (保证光在纤芯和包层界面发生全反射)满足关系式: 2221sin n n u -<(2)若n 1 = 1.62,n 2 = 1.52,求最大孔径角2u = ?部分习题解答1-4. 证:由图可以看出:12tan a a =α, 所以:2221212121222)(12tan 1tan 22tan a a a a a a a a -=-=-=ααα 若要求证 220000cos 22tan y x y x E E E E -=ϕα,可以按以下方法计算:1-14题用图1-13题用图设 ⎪⎩⎪⎨⎧=+=)cos()cos(00t E E t E E y yx x ωϕω 可得: ϕϕ2002020sin cos 2)()(=-+y y x x y y x x E E E E E E E E进行坐标变换:⎪⎩⎪⎨⎧+=-=ααααcos 'sin 'sin 'cos 'y x yy x x E E E E E E 代入上面的椭圆方程: 222220)cos sin ''2sin 'cos '(y E E E E E y x y x αααα-+222220)cos sin ''2cos 'sin '(x E E E E E y x y x αααα+++ααααα222cos ''cos sin 'cos sin '(2E E E E E y x y x -+--222220)2sin ''sin 'cos '(y E E E E E y x y x ααα-+222220)2sin ''cos 'sin '(x E E E E E y x y x ααα+++ ϕϕαα22222sin cos )2cos ''22sin )''((0000y x y x E E E E E E E E y x y x =+-- )cos 2sin cos sin (')cos 2sin sin cos ('002222200222220000ϕαααϕαααy x y y x x E E E E E E E E E E x y x y +++-+ ϕϕαα22222sin )cos 2cos 22sin )((''000000y x y x y x E E E E E E E E y x =-- 在0cos 2cos 22sin )(000022=--ϕααy x y x E E E E 时,即交叉项系数为零时,这时的'x E 、'y E 轴即为椭圆的长轴和短轴。
由0cos 2cos 22sin )(000022=--ϕααy x y x E E E E 解得: ϕαcos 22tan 220000y x y x E E E E -=1-11. 证:依照Fresnel's Fomula , )sin()sin(212100θθθθ+--=s i s r E E )tan()tan(212100θθθθ+-=p i p r E E)sin(sin cos 2212100θθθθ+=s i s t E E )cos()sin(sin cos 221212100θθθθθθ-+=p i p t E E ①、②依据题意,介质平板处在同一种介质中,由Fresnel's Fomula 的前两项,可以看出不论从介质1到介质2,还是由介质2到介质1的反射,入射角和折射角调换位置后振幅反射率大小不变,要出一个负号,所以'⊥⊥-=r r ,'////r r -=。
③=⋅⊥⊥'t t )sin(sin cos 2)sin(sin cos 221122121θθθθθθθθ+⋅+=)(sin 2sin 2sin 21221θθθθ+ )(sin )(sin 2122122θθθθ+-=⊥r )(sin )sin cos cos (sin 21222121θθθθθθ+-= )(sin sin cos cos sin 2sin cos cos sin 212212122122212θθθθθθθθθθ+-+=1-4题用图)(sin sin cos cos sin 4)sin cos cos (sin 212212122121θθθθθθθθθθ+-+=)(sin 2sin 2sin )(sin 21221212θθθθθθ+-+=)(sin 2sin 2sin 121221θθθθ+-== 1-'⊥⊥⋅t t , 所以 1'2=+⋅⊥⊥⊥r t t 。
④'////t t ⋅=⋅-+)cos()sin(sin cos 2212121θθθθθθ)cos()sin(sin cos 2122112θθθθθθ-+)(cos )(sin 2sin 2sin 21221221θθθθθθ-+=)(cos )(sin )(cos )(sin )(tan )(tan 2122122122122122122//θθθθθθθθθθθθ-++-=+-=r )(cos )(sin )(cos )(sin )(cos )(sin 12122122122122122122//θθθθθθθθθθθθ-++---+=-r )(cos )(sin )sin sin cos cos cos )(sin cos cos sin cos sin (sin 42122122211122121222212θθθθθθθθθθθθθθθθ-+++=)(cos )(sin cos sin cos sin 42122121122θθθθθθθθ-+=)(cos )(sin 2sin 2sin 21221212θθθθθθ-+='////t t ⋅=, 所以 1'////2//=⋅+t t r 。
⑤因为'////r r -=, 所以'////r r ⋅1'////2//-⋅=-=t t r , 即得:=⋅+'1////r r '////t t ⋅也可以按上述方法计算:'////r r ⋅)tan()tan(2121θθθθ+-=)tan()tan(1212θθθθ+-⋅)(tan )(tan 212212θθθθ+--=)(cos )(sin 2sin 2sin 21221221θθθθθθ-+-=1-14. (1)证:由110sin sin θn u n =,得)sin arcsin(11u n n =θ,而190θθ-︒=c , 11cos )90sin(sin θθθ=-︒=c ,即可得到:12210)sin (1n nu n n >-时在光纤内表面上发生全反射, 解得:02221sin n n n u -<,在空气中n 0 = 1。
