八下数学培优( 含答案)
北师大版2020八年级数学下册期末综合复习培优测试题C(附答案)
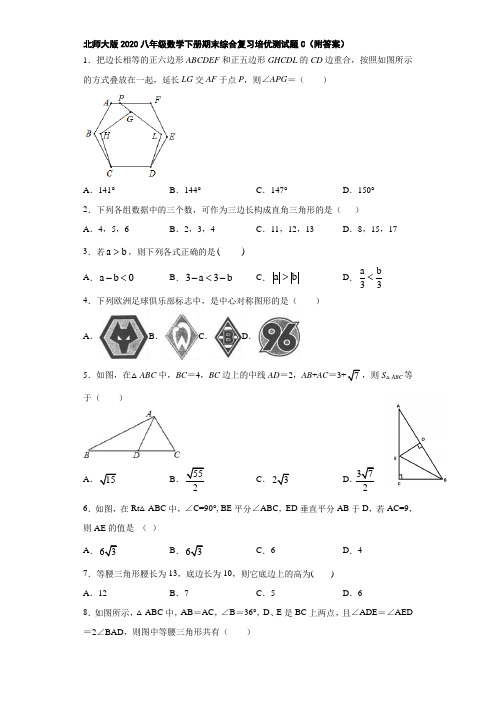
27.如图1,在四边形 中, , .
(1)求证: ;
(2)如图2,点 在线段 上,点 在线段 的延长线上,连接 , ,求证: 是 的平分线;
(3)如图3,在(2)的条件下,点 在线段 的延长线上, 的平分线 交 于点 ,若 .,求 的度数.
【详解】
解:A、∵42+52≠62,
∴以4、5、6为边不能组成直角三角形,故本选项不符合题意;
B、∵22+32≠42,
∴以2、3、4为边不能组成直角三角2≠132,
∴以11、12、13为边不能组成直角三角形,故本选项不符合题意;
D、∵82+152=172,
∴8、15、17为边能组成直角三角形,故本选项符合题意;
A.4,5,6B.2,3,4C.11,12,13D.8,15,17
3.若 ,则下列各式正确的是
A. B. C. D.
4.下列欧洲足球俱乐部标志中,是中心对称图形的是( )
A. B. C. D.
5.如图,在△ABC中,BC=4,BC边上的中线AD=2,AB+AC=3+ ,则S△ABC等于( )
A. B. C. D.
21.如图,在 中, , 是 的平分线, 于点 ,点 在 上, ,求证: .
22.如图,已知 ,请解答下列问题:
(1)利用尺规作图方法,作 的角平分线 ;(保留做图痕迹,不写作法)
(2)在(1)的条件下,若 的长为 , 的长为 ,请直接写出 与 的面积比值.
23.如图,在 中, , , 是 的角平分线, ,垂足为 .
一元二次方程 浙教版八年级数学下册期中培优训练卷1(含答案)

2021年度浙教版八年级数学下册《第2章一元二次方程》单元综合优生辅导训练1.关于x的方程x2﹣2mx﹣m﹣1=0的根的情况()A.没有实数根B.有两个不相等的实数根C.有两个相等的实数根D.不能确定2.已知m、n、3分别是等腰三角形(非等边三角形)三边的长,且m、n是关于x的一元二次方程x2﹣4x+k+2=0的两个根,则k的值等于()A.1B.﹣2C.1或2D.1或﹣23.若x0是方程ax2+2x+c=0(a≠0)的一个根,设M=2﹣ac,N=(ax0+1)2,则M与N 的大小关系正确的为()A.M>N B.M=N C.M<N D.不确定4.某初三毕业班同学之间互赠一寸相片留念,送出的相片总共2256张,如果设这个班有x 个学生,则可列方程()A.B.x(x﹣1)=2256C.(x﹣1)2=2256D.x(x+1)=22565.已知实数x满足(x2﹣2x+1)2+4(x2﹣2x+1)﹣5=0,那么x2﹣2x+1的值为()A.﹣5或1B.﹣1或5C.1D.56.如果关于x的一元二次方程ax2+bx+c=0有两个实数根,且其中一个根为另一个根的2倍,则称这样的方程为“倍根方程”,以下关于倍根方程的说法,正确的有()个.①方程x2﹣x﹣2=0是倍根方程;②若(x﹣2)(mx+n)=0是倍根方程,则4m2+5mn+n2=0;③若p、q满足pq=2,则关于x的方程px2+3x+q=0是倍根方程;④若方程ax2+bx+c=0是倍根方程,则必有2b2=9ac.A.1B.2C.3D.47.如图,在△ABC中,∠ABC=90°,AB=8cm,BC=6cm,动点P,Q分别从点A,B同时开始移动(移动方向如图所示),点P的速度为1cm/s,点Q的速度为2cm/s,点Q移动到点C后停止,点P也随之停止运动,若使△PBQ的面积为15cm2,则点P运动的时间是()A.2s B.3s C.4s D.5s8.如果一个三角形的三边长都是一元二次方程x2﹣12x+36=0的根,那么这个三角形的面积等于.9.已知矩形的长和宽分别是关于x的方程2x2+mx+8=0(m≥8)的两根,则矩形的面积是.10.如果一元二次方程x(x﹣6)=3(x﹣6)的两个根是等腰三角形的两条边的长,那么这个等腰三角形的周长为.11.等腰三角形的一边长是3,另两边的长是关于x的方程x2﹣4x+k=0的两个根,则k的值为.12.若m是方程x2﹣x﹣5=0的一个实数根,则代数式(m2﹣m)(m﹣+1)的值为.13.已知a是方程x2﹣2021x+1=0的一个根,则a3﹣2021a2﹣=.14.已知三角形的两边长分别是方程x2﹣11x+30=0的两个根,则该三角形第三边m的取值范围是.15.已知m、n是方程x2+2x﹣2021=0的两个实数根,则代数式m2+mn+3m+n=.16.方程3(x﹣4)=x(x﹣4)的解是.17.在研究:“任意给定一个矩形A,是否存在另一个矩形B,它的周长和面积分别是已知矩形周长和面积的一半”时,小明发现:当已知矩形A的长和宽分别为6和1时,存在一个矩形B的周长和面积分别是矩形A周长和面积的一半,那么矩形B的长为.18.将一元二次方程x2﹣3x+1=0变形为(x+h)2=k的形式为.19.已知关于x的一元二次方程(a﹣2)x2+2x+1=0有两个不相等的实数根,则a的取值范围是.20.某水果商场经销一种高档水果,原价每千克50元,连续两次降价后每千克32元,若每每次下降的百分率相同(1)求每次下降的百分率;(2)若每千克盈利10元,每天可售出500千克,经市场调查发现,在进货价不变的情况下,商场决定采取适当的涨价措施,若每千克涨价1元,日销售量将减少20千克,现该商场要保证每天盈利6000元,且要尽快减少库存,那么每千克应涨价多少元?21.已知关于x的方程x2+(2m﹣1)x+m2=0有实数根.(1)求m的取值范围;(2)设α,β是方程的两个实数根,是否存在实数m使得α2+β2﹣αβ=6成立?如果存在,请求出来;若不存在,请说明理由.22.已知关于x的一元二次方程x2﹣5x+m=0.(1)若方程有实数根,求实数m的取值范围;(2)若方程两实数根为x1,x2,且满足3x1﹣2x2=5,求实数m的值.23.我市南湖生态城某楼盘准备以每平方米4800元的均价对外销售,由于国务院有关房地产的新政策出台后,购房者持币观望,房地产开发商为了加快资金周转,对价格经过两次下调后,决定以每平方米3888元的均价开盘销售.(1)求平均每次下调的百分率;(2)王先生准备以开盘价均价购买一套100平方米的住房,开发商给予以下两种优惠方案:①打9.5折销售;②不打折,一次性送装修费每平方米188元,试问那种方案更优惠?24.某农科所研究出一种新型的花生摘果设备,一期研发成本为每台6万元,该摘果机的销售量y(台)与售价x(万元/台)之间存在函数关系:y=﹣x+24.(1)设这种摘果机一期销售的利润为W1(万元),问一期销售时,在抢占市场份额(提示:销量尽可能大)的前提下利润达到32万元,此时售价为多少?(2)由于环保局要求该机器必须增加除尘设备,科研所投入了7万元研究经费,使得环保达标且机器的研发成本每台降低了1万元,若科研所的销售战略保持不变,请问在二期销售中利润达到63万元时,该机器单台的售价为多少?25.如图,在△ABC中,AB=6cm,BC=7cm,∠ABC=30°,点P从A点出发,以1cm/s 的速度向B点移动,点Q从B点出发,以2cm/s的速度向C点移动.如果P、Q两点同时出发,经过几秒后△PBQ的面积等于4cm2?26.阅读下面材料:若设关于x的一元二次方程ax2+bx+c=0(a≠0)的两个根为x1,x2,那么由根与系数的关系得:x1+x2=﹣,x1x2=.∵,∴=a[x2﹣(x1+x2)x+x1x2]=a(x﹣x1)(x﹣x2).于是,二次三项式就可以分解因式ax2+bx+c=a(x﹣x1)(x﹣x2).(1)请用上面的方法将多项式4x2+8x﹣1分解因式.(2)判断二次三项式2x2﹣4x+7在实数范围内是否能利用上面的方法因式分解,并说明理由.(3)如果关于x的二次三项式mx2﹣2(m+1)x+(m+1)(1﹣m)能用上面的方法分解因式,试求出m的取值范围.27.等腰三角形边长分别为a、b、2,且a,b是关于x的一元二次方程x2﹣6x+n﹣1=0的两根,求n的值.参考答案1.解:关于x的方程x2﹣2mx﹣m﹣1=0中,a=1,b=﹣2m,c=﹣m﹣1,∴△=b2﹣4ac=(﹣2m)2﹣4×(﹣m﹣1)=(2m+1)2+3>0.∴有两个不相等的实数根.故选:B.2.解:①当m、n为腰时,m=n,∵m、n是关于x的一元二次方程x2﹣4x+k+2=0的两个根,∴方程有两个相等的实数根,∴△=(﹣4)2﹣4×1×(k+2)=0,解得:k=2;②当m和3(或n和3)是腰时,m=3,∵三角形不是等边三角形,∴此时方程有两个不相等的实数根,∵m、n是关于x的一元二次方程x2﹣4x+k+2=0的两个根,∴把m=3代入方程得9﹣12+k+2=0,解得:k=1;所以k=1或2,故选:C.3.解:∵x0是方程ax2+2x+c=0(a≠0)的一个根,∴ax02+2x0+c=0,即ax02+2x0=﹣c,则N﹣M=(ax0+1)2﹣(2﹣ac)=a2x02+2ax0+1﹣2+ac=a(ax02+2x0)+ac﹣1=﹣ac+ac﹣1=﹣1,∵﹣1<0,∴M>N,故选:A.4.解:若这个班有x个学生,则每名同学要送出贺卡(x﹣1)张,又因为是互送相片,所以总共送的张数应该是x(x﹣1)=2256.故选:B.5.解:设y=x2﹣2x+1,则y2+4y﹣5=0.整理,得(y+5)(y﹣1)=0.解得y=﹣5(舍去)或y=1.即x2﹣2x+1的值为1.故选:C.6.解:①解方程x2﹣x﹣2=0得,x1=2,x2=﹣1,得,x1≠2x2,∴方程x2﹣x﹣2=0不是倍根方程;故①不正确;②若(x﹣2)(mx+n)=0是倍根方程,x1=2,因此x2=1或x2=4,当x2=1时,m+n=0,当x2=4时,4m+n=0,∴4m2+5mn+n2=(m+n)(4m+n)=0,故②正确;③∵pq=2,则px2+3x+q=(px+1)(x+q)=0,∴,x2=﹣q,∴,因此是倍根方程,故③正确;④方程ax2+bx+c=0的根为:,,若x1=2x2,则,即,∴,∴,∴,∴9(b2﹣4ac)=b2,∴2b2=9ac.若2x1=x2时,则,则,∴,∴,∴,∴b2=9(b2﹣4ac),∴2b2=9ac.故④正确,∴正确的有:②③④共3个.故选:C.7.解:设动点P,Q运动t秒后,能使△PBQ的面积为15cm2,则BP为(8﹣t)cm,BQ为2tcm,由三角形的面积计算公式列方程得,×(8﹣t)×2t=15,解得t1=3,t2=5(当t=5时,BQ=10,不合题意,舍去).∴动点P,Q运动3秒时,能使△PBQ的面积为15cm2.故选:B.8.解:解方程x2﹣12x+36=0,得x1=x2=6.∵一个三角形的单边均满足方程x2﹣12x+36=0,∴该三角形是以6为边长的等边三角形,∴该三角形的面积为:×=9.故答案是:9.9.解:设矩形的长和宽分别为a、b,∵矩形的长和宽分别是关于x的方程2x2+mx+8=0(m≥8)的两根,∴a+b=﹣,ab==4,即矩形的面积是4,故答案为:4.10.解:解方程x(x﹣6)=3(x﹣6)得:x1=3,x2=6.当长度为3的线段为等腰三角形底边时,则腰长为6,此时三角形的周长为:6+6+3=15;当长度为6的线段为等腰三角形底边时,则腰长为3,此时3+3=6,不能构成三角形.综上所述,这个等腰三角形的周长为15.故答案是:15.11.解:当3为腰长时,将x=3代入x2﹣4x+k=0,得:32﹣4×3+k=0,解得:k=3,当k=3时,原方程为x2﹣4x+3=0,解得:x1=1,x2=3,∵1+3=4,4>3,∴k=3符合题意;当3为底边长时,关于x的方程x2﹣4x+k=0有两个相等的实数根,∴△=(﹣4)2﹣4×1×k=0,解得:k=4,当k=4时,原方程为x2﹣4x+4=0,解得:x1=x2=2,∵2+2=4,4>3,∴k=4符合题意.∴k的值为3或4.故答案是:3或4.12.解:∵m是方程x2﹣x﹣5=0的一个实数根,∴m2﹣m=5,m﹣1﹣=0,故m﹣=1,则(m2﹣m)(m﹣+1)=5×2=10.故答案为:10.13.解:∵a是方程x2﹣2021x+1=0的一个根,∴x2﹣2021x+1=0,即a2+1=2021a,a2﹣2021a=﹣1,则a3﹣2021a2﹣=a(a2﹣2021a)﹣=﹣a﹣=﹣=﹣=﹣2021.故答案是:﹣2021.14.解:∵x2﹣11x+30=0,∴(x﹣5)(x﹣6)=0,则x﹣5=0或x﹣6=0,解得x1=5,x2=6,则该三角形第三边m的取值范围是6﹣5<m<6+5,即1<m<11,故答案为:1<m<11.15.解:∵m、n是方程x2+2x﹣2021=0的两个实数根,∴m+n=﹣2,mn=﹣2021,m2+2m=2021,∴m2+mn+3m+n=m2+2m+mn+(m+n)=2021﹣2021﹣2=﹣2.故答案是:﹣2.16.解:∵3(x﹣4)=x(x﹣4),∴3(x﹣4)﹣x(x﹣4)=0,则(x﹣4)(3﹣x)=0,∴x﹣4=0或3﹣x=0,解得x1=4,x2=3,故答案为:x1=4,x2=3.17.解:由已知可得,矩形A的周长是(6+1)×2=14,面积是6×1=6,则矩形B的周长是7,面积是3,设矩形B的长为x,则宽为3.5﹣x,则x(3.5﹣x)=3,解得,x1=2,x2=1.5,当x=2时,3.5﹣x=1.5,此时长大于宽,符合实际;当x=1.5时,3.5﹣x=2,此时长小于宽,不符合实际;由上可得,矩形B的长为2,故答案为:2.18.解:x2﹣3x+1=0,x2﹣3x=﹣1,x2﹣3x+()2=﹣1+()2,(x﹣)2=,故答案为:(x﹣)2=.19.解:∵关于x的一元二次方程(a﹣2)x2+2x+1=0有两个不相等的实数根,∴,解得:a<3且a≠2.故答案为:a<3且a≠2.20.解:(1)设每次下降的百分率为a,根据题意,得:50(1﹣a)2=32,解得:a=1.8(舍)或a=0.2,答:每次下降的百分率为20%;(2)设每千克应涨价x元,由题意,得(10+x)(500﹣20x)=6000,整理,得x2﹣15x+50=0,解得:x1=5,x2=10,因为要尽快减少库存,所以x=5符合题意.答:该商场要保证每天盈利6000元,那么每千克应涨价5元.21.解:(1)根据题意得△=(2m﹣1)2﹣4m2≥0,解得m≤;(2)存在.根据题意得α+β=﹣(2m﹣1),αβ=m2,∵α2+β2﹣αβ=6,∴(α+β)2﹣3αβ=6,即(2m﹣1)2﹣3m2=6,整理得m2﹣4m﹣5=0,解得m1=5,m2=﹣1,∵m≤;∴m的值为﹣1.22.解:(1)∵方程有实数根,∴△=25﹣4m≥0,解得,m≤;(2)由一元二次方程根与系数的关系可知,x1+x2=5,x1•x2=m,∵3x1﹣2x2=5,∴3x1+3x2﹣5x2=5,∴﹣5x2=﹣10,解得,x2=2,把x=2代入原方程得,m=6.23.解:(1)设平均每次下调的百分率为x,则4800(1﹣x)2=3888,解得:x1=0.1=10%,x2=1.9(舍去),故平均每次下调的百分率为10%;(2)方案①购房优惠:3888×100×(1﹣0.95)=19440(元);方案②可优惠:188×100=18800(元).故选择方案①更优惠.24.解:(1)根据题意列出函数关系式如下:.当W1=32时,﹣(x﹣15)2+81=32,解得x1=8,x2=22.∵要抢占市场份额,故x=8.答:在抢占市场份额的前提下利润要达到32万元,此时售价为8万元/台.(2)降低成本之后,每台的成本为5万元,每台利润为(x﹣5)万元,销售量y=﹣x+24.依据题意得,当W2=63时,﹣x2+29x﹣127=63,解得x1=10,x2=19.∵要继续保持扩大销售量的战略,故x=10.答:要使二期利润达到63万元,销售价应该为10万元/台.25.解:如图,过点Q作QE⊥PB于E,则∠QEB=90°.∵∠ABC=30°,∴2QE=QB.∴S△PQB=•PB•QE.设经过t秒后△PBQ的面积等于4cm2,则PB=6﹣t,QB=2t,QE=t.根据题意,•(6﹣t)•t=4.t2﹣6t+8=0.t1=2,t2=4.当t=4时,2t=8,8>7,不合题意舍去,取t=2.当点Q到达C点时,S△PQB=××(6﹣t)=4∴t=答:经过2秒或秒后△PBQ的面积等于4cm2.26.解:(1)令4x2+8x﹣1=0,∵a=4,b=8,c=﹣1,b2﹣4ac=64+16=80>0,∴x1=,x2=,则4x2+8x﹣1=4(x﹣)(x﹣);(2)二次三项式2x2﹣4x+7在实数范围内不能利用上面的方法分解因式,理由如下:令2x2﹣4x+7=0,∵b2﹣4ac=(﹣4)2﹣56=﹣40<0,∴此方程无解,则此二次三项式不能用上面的方法分解因式;(3)令mx2﹣2(m+1)x+(m+1)(1﹣m)=0,由此二次三项式能用上面的方法分解因式,即有解,∴b2﹣4ac=4(m+1)2﹣4m(m+1)(1﹣m)≥0,化简得:(m+1)[4(m+1)+4m(m﹣1)]≥0,即4(m+1)(m2+1)≥0,∵m2+1≥1>0,∴m+1≥0,解得m≥﹣1,又m≠0,1﹣m≠0则m≥﹣1且m≠0且m≠1时,此二次三项式能用上面的方法分解因式.27.解:∵三角形是等腰三角形,∴①a=2,或b=2,②a=b两种情况,①当a=2,或b=2时,∵a,b是关于x的一元二次方程x2﹣6x+n﹣1=0的两根,∴x=2,把x=2代入x2﹣6x+n﹣1=0得,22﹣6×2+n﹣1=0,解得:n=9,当n=9,方程的两根是2和4,而2,4,2不能组成三角形,故n=9不合题意,②当a=b时,方程x2﹣6x+n﹣1=0有两个相等的实数根,∴△=(﹣6)2﹣4(n﹣1)=0解得:n=10,综上所述,n=10。
2020-2021年度青岛版八年级数学下册《第6章平行四边形》综合培优训练(附答案)
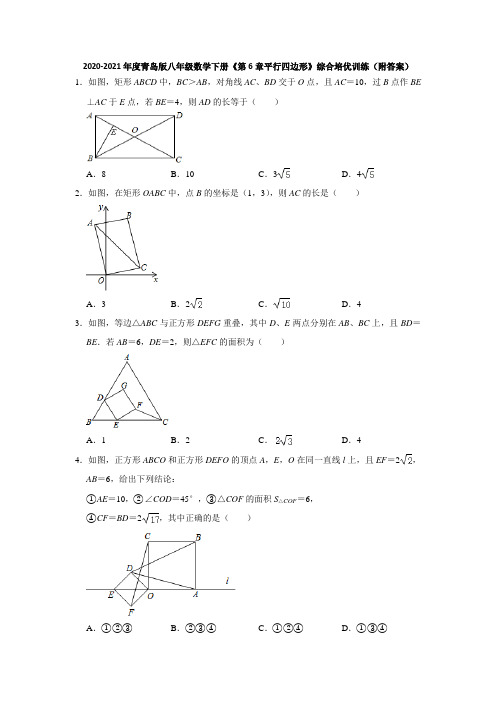
2020-2021年度青岛版八年级数学下册《第6章平行四边形》综合培优训练(附答案)1.如图,矩形ABCD中,BC>AB,对角线AC、BD交于O点,且AC=10,过B点作BE ⊥AC于E点,若BE=4,则AD的长等于()A.8B.10C.3D.42.如图,在矩形OABC中,点B的坐标是(1,3),则AC的长是()A.3B.2C.D.43.如图,等边△ABC与正方形DEFG重叠,其中D、E两点分别在AB、BC上,且BD=BE.若AB=6,DE=2,则△EFC的面积为()A.1B.2C.D.44.如图,正方形ABCO和正方形DEFO的顶点A,E,O在同一直线l上,且EF=2,AB=6,给出下列结论:①AE=10,②∠COD=45°,③△COF的面积S△COF=6,④CF=BD=2,其中正确的是()A.①②③B.②③④C.①②④D.①③④5.如图,在矩形ABCD中,DE⊥AC于E,∠EDC:∠EDA=1:3,且AC=10,则OE的长度是()A.B.5C.3D.6.如图,四边形ABCD为正方形,O为AC、BD的交点,△DCE为Rt△,∠CED=90°,OE=2,若CE•DE=5,则正方形的面积为()A.5B.6C.7D.87.如图,矩形ABCD中,AB=6,AD=8,点E在边AD上,且AE:ED=1:3.动点P 从点A出发,沿AB运动到点B停止,过点E作EF⊥PE交射线BC于点F,联结PF,设M是线段PF的中点,则点P运动的整个过程中,线段DM长的最小值为()A.B.C.3D.8.如图,在矩形ABCD中,AB=2,AD=1,E为AB的中点,F为EC上一动点,P为DF 中点,连接PB,则PB的最小值是()A.2B.4C.D.29.如图,▱ABCD中,∠B=60°,AB=4,BC=5,P是对角线AC上任一点(点P不与点A,C重合),且PE∥BC交AB于E,PF∥CD交AD于F,则阴影部分的面积是.10.矩形ABCD的对角线交于O点,一条边的长为1,△AOB是正三角形,则这个矩形的周长为.11.如图,在四边形ABCO中,AB∥OC,AO⊥OC,AB=1,OC=4,P为AO边上一个动点,连接PB并延长至点E,使得点E落在直线x=3上,以PE,PC为边作▱PEFC,连接PF,则PF长的最小值为.12.如图,正方形ABCD的边长为4,E为BC上任意一点,EF⊥AC于F,EG⊥BD于G,则EF+EG的值为.13.如图,▱ABCD中,AB=10cm,AD=15cm,点P在AD边上以每秒1cm的速度从点A 向点D运动,点Q在BC边上,以每秒4cm的速度从点C出发,在CB间往返运动,两个点同时出发,点P到达点D时停止(同时点Q也停止运动),在运动以后,当以点P、D、Q、B为顶点组成平行四边形时,运动时间t为秒.14.菱形ABCD的对角线AC=6cm,BD=4cm,以AC为边作正方形ACEF,则BF长为.15.矩形ABCD的周长是34cm,对角线相交于O,△AOD与△AOB的周长相差1cm,则AB的长是.16.如图,在四边形ABCD中,AB⊥BC,对角线AC、BD相交于点E,E为BD中点,且AD=BD,AB=2,∠BAC=30°,则DC=.17.如图,以正方形ABCD的边AD为一边作等边三角形ADE,F是DE的中点,BE、AF 相交于点G,连接DG,若正方形ABCD的面积为36,则BG=.18.如图,正方形ABCD的边长为15,AG=CH=12,BG=DH=9,连接GH,则线段GH 的长为.19.如图,△ABC中,AB=10,AC=7,AD平分∠BAC,AE是BC边上的中线,过点C 作CG⊥AD于F,交AB于G,连接EF,则线段EF的长为.20.如图,在平行四边形ABCD中,AC是对角线,且AB=AC,CF是∠ACB的角平分线交AB于点F,在AD上取一点E,使AB=AE,连接BE交CF于点P.(1)求证:BP=CP;(2)若BC=4,∠ABC=45°,求平行四边形ABCD的面积.21.在△ABC中,点M是边BC的中点,AD平分∠BAC,BD⊥AD,BD的延长线交AC于点E,AB=12,AC=20.(1)求证:BD=DE;(2)求DM的长.22.如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE∥AC且DE=AC,连接CE、OE,连接AE交OD于点F.(1)求证:OE=CD;(2)若菱形ABCD的边长为2,∠ABC=60°.求AE的长.23.如图,在正方形ABCD中,M为AB上的一点,N为BC上的一点,且BM=BN,BP⊥MC于点P,求证:DP⊥NP.24.如图,在正方形ABCD中,点E在边AD上,点F在边BC的延长线上,连接EF与边CD相交于点G,连接BE与对角线AC相交于点H,AE=CF,BE=EG.(1)求证:EF∥AC;(2)求∠BEF大小.25.(1)如图1,在四边形ABCD中,AB=CD,E,F分别是AD,BC的中点,连接FE并延长,分别与BA,CD的延长线交于点M,N.求证:∠BME=∠CNE;(提示:取BD的中点H,连接FH,HE作辅助线)(2)如图2,在△ABC中,F是BC边的中点,D是AC边上一点,E是AD的中点,直线FE交BA的延长线于点G,若AB=DC=2,∠FEC=45°,求FE的长度.26.已知正方形ABCD中,点E、F分别为BC、CD上的点,连接AE,BF相交于点H,且AE⊥BF.(1)如图1,连接AC交BF于点G,求证:∠AGF=∠AEB+45°;(2)如图2,延长BF到点M,连接MC,若∠BMC=45°,求证:AH+BH=BM;(3)如图3,在(2)的条件下,若点H为BM的三等分点,连接BD,DM,若HE=1,求△BDM的面积.27.(1)如图1,在正方形ABCD中,点O是对角线AC的中点,点E是边BC上一点,连接OE,过点O作OE的垂线交AB于点F.求证:OE=OF.(2)若将(1)中,“正方形ABCD”改为“矩形ABCD”,其他条件不变,如图2,连接EF.ⅰ)求证:∠OEF=∠BAC.ⅱ)试探究线段AF,EF,CE之间数量上满足的关系,并说明理由.参考答案1.解:∵四边形ABCD是矩形,∴∠BAD=90°,设AD=BC=a,AB=DC=b,∵AC=10,BE⊥AC,BE=4,∴a2+b2=102,又∵S矩形ABCD=2S△ABC∴ab=2××10×4=40,∵BC>AB,解得:a=4,b=2,即AD=4,故选:D.2.解:连接OB,过B作BM⊥x轴于M,∵点B的坐标是(1,3),∴OM=1,BM=3,由勾股定理得:OB==,∵四边形OABC是矩形,∴AC=OB,∴AC=,故选:C.3.解:过F作FQ⊥BC于Q,则∠FQE=90°,∵△ABC是等边三角形,AB=6,∴BC=AB=6,∠B=60°,∵BD=BE,DE=2,∴△BED是等边三角形,且边长为2,∴BE=DE=2,∠BED=60°,∴CE=BC﹣BE=4,∵四边形DEFG是正方形,DE=2,∴EF=DE=2,∠DEF=90°,∴∠FEC=180°﹣60°﹣90°=30°,∴QF=EF=1,∴△EFC的面积为==2,故选:B.4.解:①∵EF=2,∴OE=4,∵AO=AB=6,∴AE=AO+OE=6+4=10,故正确;②∵∠AOC=90°,∠DOE=45°,∴∠COD=180°﹣∠AOC﹣∠DOE=45°,故正确;③作FG⊥CO交CO的延长线于G,则FG=2,∴△COF的面积S△COF=×6×2=6,故正确;④作DH⊥AB于H,CF==2,BH=6﹣2=4,DH=6+2=8,BD==4,故错误.故选:A.5.解:∵四边形ABCD是矩形,∴∠ADC=90°,AC=BD=10,OA=OC=AC=5,OB=OD=BD=5,∴OC=OD,∴∠ODC=∠OCD,∵∠EDC:∠EDA=1:3,∠EDC+∠EDA=90°,∴∠EDC=22.5°,∠EDA=67.5°,∵DE⊥AC,∴∠DEC=90°,∴∠DCE=90°﹣∠EDC=67.5°,∴∠ODC=∠OCD=67.5°,∴∠ODC+∠OCD+∠DOC=180°,∴∠COD=45°,∴OE=DE,∵OE2+DE2=OD2,∴(2DE)2=OD2=25,∴DE=,故选:D.6.解:如图,过点O作OM⊥CE于M,作ON⊥DE交ED的延长线于N,∵∠CED=90°,∴四边形OMEN是矩形,∴∠MON=90°,∵∠COM+∠DOM=∠DON+∠DOM,∴∠COM=∠DON,∵四边形ABCD是正方形,∴OC=OD,在△COM和△DON中,,∴△COM≌△DON(AAS),∴OM=ON,CM=DN,∴四边形OMEN是正方形,∵OE=2,∴2NE2=OE2=(2)2=8,∴NE=ON=2,∵DE+CE=DE+EM+MC=DE+EM+DN=EN+EM=2EN=4,设DE=a,CE=b,∴a+b=4,∵CE•DE=5,∴CD2=a2+b2=(a+b)2﹣2ab=42﹣2×5=6.∴S正方形ABCD=6.故选:B.7.解:连接BE、EM、BM,作BE的垂直平分线GH分别与DA的延长线、BC的延长线交于点G、H,过D作DN⊥GH于点N,连接EH,过H作HK⊥AD,与AD的延长线交于点K,∵∠ABC=∠PEF=90°,M是PF的中点,∴BM=EM,∴无论P点运动到什么位置时,M点始终在BE的垂直平分线上,∴M点在GH上,当M与N点重合时,DM=DN的值最小,设EH=x,∵GH是BE的垂直平分线,∴BH=EH=x,∴∠EHG=∠BHG,∵GD∥BH,∴∠EHG=∠BHG=∠G,∴EG=EH=x,∵∠ABH=∠BAK=∠K=90°,∴四边形ABHK为矩形,∴AK=BH=x,AB=KH=6,∵AD=8,点E在边AD上,且AE:ED=1:3,∴AE=2,ED=6,∴EK=AK﹣AE=x﹣2,∵EH2﹣EK2=KH2,∴x2﹣(x﹣2)2=62,解得,x=10,∴GE=x=10,GD=EG+DE=x+6=10+6=16,∵OE∥DN,∴△GEO∽△GDN,∴,∴DN=EO,∵,∴EO=BE=,∴,即线段DM长的最小值为,解法二:建立如图坐标系,过点F作FJ⊥AD于J.则D(8,6),E(2,6),设P(0,a),由△P AE∽△EJF,可得EM=18﹣3a,∴F(20﹣3a,0),∵PM=MF,∴M(10﹣0.5a,0.5a),∴DM==,∴当a=﹣=时,DM的值最小,此时DM=.故选:A.8.解:如图:当点F与点C重合时,点P在P1处,CP1=DP1,当点F与点E重合时,点P在P2处,EP2=DP2,∴P1P2∥CE且P1P2=CE.当点F在EC上除点C、E的位置处时,有DP=FP.由中位线定理可知:P1P∥CE且P1P=CF.∴点P的运动轨迹是线段P1P2,∴当BP⊥P1P2时,PB取得最小值.∵矩形ABCD中,AB=2,AD=1,E为AB的中点,∴△CBE、△ADE、△BCP1为等腰直角三角形,CP1=1.∴∠ADE=∠CDE=∠CP1B=45°,∠DEC=90°.∴∠DP2P1=90°.∴∠DP1P2=45°.∴∠P2P1B=90°,即BP1⊥P1P2,∴BP的最小值为BP1的长.在等腰直角BCP1中,CP1=BC=1.∴BP1=.∴PB的最小值是.故选:C.9.解:∵▱ABCD,∴AB∥CD,AD∥BC∵PE∥BC,∴PE∥AD∵PF∥CD,∴PF∥AB,∴四边形AEPF为▱.设▱AEPF的对角线AP、EF相交于O,则AO=PO,EO=FO,∠AOE=∠POF ∴△POF≌△AOE,∴图中阴影部分的面积等于△ABC的面积,过A作AM⊥BC交BC于M,∵∠B=60°,AB=4,∴AM=2,S△ABC=×5×2=5,即阴影部分的面积等于5.故填5.10.解:在矩形ABCD中,AC=2OB,∵△AOB是正三角形,∴OB=AB,∴AC=2AB,①AB=1时,AC=2,根据勾股定理,BC===,所以,矩形的周长=2(AB+BC)=2(1+)=2+2;②BC=1时,根据勾股定理,AB2+BC2=AC2,所以,AB2+12=(2AB)2,解得AB=,所以,矩形的周长=2(AB+BC)=2(+1)=+2;综上所述,矩形的周长为2+2或+2.故答案为:2+2或+2.11.解:作FN⊥x轴于N,EM⊥y轴于M,连接PF.∵四边形PEFC是平行四边形,∴PE=CF,PE∥CF,∴∠FCN=∠ETC,∵EM⊥y轴,FN⊥x轴,∴∠EMP=∠FNC=90°,∵EM∥TC,∴∠MEP=∠ETC,∴∠MEP=∠FCN,∴△EMC≌△CNF(AAS),∴EM=CN=3,∴ON=OC+CN=4+3=7,当PF⊥FN时,PF的值最小,此时PF=ON=7,∴PF的最小值为7.故答案为7.12.解:∵四边形ABCD是正方形,边长为4,∴AD=CD=4 AC⊥BD∠DAO=45°;∴AC2=AD2+CD2=42+42=32,则AC=4,∵EF⊥AC,GE⊥BD,∴∠OGE=∠OFE=90°;又∵AC⊥BD,∴四边形OGEF是矩形;∴EG=OF,又∵∠DAO=∠FCE=45°,∴EF=CF;∵OF+CF=OC=×4=2,∴GE+EF=2.故答案为213.解:设经过t秒,以点P、D、Q、B为顶点组成平行四边形,∵P在AD上运动,∴t≤,即t≤15,∵以点P、D、Q、B为顶点组成平行四边形,∴DP=BQ,分为以下情况:①点Q的运动路线是C﹣B﹣C,方程为4t﹣15=15﹣t,解得:t=6;②点Q的运动路线是C﹣B﹣C﹣B,方程为15﹣(4t﹣30)=15﹣t,③点Q的运动路线是C﹣B﹣C﹣B﹣C,方程为4t﹣45=15﹣t,解得:t=12;故答案为:6或10或12.14.解:∵AC=6cm,BD=4cm,∴AO=AC=×6=3cm,BO=BD=×4=2m,如图1,正方形ACEF在AC的上方时,过点B作BG⊥AF交F A的延长线于G,BG=AO=3cm,FG=AF+AG=6+2=8cm,在Rt△BFG中,BF===cm,如图2,正方形ACEF在AC的下方时,过点B作BG⊥AF于G,BG=AO=3cm,FG=AF﹣AG=6﹣2=4cm,在Rt△BFG中,BF===5cm,综上所述,BF长为5cm或cm.故答案为:5cm或cm.15.解:由图易得:OB=OD,那么△AOD与△AOB的周长相差1cm其实就是AD与AB相差1cm 当AD比AB长1cm时,AD+AB=AB+1+AB=17,AB=8;当AD比AB短1cm时,AD+AB=AB﹣1+AB=17,AB=9.因此AB的长为8或9cm.故AB的长为8或9cm.16.解:如图,在EA上取一点K,使得EK=CE,连接DK,BK,延长DK交AB于H.∵DE=EB,CE=EK,∴四边形BCDK是平行四边形,∴CD=BK,DK∥BC,∵BC⊥AB,∴DH⊥AB,∵DA=DB,∴AH=HB=1,∴KA=KB=CD,在Rt△AKH中,AK=AH÷cos30°=,∴CD=,故答案为.17.解:如图所示,连接BD,∵S正方形ABCD=36,∴AD=6,BD=6,在正方形ABCD和等边△ADE中,∠BAE=∠BAD+∠DAE=90°+60°=150°,AB=AD=AE,∴∠AEB=(180°﹣∠BAE)=(180°﹣150°)=15°,∴∠DEG=∠AED﹣∠AEB=60°﹣15°=45°,∵F为DE的中点,∴AF垂直平分DE,DF=DE=×6=3,∴DG=EG,∴∠GDE=45°=∠DEG,∴△DEG是等腰直角三角形,∴DG=DF=3,∠DGE=90°,∴Rt△BDG中,BG===3.故答案为:3.18.解:如图,延长BG交CH于点E,在△ABG和△CDH中,,∴△ABG≌△CDH(SSS),AG2+BG2=AB2,∴∠1=∠5,∠2=∠6,∠AGB=∠CHD=90°,∴∠1+∠2=90°,∠5+∠6=90°,又∵∠2+∠3=90°,∠4+∠5=90°,∴∠1=∠3=∠5,∠2=∠4=∠6,在△ABG和△BCE中,,∴△ABG≌△BCE(ASA),∴BE=AG=12,CE=BG=9,∠BEC=∠AGB=90°,∴GE=BE﹣BG=12﹣9=3,同理可得HE=3,在Rt△GHE中,GH=,故答案为:3.19.解:∵AD平分∠BAC,∴∠GAF=∠CAF,∵CG⊥AD,∴∠AFG=∠AFC,在△AGF和△ACF中,,∴△AGF≌△ACF(ASA),∴AG=AC=7,GF=CF,则BG=AB﹣AG=10﹣7=3.又∵BE=CE,∴EF是△BCG的中位线,∴EF=BG=1.5.故答案是:1.5.20.解:(1)设AP与BC交于H,∵在平行四边形ABCD中,AD∥BC,∴∠AEB=∠CBE,∵AB=AE,∴∠ABE=∠AEB,∴∠ABE=∠CBE,∴BE平分∠ABC,∵CF是∠ACB的角平分线,BE交CF于点P,∴AP平分∠BAC,∵AB=AC,∴AH垂直平分BC,∴PB=PC;(2)∵AH垂直平分BC,∴AH⊥BC,BH=CH=BC=2,∵∠ABH=45°,∴AH=BH=2,∴平行四边形ABCD的面积=4×2=8.21.(1)证明:∵AD平分∠BAC,∴∠BAD=∠DAE.∵AD⊥BD,∴∠ADB=∠ADE=90°.在△ADB与△ADE中,∴△ADB≌△ADE,∴BD=DE.(2)∵△ADB≌△ADE,∴AE=AB=12,∴EC=AC﹣AE=8.∵M是BC的中点,BD=DE,∴DM=EC=4.22.(1)证明:在菱形ABCD中,OC=AC.∴DE=OC.∵DE∥AC,∴四边形OCED是平行四边形.∴平行四边形OCED是矩形.∴OE=CD.(2)在菱形ABCD中,∠ABC=60°,∴AC=AB=2.∴在矩形OCED中,CE=OD=.在Rt△ACE中,AE=.23.解:如图,∵四边形ABCD为正方形,∴BC=CD,AB∥CD,∠ABC=∠BCD,∴∠PCD=∠BMC,∵BP⊥MC,∴∠PBC+∠BCM=90°,而∠PBC+∠PBM=90°,∴∠PBC=∠BMC,∠MCB=∠BCP,∴△BPC∽△MBC;∴CP:BC=BP:BM=BC:MC,∵BM=BN,BC=CD,∴CP:CD=BP:BN,而∠PCD=∠BMC=∠PBC,∴△BPN∽△CPD,∴∠BPN=∠CPD,∠CPD+∠NPC=90°,∴DP⊥PN.24.(1)证明:∵四边形ABCD是正方形,∴AD∥BF,∴四边形ACFE是平行四边形,∴EF∥AC,(2)解:连接BG,如图所示:∵EF∥AC,∴∠F=∠ACB=45°,∵∠GCF=90°,∴∠CGF=∠F=45°,∴CG=CF,∵AE=CF,∴AE=CG,在△BAE与△BCG中,,∴△BAE≌△BCG(SAS)∴BE=BG,∵BE=EG,∴△BEG是等边三角形,∴∠BEF=60°.25.(1)证明:连接BD,取DB的中点H,连接EH,FH,∵E,H分别是AD,BD的中点,∴EH∥AB,EH=AB,∴∠BME=∠HEF,∵F,H分别是BC,BD的中点,∴FH∥CD,FH=CD,∵AB=CD∴HE=FH,∴∠HEF=∠HFE∴∠BME=∠CNE;(2)连接BD,取DB的中点H,连接EH,FH,∵E,F分别是AD,BC的中点,∴EH=AB,FH=CD,FH∥AC,∴∠HFE=∠FEC=45°,∵AB=CD=2,∴HF=HE=1,∴∠HEF=∠HFE=45°,∴∠EHF=180°﹣∠HFE﹣HEF=90°,∴.26.(1)证明:∵四边形ABCD是正方形,∴∠ABC=∠BCD=90°,∴∠ACB=∠ACD=45°,∵AE⊥BF,∴∠AEB+∠FBC=90°,∵∠FBC+∠BFC=90°∴∠AEB=∠BFC,∵∠AGF=∠BFC+∠ACF,∴∠AGF=∠AEB+45°;(2)解:过C作CK⊥BM于K,∵∠BMC=45°,∴CK=MK,∵四边形ABCD是正方形,∴AB=BC,∠ABC=∠BCD=90°,∴∠ABH=∠BCK,在△ABH与△BCK中,,∴△ABH≌△BCK,∴BH=CK=MK,AH=BK,∴BM=BK+MK=AH+BH;(3)解:由(2)得,BH=CK=BH,∵H为BM的三等分点,∴BH=HK=KM,过E作EN⊥CK于N,∴四边形HENK是矩形,∴HK=EN=BH,∠BHE=∠NEC,在△BHE与△ENC中,,∴△BHE≌△ENC,∴HE=CN=NK=1,∴CK=BH=2,∴BM=6,连接CH,∵HK=MK,CK⊥MH,∠BMC=45°,∴CH=CM,∠MCH=90°,∴∠BCH=∠DCM,在△BHC与△DMC中,,∴△BHC≌△DMC,∴BH=DM=2,∠BHC=∠DMC=135°∴∠DMB=90°,∴△BDM的面积=6.27.证明:(1)连接OB,∵在正方形ABCD中,O是AC的中点,∴OB=OA,∠OAB=∠OBA=∠OBC=45°,∴∠AOB=90°,又∵OE⊥OF,∴∠AOF=∠BOE,在△AOF和△BOE中,,∴△AOF≌△BOE,∴OE=OF;(2)①∵∠EOF=∠FBE=90°,∴O,E,F,B四点共圆,∴∠OBA=∠OEF,∵在矩形ABCD中,O是AC的中点,∴OA=OB,∠OAB=∠OBA,∴∠OEF=∠BAC;②如图,连接BD,延长EO交AD于G,∵BD与AC交于O,则△OGD≌△DEB,∴OG=OE,∴AG=CE,∵OF⊥GE,∴FG=EF,在Rt△AGF中,GF2=AG2+AF2,即EF2=CE2+AF2.。
八年级下册第17章勾股定理培优试题(含答案)

人教版数学八年级下册第17章勾股定理培优试题一.选择题(共10小题)1.在△ABC 中,∠B=90°,若BC=3,AC=5,则AB 等于( )A .2B .3C .4D .342.如图,有一长方形空地ABCD,如果AB=6米,AD=8米,要从A 走到C ,至少要走( ) A .6米 B .8米 C .10米 D .14米3.以下各组数为三角形的三边长,其中不能够构成直角三角形的是( )A .32、42、52B .7、24、25C .0.3、0.4、0.5D .9、12、154.“折竹抵地”问题源自《九章算术》中,即:今有竹高一丈,末折抵地,去本四尺,问折者高几何?意思是:一根竹子,原高一丈,一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部4尺远(如图),则折断后的竹子高度为多少尺?(1丈=10尺)( ) A .3 B .5 C .4.2 D .45.某直角三角形的一直角边长为8,另一直角边长与斜边长的和为32,则斜边的长为( ) A .8 B .10 C .15 D .176.满足下列条件的△ABC,不是直角三角形的是( )A .∠C=∠A+∠BB .∠C=∠A-∠BC .a :b :c=3:4:5D .∠A :∠B :∠C=3:4:57.小明想知道学校旗杆的高度,她发现旗杆上的绳子刚好垂到地面,当她把绳子的下端拉开5米后,发现绳子下端距离地面1米,则旗杆的高是( )A .8米B .10米C .12米D .13米8.下列各组数中,不是勾股数的是( )A .9,12,15B .8,15,17C .12,18,22D .5,12,13 9.下列结论中,错误的有( )①在Rt △ABC 中,已知两边长分别为3和4,则第三边的长为5;②△ABC 的三边长分别为AB,BC,AC,若BC 2+AC 2=AB 2,则∠A=90°;③在△ABC 中,若∠A :∠B :∠C=1:5:6,则△ABC 是直角三角形;④若三角形的三边长之比为3:4:5,则该三角形是直角三角形;A .0个B .1个C .2个D .3个10.如图,△ABC 中,AB=AC,AB=5,BC=8,AD 是∠BAC 的平分线,则AD 的长为( ) A .5 B .4 C .3 D .2二.填空题(共6小题)11.已知一个直角三角形的两直角边长分别是1和2,则斜边长为 .12.如图,在△ABC 中,∠C=90°,AD 平分∠CAB,DE ⊥AB 于E ,且DE=15cm,BE=8cm,则 BC= cm .13.平面直角坐标系上有点A(-3,4),则它到坐标原点的距离为 .14.如图,分别以直角△ABC 的三边为直径作半圆,若两直角边分别为6,8,则阴影部分的面积是 .15.定义:如图,点P 、Q 把线段AB 分割成线段AP 、PQ 和BQ ,若以AP 、PQ 、BQ 为边的三角形是一个直角三角形,则称点P 、Q 是线段AB 的勾股分割点.已知点P 、Q 是线段AB的勾股分割点,如果AP=8,PQ=12(PQ>BQ),那么BQ= .16.如图,一架长5米的梯子A1B1斜靠在墙A1C上,B1到墙底端C的距离为3米,此时梯子的高度达不到工作要求,因此把梯子的B1端向墙的方向移动了1.6米到B处,此时梯子的高度达到工作要求,那么梯子的A1端向上移动了米.三.解答题(共8小题)17.如图,在正方形网格中,小正方形的边长为1,A,B,C为格点(1)判断△ABC的形状,并说明理由.(2)求BC边上的高.18.已知:如图,在△ABC中,AB=13,AC=20,AD=12,且AD⊥BC,垂足为点D,求BC的长.19.我市鸭绿江边的景观区内有一块四边形空地,如图所示,景区管理人员想在这块空地上铺满观赏草坪,需要测量其面积,经技术人员测量∠ABC=90°,AB=20米,BC=15米,CD=7米,AD=24米.(1)请你帮助管理人员计算出这个四边形对角线AC的长度;(2)请用你学过的知识帮助管理员计算出这块空地的面积.20.某广场内有一块空地ABCD如图所示,现计划在空地上种草皮,经测量,∠B=90°,AB=6m,BC=8m,CD=26m,AD=24m.求四边形ABCD空地的面积.21.在△ABC中,CD是AB边上的高,AC=4,BC=3,DB=1.8.(1)求CD的长;(2)求AB的长;(3)△ABC是直角三角形吗?请说明理由.22.如图,小巷左石两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离BC 为0.7米,梯子顶端到地面的距离AC 为2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,梯子顶端到地面的距离A ′D 为1.5米,求小巷有多宽.23.如图,长7.5m 的梯子靠在墙上,梯子的底部离墙的底端4.5m .(1)求梯子的顶端到地面的距离;(2)由于地面有水,梯子底部向右滑动1.5m,则梯子顶端向下滑多少米?24.阅读下列一段文字,然后回答下列问题.已知在平面内有两点P 1()x 1,y 1、P 2()x 2,y 2,其两点间的距离P 1P 2=()x 1-x 22+()y 1-y 22,同时,当两点所在的直线在坐标轴或平行于坐标轴或垂直于坐标轴时,两点间距离公式可化简为|x 2-x 1|或|y 2-y 1|.(1)已知A(2,4)、B(-3,-8),试求A、B两点间的距离;(2)已知M、N在平行于y轴的直线上,点M的纵坐标为4,点N的纵坐标为-1,试求M、N两点的距离为;(3)已知一个三角形各顶点坐标为D(1,6)、E(-2,2)、F(4,2),你能判定此三角形的形状吗?说明理由.答案:1-5 CCACD6-10 DDCCC11.12.3213.514.2415.416.0.817. 解:(1)结论:△ABC是直角三角形.理由:∵BC2=12+82=65,AC2=22+32=13,AB2=62+42=52,∴AC2+AB2=BC2,∴△ABC是直角三角形.(2)设BC边上的高为h.则有•AC•AB=•BC•h,∵AC=,AB=2,BC=∴h=18.解:∵AB=13,AC=20,AD=12,AD⊥BC,∴Rt△ABD中,BD===5,Rt△ACD中,CD===16,∴BC=BD+CD=5+16=21.19.解:(1)连接AC.在Rt△ABC中,∵∠ABC=90°,AB=20,BC=15,∴AC===25(米).∴这个四边形对角线AC的长度为25米.(2)在△ADC中,∵CD=7,AD=24,AC=25,∴AD2+CD2=242+72=252=AC2,∴△ADC为直角三角形,∠ADC=90°,∴S四边形ABCD=S△ADC+S△ABC=×15×20+×7×24=234(平方米),∴四边形ABCD的面积为234平方米.20. 解:连接AC,在Rt△ABC中,AC2=AB2+BC2=62+82=102,∴AC=10.在△DAC中,CD2=262,AD2=242,而242+102=262,即AC2+AD2=CD2,∴∠DCA=90°,S四边形ABCD=S△BAC+S△DAC=•BC•AB+DC•AC,=×8×6+×24×10=144(m)2,答:四边形ABCD空地的面积是144m2.21.解:(1)∵CD是AB边上的高,∴△BDC是直角三角形,∴CD===2.4;(2)同(1)可知△ADC也是直角三角形,∴AD===3.2,∴AB=AD+BD=3.2+1.8=5;(3)△ABC是直角三角形,理由如下:又∵AC=4,BC=3,AB=5,∴AC2+BC2=AB2,∴△ABC是直角三角形.22.解:在Rt△ACB中,∵∠ACB=90°,BC=0.7米,AC=2.4米,∴AB2=0.72+2.42=6.25.在Rt△A′BD中,∵∠A′DB=90°,A′D=2米,BD2+A′D2=A′B′2,∴BD2+1.52=6.25,∴BD2=4.∵BD>0,∴BD=2米.∴CD=BC+BD=0.7+2=2.7米.答:小巷的宽度CD为2.7米.23.解:(1)如图,在Rt△ABC中,AC2=AB2-BC2,∵AB=7.5m,BC=4.5m,∴AC==6(m),答:梯子的顶端到地面的距离为6m;(2)如图,∵BF=1.5m,∴CF=6m,∴EC==4.5(m),∴AE=1.5,答:梯子顶端向下滑1.5米.24.解:(1)AB==13,故答案为:13;(2)MN=4-(-1)=5;故答案为:5;(3)△ABC为等腰三角形.理由如下:∵DE=5,EF=4-(-2)=6,DF==5,∴DE=DF,∴△DEF为等腰三角形;。
2020——2021学年人教版 八年级数学下册 第十九章 一次函数 培优训练(含答案)

人教版 八年级下册 第十九章 一次函数 培优训练一、选择题1. (2019•陕西)在平面直角坐标系中,将函数3y x 的图象向上平移6个单位长度,则平移后的图象与x 轴的交点坐标为 A .(2,0) B .(–2,0) C .(6,0) D .(–6,0)2. 函数y =kx +b 的图象如图,则当y <0时,x 的取值范围是( ) A .x <-2 B .x >-2 C .x <-1 D .x >-13. 设点A (a ,b )是正比例函数y =-32x 图象上的任意一点,则下列等式一定成立的是( )A. 2a +3b =0B. 2a -3b =0C. 3a -2b =0D. 3a +2b =04. 若k ≠0,b <0,则y =kx +b 的图象可能是( )5. 如图,一次函数y 1=x +b与一次函数y 2=kx +4的图象交于点P (1,3),则关于x 的不等式x +b >kx +4的解集是( ) A. x >-2 B. x >0 C. x >1 D. x <16. 某通信公司就上宽带网推出了A ,B ,C 三种月收费方式,这三种收费方式每月所需的费用y (元)与上网时间x (h)的函数关系如图所示,则下列判断错误..的是( )A .每月上网时间不足25 h 时,选择A 方式最省钱B .每月上网费用为60元时,B 方式可上网的时间比A 方式多C .每月上网时间为35 h 时,选择B 方式最省钱D .每月上网时间超过70 h 时,选择C 方式最省钱7. 在坐标平面上,某个一次函数的图象经过(5,0)、(10,-10)两点,则此函数图象还会经过下列哪点( )A. (17,947)B. (18,958)C. (19,979)D. (110,9910)8. 如图所示,向一个半径为R ,容积为V 的球形容器内注水,则能够反映容器内水的体积y 与容器内水深x 间的函数关系的图象可能是( )二、填空题9. 已知3a y ax -=,若y 是x 的正比例函数,则a 的值是 .10. 若一次函数y =-2x +b (b 为常数)的图象经过第二、三、四象限,则b 的值可以是________(写出一个即可).11. 如图所示的是函数y kx b =+与y mx n =+的图象,求方程组kx b ymx n y +=⎧⎨+=⎩的解关于原点对称的点的坐标是________.12. (2019•上海)在登山过程中,海拔每升高1千米,气温下降6 °C,已知某登山大本营所在的位置的气温是2 °C,登山队员从大本营出发登山,当海拔升高x 千米时,所在位置的气温是y °C,那么y关于x的函数解析式是__________.13. 某油桶内有油20升,它有一个进油管和一个出油管,进油管每分钟进油4升,出油管每分钟出油6升.现同时打开两管,则油桶中剩余油量Q(升)与开管时间t (分)之间的函数关系式是,自变量t的取值范围是.14. 若点M(k-1,k+1)关于y轴的对称点在第四象限内,则一次函数y=(k-1)x +k的图象不经过...第________象限.15. 甲、乙两人在直线道路上同起点、同终点、同方向,分别以不同的速度匀速跑步1500米,先到终点的人原地休息,已知甲先出发30秒后,乙才出发.在跑步的整个过程中,甲、乙两人的距离y(米)与甲出发的时间x(秒)之间的关系如图所示.则乙到终点时,甲距终点的距离是________米.16. 如图所示,已知点C(1,0),直线y=-x+7与两坐标轴分别交于A,B两点,D,E分别是AB,OA上的动点,则△CDE周长的最小值是________.三、解答题17. 某商品的进价为每件40元,在销售过程中发现,每周的销售量y(件)与销售单价x(元)之间的关系可以近似看作一次函数y=kx+b,且当售价定为50元/件时,每周销售30件,当售价定为70元/件时,每周销售10件. (1)求k ,b 的值;(2)求销售该商品每周的利润w (元)与销售单价x (元)之间的函数解析式,并求出销售该商品每周可获得的最大利润.18. 小明同学骑自行车去郊外春游,下图表示他离家的距离y (千米)与所用的时间x (时)之间关系的函数图象.⑴根据图象回答:小明到达离家最远的地方需几小时?此时离家多远? ⑵小明出发两个半小时离家多远? ⑶小明出发多长时间距家12千米?时间(小时)4653212051015253019. 公司有330台机器需要一次性运送到某地,计划租用甲、乙两种货车共8辆.已知每辆甲种货车一次最多运送机器45台,租车费用为400元,每辆乙种货车一次最多运送机器30台,租车费用为280元.(1)设租用甲种货车x 辆(x 为非负整数),试填写表格:(2)给出能完成此项运送任务的最节省费用的租车方案,并说明理由.20. 阅读:我们知道,在数轴上,1x =表示一个点,而在平面直角坐标系中,1x =表示一条直线;我们还知道,以二元一次方程210x y -+=的所有解为坐标的点组成的图形就是一次函数21y x =+的图象,它也是一条直线,如图①.观察图①可以得出:直线1x =与直线21y x =+的交点P 的坐标(1,3)就是方程组1210x x y =⎧⎨-+=⎩的解,所以这个方程组的解为13x y =⎧⎨=⎩; 在直角坐标系中,1x ≤表示一个平面区域,即直线1x =以及它左侧的部分,如图②;21y x ≤+也表示一个平面区域,即直线21y x =+以及它下方的部分,如图③.(1)y=2x+1x=1yxO P (1,3)Ox yx=1(2)O xyy=2x+1(3)回答下列问题.⑴在下面的直角坐标系中,用作图象的方法求出方程组122x y x =-⎧⎨=-+⎩的解;O xyO xy2O x yy 1=2x+1(4)⑵在上面的直角坐标系中,用阴影表示2220x y x y ≥-⎧⎪≤-+⎨⎪≥⎩所围成的区域.⑶如图⑷,表示阴影区域的不等式组为: .人教版 八年级下册 第十九章 一次函数 培优训练-答案一、选择题 1. 【答案】B【解析】根据函数图象平移规律,可知3y x =向上平移6个单位后得函数解析式应为36y x =+,此时与x 轴相交,则0y =, ∴360x +=,即2x =-, ∴点坐标为(–2,0), 故选B .2. 【答案】B3. 【答案】D【解析】把点A (a ,b )代入y =-32x ,得b =-32a ,即2b =-3a ,∴3a +2b =0.4. 【答案】B 【解析】由k ≠0可知y =kx +b 是一次函数,图象不是上升就是下降,排除D ,由b <0可知,直线y =kx +b 与y 轴交于负半轴,排除A 、C ,故选B.5. 【答案】C 【解析】结合题图可知不等式x +b >kx +4的解集为函数图象y 1在y 2上方的函数图象所对的自变量取值,即x >1.6. 【答案】D [解析] 当x ≥50时,由(50,50)和(55,65)求得B 方式的解析式为y =3x-100.令y=120,得120=3x-100,解得x=.所以当x>时,选C 方式更省钱,可见选项D 错误.故选D .7. 【答案】C【解析】设该一次函数的解析式为y =kx +b (k ≠0),将点(5,0)、(10,-10)代入到y =kx +b 中得,⎩⎨⎧0=5k +b -10=10k +b ,解得⎩⎨⎧k =-2b =10,∴该一次函数的解析式为y =-2x +10.A.y =-2×17+10=957≠947,该点不在直线上;B.y =-2×18+10=934≠958,该点不在直线上;C.y =-2×19+10=979,该点在直线上;D.y =-2×110+10=945≠9910,该点不在直线上.8. 【答案】A【解析】在函数图象上,图象越靠近y 轴正半轴,则容器内水体积增大的速度越大;当x <R 时,球形容器中水平面圆的半径逐渐增大,故随着x 的增大,容器内水的体积增大的速度为先小后大,故排除B 、C 、D ;当x >R 时,球形容器中水平面圆的半径逐渐减小,故随着x 的增大,容器内水的体积增大的速度为先大后小,故选A.二、填空题 9. 【答案】4【解析】正比例函数的比例系数0a ≠且31a -=10. 【答案】-1(答案不唯一,满足b <0即可) 【解析】∵一次函数y =-2x +b 的图象经过第二、三、四象限,∴b <0,故b 的值可以是-1.11. 【答案】()34--,【解析】考察一次函数与二元一次方程组的关系,在平面直角坐标系内可知两个直线的交点坐标为()34,,所以它关于远点的对称的点的坐标是()34--,12. 【答案】y=-6x+2【解析】根据题意得y=–6x+2,故答案为:y=–6x+2.13. 【答案】Q=20-2t0≤t ≤1014. 【答案】一【解析】依据题意,M 关于y 轴对称点在第四象限,则M 点在第三象限,即k -1<0,k +1<0, 解得k<-1.∴一次函数y =(k -1)x +k 的图象过第二、三、四象限,故不经过第一象限.15. 【答案】175 【解析】由图象可知,甲前30秒跑了75米,则甲的速度为7530=2.5米/秒,甲出发180秒时,两人相离0千米,这说明甲出发后180秒时,乙追上了甲,此时两人所行路程相等为180×2.5=450米,乙用的时间为180-30=150秒,所以乙的速度为:450150=3米/秒,由此可以求出乙跑到终点所用时间为:15003=500秒,此时甲跑的时间为500+30=530秒,甲已跑路程为530×2.5=1325米,甲距终点的距离为1500-1325=175米.16. 【答案】10 【解析】作点C 关于y 轴的对称点C 1(-1,0),点C 关于直线AB 的对称点C 2,连接C 1C 2交OA 于点E ,交AB 于点D ,则此时△CDE 的周长最小,且最小值等于C 1C 2的长.∵OA =OB =7,∴CB =6,∠ABC =45°.∵AB 垂直平分CC 2,∴∠CBC 2=90°,∴C 2的坐标为(7,6).在Rt △C 1BC 2中,C 1C 2=C 1B 2+C 2B 2=82+62=10.即△CDE 周长的最小值是10.三、解答题17. 【答案】解:(1)根据题意,得 .k b k b =+⎧⎨=+⎩3050,1070 解得,.k b =-⎧⎨=⎩180∴k 的值为-1,b 的值为80;(2)∵w = (x -40) ( -x +80) =- (x - 60) 2+400, ∴当x =60时,w 有最大值为400元.答:销售该商品每周可获得的最大利润为400元.18. 【答案】⑴3小时,30千米;⑵22.5千米;⑶48分或5小时12分【解析】⑴由图象可知小明到达离家最远的地方需3小时,此时,他离家30千米.⑵∵小明出发2小时时,离家15千米.由于在CD 段小明走的路程为15千米,时间为1小时,故小明这一段的速度为15千米/时.∴150.57.5⨯=(千米)∴7.51522.5+=(千米)∴小明出发两个半小时离家22.5千米.⑶由图象可以看出小明从出发到距离家12千米有两个时刻,一是在AB段,二是在EF段,故分两种情况:①∵小明出发到1小时时,匀速前行,其速度为15千米/时∴12150.8÷=(时),0.8小时=48分②∵小明出发4小时后返回,∴返回时速度为30215÷=(千米/时)∴301215 1.2-÷=()(时)1.2时=1小时12分∴4小时+1小时12分=5小时12分故小明出发48分和出发5小时12分时离家都为12千米.19. 【答案】解:(1)由题意可得,在表一中,当租用甲种货车7辆时,最多运送的机器数量为45×7=315(台),则租用乙种货车8-7=1(辆),最多运送的机器数量为30×1=30 (台).当租用甲种货车x辆时,最多运送的机器数量为45x台,则租用乙种货车(8 -x)辆,最多运送的机器数量为30(8-x)=(-30x+240)台.在表二中,当租用甲种货车3辆时,租用甲种货车的费用为400×3=1200(元),则租用乙种货车8-3=5(辆),租用乙种货车的费用为280×5=1400(元);当租用甲种货车x辆时,租用甲种货车的费用为400x元,则租用乙种货车(8 -x)辆,租用乙种货车的费用为280(8-x)=(-280x+2240)元.故答案为:表一:315,45x,30,-30x+240;表二:1200,400x,1400,-280x+2240.(2)能完成此项运送任务的最节省费用的租车方案是租用甲种货车6辆,乙种货车2辆.理由:当租用甲种货车x辆时,设租用两种货车的总费用为y元,则y=400x+(-280x+2240)=120x+2240.因为45x+(-30x+240)≥330,所以x≥6.又因为8-x≥0,所以x≤8,所以x的取值范围为6≤x≤8且x为整数.因为在函数y=120x+2240中,120>0,所以在函数y=120x+2240中,y 随x 的增大而增大,所以当x=6时,y 取得最小值.即能完成此项运送任务的最节省费用的租车方案是租用甲种货车6辆,乙种货车2辆.20. 【答案】⑴如图⑸,解为14x y =-⎧⎨=⎩;⑵如图⑹;⑶根据图示信息求得2332y x =-+,则021332x y x y x ⎧⎪⎪+⎨⎪⎪-+⎩≥≥≤x=-1x(5)x(6)。
人教版 八年级数学下册 18.1 平行四边形 培优训练(含答案)

人教版 八年级数学 18.1 平行四边形 培优训练一、选择题(本大题共8道小题)1. 以三角形的三个顶点作平行四边形,最多可以作( ) A .2个 B .3个 C .4个 D .5个2. 如图,将▱ABCD 沿对角线AC 折叠,使点B 落在点B′处.若∠1=∠2=44°,则∠B 为( )A . 66°B . 104°C . 114°D . 124°3. 如图,平行四边形ABCD 的周长是26 cm ,对角线AC 与BD 交于点O ,AC ⊥AB ,E 是BC 中点,△AOD 的周长比△AOB 的周长多3 cm ,则AE 的长度为( ) A . 3 cm B . 4 cm C . 5 cm D . 8 cm4. 如图,ABCD 中,AB=2,AD=4,对角线AC ,BD 相交于点O ,且E ,F ,G ,H 分别是AO ,BO ,CO ,DO 的中点,则下列说法正确的是A .EH=HGB .四边形EFGH 是平行四边形C .AC ⊥BDD .△ABO 的面积是△EFO 的面积的2倍5. 在平行四边形ABCD 中,点1A 、2A 、3A 、4A 和1C 、2C 、3C 、4C 分别为AB 和CD 的五等分点,点1B 、2B 和1D 、2D 分别是BC 和DA 的三等分点,已知四边形4242A B C D 的面积为1,则平行四边形ABCD 面积为( )A .2B .35C .53D .156. (2019▪广西池河)如图,在△ABC中,D ,E 分别是AB ,BC 的中点,点F 在DE 延长线上,添加一个条件使四边形ADFC 为平行四边形,则这个条件是A .∠B=∠FB .∠B=∠BCFC .AC=CFD .AD=CF7.已知四边形的四条边长分别是a b c d ,,,,其中a b ,为对边,并且满足222222a b c d ab cd +++=+则这个四边形是( )A .任意四边形B .平行四边形C .对角线相等的四边形D .对角线垂直的四边形8.(2020·临沂)如图,P 是面积为S 的ABCD 内任意一点,PAD ∆的面积为1S ,PBC ∆的面积为2S ,则( )A.122SS S +>B.122SS S +<C.212SS S += D.21S S +的大小与P 点位置有关二、填空题(本大题共8道小题)9. 如图所示,四边形ABCD 的对角线相交于点O ,若AB ∥CD ,请添加一个条件________(写一个即可),使四边形ABCD 是平行四边形.10.(2020·牡丹江)如图,在四边形ABCD 中,AD//BC ,在不添加任何辅助线的情况下,请你添加一个条件__________________,使四边形ABCD 是平行四边形(填一个即可).11. 已知平行四边形ABCD 的周长为60cm ,对角线AC 、BD 相交于O 点,AOB ∆的周长比BOC ∆的周长多8cm ,则AB的长度为cm .OD CBA12. 如图所示,在▱ABCD中,∠C =40°,过点D 作AD 的垂线,交AB 于点E ,交CB 的延长线于点F ,则∠BEF 的度数为__________.13. (2020·凉山州)如图,平行四边形ABCD 的对角线AC 、BD 相交于点O ,OE ∥AB 交AD 于点E .若OA =1,△AOE 的周长等于5,则平行四边形ABCD 的周长等于 .O EDCB A14. 如图,在ABCD 中,E.F 是对角线AC 上两点,AE=EF=CD ,∠ADF=90°,∠BCD=63°,则∠ADE 的大小为__________.15. 如图,在▱ABCD中,E 为边CD 上一点,将△ADE 沿AE 折叠至△AD′E 处,AD ′与CE 交于点F ,若∠B =52°,∠DAE =20°,则∠FED′的大小为________.ABC16. 如图,一个平行四边形被分成面积为1S 、2S 、3S 、4S 四个小平行四边形,当CD 沿AB 自左向右在平行四边形内平行滑动时.① 14S S 与23S S 的大小关系为.② 已知点C 与点A 、B 不重合时,图中共有 个平行四边形,S 4S 3S 2S 1(3)DCBA三、解答题(本大题共4道小题) 17. (2020·重庆B 卷)如图,在平行四边形ABCD 中,AE ,CF 分别平分∠BAD 和∠DCB ,交对角线BD 于点E ,F . (1)若∠BCF =60°,求∠ABC 的度数; (2)求证:BE =DF .18. 如图所示,P 为平行四边形ABCD 内一点,求证:以AP 、BP 、CP 、DP 为边可以构成一个四边形,并且所构成的四边形的对角线的长度恰好分别等于AB 和BC .DPCBA19. (2020·泰安)(12分)若△ABC 和△AED 均为等腰三角形,且∠BAC ﹦∠EAD﹦90°.(1)如图(1),点B 是DE 的中点,判断四边形BEAC 的形状,并说明理由;(2)如图(2),若点G 是EC 的中点,连接GB 并延长至点F ,使CF ﹦CD . 求证:①EB ﹦DC ,②∠EBG ﹦∠BFC .GFABCDEABCDE20. 如图,AC 是平行四边形ABCD 较长的一条对角线,点O 是ABCD 内部一点,OE AB ⊥于点E ,OF AD ⊥于点F ,OG AC ⊥于点G ,求证:AE AB AF AD AG AC ⋅+⋅=⋅.人教版 八年级数学 18.1 平行四边形 培优训练-答案一、选择题(本大题共8道小题) 1. 【答案】B2. 【答案】C 【解析】设∠ACD =x ,∠B =y ,则根据题意可列方程组⎩⎨⎧x +y +44°=180°180°-y -(44°-x )=44°,解得y =114°.3. 【答案】B【解析】在▱ABCD 中,AD =BC ,AB =CD ,BO =DO ,∵平行四边形ABCD 的周长为26 cm ,∴AB +BC =13 cm ,又∵△AOD 的周长比△AOB 的周长多3 cm ,∴AD -AB =BC -AB =3 cm ,解得AB =5 cm ,BC =8 cm ,又AB ⊥AC ,E 是BC 的中点,∴AE =BE =CE =12BC =4 cm.4. 【答案】B【解析】∵E,F,G,H分别是AO,BO,CO,DO的中点,在ABCD中,A B=2,AD=4,∴EH=12AD=2,HG=1122CD=AB=1,∴EH≠HG,故选项A 错误;∵E,F,G,H分别是AO,BO,CO,DO的中点,∴EH=1122AD BC FG==,∴四边形EFGH是平行四边形,故选项B正确;由题目中的条件,无法判断AC和BD是否垂直,故选项C错误;∵点E、F分别为OA和OB的中点,∴EF=12AB,EF∥AB,∴△OEF∽△OAB,∴214AEFOABS EFS AB⎛⎫==⎪⎝⎭,即△ABO的面积是△EFO的面积的4倍,故选项D错误,故选B.5. 【答案】C6. 【答案】B【解析】∵在△ABC中,D,E分别是AB,BC的中点,∴DE是△ABC的中位线,∴DE=12 AC.A.根据∠B=∠F不能判定AC∥DF,即不能判定四边形ADFC为平行四边形,故本选项错误.B.根据∠B=∠BCF可以判定CF∥AB,即CF∥AD,由“两组对边分别平行的四边形是平行四边形”得到四边形ADFC为平行四边形,故本选项正确.C.根据AC=CF不能判定AC∥DF,即不能判定四边形ADFC为平行四边形,故本选项错误.D.根据AD=CF,FD∥AC不能判定四边形ADFC为平行四边形,故本选项错误.故选B.7. 【答案】B8. 【答案】C【解析】可以利用割补法对平行四边形进行分割,然后使分割后的图形与PAD ∆的面积1S ,PBC ∆的面积2S 发生关联,然后求出其数量关系,如下图,过点P 作AD 的平行线,分别交ABCD 的边于点M 、N :2111(21222)AMND MbCN AMND MbCN SS S S S S S =+++==.二、填空题(本大题共8道小题) 9. 【答案】AD ∥BC (答案不唯一) 【解析】根据平行四边形的判定,在已有AB ∥DC 的条件下,可再加另一组对边平行即可证得它是平行四边形,即加“AD ∥BC”.10. 【答案】AD=BC【解析】当添加条件AD=BC 时,根据一组对边平行且相等的四边形是平行四边形,可得四边形ABCD 是平行四边形.11. 【答案】19【解析】如图,AOB ∆的周长为AB AO BO ++,BOC ∆的周长为BC BO CO ++ 由平行四边形的对角线互相平分可得()()8AB AO BO BC BO CO AB BC ++-++=-= ∴6082194AB +⨯==.12. 【答案】50°【解析】在平行四边形ABCD 中,AB ∥CD ,AD ∥BC ,∴∠FBA=∠C =40°,∵FD ⊥AD ,∴∠ADF =90°,∵AD ∥BC ,∴∠F =∠ADF =90°,∴∠BEF =180°-90°-40°=50°.13. 【答案】16【解析】∵四边形ABCD 是平行四边形,∴OA =OC ,AB =CD ,AD =BC .∵OE ∥AB ,∴OE 是△ACD 的中位线.∴AE =12AD ,OE =12CD .∵OA =1,△AOE 的周长等于5,∴AE +OE =4.∴AD +CD =8.∴平行四边形ABCD 的周长=16.故答案为16.14. 【答案】21° 【解析】设∠ADE=x ,∵AE=EF ,∠ADF=90°,∴∠DAE=∠ADE=x ,DE=12AF=AE=EF ,∵AE=EF=CD ,∴DE=CD , ∴∠DCE=∠DEC=2x ,∵四边形ABCD 是平行四边形,∴AD ∥BC , ∴∠DAE=∠BCA=x ,∴∠DCE=∠BCD ﹣∠BCA=63°﹣x ,∴2x=63°﹣x ,解得x=21°,即∠ADE=21°; 故答案为:21°.15. 【答案】36°【解析】∵在▱ABCD 中,∠D =∠B =52°,∴∠AEF =∠DAE +∠D =20°+52°=72°,∴∠AED =180°-∠AEF =108°,由折叠的性质得,∠AED ′=∠AED =108°,∴∠FED ′=∠AED′-∠AEF =108°-72°=36°.16. 【答案】①1423S S S S =;②9三、解答题(本大题共4道小题)17. 【答案】(1)解: ∵CF 平分∠BCD ,∴∠BCD =2∠BCF .∵∠BCF =60°,∴∠BCD =2×60°=120°.∵四边形ABCD 是平行四边形,∴AB ∥CD ,∴∠ABC +∠BCD =180°. ∴∠ABC =180°-120°=60°.(2)证明:∵四边形ABCD 是平行四边形,∴AB =CD ,AB ∥CD ,∠BAD =∠DCB .∴∠ABE =∠CDF .∵AE ,CF 分别平分∠BAD 和∠DCB ,∴∠BAE =12∠BAD =12∠DCB =∠DCF .在△ABE 和△CDF 中,∵∠ABE =∠CDF ,AB =CD ,∠BAE =∠DCF , ∴△ABE ≌△CDF . ∴BE =DF .18. 【答案】如图所示,将PAB ∆平移至QDC ∆的位置,易证DQ AP =,CQ BP =,则四边形DPCQ 恰好是一个以AP 、BP 、CP 、DP 为边的四边形,并且它的对角线恰好等于平行四边形ABCD 的两条邻边.QDPCBA19. 【答案】(1)证明:四边形BEAC 是平行四边形. 理由如下:∵△EAD 为等腰三角形且∠EAD ﹦90°, ∴∠E ﹦45°.∵B 是DE 的中点, ∴AB ⊥DE . ∴∠BAE ﹦45°.∵△ABC 为等腰三角形且∠BAC ﹦90°, ∴∠CBA ﹦45°. ∴∠BAE ﹦∠CBA . ∴BC ∥EA . 又∵AB ⊥DE ,∴∠EBA ﹦∠BAC ﹦90°. ∴BE ∥AC .∴四边形BEAC 是平行四边形.(2)证明:①∵△AED 和△ABC 为等腰三角形, ∴AE ﹦AD ,AB ﹦AC . ∵∠EAD ﹦∠BAC ﹦90°,∴∠EAD +∠DAB ﹦∠BAC +∠DAB .即∠EAB ﹦∠DAC . ∴△AEB ≌△ADC . ∴EB ﹦DC .②延长FG 至点H ,使GH ﹦FG . ∵G 是EC 中点,∴EG ﹦CG .又∠EGH ﹦∠FGC , ∴△EHG ≌△CFG ,∴∠BFC ﹦∠H ,CF ﹦EH . 又∵CF ﹦CD , ∴BE ﹦CF . ∴BE ﹦EH .∴∠EBG ﹦∠H . ∴∠EBG ﹦∠BFC .AB CDEEDCBA FGH20. 【答案】如图所示,,分别过点B 、C 、D 作直线AO 的垂线,EG CP DL ∥∥、Q 、N 为垂足;分别过B 、D 作AC 的垂线,L 、K 为垂足. 显然,A 、E 、O 、G 、F 五点共圆,AO 是直径.由DN AO ⊥,CQ AO ⊥,BM AO ⊥,DC AB ∥且DC AB =可知NQ AM =. 已知AF AD AN AO ⋅=⋅,AE AB AM AO ⋅=⋅, 则AF AD AE AB ⋅+⋅ AN AO AM AO =⋅+⋅ ()AO AN AM =+ ()AO AN NQ =+ AO AQ =⋅ AG AC =⋅故AE AB AF AD AG AC ⋅+⋅=⋅.点评:ab cd ef +=类型的问题一般要转化为ab mn =型的问题(当然,如果能够使用勾股定理、余弦定理等,大家也可以踊跃尝试),把握了这一点,就能及时调整思路,确保解题不会误入歧途.图(1)图(2)。
人教版 八年级数学 第12章 全等三角形 培优训练 (含答案)

人教版八年级数学第12章全等三角形培优训练一、选择题1. 下列各组的两个图形属于全等图形的是()2. 如图,点E,F在线段BC上,△ABF与△DCE全等,点A与点D,点B与点C是对应顶点,AF与DE相交于点M,则∠DCE等于()A.∠B B.∠A C.∠EMF D.∠AFB3. 如图所示,P是∠BAC内一点,且点P到AB,AC的距离PE,PF相等,则△PEA≌△PF A的依据是()A.HL B.ASA C.SSS D.SAS4. 根据下列条件,能画出唯一的△ABC的是()A.AB=3,BC=4,AC=8 B.AB=4,BC=3,∠A=30°C.AB=5,AC=6,∠A=50°D.∠A=30°,∠B=70°,∠C=80°5. 如图,点A在点O的北偏西30°的方向上,AB⊥OA,垂足为A.根据已知条件和图上尺规作图的痕迹判断,下列说法正确的是()A.点O在点A的南偏东60°方向上B.点B在点A的北偏东30°方向上C.点B在点O的北偏东60°方向上D.点B在点O的北偏东30°方向上6. 如图,有一张三角形纸片ABC,已知∠B=∠C=x°,按下列方案用剪刀沿着箭头方向剪开,可能得不到全等三角形纸片的是()7. 现已知线段a,b(a<b),∠MON=90°,求作Rt△ABO,使得∠O=90°,OA=a,AB=b.小惠和小雷的作法分别如下:小惠:①以点O为圆心、线段a的长为半径画弧,交射线ON于点A;②以点A为圆心、线段b的长为半径画弧,交射线OM于点B,连接AB,△ABO即为所求.小雷:①以点O为圆心、线段a的长为半径画弧,交射线ON于点A;②以点O为圆心、线段b的长为半径画弧,交射线OM于点B,连接AB,△ABO即为所求.则下列说法中正确的是()A.小惠的作法正确,小雷的作法错误B.小雷的作法正确,小惠的作法错误C.两人的作法都正确D.两人的作法都错误8. 如图,点G在AB的延长线上,∠GBC,∠BAC的平分线相交于点F,BE⊥CF 于点H.若∠AFB=40°,则∠BCF的度数为()A.40°B.50°C.55°D.60°二、填空题9. 如图,在Rt△ABC中,∠C=90°,∠B=20°,以点A为圆心,小于AC的长为半径画弧与AB,AC分别交于点M,N,再分别以点M,N为圆心,大于MN的长为半径画弧,两弧相交于点P,连接AP并延长交BC于点D,则∠ADB=°.10. 如图,在△ABC中,AD⊥BC于点D,要使△ABD≌△ACD,若根据“HL”判定,还需要添加条件:____________.11. 如图,若AB=AC,BD=CD,∠A=80°,∠BDC=120°,则∠B=________°.12. 在△ABC中,AB=4,AC=3,AD是△ABC的角平分线,则△ABD与△ACD 的面积之比是________.13. (2019•南通)如图,△ABC中,AB=BC,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF,若∠BAE=25°,则∠ACF=__________度.14. 如图所示,已知AD∥BC,则∠1=∠2,理由是________________;又知AD =CB,AC为公共边,则△ADC≌△CBA,理由是______,则∠DCA=∠BAC,理由是__________________,则AB∥DC,理由是________________________________.15. 如图,在△ABC中,∠C=90°,AC=BC,AD是∠BAC的平分线,DE⊥AB,垂足为E.若△DBE的周长为20,则AB=________.16. 如图,△ABC的两条外角平分线BP,CP相交于点P,PE⊥AC交AC的延长线于点E.若△ABC的周长为11,PE=2,S△BPC =2,则S△ABC=.三、解答题17. 育新中学校园内有一块直角三角形(Rt△ABC)空地,如图所示,园艺师傅以角平分线AD为界,在其两侧分别种上了不同的花草,在△ABD区域内种植了一串红,在△ACD区域内种植了鸡冠花,并量得两直角边AB=20 m,AC=10 m,分别求一串红与鸡冠花两种花草的种植面积.18. 如图,已知△ACF≌△DBE,且点A,B,C,D在同一条直线上.若AD=16,BC=10,求AB的长.19. 我们把两组邻边分别相等的四边形叫做“筝形”.如图,四边形ABCD是筝形,其中AB=AD,CB=CD,P是对角线AC上除A,C外的任意一点.求证:∠ABP =∠ADP.20. 如图,已知AP∥BC,∠P AB的平分线与∠CBA的平分线相交于点E,过点E 的直线分别交AP,BC于点D,C.求证:AD+BC=AB.21. (1)如图①,在△ABC中,∠BAC=90°,AB=CA,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为D,E.求证:DE=BD+CE.(2)如图②,将(1)中的条件改为:在△ABC中,AB=CA,D,A,E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角,则结论DE=BD+CE是否成立?若成立,请你给出证明;若不成立,请说明理由.人教版八年级数学第12章全等三角形培优训练-答案一、选择题1. 【答案】A2. 【答案】A[解析] ∵△ABF与△DCE全等,点A与点D,点B与点C是对应顶点,∴∠DCE=∠B.故选A.3. 【答案】A4. 【答案】C[解析] 对于选项A来说,AB+BC<AC,不能画出△ABC;对于选项B来说,可画出△ABC为锐角三角形或者钝角三角形;对于选项C来说,已知两边及其夹角,△ABC是唯一的;对于选项D来说,△ABC的形状可确定,但大小不确定.5. 【答案】D[解析] 如图,由题意知∠AOD=30°,∠COD=90°,∴∠AOC=120°.由作图可知,OB平分∠AOC,∴∠AOB=∠AOC=60°.∴∠DOB=30°.∴点B在点O的北偏东30°方向上.6. 【答案】C[解析] 选项A中由全等三角形的判定定理“SAS”证得图中两个小三角形全等.选项B中由全等三角形的判定定理“SAS”证得图中两个小三角形全等.选项C中,如图①,∵∠DEC=∠B+∠BDE,∴x°+∠FEC=x°+∠BDE.∴∠FEC=∠BDE.这两个角所对的边是BE和CF,而已知条件给的是BD=CF=3,故不能判定两个小三角形全等.选项D中,如图②,∵∠DEC=∠B+∠BDE,∴x°+∠FEC=x°+∠BDE.∴∠FEC=∠BDE.又∵BD=CE=2,∠B=∠C,∴△BDE≌△CEF.故能判定两个小三角形全等.7. 【答案】A[解析] AB=b,AB是斜边,小惠作的斜边长是b符合条件,而小雷作的是一条直角边长是b.故小惠的作法正确,小雷的作法错误.8. 【答案】B[解析] 如图,过点F分别作FZ⊥AE于点Z,FY⊥CB于点Y,FW⊥AB于点W.∵AF平分∠BAC,FZ⊥AE,FW⊥AB,∴FZ=FW.同理FW=FY.∴FZ=FY.又∵FZ⊥AE,FY⊥CB,∴∠FCZ=∠FCY.由∠AFB=40°,易得∠ACB=80°.∴∠ZCY=100°.∴∠BCF=50°.二、填空题9. 【答案】125[解析] 由题意可得AD平分∠CAB.∵∠C=90°,∠B=20°,∴∠CAB=70°.∴∠CAD=∠BAD=35°.∴∠ADB=180°-20°-35°=125°.10. 【答案】AB =AC11. 【答案】20[解析] 如图,过点D 作射线AF.在△BAD 和△CAD 中,⎩⎨⎧AB =AC ,AD =AD ,BD =CD ,∴△BAD ≌△CAD(SSS). ∴∠BAD =∠CAD ,∠B =∠C.∵∠BDF =∠B +∠BAD ,∠CDF =∠C +∠CAD , ∴∠BDF +∠CDF =∠B +∠BAD +∠C +∠CAD , 即∠BDC =∠B +∠C +∠BAC. ∵∠BAC =80°,∠BDC =120°, ∴∠B =∠C =20°.12. 【答案】4∶3【解析】如解图,过D 作DE ⊥AB ,DF ⊥AC ,垂足分别为E 、F ,∵AD 是∠BAC 的平分线,∴DE =DF(角平分线上的点到角两边的距离相等),设DE=DF=h,则S△ABDS△ACD =12AB·h12AC·h=43.13. 【答案】70【解析】∵∠ABC=90°,AB=AC,∴∠CBF=180°–∠ABC=90°,∠ACB=45°,在Rt△ABE和Rt△CBF中,AB CBAE CF=⎧⎨=⎩,∴Rt△ABE≌Rt△CBF,∴∠BCF=∠BAE=25°,∴∠ACF=∠ACB+∠BCF=45°+25°=70°,故答案为:70.14. 【答案】两直线平行,内错角相等SAS全等三角形的对应角相等内错角相等,两直线平行15. 【答案】20[解析] 由角平分线的性质可得CD=DE.易证Rt△ACD≌Rt△AED,则AC=AE,DE+DB=CD+DB=BC=AC=AE,故DE+DB+EB =AE+EB=AB.16. 【答案】7[解析] 过点P作PF⊥BC于点F,PG⊥AB于点G ,连接AP.∵△ABC的两条外角平分线BP,CP相交于点P,∴PF=PG=PE=2.∵S△BPC=2,∴BC·2=2,解得BC=2.∵△ABC的周长为11,∴AC+AB=11-2=9.∴S △ABC =S △ACP +S △ABP -S △BPC =AC ·PE+AB ·PG-S △BPC =×9×2-2=7.三、解答题17. 【答案】解:如图,过点D 作DE ⊥AB 于点E ,DF ⊥AC 于点F. ∵AD 是∠BAC 的平分线,∴DE =DF. ∵AB =20 m ,AC =10 m ,∴S △ABC =12×20×10=12×20·DE +12×10·DF ,解得DE =203(m).∴△ACD 的面积=12×10×203=1003(m 2),△ABD 的面积=12×20×203=2003(m 2).故一串红的种植面积为2003 m 2,鸡冠花的种植面积为1003 m 2.18. 【答案】解:∵△ACF ≌△DBE ,∴AC=DB.∴AC-BC=DB-BC ,即AB=CD.∵AD=16,BC=10,∴AB=CD=(AD-BC )=3.19. 【答案】证明:在△ABC 和△ADC 中,⎩⎨⎧AB =AD ,AC =AC ,CB =CD , ∴△ABC ≌△ADC.∴∠BAP =∠DAP.在△BAP 和△DAP 中,⎩⎨⎧AB =AD ,∠BAP =∠DAP ,AP =AP , ∴△BAP ≌△DAP.∴∠ABP =∠ADP.20. 【答案】证明:如图,在AB 上截取AF =AD ,连接EF.∵AE 平分∠PAB ,∴∠DAE =∠FAE.在△DAE 和△FAE 中,⎩⎨⎧AD =AF ,∠DAE =∠FAE ,AE =AE ,∴△DAE ≌△FAE(SAS).∴∠AFE =∠ADE.∵AD ∥BC ,∴∠ADE +∠C =180°.又∵∠AFE +∠EFB =180°,∴∠EFB =∠C.∵BE 平分∠ABC ,∴∠EBF =∠EBC.在△BEF 和△BEC 中,⎩⎨⎧∠EFB =∠C ,∠EBF =∠EBC ,BE =BE ,∴△BEF ≌△BEC(AAS).∴BF =BC.∴AD +BC =AF +BF =AB.21. 【答案】解:(1)证明:∵BD ⊥直线m ,CE ⊥直线m , ∴∠BDA =∠AEC =90°.∴∠BAD +∠ABD =90°.∵∠BAC =90°,∴∠BAD +∠CAE =90°. ∴∠CAE =∠ABD.在△ADB 和△CEA 中,⎩⎨⎧∠ABD =∠CAE ,∠BDA =∠AEC ,AB =CA ,∴△ADB ≌△CEA(AAS).∴BD =AE ,AD =CE.∴DE =AE +AD =BD +CE.(2)成立.证明:∵∠BDA =∠BAC =α,∴∠DBA +∠BAD =∠BAD +∠EAC =180°-α. ∴∠DBA =∠EAC.在△ADB 和△CEA 中,⎩⎨⎧∠DBA =∠EAC ,∠BDA =∠AEC ,AB =CA ,∴△ADB ≌△CEA(AAS).∴BD =AE ,AD =CE.∴DE =AE +AD =BD +CE.。
浙教版2022-2023学年八下数学第四章 平行四边形 培优测试卷(解析版)

浙教版2022-2023学年八下数学第四章 平行四边形 培优测试卷(解析版)一、选择题(本大题有10小题,每小题3分,共30分) 下面每小题给出的四个选项中,只有一个是正确的.1.以下分别是回收、节水、绿色包装、低碳4个标志,其中是中心对称图形的是( ).A .B .C .D .【答案】C【解析】A 、此图形不是中心对称图形,故本选项不符合题意; B 、此图形不是中心对称图形,故此选项不符合题意; C 、此图形是中心对称图形,故此选项符合题意;D 、此图形不是中心对称图形,故此选项不符合题意. 故答案为:C .2.已知平行四边形ABCD 中,∠A +∠C =240°,则∠B 的度数是( ) A .100° B .60° C .80° D .160° 【答案】B【解析】∵四边形ABCD 为平行四边形, ∴∠A=∠C ,∠A+∠B =180°. 又∵∠A+∠C=240°, ∴∠A=∠C=120°, ∠B=180°-∠A=60°. 故答案为:B3.多边形边数从n 增加到n +1,则其内角和( ) A .增加180° B .增加360° C .不变 D .减少180° 【答案】A【解析】n 边形的内角和是(n -2)•180°,边数增加1,则新的多边形的内角和是(n+1-2)•180°. 则(n+1-2)•180°-(n -2)•180°=180°. 故它的内角和增加180°. 故答案为:A .4.如图,平行四边形ABCD 的对角线AC 与BD 相交于点O ,AB∠AC .若AC =6,BD =10,则AB 的长是( )A .3B .4C .5D .6 【答案】B【解析】∵四边形ABCD 是平行四边形,BD =10,AC =6, ∴AO =OC =12AC =3,BO =DO =12BD =5,又∵AB∠AC , ∴∠BAC =90°,∴AB =√BO 2−AO 2=√52−32=4, 故答案为:B . 5.用反证法证明,“在∠ABC 中,∠A 、∠B 对边是a 、b ,若∠A <∠B ,则a <b .”第一步应假设( ) A .a >b B .a =b C .a≤b D .a≥b【答案】D【解析】根据反证法步骤,第一步应假设a <b 不成立,即a≥b . 故答案为:D.6.如图,点E 、F 分别是∠ABCD 边AD 、BC 的中点,G 、H 是对角线BD 上的两点,且BG=DH .则下列结论中错误的是( )A .GF =EHB .四边形EGFH 是平行四边形C .EG =FHD .EH ⊥BD【答案】D【解析】连接EF 交BD 于点O ,在平行四边形ABCD 中,AD=BC ,∠EDH=∠FBG , ∵E 、F 分别是AD 、BC 边的中点,∴DE=BF=12BC ,∠EDO=∠FBO ,∠DOE=∠BOF ,∴∠EDO∠∠FBO , ∴EO=FO ,DO=BO , ∵BG=DH , ∴OH=OG ,∴四边形EGFH 是平行四边形, ∴GF=EH ,EG=HF ,故答案为:A 、B 、C 不符合题意; ∵∠EHG 不一定等于90°,∴EH∠BD 错误,D 符合题意; 故答案为:D .7.如图,在四边形ABCD 中,点P 是对角线BD 的中点,点E 、F 分别是AB 、CD 的中点,AD=BC ,∠CBD=30°,∠ADB=100°,则∠PFE 的度数是( )A .15°B .25°C .30°D .35°【答案】D【解析】∵点P 是BD 的中点,点E 是AB 的中点, ∴PE 是∠ABD 的中位线, ∴PE=12AD ,PE∠AD ,∴∠EPD=180°-∠ADB=80°, 同理可得,PF=12BC ,PE∠BC ,∴∠FPD=∠CBD=30°, ∵AD=BC , ∴PE=PF ,∴∠PFE=12×(180°-110°)=35°,故答案为:D .8.如图, ▱EFGH 的四个顶点分别在 ▱ABCD 的四条边上, QF ∥AD ,分别交EH 、CD 于点P 、Q 过点P 作 MN ∥AB ,分别交AD 、BC 于点M 、N ,若要求 ▱EFGH 的面积,只需知道下列哪个四边形的面积( )A .四边形AFPMB .四边形MPQDC .四边形FBNPD .四边形PNCQ【答案】C【解析】如图,连接PG ,FN ,∵∠EFGH ,∴S △FPG =12S ▱EFGH ,∵FQ ∥BC ,∴S △FPN =S △FPG , 又∵MN∠AB ,∴四边形FBNP 为平行四边形,∴S △FPN =S △FPG =12S ▱FBNP∴S ▱FBNP =S ▱EFGH ,∴要求∠EFGH 的面积,只需要知道四边形FBNP 的面积. 故答案为:C.9.如图,已知□OABC 的顶点A ,C 分别在直线 x =1 和 x =4 上,O 是坐标原点,则对角线OB 长的最小值为( )A .3B .4C .5D .6 【答案】C【解析】过点B 作BD⊥直线x=4,交直线x=4于点D ,过点B 作BE⊥x 轴,交x 轴于点E ,直线x=1与OC 交于点M ,与x 轴交于点F ,直线x=4与AB 交于点N ,如图:∵四边形OABC是平行四边形,∴⊥OAB=⊥BCO,OC⊥AB,OA=BC.∵直线x=1与直线x=4均垂直于x轴,∴AM⊥CN,∴四边形ANCM是平行四边形,∴⊥MAN=⊥NCM,∴⊥OAF=⊥BCD.∵⊥OFA=⊥BDC=90°,∴⊥FOA=⊥DBC.在⊥OAF和⊥BCD中,⊥FOA=⊥DBC,OA=BC,⊥OAF=⊥BCD,∴⊥OAF⊥⊥BCD,∴BD=OF=1,∴OE=4+1=5,∴OB=√OE2+BE2.由于OE的长不变,所以当BE最小时,OB取得最小值,最小值为OB=OE=5.故答案为:C.10.如图,∠ ABCD的对角线AC、BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB=12BC,连接OE.下列结论:①∠ADO=30°;②S ∠ ABCD=AB·AC;③OB=AB;④S四边形OECD=32S∠AOD,其中成立的个数为()A.1个B.2个C.3个D.4个【答案】B【解析】∵四边形ABCD为平行四边形,∠ADC=60°,∴OA=OC,OB=OD,∠ABC=60°,∠BAD=120°,∵AE平分∠BAD,∴∠BAE=∠DAE=60°,∴△ABE是等边三角形,∴AB=AE=BE,∠AEB=60°,∵AB=12BC,∴BE=12BC,∴CE=BE=AE,∴∠ACE=∠CAE=30°,∴∠OAB=90°,∠OAD=30°,∴在Rt△AOB中,OB>OA,OB>AB,则结论③不成立;∴OD >OA ,∴∠ADO ≠∠OAD ,即∠ADO ≠30°,结论①不成立; ∵∠OAB =90°,即AB ⊥AC ,∴S ▱ABCD =AB ⋅AC ,则结论②成立; 设平行四边形ABCD 的面积为8a(a >0), 则S △AOD =S △COD =S △BOC =14S ▱ABCD =2a ,∵BE =CE ,∴S △BOE =S △COE =12S △BOC =a ,∴S 四边形OECD =S △COE +S △COD =3a =32S △AOD ,结论④成立;综上,成立的个数为2个, 故答案为:B .二、填空题(本大题有6小题,每小题4分,共24分)要注意认真看清题目的条件和要填写的内容,尽量完整地填写答案.11.一个多边形的内角和与外角和的和为2160∠,则这个多边形的边数为 . 【答案】12【解析】设这个多边形的边数是n , (n -2)•180°+360°=2160°, 解得n=12. 故答案为:12.12.在平面直角坐标系中,已知A 、B 、C 、D 四点的坐标依次为(0,0)、(6,0)、(8,6)、(2,6),若一次函数y=mx -6m 的图象将四边形ABCD 的面积分成1:3两部分,则m 的值为 .【答案】−35或−6【解析】∵直线y=mx -6m 经过定点B (6,0),A 、B 、C 、D 四点的坐标依次为(0,0)、(6,0)、(8,6)、(2,6),∴CD∠AB ,CD=8-2=6= AB , ∴四边形ABCD 是平行四边形,∴S∠ADC= S∠ADC=12S 平行四边形ABCD ,又∵直线y=mx -6m 把平行四边形ABCD 的面积分成1:3的两部分.∴直线y=mx -6m 经过AD 的中点M (1,3)或经过CD 的中点N (5,6), ∴m -6m=3或5m -6m=6,∴m=-35或-6,故答案为:-35或-6.13.如图,△ABC 是边长为1的等边三角形,取BC 边中点E ,作ED ∥AB ,EF ∥AC ,ED ,EF 分别交AC ,AB 于点D ,F ,得到四边形EDAF ,它的面积记作S 1;取BE 中点E 1,作E 1D 1∥FB ,E 1F 1∥EF ,E 1D 1,E 1F 1分别交EF ,BF 于点D 1,F 1,得到四边形E 1D 1FF 1,它的面积记作S 2……照此规律作下去,则S n = .【答案】√322n+1【解析】∵∠ABC 是边长为1的等边三角形,∴∠ABC 的高为:√12−(12)2=√32,∴S △ABC =12×1×√32=√34,∵DE 、EF 分别是∠ABC 的中位线,∴AF =12AC =12,∴S 1=12S △ABC =√38,同理可得S 2=√38×14;…,∴S n =√38×(14)n−1=√322n+1;故答案为:√322n+1.14.如图, ΔABC 和 ΔDEC 关于点C 成中心对称,若 AC =1 , AB =2 , ∠BAC =90° ,则 AE 的长是 .【答案】2√2【解析】∵∠DEC 与∠ABC 关于点C 成中心对称, ∴DC=AC=1,DE=AB=2,∴在Rt∠EDA 中,AE 的长是:AE =√AD 2+DE 2=√(DC +AC)2+DE 2=√(1+1)2+22=2√2 . 故答案为: 2√2 . 15.已知:如图,线段AB =6cm ,点P 是线段AB 上的动点,分别以AP 、BP 为边在AB 作等边△APC 、等边△BPD ,连接CD ,点M 是CD 的中点,当点P 从点A 运动到点B 时,点M 经过的路径的长是 cm .【答案】3【解析】如图,分别延长AC,BD交于H,过点M作GN∠AB分别交AH于G,BH于N,∵∠APC、∠BPD都是等边三角形,∴∠A=∠B=∠DPB=∠CPA=60°,∴AH∠PD,BH∠CP,∴四边形CPDH是平行四边形,∴CD与HP互相平分,∴M是PH的中点,故在P运动过程中,M始终在HP的中点,所以M的运动轨迹即为∠HAB的中位线,即线段GN,∴GN=12AB=3cm,故答案为:3.16.如图,把含45∘,30∘角的两块直角三角板放置在同一平面内,若AB//CD,AB=CD=√6则以A,B,C,D为顶点的四边形的面积是.【答案】3+2√3【解析】延长CO,交AB于点E,由题意可知:∠BAO=45°,∠CDO=30°∵AB//CD,AB=CD=√6∴四边形ABCD为平行四边形∵OC∠CD∴CE∠AB∴S∠AOB+S∠COD= 12AB·OE+12CD·OC= 12AB·(OE+OC)= 12AB·CE= 12S平行四边形ABCD∴S平行四边形ABCD=2(S∠AOB+S∠COD)在Rt∠AOB中,AO2+BO2=AB2=6,AO=BO解得:AO=BO= √3在Rt∠COD中,∠CDO=30°,OC2+CD2=OD2∴OD=2OC,OC2+6=(2OC)2解得:OC= √2,∴S∠AOB= 12AO·BO= 32,S∠COD=12CD·OC= √3∴S平行四边形ABCD=2(S∠AOB+S∠COD)=2×(32+√3)= 3+2√3故答案为:3+2√3.三、解答题(本题有8小题,第17~19题每题6分,第20、21题每题8分,第22、23题每题10分,第24题12分,共66分)解答应写出文字说明,证明过程或推演步骤.17.如图,在▱ABCD中,点E、F在对角线AC上,且AE=CF,连接BF、DE.求证:BF=DE,BF∥DE.【答案】解:∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC.∴∠DAC=∠BCA.又∵AE=CF,∴△DAE≌△BCF(SAS),∴BF=DE,∠DEA=∠BFC.∴∠DEC=∠BFA.∴BF∥DE.18.如图,在∠ABCD中,点E在边AD上,连接EB并延长至F,使BF=BE;连接EC并延长至G,使CG=CE,连接FG,点H为FG的中点,连接DH,AF.(1)若∠BAE=70°,∠DCE=20°,求∠DEC的度数;(2)求证:四边形AFHD为平行四边形.【答案】(1)解:∵四边形ABCD是平行四边形,∴∠BAE=∠BCD=70°,AD∠BC,∵∠DCE=20°,AB∠CD,∴∠CDE=180°﹣∠BAE=110°,∴∠DEC=180°﹣∠DCE﹣∠CDE=50°;(2)解:∵四边形ABCD是平行四边形,∴AD=BC,AD∠BC,∵BF=BE,CG=CE,∴BC是∠EFG的中位线,∴BC∠FG ,BC =12FG ,∵H 为FG 的中点, ∴FH =12FG ,∴BC∠FH ,BC =FH , ∴AD∠FH ,AD =FH ,∴四边形AFHD 是平行四边形.19.如图,∠ABC 中,点D ,E 分别是边AB ,AC 的中点,过点C 作CF∠AB 交DE 的延长线于点F ,连接BE .(1)求证:四边形BCFD 是平行四边形.(2)当AB =BC 时,若BD =2,BE =3,求AC 的长. 【答案】(1)证明:∵点 D ,E 分别是边 AB ,AC 的中点, ∴DE∠BC . ∵ CF∠AB ,∴四边形 BCFD 是平行四边形;(2)解:∵AB =BC ,E 为 AC 的中点, ∴BE∠AC .∵AB =2DB =4, BE =3, ∴AE =√42−32=√7 ∴AC =2AE =2√720.如图,在 5×5 的方格纸中,每个小正方形的边长均为1,A ,B 两点均在小正方形的顶点上,请按下列要求,在图1,图2,图3中各画一个四边形(所画四边形的顶点均在小正方形的项点上)(1)在图1中画四边形 ABCD ,使其为中心对称图形,但不是轴对称图形; (2)在图2中画以A ,B ,M ,N 为顶点的平行四边形,且面积为5;(3)在图3中画以A ,B ,E ,F 为顶点的平行四边形,且其中一条对角线长等于3. 【答案】(1)解:如图1中,四边形ABCD 即为所求作.(2)解:如图2中,四边形ABMN即为所求作. (3)解:如图3中,四边形ABEF即为所求作. 21.如图,在▱ABCD中,E,F是对角线AC上的两点,且AE=CF.(1)求证:四边形BEDF是平行四边形;(2)若AB⊥BF,AB=8,BF=6,AC=16.求线段EF长.【答案】(1)证明:连接BD交AC于点O.∵四边形ABCD是平行四边形,∴OA=OC,OB=OD,∵AE=CF,∴OE=OF,∵OB=OD,∴四边形BEDF是平行四边形.(2)解:在Rt△ABF中,AF=√AB2+BF2=√82+62=10,∵AC=16,∴CF=AC−AF=16−10=6,∵AE=CF,∴AE=6,∴EF=AF−AE=10−6=4.22.如图,已知:在∠ABCD中,AE∠BC,垂足为E,CE=CD,点F为CE的中点,点G为CD上的一点,连接DF,EG,AG,∠1=∠2.(1)求证:G 为CD 的中点.(2)若CF =2.5,AE =4,求BE 的长.【答案】(1)证明:∵点F 为CE 的中点,∴CF=12CE , 在∠ECG 与∠DCF 中,∵∠2=∠1, ∠C =∠C , CE =CD ,∴∠ECG∠∠DCF (AAS ),∴CG=CF= 12CE. 又CE=CD , ∴CG=12CD , 即G 为CD 的中点; (2)解:∵CE=CD ,点F 为CE 的中点,CF=2.5,∴DC=CE=2CF=5,∵四边形ABCD 是平行四边形,∴AB=CD=5,∵AE∠BC ,∴∠AEB=90°,在Rt∠ABE 中,由勾股定理得:BE=√52−42=3.23.如图,平行四边形ABCD 中,AE 平分∠BAD ,交BC 于点E ,且AB =AE ,延长AB 与DE 的延长线交于点F .下列结论中:求证:(1)∠ABE 是等边三角形;(2)∠ABC ∠∠EAD ;(3)S △ABE =S △CEF .【答案】(1)证明:∵ABCD 是平行四边形∴AD∠BC ,AD=BC ,∴∠EAD=∠AEB ,又∵AE 平分∠BAD ,∴∠BAE=∠DAE ,∴∠BAE=∠BEA ,∴AB=BE ,∵AB=AE ,∴∠ABE 是等边三角形;(2)证明:∵∠ABE 是等边三角形∴∠ABE=∠EAD=60∠,∵AB=AE ,BC=AD ,∴∠ABC∠∠EAD(SAS)(3)证明:∵∠FCD 与∠ABC 等底(AB=CD)等高(AB 与CD 间的距离相等),∴S∠FCD=S∠ABC ,又∵∠AEC与∠DEC同底等高,∴S∠AEC=S∠DEC,∴S∠ABE=S∠CEF24.我们规定:有一组邻边相等,且这组邻边的夹角为60°的凸四边形叫做“准筝形”.(1)如图1,在四边形ABCD中,∠A+∠C=270°,∠D=30°,AB=CB,求证:四边形ABCD是“准筝形”;(2)如图2,在“准筝形”ABCD中,AB=AD,∠BAD=∠BCD=60°,BC=4,CD=3,求AC的长;(3)如图3,在∠ABC中,∠A=45°,∠ABC=120°,AB=3-√3,设D是∠ABC所在平面内一点,当四边形ABCD是“准筝形”时,请直接写出四边形ABCD的面积.【答案】(1)证明:在四边形ABCD中,∠A+∠B+∠C+∠D=360°,∵∠A+∠C=270°,∠D=30°,∴∠B=360°-(∠A+∠C+∠D)=360°-(270°+30°)=60°,∵AB=BC,∴四边形ABCD是“准筝形”;(2)解:以CD为边作等边∠CDE,连接BE,过点E作EF∠BC于F,如图2所示:则DE=DC=CE=3,∠CDE=∠DCE=60°,∵AB=AD,∠BAD=∠BCD=60°,∴∠ABD是等边三角形,∴∠ADB=60°,AD=BD,∴∠ADB+∠BDC=∠CDE+∠BDC,即∠ADC=∠BDE,在∠ADC和∠BDE中,{AD=BD∠ADC=∠BDEDC=DE,∴∠ADC∠∠BDE(SAS),∴AC=BE,∵∠BCD=∠DCE=60°,∴∠ECF=180°-60°-60°=60°,∵∠EFC =90°,∴∠CEF =30°,∴CF =12CE =32 , 由勾股定理得:EF =√CE 2−CF 2=√32−(32)2=3√32 , BF =BC +CF =4+32=112, 在Rt∠BEF 中,由勾股定理得:BE =√BF 2+EF 2=√(112)2+(3√32)2=√37 , ∴AC =√37 ;(3)解:四边形ABCD 的面积为3√32或9+3√32 或 92+3√3. 【解析】(3)过点C 作CH∠AB ,交AB 延长线于H ,如图3所示:设BH =x ,∵∠ABC =120°,CH 是∠ABC 的高线,∴∠BCH =30°,∴HC =√3x ,BC =2BH =2x ,又∵∠A =45°,∴∠HAC 是等腰直角三角形,∴HA =HC ,∵AB =3-√3 ,∴√3x =3-√3+x ,解得:x =√3,∴HC =√3x =3,BC =2√3 ,∴AC = √2 HC =3 √2 ,当AB =AD =3- √3 ,∠BAD =60°时,连接BD ,过点C 作CG∠BD ,交BD 延长线于点G ,过点A 作AK∠BD ,如图4所示:则BD =3-√3 ,∠ABD =60°,BK =12AB =12(3-√3 ), ∵∠ABC =120°,∴∠CBG =60°=∠CBH ,在∠CBG 和∠CBH 中, {∠CGB =∠CHB =90°∠CBG =∠CBH BC =BC,∴∠CBG∠∠CBH (AAS ),∴GC =HC =3,在Rt∠ABK 中,由勾股定理得:AK =√AB 2−BK 2 =√(3−√3)2−[12(3−√3)]2 = 3√3−32, ∴S ∠ABD = 12 BD•AK = 12×(3-√3 )×3√3−32 =6√3−92, S ∠CBD = 12 BD•CG = 12×(3-√3 )×3=9−3√32, ∴S 四边形ABCD = 6√3−92 + 9−3√32 = 3√32; ②当BC =CD =2√3 ,∠BCD =60°时,连接BD ,作CG∠BD 于点G ,AK∠BD 于K ,如图5所示:则BD =2√3 ,CG =√32 BC =√32×2√3 =3,AK =3√3−32 , ∴S ∠BCD =12 BD•CG =12×2√3×3=3√3, S ∠ABD =12BD•AK =12×2√3×3√3−32=9−3√32, ∴S 四边形ABCD =3√3+9−3√32=9+3√32 ; ③当AD =CD =AC =3√2,∠ADC =60°时,作DM∠AC 于M ,如图6所示:则DM =√32AD =√32×3√2 =3√62 , ∴S ∠ABC =12AB•CH =12×(3-√3)×3=9−3√32, S ∠ADC = 12 AC•DM =12×3√2×3√62=9√32, ∴S 四边形ABCD =9−3√32+ 9√32=92+3√3. 综上所述,四边形ABCD 的面积为3√32或9+3√32 或 92+3√3.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数学培优 (一)
1. 如果x x >,且0<kp ,那么,在自变量x 的取值范围内,正比例函数kx y =和反比例函数x
p y =
在同一直角坐标系中的图象示意图正确的是( )B
A B C D
2.在同一坐标系内,表示函数b kx y +=与()0,0≠≠=b k x
kb y 的图象只可能是下图中的( )B
A B C D
3. 如图,在直角坐标系中,直线x y -=6与)0(4>=x x
y 的图像相交于点A 、B ,设点A 的坐标为),(11y x ,那么长为x 1,宽为y 1的矩形面积和周长分别为( )
A 、4,12
B 、8,12
C 、4,6
D 、8,6
4. 已知点()a P ,1在反比例函数()0≠=k x
k y 的图象上,其中322++=m m a (m 为实数),则这个函数的图象在第_____象限.一、三
5.已知3=b ,且反比例函数x
b y +=1的图象在每个象限内,y 随x 的增大而增大,如果点()3,a 在双曲线上x b y +=1,则_____=a .3
2-=a 6. 如果不等式0<+n mx 的解集是4>x ,点()n ,1在双曲线x
y 2=上,那么一次函数()m x n y 21+-=的图象不经过第__ _象限. 一、三、四 7.如图,反比例函数x
k y 2=和一次函数12-=x y ,其中一次函数的图象经过()b a ,、()k b a ++,1两点.(1)求反比例函数的解析式;(2)若点A 坐标是()1,1,请问:在x 轴上是否存在点P ,使AOP ∆为等腰三角形?若存在,把符合条件的点P 的坐标都求出来;若不存在,请说明理由.
解:(1)根据题意,得()⎩
⎨⎧-+=+-=.112,12a k b a b 两式相减,得2=k .
所以所求的反比例函数的解析式是x
y 1=. (2)由勾股定理,得21122=+=OA ,OA 与x 轴所夹的角为︒45.
①当OA 为AOP ∆的腰时,由OP OA =,得()0,21
P ,()0,22-P ; 由AP OA =,得()0,23P .
②当OA 为AOP ∆的底时,得()0,14P .
所以,这样的点有4个,分别是
()0,2、()0,2-、()0,2、()0,1. 8.如图,已知点()3,1在函数()0>=
x x k y 的图象上,矩形ABCD 的边BC 在x 轴上,E 是对角线BD 的中点,函数()0>=x x
k y 的图象经过A 、E 两点,若︒=∠45ABD ,求E 点的坐标. 解:由点()3,1在函数x k y =的图象上,则3=k .又E 也在函数x
k y =的图象上,故设E 点的坐标为⎪⎭
⎫ ⎝⎛m m 3,.过E 点作x EF ⊥轴于F ,则m EF 3=. 又E 是对角线BD 的中点,所以m EF CD AB 62=
==. 故A 点的纵坐标为m 6,代入x y 3=中,得A 点坐标为⎪⎭
⎫ ⎝⎛m m 6,2. 因此2
2m m m OB OF BF =-
=-=. 由︒=∠45ABD ,得︒=∠45EBF ,所以EF BF =. 即有m m 32=.解得6±=m .而0>m ,故6=m . 则E 点坐标为⎪⎪⎭
⎫ ⎝⎛26,6. 9.如图,已知正方形OABC 的面积为9,点O 为坐标原点,点A 在x 轴上,点C 在y 轴上,点
B 在函数()0,0>>=x k x
k y 的图象上,点()n m P ,为其双曲线上的任一点,过点P 分别作x 轴、y 轴的垂线,垂足分别为E 、F ,并设矩形OEPF 和正方形OABC 不重合部分的面积为S .
(1)求B 点坐标和k 的值;(2)当2
9=
S 时,求P 点坐标; (3)写出S 关于m 的函数关系式. 解:(1)设B 点坐标为()y x ,.则由条件,得⎩⎨⎧>==.
0,9y x xy
解上述方程组,得⎩⎨⎧==.
3,3y x 所以点B 的坐标是()3,3. 又由x
k y =,得9==xy k .
甲 乙
(2)因点P 的坐标为()n m ,. 当3≥m 时,如图甲,m n E P m AE 9,31=
=-= . 所以当2
9=
S 时,有291=•E P AE , 即()2993=•-m m .解得6=m . 故1P 点的坐标为⎪⎭
⎫ ⎝⎛23,6. 当30<<m 时,如图乙,393,2-=-==m
n FC m F P . 所以当29=S 时,有292=•FC F P . 即2
939=⎪⎭⎫ ⎝⎛-•m m .解得23=m . 即2P 点的坐标为⎪⎭
⎫ ⎝⎛6,23. (3)参照第(2)题可知,当3≥m 时,如图甲,
()m
m m E P AE S 279931-=•-=•=; 当30<<m 时,如图乙,
m m m FC F P S 39392-=⎪⎭⎫ ⎝⎛-•=•=.。
