MATLAB信号处理例题
数字信号处理第二章习题26、30、32解答(包括matlab运行程序)
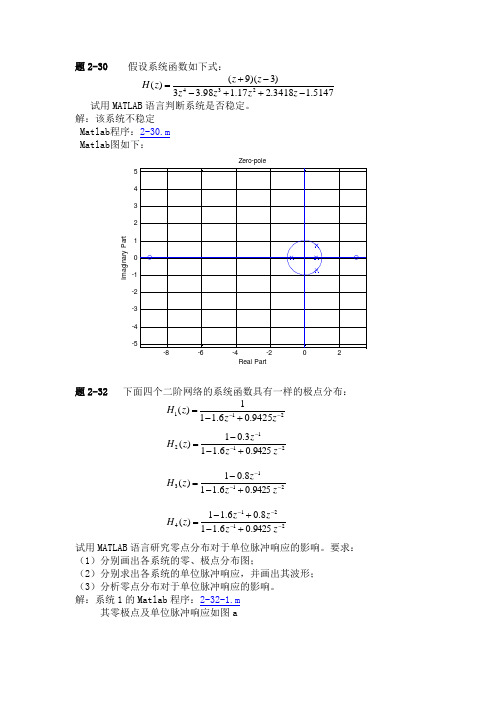
题2-30 假设系统函数如下式:5147.13418.217.198.33)3)(9()(234-++--+=z z z z z z z H试用MATLAB 语言判断系统是否稳定。
解:该系统不稳定 Matlab 程序:2-30.m Matlab 图如下:Real PartI m a g i n a r y P a r tZero-pole题2-32 下面四个二阶网络的系统函数具有一样的极点分布:2119425.06.111)(--+-=z z z H21129425.06.113.01)(---+--=z z z z H21139425.06.118.01)(---+--=z z z z H 212149425.06.118.06.11)(----+-+-=z z z z z H试用MATLAB 语言研究零点分布对于单位脉冲响应的影响。
要求: (1)分别画出各系统的零、极点分布图;(2)分别求出各系统的单位脉冲响应,并画出其波形; (3)分析零点分布对于单位脉冲响应的影响。
解:系统1的Matlab 程序:2-32-1.m 其零极点及单位脉冲响应如图a-1-0.500.51Real Part I m a g i n a r y P a r tImpulse response图 a系统2的Matlab 程序:2-32-2.m 其零极点及单位脉冲响应如图b-1-0.500.51Real Part I m a g i n a r y P a r tZero-poleImpulse response图 b系统3的Matlab 程序:2-32-3.m 其零极点及单位脉冲响应如图c-1-0.500.51Real Part I m a g i n a r y P a r t图 c系统4的Matlab 程序:2-32-4.m 其零极点及单位脉冲响应如图d-1-0.500.51Real Part I m a g i n a r y P a r tZero-pole图 d(3)零点愈靠近极点,单位脉冲响应的变化愈缓慢,因此,零点对极点的作用起到了抵消作用。
数字信号处理Matlab练习第三章-080802084朱桂香

1.编写一个Matlab程序,用一个N点的复数离散傅里叶变换计算两个长度为N的实数序列的N点离散傅里叶变换,并将结果同直接使用两个N点离散傅里叶变换得到的结果进行比较。
n=0:11; %设定n的范围x1=cos(pi/6.*n); %给定序列x1[n]x2=(4/5).^n; %给定序列x2[n]w1=x1+1i*x2; %由序列x1[n]和x2[n]组成复数序列w1[n]w2=x1-1i*x2; %序列w1[n]的共轭序列w2[n]figure,subplot(2,1,1),stem(n,x1); %指定位置1,绘制序列x1[n]xlabel('n'); %设定序列x1[n]的横轴标注和纵轴标注ylabel('x1[n]');subplot(2,1,2),stem(n,x2); %指定位置2,绘制序列x2[n]xlabel('n'); %设定序列x2[n]的横轴标注和纵轴标注ylabel('x2[n]');figure,subplot(4,1,1),stem(abs(w1)); %指定位置1,绘制序列w1[n]幅度谱xlabel('n'); %设定横轴标注,纵轴标注和标题ylabel('magnitude');title('W1的幅度谱');subplot(4,1,2),stem(angle(w1)); %指定位置2,绘制序列w1[n]相位谱xlabel('n'); %设定横轴标注,纵轴标注和标题ylabel('phase');title('W1的相位谱');subplot(4,1,3),stem(abs(w2)); %指定位置3,绘制序列w2[n]幅度谱xlabel('n'); %设定横轴标注,纵轴标注和标题ylabel('magnitude');title('W2的幅度谱');subplot(4,1,4),stem(angle(w2)); %指定位置4,绘制序列w2[n]相位谱xlabel('n'); %设定横轴标注,纵轴标注和标题ylabel('phase');title('W2的相位谱');X1=fft(x1); %求序列x1[n]的离散傅里叶变换X1(k)X2=fft(x2); %求序列x2[n]的离散傅里叶变换X2(k)W1=fft(w1); %求序列w1[n]的离散傅里叶变换W1(k)W2=fft(w2); %求序列w2[n]的离散傅里叶变换W2(k)Y1=(1/2)*(W1+W2); %由W1(k)和W2(k)来求X1(k)Y2=(1/(2*1i))*(W1-W2); %由W1(k)和W2(k)来求X2(k)figure,subplot(2,1,1),stem(abs(X1)); %指定位置1,绘制|X1(k)|xlabel('k'); %设定横轴标注和纵轴标注ylabel('|X1(k)|');subplot(2,1,2),stem(abs(Y1)); %指定位置2,绘制|Y1(k)|xlabel('k'); %设定横轴标注和纵轴标注ylabel('|Y1(k)|');figure,subplot(2,1,1),stem(abs(X2)); %指定位置1,绘制|X2(k)|xlabel('k'); %设定横轴标注和纵轴标注ylabel('|X2(k)|');subplot(2,1,2),stem(abs(Y2)); %指定位置2,绘制|Y2(k)|xlabel('k'); %设定横轴标注和纵轴标注 ylabel('|Y2(k)|');结果图:nx 1[n]024681012nx 2[n ]图1 序列x1[n]和x2[n]02468101212nm a g n i t u d eW1的幅度谱24np h a s eW1的相位谱02468101212nm a g n i t u d eW2的幅度谱024681012-4-20np h a s e图2 w1和w2的幅度谱和相位谱图246k|X 1(k )|246k|Y 1(k )|图3 两种计算X1(k)的方法比较024681012246k|X 2(k )|024681012246k|Y 2(k )|图4 两种计算X2(k)的方法比较2.编写一个Matlab 程序,用两个N 点的复数离散傅里叶变换计算一个长度为2N 的实数序列的2N 点离散傅里叶变换,并将结果同直接使用一个2N 点离散傅里叶变换得到的结果进行比较。
matlab数字信号处理85个实用案例精讲

matlab数字信号处理85个实用案例精讲MATLAB数字信号处理85个实用案例精讲MATLAB是一种强大的数学软件,广泛应用于数字信号处理领域。
本文将介绍85个实用案例,涵盖了数字信号处理的各个方面,包括信号生成、滤波、频谱分析、时频分析、数字滤波器设计等。
1. 信号生成案例:生成正弦信号在MATLAB中,可以使用sin函数生成正弦信号。
例如,生成频率为100Hz,幅度为1的正弦信号,代码如下:t = 0:0.001:1;f = 100;x = sin(2*pi*f*t);2. 滤波案例:低通滤波低通滤波器可以滤除高频信号,保留低频信号。
在MATLAB中,可以使用fir1函数设计低通滤波器。
例如,设计截止频率为100Hz的低通滤波器,代码如下:fs = 1000;fc = 100;N = 100;b = fir1(N, fc/(fs/2), 'low');3. 频谱分析案例:计算功率谱密度功率谱密度是信号在频域上的能量分布。
在MATLAB中,可以使用pwelch函数计算功率谱密度。
例如,计算频率为100Hz的正弦信号的功率谱密度,代码如下:t = 0:0.001:1;f = 100;x = sin(2*pi*f*t);[Pxx, f] = pwelch(x, [], [], [], 1000);4. 时频分析案例:计算短时傅里叶变换短时傅里叶变换可以分析信号在时间和频率上的变化。
在MATLAB中,可以使用spectrogram函数计算短时傅里叶变换。
例如,计算频率为100Hz的正弦信号的短时傅里叶变换,代码如下:t = 0:0.001:1;f = 100;x = sin(2*pi*f*t);spectrogram(x, [], [], [], 1000, 'yaxis');5. 数字滤波器设计案例:设计巴特沃斯滤波器巴特沃斯滤波器是一种常用的数字滤波器,可以实现平滑滤波和带通滤波。
matlab信号处理经典例程

实验一 离散时间信号时域和频域分析1、信号相加并作图数学描述: )()()(21n x n x n x +=MATLAB 实现: 21X X X +=设 x1=[1 0.7 0.4 0.1 0]; x2=[0.1 0.3 0.5 0.7 0.9 1]参考程序:n1=1:5;x1=[1 0.7 0.4 0.1 0];n2=3:8;x2=[0.1 0.3 0.5 0.7 0.9 1];n=1:8;x1=[x1 zeros(1,8-length(n1))];x2=[zeros(1,8-length(n2)) x2];x=x1+ x2;Subplot(3,1,1);Stem(n,x1);Subplot(3,1,2);Stem(n,x2);Subplot(3,1,3);Stem(n,x);2、信号相乘并作图数学描述: )()()(21n x n x n x *=MATLAB 实现: 2.1X X X *=x1,x2取值与上题相同。
参考程序:n1=1:5;x10=[1 0.7 0.4 0.1 0];n2=3:8;x20=[0.1 0.3 0.5 0.7 0.9 1];n=1:8;x1=[x10 zeros(1,8-length(n1))];x2=[zeros(1,8-length(n2)) x20];x=x1.*x2;Subplot(3,1,1);Stem(n,x1);Subplot(3,1,2);Stem(n,x2);Subplot(3,1,3);Stem(n,x);3、计算卷积用MATLAB 计算序列a=[-2 0 1 –1 3]和b=[1 2 0 -1]的离散卷积。
首先用手工计算,然后用MATLAB 编程计算,作图验证手工计算结果。
参考程序:a=[-2 0 1 -1 3];b=[1 2 0 -1];c=conv(a,b);M=length(c)-1;n=0:1:M;stem(n,c);xlabel('n'); ylabel('幅度');4、已知系统函数 ,作零极点图,并求z 反变换。
数字信号处理matlab版答案

数字信号处理matlab版答案【篇一:数字信号处理matlab实例】txt>例1-1 用matlab计算序列{-2 0 1 –1 3}和序列{1 2 0 -1}的离散卷积。
解 matlab程序如下:a=[-2 0 1 -1 3];b=[1 2 0 -1];c=conv(a,b);m=length(c)-1;n=0:1:m;stem(n,c);xlabel(n); ylabel(幅度);图1.1给出了卷积结果的图形,求得的结果存放在数组c中为:{-25 1 -3}。
例1-2 用matlab计算差分方程 -4 1 31当输入序列为解 matlab程序如下:时的输出结果。
脉冲响应。
n=41; a=[0.8 -0.44 0.36 0.22]; b=[1 0.7 -0.45 -0.6]; x=[1zeros(1,n-1)]; k=0:1:n-1; y=filter(a,b,x); stem(k,y)xlabel(n);ylabel(幅度) 1.2 给出了该差分方程的前41个样点的输出,即该系统的单位图例1-3 用matlab计算例1-2差分方程所对应的系统函数的dtft。
解例1-2差分方程所对应的系统函数为:0.8?0.44z?1?0.36z?2?0.02z?3h(z)?1?0.7z?1?0.45z?2?0.6z?3其dtft为 0.8?0.44e?j??0.36e?j2??0.02e?j3?)?1?0.7e?j??0.45e?j2??0.6e?j3? h(e?j?用matlab计算的程序如下:k=256; num=[0.8 -0.44 0.36 0.02]; den=[1 0.7 -0.45 -0.6];w=0:pi/k:pi; h=freqz(num,den,w); subplot(2,2,1);plot(w/pi,real(h));grid title(实部) xlabel(\omega/\pi);ylabel(幅度) subplot(2,2,2); plot(w/pi,imag(h));gridtitle(虚部) xlabel(\omega/\pi);ylabel(amplitude) subplot(2,2,3); plot(w/pi,abs(h));grid title(幅度谱) xlabel(\omega/\pi);ylabel(幅值) subplot(2,2,4); plot(w/pi,angle(h));grid title(相位谱)xlabel(\omega/\pi);ylabel(弧度)第2章离散傅里叶变换及其快速算法例2-1 对连续的单一频率周期信号按采样频率长度n分别选n =20和n =16,观察其dft结果的幅度谱。
信号与系统matlab实验习题3 绘制典型信号及其频谱图

绘制典型信号及其频谱图答案在下面四个常用信号及其傅里叶变换式如表1所示。
(1)绘制单边指数信号及其频谱图的MATLAB程序如下:close all;E=1;a=1;t=0:0.01:4;w=-30:0.01:30;f=E*exp(-a*t);F=1./(a+j*w);plot(t,f);xlabel('t');ylabel('f(t)');figure;plot(w,abs(F));xlabel('\omega');ylabel('|F(\omega)|');figure;max_logF=max(abs(F));plot(w,20*log10(abs(F)/max_logF));xlabel('\omega');ylabel('|F(\omega)| indB');figure;plot(w,angle(F));xlabel('\omega');ylabel('\phi(\omega)');请更改参数,调试此程序,绘制单边指数信号的波形图和频谱图。
观察参数a 对信号波形及其频谱的影响。
注:题目中阴影部分是幅频特性的对数表示形式,单位是(dB),请查阅相关资料,了解这种表示方法的意义及其典型数值对应的线性增益大小。
(2)绘制矩形脉冲信号、升余弦脉冲信号和三角脉冲信号的波形图和频谱图,观察并对比各信号的频带宽度和旁瓣的大小。
(3)更改参数,调试程序,绘制单边指数信号的波形图和频谱图。
观察参数a对信号波形及其频谱的影响。
答案附上程序代码:close all;E=1;a=1;t=0:0.01:4;w=-30:0.01:30;f=E*exp(-a*t);F=1./(a+j*w);plot(t,f);xlabel('t');ylabel('f(t)');figure;plot(w,abs(F));xlabel('\omega');ylabel('|F(\omega)|';E=1,a=1,波形图 频谱图更改参数E=2,a=1;更改参数a ,对信号波形及其频谱的影响。
数字信号处理课后MATLAB习题答案
30
40
50
60
70
80
90
100
cos(6*pi*t) 1 0 -1
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
cos(14*pi*t) 1 0 -1
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
cos(26*pi*t) 1 0 -1
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
cos(6*pi*t) 1 0 -1
1 Im g a P rt a in ry a 0.5 0 -0.5 -1 -3 -2 -1 0 Real Part 1 2 3 2
5 4 3 2 1 0 0 10 20 30 40 50 60 70 80 90 100
8 6 4 2 0
0
10
20
30
40
50
60
70
80
90
100
1-3(1)利用 MALTAB 语句 X=firls(511,[0 0.4 0.404],[1 1 0 0]) 产生一个 512 点的序列 x[k],并画出序列的频谱。
321012301020303210123105051015画出下列离散系统的幅度响应曲线和相位响应曲线并指出滤波器的类型
姓名:杨秀业 班级:电信 10-2
学号:3100718217
1-1 已知 g1 = cos(6πt ), g 2 = cos(14πt ) g 3 = cos( 26πt ) ,以抽样频率 fsam = 10 Hz 对上述 , 信号进行抽样。在同一张图上画出 g1,g2,和 g3 及其抽样点。对所得结果进行讨论。
现代信号处理例题及matlab代码实现

《现代信号处理》期末考核作业1 MATLAB仿真均值为0,方差为1的白噪声信号,信号长度N=1024,并用周期图法分别求500、1000和1500次实现的平均功率谱密度,画图。
程序代码如下:clear;clear all;N=1024;%数据长度Nfft=1024;%FFT所采用的数据长度n=0:N-1;wn=randn(1,N);%产生随机白噪声subplot(2,2,1);%绘出白噪声序列plot(n,wn);title('白噪声');%500次实现的平均功率谱密度s=zeros(1,N);for i=1:500wn=randn(1,N);%产生随机白噪声Pxx=10*log10(abs(fft(wn,Nfft).^2)/N);%Fourier振幅谱平方的平均值,并转换为dbs=s+Pxx;ends=s/500;f=(0:length(Pxx)-1)/length(Pxx);%绘出频率序列subplot(222);plot(f,s);xlabel('频率/Hz');ylabel('功率谱/dB');title('500次实现的平均功率谱密度');grid on;%1000次实现的平均功率谱密度s=zeros(1,N);for i=1:1000wn=randn(1,N);%产生随机白噪声Pxx=10*log10(abs(fft(wn,Nfft).^2)/N);%Fourier振幅谱平方的平均值,并转换为dbs=s+Pxx;ends=s/1000;f=(0:length(Pxx)-1)/length(Pxx);%绘出频率序列subplot(223);plot(f,s);xlabel('频率/Hz');ylabel('功率谱/dB');title('1000次实现的平均功率谱密度');grid on;%500次实现的平均功率谱密度s=zeros(1,N);for i=1:1500wn=randn(1,N);%产生随机白噪声Pxx=10*log10(abs(fft(wn,Nfft).^2)/N);%Fourier振幅谱平方的平均值,并转换为dbs=s+Pxx;ends=s/1500;f=(0:length(Pxx)-1)/length(Pxx);%绘出频率序列subplot(224);plot(f,s);xlabel('频率/Hz');ylabel('功率谱/dB');title('1500次实现的平均功率谱密度');grid on;实验结果图如下:2仿真如下随机过程:sin(n+)sin(n+)23n n x V ππ=++φφ其中:V n 是均值为0,方差为1的Gaussian 白噪声过程,Φ为随机相位,在[0,2π]间服从均匀分布。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
◆例1设方波的数学模型为:]5sin 513sin 31[sin 4)(000 t t t E t f T ,基频: T20用MATLAB 软件完成该方波的合成设计◆ MATLAB 源程序t=-10:0.1:10; %设定一个数组有201个点,方波周期为20e=5;w=pi/10; %设定方波幅值为5,w 代表w0m=-5*sign(t); %给定幅值为5的方波函数y1=(-4*e/pi)*sin(w*t); %计算1次谐波y3=(-4*e/pi)*(sin(w*t)+sin(3*w*t)/3); %计算3次谐波y5=(-4*e/pi)*(sin(w*t)+sin(3*w*t)/3+sin(5*w*t)/5); %计算5次谐波plot(t,y1,'y');hold; grid; %用黄色点线画出1次谐波及网格线,并在同一张图上画其余曲线plot(t,y3,'g'); %用绿色点线画出3次谐波plot(t,y5,'b'); %用蓝色点线画出5次谐波plot(t,m,'-k'); %用黑色实线画方波title('方波合成');xlabel('t');ylabel('f(t)'); %为图形加上标题n=50; %合成任意次方波,n 决定方波的合成次数,在此给定50yn=0; %设置初始值for i=1:nyn=yn+(-4*e/pi)*(1/(2*i-1))*sin((2*i-1)*w*t);end; %计算n 次谐波合成plot(t,yn,'r') %用红色实线画出n 次谐波合成◆ 从图中我们可以看到Gibbs 现象。
在函数的间断点附近,增加傅里叶级数的展开次数,虽然可以使其间断点附近的微小振动的周期变小,但振幅却不能变小。
此现象在控制系统表现为:当求控制系统对阶跃函数的响应时,超调量总是存在的。
◆例2(P110)MATLAB中函数FFT应用举例。
%MATLAB中函数FFT应用举例t=0:0.001:0.6;x=sin(2*pi*50*t)+sin(2*pi*120*t);y=x+2*randn(size(t))subplot(2,1,1)plot(y(1:50))xlable(‘时间轴t’)ylable(‘信号值f(t)’)title(‘正弦波+随即噪声’,’FontSize’,10)y=fft(y,512);f=1000*(0:256)/512;subplot(2,1,2)plot(f,Y(1:257))set(gca,’Xtick’,[0,50,100,150,200,250,300,350,400,450,500])set(gca,’XtickLabel’,’0|50|100|150|200|250|300|350|400|450|500|’) xlabel(‘频率轴\omega’)ylabel(‘频谱幅值F(\omega)’)title(‘信号频谱’,’FontSize’,10)◆例3例 3.8.3 有一二阶系统,阻尼比 =0.47,固有频率500 n Hz ,采样间隔0004.0 t s,采样点数N =256。
试计算理论幅频特性与由系统阶跃响应计算出的幅频特性数据值,并画出两个计算结果的幅频特性曲线。
%example 3.8.3 MA TLAB PROGRAMN=256;dt=0.0004wn=500;seta=0.47;dw=2*pi/(N*dt);a=wn^2;b=[1,2*seta*wn,a];t=[0:dt:(N-1)*dt];c=step(a,b,t);w=[0:dw:(N-1)*dw];[mag,phase]=bode(a,b,w);ycw=fft(c);Re=real(ycw);Im=imag(ycw);for i=1:NRw(i,1)=1-Im(i,1)*(i-1)*dw*dt;Iw(i,1)=Re(i,1)*(i-1)*dw*dt;endffw=Rw+Iw*sqrt(-1);Aw=abs(ffw)semilogx(w,20*log10(mag),'r-')axis([100,10000,-30,10])text(600,12,'幅频特性')hold onsemilogx(w,20*log10(Aw))axis([100,10000,-30,10])grid on◆例4例6.2.4 用MATLAB 中的函数XCORR 求出下列两个周期信号的互相关函数,式中的f=10Hz 。
),2sin()(ft t x )902sin(5.0)( ft t y%例6.2.4 中计算两个周期信号互相关函数的MA TLAB 程序N=500;Fs=500;n=0:N-1;t=n/Fs;Lag=200;x=sin(2*pi*10*t);y=0.5*sin(2*pi*10*t+90*pi/180);[c,lags]=xcorr(x,y,Lag,'unbiased');subplot(2,1,1)plot(t,x,'r')hold onplot(t,y,'b')xlabel('t');ylabel('x(t)y(t)');title('原周期信号')gridhold offsubplot(2,1,2);plot(lags/Fs,c,'k');xlabel('t');ylabel('Rxy(t)');title('互相关函数');grid◆例5例 6.2.5 若有信号为)()2sin(2)2sin()(21t t f t f t x式中,,501Hz f Hz f 1002 ,)(t 为白噪声(用MATLAB 中的函数产生)。
设采样频率2000 Fs ;试用周期法并应用MA TLAB 编程计算,当数据长度分别为2561 N 和 10242 N 两种情况下上述信号的功率谱。
%例6.2.5中周期图法计算信号功率谱的MATLAB 程序clfFs=2000;%情况1:数据长度N1=256N1=256;N1fft=256;n1=0:N1-1;t1=n1/Fs;f1=50;f2=100;xn1=sin(2*pi*f1*t1)+sin(2*pi*f2*t1)+randn(1,N1);Pxx1=10*log10(abs(fft(xn1,N1fft).^2)/N1);f1=(0:length(Pxx1)-1)*Fs/length(Pxx1);subplot(2,1,1)plot(f1,Pxx1)ylabel('功率谱(dB)');title('数据长度N1=256')grid%情况2:数据长度N2=1024N2=1024;N2fft=1024;n2=0:N2-1;t2=n2/Fs;f1=50;f2=100;xn2=sin(2*pi*f1*t2)+2*sin(2*pi*f2*t2)+randn(1,N2);Pxx2=10*log10(abs(fft(xn2,N2fft).^2)/N2);f2=(0:length(Pxx2)-1)*Fs/length(Pxx2);subplot(2,1,2)plot(f2,Pxx2)xlabel('频率(Hz)');ylabel('功率谱(dB)');title('数据长度N2=1024')◆例6(例3.8.1)分别用conv和FFT算法计算序列:x(n)为在区间[0,1]上均匀分布的N 点随机序列,表示为:x(n)=rand(1,N),h(n)为均值为零、方差为1的N点高斯分布随机序列,表示为:h(n)=rand(1,L),试求1≤N≤150时的卷积并比较其运算时间。
%例3.8.1 直接卷积和快速卷积的比较%conv_time=zeros(1,150);fft_time=zeros(1,150);%for N=1:150tc=0;tf=0; %初始化L=2*N-1; %加长序列长度nu=round((log10(L)/log10(2))+0.45);L=2^nu; %使点数成为2的幂次for I=1:100h=randn(1,N); %产生两个随机序列x=rand(1,N);t0=clock;yc=conv(h,x); %直接卷积计算t1=etime(clock,t0);tc=tc+t1; %直接卷积运算的时间t0=clock;y2=ifft(fft(h,L).*fft(x,L)); %快速卷积计算t2=etime(clock,t0);tf=tf+t2; %快速卷积计算的时间end%conv_time(N)=tc/100; %直接卷积计算的平均时间fft_time(N)=tf/100; %快速卷积计算的平均时间end%n=1:150;subplot(1,1,1); %图形显示上述两种卷积的计算时间plot(n(25:150),conv_time(25:150),n(25:150),fft_time(25:150))上述两种卷积的计算时间的比较如图3.8.5所示。
图3.8.5 两种卷积计算时间比较◆例7(例3.8.2 )运用FFT 求取矩形脉冲 1,01t 0 ,1)(t t 的谱,说明采样频率低引起的混叠现象。
(1) 先编写有一定通用性的函数文件cftbyfft.m[cftbyfft.m]function [AW,f]=cftbyfft(wt,t,flag)%cftbyfft.m%本程序采用FFT 计算连续时间Fouie 变换。
输出幅频数据对(f,AW)。
%输入量(wt,t)为已经窗口化了的时间函数wt(t),它们分别是长度为N 的向量。
%对于时限信号,应使该取值时段与窗口长度相比足够小。
以提高频率分辨率。
%对于非时限信号,窗口长度的选取应使窗口外的函数值小%到可忽略,以提高近似精度。
%输入宗量flag 控制输出CFT 的频率范围。
% flag 取非0时(缺省使用),频率范围在[0,fs);% flag 取0时,频率范围在[-fs/2,fs/2)。
if nargin==2;flag=1;endN=length(t); %采样点数,应为2的幂次,以求快速。
T=t(length(t))-t(1); %窗口长度dt=T/N; %时间分辨率W0=fft(wt); %实施FFT 变换W=dt*W0; %算得[0,fs]上的N 点CFT 值df=1/T; %频率分辨率n=0:1:(N-1)%把以上计算结果改写到[-fs/2,fs/2]范围if flag==0n=-N/2:(N/2-1);W=fftshift(W); %产生周期序列的频谱endf=n*df; %频率分量向量AW=abs(W); %幅频谱数据向量if nargout==0plot(f,AW);grid,xlabel('频率f');ylabel('|w(f)|')end(2)运行以下指令,绘制时域波形和幅频谱M=5; %做2的幂次用。
