【精准解析】山东省泰安市东平高级中学2019-2020学年高二下学期期中考试数学试题
山东省东平县高二下学期期中联考语文试题

山东省东平县高二下学期期中联考语文试题姓名:________ 班级:________ 成绩:________一、选择题 (共4题;共8分)1. (2分) (2015高一上·宁夏期中) 下列各组词语中,没有错别字的一组是()A . 忸怩尾尾动听彳亍不同凡响B . 寂寥星辉班斓火钵剑拔弩张C . 戮没大汗淋漓峥嵘黯然泣下D . 惆怅见贤思起彷徨秋亳无犯2. (2分)下列各句中,划线的成语使用恰当的一项是()A . 罕台川水从它的前面流过,孤子梁与它临川相视,一道缆车临空飞架其间,形成一道大漠旅游的独特风景线,此次旅游虽为一日千里,行程很紧,但仍给我留下极深刻的印象。
B . 袁隆平培育出的杂交水稻亩产926.6公斤,再创新纪录,用“大师”一词已不足以形容其贡献,称他为“活着的国宝”才是实至名归。
C . 一踏入这繁华的都市,他便被这灯红酒绿的花花世界迷惑,什么母亲的耳提,父亲的面命,早已灰飞烟灭,心中充满的惟有消费,惟有享乐!D . 购物能给女人带来幸福感,特别是面对打折等促销活动,那种以便宜的价格买到自己心仪的物品的快乐,更是男人所不可理喻的。
3. (2分)下面标点符号使用正确的一项是()A . 周朴园什么,鲁大海?他!我的儿子?B . 周朴园你的生日,四月十八,每年我总记得。
C . 鲁侍萍你?(笑)三十年我一个人都过了,现在我反而要你的钱!D . 鲁侍萍老爷那种绸衬衣不是一共有五件?您要哪一件?4. (2分)下列各项中,没有语病的一项是()A . 中俄双方都有维护海上通道的安全,维护海域安全的利益诉求,因此中俄举行了“海上联合-2014”军事演习。
两国最高领导人共同出席了这次海上联合军事演习的开始仪式,并共同检阅了海军仪仗队。
B . 根据诺贝尔奖官网发布的消息显示,加拿大女作家爱丽丝·门罗获得2013年诺贝尔文学奖,她以短篇小说闻名全球,被称为“当代短篇小说大师”,其影响巨大的《逃离》2004年出版,以其精致的讲故事方式著称。
山东省泰安市东平高级中学2019-2020学年高二数学下学期期中试题(含解析)

故选:A
【点睛】本题主要考查利用函数的单调性求参数的取值范围,分离变量是解决本题的关键.
二、多项选择题:在每小题给出的四个选项中,有多项符合题目要求.
a b9
9.关于
的说法,正确的是( )
A. 展开式中的二项式系数之和为 512
B. 展开式中只有第 5 项的二项式系
数最大
C. 展开式中第 5 项和第 6 项的二项式系数最大
判断每个选项得到答案.
f x x3 ax2 bx c f x 3x2 2ax b
【详解】
,则
,
取 a = b = 0 ,函数单调递增,无极值点,A 错误;
当
x
时,
f
x
,当
x
时,
f
x
,故 x0
R
,使
f
x0
0
,
B 正确;
若
x0
是
f
x 的极值点,则
f
x0
0 ,C
正确;
( ) 取 a 0 , b 3 ,得到 f ¢ x
能力,属于基础题.
x
6.若
14
a0
a1x
a2 x2
a3 x3
a4 x4
.则
a1
a2
a3
a4
的值为(
A. 1
B. 1
C. 0
【答案】B
) D. 2
【解析】
【分析】
令 x 0 得 a0 1,令 x 1 得 a0 a1 a2 a3 a4 0 ,从而计算可得;
x
【详解】解:因为
14
a0
a1x
掉丙、丁两名专家在同一地工作的排列数,即可得到答案.
山东省泰安市东平高级中学2021-2020学年高二数学下学期期中试题(含解析)

山东省泰安市东平高级中学2019-2020学年高二数学下学期期中试题(含解析)考试时间120分钟,满分150分★祝考试顺利★注意事项:1.答卷前,考生务必将自己的姓名、考生号等填写在答题卡和试卷指定位置上.2.作答选择题时,选出每小题答案后,用2B铅笔在答题:卡上对应题目选项的答案信息点涂黑:如需改动,用橡皮擦干净后,再选涂其他答案.答案不能答在试卷上.3.非选择题必领用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区城内相应位置上,如需改动,先划掉原来的答案,然后再写上新答案.不准使用铅笔和涂改液.不按以上要求作答无效.一、单项选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知i是虚数单位,复数z=z的共轭复数z=( )A. 1B. 1C. 1--D.1-+【答案】B【解析】【分析】先计算z,由共轭复数概念即可得z.详解】∵)()21i izi-===--,∴1z=+.故选:B【点睛】本题主要考查了复数的除数运算,共轭复数的概念,考查学生对基本概念的理解.2.在61(2)xx-的展开式中,常数项为()A. 120- B. 120 C. 160- D. 160 【答案】C【分析】写出二项式展开式的通项公式求出常数项. 【详解】61(2)x x-展开式的通项2616(1)2k k k k kT C x ,令260,3k k常数项333316(1)2=160T C故选:C .【点睛】本题考查二项定理. 二项展开式问题的常见类型及解法:(1)求展开式中的特定项或其系数.可依据条件写出第1k +项,再由特定项的特点求出k 值即可.(2)已知展开式的某项或其系数求参数.可由某项得出参数项,再由通项公式写出第1k +项,由特定项得出k 值,最后求出其参数.3.已知()f x =()8f '等于( )A. 0B.D. 1-【答案】C 【解析】 【分析】根据基本初等函数的导数公式求出()f x ',再求()8f '.【详解】由()f x =()11-1-?2211=x =x 22f x ',∴()()121882f -⨯'==故选C【点睛】本题考查了基本初等函数的导数公式,若()a*f x =x a Q ∈(),则()a-1=ax f x ' .4.已知某篮球队员在比赛中每次罚球的命中率相同,且在两次罚球中至少命中一次的概率为2125,则该队员每次罚球的命中率p 为( ) A. 45 B. 35C.25D.15【答案】B 【解析】利用相互独立事件概率乘法公式和互斥事件概率加法公式能求出该队员每次罚球的命中率p .【详解】解:某篮球队员在比赛中每次罚球的命中率相同,该队员每次罚球的命中率为p , 且在两次罚球中至少命中一次的概率为2125, 212(1)2521p C p p ∴+-=, 解得35p =或75p =(舍去)∴该队员每次罚球的命中率p 为35.故选:B .【点睛】本题考查概率的求法,考查相互独立事件概率乘法公式和互斥事件概率加法公式等基础知识,考查运算求解能力,属于基础题.5.已知函数()323f x x ax ax b =+++的图象在点()()1,1f 处的切线方程为12y x m =-+,若函数()f x 恰有三个不同的零点,则实数b 的取值范围是( )A. ()5,27-B. []5,27-C. (]1,3-D. []1,3-【答案】A 【解析】 【分析】先根据函数在()()1,1f 处的切线为12y x m =-+得到一个关于a ,b 的关系,然后再根据()f x 恰有三个不同的零点,列出关于b 的不等式.【详解】解:2()323f x x ax a '=++,因为函数在()()1,1f 处的切线方程为12y x m =-+ 所以()13512f a '=+=-,3a ∴=-,2()369f x x x ∴'=--. 令()0f x '=,得11x =-,23x =.当1x <-或3x >时,()0f x '>,()f x 是增函数;当13x 时,()0f x '<,()f x 是减函数.所以1x =-时,()f x 有极大值(1)5f b -=+;当3x =时,()f x 有极小值()327f b =-.所以,若函数()f x 恰有三个不同的零点,则50270b b +>⎧⎨-<⎩,解得527b -<<. 故选:A .【点睛】本题考查导数的几何意义,应用导数求函数的极值和零点,同时考查学生的运算能力,属于基础题.6.若()4234012341x a a x a x a x a x -=++++.则1234a a a a +++的值为( ) A. 1 B. 1-C. 0D. 2【答案】B 【解析】 【分析】令0x =得01a =,令1x =得012340a a a a a ++++=,从而计算可得; 【详解】解:因为()4234012341x a a x a x a x a x -=++++ 令0x =得01a =令1x =得012340a a a a a ++++= 所以12341a a a a +++=- 故选:B【点睛】本题考查利用赋值法求二项式展开式的系数和,属于基础题.7.为抗击新冠病毒,某部门安排甲、乙、丙、丁、戊五名专家到三地指导防疫工作.因工作需要,每地至少需安排一名专家,其中甲、乙两名专家必须安排在同一地工作,丙、丁两名专家不能安排在同一地工作,则不同的分配方法总数为( ) A. 18 B. 24 C. 30 D. 36【答案】C 【解析】 【分析】由甲、乙两名专家必须安排在同一地工作,此时甲、乙两名专家看成一个整体即相当于一个人,所以相当于只有四名专家,先计算四名专家中有两名在同一地工作的排列数,再去掉丙、丁两名专家在同一地工作的排列数,即可得到答案.【详解】因为甲、乙两名专家必须安排在同一地工作,此时甲、乙两名专家 看成一个整体即相当于一个人,所以相当于只有四名专家,先计算四名专家中有两名在同一地工作的排列数,即从四个中选二个和其余二个看成三个元素的全排列共有:2343C A ⋅种;又因为丙、丁两名专家不能安排在同一地工作,所以再去掉丙、丁两名专家在同一地工作的排列数有33A 种,所以不同的分配方法种数有:23343336630C A A ⋅-=-=故选:C【点睛】本题考查了排列组合的应用,考查了间接法求排列组合应用问题,属于一般题. 8.已知函数()212ee x xf x mx +-=--在R 上为增函数,则m 的取值范围为( )A. (,-∞B. )⎡+∞⎣C. (,-∞D. )⎡+∞⎣【答案】A【解析】 【分析】函数()212ee x xf x mx +-=--在R 上为增函数,等价于()2122e 2e 0x x f x m +-'=+-≥对x ∈R 恒成立,然后分离变量,得2122e 2e x x m +-≤+,求出2122e 2e +-+x x 的最小值,就能确定m 的取值范围.【详解】因为函数()212ee x xf x mx +-=--在R 上为增函数,所以()2122e 2e 0x x f x m +-'=+-≥对x ∈R 恒成立,即2122e 2e x x m +-≤+对x ∈R 恒成立,又因为2122e 2e x x +-+≥=,所以m ≤ 故选:A【点睛】本题主要考查利用函数的单调性求参数的取值范围,分离变量是解决本题的关键. 二、多项选择题:在每小题给出的四个选项中,有多项符合题目要求. 9.关于()9a b -的说法,正确的是( ) A. 展开式中的二项式系数之和为512B. 展开式中只有第5项的二项式系数最大C. 展开式中第5项和第6项的二项式系数最大D. 展开式中第6项的系数最小【答案】ACD 【解析】 【分析】利用二项式定理的通项公式及其性质即可判断出正误.【详解】解:二项式()9a b -展开式的通项为()9191rrr r r T C a b -+=-对于A :二项式系数之和为92512=,故A 正确;对于B 、C :展开式共10项,中间第5、6项的二项式系数最大,故B 错误,C 正确;对于D :展开式中各项的系数为9(1)k k C -,0k =,1,⋯⋯,9 当5k =时,该项的系数最小.故D 正确. 故选:ACD .【点睛】本题考查了二项式展开式二项式系数的性质、以及系数与二项式系数的关系,需要熟记公式才能解决问题.同时考查了学生的计算能力和逻辑推理能力. 10.已知函数()32f x x ax bx c =+++,则( )A. 0b ≤时,函数()y f x =一定存在极值B. 0x R ∃∈,使()00f x =C. 若0x 是()f x 的极值点,则()00f x '=D. 若0x 是()f x 的极小值点,则()f x 在区间()0,x -∞单调递减 【答案】BC 【解析】 【分析】求导得到()232f x x ax b '=++,根据函数的极值和函数单调性的关系,零点性质,依次判断每个选项得到答案.【详解】()32f x x ax bx c =+++,则()232f x x ax b '=++,取0a b ,函数单调递增,无极值点,A 错误;当x →+∞时,()f x →+∞,当x →-∞时,()f x →-∞,故0x R ∃∈,使()00f x =,B 正确;若0x 是()f x 的极值点,则()00f x '=,C 正确; 取0a =,3b =-,得到233fxx ,则函数在(),1-∞-上单调递增,在()1,1-上单调递减,在()1,+∞上单调递增,1是()f x 的极小值点,故D 错误. 故选:BC.【点睛】本题考查了函数的极值点,零点,单调性,意在考查学生对于函数性质的综合应用,取特殊值排除是解题的关键.11.在棱长为1的正方体1111ABCD A B C D -中,则下列说法正确的是( )A. AC ⊥面11AB DB. 点1A 到面11AB D 的距离为3C. 1AA 与面11AB DD. 二面角111A B D A --的大小为4π 【答案】BC 【解析】 【分析】AC 不垂直于1AB ,A 错误,利用等体积法计算B 正确,据B 知sin θ=,C 正确,1AOA ∠为二面角111A B D A --的平面角,1tan AOA ∠,D 错误,得到答案. 【详解】易知1AB C 为等边三角形,故AC 不垂直于1AB ,故AC 不垂直平面11AB D ,A 错误;111111111326A A B D V -=⨯⨯⨯⨯=,11111111113326A AB D AB D V S h -==⨯=△,解得h ,B 正确;设1AA 与面11AB D 的夹角的余弦值为θ,据B 知sin θ=,故cos θ=,C 正确; O 为11B D 中点,易知111AO B D ⊥,11AO B D ⊥,故1AOA ∠为二面角111A B D A --的平面角,1tan 2AOA ∠=,D 错误. 故选:BC.【点睛】本题考查了线面垂直,点面距离,线面夹角,二面角,意在考查学生的计算能力和空间想象能力. 12.已知函数()2ln f x x x=+,则以下结论正确的是( ) A. 函数()f x 的单调减区间是(0,2) B. 函数()y f x x =-有且只有1个零点 C. 存在正实数k ,使得()f x kx >成立D. 对任意两个正实数1x ,2x ,且12x x >,若()()12f x f x =则124x x +> 【答案】ABD 【解析】 【分析】A 选项,对函数求导,解对应不等式,可判断A ;B 选项,令()2ln x x x xg +=-,对其求导,研究单调性,根据零点存在定理,可判断B ; C 选项,先由()f x kx >得到22ln x k x x<+,令()22ln xh x x x =+,用导数的方法判断其单调性,即可判定C ;D 选项,令()0,2t ∈,则()20,2t -∈,令()()()22g t f t f t =+--,对其求导,判定其单调性,得到()()22f t f t +<-,令122x t =+>,根据题中条件,即可判定出D. 【详解】A 选项,因为()2ln f x x x=+,所以()22212x f x x x x -'=-+=,由()0f x '>得,2x >;由()0f x '<得,02x <<,因此函数()f x 在(0,2)上单调递减,在(2,)+∞上单调递增;故A 正确;B 选项,令()2ln x x x x g +=-,则()22222172122014x x x x x x x g x ⎛⎫-+ ⎪-+⎝⎭+'=---==<-显然恒成立; 所以函数()2ln x x x xg +=-在()0,∞+上单调递减; 又()ln112110g =-=>+,()212ln 21ln 20g =-=-<+, 所以函数()2ln x x x xg +=-有且仅有一个零点;故B 正确; C 选项,若()f x kx >,可得22ln x k x x<+, 令()22ln x h x x x =+,则()42341ln ln 4x x x x x h x x x x ----'=+=, 令()ln 4u x x x x =--,则()1ln 1ln u x x x '=--=-, 由()0u x '>得01x <<;由()0u x '<得1x >;所以函数()u x 在()0,1上单调递增,在()1,+∞上单调递减; 因此()()130u x u ≤=-<;所以()3ln 40x x x h x x --'=<恒成立,即函数()22ln xh x x x=+在()0,∞+上单调递减,所以函数()22ln xh x x x=+无最小值; 因此,不存在正实数k ,使得()f x kx >成立;故C 错; D 选项,令()0,2t ∈,则()20,2t -∈,则22t +>; 令()()()()()2224222ln 2ln 2ln 2242t tg t f t f t t t t t t t+=+--=++---=++---, 则()()()()222222241624802244t t t g t t t tt ---'=+⋅=-<+---, 所以()g t 在()0,2上单调递减,则()()00g t g <=,即()()22f t f t +<-, 令122x t =+>,由()()()122f x f x f t =<-,得22x t >-,则12224x x t t +>-++=,当14≥x 时,124x x +>显然成立,所以对任意两个正实数1x ,2x ,且12x x >,若()()12f x f x =则124x x +>.故D 正确. 故选:ABD.【点睛】本题主要考查导数的应用,通常需要对函数求导,用导数的方法研究函数的性质即可,属于常考题型. 三、填空题:13.用0,1,2,3,4,5这6个数字组成的没有重复数字的四位数中,能被5整除的数的个数为______.(用数字作答) 【答案】108 【解析】 【分析】按个位数是0和5分类计数后可得所求的个数.【详解】若四位数的个位数为0,则没有重复数字的四位数的个数为3554360A =⨯⨯=, 若四位数的个位数为5,则没有重复数字的四位数的个数为24444348A =⨯⨯=,故能被5整除的数的个数为108. 故答案为:108. 【点睛】本题考查排数问题,此类问题关键是特殊元素特殊处理,本题属于基础题. 14.在某市2020年1月份的高三质量检测考试中,所有学生的数学成绩服从正态分布()29810N ,,现任取一名学生,则他的数学成绩在区间108,118内的概率为______.(附:若()2~X Nμσ,,则()0.6826P X μσμσ-<<+=,()220.9544P X μσμσ-<<+=.)【答案】0.1359 【解析】 【分析】本题首先可根据题意得出()88108P X <<以及()78118P X <<的值,然后结合正态分布的对称性即可得出结果.【详解】因为所有学生的数学成绩服从正态分布()29810N ,,所以()881080.6826P X <<=,()781180.9544P X <<=, 所以根据正态分布的对称性可知,()0.95440.68261081180.13592P X -<<==,故答案为:0.1359.【点睛】本题考查正态分布的相关性质,考查根据正态分布求概率,考查计算能力,体现了基础性,是简单题.15.已知箱中装有10个不同的小球,其中2个红球、3个黑球和5个白球,现从该箱中有放回地依次取出3个小球.则3个小球颜色互不相同的概率是_____;若变量ξ为取出3个球中红球的个数,则ξ的数学期望E (ξ)为_____. 【答案】 (1). 950 (2). 35【解析】 【分析】基本事件总数n =103=1000,3个小球颜色互不相同包含的基本事件个数m =103﹣(23+33+53222222333283755C C C +⨯⨯+⨯⨯+⨯⨯)=180,由此能求出3个小颜色互不相同的概率;若变量ξ为取出3个球中红球的个数,则ξ~(n ,210),由此能求出ξ的数学期望E (ξ).【详解】箱中装有10个不同的小球,其中2个红球、3个黑球和5个白球, 现从该箱中有放回地依次取出3个小球,基本事件总数n =103=1000, 3个小球颜色互不相同包含的基本事件个数:m =103﹣(23+33+53222222333283755C C C +⨯⨯+⨯⨯+⨯⨯)=180,则3个小球颜色互不相同的概率是P 1809100050m n ===; 若变量ξ为取出3个球中红球的个数,则ξ~(n ,210),∴ξ的数学期望E (ξ)=323105⨯=. 故答案为:950,35.【点睛】本题考查概率、数学期望的求法,考查古典概型、二项分布等基础知识,考查数据分析能力、运算求解能力,是中档题. 16.函数()()23xf x x e =-,关于x 的方程()()210fx mf x -+=恰有四个不同的实数解,则正数m 的取值范围为______.【答案】3366e m e >+【解析】 【分析】先利用导数求出函数()f x 的单调区间和极值,令()f x t =,由题意可知,方程210t mt -+=有两个不同的实数根1t ,2t ,根据数形结合和韦达定理可知,一个根在36,e ⎛⎫∞ ⎪⎝⎭内,一个根在36,e ⎛⎫∞ ⎪⎝⎭内,再令()21g t t mt =-+,因为()010g =>,所以只需360g e ⎛⎫< ⎪⎝⎭,由此即可求出m 的取值范围. 【详解】解:()()()()22331xxx x e x f e x x =+-=+-',令()0f x '=得,3x =-或1,当3x <-时,()0f x '>,函数()f x 在(),3-∞-上单调递增,且()0f x >, 当31x -<<时,()0f x '<,函数()f x 在()3,1-上单调递减, 当1x >时,()0f x '>,函数()f x 在()1,+∞上单调递增, 所以()()363f x f e=-=极大值,()()12f x f e ==-极小值, 令()f x t =, 因为关于x 的方程()()210fx mf x -+=恰有四个不同的实数解,所以方程210t mt -+=有两个不同的实数根1t ,2t ,且一个根在360,e ⎛⎫⎪⎝⎭内,一个根在36,e ⎛⎫+∞ ⎪⎝⎭内,或者两个根都在()2,0e -内,或者一根为36e ,另一根在()2,0e -内;因为m 为正数,所以121t t =,120t t m +=>,所以1t ,2t 都为正根,所以两个根不可能在()2,0e -内,也不可能一根为36e ,另一根在()2,0e -内; 所以实数根1t ,2t ,且一个根在360,e ⎛⎫ ⎪⎝⎭内,一个根在36,e ⎛⎫+∞ ⎪⎝⎭内,令()21g t t mt =-+,因为()010g =>,所以只需360g e ⎛⎫< ⎪⎝⎭,即6336610m e e -+<,得3366e m e >+,即m 的取值范围为:336,6e e ⎛⎫++∞ ⎪⎝⎭.故答案为:336,6e e ⎛⎫++∞ ⎪⎝⎭.【点睛】本题主要考查了利用导数研究函数的单调性和极值,考查了函数的零点与方程根的关系,是中档题.四、解答题:解箸应写出文字说明证明过程或演算步骤.17.函数()1xf x e x =-+()x R ∈;(1)求()f x 在点()()1,1f 处的切线方程; (2)求()f x 的极值.【答案】(1)()11y e x =-+(2)极小值2 【解析】 【分析】(1)求出1,(1)1,))((1xe f e f e f x '-=-==',用直线的点斜式公式,即可求解; (2)由()0,0f x x '==,求出()f x 在(,0),(0,)-∞+∞上的单调区间,即可求出结论. 【详解】解:(1)()'1x fx e =-设所求切线方程的斜率为k ,则()'11k f e ==- 又()1f e =,故所求切线方程为:()()11y e e x -=-- 即()11y e x =-+ (2)因为()'1x f x e =-令()'0fx >,则0x >;令()'0f x <,则0x <,故函数()f x 在(),0-∞单调递减,在()0,∞+单调递增0x =时,函数()f x 有极小值()02f =【点睛】本题考查导数的几何意义,考查函数的极值,属于基础题.18.一饮料店制作了一款新饮料,为了进行合理定价先进行试销售,其单价x (元)与销量y (杯)的相关数据如下表:(1)已知销量y 与单价x 具有线性相关关系,求y 关于x 的线性回归方程;(2)若该款新饮料每杯的成本为8元,试销售结束后,请利用(1)所求的线性回归方程确定单价定为多少元时,销售的利润最大?(结果四舍五入保留到整数)附:线性回归方程ˆˆy bxa =+中斜率和截距最小二乗法估计计算公式:1221ˆni ii nii x y nxyb xnx ==-=-∑∑,ˆˆay bx =-,51=4195i i i x y =∑,521=453.75i i x =∑. 【答案】(1)ˆ32394yx =-+(2)单价应该定为10元 【解析】 【分析】(1)首先求出x 、y ,然后再求出ˆb、ˆa ,即可求解. (2)设定价为x 元,利润函数为()()323948y x x =-+-,利用二次函数的性质即可求解. 【详解】解:(1)由表中数据,()18.599.51010.59.55x =⨯++++= ()1201101590706090y ++++==, 则12221419559.590ˆ32453.7559.5ni ii nii x y nxybxnx ==--⨯⨯===--⨯-∑∑,ˆˆ90329.5394ay bx =-=+⨯=, 所以y 关于x 的线性相关方程为ˆ32394yx =-+. (2)设定价为x 元,则利润函数为()()323948y x x =-+-, 其中8x ≥,则2326503152y x x =-+-, 所以()65010232x =-≈⨯-(元),为使得销售的利润最大,确定单价应该定为10元.【点睛】本题考查了线性回归方程、二次函数的性质,考查了计算求解能力,属于基础题. 19.已知三棱柱111ABC A B C -,1AA ⊥平面ABC ,90ABC ∠=︒,11AA AB BC ===.(1)求异面直线1AB 与1BC 所成的角; (2)求二面角1C AB C --的大小. 【答案】(1)60;(2)45. 【解析】 【分析】(1)本题首先可根据题意构造空间直角坐标系,然后写出()11,0,1AB =-与()10,1,1BC =,最后根据向量的数量积公式即可得出结果;(2)本题首先可以求出平面1ABC 的法向量n 以及平面ABC 的法向量m ,然后求出两法向量的夹角的余弦值,最后结合图像,即可得出结果.【详解】因为1AA ⊥平面ABC ,90ABC ∠=︒所以如图,以BA 为x 轴、BC 为y 轴、1BB 为z 轴建立空间直角坐标系, 因为11AA AB BC ===,所以()1,0,0A ,()0,0,0B ,()10,0,1B ,()10,1,1C (1)因为()11,0,1AB =-,()10,1,1BC =,所以1111111,22AB BC cos AB BC AB BC ⋅<>===, 所以异面直线1AB 与1BC 所成的角为60,(2)()10,1,1BC =,()1,0,0BA =,设平面1ABC 的法向量为(),,n x y z =则100n BA n BC ⎧⋅=⎪⎨⋅=⎪⎩,化简得00x y z =⎧⎨+=⎩,取()0,1,1n =-,设平面ABC 的法向量为()0,0,1m =,,2n m cos n m n m⋅<>=== 由图形可知二面角为锐角,故二面角1C AB C --的大小为45.【点睛】本题考查异面直线所成角以及二面角的求法,可通过构造空间直角坐标系的方式求解,考查向量的数量积公式,考查计算能力,考查数形结合思想,是中档题.20.2020年3月,各行各业开始复工复产,生活逐步恢复常态,某物流公司承担从甲地到乙地的蔬菜运输业务.已知该公司统计了往年同期200天内每天配送的蔬菜量X (40≤X <200,单位:件.注:蔬菜全部用统一规格的包装箱包装),并分组统计得到表格如表:若将频率视为概率,试解答如下问题:(1)该物流公司负责人决定随机抽出3天的数据来分析配送的蔬菜量的情况,求这3天配送的蔬菜量中至多有2天小于120件的概率;(2)该物流公司拟一次性租赁一批货车专门运营从甲地到乙地的蔬菜运输.已知一辆货车每天只能运营一趟,每辆货车每趟最多可装载40件,满载才发车,否则不发车.若发车,则每辆货车每趟可获利2000元;若未发车,则每辆货车每天平均亏损400元.为使该物流公司此项业务的营业利润最大,该物流公司应一次性租赁几辆货车? 【答案】(1)485512;(2)3. 【解析】【分析】(1)记事件A 为“在200天随机抽取1天,其蔬菜量小于120件”,则P (A )38=,由此能求出随机抽取的3天中配送的蔬菜量中至多有2天的蔬菜量小于120件的概率. (2)由题意得每天配送蔬菜量X 在[40,80),[80,120),[120,160),[160,200)的概率分别为11118428,,,,设物流公司每天的营业利润为Y ,若租赁1辆车,则Y 的值为2000元,若租赁2辆车,则Y 的可能取值为4000,1600,若租赁3辆车,则Y 的可能取值为6000,3600,1200,若租赁4辆车,则Y 的可能取值为8000,5600,3200,800,分别求出相应的数学期望,推导出为使该物流公司此项业务的营业利润最大,该物流公司应一次性租赁3辆货车.【详解】(1)记事件A 为“在200天随机抽取1天,其蔬菜量小于120件”, 则P (A )38=, ∴随机抽取的3天中配送的蔬菜量中至多有2天的蔬菜量小于120件的概率为:p 22120333335355485()()()88888512C C C ⎛⎫⎛⎫=++= ⎪⎪⎝⎭⎝⎭. (2)由题意得每天配送蔬菜量X 在[40,80),[80,120),[120,160),[160,200)的概率分别为11118428,,,,设物流公司每天的营业利润为Y , 若租赁1辆车,则Y 的值为2000元,若租赁2辆车,则Y 的可能取值为4000,1600,P (Y =4000)78=,P (Y =1600)18=, ∴Y 的分布列为:∴E(Y)=400071160086⨯+⨯=3700元.若租赁3辆车,则Y的可能取值为6000,3600,1200,P(Y=6000)58 =,P(Y=3600)14 =,P(Y=1200)18 =,∴Y的分布列为:∴E(Y)511 600036001200848=⨯+⨯+⨯=4800元,若租赁4辆车,则Y的可能取值为8000,5600,3200,800,P(Y=8000)18 =,P(Y=5600)12 =,P(Y=3200)14 =,P(Y=800)18 =,∴Y的分布列为:∴E(Y)1111 8000560032008008248=⨯+⨯+⨯+⨯=4700,∵4800>4700>3700>2000,∴为使该物流公司此项业务的营业利润最大,该物流公司应一次性租赁3辆货车. 【点睛】本题考查概率、离散型随机变量的分布列、数学期望的求法,考查频数分布表、古典概型等基础知识,考查运算求解能力,是中档题. 21.如图,四棱锥P ABCD -中,平面PAC ⊥平面ABCD ,PA PC =,AB CD ∥,AB AD ⊥,且244CD AD AB ===.(1)过BD 作截面与线段PC 交于点H ,使得//AP 平面BDH ,试确定点H 的位置,并给出证明;(2)在(1)的条件下,若二面角H BD C --的大小为4π,试求直线DA 与平面BDH 所成角的正弦值.【答案】(1)H 为线段PC 上靠近点P 的五等分点,即5PC PH =,证明见解析;(2)1010【解析】 【分析】(1)连接BD 交AC 于点E .证明AP EH ∥,即可证明AP ∥平面BDH .(2)以DA ,DC 为x ,y 轴的正方向,过点D 作平面ABCD 的垂线为z 轴建立空间直角坐标系,求出平面BDH 的法向量,利用空间向量的数量积求解直线DA 与平面BDH 所成角的正弦值即可.【详解】(1)如图,连接BD 交AC 于点E ,由AB CD ∥,易知AEB △相似于CED . ∴14AE AB EC CD ==, 又AP ∥平面BDH ,平面APC平面BDH EH =, ∴AP EH ∥,∴14PH AE HC EC ==,即H 为线段PC 上靠近点P 的五等分点,即5PC PH =. (2)由12AB AD AD CD ==,Rt AED △相似于Rt CED ,可得AC BD ⊥, ∵平面PAC ⊥平面ABCD ,且平面PAC平面ABCD AC =,∴BD ⊥平面PAC , ∴HEC ∠为二面角H BD C --的平面角,∵EH PA ∥,∴4PAC HEC π∠=∠=,又PA PC =,∴PC PA ⊥,PC EH ⊥,又易知PC BD ⊥,∴PC ⊥平面BDH ,即CP 是平面BDH 的法向量,如图,以DA ,DC 为x ,y 轴的正方向,过点D 作平面ABCD 的垂线为z 轴建立空间直角坐标系,则()0,0,0D ,()2,0,0A ,()0,4,0C ,(1,5P ,∴()2,0,0DA =,(1,5CP =-, ∴10sin DA CPDA CP θ⋅==DA 与平面BDH 10【点睛】本题考查直线与平面平行的判断定理的应用,直线与平面所成角的求法,考查空间想象能力以及计算能力.22.设函数()22cos f x x x =+. (1)讨论函数()f x 的单调性;(2)若0x ≥,不等式()1f x kx ≥+恒成立,求实数k 的取值范围. 【答案】(1)在区间(),0∞-上是减函数,在区间()0,∞+上是增函数;(2)(],0∞- 【解析】【分析】(1)利用导函数的正负讨论函数的单调性; (2)不等式()1f x kx ≥+化为2210x kx cos x --+≥,结合(1)的结论,分析函数单调性,讨论函数最值,根据不等式恒成立求参数的取值范围. 【详解】解:(1)()()()2222,2222120f x x cosxsinx x sin x f x cos x cos x =-=-=-=-'≥' 所以()f x '为增函数,又因为()00f '= 所以,当0x <时,()0f x '<;当0x >时,()0f x '> 所以,函数()f x 在区间()0∞-,上是减函数,在区间()0∞+,上是增函数(2)不等式()1f x kx ≥+化为2210x kx cos x --+≥设()221g x x kx cos x =--+,()022x g x x k sin x ≥=--', 由(1)可知()g x '是[)0∞+,上的增函数, 因为()0g k '=-,所以,当()000k g '≤≥时,,函数g (x )在区间[)0∞+,上的增函数 所以()()20100g x g cos ≥=-+=,所以当0k ≤时符合题意. 当0k >时,()/00g k =-<,所以存在00x >,使得()/00g x =; 并且当()000x x g x ≤'<<时,;当()00x x g x >>'时,;所以函数()g x 在区间[)00x ,上是减函数,在区间()0x ,+∞上是增函数 最小值为()()000g x g <=,不等式不恒成立 综上,使得命题成立的实数k 的取值范围是(]0,∞- 【点睛】此题考查利用导函数讨论函数的单调性,解决不等式恒成立求参数的取值范围,涉及分类讨论.。
山东省泰安市东平高中高二物理下学期期中试卷(含解析)
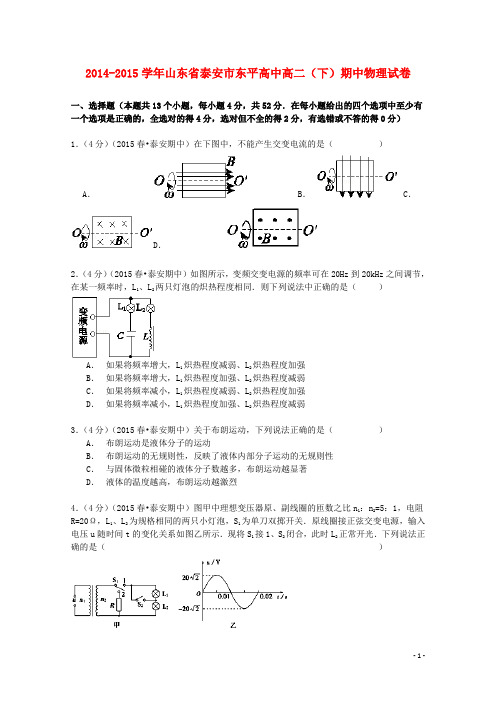
2014-2015学年山东省泰安市东平高中高二(下)期中物理试卷一、选择题(本题共13个小题,每小题4分,共52分.在每小题给出的四个选项中至少有一个选项是正确的,全选对的得4分,选对但不全的得2分,有选错或不答的得0分)1.(4分)(2015春•泰安期中)在下图中,不能产生交变电流的是()A.B.C.D.2.(4分)(2015春•泰安期中)如图所示,变频交变电源的频率可在20Hz到20kHz之间调节,在某一频率时,L1、L2两只灯泡的炽热程度相同.则下列说法中正确的是()A.如果将频率增大,L1炽热程度减弱、L2炽热程度加强B.如果将频率增大,L1炽热程度加强、L2炽热程度减弱C.如果将频率减小,L1炽热程度减弱、L2炽热程度加强D.如果将频率减小,L1炽热程度加强、L2炽热程度减弱3.(4分)(2015春•泰安期中)关于布朗运动,下列说法正确的是()A.布朗运动是液体分子的运动B.布朗运动的无规则性,反映了液体内部分子运动的无规则性C.与固体微粒相碰的液体分子数越多,布朗运动越显著D.液体的温度越高,布朗运动越激烈4.(4分)(2015春•泰安期中)图甲中理想变压器原、副线圈的匝数之比n1:n2=5:1,电阻R=20Ω,L1、L2为规格相同的两只小灯泡,S1为单刀双掷开关.原线圈接正弦交变电源,输入电压u随时间t的变化关系如图乙所示.现将S1接1、S2闭合,此时L2正常开光.下列说法正确的是()A.输入电压u的表达式u=20sin(50πt)VB.只断开S2后,L1、L2均正常发光C.只断开S2后,原线圈的输入功率增大D.若S1换接到2后,R消耗的电功率为0.8W5.(4分)(2015•新建县校级模拟)如图是某电子秤的原理图,人只要站在踏板上,仪表G就能显示人的体重,踏板下面的传感器R实质是一个阻值可随压力大小而变化的电阻,显示体重的仪表G实质是理想电流表,如果不计踏板的质量,电阻R随人的体重G变化的函数关系式为R=a﹣kG(a、k是常量,G和R的单位分别是N和Ω).下列说法正确的是()A.传感器R是一个力电传感器B.闭合电路测量时,电路中的电流随人的体重均匀变化C.该秤零刻度线(即踏板空载时的刻度线)应标在电流表G刻度盘的零刻度处D.如果要扩大电子秤的量程,滑动变阻器R′接入电路中的电阻应调大6.(4分)(2013秋•翠屏区校级期末)某电阻元件在正常工作时,通过它的电流按如图所示的规律变化.今与这个电阻元件串联一个多用电表(已调至交流电流档),则多用电表的示数为()A.4 A B.4A C.5A D. 5 A7.(4分)(2015春•泰安期中)两分子间的斥力和引力的合力F与分子间距离r的关系如图中曲线所示,曲线与r轴交点的横坐标为r0,相距很远的两分子在分子力作用下,由静止开始相互接近.若两分子相距无穷远时分子势能为零,下列说法正确的是()A.在r>r0阶段,F做正功,分子动能增加,势能也增加B.在r<r0阶段,F做负功,分子动能减小,势能增加C.在r=r0时,分子势能为零D.分子动能和势能之和在整个过程中不变8.(4分)(2015春•泰安期中)关于平衡态和热平衡,下列说法中正确的是()A.只要温度不变且处处相等,系统就一定处于平衡态B.两处系统在接触时它们的状态不发生变化,这两个系统的温度是相等的C.热平衡就是平衡态D.处于热平衡的几个系统的温度一定相等9.(4分)(2015春•泰安期中)对于分子动理论和物体内能的理解,下列说法正确的是()A.温度高的物体内能不一定大,但分子平均动能一定大B.物体的温度升高,物体中分子热运动加剧,所有分子的热运动动能都一定增大C.内能是物体内所有分子的热运动动能与分子势能的总和D.在使两个分子间的距离由很远(r>10﹣9m)减小到很难再靠近的过程中,分子间的作用力先减小后增大,分子势能不断增大10.(4分)(2014•蒙山县模拟)民间常用“拔火罐”来治疗某些疾病,方法是将点燃的纸片放入一个小罐内,当纸片燃烧完时,迅速将火罐开口端紧压在皮肤上,火罐就会紧紧地被“吸”在皮肤上.其原因是,当火罐内的气体()A.温度不变时,体积减小,压强增大B.体积不变时,温度降低,压强减小C.压强不变时,温度降低,体积减小D.质量不变时,压强增大,体积减小11.(4分)(2015春•泰安期中)如图所示,a、b、c三根完全相同的玻璃管,一端封闭,管内各用相同长度的一段水银柱封闭了质量相等的空气,a管竖直向下做自由落体运动,b管竖直向上做加速度为g的匀加速运动,c管沿倾角为45°的光滑斜面下滑,若空气温度始终不变,当水银柱相对管壁静止时,a、b、c三管内的空气柱长度L a、L b、L c间的关系为()A.L b=L c=L a B.L b<L c<L a C.L b>L c>L a D. L b<L c=L a12.(4分)(2015•上海一模)一定质量的理想气体经历如图所示的状态变化,变化顺序由a→b→c→a,ab线段延长线过坐标原点,bc线段与t轴垂直,ac线段与V轴垂直.气体在此状态变化过程中()A.从状态a到状态b,压强不变B.从状态b到状态c,压强增大C.从状态b到状态c,气体内能增大D.从状态c到状态a,单位体积内的分子数减少13.(4分)(2013•辽宁二模)如图是氧气分子在不同温度(0℃和100℃)下的速率分布,由图可得信息正确的是()A.同一温度下,氧气分子速率呈现出“中间多,两头少”的分布规律B.随着温度的升高,每一个氧气分子的速率都增大C.随着温度的升高,氧气分子中速率小的分子所占的比例高D.随着温度的升高,氧气分子的平均速率变小二、填空题(共12分)把答案填在题后的横线上(每空4分)14.(8分)(2010•徐汇区一模)在“用油膜法估测分子的大小”的实验中,以下给出的是可能的操作步骤,把你认为正确的步骤前的字母按合理的顺序填写在横线上,并请补充实验步骤D中的计算式.A.将画有油膜轮廓的玻璃板放在坐标纸上,以坐标纸上边长1cm的正方形为单位,计算出轮廓内正方形的个数m.B.将一滴油酸酒精溶液滴在水面上,待油酸薄膜的形状稳定.C.用浅盘装入约2cm深的水,然后将痱子粉均匀地撤在水面上.D.用测量的物理量估算出单个油酸分子的直径d= m.E.用滴管将事先配好的浓度为0.05%的油酸酒精溶液逐滴滴入量筒,记下滴入的溶液体积V0m3与滴数N.F.将玻璃板放在浅盘上,用笔将薄膜的外围形状描画在玻璃板上.15.(4分)(2015春•泰安期中)如图所示,L1和L2是输电导线,甲是电压互感器,乙是电流互感器.若已知变压比为100:1,变流比为1000:1,并且知道电压表示数为220V,电流表示数为100A,则输电线的输送功率为w.三、计算题(解答应写出必要的文字说明、方程式和重要演算步骤.只写出最后答案的不能得分.有数值计算的题,答案中必须明确写出数值和单位.)(共36分)16.(8分)(2008秋•鞍山期末)如图所示,变压器原线圈输入电压为220V,副线圈输出电压为36V,两只灯泡的额定电压均为36V,L1额定功率为12W,L2额定功率为6W,试求:(1)该变压器的原副线圈匝数比;(2)两灯均正常工作时原线圈的电流,以及只有L1正常工作时原线圈中的电流.17.(10分)(2015春•泰安期中)如图所示,某小型水电站发电机输出功率为10kW,发电机输出电压为400V,向远距离用户供电,为了减少电能损失,使用2kV高压输电,最后用户得到220V、9.5kW的电力(即电功率).求:(1)水电站升压变压器原、副线圈匝数比n1:n2;(2)输电线路导线电阻R线;(3)用户降压变压器原、副线圈匝数比n3:n4.18.(10分)(2015春•泰安期中)如图所示,在左端封闭右端开口的、粗细均匀的U形管中,有一段空气柱将水银分为A、B两部分,A位于封闭端的顶部.已知在温度t=87℃时,空气柱的长度L=12.5cm,水银柱A的长度h1=25cm,B部分的两液面的高度差h2=45cm,外界大气压强P0=75cmHg.试求:(1)当空气柱的温度为多少摄氏度时,A部分的水银柱恰好对U形管的顶部没有压力.(2)保持空气柱在(1)情况下的温度不变,在右管中注入多少厘米长的水银柱,可以使U形管内B部分的水银面相平.19.(11分)(2015春•泰安期中)如图1所示,水平放置的汽缸内壁光滑,活塞厚度不计,在A、B两处设有限制装置,使活塞只能在A、B之间运动,B左边汽缸的容积为V0,A、B之间的容积为0.1V0.开始时活塞在B处,缸内气体的压强为0.9p0(p0为大气压强),温度为297K,现缓慢加热缸内气体,直至399.3K.求:(1)活塞刚离开B处时的温度T B;(2)缸内气体最后的压强p;(3)在图2中画出整个过程的p﹣V图线.2014-2015学年山东省泰安市东平高中高二(下)期中物理试卷参考答案与试题解析一、选择题(本题共13个小题,每小题4分,共52分.在每小题给出的四个选项中至少有一个选项是正确的,全选对的得4分,选对但不全的得2分,有选错或不答的得0分)1.(4分)(2015春•泰安期中)在下图中,不能产生交变电流的是()A.B.C.D.考点:交变电流.分析:线圈中会不会产生感应电流,就要从感应电流的条件:闭合电路、切割磁感线运动来入手分析.如果两个条件都具备,则产生感应电流;少一个条件也不会产生.解答:解:根据题意,结合产生交流电的条件,当电路是闭合的;线圈在磁场中转动,其中的线框切割磁感线,导致磁通量变化.根据感应电流产生的条件可以确定此时会产生感应电流,再根据楞次定律,则有产生的感应电流的方向不同,故BCD中有感应电流产生,并且由于均具有周期性变化,故产生的均为交变电流;只有A图中没有感应电流产生.本题选不产生交变电流的,故选:A.点评:此题解题的关键是要将产生感应电流的两个条件,及理解楞次定律的应用,注意交流电与直流电的区别2.(4分)(2015春•泰安期中)如图所示,变频交变电源的频率可在20Hz到20kHz之间调节,在某一频率时,L1、L2两只灯泡的炽热程度相同.则下列说法中正确的是()A.如果将频率增大,L1炽热程度减弱、L2炽热程度加强B.如果将频率增大,L1炽热程度加强、L2炽热程度减弱C.如果将频率减小,L1炽热程度减弱、L2炽热程度加强D.如果将频率减小,L1炽热程度加强、L2炽热程度减弱考点:电容器和电感器对交变电流的导通和阻碍作用.分析:二个支路电压相同,当交流电频率变化时,会影响电感的感抗和电容的容抗,从而影响流过各个支路的电流.解答:解:A、二个支路电压相同,当交流电频率变大时,电感的感抗增大,电容的容抗减小,所以流过L1泡所在支路的电流变大,流过灯泡L2所在支路的电流变小.故灯泡L1变亮,灯泡L2变暗,即L1炽热程度加强、L2炽热程度减弱,故A错误,B正确;C、当交流电频率变小时,电感的感抗减小,电容的容抗增大,所以流过L1泡所在支路的电流变小,流过灯泡L2所在支路的电流变大.故灯泡L1变暗,灯泡L2变亮,即L1炽热程度减弱、L2炽热程度加强;故C正确,D错误.故选:BC.点评:解决本题的关键知道电感和电容对交流电的阻碍作用的大小与什么因素有关.记住感抗和容抗的两个公式可以帮助定性分析.X L=2πLf,X C=.3.(4分)(2015春•泰安期中)关于布朗运动,下列说法正确的是()A.布朗运动是液体分子的运动B.布朗运动的无规则性,反映了液体内部分子运动的无规则性C.与固体微粒相碰的液体分子数越多,布朗运动越显著D.液体的温度越高,布朗运动越激烈考点:布朗运动.专题:布朗运动专题.分析:布朗运动是悬浮在液体中固体颗粒的运动,是由于液体分子规则的碰撞造成的,则布朗运动反映了液体中分子的无规则运动.颗粒越小,温度越高,布朗运动越明显.解答:解:A、B、布朗运动是悬浮在液体中固体颗粒的运动,不是液体分子的运动.固体颗粒是由于液体分子规则的碰撞造成的,则布朗运动反映了液体中分子的无规则运动,故A 错误,B正确.C、D、悬浮在液体中的微粒越小,液体温度越高,布朗运动越显著,故C错误,D正确;故选:BD点评:本题考查布朗运动的定义,布朗运动既不是颗粒分子的运动,也不是液体分子的运动,而是液体分子无规则运动的反映.4.(4分)(2015春•泰安期中)图甲中理想变压器原、副线圈的匝数之比n1:n2=5:1,电阻R=20Ω,L1、L2为规格相同的两只小灯泡,S1为单刀双掷开关.原线圈接正弦交变电源,输入电压u随时间t的变化关系如图乙所示.现将S1接1、S2闭合,此时L2正常开光.下列说法正确的是()A.输入电压u的表达式u=20sin(50πt)VB.只断开S2后,L1、L2均正常发光C.只断开S2后,原线圈的输入功率增大D.若S1换接到2后,R消耗的电功率为0.8W考点:变压器的构造和原理;电功、电功率.专题:交流电专题.分析:根据电压与匝数成正比,电流与匝数成反比,变压器的输入功率和输出功率相等,逐项分析即可得出结论.解答:解:A、周期是0.02s,ω==100π,所以输入电压u的表达式应为u=20sin(100πt)V,A错误;B、只断开S2后,负载电阻变大为原来的2倍,电压不变,副线圈电流变小为原来的一半,L1、L2的功率均变为额定功率的四分之一,B错误;C、只断开S2后,原线圈的输入功率等于副线圈的功率都减小,C错误;D、若S1换接到2后,电阻R电压有效值为4V,R消耗的电功率为=0.8W,D正确.故选:D.点评:掌握住理想变压器的电压、电流及功率之间的关系,本题即可得到解决.5.(4分)(2015•新建县校级模拟)如图是某电子秤的原理图,人只要站在踏板上,仪表G就能显示人的体重,踏板下面的传感器R实质是一个阻值可随压力大小而变化的电阻,显示体重的仪表G实质是理想电流表,如果不计踏板的质量,电阻R随人的体重G变化的函数关系式为R=a﹣kG(a、k是常量,G和R的单位分别是N和Ω).下列说法正确的是()A.传感器R是一个力电传感器B.闭合电路测量时,电路中的电流随人的体重均匀变化C.该秤零刻度线(即踏板空载时的刻度线)应标在电流表G刻度盘的零刻度处D.如果要扩大电子秤的量程,滑动变阻器R′接入电路中的电阻应调大考点:传感器在生产、生活中的应用;常见传感器的工作原理.分析:根据闭合电路欧姆定律列式得到电流的表达式和量程的表达式进行讨论即可.解答:解:A、R是将压力信号转换成电信号的传感器,即力电传感器,故A正确;B、闭合电路测量时,电路中的电流:I=,显然与人的体重不成线性关系,故B错误;C、当重力为零时,电流最小,但不为零,故C错误;D、由I g=可知,kG m=a+r+R′﹣,因此变阻器接入电路中的电阻调大,可以测量的人的最大体重增大,故D正确;故选:AD.点评:本题关键是明确电子秤的工作原理,然后结合闭合电路欧姆定律和电阻R随人的体重G变化的函数关系式列式分析,不难.6.(4分)(2013秋•翠屏区校级期末)某电阻元件在正常工作时,通过它的电流按如图所示的规律变化.今与这个电阻元件串联一个多用电表(已调至交流电流档),则多用电表的示数为()A.4 A B.4A C.5A D. 5 A考点:交流的峰值、有效值以及它们的关系.专题:交流电专题.分析:有效值的定义为:把直流电和交流电分别通过两个相同的电阻器件,如果在相同时间内它们产生的热量相等,那么就把此直流电的电压、电流作为此交流电的有效值.特别的,对于正弦交变电流最大值是有效值的倍.解答:解:根据有效值的定义可得:R+(3)2R=I有效2RT,解得:I有效=5A;故选:C.点评:本题考查交变电流有效值的计算,根据交流电的定义计算即可.7.(4分)(2015春•泰安期中)两分子间的斥力和引力的合力F与分子间距离r的关系如图中曲线所示,曲线与r轴交点的横坐标为r0,相距很远的两分子在分子力作用下,由静止开始相互接近.若两分子相距无穷远时分子势能为零,下列说法正确的是()A.在r>r0阶段,F做正功,分子动能增加,势能也增加B.在r<r0阶段,F做负功,分子动能减小,势能增加C.在r=r0时,分子势能为零D.分子动能和势能之和在整个过程中不变考点:分子势能;分子间的相互作用力.分析:当分子间距离等于平衡距离时,分子力为零,分子势能最小;当分子间距离小于平衡距离时,分子力表现为斥力;根据图象分析答题.解答:解:A、r0为分子间的平衡距离,在r>r0阶段,分子力表现为引力,相互靠近时F做正功,分子动能增加,势能减小,故A错误;B、当r<r0时,分子间的作用力表现为斥力,F做负功,分子动能减小,势能增大.故B正确.C、在r=r0时,由上知在r=r0时,分子势能最小,但不一定为零,故C错误.D、由于没有其他外力做功,根据能量守恒定律可知分子动能和势能之和在整个过程中不变,故D正确;故选:BD.点评:分子间的势能及分子力虽然属于微观世界的关系,但是可运用我们所学过的力学中功能关系进行分析.8.(4分)(2015春•泰安期中)关于平衡态和热平衡,下列说法中正确的是()A.只要温度不变且处处相等,系统就一定处于平衡态B.两处系统在接触时它们的状态不发生变化,这两个系统的温度是相等的C.热平衡就是平衡态D.处于热平衡的几个系统的温度一定相等考点:阿伏加德罗常数.分析:首先知道平衡态和热平衡的定义,知道影响的因素是不同;知道温度是判断系统热平衡的依据;据此分析判断即可解答:解:A、一般来说,平衡态是针对某一系统而言的,描述系统状态的参量不只温度一个,还与体积压强有关,当温度不变时,系统不一定处于平衡态,故A错误;BD、热平衡是两个系统相互影响的最终结果,根据热平衡的定义可知,系统在接触时它们的状态不发生变化,这两个系统的温度是相等的,故BD正确;C、据以上分析可知,两者是不同的,故C错误.故选:BD.点评:一般来说,描述系统状态的参量不只温度一个,平衡态是针对某一系统而言的,热平衡是两个系统相互影响的最终结果9.(4分)(2015春•泰安期中)对于分子动理论和物体内能的理解,下列说法正确的是()A.温度高的物体内能不一定大,但分子平均动能一定大B.物体的温度升高,物体中分子热运动加剧,所有分子的热运动动能都一定增大C.内能是物体内所有分子的热运动动能与分子势能的总和D.在使两个分子间的距离由很远(r>10﹣9m)减小到很难再靠近的过程中,分子间的作用力先减小后增大,分子势能不断增大考点:温度是分子平均动能的标志;分子的热运动.分析:内能是物体内所有分子的热运动动能与分子势能的总和,物体的内能由物体的体积、温度和物质的量共同决定;温度是分子平均动能的标志.根据分子力做功情况判断分子势能的变化.解答:解:A、物体的内能由物体的体积、温度和物质的量共同决定,故温度高的物体内能不一定大,但温度越高,分子的平均动能一定越大,故A错误.B、物体的温度升高,物体中分子热运动加剧,分子的平均动能增大,由于分子运动是杂乱无章的,不是所有分子的热运动动能都增大,故B错误.C、内能是物体内所有分子的热运动动能与分子势能的总和,故C正确.D、在使两个分子间的距离由很远(r>10﹣9m)减小到很难再靠近的过程中,分子间的作用力先减小后增大,分子力先做正功后做负功,分子势能先减小后增大,故D错误.故选:AC.点评:热学中很多知识点要需要记忆,注意平时的积累,在平时训练中加强练习.关键要掌握温度的微观意义:温度是分子平均动能的标志.了解内能的含义和决定因素.10.(4分)(2014•蒙山县模拟)民间常用“拔火罐”来治疗某些疾病,方法是将点燃的纸片放入一个小罐内,当纸片燃烧完时,迅速将火罐开口端紧压在皮肤上,火罐就会紧紧地被“吸”在皮肤上.其原因是,当火罐内的气体()A.温度不变时,体积减小,压强增大B.体积不变时,温度降低,压强减小C.压强不变时,温度降低,体积减小D.质量不变时,压强增大,体积减小考点:理想气体的状态方程.专题:理想气体状态方程专题.分析:拨火罐“粘”在皮肤上,是利用了大气压.火罐内气体体积不变,温度降低,压强减小,小于大气压,火罐在内外气体压力差作用下,吸在皮肤上.解答:解:把罐扣在皮肤上,罐内空气的体积等于火罐的容积,体积不变,气体经过热传递,温度不断降低,气体发生等容变化,由查理定律可知,气体压强减小,火罐内气体压强小于外界大气压,大气压就将罐紧紧地压在皮肤上.故选B.点评:本题考查了查理定律在生活中的应用,对于生活现象的解释,关键在于判断此现象与哪些物理知识有关.11.(4分)(2015春•泰安期中)如图所示,a、b、c三根完全相同的玻璃管,一端封闭,管内各用相同长度的一段水银柱封闭了质量相等的空气,a管竖直向下做自由落体运动,b管竖直向上做加速度为g的匀加速运动,c管沿倾角为45°的光滑斜面下滑,若空气温度始终不变,当水银柱相对管壁静止时,a、b、c三管内的空气柱长度L a、L b、L c间的关系为()A.L b=L c=L a B.L b<L c<L a C.L b>L c>L a D. L b<L c=L a考点:理想气体的状态方程.专题:理想气体状态方程专题.分析:根据牛顿第二定律分别求出管内封闭气体的压强与大气压的关系,再由玻意耳定律列式分析.解答:解:设大气压为p0.对a管:a管竖直向下做自由落体运动,处于完全失重状态,封闭气体的压强等于大气压,即p a=p0;对b管:以水银为研究对象,根据牛顿第二定律得:p b S﹣p0S﹣mg=ma,则得:p b>p0;对c管:以水银为研究对象,根据牛顿第二定律得:p c S﹣p0S+mgsin45°=ma,又对管子和水银整体,有:Mgsin45°=Ma,得a=gsin45°,可解得:p c=p0;所以可得:p b>p a=p c;根据玻意耳定律pV=c得:l b<l c=l a.故选:D.点评:解决本题的关键是根据牛顿第二定律研究封闭气体的压强,常常以与气体接触的水银或活塞为研究对象,由力学规律求解封闭气体的压强.12.(4分)(2015•上海一模)一定质量的理想气体经历如图所示的状态变化,变化顺序由a→b→c→a,ab线段延长线过坐标原点,bc线段与t轴垂直,ac线段与V轴垂直.气体在此状态变化过程中()A.从状态a到状态b,压强不变B.从状态b到状态c,压强增大C.从状态b到状态c,气体内能增大D.从状态c到状态a,单位体积内的分子数减少考点:理想气体的状态方程.专题:理想气体状态方程专题.分析:解决本体需明确:V﹣T图象中倾斜的直线为等压变化,斜率越大,压强越小.解答:解:A、过各点的等压线如图,从状态a到状态b,斜率变大,则压强变小,故A错误;B、从状态b到状态c,斜率变小,则压强变大,故B正确;C、从状态b到状态c,温度不变,则内能不变,故C错误;D、从状态c到状态a,体积不变,则单位体积内的分子数不变,故D错误;故选:B.点评:本题中,要抓住过绝对零度的直线表示等压变化进行分析.13.( 4分)(2013•辽宁二模)如图是氧气分子在不同温度(0℃和100℃)下的速率分布,由图可得信息正确的是()A.同一温度下,氧气分子速率呈现出“中间多,两头少”的分布规律B.随着温度的升高,每一个氧气分子的速率都增大C.随着温度的升高,氧气分子中速率小的分子所占的比例高D.随着温度的升高,氧气分子的平均速率变小考点:温度是分子平均动能的标志.分析:温度是分子平均动能的标志,温度升高分子的平均动能增加,不同温度下相同速率的分子所占比例不同.解答:解:A、同一温度下,中等速率大的氧气分子数所占的比例大,出现“中间多、两头少”的分布规律,故A正确.B、温度升高使得氧气分子的平均速率增大,不一定每个分子的速率都增大,故B错误.C、温度升高使得速率较小的氧气分子所占的比例变小,故C错误.D、温度升高使得氧气分子的平均速率增大,故D错误.故选:A点评:本题考查了分子运动速率的统计分布规律,记住图象的特点.二、填空题(共12分)把答案填在题后的横线上(每空4分)14.(8分)(2010•徐汇区一模)在“用油膜法估测分子的大小”的实验中,以下给出的是可能的操作步骤,把你认为正确的步骤前的字母按合理的顺序填写在横线上ECBFAD,并请补充实验步骤D中的计算式.A.将画有油膜轮廓的玻璃板放在坐标纸上,以坐标纸上边长1cm的正方形为单位,计算出轮廓内正方形的个数m.B.将一滴油酸酒精溶液滴在水面上,待油酸薄膜的形状稳定.C.用浅盘装入约2cm深的水,然后将痱子粉均匀地撤在水面上.D.用测量的物理量估算出单个油酸分子的直径d= m.E.用滴管将事先配好的浓度为0.05%的油酸酒精溶液逐滴滴入量筒,记下滴入的溶液体积V0m3与滴数N.F.将玻璃板放在浅盘上,用笔将薄膜的外围形状描画在玻璃板上.考点:用油膜法估测分子的大小.。
山东省泰安市东平高级中学2019_2020学年高二数学下学期期中试题含解析

山东省泰安市东平高级中学2019-2020学年高二数学下学期期中试题(含解析)考试时间120分钟,满分150分★祝考试顺利★注意事项:1.答卷前,考生务必将自己的姓名、考生号等填写在答题卡和试卷指定位置上.2.作答选择题时,选出每小题答案后,用2B 铅笔在答题:卡上对应题目选项的答案信息点涂黑:如需改动,用橡皮擦干净后,再选涂其他答案.答案不能答在试卷上.3.非选择题必领用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区城内相应位置上,如需改动,先划掉原来的答案,然后再写上新答案.不准使用铅笔和涂改液.不按以上要求作答无效.一、单项选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知i 是虚数单位,复数z =z 的共轭复数z =( )A. 1B. 1C. 1--D.1-+2.在61(2)x x-的展开式中,常数项为( )A. 120-B. 120C. 160-D. 1603.已知()f x =()8f '等于( )A. 0B.D. 1-4.已知某篮球队员在比赛中每次罚球的命中率相同,且在两次罚球中至少命中一次的概率为2125,则该队员每次罚球的命中率p 为( ) A. 45 B. 35C.25D.155.已知函数()323f x x ax ax b =+++的图象在点()()1,1f 处的切线方程为12y x m =-+,若函数()f x 恰有三个不同的零点,则实数b 的取值范围是( )A. ()5,27-B. []5,27-C. (]1,3-D. []1,3-6.若()4234012341x a a x a x a x a x -=++++.则1234a a a a +++的值为( ) A. 1B. 1-C. 0D. 27.为抗击新冠病毒,某部门安排甲、乙、丙、丁、戊五名专家到三地指导防疫工作.因工作需要,每地至少需安排一名专家,其中甲、乙两名专家必须安排在同一地工作,丙、丁两名专家不能安排在同一地工作,则不同的分配方法总数为( ) A. 18B. 24C. 30D. 368.已知函数()212ee x xf x mx +-=--在R 上为增函数,则m 的取值范围为( )A. (,-∞B. )⎡+∞⎣C. (,-∞D. )⎡+∞⎣二、多项选择题:在每小题给出的四个选项中,有多项符合题目要求. 9.关于()9a b -的说法,正确的是( ) A. 展开式中的二项式系数之和为512 B. 展开式中只有第5项的二项式系数最大C. 展开式中第5项和第6项的二项式系数最大D. 展开式中第6项的系数最小10.已知函数()32f x x ax bx c =+++,则( )A. 0b ≤时,函数()y f x =一定存在极值B. 0x R ∃∈,使()00f x =C. 若0x 是()f x 的极值点,则()00f x '=D. 若0x 是()f x 的极小值点,则()f x 在区间()0,x -∞单调递减11.在棱长为1的正方体1111ABCD A B C D -中,则下列说法正确的是( )A. AC ⊥面11AB DB. 点1A 到面11AB DC. 1AA 与面11AB DD. 二面角111A B D A --的大小为4π12.已知函数()2ln f x x x=+,则以下结论正确的是( ) A. 函数()f x 的单调减区间是(0,2) B. 函数()y f x x =-有且只有1个零点 C. 存在正实数k ,使得()f x kx >成立D. 对任意两个正实数1x ,2x ,且12x x >,若()()12f x f x =则124x x +> 三、填空题:13.用0,1,2,3,4,5这6个数字组成的没有重复数字的四位数中,能被5整除的数的个数为______.(用数字作答)14.在某市2020年1月份的高三质量检测考试中,所有学生的数学成绩服从正态分布()29810N ,,现任取一名学生,则他的数学成绩在区间108,118内的概率为______.(附:若()2~X Nμσ,,则()0.6826P X μσμσ-<<+=,()220.9544P X μσμσ-<<+=.)15.已知箱中装有10个不同的小球,其中2个红球、3个黑球和5个白球,现从该箱中有放回地依次取出3个小球.则3个小球颜色互不相同的概率是_____;若变量ξ为取出3个球中红球的个数,则ξ的数学期望E (ξ)为_____. 16.函数()()23xf x x e =-,关于x 的方程()()210fx mf x -+=恰有四个不同的实数解,则正数m 的取值范围为______.四、解答题:解箸应写出文字说明证明过程或演算步骤. 17.函数()1xf x e x =-+()x R ∈;(1)求()f x 在点()()1,1f 处的切线方程; (2)求()f x 的极值.18.一饮料店制作了一款新饮料,为了进行合理定价先进行试销售,其单价x (元)与销量y (杯)的相关数据如下表:(1)已知销量y与单价x具有线性相关关系,求y关于x的线性回归方程;(2)若该款新饮料每杯的成本为8元,试销售结束后,请利用(1)所求的线性回归方程确定单价定为多少元时,销售的利润最大?(结果四舍五入保留到整数)附:线性回归方程ˆˆy bx a=+中斜率和截距最小二乗法估计计算公式:1221ˆni iiniix y nxybx nx==-=-∑∑,ˆˆa y bx=-,51=4195i iix y=∑,521=453.75iix=∑.19.已知三棱柱111ABC A B C-,1AA⊥平面ABC,90ABC∠=︒,11AA AB BC===. (1)求异面直线1AB与1BC所成的角;(2)求二面角1C AB C--的大小.20.2020年3月,各行各业开始复工复产,生活逐步恢复常态,某物流公司承担从甲地到乙地的蔬菜运输业务.已知该公司统计了往年同期200天内每天配送的蔬菜量X(40≤X<200,单位:件.注:蔬菜全部用统一规格的包装箱包装),并分组统计得到表格如表:蔬菜量X [40,80)[80,120)[120,160)[160,200)天数25 50 100 25若将频率视为概率,试解答如下问题:(1)该物流公司负责人决定随机抽出3天的数据来分析配送的蔬菜量的情况,求这3天配送的蔬菜量中至多有2天小于120件的概率;(2)该物流公司拟一次性租赁一批货车专门运营从甲地到乙地的蔬菜运输.已知一辆货车每天只能运营一趟,每辆货车每趟最多可装载40件,满载才发车,否则不发车.若发车,则每辆货车每趟可获利2000元;若未发车,则每辆货车每天平均亏损400元.为使该物流公司此项业务的营业利润最大,该物流公司应一次性租赁几辆货车? 21.如图,四棱锥P ABCD -中,平面PAC ⊥平面ABCD ,PA PC =,AB CD ∥,AB AD ⊥,且244CD AD AB ===.(1)过BD 作截面与线段PC 交于点H ,使得//AP 平面BDH ,试确定点H 的位置,并给出证明;(2)在(1)的条件下,若二面角H BD C --的大小为4π,试求直线DA 与平面BDH 所成角的正弦值.22.设函数()22cos f x x x =+.(1)讨论函数()f x 的单调性;(2)若0x ≥,不等式()1f x kx ≥+恒成立,求实数k 的取值范围.山东省泰安市东平高级中学2019-2020学年高二数学下学期期中试题(含解析)考试时间120分钟,满分150分★祝考试顺利★注意事项:1.答卷前,考生务必将自己的姓名、考生号等填写在答题卡和试卷指定位置上.2.作答选择题时,选出每小题答案后,用2B 铅笔在答题:卡上对应题目选项的答案信息点涂黑:如需改动,用橡皮擦干净后,再选涂其他答案.答案不能答在试卷上.3.非选择题必领用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区城内相应位置上,如需改动,先划掉原来的答案,然后再写上新答案.不准使用铅笔和涂改液.不按以上要求作答无效.一、单项选择题:在每小题给出的四个选项中,只有一项是符合题目要求的. 1.已知i是虚数单位,复数z =z 的共轭复数z =( )A. 1B. 1C. 1--D.1-+【答案】B 【解析】 【分析】先计算z ,由共轭复数概念即可得z .【详解】∵)()21i i z i-===-,∴1z =+. 故选:B【点睛】本题主要考查了复数的除数运算,共轭复数的概念,考查学生对基本概念的理解. 2.在61(2)x x-的展开式中,常数项为( )A. 120-B. 120C. 160-D. 160【答案】C 【解析】 【分析】写出二项式展开式的通项公式求出常数项.【详解】61(2)x x-展开式的通项2616(1)2k k k k kT C x ,令260,3k k常数项333316(1)2=160T C故选:C .【点睛】本题考查二项定理. 二项展开式问题的常见类型及解法:(1)求展开式中的特定项或其系数.可依据条件写出第1k +项,再由特定项的特点求出k 值即可.(2)已知展开式的某项或其系数求参数.可由某项得出参数项,再由通项公式写出第1k +项,由特定项得出k 值,最后求出其参数.3.已知()f x =()8f '等于( )A. 0B.D. 1-【答案】C 【解析】 【分析】根据基本初等函数的导数公式求出()f x ',再求()8f '.【详解】由()f x =()11-1-?2211=x =x 22f x ',∴()()1218828f -⨯'==,故选C【点睛】本题考查了基本初等函数的导数公式,若()a*f x =x a Q ∈(),则()a-1=ax f x ' .4.已知某篮球队员在比赛中每次罚球的命中率相同,且在两次罚球中至少命中一次的概率为2125,则该队员每次罚球的命中率p 为( ) A. 45 B. 35C. 25D. 15【答案】B 【解析】 【分析】利用相互独立事件概率乘法公式和互斥事件概率加法公式能求出该队员每次罚球的命中率p .【详解】解:某篮球队员在比赛中每次罚球的命中率相同,该队员每次罚球的命中率为p , 且在两次罚球中至少命中一次的概率为2125, 212(1)2521p C p p ∴+-=, 解得35p =或75p =(舍去)∴该队员每次罚球的命中率p 为35.故选:B .【点睛】本题考查概率的求法,考查相互独立事件概率乘法公式和互斥事件概率加法公式等基础知识,考查运算求解能力,属于基础题.5.已知函数()323f x x ax ax b =+++的图象在点()()1,1f 处的切线方程为12y x m =-+,若函数()f x 恰有三个不同的零点,则实数b 的取值范围是( )A. ()5,27-B. []5,27-C. (]1,3-D. []1,3-【答案】A 【解析】 【分析】先根据函数在()()1,1f 处的切线为12y x m =-+得到一个关于a ,b 的关系,然后再根据()f x 恰有三个不同的零点,列出关于b 的不等式.【详解】解:2()323f x x ax a '=++,因为函数在()()1,1f 处的切线方程为12y x m =-+ 所以()13512f a '=+=-,3a ∴=-,2()369f x x x ∴'=--. 令()0f x '=,得11x =-,23x =.当1x <-或3x >时,()0f x '>,()f x 是增函数;当13x 时,()0f x '<,()f x 是减函数.所以1x =-时,()f x 有极大值(1)5f b -=+;当3x =时,()f x 有极小值()327f b =-.所以,若函数()f x 恰有三个不同的零点,则50270b b +>⎧⎨-<⎩,解得527b -<<.故选:A .【点睛】本题考查导数的几何意义,应用导数求函数的极值和零点,同时考查学生的运算能力,属于基础题.6.若()4234012341x a a x a x a x a x -=++++.则1234a a a a +++的值为( ) A. 1 B. 1-C. 0D. 2【答案】B 【解析】 【分析】令0x =得01a =,令1x =得012340a a a a a ++++=,从而计算可得; 【详解】解:因为()4234012341x a a x a x a x a x -=++++ 令0x =得01a =令1x =得012340a a a a a ++++= 所以12341a a a a +++=- 故选:B【点睛】本题考查利用赋值法求二项式展开式的系数和,属于基础题.7.为抗击新冠病毒,某部门安排甲、乙、丙、丁、戊五名专家到三地指导防疫工作.因工作需要,每地至少需安排一名专家,其中甲、乙两名专家必须安排在同一地工作,丙、丁两名专家不能安排在同一地工作,则不同的分配方法总数为( ) A. 18 B. 24 C. 30 D. 36【答案】C 【解析】 【分析】由甲、乙两名专家必须安排在同一地工作,此时甲、乙两名专家看成一个整体即相当于一个人,所以相当于只有四名专家,先计算四名专家中有两名在同一地工作的排列数,再去掉丙、丁两名专家在同一地工作的排列数,即可得到答案.【详解】因为甲、乙两名专家必须安排在同一地工作,此时甲、乙两名专家 看成一个整体即相当于一个人,所以相当于只有四名专家,先计算四名专家中有两名在同一地工作的排列数,即从四个中选二个和其余二个看成三个元素的全排列共有:2343C A ⋅种;又因为丙、丁两名专家不能安排在同一地工作,所以再去掉丙、丁两名专家在同一地工作的排列数有33A 种,所以不同的分配方法种数有:23343336630C A A ⋅-=-=故选:C【点睛】本题考查了排列组合的应用,考查了间接法求排列组合应用问题,属于一般题. 8.已知函数()212ee x xf x mx +-=--在R 上为增函数,则m 的取值范围为( )A. (,-∞B. )⎡+∞⎣C. (,-∞D. )⎡+∞⎣【答案】A【解析】 【分析】函数()212ee x xf x mx +-=--在R 上为增函数,等价于()2122e 2e 0x x f x m +-'=+-≥对x ∈R 恒成立,然后分离变量,得2122e 2e x x m +-≤+,求出2122e 2e +-+x x 的最小值,就能确定m 的取值范围.【详解】因为函数()212ee x xf x mx +-=--在R 上为增函数,所以()2122e 2e 0x x f x m +-'=+-≥对x ∈R 恒成立,即2122e 2e x x m +-≤+对x ∈R 恒成立,又因为2122e 2e x x +-+≥=,所以m ≤ 故选:A【点睛】本题主要考查利用函数的单调性求参数的取值范围,分离变量是解决本题的关键. 二、多项选择题:在每小题给出的四个选项中,有多项符合题目要求. 9.关于()9a b -的说法,正确的是( ) A. 展开式中的二项式系数之和为512 B. 展开式中只有第5项的二项式系数最大C. 展开式中第5项和第6项的二项式系数最大D. 展开式中第6项的系数最小【答案】ACD【解析】 【分析】利用二项式定理的通项公式及其性质即可判断出正误.【详解】解:二项式()9a b -展开式的通项为()9191rrr r r T C a b -+=-对于A :二项式系数之和为92512=,故A 正确;对于B 、C :展开式共10项,中间第5、6项的二项式系数最大,故B 错误,C 正确;对于D :展开式中各项的系数为9(1)k k C -,0k =,1,⋯⋯,9 当5k =时,该项的系数最小.故D 正确. 故选:ACD .【点睛】本题考查了二项式展开式二项式系数的性质、以及系数与二项式系数的关系,需要熟记公式才能解决问题.同时考查了学生的计算能力和逻辑推理能力. 10.已知函数()32f x x ax bx c =+++,则( )A. 0b ≤时,函数()y f x =一定存在极值B. 0x R ∃∈,使()00f x =C. 若0x 是()f x 的极值点,则()00f x '=D. 若0x 是()f x 的极小值点,则()f x 在区间()0,x -∞单调递减 【答案】BC 【解析】 【分析】求导得到()232f x x ax b '=++,根据函数的极值和函数单调性的关系,零点性质,依次判断每个选项得到答案.【详解】()32f x x ax bx c =+++,则()232f x x ax b '=++,取0a b ,函数单调递增,无极值点,A 错误;当x →+∞时,()f x →+∞,当x →-∞时,()f x →-∞,故0x R ∃∈,使()00f x =,B 正确;若0x 是()f x 的极值点,则()00f x '=,C 正确;取0a =,3b =-,得到233f xx ,则函数在(),1-∞-上单调递增,在()1,1-上单调递减,在()1,+∞上单调递增,1是()f x 的极小值点,故D 错误. 故选:BC.【点睛】本题考查了函数的极值点,零点,单调性,意在考查学生对于函数性质的综合应用,取特殊值排除是解题的关键.11.在棱长为1的正方体1111ABCD A B C D -中,则下列说法正确的是( )A. AC ⊥面11AB DB. 点1A 到面11AB DC. 1AA 与面11AB DD. 二面角111A B D A --的大小为4π 【答案】BC 【解析】 【分析】AC 不垂直于1AB ,A 错误,利用等体积法计算B 正确,据B 知sin 3θ=,C 正确,1AOA ∠为二面角111A B D A --的平面角,1tan AOA ∠,D 错误,得到答案. 【详解】易知1AB C 为等边三角形,故AC 不垂直于1AB ,故AC 不垂直平面11AB D ,A 错误;111111111326A A B D V -=⨯⨯⨯⨯=,111111111133226A AB D AB D V S h h -==⨯=△,解得h ,B 正确;设1AA 与面11AB D 的夹角的余弦值为θ,据B 知sin 3θ=,故cos 3θ=,C 正确; O 为11B D 中点,易知111AO B D ⊥,11AO B D ⊥,故1AOA ∠为二面角111A B D A --的平面角,1tan AOA ∠,D 错误. 故选:BC.【点睛】本题考查了线面垂直,点面距离,线面夹角,二面角,意在考查学生的计算能力和空间想象能力. 12.已知函数()2ln f x x x=+,则以下结论正确的是( ) A. 函数()f x 的单调减区间是(0,2) B. 函数()y f x x =-有且只有1个零点 C. 存在正实数k ,使得()f x kx >成立D. 对任意两个正实数1x ,2x ,且12x x >,若()()12f x f x =则124x x +> 【答案】ABD 【解析】 【分析】A 选项,对函数求导,解对应不等式,可判断A ;B 选项,令()2ln x x x xg +=-,对其求导,研究单调性,根据零点存在定理,可判断B ; C 选项,先由()f x kx >得到22ln x k x x<+,令()22ln xh x x x =+,用导数的方法判断其单调性,即可判定C ;D 选项,令()0,2t ∈,则()20,2t -∈,令()()()22g t f t f t =+--,对其求导,判定其单调性,得到()()22f t f t +<-,令122x t =+>,根据题中条件,即可判定出D. 【详解】A 选项,因为()2ln f x x x=+,所以()22212x f x x x x -'=-+=,由()0f x '>得,2x >;由()0f x '<得,02x <<,因此函数()f x 在(0,2)上单调递减,在(2,)+∞上单调递增;故A 正确;B 选项,令()2ln x x x xg +=-,则()22222172122014x x x x x x x g x ⎛⎫-+ ⎪-+⎝⎭+'=---==<-显然恒成立; 所以函数()2ln x x x xg +=-在()0,∞+上单调递减; 又()ln112110g =-=>+,()212ln 21ln 20g =-=-<+, 所以函数()2ln x x x xg +=-有且仅有一个零点;故B 正确; C 选项,若()f x kx >,可得22ln x k x x<+, 令()22ln x h x x x =+,则()42341ln ln 4x x x x x h x x x x ----'=+=, 令()ln 4u x x x x =--,则()1ln 1ln u x x x '=--=-, 由()0u x '>得01x <<;由()0u x '<得1x >;所以函数()u x 在()0,1上单调递增,在()1,+∞上单调递减; 因此()()130u x u ≤=-<;所以()3ln 40x x x h x x --'=<恒成立,即函数()22ln xh x x x=+在()0,∞+上单调递减,所以函数()22ln xh x x x=+无最小值; 因此,不存在正实数k ,使得()f x kx >成立;故C 错; D 选项,令()0,2t ∈,则()20,2t -∈,则22t +>; 令()()()()()2224222ln 2ln 2ln 2242t tg t f t f t t t t t t t+=+--=++---=++---, 则()()()()222222241624802244t t t g t t t t t ---'=+⋅=-<+---, 所以()g t 在()0,2上单调递减,则()()00g t g <=,即()()22f t f t +<-, 令122x t =+>,由()()()122f x f x f t =<-,得22x t >-,则12224x x t t +>-++=,当14≥x 时,124x x +>显然成立,所以对任意两个正实数1x ,2x ,且12x x >,若()()12f x f x =则124x x +>.故D 正确. 故选:ABD.【点睛】本题主要考查导数的应用,通常需要对函数求导,用导数的方法研究函数的性质即可,属于常考题型. 三、填空题:13.用0,1,2,3,4,5这6个数字组成的没有重复数字的四位数中,能被5整除的数的个数为______.(用数字作答) 【答案】108 【解析】 【分析】按个位数是0和5分类计数后可得所求的个数.【详解】若四位数的个位数为0,则没有重复数字的四位数的个数为3554360A =⨯⨯=, 若四位数的个位数为5,则没有重复数字的四位数的个数为24444348A =⨯⨯=,故能被5整除的数的个数为108. 故答案为:108. 【点睛】本题考查排数问题,此类问题关键是特殊元素特殊处理,本题属于基础题. 14.在某市2020年1月份的高三质量检测考试中,所有学生的数学成绩服从正态分布()29810N ,,现任取一名学生,则他的数学成绩在区间108,118内的概率为______.(附:若()2~X Nμσ,,则()0.6826P X μσμσ-<<+=,()220.9544P X μσμσ-<<+=.)【答案】0.1359 【解析】 【分析】本题首先可根据题意得出()88108P X <<以及()78118P X <<的值,然后结合正态分布的对称性即可得出结果.【详解】因为所有学生的数学成绩服从正态分布()29810N ,,所以()881080.6826P X <<=,()781180.9544P X <<=,所以根据正态分布的对称性可知,()0.95440.68261081180.13592P X -<<==,故答案为:0.1359.【点睛】本题考查正态分布的相关性质,考查根据正态分布求概率,考查计算能力,体现了基础性,是简单题.15.已知箱中装有10个不同的小球,其中2个红球、3个黑球和5个白球,现从该箱中有放回地依次取出3个小球.则3个小球颜色互不相同的概率是_____;若变量ξ为取出3个球中红球的个数,则ξ的数学期望E (ξ)为_____. 【答案】 (1). 950 (2). 35【解析】 【分析】基本事件总数n =103=1000,3个小球颜色互不相同包含的基本事件个数m =103﹣(23+33+53222222333283755C C C +⨯⨯+⨯⨯+⨯⨯)=180,由此能求出3个小颜色互不相同的概率;若变量ξ为取出3个球中红球的个数,则ξ~(n ,210),由此能求出ξ的数学期望E (ξ).【详解】箱中装有10个不同的小球,其中2个红球、3个黑球和5个白球, 现从该箱中有放回地依次取出3个小球,基本事件总数n =103=1000, 3个小球颜色互不相同包含的基本事件个数:m =103﹣(23+33+53222222333283755C C C +⨯⨯+⨯⨯+⨯⨯)=180,则3个小球颜色互不相同的概率是P 1809100050m n ===; 若变量ξ为取出3个球中红球的个数,则ξ~(n ,210),∴ξ的数学期望E (ξ)=323105⨯=. 故答案为:950,35.【点睛】本题考查概率、数学期望的求法,考查古典概型、二项分布等基础知识,考查数据分析能力、运算求解能力,是中档题.16.函数()()23xf x x e =-,关于x 的方程()()210fx mf x -+=恰有四个不同的实数解,则正数m 的取值范围为______.【答案】3366e m e >+【解析】 【分析】先利用导数求出函数()f x 的单调区间和极值,令()f x t =,由题意可知,方程210t mt -+=有两个不同的实数根1t ,2t ,根据数形结合和韦达定理可知,一个根在36,e ⎛⎫∞ ⎪⎝⎭内,一个根在36,e ⎛⎫∞ ⎪⎝⎭内,再令()21g t t mt =-+,因为()010g =>,所以只需360g e ⎛⎫< ⎪⎝⎭,由此即可求出m 的取值范围. 【详解】解:()()()()22331xxx x e x f e x x =+-=+-',令()0f x '=得,3x =-或1,当3x <-时,()0f x '>,函数()f x 在(),3-∞-上单调递增,且()0f x >, 当31x -<<时,()0f x '<,函数()f x 在()3,1-上单调递减, 当1x >时,()0f x '>,函数()f x 在()1,+∞上单调递增, 所以()()363f x f e=-=极大值,()()12f x f e ==-极小值, 令()f x t =, 因为关于x 的方程()()210fx mf x -+=恰有四个不同的实数解,所以方程210t mt -+=有两个不同的实数根1t ,2t ,且一个根在360,e ⎛⎫⎪⎝⎭内,一个根在36,e ⎛⎫+∞ ⎪⎝⎭内,或者两个根都在()2,0e -内,或者一根为36e ,另一根在()2,0e -内;因为m 为正数,所以121t t =,120t t m +=>,所以1t ,2t 都为正根,所以两个根不可能在()2,0e -内,也不可能一根为36e ,另一根在()2,0e -内; 所以实数根1t ,2t ,且一个根在360,e ⎛⎫ ⎪⎝⎭内,一个根在36,e ⎛⎫+∞ ⎪⎝⎭内,令()21g t t mt =-+,因为()010g =>,所以只需360g e ⎛⎫< ⎪⎝⎭,即6336610m e e -+<,得3366e m e>+,即m 的取值范围为:336,6e e ⎛⎫++∞ ⎪⎝⎭.故答案为:336,6e e ⎛⎫++∞ ⎪⎝⎭.【点睛】本题主要考查了利用导数研究函数的单调性和极值,考查了函数的零点与方程根的关系,是中档题.四、解答题:解箸应写出文字说明证明过程或演算步骤.17.函数()1xf x e x =-+()x R ∈;(1)求()f x 在点()()1,1f 处的切线方程; (2)求()f x 的极值.【答案】(1)()11y e x =-+(2)极小值2 【解析】 【分析】(1)求出1,(1)1,))((1xe f e f e f x '-=-==',用直线的点斜式公式,即可求解; (2)由()0,0f x x '==,求出()f x 在(,0),(0,)-∞+∞上的单调区间,即可求出结论. 【详解】解:(1)()'1x fx e =-设所求切线方程的斜率为k ,则()'11k f e ==- 又()1f e =,故所求切线方程为:()()11y e e x -=-- 即()11y e x =-+ (2)因为()'1x f x e =-令()'0fx >,则0x >;令()'0f x <,则0x <,故函数()f x 在(),0-∞单调递减,在()0,∞+单调递增0x =时,函数()f x 有极小值()02f =【点睛】本题考查导数的几何意义,考查函数的极值,属于基础题.18.一饮料店制作了一款新饮料,为了进行合理定价先进行试销售,其单价x (元)与销量y (杯)的相关数据如下表:(1)已知销量y 与单价x 具有线性相关关系,求y 关于x 的线性回归方程;(2)若该款新饮料每杯的成本为8元,试销售结束后,请利用(1)所求的线性回归方程确定单价定为多少元时,销售的利润最大?(结果四舍五入保留到整数)附:线性回归方程ˆˆy bxa =+中斜率和截距最小二乗法估计计算公式:1221ˆni ii nii x y nxyb xnx ==-=-∑∑,ˆˆay bx =-,51=4195i i i x y =∑,521=453.75i i x =∑. 【答案】(1)ˆ32394yx =-+(2)单价应该定为10元 【解析】 【分析】(1)首先求出x 、y ,然后再求出ˆb、ˆa ,即可求解. (2)设定价为x 元,利润函数为()()323948y x x =-+-,利用二次函数的性质即可求解. 【详解】解:(1)由表中数据,()18.599.51010.59.55x =⨯++++= ()1201101590706090y ++++==, 则12221419559.590ˆ32453.7559.5ni ii nii x y nxybxnx ==--⨯⨯===--⨯-∑∑, ˆˆ90329.5394ay bx =-=+⨯=, 所以y 关于x 的线性相关方程为ˆ32394yx =-+. (2)设定价为x 元,则利润函数为()()323948y x x =-+-, 其中8x ≥,则2326503152y x x =-+-, 所以()65010232x =-≈⨯-(元),为使得销售的利润最大,确定单价应该定为10元.【点睛】本题考查了线性回归方程、二次函数的性质,考查了计算求解能力,属于基础题.19.已知三棱柱111ABC A B C -,1AA ⊥平面ABC ,90ABC ∠=︒,11AA AB BC ===.(1)求异面直线1AB 与1BC 所成的角; (2)求二面角1C AB C --的大小. 【答案】(1)60;(2)45. 【解析】 【分析】(1)本题首先可根据题意构造空间直角坐标系,然后写出()11,0,1AB =-与()10,1,1BC =,最后根据向量的数量积公式即可得出结果;(2)本题首先可以求出平面1ABC 的法向量n 以及平面ABC 的法向量m ,然后求出两法向量的夹角的余弦值,最后结合图像,即可得出结果.【详解】因为1AA ⊥平面ABC ,90ABC ∠=︒所以如图,以BA 为x 轴、BC 为y 轴、1BB 为z 轴建立空间直角坐标系, 因为11AA AB BC ===,所以()1,0,0A ,()0,0,0B ,()10,0,1B ,()10,1,1C (1)因为()11,0,1AB =-,()10,1,1BC =,所以1111111,22AB BC cos AB BC AB BC ⋅<>===, 所以异面直线1AB 与1BC 所成的角为60,(2)()10,1,1BC =,()1,0,0BA =,设平面1ABC 的法向量为(),,n x y z =则100n BA n BC ⎧⋅=⎪⎨⋅=⎪⎩,化简得00x y z =⎧⎨+=⎩,取()0,1,1n =-,设平面ABC 的法向量为()0,0,1m =,,2n m cos n m n m⋅<>=== 由图形可知二面角为锐角,故二面角1C AB C --的大小为45.【点睛】本题考查异面直线所成角以及二面角的求法,可通过构造空间直角坐标系的方式求解,考查向量的数量积公式,考查计算能力,考查数形结合思想,是中档题.20.2020年3月,各行各业开始复工复产,生活逐步恢复常态,某物流公司承担从甲地到乙地的蔬菜运输业务.已知该公司统计了往年同期200天内每天配送的蔬菜量X (40≤X <200,单位:件.注:蔬菜全部用统一规格的包装箱包装),并分组统计得到表格如表:若将频率视为概率,试解答如下问题:(1)该物流公司负责人决定随机抽出3天的数据来分析配送的蔬菜量的情况,求这3天配送的蔬菜量中至多有2天小于120件的概率;(2)该物流公司拟一次性租赁一批货车专门运营从甲地到乙地的蔬菜运输.已知一辆货车每天只能运营一趟,每辆货车每趟最多可装载40件,满载才发车,否则不发车.若发车,则每辆货车每趟可获利2000元;若未发车,则每辆货车每天平均亏损400元.为使该物流公司此项业务的营业利润最大,该物流公司应一次性租赁几辆货车? 【答案】(1)485512;(2)3. 【解析】【分析】(1)记事件A 为“在200天随机抽取1天,其蔬菜量小于120件”,则P (A )38=,由此能求出随机抽取的3天中配送的蔬菜量中至多有2天的蔬菜量小于120件的概率. (2)由题意得每天配送蔬菜量X 在[40,80),[80,120),[120,160),[160,200)的概率分别为11118428,,,,设物流公司每天的营业利润为Y ,若租赁1辆车,则Y 的值为2000元,若租赁2辆车,则Y 的可能取值为4000,1600,若租赁3辆车,则Y 的可能取值为6000,3600,1200,若租赁4辆车,则Y 的可能取值为8000,5600,3200,800,分别求出相应的数学期望,推导出为使该物流公司此项业务的营业利润最大,该物流公司应一次性租赁3辆货车.【详解】(1)记事件A 为“在200天随机抽取1天,其蔬菜量小于120件”, 则P (A )38=, ∴随机抽取的3天中配送的蔬菜量中至多有2天的蔬菜量小于120件的概率为:p 22120333335355485()()()88888512C C C ⎛⎫⎛⎫=++= ⎪⎪⎝⎭⎝⎭. (2)由题意得每天配送蔬菜量X 在[40,80),[80,120),[120,160),[160,200)的概率分别为11118428,,,,设物流公司每天的营业利润为Y , 若租赁1辆车,则Y 的值为2000元,若租赁2辆车,则Y 的可能取值为4000,1600,P (Y =4000)78=,P (Y =1600)18=, ∴Y 的分布列为:∴E(Y)=400071160086⨯+⨯=3700元.若租赁3辆车,则Y的可能取值为6000,3600,1200,P(Y=6000)58 =,P(Y=3600)14 =,P(Y=1200)18 =,∴Y的分布列为:∴E(Y)511 600036001200848=⨯+⨯+⨯=4800元,若租赁4辆车,则Y的可能取值为8000,5600,3200,800,P(Y=8000)18 =,P(Y=5600)12 =,P(Y=3200)14 =,P(Y=800)18 =,∴Y的分布列为:∴E(Y)1111 8000560032008008248=⨯+⨯+⨯+⨯=4700,∵4800>4700>3700>2000,∴为使该物流公司此项业务的营业利润最大,该物流公司应一次性租赁3辆货车. 【点睛】本题考查概率、离散型随机变量的分布列、数学期望的求法,考查频数分布表、古典概型等基础知识,考查运算求解能力,是中档题. 21.如图,四棱锥P ABCD -中,平面PAC ⊥平面ABCD ,PA PC =,AB CD ∥,AB AD ⊥,且244CD AD AB ===.(1)过BD 作截面与线段PC 交于点H ,使得//AP 平面BDH ,试确定点H 的位置,并给出证明;(2)在(1)的条件下,若二面角H BD C --的大小为4π,试求直线DA 与平面BDH 所成角的正弦值.【答案】(1)H 为线段PC 上靠近点P 的五等分点,即5PC PH =,证明见解析;(2)1010【解析】 【分析】(1)连接BD 交AC 于点E .证明AP EH ∥,即可证明AP ∥平面BDH .(2)以DA ,DC 为x ,y 轴的正方向,过点D 作平面ABCD 的垂线为z 轴建立空间直角坐标系,求出平面BDH 的法向量,利用空间向量的数量积求解直线DA 与平面BDH 所成角的正弦值即可.【详解】(1)如图,连接BD 交AC 于点E ,由AB CD ∥,易知AEB △相似于CED .∴14AE AB EC CD ==, 又AP ∥平面BDH ,平面APC 平面BDH EH =,∴AP EH ∥,∴14PH AE HC EC ==,即H 为线段PC 上靠近点P 的五等分点,即5PC PH =. (2)由12AB AD AD CD ==,Rt AED △相似于Rt CED ,可得AC BD ⊥, ∵平面PAC ⊥平面ABCD ,且平面PAC平面ABCD AC =,∴BD ⊥平面PAC ,∴HEC ∠为二面角H BD C --的平面角,∵EH PA ∥,∴4PAC HEC π∠=∠=,又PA PC =,∴PC PA ⊥,PC EH ⊥,又易知PC BD ⊥,∴PC ⊥平面BDH ,即CP 是平面BDH 的法向量,如图,以DA ,DC 为x ,y 轴的正方向,过点D 作平面ABCD 的垂线为z 轴建立空间直角坐标系,则()0,0,0D ,()2,0,0A ,()0,4,0C ,(1,5P ,∴()2,0,0DA =,(1,5CP =-, ∴10sin DA CP DA CPθ⋅==DA 与平面BDH 10【点睛】本题考查直线与平面平行的判断定理的应用,直线与平面所成角的求法,考查空间想象能力以及计算能力. 22.设函数()22cos f x x x =+.(1)讨论函数()f x 的单调性; (2)若0x ≥,不等式()1f x kx ≥+恒成立,求实数k 的取值范围.【答案】(1)在区间(),0∞-上是减函数,在区间()0,∞+上是增函数;(2)(],0∞-【解析】 【分析】 (1)利用导函数的正负讨论函数的单调性;(2)不等式()1f x kx ≥+化为2210x kx cos x --+≥,结合(1)的结论,分析函数单调性,讨论函数最值,根据不等式恒成立求参数的取值范围.【详解】解:(1)()()()2222,2222120f x x cosxsinx x sin x f x cos x cos x =-=-=-=-'≥'所以()f x '为增函数,又因为()00f '=所以,当0x <时,()0f x '<;当0x >时,()0f x '>所以,函数()f x 在区间()0∞-,上是减函数,在区间()0∞+,上是增函数。
山东省泰安市2020年高二下学期期中考试地理试题C卷

山东省泰安市2020年高二下学期期中考试地理试题C卷姓名:________ 班级:________ 成绩:________一、选择题 (共13题;共50分)1. (4分) (2018高三上·牡丹江期末) 中国地学会首任会长张相文早在1908年就提出了中国南北分界(即秦岭—淮河)的观点,而兰州大学陈全功教授等人则首次对中国南北分界线给出了定量、定位分析,最窄处约26.42公里,最宽处约195.41公里,将“线”还原成“带”(如下图)。
据此完成下面小题。
(1)将中国南北分界由“线”还原成“带”,主要运用的地理信息技术是()A . 遥感技术(RS)B . 全球定位系统(GPS)C . 地理信息系统(GIS)D . 计算机网络技术(CNT)(2)中国南北分界带西端,最接近我国的()A . 种植业与畜牧业的交错带B . 季风区与非季风区界线C . 地势二、三级阶梯分界线D . 外流河区域与内流河区域分界线2. (4分) (2016高二上·广东期末) 区域的发展一般可分为三个阶段:初期阶段、成长阶段和衰落阶段。
初期阶段主要表现为以传统农业为主体,成长阶段可分为工业化阶段和高效益的综合发展阶段。
结合图回答下列各题。
(1)在区域发展的初期阶段,下列关于区域内的产业结构及产业特征的说法,正确的是()A . 第二产业所占的比重迅速上升,第三产业表现出加速发展的趋势B . 传统农业占较大比重,工业化处于起步阶段C . 工业化的起步源于本阶段科技的创新D . 人地关系的不协调已表现得比较明显(2)右图中A,B,C各点分别代表区域发展不同时期的产业结构特征。
从区域发展的过程来看,其正确的顺序应该是()A . A—B—CB . B—C—AC . C—A—BD . B—A—C3. (2分) (2019高三上·黑龙江月考) 读黄河流域局部图,完成下题。
a地区治沙工作卓有成效,下列说法正确的是()A . 利用麦草、稻草、芦苇等材料扎设方格状的沙障是因地制宜治沙的典型B . 草方格沙障能大量吸引地下水,促进植物生长,固定沙漠C . 沙障固沙成本低,应大规模推广D . 沙障可增加地表粗糙度,削减风力,但不能截留水分,提高沙层含水量4. (4分) (2019高二上·陕西期中) 流域的开发都以河流的利用与治理为核心,结合流域的具体特征,对资源进行综合开发和利用。
山东省泰安市2019-2020年度高二下学期地理期中考试试卷B卷

山东省泰安市2019-2020年度高二下学期地理期中考试试卷B卷姓名:________ 班级:________ 成绩:________一、选择题(本卷共25个小题,每小题2分,共50分。
在每小题给出 (共11题;共50分)1. (6分) (2018高一下·长安期末) 读下图,回答下列各题。
(1)与美国相比,墨西哥发展农业的优势条件是()A . 耕地面积大B . 农业科技水平高C . 积温高D . 交通便利(2)在与美国的双边贸易中,墨西哥最具有出口优势的农产品是()A . 小麦B . 玉米C . 大豆D . 剑麻(3)为适应加入北美自由贸易区,墨西哥应该()A . 调整农业产业结构B . 大力发展农业机械C . 加大劳动力投入D . 降低农产品价格2. (4分) (2018高二下·洛阳期末) 区城产业竞争力系数,表示该区域某产业产品的输出额占一定区域市场的比重,产业竞争力系教越大,产业竞争力也就越强。
各地产业竞争力系数的变化,可以反映产生转移的动态趋势。
读上海市与浙江省各产业竞争力系数变化图,回答下面小题。
(1) 1990年—2010年,从上海向浙江转移趋势最明显的产业是()A . 家具与皮革B . 烟草与机械C . 机械与通信D . 皮革与文体用品(2)有关产业转移对移出地的影响,主要是()A . 工业产值降低,促进第三产业的发展B . 有利于产业升级,改善环境质量C . 加强国际分工合作,推动国际经济一体化D . 短期内增加就业机会,缓解就业压力3. (4分) (2019高二上·渭滨期末) 下图是美国本土某类电站分布图。
读图回答,该类电站使用的能源最可能是()A . 地热能B . 核能C . 太阳能D . 水能4. (4分) (2019高二下·赤峰期末) 光热发电是利用镜面收集太阳能,再通过换热装置提供蒸汽进行发电。
光伏发电是利用较昂贵的硅晶光电转换工艺将光能直接转变为电能。
山东省泰安市2019-2020学年高二下学期地理期中考试试卷(II)卷

山东省泰安市2019-2020学年高二下学期地理期中考试试卷(II)卷姓名:________ 班级:________ 成绩:________一、单选题。
(共18题;共56分)1. (6分) (2019高一下·盐城期末) 读中国人口分布图,完成下面小题。
(1)下列地区中人口最稀疏的是()A . 内蒙古高原B . 青藏高原C . 黄土高原D . 云贵高原(2)与西部省份相比,江苏省人口密度较大,造成该差异的主要影响因素是()A . 气候条件B . 地形差异C . 交通条件D . 经济水平2. (2分) (2015高二上·南昌期中) 下图为某岛屿等高线分布图(单位:米)。
该岛位于()①东半球②西半球③北半球④南半球A . ①③B . ①④C . ②③D . ②④3. (6分) (2017高二下·龙岩期末) “雨舌”是指丰沛降水区域呈“舌头”状向某地方向延伸的现象。
读西藏年等降水量线(单位:mm)和“雨舌”位置图,完成下列问题。
(1)影响“雨舌”区域的主要降水因素是()A . 洋流B . 地形C . 植被D . 纬度(2)位于“舌尖”上的波密县,拥有独特的自然景观是()A . 喀斯特地貌广布B . 冰川与森林相连C . 水网密布,水流湍急D . 土壤深厚,有机质多4. (2分) (2018高三上·黑龙江月考) 某太阳能设备生产公司,测试新研发的“追日型”太阳能发电设备。
聚热板可沿水平方向和竖直方向旋转,使聚热板始终正对太阳,从而提高太阳能利用率。
据图,回答下列各题。
(1)为更好的开发销售市场,对主要销售目标城市进行测试,下列城市不适合作为测试地的城市是()A . 广州B . 上海C . 杭州D . 乌鲁木齐(2)在各城市中,经一年测试,下列测试结论正确的是()A . 纬度越高的城市,水平旋转角度越大B . 纬度越高的城市,水平旋转角度越小C . 纬度越高的城市,水平旋转角度的年度化幅度越大D . 纬度越高的城市,水平旋转角度的年度化幅度越小5. (2分) (2017高二下·济南期末) 读图,完成下列各题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
力,属于基础题.
6.若 x 14 a0 a1x a2x2 a3x3 a4x4 .则 a1 a2 a3 a4 的值为(
A. 1
B. 1
C. 0
【答案】B
【解析】
) D. 2
【分析】
令 x 0 得 a0 1 ,令 x 1 得 a0 a1 a2 a3 a4 0 ,从而计算可得;
【详解】解: f (x) 3x2 2ax 3a ,因为函数在 1, f 1 处的切线方程为 y 12x m
所以 f 1 3 5a 12 , a 3 , f (x) 3x2 6x 9 .
令 f (x) 0 ,得 x1 1, x2 3 . 当 x 1或 x 3 时, f (x) 0 , f (x) 是增函数;当 -1 < x < 3 时, f (x) 0 , f (x) 是减
故选:C.
【点睛】本题考查二项定理. 二项展开式问题的常见类型及解法:
(1)求展开式中的特定项或其系数.可依据条件写出第 k 1 项,再由特定项的特点求出 k 值
即可.
(2)已知展开式的某项或其系数求参数.可由某项得出参数项,再由通项公式写出第 k 1 项,
由特定项得出 k 值,最后求出其参数.
3.已知 f x x ,则 f 8 等于( )
函数.
所以 x 1 时, f (x) 有极大值 f (1) b 5 ;当 x 3 时, f (x) 有极小值 f 3 b 27 .
3
所以,若函数
f
x
b 恰有三个不同的零点,则 b
50
,
27 0
解得 5 b 27 .
故选:A.
【点睛】本题考查导数的几何意义,应用导数求函数的极值和零点,同时考查学生的运算能
4.已知某篮球队员在比赛中每次罚球的命中率相同,且在两次罚球中至少命中一次的概率为
21 ,则该队员每次罚球的命中率 p 为( ) 25
4
A.
5
3
B.
5
2
C.
5
1
D.
5
【答案】B
【解析】
2
【分析】
利用相互独立事件概率乘法公式和互斥事件概率加法公式能求出该队员每次罚球的命中率
p.
【详解】解:某篮球队员在比赛中每次罚球的命中率相同,该队员每次罚球的命中率为 p ,
21
且在两次罚球中至少命中一次的概率为 ,
25
p2
C21 p(1
p)
21 25
,
解得 p 3 或 p 7 (舍去)
5
5
该队员每次罚球的命中率 p 为 3 . 5
故选:B.
【点睛】本题考查概率的求法,考查相互独立事件概率乘法公式和互斥事件概率加法公式等
基础知识,考查运算求解能力,属于基础题.
5.已知函数 f x x3 ax2 3ax b 的图象在点 1, f 1 处的切线方程为
4
【详解】因为甲、乙两名专家必须安排在同一地工作,此时甲、乙两名专家
看成一个整体即相当于一个人,所以相当于只有四名专家,
A. 0
B. 2 2
C. 2 8
【答案】C
D. 1
【解析】
【分析】
根据基本初等函数的导数公式求出 f x ,再求 f 8 .
【详解】由 f x
x
,得fLeabharlann x=11 -1
x2 =
1
-1
x2
,∴
f
8
1
8
1 2
2,
22
2
8
故选 C
【点睛】本题考查了基本初等函数的导数公式,若 f x =x(a a Q*),则 f x =axa-1 .
2.在 (1 2x)6 的展开式中,常数项为( ) x
A. 120
B. 120
C. 160
D. 160
【答案】C
1
【解析】
【分析】
写出二项式展开式的通项公式求出常数项.
【详解】
(1 x
2x)6
展开式的通项 Tk+1
=
(-1)k
2k
C6k
x2k-6
,令 2k - 6 = 0, k = 3
常数项 T3+1 = (-1)3 23C63 = -160
i
A. 1 3i
B. 1 3i
C. 1 3i
D.
1 3i
【答案】B 【解析】
【分析】
先计算 z ,由共轭复数概念即可得 z .
【详解】∵ z 3 i i
3 i i
i 2
1 3i ,
∴ z 1 3i .
故选:B
【点睛】本题主要考查了复数的除数运算,共轭复数的概念,考查学生对基本概念的理解.
y 12x m ,若函数 f x 恰有三个不同的零点,则实数 b 的取值范围是( )
A. 5,27
B. 5, 27
C. 1,3
D. 1,3
【答案】A 【解析】 【分析】
先根据函数在 1, f 1 处的切线为 y 12x m 得到一个关于 a , b 的关系,然后再根据
f (x) 恰有三个不同的零点,列出关于 b 的不等式.
家不能安排在同一地工作,则不同的分配方法总数为( )
A. 18 【答案】C 【解析】
B. 24
C. 30
D. 36
【分析】
由甲、乙两名专家必须安排在同一地工作,此时甲、乙两名专家看成一个整体即相当于一个
人,所以相当于只有四名专家,先计算四名专家中有两名在同一地工作的排列数,再去掉丙、
丁两名专家在同一地工作的排列数,即可得到答案.
【详解】解:因为 x 14 a0 a1x a2x2 a3x3 a4x4
令 x 0 得 a0 1
令 x 1 得 a0 a1 a2 a3 a4 0
所以 a1 a2 a3 a4 1
故选:B 【点睛】本题考查利用赋值法求二项式展开式的系数和,属于基础题. 7.为抗击新冠病毒,某部门安排甲、乙、丙、丁、戊五名专家到三地指导防疫工作.因工作需 要,每地至少需安排一名专家,其中甲、乙两名专家必须安排在同一地工作,丙、丁两名专
高二下学期期中检测数学试题
考试时间 120 分钟,满分 150 分 ★祝考试顺利★
注意事项: 1.答卷前,考生务必将自己的姓名、考生号等填写在答题卡和试卷指定位置上. 2.作答选择题时,选出每小题答案后,用 2B 铅笔在答题:卡上对应题目选项的 答案信息点涂黑:如需改动,用橡皮擦干净后,再选涂其他答案.答案不能答在 试卷上. 3.非选择题必领用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指 定区城内相应位置上,如需改动,先划掉原来的答案,然后再写上新答案.不准 使用铅笔和涂改液.不按以上要求作答无效. 一、单项选择题:在每小题给出的四个选项中,只有一项是符合题目要求的. 1.已知 i 是虚数单位,复数 z 3 i ,则 z 的共轭复数 z ( )
