噪声振动第6章1汇总
第3篇 舱室设备和内装——第6章 舱室隔声

防振 措施 。
舱室 防振措施 应从 大处 着 手 , 方法 之一 是在上层 建 筑和 主船体 之 间采取 振动 隔阻措 施 , 弹性安 装 的 其 即
的钢质 槽形 材里 , 天花 板衬层 采 用橡胶 减 振件 吊装 。
近 年来许 多船 舶 内装要 求采 用不 燃材 料 , 以橡胶 减 振层 已不适 用 。最 近 开 发 了金 属 网 吊装 天 花 板 和 所 用 金属 网加 工成 与橡胶 减振 件形 状相 仿 的减振 件 , 以及 用 不燃 材料 制 成 的织 品带 减振 件 。 图 36 34为 用 . .. 金 属 网 吊装 天花板 的典 型结 构 。
61
维普资讯
20 0 7年 2月
船
舶
F b a ,2 0 em  ̄ 0 7
N . O I
第 1期
S P& Bb 为烟囱与居住舱室分离 的支承形式 ;c 、d 为烟 囱穿过居住舱室的支承形式 ; () ( ) () e 有两根箱形轨道 的弹性 支承 ;f安全装置 ;g 限位器 ; h 隔振器的 固定。 () () () l —保 险螺栓 ;0 2 一橡胶元 件 ;一下 部箱 形轨道 ;一上层 建筑 的下部 甲板 ;一上 部箱形轨 道 ;一 主 甲板 ; 3 4 5 6 7 隔振器 ;6 一 l一橡胶垫块 ;一纵 向保 险橡 胶元件 ;0 9 l一上层 建筑 ;1 1 一上 轨道 ;2 隔振器 ;3 角钢 ;4 l一 l一 l一 下轨道 ;5 l一主 甲板 ;7 l一螺母 ;8 垫圈 ;9 间隙 ;l 粘结剂。 l一 l一 2一 图 3 63 2 弹性 上层 建筑 示意图 .. .
射频电路设计技术第六章资料

第6章 噪声与 非线性失真
• 评价一个射频系统性能的优劣时,有两 个很重要的指标: (1)噪声系数 (2)非线性失真 当一个系统处于小信号工作时,其许多 性能指标都与噪声有关;当信号增大时, 二极管和晶体管都存在非线性失真。
6.1 噪 声 系 数
• 噪声系数定义为输入信噪功率比(SNR)i Si / Ni 与输出信噪功率比 (SNR)o So / No 的比值:
6.4 交 调 失 真
• 在由各种有源器件构成的线性放大器中, 由于有源器件的特性是非线性的,在放 大过程中总会产生各种各样的失真。 • 讨论有源器件非线性特性对线性放大器 的影响,可分为两种不同的情况: 一是电路输入端只有一个有用信号输入 时; 二是输入端除有用信号外,还输入一个 或多个信号的情况。
• 这些组合频率分量形成对有用信号的干 扰。这些干扰并不是由两输入信号的谐 波产生,而是由这两个输入信号的相互 调制(相乘)引起的,所以称为互相调 制失真,又称为互调失真。
• 可在下面两个指标中选一个来衡量放大 器的互调失真程度: (1)互调失真比 (2)三阶互调截点
• 5.三阶互调截点 若忽略增益压缩,则基波分量幅度为 , a1V 互调失真比 IMR定义为在输入信号幅度 为V时,三阶互调分量的幅度与基波幅 3 度之比: a3V 3
• 6.估计IIP3的几种方法 (1)求IIP3的一种方法是通过瞬态模拟, 使两个幅值相等频率近似相同的正弦输 入信号驱动该放大器。当输入幅值改变 时计算交调,并比较输出频谱中的三次 相互调制乘积项及基波项。 (2)采用功率级数两个系数的比可计算 出三阶交调的简单表达式,并且可推导 出另一种适合于手工计算的方法。
P
• 则无杂散动态范围定义为:
DRf Pin, max Pin, min
集成电路版图第6(1)章:噪声问题

同轴屏蔽:
信号沿内部导线传送,外层的屏蔽线接地。 外界出现的任何噪声都由接地信号线接收而不会被 内部的信号线接收。 版图中可以采用同样的方法。想办法用360度的屏 蔽包围信号线。
M3 M2 GND M2 GND M2 M3 GND M2 GND
signal
signals
M3
M3
surrounded by shielding
6
利用常识解决噪声的方法
回到自己的屋里: 不仅在噪声模块周围放置保护带,把安静 模块也用保护带围起来。 双重隔离
noisy block
quiet block
7
利用常识解决噪声的方法
关闭所有的门窗: 要用保护带包围整个噪声模块,而不要留 有任何缝隙。因有些噪声会从此处溜出去。
8
利用常识解决噪声的方法
differential A-B
signal through line A
paired lines will be hit by the same noise spikes.
12
导线方面的解决方法
去耦供电轨线: 供电轨线上放置尺寸很大的去耦电容。 闯入供电轨线的任何噪声首先被吸收到接 地线,只有很少的噪声能越过这个电容进入电 路。
和祖母聊天 – 摇滚乐队 – 调小声音 – 乐队回屋 关好门窗 - 和祖母回屋 (搬家) (拒绝回屋 - 司法长官 – 定时排练 – 轮换错开)
2
利用常识解决噪声的方法
调小音量:
在电路中相当于减小信号摆幅。 在一个混合信号芯片中,主要是让数字部分保持安 静,即采用电压摆幅小的数字逻辑。 电压摆幅基本上不属于版图问题,但可在某些时候 也可以成为版图问题,如可以选择电压摆幅小的库。
《噪声基础知识》PPT课件

整理课件
37
1.单极子
媒质中流入的质量或热量不均匀时形成单极子 源声器(或叫做简单声源)。
W m ~2 V 4 D 2 0 c 02 V 3 D 2 M 0
V 是喷注速度;D 是喷口直径;M 是流动马赫数; 是喷 注密度; 0 是环境媒质密度;c 0 是环境媒质中的声速。
整理课件
38
在实际生活中,有不少近似单声源辐射的例子,如笛子 的发声孔,汽笛和火焰的燃烧吼声。氢弹爆炸是世界上最大 的单极子源。
W q~2 V 8 D 2 0 c 0 52 V 3 D 2 M 5 0
整理课件
41
第五章 风机噪声
5.1 噪声分类 5.2 旋转噪声和湍流噪声 5.3 轴流风机的声功率 5.4 降低轴流风机噪声的途径 5.5 离心风机的声功率
整理课件
42
5.1 噪声的分类
机械噪声 电磁噪声 空气动力性噪声
整理课件
24
•
声波透过孔洞
整理课件
25
声波的干涉
复杂声波的干涉是声波的重要特性。当空间存 在两个以上声源分别发出的声波时,每个声波不因 为其他声波的存在而改变其传播规律。
空间任一点的声能是各个声波分量在该点激发 振动的和,这就是叠加原理。当频率相同或接近的 两个或两个以上的声波叠加时,在叠加区的不同位 置会出现加强或减弱的现象,称为声波干涉。
2.改进工艺和操作方式。
3.提高加工精度和装配质量。
1.4.2 传输途径中的控制是最常用的办法,机器已经完成, 再从声源上控制就受局限,途径上控制大有可为。如消声、 隔声、隔振、减振等。
1.4.3 在机器多而人少或降低机器噪声不现实或不经济的情 况下,对受者的保护是个重要手段。
物理学教程(第二版)上册课后答案第六章
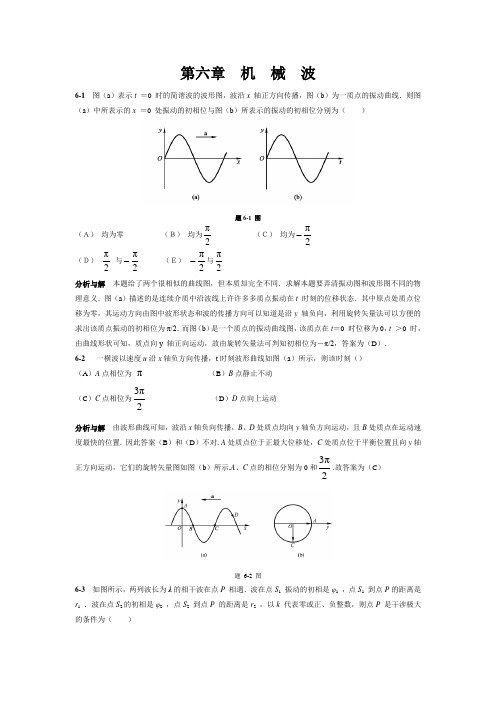
第六章 机 械 波6-1 图(a )表示t =0 时的简谐波的波形图,波沿x 轴正方向传播,图(b )为一质点的振动曲线.则图(a )中所表示的x =0 处振动的初相位与图(b )所表示的振动的初相位分别为( )题6-1 图(A) 均为零 (B) 均为2π (C) 均为2π- (D) 2π 与2π- (E) 2π-与2π 分析与解 本题给了两个很相似的曲线图,但本质却完全不同.求解本题要弄清振动图和波形图不同的物理意义.图(a )描述的是连续介质中沿波线上许许多多质点振动在t 时刻的位移状态.其中原点处质点位移为零,其运动方向由图中波形状态和波的传播方向可以知道是沿y 轴负向,利用旋转矢量法可以方便的求出该质点振动的初相位为π/2.而图(b )是一个质点的振动曲线图,该质点在t =0 时位移为0,t >0 时,由曲线形状可知,质点向y 轴正向运动,故由旋转矢量法可判知初相位为-π/2,答案为(D ). 6-2 一横波以速度u 沿x 轴负方向传播,t 时刻波形曲线如图(a )所示,则该时刻()(A )A 点相位为π (B )B 点静止不动 (C )C 点相位为2π3 (D )D 点向上运动分析与解 由波形曲线可知,波沿x 轴负向传播,B 、D 处质点均向y 轴负方向运动,且B 处质点在运动速度最快的位置. 因此答案(B )和(D )不对. A 处质点位于正最大位移处,C 处质点位于平衡位置且向y 轴正方向运动,它们的旋转矢量图如图(b )所示.A 、C 点的相位分别为0和2π3.故答案为(C )题 6-2 图6-3 如图所示,两列波长为λ的相干波在点P 相遇.波在点S 1 振动的初相是φ1 ,点S 1 到点P 的距离是r 1 .波在点S 2的初相是φ2 ,点S 2 到点P 的距离是r 2 ,以k 代表零或正、负整数,则点P 是干涉极大的条件为( )()()()()()()π2/π2A π2/π2A π2A πA 211212121212k r r k r r k k r r =-+-=-+-=-=-λϕϕλϕϕϕϕ 分析与解 P 是干涉极大的条件为两分振动的相位差π2Δk =,而两列波传到P 点时的两分振动相位差为()λϕϕϕ/π2Δ1212r r ---=,故选项(D )正确.题6-3 图6-4 在波长为λ的驻波中,两个相邻波腹之间的距离为( )(A ) 4λ (B ) 2λ(C ) 43λ (D ) λ分析与解 驻波方程为t λx A y v π2cos π2cos 2=,它不是真正的波.其中λx A π2cos 2是其波线上各点振动的振幅.显然,当Λ,2,1,0,2=±=k k x λ时,振幅极大,称为驻波的波腹.因此,相邻波腹间距离为2λ.正确答案为(B ).6-5 一横波在沿绳子传播时的波动方程为()x y ππ5.2cos 20.0-=,式中y 的单位为m ,t 的单位为s .(1) 求波的振幅、波速、频率及波长;(2) 求绳上质点振动时的最大速度;(3) 分别画出t =1s 和t =2 s 时的波形,并指出波峰和波谷.画出x =1.0 m处质点的振动曲线并讨论其与波形图的不同. 分析 (1) 已知波动方程(又称波函数)求波动的特征量(波速u 、频率υ、振幅A 及波长λ等),通常采用比较法.将已知的波动方程按波动方程的一般形式⎥⎦⎤⎢⎣⎡+⎪⎭⎫ ⎝⎛=0cos ϕωu x t A y μ书写,然后通过比较确定各特征量(式中ux 前“-”、“+”的选取分别对应波沿x 轴正向和负向传播).比较法思路清晰、求解简便,是一种常用的解题方法.(2) 讨论波动问题,要理解振动物理量与波动物理量之间的内在联系与区别.例如区分质点的振动速度与波速的不同,振动速度是质点的运动速度,即v =d y /d t ;而波速是波线上质点运动状态的传播速度(也称相位的传播速度、波形的传播速度或能量的传播速度),其大小由介质 的性质决定.介质不变,波速保持恒定.(3) 将不同时刻的t 值代入已知波动方程,便可以得到不同时刻的波形方程y =y (x ),从而作出波形图.而将确定的x 值代入波动方程,便可以得到该位置处质点的运动方程y =y (t ),从而作出振动图.解 (1) 将已知波动方程表示为()[]()m 5.2/π5.2cos 20.0x t y -=与一般表达式()[]0cos ϕω+-=u x t A y /比较,可得0s m 52m 20001=⋅==-ϕ,.,.u A则 m 0.2/,Hz 25.1π2/====v u λωv(2) 绳上质点的振动速度()[]()1s m 5.2/π5.2sin π5.0d /d -⋅--==x t t y v 则 1max s m 57.1-⋅=v(3) t =1s 和t =2s 时的波形方程分别为()()()()m ππ5cos 20.0m ππ5.2cos 20.021x y x y -=-=波形图如图(a )所示.x =1.0m 处质点的运动方程为 ()()m π5.2cos 20.0t y -=振动图线如图(b )所示.波形图与振动图虽在图形上相似,但却有着本质的区别.前者表示某确定时刻波线上所有质点的位移情况,而后者则表示某确定位置的一个质点,其位移随时间变化的情况.题6-5 图6-6 波源作简谐运动,其运动方程为()m t πcos240100.43-⨯=y ,它所形成的波形以30m·s-1 的速度沿一直线传播.(1) 求波的周期及波长;(2) 写出波动方程.分析 已知波源运动方程求波动物理量及波动方程,可先将运动方程与其一般形式进行比较,求出振幅A 、角频率ω及初相φ0 ,而这三个物理量与波动方程的一般形式()[]0cos ϕω+-=u x t A y /中相应的三个物理量是相同的.再利用题中已知的波速u 及公式ω=2πν =2π/T 和λ=u T 即可求解.解 (1) 由已知的运动方程可知,质点振动的角频率1s π240-=ω.根据分析中所述,波的周期就是振动的周期,故有 s 1033.8/π23-⨯==ωT波长为λ=uT =0.25 m(2) 将已知的波源运动方程与简谐运动方程的一般形式比较后可得A =4.0 ×10-3m ,1s π240-=ω,φ0 =0故以波源为原点,沿x 轴正向传播的波的波动方程为 ()[]()()m π8π240cos 100.4/cos 30x t u x t ωA y -⨯=+-=-6-7 波源作简谐运动,周期为0.02s,若该振动以100m·s-1 的速度沿直线传播,设t =0时,波源处的质点经平衡位置向正方向运动,求:(1) 距波源15.0m 和5.0 m 两处质点的运动方程和初相;(2) 距波源为16.0 m 和17.0m 的两质点间的相位差.分析 (1) 根据题意先设法写出波动方程,然后代入确定点处的坐标,即得到质点的运动方程.并可求得振动的初相.(2) 波的传播也可以看成是相位的传播.由波长λ的物理含意,可知波线上任两点间的相位差为Δφ=2πΔx /λ.解 (1) 由题给条件1s m 100s 020-⋅==u T ,.,可得m 2;s m π100/π21==⋅==-uT λT ω当t =0 时,波源质点经平衡位置向正方向运动,因而由旋转矢量法可得该质点的初相为φ0 =-π/2(或3π/2).若以波源为坐标原点,则波动方程为()[]2/π100π100cos --=x/t A y距波源为x 1 =15.0 m 和x 2 =5.0 m 处质点的运动方程分别为()()π5.5t π100cos π15.5t π100cos 21-=-=A y A y它们的初相分别为φ10 =-15.5π和φ20 =-5.5π(若波源初相取φ0=3π/2,则初相φ10 =-13.5π,φ20 =-3.5π.)(2) 距波源16.0m 和17.0 m 两点间的相位差()π/π2Δ1212=-=-=λϕϕϕx x6-8 图示为平面简谐波在t =0 时的波形图,设此简谐波的频率为250Hz ,且此时图中质点P 的运动方向向上.求:(1) 该波的波动方程;(2) 在距原点O 为7.5 m 处质点的运动方程与t =0 时该点的振动速度.分析 (1) 从波形曲线图获取波的特征量,从而写出波动方程是建立波动方程的又一途径.具体步骤为:1. 从波形图得出波长λ、振幅A 和波速u =λυ;2. 根据点P 的运动趋势来判断波的传播方向,从而可确定原点处质点的运动趋向,并利用旋转矢量法确定其初相φ0 .(2) 在波动方程确定后,即可得到波线上距原点O 为x 处的运动方程y =y (t ),及该质点的振动速度υ=d y /d t .解 (1) 从图中得知,波的振幅A =0.10 m ,波长λ=20.0m ,则波速u =λυ=5.0 ×103 m·s-1 .根据t =0 时点P 向上运动,可知波沿Ox 轴负向传播,并判定此时位于原点处的质点将沿Oy 轴负方向运动.利用旋转矢量法可得其初相φ0 =π/3.故波动方程为()[]()[]()m 3/π5000/π500cos 10.0/cos 0++=++=x t u x t A y ϕω(2) 距原点O 为x =7.5m 处质点的运动方程为 ()()m 12π13π5000.10cos y /t +=t =0 时该点的振动速度为 ()-10s m 40.6/12π13sin π50/d d ⋅=-===t t y v题6-8 图6-9 一平面简谐波以速度1s m 08.0-⋅=u 沿Ox 轴正向传播,图示为其在t =0 时刻的波形图,求(1)该波的波动方程;(2)P 处质点的运动方程.题6-9 图分析 (1) 根据波形图可得到波的波长λ、振幅A 和波速u ,因此只要求初相φ,即可写出波动方程.而由图可知t =0 时,x =0 处质点在平衡位置处,且由波的传播方向可以判断出该质点向y 轴正向运动,利用旋转矢量法可知φ=-π/2.(2) 波动方程确定后,将P 处质点的坐标x 代入波动方程即可求出其运动方程y P =y P (t ).解 (1) 由图可知振幅A =0.04 m, 波长λ=0.40 m, 波速u =0.08m·s-1 ,则ω=2π/T =2πu /λ=(2π/5)s-1 ,根据分析已知φ=-π/2,因此波动方程为()m 2π08.05π20.04cos y ⎥⎦⎤⎢⎣⎡-⎪⎭⎫ ⎝⎛-=x t(2) 距原点O 为x =0.20m 处的P 点运动方程为 ()m 2π52π0.04cos y ⎥⎦⎤⎢⎣⎡+= *6-10 一平面简谐波,波长为12 m ,沿O x 轴负向传播.图(a )所示为x =1.0 m 处质点的振动曲线,求此波的波动方程.题6-10图分析 该题可利用振动曲线来获取波动的特征量,从而建立波动方程.求解的关键是如何根据图(a ) 写出它所对应的运动方程.较简便的方法是旋转矢量法.解 由图(a )可知质点振动的振幅A =0.40 m,t =0 时位于x =1.0 m 处的质点在A /2 处并向Oy 轴正向移动.据此作出相应的旋转矢量图(b ),从图中可知3/π0-='ϕ.又由图(a )可知,t =5 s 时,质点第一次回到平衡位置,由图(b )可看出ωt =5π/6,因而得角频率ω=(π/6) rad .s -1 .由上述特征量可写出x =1.0 m 处质点的运动方程为 ()m 3π6π0.04cos y ⎥⎦⎤⎢⎣⎡-=t 将波速1s m 0.1π2//-⋅===ωλT λu 及x =1.0 m 代入波动方程的一般形式()[]0cos ϕω++=u x t A y /中,并与上述x =1.0 m 处的运动方程作比较,可得φ0 =-π/2,则波动方程为()()m 2π10/6π0.04cos ⎥⎦⎤⎢⎣⎡-+=x t y 6-11 平面简谐波的波动方程为()x t y π2π4cos 08.0-=,式中y 和x 的单位为m ,t 的单位为s,求:(1) t =2.1 s 时波源及距波源0.10m 两处的相位;(2) 离波源0.80 m 及0.30 m 两处的相位差. 解 (1)将t =2.1 s 和x =0 代入题给波动方程,可得波源处的相位π4.81=ϕ将t =2.1 s 和x ′=0.10 m 代入题给波动方程,得0.10 m 处的相位为π2.82=ϕ(2)从波动方程可知波长λ=1.0 m .这样,x 1=0.80 m 与x 2=0.30 m 两点间的相位差πΔπ2Δ=⋅=λϕx6-12 为了保持波源的振动不变,需要消耗4.0 W 的功率.若波源发出的是球面波(设介质不吸收波的能量).求距离波源5.0 m 和10.0 m 处的能流密度.分析 波的传播伴随着能量的传播.由于波源在单位时间内提供的能量恒定,且介质不吸收能量,故对于球面波而言,单位时间内通过任意半径的球面的能量(即平均能流)相同,都等于波源消耗的功率P .而在同一个球面上各处的能流密度相同,因此,可求出不同位置的能流密度I =P /S .解 由分析可知,半径r 处的能流密度为2π4/r P I =当r 1 =5.0 m 、r 2 =10.0m 时,分别有22211m W 1027.1π4/--⋅⨯==r P I22222m W 1027.1π4/--⋅⨯==r P I6-13 两相干波波源位于同一介质中的A 、B 两点,如图(a )所示.其振幅相等、频率皆为100 Hz ,B 比A 的相位超前π.若A 、B 相距30.0 m ,波速为u =400 m·s -1 ,试求AB 连线上因干涉而静止的各点的位置.题6-13 图分析 两列相干波相遇时的相位差λϕϕϕr Δπ2Δ12--=.因此,两列振幅相同的相干波因干涉而静止的点的位置,可根据相消条件()π12Δ+=k ϕ获得.解 以A 、B 两点的中点O 为原点,取坐标如图(b )所示.两波的波长均为λ=u /υ=4.0 m .在A 、B 连线上可分三个部分进行讨论.1. 位于点A 左侧部分()π14π2ΔA B A B -=---=r r ϕϕϕ因该范围内两列波相位差恒为2π的整数倍,故干涉后质点振动处处加强,没有静止的点.2. 位于点B 右侧部分()π16π2ΔA B A B =---=r r ϕϕϕ显然该范围内质点振动也都是加强,无干涉静止的点.3. 在A 、B 两点的连线间,设任意一点P 距原点为x .因x r -=15B,x r +=15A ,则两列波在点P的相位差为 ()()π1/π2ΔA B A B +=---=x r r λϕϕϕ根据分析中所述,干涉静止的点应满足方程()()π152π1+=+k x x得 ()2,...1,0,k m 2±±==k x因x ≤15 m ,故k ≤7.即在A 、B 之间的连线上共有15 个静止点.6-14 图(a )是干涉型消声器结构的原理图,利用这一结构可以消除噪声.当发动机排气噪声声波经管道到达点A 时,分成两路而在点B 相遇,声波因干涉而相消.如果要消除频率为300 Hz 的发动机排气噪声,则图中弯管与直管的长度差Δr =r 2 -r 1 至少应为多少? (设声波速度为340 m·s -1 )题6-14 图分析 一列声波被分成两束后再相遇,将形成波的干涉现象.由干涉相消条件,可确定所需的波程差,即两管的长度差Δr .解 由分析可知,声波从点A 分开到点B 相遇,两列波的波程差Δr =r 2 - r 1 ,故它们的相位差为()λλϕ/Δπ2/π2Δ12r r r =-=由相消静止条件Δφ=(2k +1)π,(k =0,±1,±2,…)得 Δr =(2k +1)λ/2根据题中要求令k =0 得Δr 至少应为m 57022.//===∆v u r λ讨论 在实际应用中,由于噪声是由多种频率的声波混合而成,因而常将具有不同Δr 的消声单元串接起来以增加消除噪声的能力.图(b )为安装在摩托车排气系统中的干涉消声器的结构原理图.*6-15 如图所示,x =0 处有一运动方程为t A y ωcos =的平面波波源,产生的波沿x 轴正、负方向传播.MN 为波密介质的反射面,距波源3λ/4.求:(1) 波源所发射的波沿波源O 左右传播的波动方程;(2) 在MN 处反射波的波动方程;(3) 在O ~MN 区域内形成的驻波方程,以及波节和波腹的位置;(4) x >0区域内合成波的波动方程.题6-15 图分析 知道波源O 点的运动方程t A y ωcos =,可以写出波沿x 轴负向和正向传播的方程分别为()u x t A y /+=ωcos 1和()u x t A y /-=ωcos 2.因此可以写出y 1 在MN 反射面上P 点的运动方程.设反射波为y 3 ,它和y 1 应是同振动方向、同振幅、同频率的波,但是由于半波损失,它在P 点引起的振动和y 1 在P 点引起的振动反相.利用y 1 在P 点的运动方程可求y 3 在P 点的运动方程,从而写出反射波y 3 .在O ~MN 区域由y 1 和Y 3 两列同频率、同振动方向、同振幅沿相反方向传播的波合成形成驻波.在x >0区域是同传播方向的y 2 和y 3 合成新的行波.解 (1) 由分析已知:沿左方向和右方向传播的波动方程分别为()u x t A y /+=ωcos 1和()u x t A y /-=ωcos 2(2) y 1 在反射面MN 处引起质点P 振动的运动方程⎪⎭⎫ ⎝⎛-=⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-+=2π3π2cos 43π2π2cos 1t T A t T A y pλλ 因半波损失反射波y 3 在此处引起的振动为⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛+-=2ππ2cos ππ23π2cos 3t T A t T A y p设反射波的波动方程为()ϕλ+-=/π2/π2cos 3x T t A y ,则反射波在x =-3λ/4处引起的振动为⎪⎭⎫ ⎝⎛++=ϕπ23π2cos 3t T A y p与上式比较得π2-=ϕ,故反射波的波动方程为⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛--=x λt TA x λt T A y π2π2cos π2π2π2cos 3 (3) 在O ~MN 区域由y 1 和y 3 合成的驻波y 4 为()⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛+=+=t T x λA x λt T A x λt T A y y x t y π2cos π2cos 2π2π2cos π2π2cos ,314 波节的位置:4/2/,2/ππ/π2λλk x k λx +=+=,取k =-1, -2,即x =-λ/4, -3λ/4 处为波节.波腹的位置:2/,π/π2λk x k λx ==,取k =0,-1,即x =0,-λ/2 处为波腹.(4) 在x >0 区域,由y 2 和y 3 合成的波y 5 为()⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-=+=x λt TA x λt T A x λt T A y y x t y π2π2cos 2π2π2cos π2π2cos ,325 这表明:x >0 区域内的合成波是振幅为2A 的平面简谐波.6-16 如图(a )所示,将一块石英晶体相对的两面镀银作电极,它就成为压电晶体,两极间加上频率为ν的交变电压,晶片就沿竖直方向作频率为ν的驻波振动,晶体的上下两面是自由的,故而成为波腹.设晶片d =2.00 mm ,沿竖直方向的声速13s m 1074.6-⋅⨯=u,试问要激起石英片发生基频振动,外加电压的频率应是多少?分析 根据限定区域内驻波形成条件(如图(b )所示),当晶体的上下两面是自由的而成为波腹时,其厚度与波长有关系式 k k d λ2=成立,k 为正整数.可见取不同的k 值,得到不同的k λ,晶体内就出现不同频率k ν的波.对应k =1称为基频,k =2,3,4,…称为各次谐频.解 根据分析基频振动要求2λ=d ,于是要求频率Hz 10685.126⨯===d u u λν题 6-16 图6-17 一平面简谐波的频率为500 Hz ,在空气(ρ=1.3 kg·m -3 )中以u =340 m·s -1 的速度传播,到达人耳时,振幅约为A =1.0 ×10 -6 m .试求波在耳中的平均能量密度和声强.解 波在耳中的平均能量密度2622222m J 1042.6π221--⋅⨯===v A A ρωρω声强就是声波的能流密度,即23m W 10182--⋅⨯==.ωu I这个声强略大于繁忙街道上的噪声,使人耳已感到不适应.一般正常谈话的声强约1.0×10-6W·m -2 左右. 6-18 面积为1.0 m 2 的窗户开向街道,街中噪声在窗口的声强级为80 dB .问有多少“声功率”传入窗内? 分析 首先要理解声强、声强级、声功率的物理意义,并了解它们之间的相互关系.声强是声波的能流密度I ,而声强级L 是描述介质中不同声波强弱的物理量.它们之间的关系为L =lg (I /I 0 ),其中I 0 =1.0 ×10-12 W·m -2为规定声强.L 的单位是贝尔(B ),但常用的单位是分贝(dB ),且1 B =10 dB .声功率是单位时间内声波通过某面积传递的能量,由于窗户上各处的I 相同,故有P =IS .解 根据分析,由L =lg (I /I 0 )可得声强为I =10LI 0则传入窗户的声功率为 P =IS =10L I 0S =1.0 ×10-4 W6-19 一警车以25 m·s -1 的速度在静止的空气中行驶,假设车上警笛的频率为v =800 Hz .求:(1) 静止站在路边的人听到警车驶近和离去时的警笛声波频率;(2) 如果警车追赶一辆速度为15m·s -1 的客车,则客车上人听到的警笛声波的频率是多少? (设空气中的声速u =330m·s -1 )分析 由于声源与观察者之间的相对运动而产生声多普勒效应,由多普勒频率公式可解得结果.在处理这类问题时,不仅要分清观察者相对介质(空气)是静止还是运动,同时也要分清声源的运动状态. 解 (1) 根据多普勒频率公式,当声源(警车)以速度υs =25 m·s -1 运动时,静止于路边的观察者所接收到的频率为s u u vv υμ='警车驶近观察者时,式中υs 前取“-”号,故有Hz 6.8651=-='su u v v υ 警车驶离观察者时,式中υs 前取“+”号,故有 Hz 7.7432=+='s u u v v υ (2) 客车的速度为0υ=15 m·s -1 ,声源(警车)与客车上的观察者作同向运动时,观察者收到的频率为Hz 2.82603=--='su u v v υυ 6-20 蝙蝠在洞穴中飞来飞去,能非常有效地用超声波脉冲导航.假如蝙蝠发出的超声波频率为39 kHz ,当它以声速的401的速度朝着表面平直的岩壁飞去时,试求它听到的从岩壁反射回来的超声波频率为多少?分析 由题意可知,蝙蝠既是波的发出者,又是波的接收者.设超声波的传播速度为u .首先,蝙蝠是声源,发出信号频率为v ,运动速度为40s u =υ,岩壁是接收者,利用多普勒频率公式,即可求得岩壁接收到的信号频率v '.经岩壁反射后频率不变,即岩壁发射信号频率为v ',这时蝙蝠是波的接收者,其运动速度为400u =υ,再次利用多普勒频率公式,可求得蝙蝠接收到的信号频率v ''. 解 将蝙蝠看成波源,则由分析可知,岩壁接收到的信号频率为s υ-='u uvv ,在蝙蝠接收岩壁反射信号时,又将它看成接收者.则蝙蝠接收到的信号频率为kHz 41kHz 3940/1140/11/1/1s 0s 00=⨯-+=-+=-+='+=''v u u v u u v u u v υυυυυ。
噪声控制工程习题解答

环境噪声控制工程(第一版)(32学时)习题解答环境学院环境工程系主讲教师:高永华二 一 年十月第二篇 《噪声污染控制工程》部分第二章 习 题3.频率为500Hz 的声波,在空气中、水中和钢中的波长分别为多少? (已知空气中的声速是340 m/s ,水中是1483 m/s ,钢中是6100 m/s) 解:由 C = λf (见p8, 式2-2) λ空气= C 空气/f= 340/500 = 0.68 m λ水= C 水/f = 1483/500 = 2.966 m λ钢= C 钢/f = 6100/500 = 12.2 m6.在空气中离点声源2m 距离处测得声压p=0.6Pa ,求此处的声强I 、声能密度D 和声源的声功率W 各是多少?解:由 c p I e 02/ρ=(p14, 式2-18)= 0.62/415 (取20℃空气的ρc=415 Pa·s/m, 见p23)= 8.67×10-4 W/m 2202/c p D e ρ=(p14, 式2-17)= 0.62/415×340 (取20℃空气的ρc=415 Pa·s/m, c=340 m/s, 见p23)= 2.55×10-6 J/m 3对点声源,以球面波处理,则在离点声源2m 处波阵面面积为S=4πr 2=50.3 m 2, 则声源的声功率为: W=IS (p14, 式2-19) =8.67×10-4 W/m 2 × 50.3 m 2 =4.36×10-2 W11.三个声音各自在空间某点的声压级为70 dB 、75 dB 和65 dB ,求该点的总声压级。
解:三个声音互不相干,由n 个声源级的叠加计算公式:= 10×lg (100.1Lp1 + 100.1Lp2 +100.1Lp3) = 10×lg (100.1×70 +100.1×75 +100.1×65) = 10×lg (107 +107.5 +106.5) = 10×lg [106.5×(3.16+10+1)]= 65 + 11.5= 76.5 dB该点的总声压级为76.5 dB。
第6章(832)
第6章 测试技术在工程中的应用
在测量过程中,噪声总是与有用的信号联系在一起,为了
衡量噪声对有用信号的影响,引入信噪比(S/N)的概念。所
谓信噪比,是通道中有用信号成分与噪声信号成分之比。设有
用信号功率为PS,有用信号电压为US,噪声功率为PN,噪声电
压为UN,则有
S 10 lg PS 20 lg US
第6章 测试技术在工程中的应用
图6.4 (a) 串联式; (b) 并联式
第6章 测试技术在工程中的应用 图6.5 多点接地方式
第6章 测试技术在工程中的应用
2)
电气设备的某些部分与大地相连接可以起到抑制干扰的作 用。 例如, 金属屏蔽层接地可以避免电荷积累引起的静电效 应, 抑制变化电场的干扰;大功率电路的接地可减小电路对其 它电路的电磁冲击与噪声干扰;大型电子设备往往具有很大的 对地分布电容,合理选择接地点可以削弱分布电容的影响等。
在测试系统设计、组装和使用中,主要通过屏蔽接地、 隔离、合理布线、灭弧、滤波和采用专门电路与器件等措施 抑制干扰与噪声。
第6章 测试技术在工程中的应用
6.1.2 屏蔽、接地、隔离、 1. 1) 屏蔽一般是指电磁屏蔽。电磁屏蔽就是利用电导率和磁导
率高的材料制成封闭的容器,将受扰的电路置于该容器中, 从而抑制该容器外的干扰与噪声对容器内电路的影响。也可以 将产生干扰与噪声的电路置于该容器之中,从而减弱或消除其 对外部电路的影响。
U2 1
1 1
U1
jCZ 2
(6.2)
第6章 测试技术在工程中的应用
2)
互感耦合是由电路间的寄生互感造成的,又称电感性耦
合,其简化电路模型如图6.1(b)所示。图中,I1为a、b间干扰 源的电流源,Z2为c、d间受扰电路的等效输入阻抗,M为干扰
第六章 声环境影响评价剖析
一测点距平直公路中心线20m,测得等效声级68dB,试 求距中心线200m处的等效声级。若在路旁建一医院,医院
位于声环境质量1类功能区内,在不考虑背景噪声情况下,
问至少应距公路中心线多远处方能噪声达标? 解:设公路为无限长线声源 △L=10lg(r2/r1)=10lg(200/20)=10dB L200m=68-10=58dB
质量标准
《铁路边界噪声限值及测量方法》(GB12525-1990)
《社会生活环境噪声排放标准》(GB22337-2008)
*《声环境质量标准》 (GB3096-2008)
1. 声环境功能区划 • 0类标准:康复疗养区等特别需要安静的区域。 • 1类标准:以居民住宅、医疗卫生、文化教育、科研设计、 行政办公为主要功能,需要保持安静的区域。 • 2类标准:以商业金融、集市贸易为主要功能,或者居住、 商业工业混杂,需要维护住宅安静的区域。
Abar 1 10 lg 3 20 N 1
(3)绿化林带噪声衰减
阔叶林地带的声衰减值 频率 (Hz) 衰减值 250 1 500 2 1000 3
单位:dB/10 m 2000 4 4000 4.5 8000 5
附加衰减
在下列条件下考虑地面效应的影响: 预测点距离声源50m以上; 声源距地面高度和预测点距地面高度的平均值小于30m; 声源与预测点之间的地坪被草地、灌木等覆盖。
1000
α——每1km空气吸收系数,dB;
r——声波传播距离,m。
声屏障衰减
• 有限长薄屏障在点声源中
菲涅耳数N1,2,3 2(SO+OP-SP)
P
1 1 1 Abar 10 lg 3 20 N 3 20 N 3 20 N 1 2 3
高频第6章_噪声、干扰及其抑制
第
噪声温度( 噪声温度(一)
声 噪声温度 一 温度 噪声 噪
第 二 节 : 噪 声 电 路 的 计 算
温度 Te 温度 Te
ue2
噪声
Rs
噪声温度
噪声温度( 噪声温度(二)
PnA Te = Apm k f
低频噪声
噪声
第 一 节 : 元 器 件 内 部 噪 声 产 生 的 原 因 及 其 表 示 方 法
分配噪声
噪声 分配 噪声 噪声
| α |2 Si ( f ) = 2qI C 1 α0 | α |2 2 or dicp = 2qIC 1 df α0
分配噪声
I C、I B 分配
第 四 节
电 干扰 磁 干扰 来
的
方 合
的 的 来抑制干扰
: 减 小 元 器 件 外 部 干 扰 提 高 输 出 信 噪 比 的 方 法
公共地线连接不当造成的干扰及其抑制( 公共地线连接不当造成的干扰及其抑制(一)
的连接
的
的
一 的 的
公共地线
第 四 节
线 的 不 的
不 的
不 干扰 扰
Z s , R5 , R6
热
热噪声 噪声
表 示 方 法
噪声
热噪声(二) 热噪声(
e = 4kTRf
2 n
f
热噪声
R
R
第 一 节 : 元 器 件 内 部 噪 声 产 生 的 原 因 及 其 表 示 方 法
i = 4kTGf
2 n
G = 1/ R
散弹噪声
噪声
散弹噪声
散弹噪声 噪声 噪声
噪声学-复习整理
噪声学-复习整理环境噪声控制⼯程第⼀章:绪论⼀、环境噪声标准分为以下三种:1.城市区域环境噪声标准GB3096-93;2.⼯业企业⼚界标准GB12348-90;3.⼯业企业⼚区各类场所噪声限制(噪声卫⽣标准)GBJ87-85。
掌握1和2的功能区分类等,如下:第⼆章:声波的物理基础⼀、频谱频谱图:把某⼀信号中所包含的频率成分,按其幅值或相位作为频率的函数作出的分布图,称作该信号的频谱图。
分:1.离散谱:2.连续谱3.复合谱(见书11)⼆、频程把某⼀范围的频率划分成若⼲⼩的频率段,每⼀段以它的中⼼频率为代表,然后求出声信号在各频率段的中⼼频率上的幅值,作为⼀种频谱,将这样分出来的频率段叫频程。
在划分频程时,使每⼀个频率段的下限频率与上限频率的⽐值为确定的常数。
掌握概念:倍频程和1/3倍频程(见书11)三、声强级、声压级、声功率级定义声强级:⼀个声⾳的声强级L I是该声⾳的声强与基准声强之⽐的常⽤对数乘以10,以分贝计,即: 基准声强I0在空⽓中为10-12W/m2,它是1000Hz声⾳的可听阈声强。
声压级:某声压p与基准声压p0之⽐的常⽤对数乘以20称为该乘以的声压级,以分贝计,即: 基准声压p0在空⽓中为2×10-5Pa。
声功率级:某声功率W与基准声功率W0之⽐的常⽤对数乘以10称为该乘以的声功率级,以分贝计,即:基准声压p0在空⽓中为10-12W。
四、声压级的叠加(计算)有n个不同的噪声源互不相⼲,其中第i个噪声源在某测点处测得的声压级为Lpi,当n个噪声源同时发声,在该点处产⽣的总声压级为:注意:2个⼤⼩相等的噪声叠加后,总声压级⽐原来单独时⾼3(dB)五、声波的反射和透射反射系数r p:反射声压幅值与⼊射声压幅值之⽐。
r p⼤,则吸声差,r值⼩的材料称为吸声材料。
声压透射系数t p:透射声压幅值与⼊射声压幅值之⽐。
t p⼤,则隔声差,t p值⼩的材料称为隔声材料。
六、声传播中的距离衰减(计算)点源:计算从距离r1传播到距离r2时,声强级或声压级衰减量△L,则有:连续线声源:当传播距离从r0⾄r2时,声压级或声强级的衰减量为:第三章:噪声基本评价量⼀、响度级以1KHz纯⾳为基准声⾳,任何声⾳如果听起来和某个1KHz纯⾳⼀样响,那么这个1KHz纯⾳声压级的分贝值就是该声⾳的响度级,单位phon。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第6章环境噪声及其控制随着工业和交通运输的发展,人口迅猛膨胀,噪声对环境质量的影响日趋严重。
据不完全统计,近年来向环境保护部门写信或控告的污染事件中,噪声事件所占的比重已上升到第一位。
噪声不但会影响人的正常生活、学习和工作,还会危害人体健康。
因此,降低周围环境的噪声,防止噪声的危害,已成为人们的迫切愿望。
6.1 噪声污染6.1.1 噪声的定义一般认为凡是不需要的,使人厌烦并对人类生活和生产有妨碍的声音都是噪声(noise)。
因此,它不单独取决于声音的物理性质,而且和人类的生活状态有关。
例如,听音乐会时,除演员和乐队的声音外,其他都是噪声;但当睡眠时,再悦耳的音乐也是噪声。
看来,要对噪声下一个确切的定义是较难的,但是,作为感觉公害,归纳起来,噪声大致可分为四类:(1) 过响声。
如喷气发动机发出的轰隆声。
(2) 妨碍声。
此种声音虽不太响,但它妨碍人的交谈、思考、学习、睡眠和休息。
(3) 不愉快声。
如摩擦声、刹车声均属此类。
(4) 无影响声。
日常生活中,人们习以为常的声音,如湖外风吹树叶的沙沙声等。
由于噪声会妨碍人的休息和健康、降低工作效率,因此它对周围环境造成的不良影响叫噪声污染(noise pollution)。
6.1.2 噪声的特征由于噪声属于感觉公害,所以它与其他由有毒物质引起的公害不同,与大气污染、水污染相比,有以下四个特点。
(1) 噪声是人们不需要的声音的总称,因此一种声音是否属于噪声完全由判断者心理和生理上的因素所决定。
对于某人喜欢的声音,对于另外一个人是噪声的情况是很多的,例如优美的音乐对于正在思考的人却是噪声。
所以,可以说任何声音都可以成为噪声。
(2) 噪声具有局部性。
声音在空气中传播时衰减很快,它不像大气污染和水污染影响面广,而是带有局部的特点。
但是在某些情况下,噪声的影响范围很广,例如发电厂高压排气放空,其噪声可能干扰周围几十公里内居民生活的安宁。
(3) 噪声污染属物理污染,在环境中不留下任何物质,也不积累,随声源的停止噪声也随即消失。
(4) 噪声污染一般不会直接致命或致病,它的危害是间接的和慢性的。
6.1.3 噪声的分类按噪声的来源,可分为工业噪声、交通噪声和生活噪声。
按噪声产生的机理,工业交通噪声又可分为空气动力性噪声、机械性噪声和电磁性噪声;生活噪声又可分为电声性噪声、声乐性噪声和人类语言性噪声。
(1) 空气动力性噪声:这类噪声是高速气流、不稳定气流中由于涡流或压力的突变引起了气体的振动而产生的。
例如通风机、鼓风机、空压机、燃气轮机、锅炉排气放空等所产生的噪声都属于这一类。
(2) 机械性噪声:这类噪声是在撞击、摩擦和交变的机械力作用下部件发生振动而产生的。
例如织布机、球磨机、破碎机、电锯、汽锤、打桩机等产生的噪声都属于这一类。
(3) 电磁性噪声:这类噪声是由于磁场脉动、磁场伸缩引起电器部件振动而产生的。
例如电动机、变压器等产生的噪声属于此类。
(4) 电声性噪声:此类噪声是由于电-声转换而产生的。
例如广播、电视、收录机、电话机、电子计算机等产生的噪声属于此类。
其余几类噪声是我们日常生活中经常遇到的,在此不一一介绍了。
6.1.4 噪声的危害40dB是正常的环境声音,一般被认为是噪声的卫生标准。
在此以上便是有害的噪声,它影响睡眠和休息、干扰工作、妨碍谈话、使听力受损伤,甚至引起心血管系统、神经系统、消化系统等方面的疾病。
归纳起来,噪声的危害主要表现在以下几个方面:1.干扰睡眠睡眠是人消除疲劳、恢复体力和维持健康的一个重要条件。
但是噪声会影响人的睡眠质量和数量,老年人和病人对噪声干扰更为敏感。
当睡眠受干扰而辗转不能入睡时,就会出现呼吸频繁、脉搏跳动加剧、神经兴奋等现象,第二天会觉得疲劳、易累,从而影响工作效率。
久而久之,就会引起失眠、耳鸣多梦、疲劳无力、记忆力衰退,在医学上为神经衰弱症侯群。
在高噪声环境下,这种病的发病率可达50%~60%以上。
2.损伤听力噪声可以使人造成暂时性的或持久的听力损伤,后者即耳聋。
一般说来,85dB以下的噪声不至于危害到听觉,而超过85dB可能发生危险。
表6-1列出不同噪声级下长期工作时,耳聋发病率的统计情况。
表6-1 工作40年后噪声性耳聋发病率(%)由表可见,90dB的噪声,耳聋发病率明显增加。
但是,即使高至90dB的噪声,也只能产生暂时性的病患,休息后即可恢复。
因此噪声的危害,关键在于它的长期作用。
3.对人体的生理影响一些实验表明,噪声会引起人体的紧张反应,刺激肾上素的分泌,因而引起心率改变和血压升高。
可以说,20世纪生活中的噪声,是心脏病恶化和发病率增加的一个重要原因。
噪声会使人的唾液、胃液分泌减少,胃酸降低,从而导致胃溃疡和十二指肠溃疡。
一些研究指出,某些喧闹的工业企业里,溃疡症的发病率比安静环境的高5倍。
噪声对人的内分泌机能也会产生影响。
在高环境噪声下,会使一些女性的性机能紊乱,月经失调,孕妇流产率增高。
近年还有人指出,噪声是刺激癌症的病因之一。
有些生理学家和肿瘤学家指出:人的细胞是产生热量的器官,当人受到噪声或各种神经刺激时,血液中的肾上腺素显著增加,促使细胞产生的热能增加,而癌细胞因为热能的增高而有明显的增殖倾向,特别是在睡眠当中。
4.对儿童和胎儿的影响在噪声环境下,儿童的智力发展缓慢。
有人作过调查,吵闹环境下,儿童智力发育比安静环境中的低20%。
噪声也会对胎儿产生有害影响。
研究表明,噪声使母体产生紧张反应,会引起子宫血管收缩,以至影响供给胎儿发育所必须的养料和氧气。
有人对机场附近居民的一个初步研究发现,噪声与胎儿畸形有关。
此外,噪声还影响胎儿的体重。
有人发现,吵闹区婴儿体重轻的比例较高。
5. 对动物的影响强噪声会使鸟类的羽毛脱落,不下蛋,甚至内出血,最终死亡。
60年代初,美国F104喷气机作超声速飞行实验,地点是俄克拉荷马市上空,飞行高度为10000m ,每天飞跃8次,共飞行6个月。
结果,在飞机轰隆声的作用下,一个农场的10000只鸡被轰声杀死6000只。
6. 对建筑物的损害50年代曾有报道,一架以每小时1100km 的速度(亚音速)飞行的飞机,做60m 的低空飞行时,噪声使地面的一幢楼房遭到破坏。
在美国统计的3000件喷气飞机使建筑物受损害的事件中,抹灰开裂的占43%,损坏的占32%,墙开裂的占15%,瓦损坏的占6%。
此外,由于飞机噪声造成的经济损失,1968年约为40~185亿美元,1978年约为60~277亿美元。
由于汽车、飞机等与日俱增,噪声污染已引起人们的高度重视。
控制噪声污染已成为当务之急。
这里有两方面的问题需要解决,一是控制到什么程度,二是如何控制。
6.2 噪声的评价与测量6.2.1 噪声的物理度量空气中传播的声是一种疏密波,描述波动的三个物理量是波长λ(m)、频率ƒ(Hz)和声速C (m/s),它们之间的关系是:C =λf (6-1)声音音调的高低取决于声波的频率,频率高的声音叫高音,频率低的声音叫低音。
人能听到的声音的频率范围上20~20000Hz ,而对频率在3000~4000Hz 的声音最为敏感。
对噪声的量度,主要有噪声强弱的量度和噪声频谱的分析。
前者主要包括声强和声强级、声压和声压级、声功率和声功率级。
1. 声强与声强级声波具有能量,声波的传播过程实质就是声振动能量的传播过程。
垂直于声波传播方向上,单位时间内通过单位面积的声能量称为声强(sound intensity),用符号I 表示,单位是W/m 2。
很显然,声强越大表示声音越强。
听力正常的年轻人对频率为1000Hz 的纯音的听觉范围是10-12~10W/m 2,高限(痛阈)和低限(听阈)之间相差1013倍。
下面要提到的声压和声功率等参量变化范围也很大,所以,用线性标度来表示这些量是不方便的,而且人的听觉机构对声音大小的感觉不是与声强或声压的绝对值成线性关系,而是成对数关系的。
因此,常用对数标度来表示声强、声压或声功率的大小。
由于对数的自变量是无量纲的,用对数标度必须先选定基准量(或称参考量),然后取被量度的量与基准量比值的对数值,这个对数值被称为被量度量的“级”。
“级”的单位是贝尔,贝尔的1/10称为分贝,用符号dB 表示。
下式表示的量L 1就称为声强级(sound intensity level):01lg 10I IL = (6-2)式中:I 0—基准声强,I 0=10-12W/m 2。
2. 声压与声压级声波是疏密波,声波传播时,使空气发生压缩和膨胀的变化,压缩时使压强增加,膨胀时使压强减小。
设某体积元内,平衡时的静压强为P 0,声波作用下变化的压强为P ,则压强增量⊿P=P-P 0叫做声压(sound pressure)。
声压的单位与压强的相同,在国际单位制中压强的单位是Pa ,1Pa=1N/m 2。
声波在空气中传播时,声压P 实际上随时间迅速变化,对应于某一瞬时的声压叫做瞬时声压。
瞬时声压对时间取均方值(把瞬时声压平方,再对时间取平均,然后开方)称为有效声压。
在实际问题中,如不做说明,所谓声压指的是有效声压。
声压与声强的区别在于一个是压强,一个是能量。
在自由声场中,某点的声强I 与该点的有效声压P 间有如下关系:CP I ρ2= (6-3)式中:ρ—空气密度(kg/m);C —空气中声速(m/s)。
ρC 为空气的特性阻抗,其值随媒质的性质而异。
在P=1.013⨯105Pa 及15o C 时,空气的特性阻抗为400N ⋅s/m 3左右。
在噪声控制中,常用声压级(sound pressure level)衡量声音的强弱。
声压级L p 可用下式表示:L p =20lg(P/P 0) (6-4)式中:L p —对应于声压P 的声压级(dB);P 0—基准声压,P 0=2⨯10-5P a 。
人类的听觉对于1000Hz 的纯音,能感觉到的声压范围为2⨯10-5~20P a ,相应的声压级的范围为0~120dB 。
一些典型噪声源产生的声压级的大概值列于表6-2中。
表6-2 一些典型噪声源产生的声压级3. 声功率与声功率级每秒从声源放射出的声波能量叫声功率(sound power),用符号W 表示,单位是瓦(W)。
声功率的大小反映声源辐射声波本领的高低,是从能量角度描述噪声特性的重要物理量。
对应于声功率W 的声功率级(sound power level)L w (dB)可用下式表示:0lg 10W WL w = (6-5) 式中:W 0—基准声功率,W 0=10-12W 。
对于点声源发出的球对称的球面声波,如果声源的声功率为W ,距离声源r(m)处的声强为I (W/m 2),可得:W=SI=4πr 2I (6-6)式中:S —距离r 处的球面面积(m 2)。
由此可得声功率级L w 和声强级L I 之间的关系:L w =L I +20lgr+11.0 (6-7)根据式(6-3)和式(6-4)可得声功率L w 和声压级L P 间的关系:L w =L P +20lgr+11.0+10lg(Cρ400) (6-8) 6.2.2 噪声的评价声压和声压级是衡量声音强度的物理量,声压级越高,声音越强。
