高二立体几何大全
高二立体几何知识点
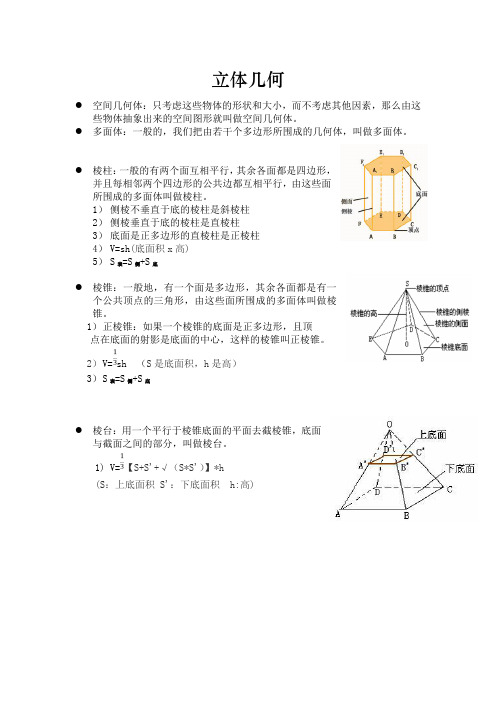
立体几何●空间几何体:只考虑这些物体的形状和大小,而不考虑其他因素,那么由这些物体抽象出来的空间图形就叫做空间几何体。
●多面体:一般的,我们把由若干个多边形所围成的几何体,叫做多面体。
●棱柱:一般的有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的多面体叫做棱柱。
1)侧棱不垂直于底的棱柱是斜棱柱2)侧棱垂直于底的棱柱是直棱柱3)底面是正多边形的直棱柱是正棱柱4)V=sh(底面积x高)5)S表=S侧+S底●棱锥:一般地,有一个面是多边形,其余各面都是有一个公共顶点的三角形,由这些面所围成的多面体叫做棱锥。
1)正棱锥:如果一个棱锥的底面是正多边形,且顶点在底面的射影是底面的中心,这样的棱锥叫正棱锥。
2)V=sh (S是底面积,h是高)3)S表=S侧+S底●棱台:用一个平行于棱锥底面的平面去截棱锥,底面与截面之间的部分,叫做棱台。
1)V=【S+S'+√(S*S')】*h(S:上底面积 S':下底面积 h:高)●圆柱:以矩形的一边所在直线为旋转轴,其余三边旋转360°形成的曲面所围成的几何体叫作圆柱。
(轴截面为矩形)1)V=r2h=sh (公式中s为圆柱的底面积,h为圆柱的高。
)2)S=2r2+2rh (公式中r为圆柱底面半径,h为圆柱的高。
)●圆锥:以直角三角形的直角边所在直线为旋转轴,其余两边旋转360度而成的曲面所围成的几何体叫做圆锥(轴截面为等腰三角形)1)V=sh(S是底面积,h是高)2)S=rl+r2 (公式中r为底面半径,l为圆锥母线)●圆台:用一个平行于圆锥底面的平面去截圆锥,底面与截面之间的部分叫做圆台(轴截面为直角梯形)1)V=h(R2+r2+R*r)公式中r为上底半径、R为下底半径、h为高。
2)S=(R2+r2+Rl+rl)公式中r为上底半径、R为下底半径、l为母线●球:球是以半圆的直径所在直线为旋转轴,半圆面旋转一周形成的旋转体,也叫做球体。
高中数学—立体几何知识点总结(精华版)

立体几何知识点一.根本概念和原理:1.公理1:如果一条直线上的两点在一个平面内,那么这条直线上的所有的点都在这个平面内。
公理2:如果两个平面有一个公共点,那么它们有且只有一条通过这个点的公共直线。
公理3:过不在同一条直线上的三个点,有且只有一个平面。
推论1: 经过一条直线和这条直线外一点,有且只有一个平面。
推论2:经过两条相交直线,有且只有一个平面。
推论3:经过两条平行直线,有且只有一个平面。
公理4 :平行于同一条直线的两条直线互相平行。
如果一个角的两边和另一个角的两边分别平行并且方向相同,那么这两个角相等。
异面直线判定定理:用平面内一点与平面外一点的直线,与平面内不经过该点的直线是异面直线。
两异面直线所成的角:范围为( 0°,90° ) esp.空间向量法两异面直线间距离: 公垂线段(有且只有一条) esp.空间向量法2平面的一条斜线和它在这个平面内的射影所成的锐角。
esp.空间向量法(找平面的法向量)〔规定:a、直线与平面垂直时,所成的角为直角,b、直线与平面平行或在平面内,所成的角为0°角由此得直线和平面所成角的取值范围为[0°,90°]〕斜线与平面所成的角是斜线与该平面内任一条直线所成角中的最小角如果平面内的一条直线,与这个平面的一条斜线的射影垂直,那么它也与这条斜线垂直。
a和一个平面内的任意一条直线都垂直,就说直线a和平面互相垂直.直线a叫平面的垂线,平面叫做直线a的垂面。
直,那么这条直线垂直于这个平面。
如果两条直线同垂直于一个平面,那么这两条直线平行。
如果一条直线和一个平面没有公共点,那么我们就说这条直线和这个平面平行。
行,那么这条直线和这个平面平行。
如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行。
面,那么这两个平面平行。
行。
8.〔1〕二面角:从一条直线出发的两个半平面所组成的图形叫做二面角。
二面角的取值范围为[0°,180°]〔2〕二面角的平面角:以二面角的棱上任意一点为端点,在两个面内分别作垂直于棱的两条射线,这两条射线所成的角叫做二面角的平面角。
(完整版)高中数学必修2立体几何知识点

高中数学必修 2 知识点第一章空间几何体1.1 柱、锥、台、球的构造特色(略)棱柱:棱锥:棱台:圆柱:圆锥:圆台:球:1.2 空间几何体的三视图和直观图1三视图:正视图:以前去后侧视图:从左往右俯视图:从上往下2画三视图的原则:长对齐、高对齐、宽相等3直观图:斜二测画法4斜二测画法的步骤:(1).平行于坐标轴的线依旧平行于坐标轴;(2).平行于 y 轴的线长度变半,平行于x,z 轴的线长度不变;(3).画法要写好。
5用斜二测画法画出长方体的步骤:(1)画轴( 2)画底面( 3)画侧棱( 4)成图1.3 空间几何体的表面积与体积(一)空间几何体的表面积1 棱柱、棱锥的表面积:各个面面积之和2圆柱的表面积4圆台的表面积S 2 rl2r 2 3 圆锥的表面积S rlr 2 S rl r 2Rl R2 5 球的表面积S 4R26扇形的面积公式S扇形n R21lr (此中l表示弧长,r表示半径)3602(二)空间几何体的体积1柱体的体积 V S底h 2 锥体的体积1S底h V33台体的体积V1S上h4 球体的体积V4R3(下下3S上 SS )3第二章直线与平面的地点关系2.1 空间点、直线、平面之间的地点关系1平面含义:平面是无穷延展的 , 无大小,无厚薄。
2平面的画法及表示450,且横边画成邻边的(1)平面的画法:水平搁置的平面往常画成一个平行四边形,锐角画成 2 倍长(2)平面往常用希腊字母α、β、γ等表示,如平面α、平面β等,也能够用表示平面的平行四边形的四个极点或许相对的两个极点的大写字母来表示,如平面AC、平面 ABCD等。
3三个公义:(1)公义 1:假如一条直线上的两点在一个平面内,那么这条直线在此平面内A l符号表示为B ll AB公义 1 作用:判断直线能否在平面内(2)公义 2:过不在一条直线上的三点,有且只有一个平面。
符号表示为: A、B、C 三点不共线有且只有一个平面α,使A∈α、 B∈α、 C∈α。
必修二立体几何知识点+例题+练习+答案

行于底面的截面是相似的正多边形 5.旋转体:由一个平面图形绕一条定直线旋转所形成的封闭几何体叫旋转体,这条定
直线叫做旋转体的轴,
6.圆柱、圆锥、圆台:分别以矩形的一边、直角三角形的直角边、直角梯形垂直于 底边的腰所在的直线为旋转轴,其余各边旋转而形成的曲面所围成的几何体分别叫 做圆柱、圆锥、圆台。
必修二立体几何知识点+例题+练习+答案(word 版可编辑修改)
必修二立体几何知识点+例题+练习+答案(word 版可编辑修改) 编辑整理:
尊敬的读者朋友们: 这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对 文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(必修二立体几何知识点+例题+ 练习+答案(word 版可编辑修改))的内容能够给您的工作和学习带来便利。同时也真诚的希望收 到您的建议和反馈,这将是我们进步的源泉,前进的动力。 本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快 业绩进步,以 下为必修二立体几何知识点+例题+练习+答案(word 版可编辑修改)的全部内容。
主主主
主主主
主主主
[来源:学_科_网]
主主主
主主主
主主主
主主主
主主主
主主主
A
主主主
B
主主主
C
主主主
D
(3).空间几何体的直观图-—斜二测画法特点:
①斜二测坐标系的 y 轴与 x 轴正方向成 45 角;②原来与 x 轴平行的线段仍然与 x 平行,
高中数学必修二立体几何知识点梳理

高中数学必修二立体几何知识点梳理立体几何初步1、柱、锥、台、球的结构特征1) 棱柱:定义为有两个面互相平行,其余各面都是四边形,且每相邻两个四边形的公共边都互相平行,由这些面所围成的几何体。
按底面多边形的边数分类,可分为三棱柱、四棱柱、五棱柱等。
表示可用各顶点字母,如五棱柱ABCDE或用对角线的端点字母,如五棱柱AD''''。
几何特征为两底面是对应边平行的全等多边形;侧面、对角面都是平行四边形;侧棱平行且相等;平行于底面的截面是与底面全等的多边形。
2) 棱锥:定义为有一个面是多边形,其余各面都是有一个公共顶点的三角形,由这些面所围成的几何体。
按底面多边形的边数分类,可分为三棱锥、四棱锥、五棱锥等。
表示可用各顶点字母,如五棱锥P-ABCDE。
几何特征为侧面、对角面都是三角形;平行于底面的截面与底面相似,其相似比等于顶点到截面距离与高的比的平方。
3) 棱台:定义为用一个平行于棱锥底面的平面去截棱锥,截面和底面之间的部分。
按底面多边形的边数分类,可分为三棱台、四棱台、五棱台等。
表示可用各顶点字母,如五棱台P-ABCDE。
几何特征为上下底面是相似的平行多边形;侧面是梯形;侧棱交于原棱锥的顶点。
4) 圆柱:定义为以矩形的一边所在的直线为轴旋转,其余三边旋转所成的曲面所围成的几何体。
几何特征为底面是全等的圆;母线与轴平行;轴与底面圆的半径垂直;侧面展开图是一个矩形。
5) 圆锥:定义为以直角三角形的一条直角边为旋转轴,旋转一周所成的曲面所围成的几何体。
几何特征为底面是一个圆;母线交于圆锥的顶点;侧面展开图是一个扇形。
6) 圆台:定义为用一个平行于圆锥底面的平面去截圆锥,截面和底面之间的部分。
几何特征为上下底面是两个圆;侧面母线交于原圆锥的顶点;侧面展开图是一个弓形。
7) 球体:定义为以半圆的直径所在直线为旋转轴,半圆面旋转一周形成的几何体。
几何特征为球的截面是圆;球面上任意一点到球心的距离等于半径。
高二上册立体几何知识点

高二上册立体几何知识点一、几何体的定义和分类几何体是指由许多平面图形组成的立体图形,主要包括以下几种分类:1. 三棱柱:由两个底面和三个矩形的侧面组成。
2. 四棱柱:由两个底面和四个矩形的侧面组成。
3. 五棱柱:由两个底面和五个等边三角形的侧面组成。
4. 六棱柱(正六棱柱):由两个底面和六个全等的正三角形的侧面组成。
5. 正四棱锥:由一个底面(正四边形)和四个全等的三角形的侧面组成。
6. 正四面体:由四个全等的正三角形的面组成。
7. 正六面体(立方体):由六个全等的正方形的面组成。
8. 正八面体:由八个全等的正三角形的面组成。
9. 正十二面体:由十二个全等的正五边形的面组成。
10. 正二十面体:由二十个全等的正三角形的面组成。
二、常见几何体的性质1. 体积和表面积:体积是指几何体所占的三维空间大小,表面积是指几何体外表面的总面积。
2. 相交关系:几何体之间可以相交、相切或者不相交。
3. 对称性:一些几何体具有对称性,可以根据某些轴或平面进行对称。
4. 轴对称几何体:具有轴对称性的几何体可以围绕某个轴进行旋转,使得旋转后的形状与原始形状完全相同。
5. 平面对称几何体:具有平面对称性的几何体可以通过平面反射,使得反射后的形状与原始形状完全相同。
三、立体几何的计算公式1. 三棱柱的体积计算公式:V = 底面积 ×高,其中底面积指底面的面积,高指垂直于底面的高度。
2. 四棱柱的体积计算公式:V = 底面积 ×高,其中底面积指底面的面积,高指垂直于底面的高度。
3. 六棱柱(正六棱柱)的体积计算公式:V = 底面积 ×高,其中底面积指底面的面积,高指垂直于底面的高度。
4. 正四棱锥的体积计算公式:V = (底面积 ×高)/ 3,其中底面积指底面的面积,高指锥的高度。
5. 正四面体的体积计算公式:V = (底面积 ×高)/ 3,其中底面积指底面的面积,高指四面体的高度。
高中数学立体几何公式大全

高中数学立体几何公式大全高中数学立体几何公式整理如下:1. 正方体:a-边长,S=6a²,V=a³2. 长方体:a-长,b-宽,c-高,S=2(ab+ac+bc),V=abc3. 圆柱:r-底半径,h-高,C=2πr,S底=πr²,S侧=Ch,S表=Ch+2S底,V=S底h=πr²h4. 空心圆柱:R-外圆半径,r-内圆半径,h-高,V=πh(R²-r²)5. 直圆锥:r-底半径,h-高,V=πr²h/36. 圆台:r-上底半径,R-下底半径,h-高,V=πh(R²+Rr+r²)/37. 棱柱:S-底面积,h-高,V=Sh8. 棱锥:S-底面积,h-高,V=Sh/39. 棱台:S1和S2-上、下底面积,h-高,V=h[S1+S2+(S1S1)1/2]/310. 拟柱体:S1-上底面积,S2-下底面积,S0-中截面积,h-高,V=h(S1+S2+4S0)/611. 球:r-半径,d-直径,V=4/3πr³=πd²/612. 球缺:h-球缺高,r-球半径,a-球缺底半径,V=πh(3a²+h²)/6=πh²(3r-h)/3a²=h(2r-h)13. 球台:r1和r2-球台上、下底半径,h-高,V=πh[3(r1²+r2²)+h²]/614. 圆环体:R-环体半径,D-环体直径,r-环体截面半径,d-环体截面直径,V=2π²Rr²=π²Dd²/415. 桶状体:D-桶腹直径,d-桶底直径,h-桶高,V=πh(2D²+d²)/12以上公式涵盖了几何体各个方面的内容。
必修二立体几何知识点

必修二立体几何知识点一、引言本文档旨在概述高中必修二课程中立体几何的核心知识点,为教师和学生提供一个清晰的学习指南。
二、立体图形的基础1. 点、线、面的关系- 点的位置关系:共面、异面- 线的位置关系:平行、相交、异面- 面的位置关系:平行、相交2. 立体图形的分类- 多面体:棱柱、棱锥、圆柱、圆锥、球体- 旋转体:球面、圆锥面、圆柱面三、多面体1. 棱柱- 棱柱的结构特征- 棱柱的体积和表面积计算2. 棱锥- 棱锥的结构特征- 棱锥的体积和表面积计算3. 棱台- 棱台的结构特征- 棱台的体积计算四、旋转体1. 圆柱和圆锥- 结构特征- 体积和表面积计算- 旋转体的方程表示2. 球体- 结构特征- 体积和表面积计算五、立体图形的截面1. 截面的概念- 截面的定义- 截面的形状分类2. 截面的性质- 截面与原图形的关系- 截面的计算方法六、空间向量1. 空间向量的定义- 空间向量的基本概念- 空间向量的加法、减法和数乘2. 空间向量的应用- 点到直线的距离- 直线到平面的距离- 立体图形的体积计算七、立体角1. 立体角的定义- 立体角的概念- 立体角的度量2. 立体角的性质- 立体角与平面角的关系- 立体角的计算方法八、结语本文档提供的知识点是理解和掌握立体几何的基础。
教师应根据学生的实际情况,适当调整教学进度和深度。
文档格式说明:- 本文档应使用Word格式编写,确保所有文本清晰可读。
- 各主要部分应使用标题和子标题进行区分,以便快速导航。
- 公式和图表应使用适当的工具插入,并确保其准确性和清晰度。
- 文档应进行适当的排版,以确保整体观感良好,易于阅读和理解。
- 应提供足够的页边距和行间距,以便于打印和复制。
- 文档应保存为.docx格式,以确保可编辑性和可修改性。
请注意,这是一个教学文档的概要结构,具体内容需要根据教学大纲和实际教学需求进行填充和调整。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
立体几何习题1. 如图,四棱锥P-ABCD 的底面是正方形,,,//,PA ABCD AE PD EF CD AM EF ⊥⊥=底面(1) 证明MF 是异面直线AB 与PC 的公垂线;(2) 若3PA AB =,求直线AC 与平面EAM 所成角的正弦值2. 已知三棱柱ABC -A 1B 1C 1中,底面边长和侧棱长均为a ,侧面A 1ACC 1⊥底面ABC ,A 1B =26a , (Ⅰ)求异面直线AC 与BC 1所成角的余弦值; (Ⅱ)求证:A 1B ⊥面AB 1C .3. 如图,四棱锥S ABCD -的底面是边长为1的正方形,SD 垂直于底面ABCD ,SB =31.求证BC SC ⊥;2.求面ASD 与面BSC 所成二面角的大小;3.设棱SA 的中点为M ,求异面直线DM 与SB 所成角的大小BC DA PM FE4. 在三棱锥S —ABC 中,△ABC 是边长为4的正三角形,平面SAC ⊥平面ABC ,SA=SC=23,M 、N 分别为AB 、SB 的中点.(Ⅰ)证明:AC ⊥SB ;(Ⅱ)求二面角N —CM —B 的大小; (Ⅲ)求点B 到平面CMN 的距离.5. 如右下图,在长方体ABCD —A 1B 1C 1D 1中,已知AB= 4, AD =3, AA 1= 2. E 、F 分别是线段AB 、BC 上的点,且EB= FB=1.(1) 求二面角C —DE —C 1的正切值;(2) 求直线EC 1与FD 1所成的余弦值.6. 如图,在底面是菱形的四棱锥P —ABC D中,∠ABC=600,PA=AC=a ,PB=PD=a 2,点E 在PD 上,且PE:ED=2:1.(I )证明PA ⊥平面ABCD ;(II )求以AC 为棱,EAC 与DAC 为面的二面角 的大小;(Ⅲ)在棱PC 上是否存在一点F ,使BF//平面AEC ?证明你的结论.1B 1D BA 1EFB CDA P E7. 在棱长为4的正方体ABCD-A 1B 1C 1D 1中,O 是正方形A 1B 1C 1D 1的中心,点P 在棱CC 1上,且CC 1=4CP. (Ⅰ)求直线AP 与平面BCC 1B 1所成的角的大小(结果用反三角函数值表示);(Ⅱ)设O 点在平面D 1AP 上的射影是H ,求证:D 1H ⊥AP ;(Ⅲ)求点P 到平面ABD 1的距离.8. 如图,已知四棱锥 P —ABCD ,PB ⊥AD 侧面PAD 为边长等于2的正三角形,底面ABCD 为菱形,侧面PAD 与底面ABCD 所成的二面角为120°.(I )求点P 到平面ABCD 的距离,(II )求面APB 与面CPB 所成二面角的大小.9. 如图,直三棱柱ABC -A 1B 1C 1中,∠ACB =90o ,AC =1,CB =2,侧棱AA 1=1,侧面AA 1B 1B 的两条对角线交点为D ,B 1C 1的中点为M . (Ⅰ)求证:CD ⊥平面BDM ;(Ⅱ)求面B 1BD 与面CBD 所成二面角的大小. · B 1 PA C D A 1 C 1 D 1B O H ·CAC10. 三棱锥P-ABC 中,侧面P AC 与底面ABC 垂直,P A =PB =PC =3. (1)求证 AB ⊥BC;(II)如果 AB=BC=AC 与侧面P AC 所成角的大小.11. 如图,四棱锥P —ABCD 中,底面ABCD 为矩形,AB=8,AD=43,侧面PAD 为等边三角形,并且与底面所成二面角为60°.(Ⅰ)求四棱锥P —ABCD 的体积; (Ⅱ)证明PA ⊥BD.12.已知四棱锥P —ABCD ,底面ABCD 是菱形,⊥︒=∠PD DAB ,60平面ABCD ,PD=AD , 点E 为AB 中点,点F 为PD 中点. (1)证明平面PED ⊥平面PAB ;(2)求二面角P —AB —F 的平面角的余弦值.C13. 如图,在四棱锥P—ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F(1)证明PA//平面EDB;(2)证明PB⊥平面EFD;(3)求二面角C—PB—D的大小14. 如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=2,AF=1,M是线段EF的中点(Ⅰ)求证AM∥平面BDE;(Ⅱ)求二面角A—DF—B的大小;BAC参考答案1.解:(I )证明:因PA ⊥底面,有PA ⊥AB ,又知AB ⊥AD ,故AB ⊥面PAD ,推得BA ⊥AE , 又AM ∥CD ∥EF ,且AM=EF , 证得AEFM 是矩形,故AM ⊥MF.又因AE ⊥PD ,AE ⊥CD ,故AE ⊥面PCD , 而MF ∥AE ,得MF ⊥面PCD , 故MF ⊥PC ,因此MF 是AB 与PC 的公垂线.(II )解:连结BD 交AC 于O ,连结BE ,过O 作BE 的垂线OH , 垂足H 在BE 上. 易知PD ⊥面MAE ,故DE ⊥BE , 又OH ⊥BE ,故OH//DE , 因此OH ⊥面MAE. 连结AH ,则∠HAO 是所要求的线AC 与面NAE 所成的角 设AB=a ,则PA=3a , a AC AO 2221==.因Rt △ADE~Rt △PDA ,故中从而在AHO Rt a ED OH a a a a PDAD ED ∆===+==.10221,10)3(2222.10520122102sin ==⨯==a a AO OH HAO 2. 解:;(Ⅱ)略. 3.解:(底面ABCD 是正方形 ∴⊥BC DCSD ⊥底面ABCD ∴DC 是SC 在平面ABCD 上的射影 由三垂线定理得BC SC ⊥(II )解:SD ⊥底面ABCD ,且ABCD 为正方形∴可以把四棱锥S ABCD -补形为长方体A B C S ABCD 111-,如图2 面ASD 与面BSC 所成的二面角就是面ADSA 1与面BCSA 1所成的二面角,SC BC BC A SSC A S⊥∴⊥,//11 又SD A S ⊥1 ∴∠CSD 为所求二面角的平面角在Rt SCB ∆中,由勾股定理得SC =2 在Rt SDC ∆中,由勾股定理得SD =1即面ASD 与面BSC 所成的二面角为图2图3∴∆SDA 是等腰直角三角形 又M 是斜边SA 的中点∴⊥⊥⊥=DM SABA AD BA SD AD SD D,, ∴⊥BA 面ASD ,SA 是SB 在面ASD 上的射影由三垂线定理得DM SB ⊥ ∴异面直线DM 与SB 所成的角为90︒DABMSCP4. 解法一:(Ⅰ)取AC 中点D ,连结SD 、DB. ∵SA=SC ,AB=BC , ∴AC ⊥SD 且AC ⊥BD ,∴AC ⊥平面SDB ,又SB ⊂平面SDB , ∴AC ⊥SB.(Ⅱ)∵AC ⊥平面SDB ,AC ⊂平面ABC , ∴平面SDB ⊥平面ABC.过N 作NE ⊥BD 于E ,NE ⊥平面ABC , 过E 作EF ⊥CM 于F ,连结NF , 则NF ⊥CM.∴∠NFE 为二面角N -CM -B 的平面角.∵平面SAC ⊥平面ABC ,SD ⊥AC ,∴SD ⊥平面ABC. 又∵NE ⊥平面ABC ,∴NE ∥SD. ∵SN=NB ,∴NE=21SD=2122AD SA -=21412-=2,且ED=EB.在正△ABC 中,由平几知识可求得EF=41MB=21, 在Rt △NEF 中,tan ∠NFE=EFEN=22, ∴二面角N —CM —B 的大小是arctan22. (Ⅲ)在Rt △NEF 中,NF=22EN EF +=23, 13313∵V B-CMN =V N-CMB ,NE ⊥平面CMB ,∴31S △CMN ·h=31S △CMB ·NE , ∴h=CMNCMB S NE S ⋅=324.即点B 到平面CMN 的距离为324.解法二:(Ⅰ)取AC 中点O ,连结OS 、OB.∵SA=SC ,AB=BC , ∴AC ⊥SO 且AC ⊥BO.∵平面SAC ⊥平面ABC ,平面SAC ∩平面 ABC=AC ∴SO ⊥面ABC ,∴SO ⊥BO.如图所示建立空间直角坐标系O -x yz.则A (2,0,0),B (0,23,0),C (-2,0,0), S (0,0,22),M(1,3,0),N(0,3,2). ∴AC =(-4,0,0),SB =(0,23,22), ∵AC ·SB =(-4,0,0)·(0,23,22)=0, ∴AC ⊥SB.(Ⅱ)由(Ⅰ)得CM =(3,3,0),MN =(-1,0,2).设n=(x ,y ,z )为平面CMN 的一个法向量,CM ·n=3x +3y=0, 则 取z=1,则x =2,y=-6,MN ·n=-x +2z=0,∴n=(2,-6,1),又OS =(0,0,22)为平面ABC 的一个法向量, ∴cos(n ,OS ||||OS n OS⋅=31. ∴二面角N -CM -B 的大小为arccos31. (Ⅲ)由(Ⅰ)(Ⅱ)得MB =(-1,3,0),n=(2,-6,1)为平面CMN 的一个法向量,∴点B 到平面CMN 的距离d=|·|MB n =24.5解:(I )以A 为原点,1,,AA AD AB 分别为x 轴,y 轴,z轴的正向建立空间直角坐标系,则有D(0,3,0)、D 1(0,3,2)、E(3,0,0)、F(4,1,0)、C 1(4,3,2) 于是,)2,2,4(),2,3,1(),0,3,3(11-==-=FD EC DE设向量),,(z y x n =与平面C 1DE 垂直,则有133013202n DE x y x y z x y z n EC ⎫⊥-=⎫⎪⇒⇒==-⎬⎬++=⊥⎭⎪⎭(,,)(1,1,2),0222z z zn z z ∴=--=-->其中001(1,1,2),,n n C DE =--取则是一个与平面垂直的向量1011(0,0,2),AA CDE n AA C DE C θ=∴--向量与平面垂直与所成的角为二面角的平面角0101cos 3||||1n AA n AA θ•-===⨯tan θ∴= (II )设EC 1与FD 1所成角为β,则142122)4(2312223)4(1||||cos 2222221111=++-⨯++⨯+⨯+-⨯=⨯=FD EC FD EC β 6.BD(Ⅰ)证明 因为底面ABCD 是菱形,∠ABC=60°,所以AB=AD=AC=a , 在△PAB 中, 由PA 2+AB 2=2a 2=PB 2 知PA ⊥AB. 同理,PA ⊥AD ,所以PA ⊥平面ABCD. (Ⅱ)解 作EG//PA 交AD 于G , 由PA ⊥平面ABCD.知EG ⊥平面ABCD.作GH ⊥AC 于H ,连结EH , 则EH ⊥AC ,∠EHG 即为二面角θ的平面角. 又PE : ED=2 : 1,所以.3360sin ,32,31a AG GH a AG a EG =︒=== 从而 ,33tan ==GH EG θ .30︒=θ (Ⅲ)解法一 以A 为坐标原点,直线AD 、AP 分别为y 轴、z 轴,过A 点垂直平面PAD 的直线为xD CABB).0,21,23(),0,21,23(),0,0,0(a a C a a B A - ).31,32,0(),,0,0(),0,,0(a a E a P a D所以 ).0,21,23(),31,32,0(a a AC a a AE == ).,21,23(),,0,0(a a a PC a AP -== ).,21,23(a a a BP -=设点F 是棱PC 上的点,,10),,21,23(<<-==λλλλλ其中a a a PC PF 则 ),21,23(),21,23(λλλa a a a a a PF BP BF -+-=+=)).1(),1(21),1(23(λλλ-+-=a a a 令 AE AC BF 21λλ+= 得 ⎪⎪⎪⎩⎪⎪⎪⎨⎧=-+=+=-⎪⎪⎪⎩⎪⎪⎪⎨⎧=-+=+=-.311,341,1.31)1(,3221)1(21,23)1(2322112211λλλλλλλλλλλλλλ即a a a a a a a 解得.23,21,2121=-==λλλ 即 21=λ时,.2321AE AC BF +-= 亦即,F 是PC 的中点时,BF 、AC 、AE 共面.又 BF ⊄平面AEC ,所以当F 是棱PC 的中点时,BF//平面AEC. 解法二 当F 是棱PC 的中点时,BF//平面AEC ,证明如下, 证法一 取PE 的中点M ,连结FM ,则FM//CE. ①由 ,21ED PE EM ==知E 是MD 的中点. 连结BM 、BD ,设BD ⋂AC=O ,则O 为BD 的中点.所以 BM//OE. ②由①、②知,平面BFM//平面AEC.又 BF ⊂平面BFM ,所以BF//平面AEC. 证法二因为 )(2121DP CD AD CP BC BF ++=+= .2123)(23)(212321AC AE AD AE AC AD AD DE CD AD -=-+-+=++=所以 BF 、AE、AC 共面.又 BF ⊄平面ABC ,从而BF//平面AEC.7. 解(1)APB ∠=· B 1PACDA 1C 1D 1BO H·(2)略 (33228.(I )解:如图,作PO ⊥平面ABCD ,垂足为点O.连结OB 、OA 、OD 、OB 与AD 交于点E ,连结PE. ∵AD ⊥PB ,∴AD ⊥OB ,∵PA=PD ,∴OA=OD ,于是OB 平分AD ,点E 为AD 的中点,所以PE ⊥AD.由此知∠PEB 为面PAD 与面ABCD 所成二面角的平面角, ∴∠PEB=120°,∠PEO=60°由已知可求得PE=3∴PO=PE ·sin60°=23233=⨯, 即点P 到平面ABCD 的距离为23. (II )解法一:如图建立直角坐标系,其中O 为坐标原点,x 轴平行于DA.)43,433,0(),0,233,0(),23,0,0(的坐标为中点G PB B P .连结AG.又知).0,233,2(),0,23,1(-C A 由此得到: 0,0).0,0,2(),23,233,0(),43,43,1(=⋅=⋅-=-=--=PB BC PB GA BC PB GA 于是有所以θ的夹角BC GA PB BC PB GA ,.⊥⋅⊥ 等于所求二面角的平面角, 于是,772||||cos -=⋅=BC GA BC GA θ 所以所求二面角的大小为772arccos-π . 解法二:如图,取PB 的中点G ,PC 的中点F ,连结EG 、AG 、GF ,则AG ⊥PB ,FG//BC ,FG=21BC. ∵AD ⊥PB ,∴BC ⊥PB ,FG ⊥PB , ∴∠AGF 是所求二面角的平面角. ∵AD ⊥面POB ,∴AD ⊥EG.又∵PE=BE ,∴EG ⊥PB ,且∠PEG=60°. 在Rt △PEG 中,EG=PE ·cos60°=23.在Rt △PEG 中,EG=21AD=1. 于是tan ∠GAE=AE EG =23, 又∠AGF=π-∠GAE.所以所求二面角的大小为π-arctan23. 9.解法一:(I)如图,连结CA 1、AC 1、CM ,则CA 1=2, ∵CB=CA 1=2,∴△CBA 1为等腰三角形, 又知D 为其底边A 1B 的中点,∴CD ⊥A 1B , ∵A 1C 1=1,C 1B 1=2,∴A 1B 1=3, 又BB 1=1,∴A 1B=2,∵△A 1CB 为直角三角形,D 为A 1B 的中点,CD=21A 1B=1,CD=CC 1又DM=21AC 1=22,DM=C 1M ,∴△CDN ≌△CC 1M ,∠CDM=∠CC 1M=90°,即CD ⊥DM ,因为A 1B 、DM 为平面BDM 内两条相交直线,所以CD ⊥平面BDM(II)设F 、G 分别为BC 、BD 的中点,连结B 1G 、FG 、B 1F ,则FG ∥CD ,FG=21CD ∴FG=21,FG ⊥BD.由侧面矩形BB 1A 1A 的对角线的交点为D,知BD=B 1D=21A 1B=1, 所以△BB 1D 是边长为1的正三角形,于是B 1G ⊥BD ,B 1G=23, ∴∠B 1GF 是所求二面角的平面角又B 1F 2=B 1B 2+BF 2=1+(22)2=23. ∴cos ∠B 1GF=332123223)21()23(222121221-=••-+=•-+FG G B F B FG G B 即所求二面角的大小为π-arccos33 解法二:如图以C 为原点建立坐标系(I):B(2,0,0),B 1(2,1,0),A 1(0,1,1),D(22,21,21), M(22,1,0),=CD (22,21,21),=B A 1(2,-1,-1), =DM (0,21,-21),,0,01=•=•DM CD B A CD∴CD ⊥A 1B,CD ⊥DM.因为A 1B 、DM 为平面BDM 内两条相交直线, 所以CD ⊥平面BDM(II):设BD 中点为G ,连结B 1G ,则G ),41,41,423(=BD (-22,21,21),=G B 1),41,43,42(--∴01=•G B BD ,∴BD ⊥B 1G ,又CD ⊥BD ,∴CD 与G B 1的夹角θ等于所求二面角的平面角, cos .33||||11-=••=G B CD G B CD θ A'CBA C'B'MD A BC A'B'C'DM F Gz XA'C B AC'B'F MDGC所以所求二面角的大小为π10.C⑴证明:取AC 中点O , 连结PO 、BO .∵P A =PC ∴PO ⊥AC 又∵侧面P AC ⊥底面ABC ∴PO ⊥底面ABC又P A =PB =PC ∴AO =BO =CO ∴△ABC 为直角三角形 ∴AB ⊥BCC⑵解:取BC的中点为M ,连结OM,PM ,所以有OM=12=∴PO ==由⑴有PO ⊥平面ABC,OM⊥BC ,由三垂线定理得PM ⊥BC ∴平面POM ⊥平面PBC ,又∵∴△POM 是等腰直角三角形,取PM 的中点N ,连结ON, NC则ON ⊥PM, 又∵平面POM ⊥平面PBC, 且交线是PM, ∴ON ⊥平面PBC ∴∠ONC 即为AC 与平面PBC 所成的角.122ON PM OC ==== ∴1sin 2ON ONC OC ∠== ∴6ONC π∠=.故AC 与平面PBC 所成的角为6π. 11. 解:(Ⅰ)如图1,取AD 的中点E ,连结PE ,则PE 作PO ⊥平面在ABCD ,垂足为O ,连结OE.图2CACAC根据三垂线定理的逆定理得OE ⊥AD ,所以∠PEO 为侧面PAD 与底面所成的二面角的平面角, 由已知条件可知∠PEO=60°,PE=6, 所以PO=33,四棱锥P —ABCD 的体积 V P —ABCD =.963334831=⨯⨯⨯ (Ⅱ)解法一:如图1,以O 为原点建立空间直角坐标系.通过计算可得P (0,0,33),A (23,-3,0),B (23,5,0),D (-23,-3,0) 所以).0,8,34(),33,3,32(--=--=BD PA 因为,002424=++-=⋅BD PA 所以PA ⊥BD.解法二:如图2,连结AO ,延长AO 交BD 于点F.通过计算可得AE=23,又知AD=43,AB=8,得.ABADAE EO = 所以 Rt △AEO ∽Rt △BAD. 得∠EAO=∠ABD.所以∠EAO+∠ADF=90°所以 AF ⊥BD.因为 直线AF 为直线PA 在平面ABCD 内的身影,所以PA ⊥BD.12.(1)证明:连接BD.ADB DAB AD AB ∆∴︒=∠=,60, 为等边三角形.E 是AB 中点,.DE AB ⊥∴…………2分⊥PD 面ABCD ,AB ⊂面ABCD ,.PD AB ⊥∴⊂DE 面PED ,PD ⊂面PED ,⊥∴=AB D PD DE , 面PED.…………4分⊂AB 面PAB ,⊥∴PED 面面PAB. ……………………6分(2)解:⊥AB 平面PED ,PE ⊂面PED ,.PE AB ⊥∴ 连接EF ,⊂EF PED ,.EF AB ⊥∴PEF ∠∴为二面角P —AB —F 的平面角. ………… 9分 设AD=2,那么PF=FD=1,DE=3. 在,1,2,7,===∆PF EF PE PEF 中,147572212)7(cos 22=⨯-+=∠∴PEF即二面角P —AB —F 的平面角的余弦值为.1475…12分13.AC方法一:(1)证明:连结AC ,AC 交BD 于O ,连结EO ∵底面ABCD 是正方形,∴点O 是AC 的中点 在PAC ∆中,EO 是中位线,∴PA // EO 而⊂EO 平面EDB 且⊄PA 平面EDB , 所以,PA // 平面EDBAC(2)证明:∵PD ⊥底面ABCD 且⊂DC 底面ABCD ,∴DC PD ⊥∵PD=DC ,可知PDC ∆是等腰直角三角形,而DE 是斜边PC 的中线, ∴DE ⊥ ①同样由PD ⊥底面ABCD ,得PD ⊥BC∵底面ABCD 是正方形,有DC ⊥BC ,∴BC ⊥平面PDC 而⊂DE 平面PDC ,∴BC ⊥ ② 由①和②推得⊥DE 平面PBC 而⊂PB 平面PBC ,∴PB DE ⊥又PB EF ⊥且E EF DE = ,所以PB ⊥平面EFD(3)解:由(2)知,DF PB ⊥,故EFD ∠是二面角C —PB —D 的平面角由(2)知,PD EF DE ⊥⊥,设正方形ABCD 的边长为a ,则a BD a DC PD 2,===a BD PD PB 322=+=, a DC PD PC 222=+=PC DE 2221==在PDB Rt ∆中,aa a PB BD PD DF 3632=⋅=⋅=在EFD Rt ∆中,233622sin ===a aDF DE EFD ,∴3=∠EFD 所以,二面角C —PB —D 3方法二:如图所示建立空间直角坐标系,D 为坐标原点,设a DC = (1)证明:连结AC ,AC 交BD 于G ,连结EG依题意得)2,2,0(),,0,0(),0,0,(a a E a P a A ∵底面ABCD 是正方形,∴G 是此正方形的中心,故点G 的坐标为)0,2,2(aa 且 2,0,2(),,0,(aa EG a a PA -=-=∴EG PA 2=,这表明PA//EG而⊂EG 平面EDB 且⊄PA 平面EDB ,∴PA//平面EDB(2)证明;依题意得)0,,(a a B ,,,(a a a PB -=)2,2,0(aa DE =,故22022=-+=⋅a a DE PB ∴PB ⊥由已知PB EF ⊥,且E DE EF = ,所以⊥PB 平面EFD (3)解:设点F 的坐标为),,(000z y x ,PB PF λ=,则),,(),,(000a a a a z y x -=-λ从而z a y a x )1(,,000λλλ-===所以))21(,)21(,()2,2,(000a a a z a y a x FE ---=---=λλλ 由条件PB EF ⊥知,0=⋅PB FE ,即0)21()21(222=---+-a a a λλλ,解得31=λ∴点F 的坐标为)32,3,3(aa a ,且 )6,6,3(a a a FE --=,)32,3,3(aa a FD ---=∴03233222=+--=⋅a a a FD PB 即FD PB ⊥,故EFD ∠是二面角C —PB —D 的平面角∵691892222a a a a FD FE =+-=⋅,且 a a a a FE 6636369||222=++=,a a a a FD 369499||222=++=,∴236666||||cos 2=⋅==a a a FD FE EFD ∴3=∠EFD所以,二面角C —PB —D 314. 方法一解: (Ⅰ)记AC 与BD 的交点为O,连接OE, ∵O 、M 分别是AC 、EF 的中点,ACEF 是矩形,∴四边形AOEM 是平行四边形, ∴AM ∥OE∵⊂OE 平面BDE , ⊄AM 平面BDE ,∴AM ∥平面BDEBB(Ⅱ)在平面AFD 中过A 作AS ⊥DF 于S ,连结BS , ∵AB ⊥AF , AB ⊥AD , ,A AF AD = ∴AB ⊥平面ADF ,∴AS 是BS 在平面ADF 上的射影, 由三垂线定理得BS ⊥DF∴∠BSA 是二面角A —DF —B 的平面角在RtΔASB 中,,2,36==AB ASB∴,60,3tan ︒=∠=∠ASB ASB∴二面角A —DF —B 的大小为60º(Ⅲ)设CP=t (0≤t≤2),作PQ ⊥AB 于Q ,则PQ ∥AD , ∵PQ ⊥AB ,PQ ⊥AF ,A AF AB = , ∴PQ ⊥平面ABF ,⊂QE 平面ABF , ∴PQ ⊥QF在RtΔPQF 中,∠FPQ=60º, PF=2PQ∵ΔPAQ 为等腰直角三角形,∴).2(22t PQ -=又∵ΔPAF 为直角三角形, ∴1)2(2+-=t PF ,∴).2(2221)2(2t t -⋅=+- 所以t=1或t=3(舍去) 即点P 是AC 的中点方法二(Ⅰ)建立如图所示的空间直角坐标系 设N BD AC = ,连接NE ,则点N 、E 的坐标分别是()0,22,22、(0,0,1), ∴ NE =()1,22,22--, 又点A 、M 的坐标分别是(022,,)、()1,22,22 ∴ AM =()1,22,22-- ∴NE =AM 且NE 与AM 不共线, ∴NE ∥AM又∵⊂NE 平面BDE , ⊄AM 平面BDE , ∴AM ∥平面BDF(Ⅱ)∵AF ⊥AB ,AB ⊥AD ,AF ,A AD = ∴AB ⊥平面ADF∴(AB =-为平面DAF 的法向量∵NE DB •=()1,22,22--·)0,2,2(-=0, ∴NE NF •=()1,22,22--·)0,2,2(=0得 NE DB ⊥,NE NF ⊥∴NE 为平面BDF 的法向量∴cos<,AB NE >=21 ∴,AB NE 的夹角是60º即所求二面角A —DF —B 的大小是60º(Ⅲ)设P(t,t,0)(0≤t≤2)得(2,1),PF t t =∴CD =(2,0,0) 又∵PF 和CD 所成的角是60º∴21)2()2(2)2(60cos 22⋅+-+-⋅-=︒t t t解得22=t 或223=t (舍去), 即点P 是AC 的中点。
