2021年三角形“四心”定义与性质之欧阳学文创编
三角形四心及性质

三角形四心三角形四心要点诠释:(1)三角形的内心、重心都在三角形的内部.(2)钝角三角形的垂心、外心都在三角形的外部.(3)直角三角形的垂心为直角顶点,外心为直角三角形斜边的中点.(4)锐角三角形的垂心、外心都在三角形的内部.1、三角形外心:三角形的外心是三角形三条垂直平分线的交点(或三角形外接圆的圆心) 。
三角形的三条垂直平分线必交于一点已知:△ABC中,AB,AC的垂直平分线DO,EO相交于点O求证:O点在BC的垂直平分线上证明:连结AO,BO,CO,∵DO垂直平分AB,∴AO=BO∵EO垂直平分AC,∴AO=CO∴BO=CO即O点在BC的垂直平分线上三角形的外心的性质:1.三角形三条边的垂直平分线的交于一点,该点即为三角形外接圆的圆心.2三角形的外接圆有且只有一个,即对于给定的三角形,其外心是唯一的,但一个圆的内接三角形却有无数个,这些三角形的外心重合。
3. 锐角三角形的外心在三角形内;钝角三角形的外心在三角形外;直角三角形的外心与斜边的中点重合4.OA=OB=OC=R5.∠BOC=2∠BAC,∠AOB=2∠ACB,∠COA=2∠CBA(圆心角=2同弧圆周角)6.S△ABC=abc/4R2、三角形的内心:三角形的内心是三角形三条内角平分线的交点(或内切圆的圆心)。
三角形三条角平分线必交于一点证明己知:在△ABC中,∠A与∠B的角平分线交于点O,连接OC求证:OC平分∠ACB证明:过O点作OD,OE,OF分别垂直于AC,BC,AB,垂足分别为D,E,F∵AO平分∠BAC,∴OD=OF;∵BO平分∠ABC,∴OE=OF ;∴OD=OF∴O在∠ACB角平分线上∴CO平分∠ACB三角形内心的性质:1.三角形的三条角平分线交于一点,该点即为三角形的内心2.三角形的内心到三边的距离相等,都等于内切圆半径r3.r=2S/(a+b+c)4.在Rt△ABC中,∠C=90°,r=(a+b-c)/2.5.∠BOC = 90 °+∠A/2 ∠BOA = 90 °+∠C/2 ∠AOC = 90 °+∠B/26.S△ABC=[(a+b+c)r]/2 (r是内切圆半径)3、三角形的垂心:三角形的垂心是三角形三边上的高的交点(通常用H表示)。
三角形“四心”定义与性质

三角形“四心”定义与性质-CAL-FENGHAI.-(YICAI)-Company One1三角形“四心”定义与性质所谓三角形的“四心”是指三角形的重心、垂心、外心及内心。
当三角形是正三角形时,四心重合为一点,统称为三角形的中心。
一、三角形的外心定 义:三角形三条中垂线的交点叫外心,即外接圆圆心。
ABC ∆的重心一般用字母O 表示。
性 质:1.外心到三顶点等距,即OC OB OA ==。
2.外心与三角形边的中点的连线垂直于三角形的这一边,即AB OF AC OE BC OD ⊥⊥⊥,,. 3.AOB C AOC B BOC A ∠=∠∠=∠∠=∠21,21,21。
二、三角形的内心 定 义:三角形三条角平分线的交点叫做三角形的内心,即内切圆圆心。
ABC ∆的内心一般用字母I 表示,它具有如下性质:性 质:1.内心到三角形三边等距,且顶点与内心的连线平分顶角。
2.三角形的面积=⨯21三角形的周长⨯内切圆的半径. 3.CE CD BD BF AF AE ===,,;=++CD BF AE 三角形的周长的一半。
4.,2190A BIC ∠+=∠ B CIA ∠+=∠2190 ,C AIB ∠+=∠2190 。
三、三角形的垂心定 义:三角形三条高的交点叫重心。
ABC ∆的重心一般用字母H 表示。
性 质:1.顶点与垂心连线必垂直对边,即AB CH AC BH BC AH ⊥⊥⊥,,。
2.△ABH 的垂心为C ,△BHC 的垂心为A ,△ACH 的垂心为B 。
四、三角形的“重心”:定 义:三角形三条中线的交点叫重心。
ABC ∆的重心一般用字母G 表示。
性 质:1.顶点与重心G 的连线必平分对边。
2.重心定理:三角形重心与顶点的距离等于它与对边中点的距离的2倍。
即GF GC GE GB GD GA 2,2,2===3.重心的坐标是三顶点坐标的平均值. 即3,3C B AG C B A G y y y y x x x x ++=++=. 4.向量性质:(1)0=++GC GB GA ;(2))(31++=,5.ABC AGB CGA BGC S S S S ∆∆∆∆===31。
三角形“四心”定义与性质

三角形“四心”定义与性质三角形的“四心”是指三角形的重心、垂心、外心及内心。
当三角形是正三角形时,四心重合为一点,统称为三角形的中心。
一、三角形的外心定 义:三角形三条中垂线的交点叫外心,即外接圆圆心。
ABC ∆的重心一般用字母O 表示。
性 质:1.外心到三顶点等距,即OC OB OA ==。
〖半径〗2.外心与三角形边的中点的连线垂直于三角形的这一边,即AB OF AC OE BC OD ⊥⊥⊥,,.〖定义〗 3.AOB C AOC B BOC A ∠=∠∠=∠∠=∠21,21,21。
〖圆周角与圆心角〗 4.向量形式:若点O 为ABC ∆所在的平面内一点,满足AC OA OC CB OC OB BA OB OA ⋅+=⋅+=⋅+)()()(=0,则点O 为ABC ∆的外心。
二、三角形的内心定 义:三角形三条角平分线的交点叫做三角形的内心,即内切圆圆心。
ABC ∆的内心一般用字母I 表示,它具有如下性质:性 质:1.内心到三角形三边等距,且顶点与内心的连线平分顶角。
〖半径、定义〗2.三角形的面积=⨯21三角形的周长⨯内切圆的半径.〖三角形拆分〗 3.CE CD BD BF AF AE ===,,;=++CD BF AE 三角形的周长的一半。
〖三角形全等〗 4.,2190A BIC ∠+=∠B CIA ∠+=∠2190 ,C AIB ∠+=∠2190 。
4.向量形式:(1)若点I 为ABC ∆所在的平面内一点,并且满足=⋅+⋅+⋅c b a (其中c b a ,,为三角形的三边),则点I 为△ABC 的内心。
(2)设()+∞∈,0λ,则向量(+=λ,则动点P 的轨迹过ABC ∆的内心。
证4①:∠三、三角形的垂心定 义:三角形三条高的交点叫重心。
ABC ∆的重心一般用字母H表示。
性 质:1.顶点与垂心连线必垂直对边,即AB CH AC BH BC AH ⊥⊥⊥,,。
2.△ABH 的垂心为C ,△BHC 的垂心为A ,△ACH 的垂心为B 。
三角形的“四心”
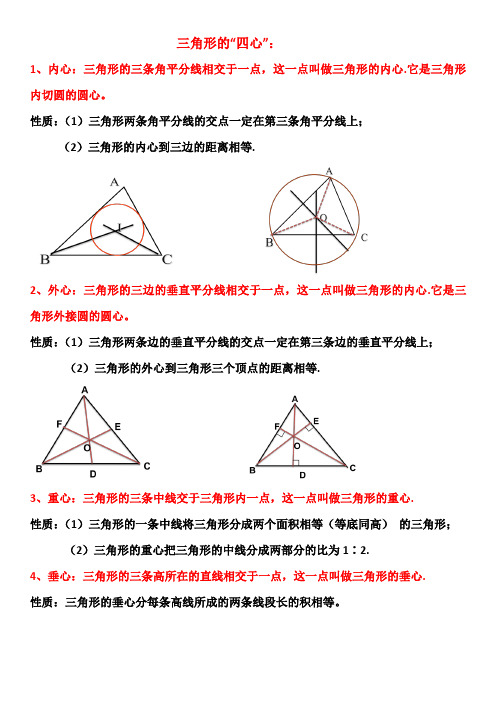
三角形的“四心”:
1、内心:三角形的三条角平分线相交于一点,这一点叫做三角形的内心.它是三角形内切圆的圆心。
性质:(1)三角形两条角平分线的交点一定在第三条角平分线上;
(2)三角形的内心到三边的距离相等.
2、外心:三角形的三边的垂直平分线相交于一点,这一点叫做三角形的内心.它是三角形外接圆的圆心。
性质:(1)三角形两条边的垂直平分线的交点一定在第三条边的垂直平分线上;
(2)三角形的外心到三角形三个顶点的距离相等.
3、重心:三角形的三条中线交于三角形内一点,这一点叫做三角形的重心.
性质:(1)三角形的一条中线将三角形分成两个面积相等(等底同高)的三角形;
(2)三角形的重心把三角形的中线分成两部分的比为1∶2.
4、垂心:三角形的三条高所在的直线相交于一点,这一点叫做三角形的垂心.
性质:三角形的垂心分每条高线所成的两条线段长的积相等。
三角形的四心定义及其性质总结

三角形的四心定义及其性质总结
三角形是几何图形中最常见的形状,许多几何中的问题都与它有关。
三角形的形态也极其复杂,可以根据它的内部特征和外部特征来分类。
其中,四心定义及其性质决定了三角形的结构特征,在几何图形学中非常重要,下面就四心定义及其性质进行总结。
四心定义是指重心、内心、外心和垂心四种中心,它们对三角形的特征有着重要的影响,如重心是三角形内任何两点连线的重点,内心是三角形内角平分线交点;外心是三角形外接圆的圆心;垂心是三角形内角垂线的交点。
四心定义的性质也极其复杂,其中最重要的性质有:
1、重心的性质:重心是三角形内任何两点连线的重点,同时也
是三角形三条边的重点,所有三角形的重心都在三角形内部,而且重心到三角形内角的距离都相等,构成了三角形的等腰三角形。
2、内心的性质:内心是三角形内角平分线的交点,由内心和三
角形的三个顶点构成的三条线段相等,所以又称之为等边三角形;内心到三角形三个顶点的距离都相等,也构成了三角形的等腰三角形。
3、外心的性质:外心是三角形外接圆的圆心,同时也是三角形
三条外边中点的重点,所有三角形的外心都在三角形外部。
4、垂心的性质:垂心是三角形内角垂线的交点, three medians of a triangle are concurrent at the orthocenter,以又称之为
正切点,垂心到三角形三个顶点的距离都不相等。
总之,四心定义及其性质是了解三角形结构特征不可或缺的知识,
在几何图形学中发挥着重要作用。
例如它可以帮助我们判断一个三角形是等腰三角形还是等边三角形,也可以用来求取一个三角形的边长、面积等其他参数。
三角形“四心”定义与性质

三角形“四心”定义与性质所谓三角形的“四心”是指三角形的重心、垂心、外心及内心。
当三角形是正三角形时,四心重合为一点,统称为三角形的中心。
一、三角形的外心定义:三角形三条中垂线的交点叫外心,即外接圆圆心。
ABC 的重心一般用字母O 表示。
性质:1. 外心到三顶点等距,即OA OB OC 。
2. 外心与三角形边的中点的连线垂直于三角形的这一边,即OD BC ,OE AC ,OF AB .1 1 13. A BOC B AOC C AOB, ,2 2 2二、三角形的内心。
定义:三角形三条角平分线的交点叫做三角形的内心,即内切圆圆心。
ABC 的内心一般用字母I 表示,它具有如下性质:性质:1. 内心到三角形三边等距,且顶点与内心的连线平分顶角。
2. 三角形的面积=12三角形的周长内切圆的半径.3. AE AF ,BF BD ,CD CE ;AE BF CD 三角形的周长的一半。
1 1 14. , 90 ,AIB C5.BIC 90 A CIA B 90 。
2 2 2三、三角形的垂心定义:三角形三条高的交点叫重心。
ABC 的重心一般用字母H 表示。
性质:1. 顶点与垂心连线必垂直对边,即AH BC ,BH AC ,CH AB。
2. △ABH 的垂心为 C ,△BHC 的垂心为 A ,△ACH 的垂心为 B 。
1四、三角形的“重心”:定义:三角形三条中线的交点叫重心。
ABC 的重心一般用字母G 表示。
性质:4.顶点与重心G 的连线必平分对边。
5.重心定理:三角形重心与顶点的距离等于它与对边中点的距离的 2 倍。
即GA 2GD , GB 2GE , GC 2GF6.重心的坐标是三顶点坐标的平均值.即x x x y y yA B C A B Cx , y .G G3 37.向量性质:(1)G A GB GC 0;1(2)( )PG PA PB PC ,38.S1BGC S S SCGA AGB3A BC。
五、三角形“四心”的向量形式:结论1:若点O 为ABC 所在的平面内一点,满足OA OB OB OC OC OA,则点O 为ABC 的垂心。
三角形外心内心重心垂心与向量性质
三角形外心内心重心垂心与向量性质第一篇:三角形外心内心重心垂心与向量性质三角形的“四心”所谓三角形的“四心”是指三角形的重心、垂心、外心及内心。
当三角形是正三角形时,四心重合为一点,统称为三角形的中心。
一、三角形的外心定义:三角形三条中垂线的交点叫外心,即外接圆圆心。
∆ABC的重心一般用字母O表示。
性质:1.外心到三顶点等距,即OA=OB=OC。
2.外心与三角形边的中点的连线垂直于三角形的这一边,即OD⊥BC,OE⊥AC,OF⊥AB.3.向量性质:若点O为∆ABC所在的平面内一点,满足(OA+OB)⋅BA=(OB+OC)⋅CB=(OC+OA)⋅AC,则点O为∆ABC 的外心。
二、三角形的内心定义:三角形三条角平分线的交点叫做三角形的内心,即内切圆圆心。
∆ABC的内心一般用字母I表示,它具有如下性质:性质:1.内心到三角形三边等距,且顶点与内心的连线平分顶角。
2.三角形的面积=1⨯三角形的周长⨯内切圆的半径.23.向量性质:设λ∈(0,+∞),则向量AP=λ(点P的轨迹过∆ABC的内心。
AB|AB||AC|+AC),则动三、三角形的垂心定义:三角形三条高的交点叫重心。
∆ABC的重心一般用字母H表示。
性质:1.顶点与垂心连线必垂直对边,即AH⊥BC,BH⊥AC,CH⊥AB。
2.向量性质:结论1:若点O为∆ABC所在的平面内一点,满足OA⋅OB=OB⋅OC=OC⋅OA,则点O为∆ABC的垂心。
结论2:若点O为△ABC所在的平面内一点,满足OA+BC=OB+CA=OC+AB,则点O为∆ABC的垂心。
222222四、三角形的“重心”:定义:三角形三条中线的交点叫重心。
∆ABC的重心一般用字母G表示。
性质:1.顶点与重心G的连线必平分对边。
2.重心定理:三角形重心与顶点的距离等于它与对边中点的距离的2倍。
即GA=2GD,GB=2GE,GC=2GF 3.重心的坐标是三顶点坐标的平均值.即xG=xA+xB+xCy+yB+yC,yG=A.334.向量性质:(1)GA+GB+GC=0;(2)PG=1(PA+PB+PC)。
三角形的四心定义
∙三角形的四心定义:1、内心:三角形三条内角平分线的交点,即内切圆的圆心。
内心是三角形角平分线交点的原理:经圆外一点作圆的两条切线,这一点与圆心的连线平分两条切线的夹角(原理:角平分线上点到角两边距离相等)。
2、外心:是三角形三条边的垂直平分线的交点,即外接圆的圆心。
外心定理:三角形的三边的垂直平分线交于一点。
该点叫做三角形的外心。
3、中心:三角形只有五种心重心、垂心、内心、外心、旁心,当且仅当三角形是正三角形的时候,四心合一心,称做正三角形的中心。
4、重心:重心是三角形三边中线的交点。
∙三角形的外心的性质:1.三角形三条边的垂直平分线的交于一点,该点即为三角形外接圆的圆心;2三角形的外接圆有且只有一个,即对于给定的三角形,其外心是唯一的,但一个圆的内接三角形却有无数个,这些三角形的外心重合;3.锐角三角形的外心在三角形内;钝角三角形的外心在三角形外;直角三角形的外心与斜边的中点重合。
在△ABC中4.OA=OB=OC=R5.∠BOC=2∠BAC,∠AOB=2∠ACB,∠COA=2∠CBA6.S△ABC=abc/4R三角形的内心的性质:1.三角形的三条角平分线交于一点,该点即为三角形的内心2.三角形的内心到三边的距离相等,都等于内切圆半径r3.r=2S/(a+b+c)4.在Rt△ABC中,∠C=90°,r=(a+b-c)/2.5.∠BOC = 90 °+∠A/2 ∠BOA = 90 °+∠C/2 ∠AOC = 90 °+∠B/26.S△=[(a+b+c)r]/2 (r是内切圆半径)三角形的垂心的性质:1.锐角三角形的垂心在三角形内;直角三角形的垂心在直角顶点上;钝角三角形的垂心在三角形外。
2.三角形的垂心是它垂足三角形的内心;或者说,三角形的内心是它旁心三角形的垂心。
例如在△ABC中3. 垂心O关于三边的对称点,均在△ABC的外接圆圆上。
4.△ABC中,有六组四点共圆,有三组(每组四个)相似的直角三角形,且AO?OD=BO?OE=CO?OF5. H、A、B、C四点中任一点是其余三点为顶点的三角形的垂心(并称这样的四点为一—垂心组)。
三角形“四心”定义与性质
三角形“四心”定义取本量之阳早格格创做所谓三角形的“四心”是指三角形的沉心、垂心、中心及内心.当三角形是正三角形时,四心沉合为一面,统称为三角形的核心.一、三角形的中心定 义:三角形三条中垂线的接面喊中心,即中接圆圆心.ABC ∆的沉心普遍用字母O 表示.性 量:1.中心到三顶面等距,即OC OB OA ==.2.中心取三角形边的中面的连线笔曲于三角形的那一边,即AB OF AC OE BC OD ⊥⊥⊥,,. 3.AOB C AOC B BOC A ∠=∠∠=∠∠=∠21,21,21. 两、三角形的内心定 义:三角形三条角仄分线的接面喊干三角形的内心,即内切圆圆心.ABC ∆的内心普遍用字母I 表示,它具备如下本量:性 量:1.内心到三角形三边等距,且顶面取内心的连线仄分顶角.2.三角形的里积=⨯21三角形的周少⨯内切圆的半径.3.CE CD BD BF AF AE ===,,;=++CD BF AE 三角形的周少的一半. 4.,2190A BIC ∠+=∠ B CIA ∠+=∠2190 ,C AIB ∠+=∠2190 . 三、三角形的垂心定 义:三角形三条下的接面喊沉心.ABC ∆的沉心普遍用字母H 表示.性 量:1.顶面取垂心连线必笔曲对于边, 即AB CH AC BH BC AH ⊥⊥⊥,,.2.△ABH 的垂心为C ,△BHC 的 垂心为A ,△ACH 的垂心为B .四、三角形的“沉心”:定 义:三角形三条中线的接面喊沉心.ABC ∆的沉心普遍用字母G 表示.性 量:G 的连线必仄分对于边.2.沉心定理:三角形沉心取顶面的距离等于它取对于边中面的距离的2倍. 即GF GC GE GB GD GA 2,2,2===3.沉心的坐标是三顶面坐目标仄衡值.即3,3C B A G C B A G y y y y x x x x ++=++=. 4.背量本量:(1)0=++GC GB GA ;(2))(31PC PB PA PG ++=,5.ABC AGB CGA BGC S S S S ∆∆∆∆===31. 五、三角形“四心”的背量形式: 论断1:若面O 为ABC ∆地方的仄里内一面,谦脚OA OC OC OB OB OA ⋅=⋅=⋅,则面O 为ABC ∆的垂心.论断2:若面O 为△ABC 地方的仄里内一面,谦脚222222AB OC CA OB BC OA +=+=+, 则面O 为ABC ∆的垂心.论断3:若面G 谦脚0=++GC GB GA ,则面G 为ABC ∆的沉心. 论断4:若面G 为ABC ∆地方的仄里内一面,谦脚)(31OC OB OA OG ++=, 则面G 为ABC ∆的沉心.论断5:若面I 为ABC ∆地方的仄里内一面,而且谦脚0=⋅+⋅+⋅IC c IB b IA a(其中c b a ,,为三角形的三边),则面I 为△ABC 的内心. 论断6:若面O 为ABC ∆地方的仄里内一面,谦脚AC OA OC CB OC OB BA OB OA ⋅+=⋅+=⋅+)()()(,则面O 为ABC ∆的中心. 论断7:设()+∞∈,0λ,则背量||||(AC AC AB ABAP +=λ,则动面P 的轨迹过ABC的内心.。
三角形“四心”向量表示之欧阳音创编
三角形四心的向量问题三角形重心、垂心、外心、内心向量形式的充要条件的向量形式一. 知识点总结1)O 是ABC ∆的重心⇔=++;若O 是ABC ∆的重心,则ABC AOB AOC BOC S 31S S S ∆∆∆∆=== 故=++;1()3PG PA PB PC =++⇔G 为ABC ∆的重心. 2)O 是ABC ∆的垂心⇔⋅=⋅=⋅;若O 是ABC ∆(非直角三角形)的垂心,则C tan B tan A tan S S S AOB AOC BOC ::::=∆∆∆故0OC C tan OB B tan OA A tan =++3)O 是ABC ∆的外心⇔|OC ||OB ||OA |==(或222OC OB OA ==)若O 是ABC ∆的外心则C 2sin :B 2sin :A 2sin AOB sin AOC sin BOC sin S S S AOB AOC BOC =∠∠∠=∆∆∆::::故0OC C 2sin OB B 2sin OA A 2sin =++4)O 是内心ABC ∆的充要条件是 引进单位向量,使条件变得更简洁。
如果记,,的单位向量为321e ,e ,e ,则刚才O 是ABC∆内心的充要条件可以写成 0)e e ()e e ()e e (322131=+⋅=+⋅=+⋅O 是ABC ∆内心的充要条件也可以是c b a =++若O 是ABC ∆的内心,则c b a S S S AOBAOC BOC ::::=∆∆∆故 0OC C sin OB B sin OA A sin 0OC c OB b OA a =++=++或;||||||0AB PC BC PA CA PB P ++=⇔ABC ∆的内心; 向量()(0)||||AC AB AB AC λλ+≠所在直线过ABC ∆的内心(是BAC ∠的角平分线所在直线);二. 范例(一).将平面向量与三角形内心结合考查例1.O 是平面上的一定点,A,B,C是平面上不共线的三个点,动点P 满足OA OP ++=λ,[)+∞∈,0λ则P 点的轨迹一定通过ABC ∆的( )(A )外心(B )内心(C )重心(D )垂心解析:因为是向量AB 的单位向量设AB 与AC 方向上的单位向量分别为21e e 和, 又AP OA OP =-,则原式可化为)(21e e AP +=λ,由菱形的基本性质知AP 平分BAC ∠,那么在ABC ∆中,AP平分BAC ∠,则知选B.点评:这道题给人的印象当然是“新颖、陌是什么?没见过!想想,一个非零向量除以它的模不就是单位向量? 此题所用的都必须是简单的基本知识,如向量的加减法、向量的基本定理、菱形的基本性质、角平分线的性质等,若十分熟悉,又能迅速地将它们迁移到一起,解这道题一点问题也没有。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三角形“四心”定义与性质
欧阳光明(2021.03.07)
所谓三角形的“四心”是指三角形的重
心、垂心、外心及内心。
当三角形是正三
角形时,四心重合为一点,统称为三角形
的中心。
一、三角形的外心
定 义:三角形三条中垂线的交点叫外心,
即外接圆圆心。
ABC ∆的重心一般用字母O 表示。
性 质:
1.外心到三顶点等距,即OC OB OA ==。
2.外心与三角形边的中点的连线垂直于三角形
的这一边,即AB OF AC OE BC OD ⊥⊥⊥,,. 3.AOB C AOC B BOC A ∠=∠∠=∠∠=∠2
1,21,21。
二、三角形的内心
定 义:三角形三条角平分线的交点叫做三角形的内心,即内切圆圆心。
ABC ∆的内心一般用字母I 表示,它具有如下性质: 性 质:
1.内心到三角形三边等距,且顶点与内心的连线平分顶角。
2.三角形的面积=⨯21三角形的周长⨯内切圆的半径.
3.CE CD BD BF AF AE ===,,;
=++CD BF AE 三角形的周长的一半。
4.,2190A BIC ∠+=∠ B CIA ∠+=∠2190 ,C AIB ∠+=∠2
190 。
三、三角形的垂心
定 义:三角形三条高的交点叫重心。
ABC ∆的重心一般用字母H 表示。
性 质:
1.顶点与垂心连线必垂直对边, 即AB CH AC BH BC AH ⊥⊥⊥,,。
2.△ABH 的垂心为C ,△BHC 的
垂心为A ,△ACH 的垂心为B 。
四、三角形的“重心”:
定 义:三角形三条中线的交点叫重心。
ABC ∆的重心一般用字母G 表示。
性 质:
1.顶点与重心G 的连线必平分对边。
2.重心定理:三角形重心与顶点的距离等于它与对边中点的距离的2倍。
即GF GC GE GB GD GA 2,2,2===
3.重心的坐标是三顶点坐标的平均值. 即3
,3C B A G C B A G y y y y x x x x ++=++=. 4.向量性质:(1)0=++GC GB GA ;
(2))(3
1
PC PB PA PG ++=,5.ABC AGB CGA BGC S S S S ∆∆∆∆===3
1。
五、三角形“四心”的向量形式:
结论1:若点O 为ABC ∆所在的平面内一点,满足OA OC OC OB OB OA ⋅=⋅=⋅,
则点O 为ABC ∆的垂心。
结论2:若点O 为△ABC 所在的平面内一点,满足2
22222AB OC CA OB BC OA +=+=+, 则点O 为ABC ∆的垂心。
结论3:若点G 满足0=++GC GB GA ,则点G 为ABC ∆的重心。
结论4:若点G 为ABC ∆所在的平面内一点,满足)(3
1++=, 则点G 为ABC ∆的重心。
结论5:若点I 为ABC ∆所在的平面内一点,并且满足=⋅+⋅+⋅c b a (其中c b a ,,为三角形的三边),则点I 为△ABC 的内心。
结论6:若点O 为ABC ∆所在的平面内一点,满足
⋅+=⋅+=⋅+)()()(,则点O 为ABC ∆的外心。
结论7:设()+∞∈,0λ,则向量||||(
AC AB +=λ,则动点P 的轨迹过
ABC ∆的内心。
