已知平行截面面积函数的立体体积
§2已知幂势平行截面面积求体积

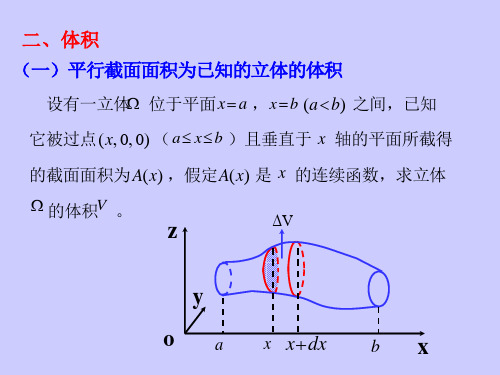
1 §2 由平行截面面积求体积一、已知平行截面面积函数的一般体积公式:设一几何体夹在x =a 和x =b (a<b )这两个平行平面之间,用垂直于X 轴的平面去截此几何体,设载面与X 轴交点为(x ,0),可得的截面面积为S (x ),如果S(x)是[a,b]上的(R )可积函数,则该几何体的体积V 等于:()ba V S x dx =⎰。
注:利用微元法推导公式例1 求由两个圆柱面 222a y x =+ 和 222a z x =+所围立体体积 . ( 3316a ) 例2 求由椭球面2222221x y z a b c ++=所围的几何体体积。
(a,b,c>0) ( abc π34 ) 祖暅原理: 夫幂势即同 , 则积不容异 . ( 祖暅系祖冲之之子,齐梁时人,大约在五世纪下半叶到六世纪初 )补例1 求底面积为S ,高为h 的斜柱体的体积V 。
补例2 求底面积为S ,高为h 的圆锥体的体积V 。
二、旋转体的体积定义旋转体并推导出体积公式.设y =y(x)于[a,b](R )可积,曲线y =y(x),a ≤x ≤b ,绕x 轴产生旋转体的截面积为S(x)=2()y x π,则 V 旋体=2()b ba a S x dx y dx π=⎰⎰ 注:利用微元法推导公式例3 推导高为h , 底面半径为r 的正圆锥体体积公式.例4求由圆)0(,)(222R r r R y x <<≤-+绕X 轴一周所得旋转体体积.特别有 25)20(22≤-+y x 对应的面积为10002π补例3 求抛物线22y x =,0≤x ≤1分别绕x 轴和y 轴所产生的旋转体体积。
补例4 求由曲线02=-y x 和0=-y x 所围平面图形绕X 轴旋转所得立体体积.补例5 ,0 , :==-x e y D x X 轴正半轴 . D 绕X 轴旋转 . 求所得旋转体体积.作业 P 246:1,2(1)、(2)、(3)、5*。
已知平行截面面积求立体的体积:图形、动画、计算

四川大学数学学院 徐小湛
July 1, 2012
切片法 3
例 1立 体 以 f(x ) x 2 1 和 g (x ) x 4 1 ( 3 x 3 ) 之 间 的 区 域 为 底 ,
1 0
1 5 0
在 x 处 的 垂 直 于 x 轴 的 截 面 是 一 个 高 H 3 的 等 腰 三 角 形 。
3
3 2 1 01 5 0 1 2 5
3
-3230x21100x432709 dx125
f:=x->(3/2)*(x^2/10+x^4/150+2): a:=-3:b:=3: Integrate(f(x),x=a..b)=integrate(f(x),x=a..b);
四川大学数学学院 徐小湛
July 1, 2012
切片法 5
现在来求这个立体的体积
截面面积 A(x) 1 3 [ f (x) g (x)]
2 3 x2 x4 ( 2) 2 10 150
立 体 体 积 V 3A ( x ) d x 33 (x 2 x 4 2 ) d x 2 7 0 9
切片法 1
已知平行截面的面积求体积
(切片法)
h蜀ttp南://xu竹xzm海
四川大学数学学院 徐小湛
July 1, 2012
切片法 2
用数学软件Maple作了有关动画 这些动画生动地显示了立体的形成过程
计算了一些立体的体积
g(x) x4 1 150
x
y
f (x) x2 1 10
四川大学数学学院 徐小湛
July 1, 2012
切片法 4
动画的Maple程序
数学分析10.2由平行截面面积求体积

第十章 定积分的应用 2 由平行截面面积求体积定义:设Ω为三维空间中的一立体,它夹在垂直于x 轴的两平面x=a 与x=b 之间(a<b). 称Ω为位于[a,b]的立体. 若在任意一点x ∈[a,b]处作垂直于x 轴的平面,它截得Ω的截面面积显然是x 的函数,记为A(x), x ∈[a,b],并称之为Ω的截面面积函数.公式1:设截面面积函数A(x)是[a,b]上的一个连续函数,对[a,b]作分割T :a=x 0<x 1<…<x n =b. 过各分点作垂直于x 的平面x=x i , i=1,2,…,n ,它们把Ω切割成n 个薄片. 设A(x)在每个小区间△i =[x i-1,x i ]上的最大, 最小值分别为M i 与m i ,那么每一薄片的体积△V i 满足 m i △x i ≤△V i ≤M i △x i . 于是Ω的体积V=∑=n1i i V △满足∑=n1i iix△m ≤V ≤∑=n1i i i x △M . 因为A(x)连续,从而在[a,b]上可积,所以当T 足够小时,能使i n1i i x △ω∑==∑=n1i i i i x )△m -(M <ε,ε为任意小的正数.∴V=∑=→n 1i i 0T M lim △x i (或∑=→n 1i i 0T m lim △x i )=∑=→n1i 0T A lim (ξi )△x i . 其中A(ξi )=M i (或m i ). ∴V=⎰ba A(x )dx.例1:求由两个圆柱面x 2+y 2=a 2与z 2+x 2=a 2 所围立体的体积.解:如图取该立体的第一卦限,即81部分.对任一x 0∈[0,a],平面x=x 0与这部分立体的截面是正方形,边长为:202x a -,即A(x)=a 2-x 2, x ∈[0,a]. ∴V=8⎰a 0A(x )dx=8⎰-a22)x (a dx=316a 3.例2:求由椭球面222222cz b y a x ++=1所围立体(椭球)的体积.解:以平面x=x 0(|x 0|≤a)截椭球面,得椭圆:⎪⎪⎭⎫ ⎝⎛-+⎪⎪⎭⎫ ⎝⎛-220222222a x 1c z a x 1b y =1.∴截面面积函数为:A(x)=πbc ⎪⎪⎭⎫ ⎝⎛-22a x 1, x ∈[-a,a]. ∴V=⎰aa -A(x )dx=⎰⎪⎪⎭⎫ ⎝⎛-aa -22a x 1πbc dx=34πabc.注:当a=b=c=r 时,就等于球的体积34πr 3.定理:设ΩA ,ΩB 为位于同一区间a,b 的两个立体,其体积分别V A ,V B .若在[a,b]上它们的截面面积函数A(x)与B(x)皆连续,且A(x)=B(x)则V A =V B .公式2:设f 是[a,b]上的连续函数,Ω是由平面图形0≤|y|≤|f(x)|, a ≤x ≤b 绕x 轴旋转一周的旋转体,则截面面积函数为A(x)=π[f(x)]2, x ∈[a,b]. ∴旋转体Ω的体积为:V=π⎰ba2[f(x )]dx.例3:试用公式2导出圆锥体的体积公式.解:设正圆锥的高为h ,底圆半径为r ,则有0≤|y|≤hrx, x ∈[0,h].∴V=π⎰⎪⎭⎫⎝⎛h02x h r dx=31πr 2h.例4:求由圆x 2+(y-R)2≤r 2 (0<r<R)绕x 轴旋转一周所得环状立体体积.解:圆的上下半圆分别为:y=f(x)=R+22x r -;y=g(x)=R-22x r -, |x|≤r. ∴圆环体截面面积函数为:A(x)=π[f(x)]2-π[g(x)]2=4πR 22x r -, x ∈[-r,r]. ∴V=2⎰-r022x r πR 4dx=8πR ⎰-r022x r dx= 2π2r 2R.习题1、如图所示,直椭圆柱体被通过底面短轴的斜平面所截,试求截得楔形体的体积.解:如图所示建立直角坐标系,则椭圆柱面的方程为:16y 100x 22+=1, 斜面的方程为Z=2x.用平面x=t 截这个立体,得一长方形,其边长为:8100t 12-和2t.∴A(x)=82x 100x 12⋅-=4x 100x 12-, x ∈[0,10].∴截得楔形体的体积为:V=⎰-1002100x 1x 4dx=3400.2、求下列平面曲线绕轴旋转所围成立体的体积: (1)y=sinx, 0≤x ≤π, 绕x 轴;(2)x=a(t-sint), y=a(1-cost) (a>0), 0≤t ≤2π, 绕x 轴; (3)r=a(1+cos θ), (a>0), 绕极轴;(4)2222b y a x +=1, 绕y 轴. 解:(1)V=π⎰π02x sin dx=2π2.(2)V=π⎰2π22cost)-(1a d[a(t-sint)]=πa3⎰2π3cost)-(1dt=5a 3π2.(3)r=a(1+cos θ), (a>0)是心脏线,而心脏线极轴之上部分的参数方程为: x=a(1+cos θ)cos θ; y=a(1+cos θ)sin θ, (0≤θ≤π) ∴V=|π⎰π322y dx|-|π⎰π32π2y dx|=|π⎰+π222θsin ) cos θ(1a da(1+cos θ)cos θ|=πa3⎰+++π2333) cos θ2θ)(1θcos sin 2θcosθsin 2θ(sin d θ=38πa 3.(4)y=b 22a x 1-, ∴V=πb 2⎰⎪⎪⎭⎫ ⎝⎛-a a -22a x 1dx =34a b 2π.3、已知球半径为r ,验证高为h 的球缺体积V=πh 2(r-3h) (h ≤r). 证:球缺体积可看作曲线y=22x R -,R-h ≤x ≤R 绕x 轴旋转而得, V=π⎰Rh-R 2y dx=π⎰-Rh-R 22)x (R dx=πh 2(r-3h). 得证.4、求曲线x=Rcos3t, y=Rsin3t, (R>0)所围平面绕x轴旋转所得立体体积.解:V=π⎰RR-2y dx=π⎰0π62tsinR dRcos3t=3πR3⎰π027ttcossin dt=10516πR3.5、导出曲边梯形0≤y≤f(x), a≤x≤b绕y轴旋转所得立体的体积公式为:V=2π⎰bax f(x)dx.证:曲边梯形绕y轴旋转,在x处的截面图形为一圆柱的侧面,其面积为:A(x)=2πx·f(x), a≤x≤b. 所围立体体积为:V=⎰baA(x)dx=2π⎰b a x f(x)dx. 得证.6、求0≤y≤sinx, 0≤x≤π所示平面图形绕y轴旋转所得立体体积. 解法1:曲线y=sinx可分成两部分:x=arcsiny, x=π-arcsiny, 0≤y≤1. 用y=t截这个立体,其截面面积为:A(t)=π[(π-arcsint)2- (arcsint)2]=π3-2π2arcsint.即面积函数为A(y)=π3-2π2arcsiny.∴V=⎰123arcsiny)2π-(πdy=2π2.解法2:利用第5题的结论可得:V=2π⎰πx sinx dx=2π2.。
空间立体体积的计算方法(1)

数学积分求体积方法概述摘要:定积分在大学数学学习及应用中起着非常重要的作用,一直以来定积分问题就是大学数学学习的重点,也是本科及研究生入学考试重点考察的内容之一,在我们的生活中起着很重要的作用!空间立体体积的计算在日常生活和学习中是十分重要的,对于规则的立体,中学里已有一些求解公式,对于不规则的立体,则需要用高等数学积分法加以解决。
本文总结了几种常见的利用积分求立体体积的方法及案例,通过所学积分学知识建立了更为普遍的立体体积的求解方法和计算公式,同时也介绍了相关的物理方法,并从具体的例题入手充分挖掘了空间立体体积计算的一些思想和方法。
关键词:积分; 空间立体体积; 积分区域; 被积函数引言空间立体体积的计算是生活中常见的问题,对于规则的空间立体体积的计算在中学时就有具体的计算公式,但对于不规则的空间立体体积则难以计算。
本文就主要针对各种形状的空间立体研究计算其体积的简便方法。
其实很多文献对空间立体体积的计算问题都进行了讨论,文献[1]就基本上包括了此问题的所有积分计算方法,并给出了相应的计算公式。
文献[2]-[9]分别从不同方面对各种方法进行了细致说明,并对个别特例进行了深入分析,给出了特殊的积分计算方法。
文献[10]则主要是对部分方法做出了总结,并列出了大量相关例题辅助理解。
以上文献充分体现出积分思想在解题中应用广泛,特别是在计算空间立体体积领域。
如果我们能够在积分学的基础上掌握空间立体体积的计算方法,则能使一些复杂的问题简单化,还易让人接受。
所以我们要分析掌握积分法,以便于解决与此相关的各种复杂问题,特别是各种空间立体体积的计算问题。
空间立体体积的计算是高等数学积分法在几何上的主要应用,其主要思想是将体积表示成定积分或重积分,研究空间立体,确定积分区域及被积函数,然后综合考虑立体特征、积分区域及被积函数特点,选择恰当的积分方法,使空间立体体积的计算简单明了。
本文在上述文献的基础上,总结了中学常见的空间立体体积的计算方法。
高数上册之立体的体积

一系列圆柱形薄壳组成的, 以此柱壳的体积作为体积元素,
当dx很小时,此小柱体的高看作f(x),
即为圆柱薄壳
8
y
在区间 [ x , x dx] 上
柱壳体的体积元素为
绵 阳
师 范 学 院
y f (x)
dV 2x dx f ( x )
V dV 2 xf ( x )dx
a a
b
o
a
x
b
4
x
图1
y
绵 同理,如旋转体由图2的曲边梯 阳 师 范 学 d 形绕y轴形成. x=(y) d 2 c 则体积为 V [ ( y )] dy 院
c
例3 求如图直角三角形绕x轴 旋转而成的圆锥体的体积.
解 可求得过点O及P(h,r)的直线方程为
r y x h
o
2 3 2
o
x
例4 求阿基米德螺线r=a(a>0)上 相应于从0到2的一段弧长. 解
s
b
r ( ) r ( )d a
2 2
2
1 2 d
0
a [2 1 4 2 ln(2 1 4 2 )] 2
14
1
绵 阳
师 范 学 院
解
如图,过x的截面是直角三角形,
边长分别为y和ytan .因此
1 2 A( x ) ( R x 2 ) tan ,-R 2 o R 1 x y 2 2 V ( R x ) tandx R R 2 x 1 2 1 3 2 3 R ( R x x ) tan | R R tan 2 3 3
o
b
x
解 圆的方程为 ( x b) 2 y 2 a 2 ,则所求体积可视为
由平行截面面积求体积

方形, 所以截面面积 A(x) R 2 。 2
R2 2的正
故两圆柱面所围成的立体体积
R
V 8
R2 x2
dx 16 R3
0
3
-a
z c
x0
by
0
ax
-b
-c
例2 求由椭圆面 x2 y2 z2 1 所围立体(椭球)的体积。(如上图) a2 b2 c2
解法:画出草图,关键是求出用垂直于 x 轴(其它轴也可)的平面 截立体所得截面面积函数 A(x) 的具体表达式。
解:如上图所示,上、下半圆方程分别为:y1 R r2 x2 , y2 R r2 x2 , x r则环体体积是由上、
下两个半圆绕 x 轴旋转一周所得旋转体的体积之差 (如下图所示):
r
y
o
r
x
上半圆:y1 R r2 x2
r
o
y
r
x
下半圆:y2 R r2 x2
A(x) f (x)2 , x [a, b],
由已知平行截面面积求体积的 公式可知,旋转体的体积公式为:
b
V f (x)2dx. a
例3 求圆锥体的体积公式
y
y f (x)
o a
y
y f (x)
oa
x
x b
b
x
4
例4 求由圆 x2 ( y R)2 r2 (0 r R)绕x轴旋转 一周所得环状立体体积。
例 1 求两圆柱: x2 y 2 R2 z 2 x2 R2 所围的立体体积 .卦限对称的,因此,它的体 积是其在第一卦限体积的8倍。如何求其在第一卦限的体积? 下图就是其在第一卦限部分立体:
-体积、旋转体的侧面积、一些物理量的计算
dV A(x)dx,
b
V a A(x)dx.
例 1.设有半径为R 的正圆柱体,被通过其底的直径
而与底面交成 的平面所截,求截得的圆柱楔的体积。
解:如图建立坐标系,
y tan
R
则底圆的方程为x2 y2 R2 。
x y
x[R, R] ,用过点x 且垂直于x 轴 o
x2
)dx
a
V
a a
b2 a2
(a
2
x2
)dx
ox
b
Байду номын сангаасax
x dx
2
b2 a2
a 0
(a2 x2)dx
2b2 a2
(a
2
x
1 3
x3
)
a 4 ab2. 03
例 3.已知圆台的上底半径为 r1 ,下底半径为r2 ,高为h ,
求它的体积。
解:如图选择坐标系,母线 AB 的方程为
y
0
r1
h r2
y
o a x xdx b x
设[x,x dx] 是[a,b] 上的代表小区间,相应的一小块立体
的体积记为V ,设 A(x) 在[x,x dx] 上的最小值和最大值分
别为m 和 M ,则 mdxV Mdx,
取近似
V A(x)dx,
其误差为 V A(x)dx (M m)dx ,
∵当dx0 时,(M m) 0 ,
则 dA 2f (x)dL ,
oa
故
A 2
b
f (x)
1 y2 dx.
a
y f (x) x x dx b x
[ 圆台的侧面积= 母线长 (上底半径 下底半径 ) 。在极限 状态,母线长是弧微元dL ;上底半径 下底半径 2f(x) 。]
平行截面面积求体积

例2 求由圆 x2 ( y R)2 r 2 (0 r R) 绕 x 轴
旋转一周所得环状立体的体积.
y
r
解 x2 ( y R)2 r2 的上下半圆分别为
R
y f2(x) R r2 x2,
O
x
y f1( x) R r 2 x2 .
因此
A( x)dx.
a
i 1
i 1
因此
b
V A( x)dx.
a
例1 求由两个圆柱面 围立体的体积.
x2 y2 a2 与 z2 x2 a2 所
z
a
x
a x0
O
a
y
解 先求出立体在第一卦限的体积V1. x0 [0,a] ,
x x0 与立体的截面是边长为 a2 x02 的正方形,
所以 A( x) a2 x2 , x [0,a]. 于是求得
A( x)
f
2 2
(
x)
f12( x) 4
R
r2 x2 ,
从而
r
V 8 R
r 2 x2dx 2 2r 2R.
0
例3 求由区域 ( x, y) | 0 x 1 , x y 2 x2
绕 y 轴旋转一周所得立体的体积. y
解 旋转体由曲线
2
x
y,
y [0,1]
2 y , y [1, 2]
围成的曲边三角形绕极轴旋转一周所得旋转体的
体积公式.
作业: P246:1,2(2,4),4,5,6
[ xi1, xi ] 上 A( x) 的最大、最小值分别为 Mi , mi ,
则第 i 个小薄片的体积 Vi 满足
mi xi Vi Mi xi ,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
思考: 可否选择 y 作积分变量 ? 此时截面面积函数是什么 ?
如何用定积分表示体积 ? 提示:
A( y) 2x y tan 2 tan y R2 y2
V 2 tan Ry R2 y2 dy 0
y
o
R (x, y) x
机动 目录 上页 下页 返回 结束
例2. 计算由曲面
所围立体(椭球体)
解: 如图所示取坐标系, 则圆的方程为 x2 y2 R2
垂直于x 轴 的截面是直角三角形, 其面积为
A(x) 1 (R2 x2 ) tan (R x R)
2
利用对称性
V 2 R 1 (R2 x2 ) tan d x
02
2 tan R2x 1 x3 R
30
y
ox
R x
机动 目录 上页 下页 返回 结束
已知平行截面面积函数的立体体积
设所给立体垂直于x 轴的截面面积为A(x),
上连续, 则对应于小区间
的体积元素为
dV A(x) d x
因此所求立体体积为
b
V a A(x) d x
A( x)
ax
bx
机动 目录 上页 下页 返回 结束
特别 , 当考虑连续曲线段
轴旋转一周围成的立体体积时, 有
V
b
的体积.
解: 垂直 x 轴的截面是椭圆
b2
y2 (1
x2 a2
)
z2 c2 (1
x2 a2
)
1
它的面积为
c
xo
a
b
因此椭球体体积为
V
2
a 2
)
d
x
2
bc
x
x3 3a 2
a
0
4 abc
3
特别当 a = b = c 时就是球体体积 .
机动 目录 上页 下页 返回 结束
例3. 求曲线 y 3 x2 1 与 x 轴围成的封闭图形
[
f
(
x)]2
dx
a
y
y f (x)
当考虑连续曲线段
o ax b x
绕 y 轴旋转一周围成的立体体积时,
有
V d [ ( y)]2dy c
y
d y x (y)
c
o
x
机动 目录 上页 下页 返回 结束
例1. 一平面经过半径为R 的圆柱体的底圆中心 , 并
与底面交成 角, 计算该平面截圆柱体所得立体的体积 .
36 2
21
(1x
2x12))22
dd
xx
24482
(x2
1) 2
d
x
00
15 1
机动 目录 上页 下页 返回 结束
绕直线 y=3 旋转得的旋转体体积. (94 考研)
解: 利用对称性 , 在第一象限
y
x2 2, 4 x2 ,
0 x 1 1 x 2
yB 3 A
故旋转体体积为
V 32 4 2 1 [3 (x2 2)]2 d x 0
C
o 1 2x
2 2 [3 (4 x2 )]2 d x 1
