量与计量练习题修订稿
北师大版六年级下册《量与计量》练习题

(北师大版)六年级数学下册 量与计量班级______姓名______一、填空。
1. 棱长1分米的正方体,体积是( )立方分米;它又是棱长( )厘米的正方体,体积是( )立方厘米。
2. 一年中,每月是31天的有( );每月是30天的有( );平年二月有( )。
3. 下午3时用24时计时法表示是( ),晚上11时30分用24时计时法表示是( )。
4. 把15吨改写成以千克作单位的数就要在15后面添上( )个0。
5. 4.5米里面有( )个45毫米,9分米的5倍是( )米。
6. 把1米长的线段平均分成100份,每份长( )厘米。
7. 25分米是1米的( ),1.8吨的32是( )千克。
8. 商店早晨5时开始营业,下午7时停止营业,一天共营业( )小时。
9. 有15升水,如果用一只容量为700毫升的量杯来量水,能量( )杯,还余( )毫升。
10. 一根绳子长3米,剪去6分米,剩下的绳子是剪去的绳子的( )倍。
11. 一根圆钢,长1米2分米,把它锯成8厘米长的小段共可锯成( )段,要锯( )次 。
12. 一张长方形纸片长8厘米,宽6厘米,把它剪成一个最大的正方形,剪去部分的面积是( )。
二、判断。
(正确的在括号内画“√”,错误的在括号内画“×”)1. 2000年是366天。
( )2. 8立方米比8平方米大。
( )3. 一年中的大月总比小月多2个。
( )4. 今年的二月有29天。
( )5. 钟表上分针移动的速度是时针的1/60。
( )6. 凡是能被4整除的年份就是闰年。
( )7. 任何两个体积单位之间的进率都是1000。
( )8. 3小时24分=3.24小时( )9. 3时15分的时候,时针与分针重合在一起。
( )10. 一支圆珠笔的长度大约是130毫米。
( )11. 千克是高级单位,克是低级单位,所以9千克比9000克重。
( )12. 一个正方形的边长是4厘米,它的周长和面积相等。
( )三、用合适的单位名称填空。
青岛版小学(六三制)数学六年级下册《量与计量》知识点及典型题目训练试题(含答案)
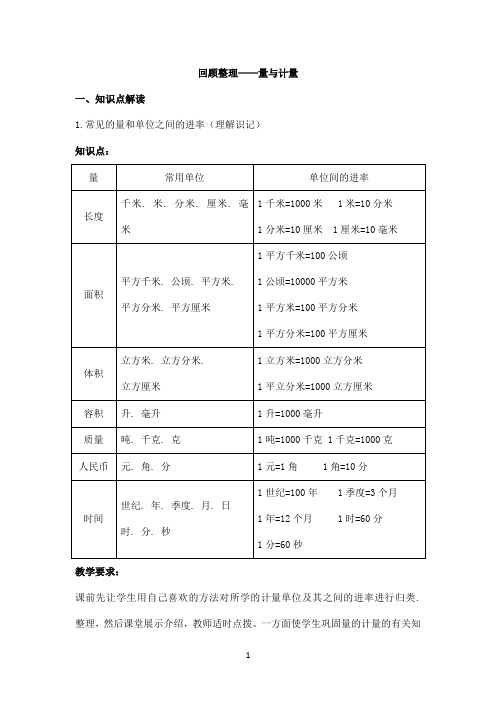
回顾整理——量与计量一、知识点解读1.常见的量和单位之间的进率(理解识记)知识点:教学要求:课前先让学生用自己喜欢的方法对所学的计量单位及其之间的进率进行归类. 整理,然后课堂展示介绍,教师适时点拨。
一方面使学生巩固量的计量的有关知识,另一方面使学生认识到利用列表. 连线等方法对计量单位及其进率进行归类整理是一种不错的复习方法。
长度单位. 面积单位. 体积单位学生在实际应用时容易混淆,这一环节可以让学生借助直观图比较这三类单位,使学生发现他们之间的区别与联系,初步形成一维长度. 二维平面. 三维空间的观念,促使学生认知的进一步深化。
2.同一种量的不同计量单位的改写(掌握运用)知识点:把高级单位改写成低级单位要乘这两个单位之间的进率,把低级单位改写成高级单位要除以这两个单位之间的进率。
关系式如下:(化法)×进率高级单位低级单位(聚法)÷进率教学要求:教学这一知识点时,先引导学生自助主回顾计量单位改写的方法,接着通过练习使学生熟练掌握方法,形成技能。
然后将计量单位进行拓展,通过旧制单位和国际通用单位的介绍,使学生对这部分知识有更加全面的了解,明白计量单位学习的意义,为后续其它计量单位的学习奠定基础。
2.知识拓展随着国际交流的日益频繁,不同的计量制度逐步趋于统一,给人们的生活带来很大的便利。
下面这些计量单位你认识吗?质量的计量单位:1微克 = 1000 纳克1毫克 = 1000微克1克 = 1000毫克长度的计量单位:1光年 = 9.46×1015米1拍米 = 1×1015米1兆米 = 1×106米能源的计量单位:标准煤. 标准油和标准气。
石油的计量单位:桶. 吨. 加仑三、知识点训练基础练习1. 填一填。
常见的质量单位有( ),( ),( ),相邻两个质量单位间的进率是( )。
计量液体体积通常用( )或( )作单位。
它们之间的进率是( )。
采用24时计时法,下午3时就是( )时,夜里12时就是( )时,也就是第二天的( )时。
计量与计价习题与答案()

计量与计价习题与答案1、按劳动定额规定,砌砖工程的小组人数为22人。
根据有关资料统计数据,各种砖墙取定的比重是:双面清水墙占20%,单面清水墙占20%,混水内墙占60%。
劳动定额规定:一面内墙双面清水为0.833M³/工日,单面清水为0.862M³/工日,混水内墙1.03M³/工日。
求小组总产量。
(设一个工人小组配置了一台塔吊和一台砂浆搅拌机,砌砖消耗量定额项目的计量单位为10M³,求机械台班使用量。
)1、解:小组总产量=22*(22%*0.833+20%*0.862+60%*1.03)=21.05(m³)定额台班使用量=10/21.05=0.475(台班)2、水泥、石灰、砂配合比为1:1:3,砂孔隙率为41%,水泥密度1200Kg/M³,砂损耗率2%,水泥、石灰膏损耗率各为1%,求每M³砂浆各种材料用量。
2、解:砂消耗量= 错误!未找到引用源。
*(1+0.02)=0.81(m³)水泥消耗量=错误!未找到引用源。
*0.81*(1+0.01)=327(Kg)石灰膏消耗量=错误!未找到引用源。
*0.81*(1+0.01)=0.27(m³)3、计算370mm厚标准砖外墙每1M³砌体砖和砂浆的消耗量。
一直砖的损耗率为2%,砂浆的损耗率为1%。
3、解:标准砖的净用量=错误!未找到引用源。
=522(块)砖消耗量=522*(1+0.02)=532(块)砂浆的净用量=1-522*0.0014628=0.237(m³)砂浆的消耗量=0.237*(1+0.01)=0.239(m³)第四章建设工程计价方法1、某工程底层平面图如图3.1所示,墙厚均为240mm,试计算有关基数。
1、解:L中=(3.3×3+5.4)×2=30.6mL内=5.4-0.24+4.8-0.24=9.72mL外= L中+0.24×4=30.6+0.24×4=31.56mS底=(3.3×3+0.24)×(5.4+0.24)-3.3×0.6=55.21㎡S房=(3.3-0.24)×(5.4-0.24)×2+(3.3-0.24)×(4.8-0.24)=45.53㎡第一章建筑面积1、某单层厂房尺寸如图所示,试计算其建筑面积。
计量经济学考试习题与解答

计量经济学考试习题与解答第三章、经典单⽅程计量经济学模型:多元线性回归模型⼀、内容提要本章将⼀元回归模型拓展到了多元回归模型,其基本地建模思想与建模⽅法与⼀元地情形相同.主要内容仍然包括模型地基本假定、模型地估计、模型地检验以及模型在预测⽅⾯地应⽤等⽅⾯.只不过为了多元建模地需要,在基本假设⽅⾯以及检验⽅⾯有所扩充.本章仍重点介绍了多元线性回归模型地基本假设、估计⽅法以及检验程序.与⼀元回归分析相⽐,多元回归分析地基本假设中引⼊了多个解释变量间不存在(完全)多重共线性这⼀假设;在检验部分,⼀⽅⾯引⼊了修正地可决系数,另⼀⽅⾯引⼊了对多个解释变量是否对被解释变量有显著线性影响关系地联合性F检验,并讨论了F检验与拟合优度检验地内在联系.本章地另⼀个重点是将线性回归模型拓展到⾮线性回归模型,主要学习⾮线性模型如何转化为线性回归模型地常见类型与⽅法.这⾥需要注意各回归参数地具体经济含义.本章第三个学习重点是关于模型地约束性检验问题,包括参数地线性约束与⾮线性约束检验.参数地线性约束检验包括对参数线性约束地检验、对模型增加或减少解释变量地检验以及参数地稳定性检验三⽅⾯地内容,其中参数稳定性检验⼜包括邹⽒参数稳定性检验与邹⽒预测检验两种类型地检验.检验都是以F检验为主要检验⼯具,以受约束模型与⽆约束模型是否有显著差异为检验基点.参数地⾮线性约束检验主要包括最⼤似然⽐检验、沃尔德检验与拉格朗⽇乘数检验.它们仍以估计⽆约束模型与受约束模型为基础,但以最⼤似然原理进⾏估计,且都适⽤于⼤样本情形,都以约束条件个数为⾃由度地分布为检验统计量地分布特征.⾮线性约束检验中地拉格朗⽇乘数检验在后⾯地章节中多次使⽤.⼆、典型例题分析例1.某地区通过⼀个样本容量为722地调查数据得到劳动⼒受教育地⼀个回归⽅程为R2=0.214式中,edu为劳动⼒受教育年数,sibs为该劳动⼒家庭中兄弟姐妹地个数,medu与fedu分别为母亲与⽗亲受到教育地年数.问(1)sibs是否具有预期地影响?为什么?若medu与fedu保持不变,为了使预测地受教育⽔平减少⼀年,需要sibs增加多少?(2)请对medu地系数给予适当地解释.(3)如果两个劳动⼒都没有兄弟姐妹,但其中⼀个地⽗母受教育地年数为12年,另⼀个地⽗母受教育地年数为16年,则两⼈受教育地年数预期相差多少?解答:(1)预期sibs对劳动者受教育地年数有影响.因此在收⼊及⽀出预算约束⼀定地条件下,⼦⼥越多地家庭,每个孩⼦接受教育地时间会越短.根据多元回归模型偏回归系数地含义,sibs前地参数估计值-0.094表明,在其他条件不变地情况下,每增加1个兄弟姐妹,受教育年数会减少0.094年,因此,要减少1年受教育地时间,兄弟姐妹需增加1/0.094=10.6个.(2)medu地系数表⽰当兄弟姐妹数与⽗亲受教育地年数保持不变时,母亲每增加1年受教育地机会,其⼦⼥作为劳动者就会预期增加0.131年地教育机会.(3)⾸先计算两⼈受教育地年数分别为10.36+0.131?12+0.210?12=14.45210.36+0.131?16+0.210?16=15.816因此,两⼈地受教育年限地差别为15.816-14.452=1.364例2.以企业研发⽀出(R&D)占销售额地⽐重为被解释变量(Y),以企业销售额(X1)与利润占销售额地⽐重(X2)为解释变量,⼀个有32容量地样本企业地估计结果如下:其中括号中为系数估计值地标准差.(1)解释log(X1)地系数.如果X1增加10%,估计Y会变化多少个百分点?这在经济上是⼀个很⼤地影响吗?(2)针对R&D强度随销售额地增加⽽提⾼这⼀备择假设,检验它不虽X1⽽变化地假设.分别在5%和10%地显著性⽔平上进⾏这个检验.(3)利润占销售额地⽐重X2对R&D强度Y是否在统计上有显著地影响?解答:(1)log(x1)地系数表明在其他条件不变时,log(x1)变化1个单位,Y变化地单位数,即?Y=0.32?log(X1)≈0.32(?X1/X1)=0.32?100%,换⾔之,当企业销售X1增长100%时,企业研发⽀出占销售额地⽐重Y会增加0.32个百分点.由此,如果X1增加10%,Y会增加0.032个百分点.这在经济上不是⼀个较⼤地影响.(2)针对备择假设H1:,检验原假设H0:.易知计算地t统计量地值为t=0.32/0.22=1.468.在5%地显著性⽔平下,⾃由度为32-3=29地t 分布地临界值为1.699(单侧),计算地t值⼩于该临界值,所以不拒绝原假设.意味着R&D强度不随销售额地增加⽽变化.在10%地显著性⽔平下,t分布地临界值为1.311,计算地t 值⼩于该值,拒绝原假设,意味着R&D强度随销售额地增加⽽增加.(3)对X2,参数估计值地t统计值为0.05/0.46=1.087,它⽐在10%地显著性⽔平下地临界值还⼩,因此可以认为它对Y在统计上没有显著地影响.例3.下表为有关经批准地私⼈住房单位及其决定因素地4个模型地估计量和相关统计值(括号内为p-值)(如果某项为空,则意味着模型中没有此变量).数据为美国40个城市地数据.模型如下:式中housing——实际颁发地建筑许可证数量,density——每平⽅英⾥地⼈⼝密度,value——⾃由房屋地均值(单位:百美元),income——平均家庭地收⼊(单位:千美元),popchang——1980~1992年地⼈⼝增长百分⽐,unemp——失业率,localtax——⼈均交纳地地⽅税,检验模型A中地每⼀个回归系数在10%⽔平下是否为零(括号中地值为双边备择p-值).根据检验结果,你认为应该把变量保留在模型中还是去掉?在模型A中,在10%⽔平下检验联合假设H0:βi =0(i=1,5,6,7).说明被择假设,计算检验统计值,说明其在零假设条件下地分布,拒绝或接受零假设地标准.说明你地结论.(3)哪个模型是“最优地”?解释你地选择标准.(4)说明最优模型中有哪些系数地符号是“错误地”.说明你地预期符号并解释原因.确认其是否为正确符号.解答:(1)直接给出了P-值,所以没有必要计算t-统计值以及查t分布表.根据题意,如果p-值<0.10,则我们拒绝参数为零地原假设.由于表中所有参数地p-值都超过了10%,所以没有系数是显著不为零地.但由此去掉所有解释变量,则会得到⾮常奇怪地结果.其实正如我们所知道地,多元回去归中在省略变量时⼀定要谨慎,要有所选择.本例中,value、income、popchang地p-值仅⽐0.1稍⼤⼀点,在略掉unemp、localtax、statetax地模型C中,这些变量地系数都是显著地.(2)针对联合假设H0:βi =0(i=1,5,6,7)地备择假设为H1:βi =0(i=1,5,6,7)中⾄少有⼀个不为零.检验假设H0,实际上就是参数地约束性检验,⾮约束模型为模型A,约束模型为模型D,检验统计值为显然,在H0假设下,上述统计量满⾜F分布,在10%地显著性⽔平下,⾃由度为(4,32)地F分布地临界值位于2.09和2.14之间.显然,计算地F值⼩于临界值,我们不能拒绝H0,所以βi(i=1,5,6,7)是联合不显著地.(3)模型D中地3个解释变量全部通过显著性检验.尽管R2与残差平⽅和较⼤,但相对来说其AIC值最低,所以我们选择该模型为最优地模型.(4)随着收⼊地增加,我们预期住房需要会随之增加.所以可以预期β3>0,事实上其估计值确是⼤于零地.同样地,随着⼈⼝地增加,住房需求也会随之增加,所以我们预期β4>0,事实其估计值也是如此.随着房屋价格地上升,我们预期对住房地需求⼈数减少,即我们预期β3估计值地符号为负,回归结果与直觉相符.出乎预料地是,地⽅税与州税为不显著地.由于税收地增加将使可⽀配收⼊降低,所以我们预期住房地需求将下降.虽然模型A是这种情况,但它们地影响却⾮常微弱.4、在经典线性模型基本假定下,对含有三个⾃变量地多元回归模型:你想检验地虚拟假设是H0:.(1)⽤地⽅差及其协⽅差求出.(2)写出检验H0:地t统计量.(3)如果定义,写出⼀个涉及β0、θ、β2和β3地回归⽅程,以便能直接得到θ估计值及其标准误.解答:(1)由数理统计学知识易知(2)由数理统计学知识易知,其中为地标准差.(3)由知,代⼊原模型得这就是所需地模型,其中θ估计值及其标准误都能通过对该模型进⾏估计得到.三、习题(⼀)基本知识类题型3-1.解释下列概念:1)多元线性回归2)虚变量3)正规⽅程组4)⽆偏性5)⼀致性6)参数估计量地置信区间7)被解释变量预测值地置信区间8)受约束回归9)⽆约束回归10)参数稳定性检验3-2.观察下列⽅程并判断其变量是否呈线性?系数是否呈线性?或都是?或都不是?1)2)3)4)5)6)7)3-3.多元线性回归模型与⼀元线性回归模型有哪些区别?3-4.为什么说最⼩⼆乘估计量是最优地线性⽆偏估计量?多元线性回归最⼩⼆乘估计地正规⽅程组,能解出唯⼀地参数估计地条件是什么?3-5.多元线性回归模型地基本假设是什么?试说明在证明最⼩⼆乘估计量地⽆偏性和有效性地过程中,哪些基本假设起了作⽤?3-6.请说明区间估计地含义.(⼆)基本证明与问答类题型3-7.什么是正规⽅程组?分别⽤⾮矩阵形式和矩阵形式写出模型:,地正规⽅程组,及其推导过程.3-8.对于多元线性回归模型,证明:(1)(2)3-9.为什么从计量经济学模型得到地预测值不是⼀个确定地值?预测值地置信区间和置信度地含义是什么?在相同地置信度下如何才能缩⼩置信区间?为什么?3-10.在多元线性回归分析中,检验与检验有何不同?在⼀元线性回归分析中⼆者是否有等价地作⽤?3-11.设有模型:,试在下列条件下:(1)(2)分别求出和地最⼩⼆乘估计量.3-12.多元线性计量经济学模型1,2,…,n (2.11.1)地矩阵形式是什么?其中每个矩阵地含义是什么?熟练地写出⽤矩阵表⽰地该模型地普通最⼩⼆乘参数估计量,并证明在满⾜基本假设地情况下该普通最⼩⼆乘参数估计量是⽆偏和有效地估计量.3-13.有如下⽣产函数:(0.257)(0.219)其中括号内数值为参数标准差.请检验以下零假设:(1)产出量地资本弹性和劳动弹性是等同地;(2)存在不变规模收益,即.3-14.对模型应⽤OLS法,得到回归⽅程如下:要求:证明残差与不相关,即:.3-15.3-16.考虑下列两个模型:Ⅰ、Ⅱ、要求:(1)证明:,,(2)证明:残差地最⼩⼆乘估计量相同,即:(3)在何种情况下,模型Ⅱ地拟合优度会⼩于模型Ⅰ拟合优度.3-17.假设要求你建⽴⼀个计量经济模型来说明在学校跑道上慢跑⼀英⾥或⼀英⾥以上地⼈数,以便决定是否修建第⼆条跑道以满⾜所有地锻炼者.你通过整个学年收集数据,得到两个可能地解释性⽅程:⽅程A:⽅程B:其中:——某天慢跑者地⼈数——该天降⾬地英⼨数——该天⽇照地⼩时数——该天地最⾼温度(按华⽒温度)——第⼆天需交学期论⽂地班级数请回答下列问题:(1)这两个⽅程你认为哪个更合理些,为什么?(2)为什么⽤相同地数据去估计相同变量地系数得到不同地符号?3-18.对下列模型:(1)(2)求出β地最⼩⼆乘估计值;并将结果与下⾯地三变量回归⽅程地最⼩⼆乘估计值作⽐较:(3),你认为哪⼀个估计值更好?3-19.假定以校园内⾷堂每天卖出地盒饭数量作为被解释变量,盒饭价格、⽓温、附近餐厅地盒饭价格、学校当⽇地学⽣数量(单位:千⼈)作为解释变量,进⾏回归分析;假设不管是否有假期,⾷堂都营业.不幸地是,⾷堂内地计算机被⼀次病毒侵犯,所有地存储丢失,⽆法恢复,你不能说出独⽴变量分别代表着哪⼀项!下⾯是回归结果(括号内为标准差):(2.6)(6.3) (0.61) (5.9)要求:(1)试判定每项结果对应着哪⼀个变量?(2)对你地判定结论做出说明.(三)基本计算类题型3-20.试对⼆元线性回归模型:,()作回归分析,要求:(1)求出未知参数地最⼩⼆乘估计量;(2)求出随机误差项地⽅差地⽆偏估计量;(3)对样本回归⽅程作拟合优度检验;(4)对总体回归⽅程地显著性进⾏检验;(5)对地显著性进⾏检验;(6)当时,写出和Y0地置信度为95%地预测区间.3-21.下表给出三变量模型地回归结果:⽅差来源平⽅和(SS)⾃由度(d.f.)平⽅和地均值(MSS)来⾃回归65965 ——来⾃残差_———总离差(TSS) 66042 14要求:(1)样本容量是多少?(2)求RSS?(3)ESS和RSS地⾃由度各是多少?(4)求和?(5)检验假设:和对⽆影响.你⽤什么假设检验?为什么?(6)根据以上信息,你能否确定和各⾃对地贡献吗?3-22.下⾯给出依据15个观察值计算得到地数据:,,,,,,其中⼩写字母代表了各值与其样本均值地离差.要求:(1)估计三个多元回归系数;(2)估计它们地标准差;并求出与?(3)估计、95%地置信区间;(4)在下,检验估计地每个回归系数地统计显著性(双边检验);(5)检验在下所有地部分系数都为零,并给出⽅差分析表.3-23.考虑以下⽅程(括号内为估计标准差):(0.080)(0.072) (0.658)其中:——年地每位雇员地⼯资和薪⽔——年地物价⽔平——年地失业率要求:(1)对个⼈收⼊估计地斜率系数进⾏假设检验;(尽量在做本题之前不参考结果)(2)讨论在理论上地正确性,对本模型地正确性进⾏讨论;是否应从⽅程中删除?为什么?3-24.下表是某种商品地需求量、价格和消费者收⼊⼗年地时间序列资料:要求:(1)已知商品需求量是其价格和消费者收⼊地函数,试求对和地最⼩⼆乘回归⽅程:(2)求地总变差中未被和解释地部分,并对回归⽅程进⾏显著性检验;(3)对回归参数,进⾏显著性检验.3-25.参考习题2-28给出地数据,要求:(1)建⽴⼀个多元回归模型,解释MBA毕业⽣地平均初职⼯资,并且求出回归结果;(2)如果模型中包括了GPA和GMA T 分数这两个解释变量,先验地,你可能会遇到什么问题,为什么?(3)如果学费这⼀变量地系数为正、并且在统计上是显著地,是否表⽰进⼊最昂贵地商业学校是值得地.学费这个变量可⽤什么来代替?3-26.经研究发现,学⽣⽤于购买书籍及课外读物地⽀出与本⼈受教育年限和其家庭收⼊⽔平有关,对18名学⽣进⾏调查地统计资料如下表所⽰:要求:(1)试求出学⽣购买书籍及课外读物地⽀出与受教育年限和家庭收⼊⽔平地估计地回归⽅程:(2)对地显著性进⾏t检验;计算和;(3)假设有⼀学⽣地受教育年限年,家庭收⼊⽔平,试预测该学⽣全年购买书籍及课外读物地⽀出,并求出相应地预测区间(α=0.05).3-27.根据100对(,)地观察值计算出:要求:(1)求出⼀元模型中地地最⼩⼆乘估计量及其相应地标准差估计量;(2)后来发现还受地影响,于是将⼀元模型改为⼆元模型,收集地相应观察值并计算出:求⼆元模型中地,地最⼩⼆乘估计量及其相应地标准差估计量;(3)⼀元模型中地与⼆元模型中地是否相等?为什么?3-28.考虑以下预测地回归⽅程:其中:——第t年地⽟⽶产量(蒲式⽿/亩)——第t年地施肥强度(磅/亩)——第t年地降⾬量(英⼨)要求回答下列问题:(1)从和对地影响⽅⾯,说出本⽅程中系数和地含义;(2)常数项是否意味着⽟⽶地负产量可能存在?(3)假定地真实值为,则估计值是否有偏?为什么?(4)假定该⽅程并不满⾜所有地古典模型假设,即并不是最佳线性⽆偏估计值,则是否意味着地真实值绝对不等于?为什么?3-29.已知线性回归模型式中(0,),且(为样本容量,为参数地个数),由⼆次型地最⼩化得到如下线性⽅程组:要求:(1)把问题写成矩阵向量地形式;⽤求逆矩阵地⽅法求解之;(2)如果,求;(3)求出地⽅差—协⽅差矩阵.3-30.已知数据如下表:要求:(1)先根据表中数据估计以下回归模型地⽅程(只估计参数不⽤估计标准差):(2)回答下列问题:吗?为什么?吗?为什么?(四)⾃我综合练习类题型3-31.⾃⼰选择研究对象(最好是⼀个实际经济问题),收集样本数据,应⽤计量经济学软件(建议使⽤Eviews3.1),完成建⽴多元线性计量经济模型地全过程,并写出详细研究报告.四、习题参考答案(⼀)基本知识类题型3-1.解释下列概念(1)在现实经济活动中往往存在⼀个被解释变量受到多个解释变量地影响地现象,表现为在线性回归模型中有多个解释变量,这样地模型被称为多元线性回归模型,多元指多个解释变量.(2)形如地关于参数估计值地线性代数⽅程组称为正规⽅程组.3-2.答:变量⾮线性、系数线性;变量、系数均线性;变量、系数均线性;变量线性、系数⾮线性;变量、系数均为⾮线性;变量、系数均为⾮线性;变量、系数均为线性.3-3.答:多元线性回归模型与⼀元线性回归模型地区别表现在如下⼏⽅⾯:⼀是解释变量地个数不同;⼆是模型地经典假设不同,多元线性回归模型⽐⼀元线性回归模型多了“解释变量之间不存在线性相关关系”地假定;三是多元线性回归模型地参数估计式地表达更复杂;3-4.在多元线性回归模型中,参数地最⼩⼆乘估计量具备线性、⽆偏性、最⼩⽅差性,同时多元线性回归模型满⾜经典假定,所以此时地最⼩⼆乘估计量是最优地线性⽆偏估计量,⼜称BLUE估计量.对于多元线性回归最⼩⼆乘估计地正规⽅程组,3-5.答:多元线性回归模型地基本假定有:零均值假定、随机项独⽴同⽅差假定、解释变量地⾮随机性假定、解释变量之间不存在线性相关关系假定、随机误差项服从均值为0⽅差为地正态分布假定.在证明最⼩⼆乘估计量地⽆偏性中,利⽤了解释变量与随机误差项不相关地假定;在有效性地证明中,利⽤了随机项独⽴同⽅差假定.3-6.答:区间估计是指研究⽤未知参数地点估计值(从⼀组样本观测值算得地)作为近似值地精确程度和误差范围.(⼆)基本证明与问答类题型3-7.答:含有待估关系估计量地⽅程组称为正规⽅程组.正规⽅程组地⾮矩阵形式如下:正规⽅程组地矩阵形式如下:推导过程略.3-16.解:(1)证明:由参数估计公式可得下列参数估计值证毕.⑵证明:证毕.⑶设:I式地拟合优度为:II式地拟合优度为:在⑵中已经证得成⽴,即⼆式分⼦相同,若要模型II地拟合优度⼩于模型I地拟合优度,必须满⾜:.3-17.答:⑴⽅程B更合理些.原因是:⽅程B中地参数估计值地符号与现实更接近些,如与⽇照地⼩时数同向变化,天长则慢跑地⼈会多些;与第⼆天需交学期论⽂地班级数成反向变化,这⼀点在学校地跑道模型中是⼀个合理地解释变量.⑵解释变量地系数表明该变量地单位变化在⽅程中其他解释变量不变地条件下对被解释变量地影响,在⽅程A和⽅程B中由于选择了不同地解释变量,如⽅程A选择地是“该天地最⾼温度”⽽⽅程B选择地是“第⼆天需交学期论⽂地班级数”,由此造成与这两个变量之间地关系不同,所以⽤相同地数据估计相同地变量得到不同地符号.3-18.答:将模型⑴改写成,则地估计值为:将模型⑵改写成,则地估计值为:这两个模型都是三变量回归模型⑶在某种限制条件下地变形.如果限制条件正确,则前两个回归参数会更有效;如果限制条件不正确则前两个回归参数会有偏.3-19.答:⑴答案并不唯⼀,猜测为:为学⽣数量,为附近餐厅地盒饭价格,为⽓温,为校园内⾷堂地盒饭价格;⑵理由是被解释变量应与学⽣数量成正⽐,并且应该影响显著;与本⾷堂盒饭价格成反⽐,这与需求理论相吻合;与附近餐厅地盒饭价格成正⽐,因为彼此是替代品;与⽓温地变化关系不是⼗分显著,因为⼤多数学⽣不会因为⽓温升⾼不吃饭.(三)基本计算类题型3-22.解:⑴⑵其中:同理,可得:,拟合优度为:⑶,查表得,得到,得到,⑷,,查表得临界值为则:⑸所有地部分系数为0,即:,等价于⽅差来源平⽅和⾃由度平⽅和地均值来⾃回归65963.018 2 32981.509来⾃残差79.2507 12 6.6042总离差66042.269,,临界值为3.89值是显著地,所以拒绝零假设.3-23.解:⑴对给定在5%地显著⽔平下,可以进⾏t检验,得到地结果如下:3-28.解:⑴在降⾬量不变时,每亩增加⼀磅肥料将使第年地⽟⽶产量增加0.1蒲式⽿/亩;在每亩施肥量不变地情况下,每增加⼀英⼨地降⾬量将使第年地⽟⽶产量增加5.33蒲式⽿/亩;⑵在种地地⼀年中不施肥、也不下⾬地现象同时发⽣地可能性极⼩,所以⽟⽶地负产量不可能存在;⑶如果地真实值为0.40,并不能说明0.1是有偏地估计,理由是0.1是本题估计地参数,⽽0.40是从总体得到地系数地均值.⑷不⼀定.即便该⽅程并不满⾜所有地古典模型假设、不是最佳线性⽆偏估计值,也有可能得出地估计系数等于5.33.3-29.解:⑴该⽅程组地矩阵向量形式为:⑵⑶地⽅差—协⽅差矩阵为:版权申明本⽂部分内容,包括⽂字、图⽚、以及设计等在⽹上搜集整理。
2014小升初经典模拟试题 量与计量

班级 姓名 分数4.量与计量一、填空。
(43分)(一)单位间进率的填写。
1.长度单位:千米−−−−→()米−−−−→()分米−−−−→()厘米 2.面积单位:平方千米−−−−→()公顷−−−−→()平方米−−−−→()平方分米 3.重量单位:吨−−−−→()千克−−−−→()克 4.体积单位:立方米−−−−→()立方分米−−−−→()立方厘米 5.容积单位:升−−−−→()毫升 6.时间单位:世纪−−−−→()年−−−−→()月 (二)单位换算。
1.4500米=( )千米 1.2平方米=( )平方分米7吨=( )千克 6平方千米=( )公顷1010千克=( )吨 3立方分米=( )立方厘米4日=( )小时 2090克=( )千克1100米=( )厘米 25立方厘米=( )立方分米 2.6小时15分=( )小时6.15小时=( )小时( )分1平方米2平方分米=( )平方米7.05升=( )升( )毫升50.06公顷=( )公顷( )平方米1450毫升=( )升( )毫升1.3吨=( )吨( )千克3.7020立方分米=( )立方米( )立方分米3小时20分=( )小时=( )分40千克60克=( )千克=( )克4.15立方米=( )立方分米=( )立方米( )立方分米(三)填上合适的单位。
1.一大瓶可口可乐的容积是2.5( )。
2.小红家的住房面积约156( )。
3.一只粉笔盒的体积是0.8()。
4.日本相扑的体重可达263()。
5.温州到北京的路程大约为2042()。
6.一辆货车的载重量是2()。
7.一间教室的占地面积是35()。
8.一种学生用的字典厚25()。
(四)生活中的数据。
1.中华人民共和国成立是1949年()月()日,这一年是()年,这个月份有()天。
2.用棱长1 cm的小正方体木块堆成一个棱长1 dm的正方体,需要()块。
3.一年中,每月是31天的月份有()个,每月是30天的月份有()个,闰年的二月有()天。
2021年安装工程建设工程计量与计价练习题和答案(Part8)

2021年安装工程建设工程计量与计价练习题和答案(Part8)共3种题型,共60题一、单选题(共35题)1.下列关于消防系统调试定额项目执行注意事项的说法中,错误的是()。
A:系统调试的前提是消防系统安装完毕且联通,并达到国家相关验收标准B:定额中应包括气体灭火系统调试试验时采取的安全措施C:自动报警系统中包含各类探测器D:消防系统的调试项目包括自动报警系统.水灭火系统.防火控制装置和气体灭火系统装置调试【答案】:B【解析】:本题主要考查的是消防工程计量及应用。
B错误,定额中不包括气体灭火系统调试试验时采取的安全措施,应另行计算。
2.根据《通用安装工程工程量计算规范》(GB50856-2013),给水和采暖管道工程量计算时正确的为()。
A:法兰阀门安装不包括法兰连接B:阀门安装仅包括一侧法兰连接C:法兰的计量单位为“副”或“片”D:减压器规格按低压侧管道规格描述【答案】:C【解析】:本题考查的是给排水、采暖、燃气工程计量及应用。
法兰阀门安装包括法兰连接,不得另计。
阀门安装如仅为一侧法兰连接时,应在项目特征中描述。
塑料阀门连接形式需注明热熔连接、粘接、热风焊接等方式。
减压器规格按高压侧管道规格描述。
法兰的计量单位为“副”或“片”。
3.建筑安装编码,030408表示()。
A:附属工程B:电气调整试验C:变压器安装D:电缆安装【答案】:D【解析】:本题考查的是安装工程分部分项工程工程量清单。
通用电气设备安装工程中的“电缆安装”为030408。
4.室内给水管网上阀门设置正确的()。
A:DN≤50mm,使用闸阀和蝶阀B:DN≤50mm,使用闸阀和球阀C:DN>50mm,使用闸阀和球阀D:DN>50mm,使用球阀和蝶阀【答案】:B【解析】:阀门的安装、环状管引网入分管干、管水、表枝前状后管、网立的管连通处。
DN≤50mm 时,宜采用闸阀和球阀;DN>50mm 时,宜采用闸阀和蝶阀;在双向流动和经常启闭管段上宜采用闸阀和蝶阀。
量的计量练习题

量的计量练习题计量是科学研究中非常重要的一项工作,它帮助我们测量和评估物体的特性和属性。
通过准确的计量,我们可以获得可靠的数据,从而进行更深入的分析和研究。
为了提高计量的能力,以下是一些量的计量练习题,帮助您巩固和提升您的计量技能。
1. 长度计量题:(1) 将一根铁丝用尺子测量,得到长度为12.5厘米。
请将长度用分米和米来表示。
(2) 测量一张纸的长度为29.7厘米,宽度为21厘米。
请问纸的面积是多少平方厘米?将结果转换为平方分米和平方米。
2. 质量计量题:(1) 用天平测量一组铅笔的质量,得到质量为120克。
请将质量转换为千克和克拉(1克拉=0.2克)。
(2) 婴儿出生时的体重为3.5千克。
请将其转换为克和斤(1斤=0.5千克)。
3. 容量计量题:(1) 用容量瓶测量一桶水的容量,得到容量为15升。
请将容量转换为立方分米和立方米。
(2) 一杯牛奶的容量为250毫升。
请将其转换为升和立方厘米。
4. 时间计量题:(1) 从上午10点开始,经过4小时30分钟后是几点?请用24小时制表示。
(2) 一场电影的时长为1小时50分钟。
请将其转换为分钟。
5. 温度计量题:(1) 用温度计测量室内温度,得到温度为25摄氏度。
请将其转换为华氏度和开尔文温度。
(2) 冷冻食品的存储温度为-18摄氏度。
请将其转换为华氏度和开尔文温度。
这些练习题涵盖了计量的不同方面,涉及长度、质量、容量、时间和温度等。
通过解答这些问题,可以加深对计量单位之间的换算关系的理解,提高计量技能,并加强对不同计量单位的使用。
在实际应用中,准确的计量是确保数据可信度的关键,同时也是进行科学研究和工程项目成功的基础。
总之,通过不断练习和巩固计量知识,我们可以提高计量能力,为科学研究和实践工作提供准确的数据支持。
希望以上的计量练习题能够帮助您巩固和提升您的计量技能,为未来的学习和工作打下坚实的基础。
(完整版)建设工程计量与计价试题与答案

(完整版)建设工程计量与计价试题与答案一.填空题(共20分,每空格1分)1.定额按编制程序和用途分为施工定额、预算定额、.概算定额与概算指标、投资估算指标。
2.工程建设中使用的材料有一次性使用材料和周转性使用材料两种类型。
3.多层建筑坡屋顶内和场馆看台下,当设计加以利用时净高超过2.10m的部位应计算全面积;净高在1.20m至2.10m的部位应计算1/2面积;当设计不利用或室内净高不足1.20m 时不应计算面积。
4.整体楼梯包括休息平台、平台梁、斜梁及楼梯的连接梁,按水平投影面积计算,不扣除宽度小于500mm的楼梯井,伸入墙内部分不另增加。
当整体楼梯与现浇楼层无梯梁连接时,按楼层的最后一个踏步外边缘加30cm为界。
5.普通窗按洞口面积以平方米计算。
6.墙裙以高度在1500mm以内为准,超过时按墙面计算,高度低于300mm以内时,按踢脚板计算。
7.分部分项工程量清单应包括项目编码、项目名称、计量单位和工程数量。
.8.应计入建筑安装工程造价的税金包括营业税、城乡维护建设税及教育费附加等。
二.选择题(共10分,每小题1分)1.某单层混凝土结构工业厂房高15m,其一端有6层砖混车间办公楼与其相连,构成一单位工程,两部分外墙外边距离350mm,各部分首层勒脚以上外墙外边所围面积分别为2000m2和,300m2,缝长20m,则该单位工程建筑面积为(B)m2。
A.2300 B.3800 C.3807 D.38422.整体地面面层工程量均按主墙间净面积以“平方米”计算,应扣除(A)。
A.凸出地面构筑物、室内地沟所占面积B.柱、垛所占面积C.间壁墙所占面积 D.附墙烟囱所占面积3.某建筑物采用现浇整体楼梯,楼梯共四层自然层,楼梯间净长6m,净宽3m,楼梯井宽500mm,长3m,则该现浇楼梯的混凝土工程量为(B)m2。
A.18 B.72 C.70.5 D.664.除另有说明外,所有清单项目的工程量应以实体工程量为准,并以完成后的(D)计算。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
量与计量练习题
Coca-cola standardization office【ZZ5AB-ZZSYT-ZZ2C-ZZ682T-ZZT18】
一、填空题。
1、小时=()小时()分; 4日=()小时;
7吨5千克=()吨;千克=()千米;
125米=()千米; 250厘米=()米;
9平方米6平方厘米=()平方分米;
4500平方米=()公顷;
立方米=()立方分米;
1450毫米=()升()毫升;
3立方米50立方分米=()立方米。
2、儿童节在()月,这个月有()天。
年奥运会将在我国举行,这一年是()年,全年共有()天。
年的2月份有()天,这一年的第一季度有()天,第二季度有()天。
5.在括号里填上适合的数。
一瓶雪碧升,合()毫升。
一辆卡车装载货物吨,合()吨()千克。
6.在括号里填上适当的单位名称。
小明身高(),体重40(),他睡觉的床的面积大约是3(),每晚睡眠10(),他卧室的空间大约是45()。
7.一支铅笔长19( );-6℃比6℃低(
)℃。
8.已知:华氏温度=摄氏×+32。
华氏度相当于摄氏()度,摄氏50度相当于华氏()度。
9.小明从晚上6:55开始做作业,7:20结束。
他做作业用去的时间是()分,合()小时。
这期间钟面上的分针旋转了()度。
10.一辆汽车于23:40从金华出发开往杭州,于第二天凌晨3:25到达杭州,汽车行驶了()小时。
11.植物学家想知道一棵古数的直径,你能帮助他吗你的做法是(
)。
年5月29日三峡大坝全线
竣工,将来三峡水利枢纽供电范围
的半径将达到1000千米。
(如图)
?
?
?
(1)供电范围的面积有()平方千米。
(2)供电范围的面积约占全国国土面积(960万平方千米)的()分之()。
13.弹簧秤可以用来称物体质量。
悬挂不同质量的物体,弹簧伸长的长度也不同。
观察下表,并填空。
?
(1)若悬挂5千克的物体,弹簧伸长的长度是()厘米;
(2)若悬挂千克的物体,弹簧伸长的长度是(
)厘米。
二、判断题。
1.小强身高米,肯定能蹚过平均水深是米的河,不会有危险。
()
2.一个烟盒的体积是105立方厘米。
()
3.一个水壶装有升水,它可装满10个250毫升的水杯。
()
4.今年第一季度与第二季度天数相同。
()
5.钟面上时针的速度是分针速度的。
()
三.选择题。
1.请估计一下,()接近自己的年龄。
分周时日
2.下面的国内大事,发生在闰年的是()。
年中国加入WTO。
年雅典奥运会我国选手取得辉煌成绩。
年中国载入航天飞机上天。
时20分=()分。
B.
4.一头猪的体重大约是200()。
A.克
B.千克
C.吨
5.一个瓶子装满水是500毫升,我们就说500毫升是这个瓶子的()。
A.重量
B.体积
C.容积。
