Ch10热力学定律
甲烷部分氧化过程的热力学

甲烷部分氧化过程的热力学首先,热力学是研究热和其他形式能量之间相互转化关系的科学。
甲烷部分氧化过程的热力学基础是热力学第一定律和第二定律。
热力学第一定律是能量守恒定律,它表明甲烷部分氧化过程中的能量变化等于吸热与放热之和。
这个过程中,甲烷燃烧释放出热量,而吸热过程是氧气与甲烷反应所需的能量。
热力学第二定律涉及熵的概念,它描述了能量的转化过程中的不可逆性。
在甲烷部分氧化过程中,反应的方向是由热力学第二定律决定的。
根据热力学第二定律,气体燃烧生成的一氧化碳和水蒸汽的熵会增加,因此这个过程是自发的。
接下来,我们可以考虑甲烷部分氧化过程的热力学性质,包括焓变、自由能变和反应熵变。
焓变是指甲烷部分氧化过程中的能量变化,可以用来评估这个过程的放热或吸热性质。
焓变(ΔH)等于反应物的焓减去生成物的焓。
在这个过程中,甲烷和氧气的焓减小于一氧化碳和水蒸汽的焓,所以整个过程是放热的。
自由能变是评估化学反应进行的驱动力的物理量,可以通过自由能变(ΔG)来描述。
自由能变等于反应物的自由能减去生成物的自由能。
在这个过程中,甲烷氧化生成的一氧化碳和水蒸汽的自由能减小,所以整个过程是自发进行的。
最后,反应熵变(ΔS)描述了甲烷部分氧化过程中物质的混乱程度的变化。
反应熵变可以通过生成物的熵减去反应物的熵来求得。
在这个过程中,一氧化碳和水蒸汽的熵大于甲烷和氧气的熵,所以反应熵变是正值,说明这是一个自发的过程。
总的来说,甲烷部分氧化的热力学性质可以通过焓变、自由能变和反应熵变来描述。
这些性质决定了反应是否进行以及反应的方向。
了解这些性质可以帮助我们优化工业过程条件,提高产率,并最大程度地利用可用的能量。
02热力学第一定律

压缩机工作时,速率很快,来不及进行热交换
Q0
W U 2731J
3. 摩尔恒压热容与摩尔恒容热容的关系
C p ,m CV ,m
H m T U m T
T2 T1
U QV n CV ,mdT
2.4.2
应用——计算单纯pVT 过程的U 恒容过程:
U QV n CV ,mdT
T2 T1
非恒容过程: U QV n
T2
T1
CV ,mdT
(理想气体)
nCV ,m (T2 T1 )
2. 摩尔定压热容
C p ,m
•自由膨胀过程
∵pamb=0 • 恒容过程 dV=0 W=0 ∴W=0
热力学能U:系统内部储存的能量,是广度量的状态函数。
分子平动能 动能 分子转动能 系统总能量 势能 分子振动能 热力学能 分子间作用能 电子运动能 核运动能
符号规定: 若热力学能增加+,若热力学能减小U 的绝对值无法求,但U可求
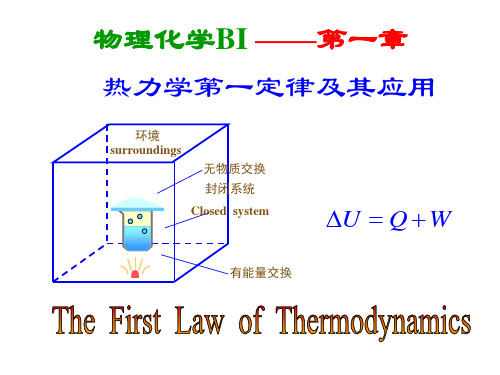
T,p 2HCl(aq)+Zn(s) ZnCl 2 (aq)+H2 (g)
这是什么体系?界面在什么位置?
如果上述反应是在恒容、绝热,不透光、不导 电的容器中进行,它又是什么体系?
作业:以电解水为例确定界面使系统分别为隔离系统、 封闭系统、敞开系统
2. 状态与状态函数 (1)状态与状态函数 系统的性质:决定系统状态的物理量(如p,V,T,Cp,m)
系统的状态:热力学用系统所有的性质来描述它所处 的状态,当系统所有性质都有确定值时,则系统处于一 定的状态
热力学第一定律

3、分析
机械能的增量 流动功
1 2 q u c f gz ( pv ) wi 2 18 2
容积变化功 机械能可以全 部转变为功 工质对机器作的功
说明:
(1)工质在状态变化过程中从热能转变而来的机械能 总等于膨胀功 。
1 2 (2)2 c f 、gz、wi
1、热力学第一定律的第二解析式
引进技术功概念后,稳定流动能量方程式(2-16)可写为
Q H Wt 2 23a
对于微元过程,有
q h wt 2 23
q dh wt 2 23b Q dH Wt 2 23c
若过程可逆,则
q h vdp, q dh vdp2 23d
1、开口系统能量方程式 2、稳定流动能量方程式 3、分析
2014-12-2
22
1、开口系统能量方程式
如图所示,一开口系统在dτ时间内进行一个微元过程:
2014-12-2
23
考察该系统微元过程的能量平衡:
进入系统的能量 离开系统的能量 控制容积的储存能增量
dE1 p1dV 1 Q
dE2 p2dV2 Wi
2014-12-2
15
一、推动功和流动功
推动功—工质在开口 系统中流动而传递的功。
mkg工质的推动功等于
pAl pV mpv
1kg工质的推动功等于
2014-12-2
pv
16
说明:
(1)推动功只有在工质移动位置时才起作用。 (2)工质在传递推动功时没有热力状态的变化,也 没有能量形态的变化。 (3)工质的作用只是单纯地运输能量。
2 1
2014-12-2
03章 热力学第二定律

一、Clausius 不等式—— 热力学第二定律的数学表达式 前面根据可逆过程的热温商定义了熵函 数,下面讨论不可逆的情况。 卡诺定理指出,工作于T1,T2两个热源间的 任意热机I与可逆热机R,其热机效率有如下的关 系:
I≤ R
说明:
1.各种说法一定是等效的。若克氏说法不成立,则开氏说法 也一定不成立; 2.要理解整个说法的完整性切不可断章取义。如不能误解为 热不能转变为功,因为热机就是一种把热转变为功的装置; 也不能认为热不能完全转变为功,因为在状态发生变化时, 热是可以完全转变为功的(如理想气体恒温膨胀即是一例) 3.虽然第二类永动机并不违背能量守恒原则,但它的本质却 与第一类永动机没什么区别。
2.卡诺定理 所有工作于同温热源和同温冷源之间的热机,其效率 都不能超过可逆机,即可逆机的效率最大。
I≤ R
3.卡诺定理的推论
所有工作于同温热源和同温冷源之间的可逆
机,其热机的效率都相等。
4.熵的数学表达式
S (
A
B
Q
T
)R
或
dS (
Q
T
)R
§3.5 Clausius 不等式与熵增加原理
(2)要使发生自发过程的系统复原,环境必 然留下永久变化的痕迹;
(3)自发过程是不可逆过程。 自然界中发生的一切实际过程都有一定的方向和限度。
§3.2
热力学第二定律
▲ Clausius 说法:不可能把热从低温物体传到高
温物体而不引起其它变化。
“It is impossible to devise an engine ,which working in a cycle, shall produce no effect other than the transfer of heat from a colder to a hotter body. ”
热力学第一定律2
对热和功的几点交待
I A II B
改变量:
U , Q, W ???
B
U I U II dU U B U A
A
QI QII ? Q QB QA ?
A
B
WI WII ? W WB WA ?
A
B
对热和功的几点交待
(2)Q和W是体系与环境之间能量传递形式,离开环 境无所谓热和功的概念。
(5)关于We
如下图所示,一个带有理想活塞贮有一定量气体 的气缸,截面积为A;环境压力为p外。设活塞在 力的方向上的位移为dl。
F’
关于体积功(教材32页)
在此微小过程中,气体克服外力所作的功:
We F dl pe A dl
pe dV
如果体系发生明显的体积变化,则:
We
V2
V1
pedV
------计算体积功的基本公式
We
V2
V1
pe dV
有关功的概念,请注意: (1) 微量体积功: 有限量体积功:
We
We
非特殊指明,可用W或δW表示。 (2) 计算体积功时必须使用外压。
例1:气体向真空膨胀(自由膨胀)
We
V2
V1
pedV 0
V2
V
多次等外压压缩
实例讨论---功与过程
3.可逆压缩 如果将蒸发掉的水气慢慢在杯中凝聚,使压力缓慢增 加,恢复到原状,所作的功为:
We,3 pe dV ( p dp)dV
V2 V2 V1 V1
p
p1
p1V1
nRT dV pdV V 2 V2 V V2 V1 nRT ln V2 nRT ln V
固体氧化物燃料电池的热力学及电化学应用基础

2012 7 C h e m i ca l I ndu stry T i m es J u l. 7. 2012do i:10. 3969 /j.i ss n. 1002 -154X. 2012. 07. 015固体氧化物燃料电池的热力学及电化学应用基础蒋先锋( 中国矿业大学,化学与环境工程学院,北京100083)摘要固体氧化物燃料电池是一种典型的电化学装置,可以把燃料气和空气( 或氧气) 的化学能直接转化为电能。
电池的整个反应过程可以根据还原剂和氧化剂反应自由焓来进行热力学计算。
对于最简单的氢气和氧气的反应来说,可以根据可逆反应平衡方程式计算电池的可逆功,而且SOFC 系统和外部环境的热交换也是可逆的。
SO F C作为一种伴生热能的发电装置,对热力学的理解必不可少。
所以本文将首先介绍一下SOFC 的热力学基础,而作为一种电化学发电装置,需要系统了解SO FC 的电化学基础,其中重点介绍SO FC 的电化学分析曲线———i-V 曲线。
关键词固体氧化物燃料电池热力学电化学开路电压i -V 曲线T h e r m o d yna m i c and E l ect r o c h e m i s t r y Foundation of Solid Ox i d e Fuel C e llX i a n fe n g J i a n g( C h e m i ca l and En v i ro nm e n t En g i n eer i n g Sc h oo l,C h i n a Un i vers i ty of Mining and Tec hn o l ogy,Be iji n g,100083) Ab st r a ct So li d ox i d e f u e l ce ll ( SOFC) i s a ty p i ca l e l ectroc h e m i ca l d ev i ce,w h i c h can d i rect l y and eff i c i e n t l y convert c h e m i ca l energy in f u e l and a i r ( or oxygen) to e l ectr i c i ty. The overa ll react i o n process of SOFC can be ex- p l a i n e d by t h er m o d y n a m i c ca l c u l at i o n based on the react i o n free e n t h a l p y of redu cto r and ox i d a n t. For the s i mp l est re- act i o n of hydrogen and oxyge n,th e revers i b l e work of ce ll can be ca l c u l ate d based on the revers i b l e react i o n b a l a n ce e qu at i o n,a nd heat exchange between SOFC syste m and exter n a l e n v i ro nm e n t i s a l so revers i b l e.I t i s necessary to un- derstan d the t h er m o d y n a m i c of SOFC as an e l ectr i c i ty d ev i ce w i t h t h er m a l ge n erat i o n.T h er m o d y n a m i c fo und at i o n of SOFC was presen ted f i rst l y,a nd e l ectroc h e m i stry fo und at i o n and a n a l ys i s c u rve—i-V curve were syste m at i ca ll y i n tro- du ce d.K e ywo r d s So li d ox i d e f u e l ce ll t h er m o d y n a m i c e l ectroc h e m i stry open c i rc u i t vo l tage i -V curve固体氧化物燃料电池( SOFC) 作为一种电化学发电装置,是化学工程、化学工艺、材料化学、电化学、热力学等诸多化学学科的综合整体[1,2]。
热力学第二定律复习题..
热⼒学第⼆定律复习题..热⼒学第⼆定律(r δ/0Q T =∑)→熵函数引出 0< (不可能发⽣的过程) 0= (可逆过程)0>(⾃发、不可逆过程)S ?环)I R ηη≤ 不等式:)0A B iA BS →→?≥函数G 和Helmholtz 函数A 的⽬的A U TS ≡-,G H TS ≡-d d d d d d d d T S p VT S V p S T p V S T V p -+---+ W ' =0,组成恒定封闭系统的可逆和不可逆过程。
但积分时要⽤可逆途径的V ~p 或T ~S 间的函数关系。
应⽤条件: V )S =-(?p /?S )V , (?T /?p )S =(?V /?S )p V )T =(?p /?T )V , (?S /?p )T =-(?V /?T )p应⽤:⽤易于测量的量表⽰不学关系式的推导和证明<0 (⾃发过程) =0 (平衡(可逆)过程)判据△A T ,V ,W ’=0判据△G T ,p ,W ’=0<0 (⾃发过程) =0 (平衡(可逆)过程)基本计算公式/()/rS Q T dU W Tδδ==-, △S环=-Q体/T环△A=△U-△(TS) ,d A=-S d T-p d V△G=△H-△(TS) ,d G=-S d T-V d p不同变化过程△S、△A、△G 的计算简单pVT变化(常压下)凝聚相及实际⽓体恒温:△S =-Q r/T;△A T≈0 ,△G T≈V△p≈0(仅对凝聚相)△A=△U-△(TS),△G=△H-△(TS); △A≈△G恒压变温21,(/)Tp mTS nC T dT=nC p,m ln(T2/T1)C p,m=常数恒容变温21(/)TV mTS nC T dT=nC V,m ln(T2/T1)C V,m=常数△A=△U-△(TS),△G=△H-△(TS); △A≈△G理想⽓体△A、△G的计算恒温:△A T=△G T=nRT ln(p2/p1)=- nRT ln(V2/V1)变温:△A=△U-△(TS),△G=△H-△(TS)计算△S△S=nC V ,m ln(T2/T1)+nR ln(V2/V1)= nC p,m ln(T2/T1)-nR ln(p2/p1)= nC V,m ln(p2/p1)+ nC p,m ln(V2/V1)纯物质两相平衡时T~p关系g?l或s两相平衡时T~p关系任意两相平衡T~p关系:m md/d /p T T V Hββαα=??(Clapeyron⽅程)微分式:vap m2d lndHpT RT定积分式:ln(p2/p1)=-△vap H m/R(1/T2-1/T1)不定积分式:ln p=-△vap H m/RT+C恒压相变化不可逆:设计始、末态相同的可逆过程计S=△H/T;△G=0;△A≈0(凝聚态间相变)=-△n(g)RT (g?l或s)化学变化标准摩尔⽣成Gibbs函数r m,BG定义r m B m,BBS Sν=∑,r m B f m,BBH Hν=∑,r m r m r mG H T S=-或r m B f m,BG Gν=∑G-H⽅程(?△G/?T)p=(△G-△H)/T或[?(△G/T)/?T]p=-△H/T2r m0()//ln1/21/6G T T H T IR a T bT cT=+---应⽤:利⽤G-H⽅程的积分式,可通过已知T1时的△G(T1)或△A(T1)求T2时的△G(T2)或△A(T2)微分式热⼒学第三定律及其物理意义规定熵、标准摩尔熵定义任⼀物质标准摩尔熵的计算⼀、选择题1.体系经历⼀个正的卡诺循环后,试判断下列哪⼀种说法是错误的?(a )体系本⾝没有任何变化(b )再沿反⽅向经历⼀个可逆的卡诺循环,最后体系和环境都没有任何变化(c )体系复原了,但环境并未复原(d )体系和环境都没有任何变化(答案) d (什么叫卡诺循环?以理想⽓体为⼯作物质,从⾼温(T h )热源吸收(Q h )的热量,⼀部分通过理想热机⽤来对外做功(Wr )另⼀部分(Qc)的热量放给低温(Tc)热源。
热力学第一定律小结
第一章 热力学第一定律核心内容:能量守恒 ΔU=Q+W主要内容:三种过程(单纯pVT 变化、相变、化学反应)W 、Q 、ΔU 、ΔH 的计算一、内容提要1.热力学第一定律与状态函数(1)热力学第一定律: ΔU=Q+W (封闭系统) 用途:可由ΔU ,Q 和W 中的任意两个量求第三个量。
(2)关于状态函数(Z )状态函数:p 、V 、T 、U 、H 、S 、A 、G ……的共性: ①系统的状态一定,所有状态函数都有定值;②系统的状态函数变化值只与始终态有关,而与变化的途径无关。
用途:在计算一定始终态间的某状态函数增量时,为了简化问题,可以撇开实际的复杂过程,设计简单的或利用已知数据较多的过程进行计算。
ΔZ (实)=ΔZ (设)。
这种方法称为热力学的状态函数法。
③对于循环过程,系统的状态函数变化值等于零,即ΔZ =0。
此外,对于状态函数还有如下关系:对于组成不变的单相封闭系统,任一状态函数Z 都是其他任意两个独立自变量(状态函数)x 、y 的单值函数,表示为Z=Z(x 、y),则dy y Z dx x Z dZ xy ⎪⎪⎭⎫ ⎝⎛∂∂+⎪⎭⎫ ⎝⎛∂∂=,)(Z y y x x Z x Z y 循环关系式1-=⎪⎭⎫⎝⎛∂∂⎪⎪⎭⎫ ⎝⎛∂∂⎪⎭⎫ ⎝⎛∂∂ )(xy Z y x Z 尤拉关系式∂∂∂=∂∂∂22 注意:因为W 和Q 为途径函数,所以Q 和W 的计算必须依照实际过程进行。
⎰-=21V V e dV p W ,其中e p 为环境压力。
Q 由热容计算或由热力学第一定律求得。
将热力学第一定律应用于恒容或恒压过程,在非体积功为零(即0=f W )的情况下有:Q V =ΔU ,Q p =ΔH (H 的定义:H=U+pV )。
此时,计算Q v 、Q p 转化为计算ΔU 、ΔH ,由于U 、H 的状态函数性质,可以利用上面提到的状态函数法进行计算。
下面1(p 1,V 1,T 1) (p'1,V 1,T 2) 2(p 2,V 2,T 2) (p 1,V'1,T 2) VT 就三种常见的过程进行展开。
中文sgwhk10
3.7 亥姆霍茨(Helmholtz)函数F与-第十讲-吉布斯(Gibbs) 函数G11. 热力学第一和第二定律的联合公式---W’{}> 不可逆T 环d S d U ≥δW exp δW { }= 可逆22. 亥姆霍茨(Helmholtz)函数(Helmholtz Function, Helmholtz Free Energy)对于等温过程为恒量对于等温过程,T 为恒量,T 体系=T 环境=T ,有S -=-d(-)--W’{}> 不可逆T d S d U d(U TS ) ≥δW exp δW { }= 可逆定义定义:Helmholtz 函数F ≡U -TS因为U ,T ,S 均为状态函数,U 和T S 均为能量量纲,2所以F 为一具有能量量纲的状态函数。
对等温、等容过程,d T =0, d V =0 (δW =0), 则(exp )-d F ≥-δW’{ }> 不可逆= 可逆对等温、等容,无其它功的过程,则-d F ≥0{ }> 不可逆= 可逆或d F ≤0{ }< 不可逆= 可逆亥姆霍茨自由能减少原理:无其它功的封闭体系,在等温等容的条件下体系的亥姆霍茨自由能在可逆过程中保持不变在的条件下,体系的亥姆霍茨自由能在可逆过程中保持不变;在不可逆过程中总是减少,减少到F 最小时体系达到平衡状态。
亥姆霍茨函数判据: 在等温、等容且W ′=0时,只能自发地3向F 减小的方向进行, 直到ΔF T,V =0 时, 体系达到平衡。
3. 吉布斯(Gibbs)函数(Gibbs Function,Gibbs Free Energy)一个封闭体系,设进行等温(T =T 环)、等压过程(p = p ex ), 体系(Gibbs Function, Gibbs Free Energy)作体积功δW exp = p d V 由第一、第二定律W’{}> 由第第定律联合公式---W’{}> 不可逆T 环d S -d U ≥-δW exp -δW { }不可逆= 可逆T d S d U p d V ≥δW { }= 可逆-(U -TS +-W’{}>不可逆不变G TS TS d (U TS + pV )≥δW { }=可逆因T,p 定义G ≡U +pV -TS =H -TS =F +pV—,,H 5G 吉布斯函数或吉布斯自由能是状态函数, 广度性质, 与H 单位相同。
热力学第零定律
dW=PdV
氣體以壓力P對外作功,熱
量可由底部流入或流出。
功的大小等於PV曲線下之面積,可由鋸齒狀線下之面積求得 近似值。
目錄 第十一章 熱力學
CH.1 CH.2
CH.3 CH.4
CH.5 CH.6 CH.7 CH.8 CH.9 CH.10 CH.11 CH.12 CH.13 CH.14
W= W=P1V1+P2V2+
nCpT=U+PV (等壓過程)
等壓過程
等容過程
當系統之狀態發生變化時,整個系統之體積若保 持一定不變,則此變化過程稱為等容過程(constant volume或isovolume或isochoric process)。
右圖為等容過程之 P-V圖。因體積保持一 不變之常數V,故為一 垂直線。線下之面積為 零,故在等容過程中, 所作之功W=0。
系統原有之內能為U0,若周遭加Q之熱量於系 統,系統對外圍作W之功。故系統最終之內能U為:
U=U0+Q-W 或 Q=U-U0+W=U+W
目錄 第十一章 熱力學
CH.1 CH.2
CH.3 CH.4 CH.5 CH.6 CH.7 CH.8 CH.9 CH.10 CH.11 CH.12 CH.13 CH.14 CH.15 CH.16 CH.17 CH.18
CH.1 CH.2
CH.3 CH.4 CH.5 CH.6 CH.7 CH.8 CH.9 CH.10
所謂節流過程,是高壓的流體, 經過一多孔的壁或一細縫(節流活門) 而摻入一低壓的區域,其間無熱的轉 移現象。
CH.11 CH.12
CH.13 CH.14
自由膨脹(free expansion)
如果在一個絕熱過程之中,系統 並未對外作功,而外界亦未對此系統
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Ch. 10 热力学定律18世纪中叶,瓦特在改进前人成果的基础上发明了真正用于生产的蒸汽机,热做功应用于生产实践中。
但此时对热的本质认识还处于“热质说”的错误理论上。
“热质说”认为热是一种微粒。
燃烧的物质放出一种“燃素”的物质,这种物质吸附普通物质,是物质表现出温度的改变。
这种理论在牛顿提出光的微粒学说后得到进一步的巩固。
直到19世纪中叶,德国医生罗伯特·迈耶(1814~1878)在观察热带气候对病人的影响时,开始关注物理力对生命力的影响。
1842年,迈耶发表《论无机自然界的力》一文,提出热是一种能量,自然界的能量守恒是包含热的。
但这种理论没有得到应用的重视。
几乎同时,1847年,英国科学家焦耳在一个普通的学术会议上作了题为“能量的普适守恒原理”的报告,提出热不是物质,而是一种运动,并进行了热功当量的实验。
热的本质问题得以充分解决。
本章主要研究热力学系统的状态发生变化时,能量所遵循的变化规律。
§10.1 准静态过程一、准静态过程当系统的外界条件改变时,它的状态就随时间发生变化,称系统经历一个“热力学过程”,简称“过程”。
如果过程进展得十分缓慢,使所经历的一系列中间状态,都无限接近平衡状态,这个过程就叫做准静态过程。
1、准静态过程:在任意时刻,系统的状态都无限接近于平衡态的热力学过程。
准静态过程的任意时刻的状态都可以当作平衡态处理。
2、弛豫时间一个系统从一个非平衡态过渡到一个平衡态,经过的时间称弛豫时间。
只有过程变化的时间远远大于弛豫时间时,这个过程才能看作准静态过程。
如,内-,而活塞一次压缩燃机气缸内的气体(空气与汽油气的混合物)的弛豫时间小于310s-,这个过程可近似为准静态过程。
气体的时间约为210s3、过程曲线由理想气体状态方程:pV RT ν=,准静态过程可以通过p-V (p-T 或V-T )的关系曲线表示。
这些曲线叫过程曲线。
二、功做功的过程是宏观机械运动能量与系统分子热运动能量之间的转化。
系统对外界做功,A ; 外界对系统做功,A '。
A A '=-1、功的计算设气缸内气体压强为p ,活塞面积S ,当活塞移动微小距离d l 时,气体经历了一个无限小的准静态过程。
d d d d A F l pS l p V ===当气体的体积由1V 到2V 时,气体对外做功为21d d V V A A p V ==⎰⎰21,0,V V A >> 表示气体对外做正功;21,0,V V A << 表示气体对外做负功,即外界对气体做正功。
2、功的图示由积分意义可知,准静态过程做功的大小等于p-V 图上过程曲线下的面积。
比较初末状态相同而中间过程不同的两个准静态过程,由于过程曲线的面积不同而做功也不同。
因此,功的数值不仅与初态和末态有关,而且还依赖于所经历的中间状态。
功与过程的路径有关——热力学系统做功是过程量!VTOT·例:理想气体等温过程做功:..C pV RT C p Vν==→=22112211.d d .ln ln V V V V V V C A p V V C RT V V V ν====⎰⎰三、内能E int英国科学家焦耳通过大量实验证明,热力学系统处于某一状态,就对应一定的能量。
当系统状态改变时,则系统的能量也随之变化。
这种由系统状态确定的能量称为热力学系统的内能。
微观上,内能是系统中所有分子的平均动能与势能之和。
int int,int,k p E E E =+内能是状态量!改变内能的方法——做功和热传递四、热量1、热传递当系统与外界的温度不同时,就会通过分子间的相互作用而发生能量传递,这种过程称为“热传递”。
热传递同样能改变系统的宏观状态(p ,V ,T )。
热传递和做功是等效的(热功当量)。
2、热量Q通过热传递方式交换的能量,称为热量。
(单位:J )Q > 0,表示系统从外界吸热; Q < 0,表示系统向外界放热。
热量是系统与外界热能转换的量度——热量也是过程量!VppV 1 2VV 12Vp§10.2热力学第一定律 热容一、热力学第一定律:任一热力学过程,外界对系统做功和传给系统的热量之和,等于系统内能的增量。
A Q E '+=∆或者说,系统从外界吸收热量Q ,一部分用来使系统的内能增加E ∆,另一部分是用于系统对外做功A 。
——热力学第一定律。
·注:(1) 内能是状态量,功和热量是过程量。
(2) 热力学定律是更加普遍的能量守恒定律,适用于任何系统的任何过程。
(3) 第一类永动机(不从外界吸收热量,系统内能无变化而对外做功)是不可能造成的:0, 0, 0A E Q >∆==不成立。
(第二类永动机:吸收全部热量都用来做功,也是不可能的——热力学第二定律。
)二、热容:系统和外界之间的热传递,通常会引起系统本身温度的变化。
不同的物质升高相同的温度所吸收的热量不同,用热容来描述。
·摩尔热容:1mol 物质温度升高d T 时,吸收热量d Q ,则摩尔热容为111d (J K mol )d m QC Tν--=⋅⋅·比热(容):单位质量的物质升高单位温度吸收的热量,111d (J K kg )d Q C m T--=⋅⋅。
讨论:如果气体压强一定,吸收热量时,温度升高(内能增加),体积增大(对外做功)。
则吸收的热量用来增加内能和对外做功。
如果气体体积一定,吸收热量,不对外做功,只用来增加内能。
因此,同一系统经过定压和定容过程,升高相同的温度吸收的热量不同,即定压热容和定体热容不同。
1、定压mol 热容,p m C对于νmol 的理想气体,进行微小的压强不变的准静态过程:吸热,内能增加同时对外做功。
(d )d d p Q E p V =+定压mol 热容:,1d 1d d ()d d d p m p Q E p VC T T Tννν==+将 2iE R T ν= 和 p V R T ν= 代入——理想气体的定压mol 热容 表示:1mol 理想气体,在压强保持不变时,温度改变1K 时,吸收或放出的热量。
2、定容mol 热容,V m C对于νmol 的理想气体,进行微小的体积不变的准静态过程:吸热,内能增加,不对外做功。
(d)d V Q E =——理想气体的定体mol 热容 表示:1mol 理想气体,在体积保持不变时,温度改变1K 时,吸收或放出的热量。
·对于一切始末态为平衡态的过程,都有,d d V m E C T ν= ,V m E C T ν∆=∆3、迈耶公式(1842)1mol 理想气体的定压热容比定体热容多一个普适气体常数R ,,,p m V m C C R =+ ——迈耶公式比热(容)比:,,2p m V mC i C iγ+==. 三、四种特殊过程研究理想气体的四种准静态过程(等体过程;等温过程;等压过程;绝热过程),是研究气体做功过程的基础。
1、等体过程理想气体的体积不发生变化(.V C =),对外不做功(0A =)。
也叫定容过程。
由理想气体状态方程:pV RT ν=,可得.pC T= ——等体过程方程,反映了等体过程的可变参量之间的关系。
根据热力学第一定律:Q E A E =∆+=∆,等体热容公式:,1d ()d V m VQ C T ν=2211,,21d d ()Q T V m V m Q T E Q Q C T C T T νν∆====-⎰⎰2、等温过程理想气体的温度不发生变化(.T C =),内能不变(0E ∆=)。
.pV C = ——等温过程方程根据热力学第一定律:Q E A A =∆+=, 和理想气体状态方程:pV RT ν=22112112d d ln ln V V V V V p VQ A p V RTRT RT V V p ννν=====⎰⎰ 3、等压过程理想气体的压强不发生变化(.p C =)。
.TC V= ——等压过程方程 对外做功:212121d ()()V V A p V p V V R T T ν==-=-⎰;内能增量:,21()V m E C T T ν∆=-系统吸热:,2121,21()()()V m p m Q E A C T T R T T C T T ννν=∆+=-+-=- 4、绝热过程系统与外界没有热量交换,或热交换可以忽略时的变化过程称为绝热过程。
绝热过程也是理想化的过程模型,没有绝对等绝热过程。
两种实现近似绝热过程的途径:(1) 用隔能壁把系统和外界隔开,尽可能阻止热传递。
(2) 状态过程进行得极快,系统在过程中来不及与外界进行热传递。
但是系统不能经历准静态过程。
(1) 准静态绝热过程绝热过程满足:d 0Q =根据热力学第一定律:Q E A =∆+ 对于一个微小的过程:d d d Q E A =+则, d d 0E A +=对于理想气体,有, ,d d d 2d d V m i E C T R TA p Vνν⎧==⎪⎨⎪=⎩ d d 02iR T p V ν+= 这是由能量守恒给出的状态参量之间的关系。
又由理想气体状态方程pV RT ν=,两边积分:d d d p V V p R T ν+=,代入上式,(1)d d 022i ip V V p ++=, 利用比热容比:221i i iγ+==+, → d d 0p V Vp γ+= 两边同除以pV , → d d 0V pV pγ+= 两边积分, → 1l n l n .l n V p C C γ+==1pV C γ= ——泊松公式。
同理,在状态参量关系式中消去p ,可得,12TV C γ-= 消去d V 可得, 13p T C γγ--=绝热过程的过程方程—— 11213pV C TV C p T C γγγγ---⎧=⎪=⎨⎪=⎩①系统吸热: 0Q =②内能增量: 2121,21()()2V m iE E E R T T C T T νν∆=-=-=- ③对外作功: 12,12()()2V m iA E R T T C T T νν=-∆=-=- 由221121i i i i γγ+==+→=-,代入上式 12112211()()11A RT RT p V p V νννγγ=-=--- **绝热线与等温线两条过程曲线的斜率对比: ·数学证明:等温过程:TT C pV C p V=→=,p-V 曲线斜率: 22d d T T TC p pV p k VV V V===-=-=- 绝热过程:Q Q C pV C p Vγγ=→=,p-V 曲线斜率11d d Q Q QC ppV p k VV V Vγγγγγγ++===-=-=-1||||Q T k k γ>→>,说明绝热线比等温线更陡。
