2014年成人高考高起点数学精选模拟试题和参
成考数学2014年理工类试题和答案(1--21题有详细答案)

,
,选 B
D
乙:a������ 2 + ������������+c=0 有实根,则
甲是乙的必要条件,但不是乙的充分条件 甲是乙的充分的条件,但不是乙的必要条件 甲既不是乙的充分的条件,也不是乙的必要条件
D 甲是乙的充分必要条件 解:显然甲是乙的充分条件,且有实数根,也必须������ 2 − 4������������ > 0, 即甲是乙的充分必要条件。应选择 D 8、二次函数y = ������ 2 + ������ − 2 的图像与x 轴的交点坐标为 A: −2, 0 和 1, 0 C 2, 0 和 1, 0 B −2, 0 和 −1, 0 D 2, 0 和 −1, 0 A
解方程������ 2 + ������ − 2 = 0,其根为������1 = −2,������2 = 1, 所以交点坐标选 A 9、设z = 1 + A
1+ 3������ 4
3 i i 是虚数单位,则 z = B
B
1− 3������ 4
1
C
2+ 3������ 4 1 ������
D
1
2− 3������ 4 1− 3������ 4
3 2
3,0 ,其长轴长为 4,
������ + ������与椭圆有两个不同的交点,求m的取值范围
解:1、长轴长为 4,则a = 2 由焦点坐标知c = 3 所以b = ������2 − ������ 2 = 4 − 3 = 1 所以本椭圆的方程为: 4 + ������ 2 = 1 2、 将y =
3 2 x2
������ + ������ 代入椭圆方程 4 + ������ 2 = 1 可得
2014年度成人高考专升本高等数学一试卷及解答

2014年成人高考专升本高等数学一试卷及解答一、选择题:每小题4分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求。
第1题参照解答:D第2题参照解答:A第3题参照解答:B第4题设函数f(x)在[a,b]连续,在(a,b)可导,f’(x)>0.若f(a)·f(b)<0,则y=f(x)在(a,b)( )A.不存在零点B.存在唯一零点C.存在极大值点D.存在极小值点参照解答:B第5题参照解答:C第6题参照解答:D 第7题参照解答:C 第8题参照解答:A 第9题参照解答:A第10题设球面方程为(x一1)2+(y+2)2+(z一3)2=4,则该球的球心坐标与半径分别为( )A.(一1,2,一3);2B.(一1,2,-3);4C.(1,一2,3);2D.(1,一2,3);4参照解答:C二、填空题:本大题共10小题。
每小题4分,共40分,将解答填在题中横线上。
第11题参照解答:2/3第12题第13题第14题参照解答:3第15题曲线y=x+cosx在点(0,1)处的切线的斜率k=_______.参照解答:1第16题参照解答:1/2第17题参照解答:1第18题设二元函数z=x2+2xy,则dz=_________.参照解答:2(x+y)dx-2xdy第19题过原点(0,0,0)且垂直于向量(1,1,1)的平面方程为________.参照解答:z+y+z=0第20题微分方程y’-2xy=0的通解为y=________.三、解答题:本大翘共8个小题,共70分。
解答应写出推理,演算步骤。
第21题第22题设Y=y(x)满足2y+sin(x+y)=0,求y’.第23题求函数f(x)一x3—3x的极大值.第24题第25题第26题第27题第28题求微分方程y”+3y’+2y=ex的通解.。
2014成人高等学校招生全国统一考试数学真题(理工类)

附录 2014年成人高等学校招生全国统一考试(高起点)数学试题(理工农医类)第Ⅰ卷(选择题,共85分)一、选择题(本大题共17小题,每小题5分,共85分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.设集合{}21|<≤-=x x M ,{}1|≤=x x N ,则集合=N MA . {}1|->x xB .{}1|>x xC .{}11|≤≤-x xD .{}21|≤≤x x 2.函数51-=x y 的定义域为 A . ()5,∞- B . ()+∞∞-, C . ()+∞,5 D .()()+∞∞-,55, 3.函数x y 6sin 2=的最小正周期为A . 3πB .2πC . π2D .π34.下列函数为奇函数的是A . x y 2log =B . x y sin =C . 2x y =D .x y 3=5.过点()1,2 且与直线x y =垂直的直线方程为A . 2+=x yB . 1-=x yC . 3+-=x yD .2+-=x y6.函数12+=x y 的反函数为A .21+=x yB .21-=x y C .12-=x y D .x y 21-= 7.若c b a ,,为实数,且0≠a .设甲:042≥-ac b ,乙:02=++c bx ax 有实数根,则A .甲是乙的必要条件,但不是乙的充分条件B .甲是乙的充分条件,但不是乙的必要条件C .甲既不是乙的充分条件,也不是乙的必要条件D .甲是乙的充分必要条件8. 二次函数22-+=x x y 的图像与x 轴的交点坐标为A . ()0,2- 和()0,1B .()0,2- 和()0,1-C .()0,2 和()0,1D .()0,2 和()0,1-9.设i z 31+=,i 是虚数单位,则=z 1 A .431i + B .431i - C .232i + D .232i - 10.设1>>b a ,则A .44b a ≤B .4log 4log b a >C .22--<b aD .b a 44<11.已知平面向量()1,1=a ,()1,1-=b ,则两向量的夹角为A . 6πB .4πC . 3πD .2π 12.3)1(xx -的展开式中的常数项为A .3B .2C .2-D .3-13.每次射击时,甲击中目标的概率为8.0,乙击中目标的概率为6.0,甲、乙各自独立地向目标射击一次,则恰有一人击中的概率为A .44.0B .6.0C .8.0D .1 14.已知一个球的体积为π332,则它的表面积为 A . π4 B .π8 C .π16 D .π2415.在等腰三角形ABC 中,A 是顶角,且21cos -=A ,则=B cos A .23 B .21 C . 21- D .23- 16. 四棱锥ABCD P -的底面为矩形,且4=AB ,3=BC ,⊥PD 底面ABCD ,5=PD ,则PB与底面所成角为A .︒30B .︒455.1C .︒60D .︒7517.将5本不同的历史书和2本不同的数学书排成一行,则2本数学书恰好在两端的概率为A .101 B .141 C .201 D .211第Ⅱ卷(非选择题,共65分)二、填空题(本大题共4小题,每小题4分,共16分) 18.已知空间向量()3,2,1=a ,()3,2,1-=b ,则=+b a 2 .19.曲线x x y 23-=在点()1,1-处的切线方程为 .20.设函数()11+=+x x x f ,则()=3f . 21.某运动员射击10次,成绩(单位:环)如下8 10 9 9 10 8 9 9 8 7则该运动员的平均成绩是 环.三、解答题(本大题共4小题,共49分.解答应写出推理、演算步骤)22.(本小题满分12分)已知ABC ∆中,︒=110A ,5=AB ,6=AC ,求BC .(精确到01.0)23.(本小题满分12分)已知数列{}n a 的前n 项和n n S 211-=,求 (Ⅰ) {}n a 的前三项;(Ⅱ) {}n a 的通项公式. 24.(本小题满分12分)设函数()x x x x f 9323--=,求(Ⅰ)函数()x f 的导数;(Ⅱ)函数()x f 在区间[]4,1的最大值与最小值.25.(本小题满分13分) 设椭圆的焦点为()0,31-F ,()0,32F ,其长轴长为4. (Ⅰ)求椭圆的方程;(Ⅱ) 若直线m x y +=23与椭圆有两个不同的交点,求m 的取值范围.参考答案一、 选择题(每小题5分,共85分)1 . C 2.D 3.A 4.B 5.C 6.B 7.D 8.A 9.B 10.C 11.D 12.D 13.A 14.C 15.A 16.B 17.D二、填空题(每小题4分,共16分,)18. ()9,2,3 19. 2-=x y 20.32 21. 7.8 三、解答题(共49分.)22.解:根据余玄定理 A AC AB AC AB BC cos 222∙∙-+=︒∙∙∙-+=110cos 652652203.9≈23.解:(Ⅰ)因为n n S 211-=,则 2121111=-==S a 41212112122=--=-=a S a 8141218112133=---=--=a a S a (Ⅱ)当2≥n 时,1--=n n n S S a⎪⎭⎫ ⎝⎛---=-1211211n n ⎪⎭⎫ ⎝⎛-=-211211n n 21=当1=n 时,211=a ,满足公式n n a 21= 所以数列的通项公式为n n a 21=. 24.解:(Ⅰ) 因为函数()x x x x f 9323--=,所以963)(2'--=x x x f(Ⅱ) 令0)('=x f ,解得3=x 或1-=x ,比较()1f ,()3f ,()4f 的大小,()111-=f ,()273-=f ,()204-=f所以函数()x x x x f 9323--=在区间[]4,1的最大值为11-,最小值为27-. 25.解:(Ⅰ)由已知,椭圆的长轴长42=a ,焦距322=c ,设其短半轴长为b ,则 13422=-=-=c a b所以椭圆的方程为1422=+y x (Ⅱ) 将直线方程m x y +=23代入椭圆方程可得01322=-++m mx x因为直线与椭圆有两个不同交点,所以()014322>--=∆m m解得 22<<-m所以m 的取值范围为()2,2-.。
2014年成人高考数学模拟试题.及其内容规范标准答案3

2014年成人高考数学模拟试题3第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 设集合{1,2,4,6,8},{1,2,3,5,6,7}M N ==,则M N I 中元素的个数为( )A .2B .3C .5D .72. 已知角α的终边经过点(4,3)-,则cos α=( )A .45B .35C .35-D .45- 3. 不等式组(2)0||1x x x +>⎧⎨<⎩的解集为( )A .{|21}x x -<<-B .{|10}x x -<<C .{|01}x x <<D .{|1}x x > 4. 已知正四面体ABCD 中,E 是AB 的中点,则异面直线CE 与BD 所成角的余弦值为( )A .16B .6 C .13D .35. 函数1)(1)y x =>-的反函数是( )A .3(1)(1)x y e x =->- B .3(1)(1)xy e x =->- C .3(1)()x y e x R =-∈ D .3(1)()xy e x R =-∈6. 已知a b r r 、为单位向量,其夹角为060,则(2)a b b -•=r r r ( ) A .-1 B .0 C .1 D .27. 有6名男医生、5名女医生,从中选出2名男医生、1名女医生组成一个医疗小组,则不同的选法共有( )A .60种B .70种C .75种D .150种8. 设等比数列{}n a 的前n 项和为n S ,若243,15,S S ==则6S =( )A .31B .32C .63D .649. 已知椭圆C :22221x y a b+=(0)a b >>的左、右焦点为1F 、2F,过2F 的直线l 交C 于A 、B 两点,若1AF B ∆的周长为C 的方程为( )A .22132x y += B .2213x y += C .221128x y += D .221124x y += 10. 正四棱锥的顶点都在同一球面上,若该棱锥的高位4,底面边长为2,则该球的表面积为( )A .814π B .16π C .9π D .274π11. 双曲线C :22221(0,0)x y a b a b-=>>的离心率为2,,则C 的焦距等于( )A .2 B. C .4 D.12. 奇函数()f x 的定义域为R ,若(2)f x +为偶函数,且(1)1f =,则(8)(9)f f +=( )A .-2B .-1C .0D .1第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上) 13. 6(2)x -的展开式中3x 的系数为 .(用数字作答) 14. 函数cos 22sin y x x =+的最大值为 .15. 设x 、y 满足约束条件02321x y x y x y -≥⎧⎪+≤⎨⎪-≤⎩,则4z x y =+的最大值为 .16. 直线1l 和2l 是圆222x y +=的两条切线,若1l 与2l 的交点为(1,3),则1l 与2l 的夹角的正切值等于 .三、解答题 (本大题共6小题. 解答应写出文字说明、证明过程或演算步骤.) 17. (本小题满分10分)数列{}n a 满足12212,2,22n n n a a a a a ++===-+.(1)设1n n n b a a +=-,证明{}n b 是等差数列; (2)求{}n a 的通项公式. 18. (本小题满分12分)ABC ∆的内角A 、B 、C 的对边分别为a 、b 、c ,已知13cos 2cos ,tan 3a C c A A ==,求B.19. (本小题满分12分)如图,三棱柱111ABC A B C -中,点1A 在平面ABC 内的射影D 在AC 上,090ACB ∠=,11,2BC AC CC ===.(1)证明:11AC A B ⊥;(2)设直线1AA 与平面11BCC B 1A AB C --的大小. 20.(本小题满分12分)设每个工作日甲、乙、丙、丁4人需使用某种设备的概率分别是0.6,0.5,0.5,0.4,各人是否使用设备相互独立,(1)求同一工作日至少3人需使用设备的概率;(2)实验室计划购买k 台设备供甲、乙、丙、丁使用,若要求“同一工作日需使用设备的人数大于k ”的概率小于0.1,求k 的最小值.21. (本小题满分12分)函数32()33(0)f x ax x x a =++≠.(1)讨论函数()f x 的单调性;(2)若函数()f x 在区间(1,2)是增函数,求a 的取值范围. 22. (本小题满分12分)已知抛物线C:22(0)y px p =>的焦点为F ,直线4y =与y 轴的交点为P ,与C 的交点为Q ,且54QF PQ =. (1)求抛物线C 的方程;(2)过F 的直线l 与C 相交于A,B 两点,若AB 的垂直平分线l '与C 相交于M,N 两点,且A,M,B,N四点在同一个圆上,求直线l 的方程.2014年成人高考数学模拟试题答案3一、选择题1.B2.D3.C4.B5.D6.B7.C8.C9.A10.A11.C12.D二、填空题13. -16014.3215. 5 16.43三、解答题:解答应写出文字说明,证明过程或演算步骤。
2014年成人高考数学命题预测试卷(文史类)(三)

成人高等学校招生全国统一考试数学命题预测试卷(三)(文史财经类)(考试时间120分钟)一、选择题:本大题共17小题,每小题5分,共85分.在每小题给出的四个选项中。
只有一项是符合题目要求的.()A.(0,+∞)B.(1,+∞)C.[0,+∞)D.[1,+∞)2.设集合A={x |x2-2x-3<0},B={x | | x-2 1>2),则A ∩ B=()A.{x |-1<x<0)B.{x| 0<x<3)C.{x |-3<x<0)D.{x | 0<x<1)3.()A.9/2B.9C.18D.274.()A.30ºB.45ºC.60ºD.75º5.y=(2x2+3)(3x-2)的导数是()A.18x2-8x+9B.6x2+9C.12x2-8xD.12x6.已知sin a>0,cosa<0,则角a在()A.第一象限B.第二象限C.第三象限D.第四象限7.数列{a n}的通项公式为a n=3n,则{a n}()A.是等差数列B.是首项为1的等比数列C.是首项为3的等比数列D.不是等比数列8.抛物线y2=-2x+2()A.开口向右,顶点为(-1,0)B.开口向右,顶点为(1,0)C.开口向左,顶点为(-1,0)D.开口向左,顶点为(1,0)9.下列函数为偶函数的是()A.ƒ(x)=tan xB.ƒ(x)=| x3 |C.ƒ(x)=(x2+x)2D.ƒ(x)=(3x)310.()A.(0,3),(0,-3)B.(3,0),(-3,0)11.函数ƒ(x)=ax3+bx+1(a,b为常数),ƒ(2)=3,则ƒ(-2)的值为()A.-3B.-1C.3D.112.设甲:四边形ABCD是平行四边形;乙:四边形ABCD是正方形,则()A.甲是乙的充分条件,但不是乙的必要条件B.甲是乙的必要条件,但不是乙的充分条件C.甲是乙的充分必要条件D.甲既不是乙的充分条件,也不是乙的必要条件13.已知M(3,-1),N(-3,5),则线段MN的垂直平分线方程为()A.x-y-2=0B.x+y-2=0C.3x-2y+3=0D.x-y+2=014.()A.4πB.2πC.πD.π/215.已知x>0,y>0,2x+y=3,则xy的最大值为().16.1位老师与6位学生站在一起拍照,要求老师站在中间,并且甲、乙两位同学要求与老师站在一起,则不同的站法种数为()17.一袋中有5个白球,3个红球,现从袋中往外取球,每次任取一个记下颜色后放回,直到红球出现10次时停止,则停止时共取12次球的概率为()二、填空题:本大题共4小题。
2014年成考数学试题

2014年成考数学试题2014年成人高考数学试题由国家教育考试中心于2014年组织编写,通过这篇文章我们将回顾和解答部分试题,帮助考生更好地应对类似的数学题型。
第一节:选择题1. 设集合A = {1, 2, 3, 4, 5},B = {3, 4, 5, 6, 7},则|(A ∪ B) - (A ∩B)| = ?解析:首先求出A ∪ B,即集合A和集合B的并集,得到{1, 2, 3, 4, 5, 6, 7}。
然后求出A ∩ B,即集合A和集合B的交集,得到{3, 4, 5}。
最后求出(A ∪ B) - (A ∩ B),即两个集合的差集,得到{1, 2, 6, 7}。
所以 |(A ∪ B) - (A ∩ B)| 的基数(即集合中元素的个数)为4。
2. 已知正方形ABCD的边长为6cm,点E在CD上且CE = 2cm,则三角形ABE的面积为?解析:首先连接AE,再连接BE,这样三角形ABE就形成了。
由题意可知,三角形ABE是以AE为底,BE为高的等腰直角三角形,所以ABE的面积等于1/2 * AE * BE。
由勾股定理可知,AE的长度为√(2^2 + 6^2) = √40 = 2√10。
所以三角形ABE的面积为1/2 * 2√10 * 2 =2√10 cm²。
第二节:计算题1. 已知函数f(x) = 3x^2 + ax + 9,若f(2) = 27,则a的值为多少?解析:将x = 2代入函数f(x),得到 f(2) = 3(2)^2 + a(2) + 9 = 27。
化简方程,得到 12 + 2a + 9 = 27。
继续化简,得到 2a + 21 = 27。
最后解方程,得到 a = 3。
2. 解方程组:{2x + 5y = 9;3x - 4y = 2。
解析:可以使用消元法来解决这个方程组。
首先将第一个方程乘以3,得到6x + 15y = 27。
然后将第二个方程乘以2,得到6x - 8y = 4。
2014年成人高考数学命题预测试卷(文史类)(二)

成人高等学校招生全国统一考试数学命题预测试卷(二)(文史财经类)(考试时间120分钟)一、选择题:本大题共17小题,每小题5分,共85分.在每小题给出的四个选项中。
只有一项是符合题目要求的.1.()A.(-∞,-6)∪(1,+∞)B.(-6,1)C.(-∞,2)∪(3,+∞)D.(2,3)2.()A.b<c<aB.a<c<bC.a<b<cD.C<b<a3.若x∈R,则“x>3”是“| x |>3”的()A.充分但不必要条件B.必要但不充分条件C.充要条件D.既不充分也不必要条件4.()5.设ƒ(x)是反比例函数,且ƒ(-2)=4,则()6.在同一坐标系中,函数y=2-x与y=log2x的图象是()7.函数ƒ(x)=| x |+cosx ()A.是奇函数B.是偶函数C.既是奇函数也是偶函数D.既不是奇函数也不是偶函数8.已知|a|=4,|b|=5,向量a与b的夹角为π/3,则a·b的值为()A.40B.20C.30D.109.经过点B(0,3)且与直线x+2y-3=0垂直的直线方程为()A.2x-y-3=0B.y-2x-3=0C.X+2y-6=0D.2x+y-3=010.Y=(1-x2)2的导数是()A.2-2x2B.2x2-2C.4x3-4xD.4x-4x311.如果椭圆的一焦点与短轴的两个端点连线互相垂直,则这个椭圆的离心率是()12.从北京开往某地的一列火车,沿途停靠车站共12个(包括起点和终点),这列火车共需车票种数为()A.12B.24C.66D.13213.()A.第n项B.第2+1项C.第n+2项D.第n+3项14.抛物线的顶点是双曲线9x2-4y2=36的中心,而焦点是双曲线的左顶点,则抛物线的方程为()A.y2=-4xB.y2=-8xC.y2=-9xD.y2=-18x15.()A.a>bB.a<bC.a=bD.a,b大小不确定16.函数y=cos2x-sin2x+2sin xcosx的最小正周期和最大值分别是()17.在人寿保险业中,要重视某一年龄的投保人的死亡率,经过随机抽样统计,得到某城市一个投保人能活到75岁的概率为詈,则两个投保人都能活到75岁的概率为()二、填空题:本大题共4小题。
温州市2014年秋成人高中“双证制”模拟卷数学模拟试卷1+答案
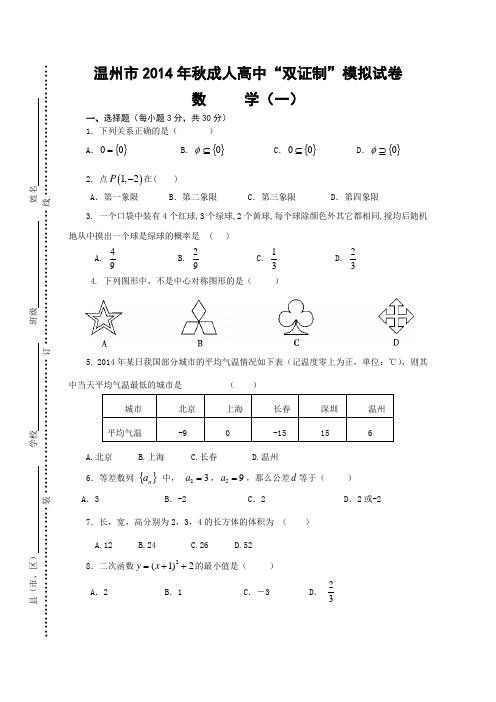
温州市2014年秋成人高中“双证制”模拟试卷数 学(一)一、选择题(每小题3分,共30分)1.下列关系正确的是( )A .{}00=B .{}0⊆φC .{}00⊆D .{}0⊇φ 2. 点()1,2P -在( )A .第一象限B .第二象限C .第三象限D .第四象限3. 一个口袋中装有4个红球,3个绿球,2个黄球,每个球除颜色外其它都相同,搅均后随机地从中摸出一个球是绿球的概率是 ( ) A.94 B.92 C.31D.32 4. 下列图形中,不是中心对称图形的是( )5. 2014年某日我国部分城市的平均气温情况如下表(记温度零上为正,单位:℃),则其中当天平均气温最低的城市是( ) 城市 北京 上海 长春 深圳 温州 平均气温-9-15156A .北京 B.上海 C.长春 D.温州6.等差数列 {}n a 中, 23a =,59a =,那么公差d 等于( ) A .3 B .-2 C .2 D .2或-2 7.长,宽,高分别为2,3,4的长方体的体积为 ( ) A.12 B.24C.26D.528.二次函数2(1)2y x =++的最小值是( )A .2B .1C .-3D . 23县(市、区) 学校 班级 姓名 ······························装·······························订·······························线······························9. 不等式5160x -<的正整数解为( )A .0,1,2,3B .3C .1,2,3D .1,210.已知直线的倾斜角60°,则此直线的斜率是( )A 、B 、C 、-1D 、1 二、填空题(每个空格4分,共28分) 11.23π是第 象限角. 12.函数cos 1y x =+的周期是________ __________. 13.找规律填数:1,-4,9,-16, ,-36.14.在100张奖券中设有一等奖1张,二等奖5张,三等奖10张,若买1张奖券,则中奖的概率是__ .15.二次函数2(1)4y x =-+的顶点坐标为_____ ____________.16.某校艺术节演出中,5位评委给某个节目打分如下:9分,9.3分,8.9分,8.7分,9.1分,则该节目的平均得分是 分;17.边长是3的正方体的表面积是_________________.三、解答题(18-20题,每题8分,第21、22题,每题9分,共42分) 18.解方程y y =-223-319.等差数列{}n a 中, 23a =,59a =,求6S20. 已知y 是x 的一次函数,当1x =时,6y =;当1x =-时, 2y =, (1)求这个函数的解析式.(2)画出这个函数的图象.21.已知圆柱的底面半径为3,母线长为5,求它的体积。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2014年成人高考高起点数学精选模拟试题和参考答案(一)
(考试时间120分钟)
一、选择题(本大题共15小题,每小题5分,共75分。
在每小题给出的四个选项中,只
有一项是符合题目要求的) 1.已知集合{}{}2,,1=
∈>=B R x x x A ,则下列关系中正确的是( )
A .
B A ∈ B .A B ∈
C .B A ⊄
D .A B ⊄ 2.下列函数为偶函数的是( )
A .x y -=
B .x x y sin =
C .x x y cos =
D .x x y +=2 3.条件甲:1=x ,条件乙:0232=+-x x ,则条件甲是条件乙的( )
A .充分但不必要条件
B .必要但不充分条件
C .充要条件
D .既不充分又不必要条件
4.复数)15cos 15(cos 3︒+︒-=i z 的辐角主值是( ) A .︒15 B .︒45 C .︒75 D .︒225
5.两条平行直线0543:1=-+y x l 与0586:2=++y x l 之间的距离是( ) A .2 B .3 C .
21 D .2
3 6.函数31+-=x y 的定义域是( )
A .R
B .[)+∞,0
C .[]2,4--
D .)2,4(--
7.a 为第二象限角,m a =tan ,则a sin 的值为( ) A .2
1m
m +±
B .
2
1m
m + C .2
1m
m +-
D .2
1m
m +-
8.下列命题中,正确的是( )
A .空间中,垂直于同一条直线的两直线平行
B .空间中,垂直于同一平面的两直线平行
C .空间中,垂直于同一平面的两平面平行
D .空间中,与同一平面所成角相等的两直线平行 9.下列等式中,成立的是( )
A .41arctan π=
B .14arctan =π
C .2)2sin(arcsin =
D .43)43arcsin(sin π
π=
10.抛物线22px y =的准线方程为( ) A .2p x -
= B .2p y -= C .p
x 81-= D .p y 81-= 11.由0,1,2,3,4五个数字组成没有重复数字的五位偶数的个数为( )
A .120个
B .60个
C .36个
D .24个
12.参数方程)(1
为参数t t y x ⎩
⎨⎧==表示的图形是( )
A .垂直于x 轴的直线
B .平行于x 轴的直线
C .以原点为圆心的圆
D .过原点的圆
13.若从一批有8件正品,2件次品组成的产品中接连抽取2件产品(第一次抽出的产品
不放回去),则第一次取得次品且第二次取得正品的概率是( )
A .91
B .92
C .458
D .4516
14.已知)2(log ax y a -=在[]1,0上是x 的减函数,则a 的取值范围是( ) A .(0,1) B .(1,2) C .(0,2) D .(2,∞+)
15.设)(x f 是),(+∞-∞上的奇函数,)()2(x f x f -=+,当10≤≤x 时,x x f =)(,则)5.7(f 的值为( )
A .0.5
B .-0.5
C .1.5
D .-1.5
二、填空题(本大题共4个小题,每小题4分,共16分。
把答案填在题中横线上) 16.函数)1(1)1(2≤+-=x x y 的反函数是 。
17.给定三点)0,1(A 、)0,1(-B 、)2,1(C ,那么通过点A ,并且与直线BC 垂直的直线方程
是 。
18.已知离散型随机变量ξ的分布列为
则ξ的期望值)(ξE = 。
19.过曲线3
3
1x y =
上一点)38,2(P 的切线方程是 。
三、解答题(本大题共5小题,共59分,解答应写出推理、演算步骤) 20.(本小题满分11分) 求函数3cos 2sin 2cos sin 2+++=x x x x y 的值域。
21.(本小题满分12分)
{}n a 是首项为2,公比为3的等比数列,将此数列的每一项取以3为底的对数构成数
列{}n b 。
(1)求{}n b 的通项公式.
(2){}n b 的前多少项和为452log 103+ 22.(本小题满分12分)
函数)3222lg(22-++-=a a ax x y 对一切实数x 都有意义,求a 的取值范围。
23.(本小题满分12分)
已知1F 、2F 分别为双曲线
12522
2=-b
y x 的左、右两焦点,P 为双曲线左支上的一点,且︒=∠=120,3211PF F PF ,求b 的值。
24.(本小题满分12分)
在直角梯形ABCD 中,︒=∠=∠90BAD D ,a AB DC AD ==
=2
1
(如图1),将ADC ∆沿AC 折起,使D 到D ',记面D AC '为a ,面ABC 为β,面D BC '为γ。
(1)若二面角βα--AC 为直二面角(如图2),求二面角γβ--BC 的大 小。
(2)若二面角βα--AC 为︒60(如图3),求三棱锥ABC D -'的体积。
参考答案
一、 选择题
1.D 2.B 3.A 4.D 5.D 6.C 7.C 8.B 9.A 10.D 11.B 12.A 13.C 14.B 15.B 二、 填空题
16.)1(11≥--=x x y 17.01=-+y x 18.1.3
19.016312=--y x
三、
解答题
20.解 原式2)cos (sin 2cos sin 21++++=x x x x
2)cos (sin 2cos cos sin 2sin 22+++++=x x x x x x 2)cos (sin 2)cos (sin 2++++=x x x x
设x x t cos sin +=,则)4
sin(2π
+=x t ,有22≤≤-t
原式1)1(2222++=++=t t t
当1-=t 时,1=最小y ;当2=t 时,224+=最大y . 故原函数值域为[]
224,1+.
21.解 (1){}n a 为等比数列,3,21==q a ,则132-⨯=n n a )32(log 13-⨯=n n b
12log 3-+=n
(2)由于[]11)1(2log )12(log 331=--+--+=--n n b b n n
{}n b 是以2log 3为首项以1为公差的等差数列,设{}n b 前n 项和等于452log 103+
有 2l o g 10452
)
1(2log 33+=-+
n n n 整理得 02l o g 2090)12(log 2332=---+n n 即 0)2l o g 29)(10(3=++-n n 解得 10=n 或2log 293--=n (舍去) 故{}n b 前10项和为452log 103+.
22.解 由题意有对一切实数x 都有0322222>-++-a a ax x
设322222-++-=a a ax x t ,则对一切x ,关于x 的二次函数的图象都在x 轴上方
因此0)322(4)2(22<-+--a a a
解得31-<>a a 或
故a 的取值范围为31-<>a a 或.
23.解 根据双曲线的定义,知1012=-PF PF ,又31=PF 13 2=∴PF 在21F PF ∆中有︒⋅-+=120cos 2212
2212
2
1PF PF PF PF F F
即)2
1(1332133)25(4222-⨯⨯⨯-+=+b
解得41172=
b ,故2
117
=b . 24.解 (1)在直角梯形ABCD 中,由已知DAC ∆为等腰直角三角形, 知︒=∠=45,2CAB a AC 过C 作AB CH ⊥,由a AB 2= 可推得a BC AC 2==
∴ BC AC ⊥
取AC 的中点E ,连结E D ',知AC E D ⊥'.
又 二面角β--AC a 为直二面角 ∴β⊥'E D 又 ⊄BC 平面β ∴E D BC '⊥ ∴ a BC ⊥,而a C D ⊄' ∴C D BC '⊥
∴ CA D '∠为二面角γβ--BC 的平面角
由于︒='∠45CA D ,所以二面角γβ--BC 为︒45.
(2)取AC 中点E ,连结E D ',再过D '作β⊥'O D ,垂足为O ,连OE E D AC '⊥ ∴OE AC ⊥
∴ EO D '∠为二面角βα--AC 的平面角 ∴ ︒='∠60EO D 在OE D Rt '∆中,a AC E D 2
221=='
∴ O D S V ABC ABC D '⋅=
∆-'3
1
O D BC AC '⋅⋅⨯=2
1
31
3126462261a a a a =⨯⨯⨯=。
