(完整word版)2019-2020厦门市八年级上学期数学质检试题(2)
人教版2019-2020学年福建省厦门市八年级(上)第一次月考数学试卷解析版

2019-2020学年福建省厦门市八年级(上)月考数学试卷一、选择题(本大题有10小题,每小题4分,共40分)1.(4分)下列图案是几种名车的标志,在这几个图案中不是轴对称图形的是()A.B.C.D.2.(4分)能将三角形面积平分的是三角形的()A.角平分线B.高C.中线D.外角平分线3.(4分)若一个多边形的内角和为1080°,则这个多边形的边数为()A.6B.7C.8D.94.(4分)已知三角形的两边长分别为4cm和9cm,则下列长度的四条线段中能作为第三边的是()A.13cm B.6cm C.5cm D.4cm5.(4分)某同学把一块三角形的玻璃打碎成了3块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事方法是()A.带①去B.带②去C.带③去D.①②③都带去6.(4分)如图,△ACB≌△A′CB′,∠BCB′=30°,则∠ACA′的度数为()A.20°B.30°C.35°D.40°7.(4分)如图,a、b、c分别表示△ABC的三边长,则下面与△ABC一定全等的三角形是()A.B.C.D.8.(4分)如图,将一副三角板和一张对边平行的纸条按下列方式摆放,两个三角板的一直角边重合,含30°角的直角三角板的斜边与纸条一边重合,含45°角的三角板的一个顶点在纸条的另一边上,则∠1的度数是()A.30°B.20°C.15°D.14°9.(4分)下列说法:①全等图形的形状相同、大小相等;②全等三角形的对应边相等;③全等三角形的对应角相等;④全等三角形的周长、面积分别相等,其中正确的说法为()A.①②③④B.①③④C.①②④D.②③④10.(4分)如图所示,BE⊥AC于点D,且AD=CD,BD=ED,若∠ABC=54°,则∠E=()A.25°B.27°C.30°D.45°二、填空题(本大题有6小题,每题4分,共24分)11.(4分)如图,一面小红旗,其中∠A=60°,∠B=30°,则∠BCD=.12.(4分)如图,为了使一扇旧木门不变形,木工师傅在木门的背后加钉了一根木条,这样做的道理是.13.(4分)如图,AB、CD相交于点O,AD=CB,请你补充一个条件,使得△AOD≌△COB,你补充的条件是.14.(4分)如图,DE是△ABC中AC边的垂直平分线,若BC=8cm,AB=10cm,则△EBC的周长为.15.(4分)若一个多边形的每个外角都为36°,则这个多边形的对角线共有条.16.(4分)如图所示,∠E=∠F=90°,∠B=∠C,AE=AF.给出下列结论:①∠1=∠2;②BE =CF;③△ACN≌△ABM;④CD=DN.其中正确的结论是.(将你认为正确的结论的序号都填上)三、解答题(本大题有9小题,共86分)17.(8分)解方程组:18.(8分)解不等式组.19.(8分)在直线l上找出一点P,使得点P到∠AOB的两边OA、OB的距离相等.(要求用尺规作图,保留作图痕迹)20.(8分)如图,AD=AE,∠1=∠2,∠B=∠C.求证:AB=AC.21.(8分)如图,已知CE⊥AB于点E,BF⊥AC于点F,CE与BF相交于点D,且AD平分∠BAC,求证:BD=CD.22.(10分)如图,△ABC中,AD⊥BC于D,BF=AC,FD=CD.求证:AC⊥BE.23.(10分)如图,AD平分∠BAC,DE⊥AB于点E,DF⊥AC于点F,且BD=CD.求证:(1)BE=CF;(2)∠ABD+∠ACD=180°.24.(12分)如图,AD是△ABC的中线,E、F分别在AB、AC上,且DE⊥DF求证:BE+CF>EF.25.(14分)CD经过∠BCA顶点C的一条直线,CA=CB.E,F分别是直线CD上两点,且∠BEC =∠CFA=∠α.(1)若直线CD经过∠BCA的内部,且E,F在射线CD上,请解决下面两个问题:①如图1,若∠BCA=90°,∠α=90°,则BE CF;EF|BE﹣AF|(填“>”,“<”或“=”);②如图2,若0°<∠BCA<180°,请添加一个关于∠α与∠BCA关系的条件,使①中的两个结论仍然成立.(2)如图3,若直线CD经过∠BCA的外部,∠α=∠BCA,请提出EF,BE,AF三条线段数量关系的合理猜想并给出理由.参考答案与试题解析一、选择题(本大题有10小题,每小题4分,共40分)1.解:根据轴对称图形定义可知:A、不是轴对称图形,符合题意;B、是轴对称图形,不符合题意;C、是轴对称图形,不符合题意;D、是轴对称图形,不符合题意.故选:A.2.解:根据等底等高可得,能将三角形面积平分的是三角形的中线.故选C.3.解:设这个多边形的边数为n,根据题意得:180(n﹣2)=1080,解得:n=8.故选:C.4.解:根据三角形的三边关系,得:第三边应大于两边之差,且小于两边之和,即9﹣4=5,9+4=13.∴第三边取值范围应该为:5<第三边长度<13,故只有B选项符合条件.故选:B.5.解:第一块和第二块只保留了原三角形的一个角和部分边,根据这两块中的任一块均不能配一块与原来完全一样的;第三块不仅保留了原来三角形的两个角还保留了一边,则可以根据ASA来配一块一样的玻璃.应带③去.故选:C.6.解:∵△ACB≌△A′CB′,∴∠ACB=∠A′CB′,即∠ACA′+∠A′CB=∠B′CB+∠A′CB,∴∠ACA′=∠B′CB,又∠B′CB=30°∴∠ACA′=30°.故选:B.7.解:A、与三角形ABC有两边相等,而夹角不一定相等,二者不一定全等;B、选项B与三角形ABC有两边及其夹边相等,二者全等;C、与三角形ABC有两边相等,但角不是夹角,二者不全等;D、与三角形ABC有两角相等,但边不对应相等,二者不全等.故选:B.8.解:如图,∠2=30°,∠1=∠3﹣∠2=45°﹣30°=15°.故选:C.9.解:由全等三角形的概念可知:全等的图形是完全重合的,所以①全等图形的形状相同、大小相等是正确的;重合则对应边、对应角是相等的,周长与面积也分别相等,所以①②③④都正确的故选:A.10.解:在△ADB和△CDB,∵BD=BD,∠ADB=∠CDB=90°,AD=CD∴△ADB≌△CDB,∴∠ABD=∠CBD,又∵∠ABC=∠ABD+∠CBD=54°,∴∠ABD=∠CBD=×∠ABC=27°.在△ADB和△EDC中,∵AD=CD,∠ADB=∠EDC=90°,BD=ED,∴△ADB≌△CDE,∴∠E=∠ABD.∴∠E=∠ABD=∠CBD=27°.所以,本题应选择B.二、填空题(本大题有6小题,每题4分,共24分)11.解:∠BCD是三角形ABC的外角,所以∠BCD=∠A+∠B=60°+30°=90°.故填90°.12.解:这样做的道理是利用三角形的稳定性.13.解:添加条件可以是:∠A=∠C或∠ADC=∠ABC.∵添加∠A=∠C根据AAS判定△AOD≌△COB,添加∠ADC=∠ABC根据ASA判定△AOD≌△COB,故填空答案:∠A=∠C或∠ADC=∠ABC.14.解:∵DE垂直平分AC,∴EA=EC.△EBC的周长=BC+BE+EC,=BC+BE+AE,=BC+AB,=8+10,=18(cm).故答案为:18cm.15.解:多边形的边数=360°÷36°=10,对角线条数==35条.故答案为:35.16.解:∵∠E=∠F=90°,∠B=∠C,AE=AF,∴△ABE≌△ACF,∴AC=AB,BE=CF,即结论②正确;∵AC=AB,∠B=∠C,∠CAN=∠BAM,∴ACN≌△ABM,即结论③正确;∵∠BAE=∠CAF,∵∠1=∠BAE﹣∠BAC,∠2=∠CAF﹣∠BAC,∴∠1=∠2,即结论①正确;∴△AEM≌△AFN,∴AM=AN,∴CM=BN,∴△CDM≌△BDN,∴CD=BD,∴题中正确的结论应该是①②③.故答案为:①②③.三、解答题(本大题有9小题,共86分)17.解:解法1:(1)+(2),得5x=10,∴x=2,(3分)把x=2代入(1),得4﹣y=3,∴y=1,(2分)∴方程组的解是.(1分)解法2:由(1),得y=2x﹣3,③(1分)把③代入(2),得3x+2x﹣3=7,∴x=2,(2分)把x=2代入③,得y=1,(2分)∴方程组的解是.(1分)18.解:,由①得:x>1,由②得:x≥﹣2,不等式组的解集为:x>1.19.解:如图,点P为所作.20.证明:∵∠1=∠2,∴∠1+∠BAC=∠2+∠BAC,即∠CAE=∠BAD.在△ABD和△ACE中,∴△ABD≌△ACE(AAS).∴AB=AC.21.证明:∵BE⊥AC,CF⊥AB,∴∠BFD=∠CED=90°,∴∠BDE+∠B=90°,∠FDC+∠90°,∵∠BDE=∠CDF,∴∠B=∠C,∵AD平分∠BAC,∴∠BAD=∠CAD,在△BAD与△CAD中,,∴△BAD≌△CAD(AAS),∴BD=CD.22.证明:∵AD⊥BC,∴∠BDF=∠ADC=90°,在Rt△BDF和Rt△ADC中∴Rt△BDF≌Rt△ADC(HL),∴∠FBD=∠DAC,∵∠BDF=90°,∴∠DBF+∠BFD=90°,∵∠BFD=∠AFE,∴∠DAC+∠AFE=90°,∴∠AEF=180°﹣90°=90°,∴AC⊥BE.23.解:(1)∵AD平分∠BAC,DE⊥AB于点E,DF⊥AC于点F,∴DE=DF,在RT△BDE和RT△CDF中,,∴RT△BDE≌RT△CDF(HL),∴BE=CF;(2)∵RT△BDE≌RT△CDF,∴∠ACD=∠DBE,∵∠DBE+∠ABD=180°,∴∠ABD+∠ACD=180°.24.证明:延长FD至G,使得GD=DF,连接BG,EG ∵在△DFC和△DGB中,,∴△DFC≌△DGB(SAS),∴BG=CF,∵在△EDF和△EDG中∴△EDF≌△EDG(SAS),∴EF=EG在△BEG中,两边之和大于第三边,∴BG+BE>EG又∵EF=EG,BG=CF,∴BE+CF>EF.25.解:(1)①如图1中,E点在F点的左侧,∵BE⊥CD,AF⊥CD,∠ACB=90°,∴∠BEC=∠AFC=90°,∴∠BCE+∠ACF=90°,∠CBE+∠BCE=90°,∴∠CBE=∠ACF,在△BCE和△CAF中,,∴△BCE≌△CAF(AAS),∴BE=CF,CE=AF,∴EF=CF﹣CE=BE﹣AF,当E在F的右侧时,同理可证EF=AF﹣BE,∴EF=|BE﹣AF|;②∠α+∠ACB=180°时,①中两个结论仍然成立;证明:如图2中,∵∠BEC=∠CFA=∠a,∠α+∠ACB=180°,∴∠CBE=∠ACF,在△BCE和△CAF中,,∴△BCE≌△CAF(AAS),∴BE=CF,CE=AF,∴EF=CF﹣CE=BE﹣AF,当E在F的右侧时,同理可证EF=AF﹣BE,∴EF=|BE﹣AF|;故答案为∠α+∠ACB=180°.(2)结论:EF=BE+AF.理由:如图3中,∵∠BEC=∠CFA=∠a,∠a=∠BCA,又∵∠EBC+∠BCE+∠BEC=180°,∠BCE+∠ACF+∠ACB=180°,∴∠EBC+∠BCE=∠BCE+∠ACF,∴∠EBC=∠ACF,在△BEC和△CFA中,,∴△BEC≌△CFA(AAS),∴AF=CE,BE=CF,∵EF=CE+CF,∴EF=BE+AF.故答案为:=,EF=|BE﹣AF|;②∠α+∠ACB=180°时.。
福建省厦门市2019届数学八上期末检测试题

福建省厦门市2019届数学八上期末检测试题注意事项:1. 答题前,考生先将自己的姓名、准考证号填写清楚,将条形码准确粘贴在考生信息条形码粘贴区。
2.选择题必须使用2B 铅笔填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整、笔迹清楚。
3.请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效。
4.保持卡面清洁,不要折叠,不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
一、选择题1在实数范围内有意义,则x 的取值范围是( ) A.x >-4B.x≥-4C.x >-4且x≠1D.x≥-4且x≠-1 2.科学家发现了一种新型病毒,其直径约为0.00000012mm ,数据0.00000012用科学记数法表示正确的是( )A .71.210⨯B .71.210-⨯C .81.210⨯D .81.210-⨯ 3.若解方程225111m x x x +=+--会产生增根,则m 等于( ) A .-10 B .-10或-3 C .-3 D .-10或-44.下列是平方差公式应用的是( )A .(x+y )(﹣x ﹣y )B .(2a ﹣b )(2a+b )C .(﹣m+2n )(m ﹣2n )D .(4x+3y )(4y ﹣3x )5.下列各式:①(-a-2b)(a+2b);②(a-2b)(-a+2b);③(a-2b)(2b+a);④(a-2b)(-a-2b),其中能用平方差公式计算的是( )A.①②B.①③C.②③D.③④ 6.下列由左到右的变形,属于因式分解的( ) A.()()2339x x x --=-B.()2481421a a x x --=--C.()()2492323x x x -=+-D.2269(3)a a a +-=-7.如图,是的高,,则度数是( )A. B. C. D.8.下列标志中,可以看作是轴对称图形的是( )A. B.C. D.9.如图,已知点 D 是∠ABC 的平分线上一点,点 P 在 BD 上,PA ⊥AB ,PC ⊥BC ,垂足分别为 A ,C .下列结论错误的是( )A.∠ADB=∠CDB .B.△ABP ≌△CBPC.△ABD ≌△CBDD.AD=CP10.已知在Rt △ABC 中,∠C =90°,∠A =60°,AC =2,则AB 的值为( )A .B .C .4D .111.如图,△ABC 和△DEF 中,AB=DE ,∠B=∠DEF ,那么添加下列一个条件后,仍无法判定△ABC ≌△DEF 的是( )A .AC=DFB .AC ∥DF C .∠A=∠D D .∠ACB=∠F12.用尺规作图,已知三边作三角形,用到的基本作图是( )A .作一个角等于已知角B .作一条线段等于已知线段C .作已知直线的垂线D .作角的平分线13.下列各组数中,不能成为直角三角形的三条边长的是( )A .3,4,5B .7,24,25C .6,8,10D .9,11,13 14.下列长度的三条线段,能组成三角形的是( ) A .3,4,8B .6,7,8C .5,6,11D .1,4,7 15.若一个多边形的内角和比外角和的2倍少180°,则这个多边形是( )A .三角形B .四边形C .五边形D .六边形 二、填空题 16.分式293x x --约分得_____. 17.计算6x 7÷2x 2的结果等于_____.18.如图,点B ,F ,C ,E 在同一条直线上,BF CE =,//AB DE ,若证明ABC ≌DEF ,还需添加一个条件是______.19.一个多边形的内角和是它外角和的1.5倍,那么这个多边形是______边形.20(b+2)2=0,则点M (a ,b )关于x 轴的对称点的坐标为_____.三、解答题21.某体育用品商场预测某品牌运动服能够畅销,就用32000元购进了一批这种运动服,上市后很快脱销,商场又用68000元购进第二批这种运动服,所购数量是第一批购进数量的2倍,但每套进价多了10元.(1)该商场两次共购进这种运动服多少套?(2)如果这两批运动服每套的售价相同,且全部售完后总利润不低于20%,那么每套售价至少是多少元?22.计算:(1)1020191()(2019)(1)2π-+--- (2)32423()(2)a a a a -⋅+÷ 23.如图,直线l 与m 分别是ABC ∆边AC 和BC 的垂直平分线,它们分别交边AB 于点D 和点E.(1)若10AB =,则CDE ∆的周长是多少?为什么?(2)若125ACB ︒∠=,求DCE ∠的度数.24.如图,已知ABC ∆中,AB AC =,点,D E 分别在,AB AC 上,且BD CE =,如何说明BE CD =呢?解:因为AB AC =( )所以A ABC CB =∠∠( )又因为BD CE =( )BC CB =( )所以BCD ∆≌ CBE ∆( )所以BE CD =( )25.已知12l l //,射线MN 分别和直线12,l l 交于点,A B ,射线ME 分别和直线12,l l 交于点,C D .点P 在MN 上(P 点与,,A B M 三点不重合).连接,PD PC .请你根据题意画出图形并用等式直接写出BDP ∠、ACP ∠、CPD ∠之间的数量关系.【参考答案】一、选择题。
2019-2020厦门市八上数学质检参考答案
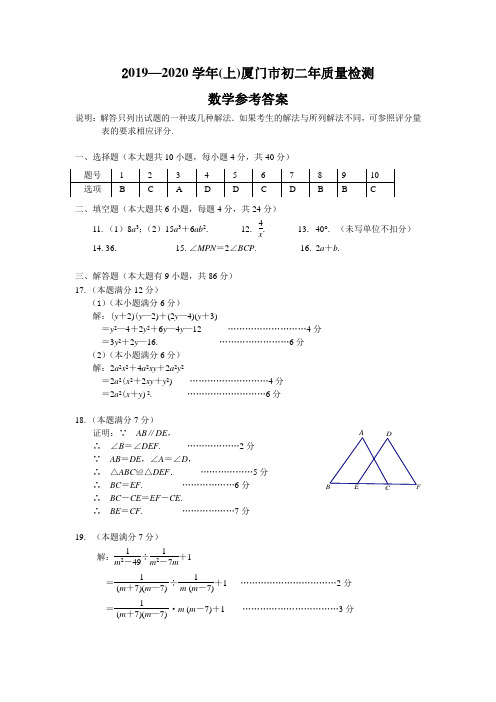
2019—2020学年(上)厦门市初二年质量检测数学参考答案说明:解答只列出试题的一种或几种解法.如果考生的解法与所列解法不同,可参照评分量表的要求相应评分.一、选择题(本大题共10小题,每小题4分,共40分)二、填空题(本大题共6小题,每题4分,共24分)11.(1)8a 3;(2)15a 3+6ab 2. 12. 4x . 13. 40°. (未写单位不扣分)14.36. 15.∠MPN =2∠BCP . 16. 2a +b .三、解答题(本大题有9小题,共86分)17.(本题满分12分) (1)(本小题满分6分)解:(y +2)(y —2)+(2y —4)(y +3)=y 2—4+2y 2+6y —4y —12 ………………………4分 =3y 2+2y —16. ……………………6分 (2)(本小题满分6分) 解:2a 2x 2+4a 2xy +2a 2y 2=2a 2(x 2+2xy +y 2) ………………………4分 =2a 2(x +y ) 2. ………………………6分18.(本题满分7分)证明:∵ AB ∥DE ,∴ ∠B =∠DEF . ………………2分 ∵ AB =DE ,∠A =∠D ,∴ △ABC ≌△DEF . ………………5分∴ BC =EF . ………………6分 ∴ BC -CE =EF -CE .∴ BE =CF . ………………7分19. (本题满分7分)解:1m 2-49÷1m 2-7m+1=1 (m +7)(m —7) ÷1m (m -7)+1 ……………………………2分=1(m +7)(m —7)·m (m -7)+1 ……………………………3分AB DCE F=mm +7 +1 ……………………………5分=m +m +7 m +7=2m +7 m +7 . ……………………………6分当m =2时,原式=2×2+7 2+7 =119. ……………………………7分20. (本题满分8分) 解:(1)(本小题满分6分)如图即为所求. …………………6分 (2)(本小题满分2分)对称点P ′在△ABC 外. …………………8分21. (本题满分8分)(1)(本小题满分5分) 证明:解法一∵ BD ⊥AC ,D 是边AC 的中点, ∴ BD 是边AC 的垂直平分线.∴ BA= BC . ………………………3分 ∵ AB =AC , ∴ AB =AC= BC .∴ △ABC 是等边三角形. ………………………5分解法二∵ BD ⊥AC ,D 是边AC 的中点, ∴ ∠BDA =∠BDC =90°,AD =CD . 又∵ BD =BD , ∴ △BAD ≌△BCD .∴ BA= BC . ………………………3分 ∵ AB =AC ,∴ AB =AC= BC .∴ △ABC 是等边三角形. ……………………5分 (2)(本小题满分3分)如图点E 即为所求. ………………………8分AB CDEAB CDAB C · · ·22.(本题满分9分) 解:(1)(本小题满分4分)设甲厂2017年日均生产该产品x 件(x >0),则甲厂2018年日均生产该产品(2x +2)件,由题意得99x =2002x +2.………………2分 解得x =99. ………………3分经检验,x =99是原方程的解,且符合题意.答:甲厂2017年日均生产该产品99件. ………………4分 (2)(本小题满分5分)设甲厂2017年日均生产该产品x 件(x >0),则甲厂2018年日均生产该产品(2x +2)件, 乙厂日均生产该产品(3x +4)件.由m :n =14:25可设m =14k ,n =25k (k >0).所以甲厂生产m 件产品所用时间t 甲=14k 2x +2,t 乙=25k3x +4. (5)t 甲-t 乙=14k 2x +2-25k3x +4………………7分=(3-4x )k ( x +1)(3x +4). 因为2017年的年产量过万件, 所以x >10000365.所以3-4x <0. 所以t 甲-t 乙<0.即t 甲<t 乙.答:甲厂先完成任务. ………………9分23.(本题满分10分)解:(1)(本小题满分1分) 算式:62×11,34×11,54×11.共同特征:三个算式均是一个两位数与11相乘. ………………1分 (2)(本小题满分4分)62×11=682,34×11=374,54×11=594.规律:一个两位数与11相乘,将这个两位数的十位和个位分别作为积的百位和个位,将这个两位数的数位上数字之和作为积的十位. ……………5分 (3)(本小题满分3分)规律:(10a +b )×11=100a +10(a +b )+b . (其中1≤a ≤9,0≤b ≤9,且a +b ≤9,a ,b 为整数)证明:(10a +b )×11=(10a +b )×10+(10a +b ) =100a +10b +10a +b=100a +10(a +b )+b . ………………8分 (4)(本小题满分2分)18×22,15×55. ………………10分24.(本题满分11分)解:(1)(本小题满分5分) ∵ △ABC 是等边三角形,∴ ∠A =∠B =∠C =60°. ……………1分设∠A =12∠B +α.可得α=30°,不符合定义. ……………2分 所以∠A 不是∠B 的差角.同理可知,△ABC 中任意一个角都不是其他角的差角. ……………3分 所以△ABC 不是“差角三角形”. ……………4分 (2)(本小题满分6分) ∵ 在△ABC 中,∠C =90°, ∴ ∠A =90°-∠B . ①设∠C =12∠A +α.即90°=12(90°-∠B )+α,所以α=12∠B +45°.因为50°≤∠B ≤70°,可得α>25°.不符合定义,所以∠C 不是∠A 的差角. ②设∠C =12∠B +α.即90°=12∠B +α,所以α=90°-12∠B .因为50°≤∠B ≤70°,可得α>25°.不符合定义,所以∠C 不是∠B 的差角. ③设∠A =12∠B +α.即90°-∠B =12∠B +α,所以α=90°-32∠B .因为50°≤∠B ≤70°,可得-15°≤α≤15°.由0°<α≤15°,可得50°≤∠B <60°. 即当50°≤∠B <60°时,△ABC 是差角三角形,且∠A 是∠B 的差角. ④设∠A =12∠C +α.即90°-∠B =45°+α,所以α=45°-∠B . 因为50°≤∠B ≤70°,可得α<0°.不符合定义,所以∠A 不是∠C 的差角. ⑤设∠B =12∠A +α.即∠B =12(90°-∠B )+α,所以α=32∠B -45°.因为50°≤∠B ≤70°,可得α>30°.不符合定义,所以∠B 不是∠A 的差角.⑥设∠B =12∠C +α.即∠B =45°+α,所以α=∠B -45°. 因为50°≤∠B ≤70°,可得5°≤α≤25°.符合定义,所以△ABC 是差角三角形,且∠B 是∠C 的差角. 综上,△ABC 是差角三角形.∠B 是∠C 的差角;当50°≤∠B <60°时,∠A 是∠B 的差角.(本小题的评分要求见评分量表)25. (本题满分14分)(1)(本小题满分3分)证明:∵ ∠ABC =∠CDA =90°, ∵ BC =CD ,AC=AC ,∴ Rt △ABC ≌Rt △ADC . ………………………2分 ∴ AB =AD . ………………………3分(2)(本小题满分4分) 证明:∵ AE =BE +DE , 又∵ AE =AD +DE ,∴ AD =BE . ……………………………4分 ∵ AB =AD ,∴ AB =BE . ……………………………5分 ∴ ∠BAD =∠BEA . ∵ ∠ABC =90°,∴ ∠BAD =180°—∠BAC2 =45°. ……………………………6分∵ 由(1)得△ABC ≌△ADC , ∴ ∠BAC =∠DAC .∴ ∠BAC =45°2 =22.5°. ……………………………7分(3)(本小题满分7分)解法一:解:当MO +PO 的值最小时,点O 与点E 可以重合,理由如下: ∵ ME ∥AB ,∴ ∠ABC =∠MEC =90°,∠2=∠3. ∵ MP ⊥DC , ∴ ∠MPC =90°.∴ ∠MPC =∠ADC =90°. ∴ PM ∥AD . ∴ ∠1=∠4.由(1)得,Rt △ABC ≌Rt △ADC , ∴ ∠1=∠2 ,∴ ∠3=∠4.即MC 平分∠PME .BE D CA654321QPACDEBM又∵MP⊥CP,ME⊥CE,∴PC=EC.连接PB,连接PE,延长ME交PD的延长线于点Q.设∠1=α,则∠2=α.在Rt△ABE中,∠5=90°—2α.在Rt△CDE中,∠ECD=90°—∠5=2α.∵PC=EC,……………………8分∴∠6=∠EPC=12 ∠ECD=α.∴∠PED=∠5+∠6=90°—α.∵ME∥AB,∴∠QED=∠BAD=2α.当∠PED=∠QED时,∵∠PDE=∠QDE,DE=DE,∴△PDE≌△QDE.∴PD=DQ.即点P与点Q关于直线AE成轴对称,也即点M、点E、点P关于直线AE的对称点Q,这三点共线,也即MO+PO的值最小时,点O与点E重合.因为当∠PED=∠QED时,90°—α=2α,也即α=30°.所以,当∠ABD=60°时,MO+PO取最小值时的点O与点E重合. ……………11分此时MO+PO的最小值即为ME+PE.∵PC=EC,∠PCB=∠ECD,CB=CD,∴△PCB≌△ECD.∴∠CBP=∠CDE=90°.∴∠CBP+∠ABC=180°.∴A,B,P三点共线. ……………………13分当∠ABD=60°时,在△PEA中,∠P AE=∠PEA=60°.∴∠EP A=60°.∴△PEA为等边三角形.∵EB⊥AP,∴AP=2AB=2a.∴EP=AE=2a.∵∠1=∠3=30°,∴EM=AE=2a.∴MO+PO的最小值为4a.……………………14分。
(完整word版)2019-2020厦门市八年级上学期数学质检试题

2019—2020学年(上)厦门市八年级质量检测数 学(试卷满分:150分 考试时间:120分钟)准考证号 姓名 座位号注意事项:1.全卷三大题,25小题,试卷共4页,另有答题卡. 2.答案必须写在答题卡上,否则不能得分. 3.可以直接使用2B 铅笔作图.一、选择题(本大题有10小题,每小题4分,共40分.每小题都有四个选项,其中有且只有一个选项正确) 1.计算2-1的结果是A . 0B . 12C . 1D .22.下列长度的三条线段能组成三角形的是A . 3,4,7B . 3,4,8C . 3,3,5D . 3,3,73.分式xx -2有意义,则x 满足的条件是A . x ≠2B . x =0C . x =2D . x >2 4. 如图1,在△ABC 中,AD 交边BC 于点D .设△ABC 的重心为M , 若点M 在线段AD 上,则下列结论正确的是A . ∠BAD =∠CADB .AM =DMC . △ABD 的周长等于△ACD 的周长 D .△ABD 的面积等于△ACD 的面积 5.已知正方形ABCD 边长为x ,长方形EFGH 的一边长为2,另一边的长为x ,则正方形ABCD 与长方形EFGH 的面积之和等于A .边长为x +1的正方形的面积B . 一边长为2,另一边的长为x +1的长方形面积C . 一边长为x ,另一边的长为x +1的长方形面积D . 一边长为x ,另一边的长为x +2的长方形面积6.从甲地到乙地有两条路:一条是全长750km 的普通公路,另一条是全长600km 高速公路.某客车从甲地出发去乙地,若走高速公路,则平均速度是走普通公路的平均速度的2倍,所需时间比走普通公路所需时间少5小时.设客车在普通公路上行驶的平均速度是x km /h ,则下列等式正确的是 A . 600x +5=7502x B . 600x -5=7502x C .6002x +5=750x D . 6002x -5=750x7.在△ABC 中,D ,E 分别是边AB ,AC 上的点,且AD =CE ,∠DEC =∠C =70°, ∠ ADE =30°,则下列结论正确的是A .DE =CEB .BC =CE C .DB =DED .AE =DB图18.在平面直角坐标系中,O 是坐标原点,点A (3,2),点P (m ,0)(m <6),若△POA 是等腰三角形,则m 可取的值最多有A . 2个B .3个C .4个D . 5个9. 下列四个多项式,可能是2x 2+mx -3 (m 是整数)的因式的是A . x -2B . 2x +3C . x +4D . 2x 2-1 10. 如图2,点D 在线段BC 上,若BC =DE ,AC =DC ,AB =EC ,且∠ACE =180°—∠ABC —2x °,则下列角中,大小为x °的角是A . ∠EFCB . ∠ABC C . ∠FDCD . ∠DFC二、填空题(本大题有6小题,每小题4分,共24分)11.计算:(1)(2a )3= ;(2)3a (5a 2+2b 2) = . 12.计算:4x 23y ·3yx3= .13. 如图3,在△ABC 中,∠ACB =90°,AD 平分∠CAB ,交边BC 于点D , 过点D 作DE ⊥AB ,垂足为E .若∠CAD =20°,则∠EDB 的度数是 . 14. 如图4,有一张边长为x 的正方形ABCD 纸板,在它的一个角上切去一个 边长为y 的正方形AEFG ,剩下图形的面积是32,过点F 作FH ⊥DC ,垂 足为H .将长方形GFHD 切下,与长方形EBCH 重新拼成一个长方形,若 拼成的长方形的较长的一边长为8,则正方形ABCD 的面积是 . 15. 已知锐角∠MPN ,依照下列步骤进行尺规作图: (1)在射线PN 上截取线段P A ;(2)分别以P ,A 为圆心,大于12P A 的长为半径作弧,两弧相交于E ,F两点; (3)作直线EF ,交射线PM 于点B ; (4)在射线AN 上截取AC =PB ; (5)连接BC .则∠BCP 与∠MPN 之间的数量关系是 .16.在△ABC 中,∠C =90°,D 是边BC 上一点,连接AD ,若∠BAD +3∠CAD =90°,DC =a ,BD =b ,则AB = . (用含a ,b 的式子表示)三、解答题(本大题有9小题,共86分)17.(本题满分12分)(1)计算:(y +2)(y —2) +(2y —4)(y +3); (2)分解因式:2a 2x 2+4a 2xy +2a 2y 2.18. (本题满分7分)如图5,点B ,E ,C ,F 在一条直线上,AB =DE ,∠A =∠D ,AB ∥DE. 求证:BE =CF .F A B CD E图2 ABCDE图3AB DCE F图5FA B CD EHG图4先化简,再求值:1m 2-49÷1m 2-7m+1,其中m =2.20. (本题满分8分) 已知点A (1,1),B (-1,1),C (0,4). (1)在平面直角坐标系中描出A ,B ,C 三点;(2)在同一平面内,点与三角形的位置关系有三种:点在三角形内、点在三角形边上、 点在三角形外.若点P 在△ABC 外,请判断点P 关于y 轴的对称点P ′与△ABC 的 位置关系,直接写出判断结果.21. (本题满分8分)如图6,在△ABC 中,AB =AC ,过点B 作BD ⊥AC ,垂足为D ,若D 是边AC 的中点, (1)求证:△ABC 是等边三角形;(2)在线段BD 上求作点E ,使得CE =2DE . (要求:尺规作图,不写画法,保留作图痕迹)22. (本题满分9分)某企业在甲地有一工厂(简称甲厂)生产某产品,2017年的年产量过万件,2018年甲 厂经过技术改造,日均生产的该产品数是该厂2017年的2倍还多2件. (1)若甲厂2018年生产200件该产品所需的时间与2017年生产99件该产品所需的时间相同,则2017年甲厂日均生产该产品多少件?(2)由于该产品深受顾客欢迎,2019年该企业在乙地建立新厂(简称乙厂)生产该产品.乙厂的日均生产的该产品数是甲厂2017年的3倍还多4件.同年该企业要求甲、乙两厂分别生产m ,n 件产品(甲厂的日均产量与2018年相同),m :n =14:25,若甲、乙两厂同时开始生产,谁先完成任务?请说明理由.图6AB CD已知一些两位数相乘的算式:62×11,78×69,34×11,63×67,18×22,15×55,12×34,54×11. 利用这些算式探究两位数乘法中可以简化运算的特殊情形:(1)观察已知算式,选出具有共同特征的3个算式,并用文字描述它们的共同特征; (2)分别计算你选出的算式.观察计算的结果,你能发现不经过乘法运算就可以快速、 直接地写出积的规律吗?请用文字描述这个规律; (3)证明你发现的规律;(4)在已知算式中,找出所有可以应用(或经过转化可以应用)上述规律的算式,并将 它们写在横线上: .24. (本题满分11分)在△PQN 中,若∠P =12∠Q +α(0°<α≤25°),则称△PQN 为“差角三角形”,且∠P 是∠Q 的“差角”.(1)已知△ABC 是等边三角形,判断△ABC 是否为“差角三角形”,并说明理由; (2)在△ABC 中,∠C =90°,50°≤∠B ≤70°,判断△ABC 是否为“差角三角形”,若是,请写出所有的“差角”并说明理由;若不是,请说明理由.25. (本题满分14分)如图7,在四边形ABCD 中,AC 是对角线,∠ABC =∠CDA =90°,BC =CD ,延长 BC 交AD 的延长线于点E . (1)求证:AB =AD ;(2)若AE =BE +DE ,求∠BAC 的值;(3)过点E 作ME ∥AB ,交 AC 的延长线于点M ,过点M 作MP ⊥DC ,交DC 的延长 线于点P ,连接PB .设PB =a ,点O 是直线AE 上的动点,当MO +PO 的值最小 时,点O 与点E 是否可能重合?若可能,请说明理由并求此时MO +PO 的值(用 含a 的式子表示);若不可能,请说明理由.图7B E DC A。
2020—2021学年(上)厦门市初二年数学质量检测

2020—2021学年(上)厦门市初二年质量检测数学一、选择题(本大题有10小题,每小题4分,共40分.每小题都有四个选项,其中有且只有一个选项正确)1.计算20的结果是( )A .0B .21C .1D .22.计算6m ÷3m 的结果是( )A .2B .2mC .3mD .2m 23.在平面直角坐标系XOY 中,点(2,1)关于y 轴对称的点在( )A .第一象限B .第二象限C .第三象限D .第四象限4.若AD 是△ABC 的中线,则下列结论正确的是( ) A .AD ⊥BC B .BD=CD C .∠BAD=∠CAD D .AD=21BC 5.如图1,点B ,C 分别在∠EAF 的边AE ,AF 上,点D 在线段AC 上,则下列是△ABD 的外角的是( )A .∠BCFB .∠CBEC .∠DBCD .∠BDF6.整式n 2-1与n 2+n 的公因式是( )A .nB .n 2C .n +1D .n -17.运用公式a 2+2ab +6=(a +b )2直接对整式4x 2+4x +1进行因式分解,公式中的a 可以是( )A .2x 2B .4x 2C .2xD .4x8.如图2,已知△ABC 与△BDE 全等,其中点D 在边AB 上,AB>BC ,BD=CA ,DE ∥AC ,BC 与DE 交于点F ,下列与AD+AC 相等的是( )A .DEB .BEC .BFD .DF9.如图3,直线AB ,CD 交于点O ,若AB ,CD 是等边△MNP 的两条对称轴,且点P 在直线CD 上(不与点O 重合),则点M ,N 中必有一个在( )A .∠AOD 的内部B .∠BOD 的内部C .∠BOC 的内部D .直线AB 上10.在平面直角坐标系XOY 中,点A (0,2),B (a ,0),C (m ,n ),其中m >a ,a <1,n >0,若△ABC 是等腰直角三角形,且AB=BC ,则m 的取值范围是( )A .0<m <2B .2<m <3C .m <3D .m >3二、填空题(本大题有6小题,每小题4分,共24分)11.计算∶(1)52x x ⋅= ;(2)23)(x = .12.五边形的外角和为 度.13.计算∶111---x x x = . 14.如图4,CE 是△ABC 外角的平分线,且AB//CE ,若∠ACB=36°,则∠A 等于 度.15.如图5,△ABC 与△BED 全等,点A ,C 分别与点B ,D 对应,点C 在BD 上,AC 与BE 交于点F .若∠ABC=90°,∠D=60°,则AF :BD 的值为 .16.如图6,在一个大正方形纸板中剪下边长为acm 和边长为bcm 的两个正方形,剩余长方形①和长方形②的面积和为8cm².若将剩余的长方形①和②平移进边长为acm 的正方形中(如图7),此时该正方形未被覆盖的面积为6cm²,则原大正方形的面积为 .三、解答题(本大题有9小题,共86分)17.(本题满分12分)计算:(1)2a ²·(3a ²-5b ) (2)(2a +b )·(2a -b )如图8,点B ,F ,C ,E 在一条直线上,AB=DE ,FB=CE ,AB//ED .求证:AC//FD .19.(本题满分7分) 先化简,再求值:m m m m m m 4)223(2-⋅++-,其中m =1.20.(本题满分8分)甲、乙两人做某种机械零件.已知甲每小时比乙多做6个,甲做90个所用的时间与乙做60个所用的时间相等.求甲、乙每小时各做零件多少个.如图9,已知锐角∠APB,M是边PB上一点,设∠APB=α,(1)尺规作图:在边PA上作点N,使得∠ANM=2α;(不写作法,保留作图痕迹)(2)在(1)的条件下,若边PA上存在点Q,使得∠QMB=3α,①证明△MNQ是等腰三角形;②直接写出α的取值范围.22.(本题满分10分)将一个三角形沿着其中一个顶点及其对边上的一点所在的直线折叠,若折叠后原三角形的一边垂直于这条对边,则称这条直线是该三角形的“对垂线”.(1)如图10,AD是等边△ABC的对垂线,把△ABC沿直线AD折叠后,点B落在点B'处,求∠BAD的度数;(2)如图11,在△ABC中,∠BAC=90°,点D在边BC上,且AB=AD,若∠B=2∠DAC,判断直线AD是否是△ABC的对垂线,并说明理由.23.(本题满分10分)观察下列等式:第1个等式∶111)211(34+=+⨯;第2个等式∶211)311(89+=+⨯;第3个等式∶311)311(1516+=+⨯;第4个等式∶411)511(2425+=+⨯;.....根据你观察到的规律,解决下列问题:(1)写出第5个等式;(2)写出第n 个等式,并证明;(3)计算∶.1-20202020 (24251516893422)⨯⨯⨯⨯⨯某国家5A级景区开展一年一度的旅游主题活动,活动将持续两周.景区内某餐厅今年活动期间推出“精品套餐”,在午餐和晚餐时间只出售该套餐,且定价相同.活动开始后,该套餐的销售情况如下:第一天,午餐、晚餐时间均按定价出售,当天销售总收入为30000元;第二天,午餐时间按定价共售出100份;晚餐时间按定价打九五折出售(即按定价的95%出售),当天销售总收入为37650元,且全天销售量比第一天多30%(销售量指售出的套餐的份数).(1)若第一天的全天销售量为m,请用含m的代数式表示第二天晚餐时间该套餐的销售量;(2)该套餐的定价为多少元?(3)第三天,餐厅在午餐时间按定价打九二折出售该套餐,晚餐按定价出售,全天销售量比第一天多32%;第四天,午餐和晚餐时间均按定价打九折出售,全天销售量比第一天多1倍.根据该餐厅往年活动期间的销售数据,午餐时间套餐的销售量和晚餐时间套餐的销售量有如下规律:①若套餐价格不变,则二者分别保持基本稳定;②若套餐按定价打折,折扣相同,则二者的增长率也会大致相同.参考前四天该套餐按定价所打折扣与销售量增长率之间的关系,若第五天午餐与晚餐时间均按定价打八八折出售该套餐,你认为全天销售量会是多少?请说明理由.在四边形ABCD中,∠ABC=90°,AC⊥BD,垂足为E.(1)如图12,若BC=DC,求证:∠ADC=90°;(2)如图13,过点C作CG∥AB,分别与BD,AD交于点F,G,点M在边AB上,连接MC并延长,交BD于点N,过D作DH⊥MC于H,∠BCG=2∠DCG,且∠BMC=∠BDC+45°.①证明NM=NB;②若BD=AE+CH,探究AB与BC的数量关系.。
学年上厦门市八年级质量检测数学试卷及答案

2018-2019学年(上)厦门市八年级质量检测数 学(试卷满分:150分 考试时间:120分钟)准考证号 姓名 座位号一、选择题(本大题有10小题,每小题4分,共40分.每小题都有四个选项,其中有且只有一个选项正确)(2019厦门八上质检1)计算12-的结果是( )A .2-B .12-C .12D .1(2019厦门八上质检2)1x =是方程22x a +=-的解,则a 的值是( ) A .4- B .3- C .0 D .4 (2019厦门八上质检3)四边形内角和是( )A .90 B . 180 C .360 D .540(2019厦门八上质检4)在平面直角坐标系xoy 中,若ABC ∆在第一象限,则ABC ∆关于x 轴对称的图形所在的位置是( )A .第一象限B .第二象限C .第三象限D .第四象限(2019厦门八上质检5)若AD 是ABC ∆的中线,则下列结论正确的是( )A .BD CD =B .AD BC ⊥ C .BAD CAD ∠=∠ D . BD CD =且AD BC ⊥ (2019厦门八上质检6)运用完全平方公式222()2a b a ab b +=++计算21()2x +,则公式中的2ab 是( )A.12x B . x C . 2x D . 4x (2019厦门八上质检7)甲完成一项工作需要n 天,乙完成该项工作需要的时间比甲多3天,则乙一天能完成的工作量是该项工作的( ) A .3nB .13n C . 113n + D . 13n + (2019厦门八上质检8)如图1,点,F C 在BE 上,ABC DEF ≌,AB 和DE ,AC 与DF 是对应边,,AC DF 交于点M ,则AMF ∠等于( ).2A B ∠ .2B ACB ∠ .C A D +∠∠ D.B ACB +∠∠(2019厦门八上质检9)在半径为R 的圆形钢板上,挖去四个半径都为r 的小圆.若16.8R =,剩余部分的面积为272π,则r 的值( ).A 3.2 .B 2.4 .C 1.6 .D 0.8(2019厦门八上质检10)在平面直角坐标系xOy 中,点()0,A a ,(),12B b b -,()23,0C a -,012a b <<<,若OB 平分AOC ∠,且AB BC =,则a b +的值为( ).A 9或12 .B 9或11 .C 10或11 .D 10或12 二、填空题(本大题有6小题,每小题每题4分,共24分) (2019厦门八上质检11)计算下列各题:()421xx x ÷=()()22=ab(2019厦门八上质检12)要使分式13x -有意义,x 应满足的条件是 (2019厦门八上质检13)如图2,在ABC 中,°90C =∠,°=30A ∠,4AB =,则BC 的长为(2019厦门八上质检14)如图3,在ABC 中,=60B AD ∠︒,平分BAC ∠,点E 在AD 延长线上,且EC AC ⊥.若=50E ∠︒,则ADC ∠的度数是(2019厦门八上质检15)如图4,已知,,,E F P Q 分别是长方形纸片()ABCD AD AB >各边的中点,将该纸片对着,使顶点,B D 重合,则折痕所在的直线可能是 .(2019厦门八上质检16)已知,a b 满足22(2)()442a b a b ab b b a a -+-++=-,且2a b ≠,则a 与b 的数量关系是 .三、解答题(本大题有9小题,共86分)(2019厦门八上质检17)(本题满分12分)计算: (1)23105;mn mn m n ÷⋅ (2)(32)(5)x x +-.(2019厦门八上质检18)(本题满分7分)如图5,在ABC 中,=60B ∠︒,过点C 作//,CD AB 若60ACD ∠=︒,求证:ABC 是等边三角形.(2019厦门八上质检19)(14分)化简并求值: (1),)42()12(22+--a a 其中;234=+a (2),4331232-+÷⎪⎭⎫ ⎝⎛+-m m m 其中4=m(2019厦门八上质检20)(7分)如图6,已知D CF AB ,//是AB 上一点,DF 交AC 于点E ,若CF BD AB +=,求证:CFE ADE ∆≅∆(2019厦门八上质检21)(7分)在平面直角坐标系xOy 中,点A 在第一象限,点B A 、关于y 轴对称。
2019—2020学年(上)厦门市八年级质量检测(数学试题)

2019—2019—2020学年(上)厦门市八年级质量检测(数学试题)数学试题(试卷满分120分;考试时间120分钟)一、选择题(本大题有7小题;每小题3分;共21分)1、下列实数中;是无理数的是( ) A . 2 B . 0 C . 5 D .31-2、下列图形中;不是轴对称图形的是( )3、直线x y 2= 经过( )A .第一、三象限B .第二、四象限C .第一、四象限D .第二、三象限 4、下列计算正确的是( )A .532a a a =+B .624a a a =⋅C .33a a a =÷ D .623)(a a -=-5、下列函数中;y 随x 的增大而减小的是( ) A .x y 21+= B .34+-=x y C .x y 31= D .12-=x y 6、下列命题是真命题的是( )A .有一边对应相等的两个直角三角形全等;B .两个等边三角形全等;C .各有一个角是450的两个等腰三角形全等;D .腰和底对应相等的两个等腰三角形全等。
7、若a 是与65最接近的整数;81=b ;则20112012b a⋅=( ) A . 8 B . 81 C . 8± D .81±二、填空题(本大题共10题;每小题4分;共40分)8.计算:⑴4= ;⑵327= ;⑶01.0= ;⑷3)2(b = ;⑸)2(42xy y -⋅= ;⑹y x y x 324728÷= ;⑺))((b a b a -+= ;9.如图1;在△ABC 中;AB =AC ;A D ⊥BC ;BC =4; 则BD = . 10.2536的平方根是 . 11.当3=x 时;函数12-=x y 的值是 .A .B .C .D . 图1D CBADA则∠DBC = 0.13.已知直线经过点(2;1);且平行于直线x y 3=;则这条直线的解析式为 . 14.在△ABC 中;∠C =900;∠ABC 的平分线BD 交AC 于点D ;若点D 到AB 边的距离为5cm ;则DC = cm.15.如图3;在△ABC 中;AB<AC ;BC 边上的垂直平分线DE 交BC 于点D ;交AC 于点E ;BD =4;△ABE 的周长为14;则△ABC 的周长为 。
2019-2020学年(上)厦门市初二数学质量检测卷及答案

2019-2020学年(上)厦门市初二质量检测数学注意事项:1.全卷三大题,25小题,试卷共4页,另有答题卡.2.答案必须写在答题卡上,否则不能得分.3.可以直接使用2B 铅笔作图.一、选择题(本大题有10小题,每小题4分,共40分.每小题都有四个选项,其中有且只有一个选项正确)1.计算1-2的结果是A.0B.21C.1D.22.下列长度的三条线段能组成三角形的是A.3,4,7B.3,4,8C.3,3,5D.3,3,73.分式2-x x 有意义,则x 满足的条件是A.2≠x B.0=x C.2=x D.2>x 4.如图1,在△ABC 中,AD 交边BC 于点D.设△ABC 的重心为M ,若点M 在线段AD 上,则下列结论正确的是A.∠BAD=∠CADB.AM=DMB. C.△ABD 的周长等于△ACD 的周长 D.△ABD 的面积等于△ACD 的面积5.已知正方形ABCD 边长为x ,长方形EFGH 的一边长为2,另一边的长为x ,则正方形ABCD 与长方形EFGH 的面积之和等于A.边长为1+x 的正方形的面积B.一边长为2,另一边的长为x +1的长方形面积C.一边长为x ,另一边的长为x +1的长方形面积D.一边长为x ,另一边的长为x +2的长方形面积6.从甲地到乙地有两条路:一条是全长750km 的普通公路,另一条是全长600km 高速公路.某客车从甲地出发去乙地,若走高速公路,则平均速度是走普通公路的平均速度的2倍,所需时间比走普通公路所需时间少5小时.设客车在普通公路上行驶的平均速度是x km/h ,则下列等式正确的是A.x x 27505600=+ B.x x 27505600=-C.x x 75052600=+ D.x x 75052600=-7.在△ABC 中,D,E 分别是边AB ,AC 上的点,且AD=CE ,∠DEC=∠C=70°,∠ADE=30°,则下列结论正确的是A.DE=CEB.BC=CEC.DB=DED.AE=DB8.在平面直角坐标系中,O 是坐标原点,点A (3,2),点P (m ,0)(m <6),若POA 是等腰三角形,则m 可取的值最多有A.2个B.3个C.4个D.5个9.下列四个多项式,可能是322-+mx x (m 是整数)的因式的是A.x -2B.2x +3C.x +4D.122-x 10.如图2,点D 在线段BC 上,若BC=DE ,AC=DC ,AB=EC ,且∠ACE=180°-∠ABC-x 2,则下列角中,大小为x °的角是A.∠EFCB.∠ABCC.∠FDCD.∠DFC二、填空题(本大题有6小题,每小题4分,共24分)11.计算:(1)()=32a ;(2)()=+22253b a a12.计算:=⋅32334x y y x 13.如图3,在△ABC 中,∠ACB=90°,AD 平分∠CAB ,交边BC 于点D ,过点D 作DE ⊥AB ,垂足为E.若∠CAD=20°,则∠EDB 的度数是.14.如图4,有一张边长为x 的正方形ABCD 纸板,在它的一个角上切去一个边长为y 的正方形AEFG ,剩下图形的面积是32,过点F 作FH ⊥DC ,垂足为H.将长方形GFHD 切下,与长方形EBCH 重新拼成一个长方形,若拼成的长方形的较长的一边长为8,则正方形ABCD 的面积是.15.已知锐角∠MPN ,依照下列步骤进行尺规作图:(1)在射线PN 上截取线段PA(2)分别以P ,A 为圆心,大于21PA 的长为半径作弧,两弧相交于E 、F 两点;(3)作直线EF ,交射线PM 于点B ;(4)在射线AN 上截取AC=PB ;(5)连接BC则∠BCP 与∠MPN 之间的数量关系是.16.在△ABC 中,∠C=90°,D 是边BC 上一点,连接AD ,若∠BAD+3∠CAD=90°,DC=a ,BD=b ,则AB=.(用含a ,b 的式子表示)三、解答题(本大题有9小题,共86分)17.(本题满分12分)(1)计算:()()()()34222+-+-+y y y y ;(2)分解因式:22222242y a xy a x a ++.18.(本题满分7分)如图5,点B ,E ,C ,F 在一条直线上,AB=DE ,∠A=∠D ,AB ∥DE.求证:BE=CF.先化简,再求值:17149122+-÷-mm m ,其中m =2.20.(本题满分8分)已知点A (1,1),B (-1,1),C (0,4).(1)在平面直角坐标系中描出A 、B 、C 三点;(2)在同一平面内,点与三角形的位置关系有三种:点在三角形内、点在三角形边上、点在三角形外.若点P 在△ABC 外,请判断点P 关于y 轴的对称点P’与△ABC 的位置关系,直接写出判断结果.21.(本题满分8分)如图6,在△ABC 中,AB=AC,过点B 作BD ⊥AC ,垂足为D ,,若D 是边AC 的中点,(1)求证:△ABC 是等边三角形;(2)在线段BD 上求作点E ,使得CE=2DE.(要求:尺规作图,不写画法,保留作图痕迹)22.(本题满分9分)某企业在甲地有一工厂(简称甲厂)生产某产品,2017年的年产量过万件,2018年甲厂经过技术改造,日均生产的该产品数是该厂2017年的2倍还多2件.(1)若甲厂2018年生产200件该产品所需的时间与2017年生产99件该产品所需的时间相同,则2017年甲厂日均生产该产品多少件?(2)由于该产品深受顾客欢迎,2019年该企业在乙地建立新厂(简称乙厂)生产该产品.乙厂的日均生产的该产品数是甲厂2017年的3倍还多4件.同年该企业要求甲、乙两厂分别生产m ,n 件产品(甲厂的日均产量与2018年相同),m :n=14:25,若甲、乙两厂同时开始生产,谁先完成任务?请说明理由.已知一些两位数相乘的算式:62×11,78×69,34×11,63×67,18×22,15×55,12×34,54×11.利用这些算式探究两位数乘法中可以简化运算的特殊情形:(1)观察已知算式,选出具有共同特征的3个算式,并用文字描述它们的共同特征;(2)分别计算你选出的算式.观察计算的结果,你能发现不经过乘法运算就可以快速、直接地写出积的规律吗?请用文字描述这个规律;(3)证明你发现的规律;(4)在已知算式中,找出可以应用(或经过转化可以应用)上述规律的所有算式,并将它们写在横线上:.24.(本题满分11分)在△PQN 中,若α+∠=∠Q 21p (0°<α≤25°),则称△PQN 为“差角三角形”,且p ∠是Q ∠的“差角”.(1)已知△ABC 是等边三角形,判断△ABC 是否为“差角三角形”,并说明理由;(2)在△ABC 中,∠C=90°,50°≤∠B ≤70°,判断△ABC 是否为“差角三角形”,若是,请写出所有的“差角”并说明理由;若不是,也请说明理由.25.(本题满分14分)如图7,在四边形ABCD 中,AC 是对角线,∠ABC=∠CDA=90°,BC=CD ,延长BC 交AD 的延长线于点E.(1)求证:AB=AD(2)若AE=BE+DE ,求∠BAC 的值;(3)过点E 作ME ∥AB ,交AC 的延长线于点M ,过点M 作MP ⊥DC ,交DC 的延长线于点P ,连接PB.设PB=a ,点O 是直线AE 上的动点,当MO+PO 的值最小时,点O 与点E 是否可能重合?若可能,请说明理由并求此时MO+PO 的值(用含a 的式子表示);若不可能,请说明理由.松鼠AI智适应—厦门金湖校区。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2019—2020学年(上)厦门市八年级质量检测
数 学
(试卷满分:150分 考试时间:120分钟)
准考证号 姓名 座位号
注意事项:
1.全卷三大题,25小题,试卷共4页,另有答题卡. 2.答案必须写在答题卡上,否则不能得分. 3.可以直接使用2B 铅笔作图.
一、选择题(本大题有10小题,每小题4分,共40分.每小题都有四个选项,其中有且只
有一个选项正确) 1.计算2-1的结果是
A . 0
B . 1
2
C . 1
D .2
2.下列长度的三条线段能组成三角形的是
A . 3,4,7
B . 3,4,8
C . 3,3,5
D . 3,3,7
3.分式x
x -2
有意义,则x 满足的条件是
A . x ≠2
B . x =0
C . x =2
D . x >2 4. 如图1,在△ABC 中,AD 交边BC 于点D .设△ABC 的重心为M , 若点M 在线段AD 上,则下列结论正确的是
A . ∠BAD =∠CAD
B .AM =DM
C . △AB
D 的周长等于△ACD 的周长 D .△ABD 的面积等于△ACD 的面积 5.已知正方形ABCD 边长为x ,长方形EFGH 的一边长为2,另一边的长为x ,则正方形ABCD 与长方形EFGH 的面积之和等于
A .边长为x +1的正方形的面积
B . 一边长为2,另一边的长为x +1的长方形面积
C . 一边长为x ,另一边的长为x +1的长方形面积
D . 一边长为x ,另一边的长为x +2的长方形面积
6.从甲地到乙地有两条路:一条是全长750km 的普通公路,另一条是全长600km 高速公路.某客车从甲地出发去乙地,若走高速公路,则平均速度是走普通公路的平均速度的2倍,所需时间比走普通公路所需时间少5小时.设客车在普通公路上行驶的平均速度是x km /h ,则下列等式正确的是 A . 600x +5=7502x B . 600x -5=7502x C .
6002x +5=750x D . 6002x -5=750x
7.在△ABC 中,D ,E 分别是边AB ,AC 上的点,且AD =CE ,∠DEC =∠C =70°, ∠ ADE =30°,则下列结论正确的是
A .DE =CE
B .B
C =CE C .DB =DE
D .A
E =DB
图1
8.在平面直角坐标系中,O 是坐标原点,点A (3,2),点P (m ,0)(m <6),若△POA 是等腰三角形,则m 可取的值最多有
A . 2个
B .3个
C .4个
D . 5个
9. 下列四个多项式,可能是2x 2+mx -3 (m 是整数)的因式的是
A . x -2
B . 2x +3
C . x +4
D . 2x 2-1 10. 如图2,点D 在线段BC 上,若BC =D
E ,AC =DC ,AB =EC ,
且∠ACE =180°—∠ABC —2x °,则下列角中,大小为x °的角是
A . ∠EFC
B . ∠AB
C C . ∠FDC
D . ∠DFC
二、填空题(本大题有6小题,每小题4分,共24分)
11.计算:(1)(2a )3= ;(2)3a (5a 2+2b 2) = . 12.计算:4x 23y ·3y
x
3= .
13. 如图3,在△ABC 中,∠ACB =90°,AD 平分∠CAB ,交边BC 于点D , 过点D 作DE ⊥AB ,垂足为E .若∠CAD =20°,则∠EDB 的度数是 . 14. 如图4,有一张边长为x 的正方形ABCD 纸板,在它的一个角上切去一个 边长为y 的正方形AEFG ,剩下图形的面积是32,过点F 作FH ⊥DC ,垂 足为H .将长方形GFHD 切下,与长方形EBCH 重新拼成一个长方形,若 拼成的长方形的较长的一边长为8,则正方形ABCD 的面积是 . 15. 已知锐角∠MPN ,依照下列步骤进行尺规作图: (1)在射线PN 上截取线段P A ;
(2)分别以P ,A 为圆心,大于1
2
P A 的长为半径作弧,两弧相交于E ,F
两点; (3)作直线EF ,交射线PM 于点B ; (4)在射线AN 上截取AC =PB ; (5)连接BC .
则∠BCP 与∠MPN 之间的数量关系是 .
16.在△ABC 中,∠C =90°,D 是边BC 上一点,连接AD ,若∠BAD +3∠CAD =90°,DC =a ,BD =b ,则AB = . (用含a ,b 的式子表示)
三、解答题(本大题有9小题,共86分)
17.(本题满分12分)
(1)计算:(y +2)(y —2) +(2y —4)(y +3); (2)分解因式:2a 2x 2+4a 2xy +2a 2y 2.
18. (本题满分7分)
如图5,点B ,E ,C ,F 在一条直线上,AB =DE ,∠A =∠D ,AB ∥DE. 求证:BE =CF .
F A B C
D E
图2 A
B
C
D
E
图3
A
B D
C
E F
图5
F
A B C
D E
H
G
图4
先化简,再求值:1m 2-49÷1
m 2-7m
+1,其中m =2.
20. (本题满分8分) 已知点A (1,1),B (-1,1),C (0,4). (1)在平面直角坐标系中描出A ,B ,C 三点;
(2)在同一平面内,点与三角形的位置关系有三种:点在三角形内、点在三角形边上、 点在三角形外.若点P 在△ABC 外,请判断点P 关于y 轴的对称点P ′与△ABC 的 位置关系,直接写出判断结果.
21. (本题满分8分)
如图6,在△ABC 中,AB =AC ,过点B 作BD ⊥AC ,垂足为D ,若D 是边AC 的中点, (1)求证:△ABC 是等边三角形;
(2)在线段BD 上求作点E ,使得CE =2DE . (要求:尺规作图,不写画法,保留作图痕迹)
22. (本题满分9分)
某企业在甲地有一工厂(简称甲厂)生产某产品,2017年的年产量过万件,2018年甲 厂经过技术改造,日均生产的该产品数是该厂2017年的2倍还多2件. (1)若甲厂2018年生产200件该产品所需的时间与2017年生产99件该产品所需的时
间相同,则2017年甲厂日均生产该产品多少件?
(2)由于该产品深受顾客欢迎,2019年该企业在乙地建立新厂(简称乙厂)生产该产
品.乙厂的日均生产的该产品数是甲厂2017年的3倍还多4件.同年该企业要求甲、乙两厂分别生产m ,n 件产品(甲厂的日均产量与2018年相同),m :n =14:25,若甲、乙两厂同时开始生产,谁先完成任务?请说明理由.
图6
A
B C
D
已知一些两位数相乘的算式:
62×11,78×69,34×11,63×67,18×22,15×55,12×34,54×11. 利用这些算式探究两位数乘法中可以简化运算的特殊情形:
(1)观察已知算式,选出具有共同特征的3个算式,并用文字描述它们的共同特征; (2)分别计算你选出的算式.观察计算的结果,你能发现不经过乘法运算就可以快速、 直接地写出积的规律吗?请用文字描述这个规律; (3)证明你发现的规律;
(4)在已知算式中,找出所有可以应用(或经过转化可以应用)上述规律的算式,并将 它们写在横线上: .
24. (本题满分11分)
在△PQN 中,若∠P =1
2∠Q +α(0°<α≤25°),则称△PQN 为“差角三角形”,且∠P 是
∠Q 的“差角”.
(1)已知△ABC 是等边三角形,判断△ABC 是否为“差角三角形”,并说明理由; (2)在△ABC 中,∠C =90°,50°≤∠B ≤70°,判断△ABC 是否为“差角三角形”,若
是,请写出所有的“差角”并说明理由;若不是,请说明理由.
25. (本题满分14分)
如图7,在四边形ABCD 中,AC 是对角线,∠ABC =∠CDA =90°,BC =CD ,延长 BC 交AD 的延长线于点E . (1)求证:AB =AD ;
(2)若AE =BE +DE ,求∠BAC 的值;
(3)过点E 作ME ∥AB ,交 AC 的延长线于点M ,过点M 作MP ⊥DC ,交DC 的延长 线于点P ,连接PB .设PB =a ,点O 是直线AE 上的动点,当MO +PO 的值最小 时,点O 与点E 是否可能重合?若可能,请说明理由并求此时MO +PO 的值(用 含a 的式子表示);若不可能,请说明理由.
图7
B E D
C A。
