材料力学上课例题
材料力学例题
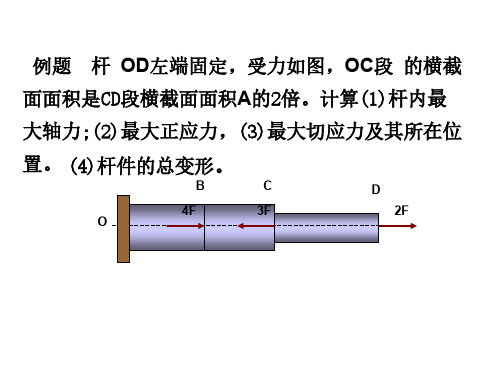
0.75m 1m
A
D 1.5m
B
F
横梁BC为刚杆,自重Q=2KN,力P=10KN可在横 梁BC上自由移动。AB杆的许用应力为[σ]=100MP a,设计AB杆的横截面面积。如果AB杆采用直径 为10毫米的细丝,需要几根?
P C
30°
B
• [例] 长为 L=2m 的圆杆受均布力偶 m=20Nm/m 的作用,如图,若杆的内外径之比为 =0.8 ,
例题 空心圆杆AB和CD杆焊接成整体结构,受力如图.AB杆的外径 D=140mm,内外 径之比α= d/D=0.8,材料的许用应力[] = 160MPa。试用第三强度理论校核AB杆的 强度。 解:(1)外力分析 将力向AB杆的B截面形心简化得
10kN
0.8m A
B D
F 25kN
M e 15 1 . 4 10 0 . 6 15 kN m
G=80GPa ,许用剪应力 []=30MPa,试设计杆
的外径;若[]=2º /m ,试校核此杆的刚度,并
求右端面转角。
[例题] 某传动轴设计要求转速n = 500 r / min,输入功率P1 = 500 马力, 输出功率分别 P2 = 200马力及 P3 = 300马力,已 知:G=80GPa ,[ ]=70M Pa,[ ]=1º /m ,试确定: ①AB 段直径 d1和 BC 段直径 d2 ? ②若全轴选同一直径,应为多少? ③主动轮与从动轮如何安排,轴的受力合理? P2 A 500 B 400 P3 C
y Me A x B l/2 F1
F2
D F2 D M e C ( F1 F 2 ) 2 2 20 F2 kN 3 F 20kN
轴产生扭转和垂直纵向对称面内的平 面弯曲
材料力学(资料例题)

材料力学(一)轴向拉伸与压缩【内容提要】材料力学主要研究构件在外力作用下的变形、受力与破坏、失效的规律。
为设计既安全可靠又经济合理的构件,提供有关强度、刚度与稳定性分析的基本理论与方法。
【重点、难点】重点考察基本概念,掌握截面法求轴力、作轴力图的方法,截面上应力的计算。
【内容讲解】一、基本概念强度——构件在外力作用下,抵抗破坏的能力,以保证在规定的使用条件下,不会发生意外的断裂或显著塑性变形。
刚度——构件在外力作用下,抵抗变形的能力,以保证在规定的使用条件下不会产生过分的变形。
稳定性——构件在外力作用下,保持原有平衡形式的能力,以保证在规定的使用条件下,不会产生失稳现象。
杆件——一个方向的尺寸远大于其它两个方向的尺寸的构件,称为杆件或简称杆。
根据轴线与横截面的特征,杆件可分为直杆与曲杆,等截面杆与变截面杆。
二、材料力学的基本假设工程实际中的构件所用的材料多种多样,为便于理论分析,根据它们的主要性质对其作如下假设。
(一)连续性假设——假设在构件所占有的空间内均毫无空隙地充满了物质,即认为是密实的。
这样,构件内的一些几何量,力学量(如应力、位移)均可用坐标的连续函数表示,并可采用无限小的数学分析方法。
(二)均匀性假设——很设材料的力学性能与其在构件中的位置无关。
按此假设通过试样所测得的材料性能,可用于构件内的任何部位(包括单元体)。
(三)各向同性假设——沿各个方向均具有相同力学性能。
具有该性质的材料,称为各向同性材料。
综上所述,在材料力学中,一般将实际材料构件,看作是连续、均匀和各向同性的可变形固体。
三、外力内力与截面法(一)外力对于所研究的对象来说,其它构件和物体作用于其上的力均为外力,例如载荷与约束力。
外力可分为:表面力与体积力;分布力与集中力;静载荷与动载荷等。
当构件(杆件)承受一般载荷作用时,可将载荷向三个坐标平面(三个平面均通过杆的轴线,其中两个平面为形心主惯性平面)内分解,使之变为两个平面载荷和一个扭转力偶作用情况。
材料力学典型例题及解析 12.冲击问题典型习题解析

击构件瞬间的速度为 υ
,只须将前面(a)式右端改为
1 2
⋅
Pυ2 g
= Vε
,即可导出 kd
=
υ2 。 g∆st
(4)、前面推导过程中,冲击物的势能取为 Ep = P(h + ∆d ) ,一般情况下 ∆d << h ,可将其忽
略,取 Ep = Ph ,读者可仿照上面推导一下,并讨论忽略后对 kd 有什么影响。
所以本问题的动载荷因数为: kd
=
∆d ∆st
=1+
1+ 2h = 1+ ∆st
1+
2
× 440 ×10 −3 2 ×10 −3 m
m
= 22
讨论:(1)、在线弹性范围内,载荷、变形、应变、应力之间都是线性关系,也就是说,当
外载荷被放大 kd 倍,则变形、应力、应变也同样被放大 kd 倍。所以有σ d = kdσ st 。有了 kd 很
动能完全转化为橡皮筋的应变能。即 Ek = Vε 。
解:设小球离开木拍瞬间速度为υ ,则其动能 Ek
=
1 2பைடு நூலகம்
W g
υ 2 ;而橡皮筋被拉至最长时应变能
Vε
=
1 2
F ⋅ ∆L ,其中
F
为小球速度为零时橡皮筋所受拉力。由于假设橡皮筋为线弹性变形,
3
所以 F
=σ
A
=
Eε
A=
∆L L0
EA ,于是Vε
=
∆d
=
∆d ∆st
P 。定义
∆d ∆st
= kd 为动载荷因数,则有
Fd P
=
∆d ∆st
= σd σ st
材料力学例题及解题指导总结

材料力学例题及解题指导(第二章至第六章)第二章拉伸、压缩与剪切例2-1试画出图a直杆的轴力图解:此直杆在A、B、C、D点承受轴向外力。
先求AB段轴力。
在段内任一截面1-1处将杆件截开,考察左段(图2-5b)。
在截面上设出正轴力2。
由此段的平衡方程ZX = 0得N L 6= 0, N i =+ 6kN图2-5理得CD段内任一截面的轴力都是一4kN。
画内力图,以水平轴x表示杆的截面位置, 的比例尺画出轴力图,如图N i得正号说明原先假设拉力是正确的,同时也就表明轴力是正的。
AB段内任一截面的轴力都等于+6kN。
再求BC段轴力,在BC段任一截面2-2处将杆件截开,仍考察左段(图2-5C),在截面上仍设正的轴力N 2,由ZX= 0得—6 + 18+ N2 = 0N2=- 12kNN2得负号说明原先假设拉力是不对的(应为压力),同时又表明轴力N2是负的。
2-5 (d)所示。
由此图可知数值最大的轴力发生在BC段内任一截面的轴力都等于—12kN。
同以垂直x的坐标轴表示截面的轴力,按选定BC段内。
解题指导:利用截面法求轴力时,在切开的截面上总是设出正轴力N,然后由3X= 0求出轴力N ,如N得正说明是正轴力(拉力),如得负则说明是负轴力(压力)。
例2-3图2-7所示两根圆截面杆材料相同,试计 算两杆的应变能,并比较其大小。
解:a 杆:U aP 2 丨=P 2 l _ 22EA 2E 「:d4二 2 P lE d例2-2试求自由悬挂的直杆(图2-6a ) 由纵向均匀分布荷载 q (力/长度)引起 的应力和纵向变形。
设杆长 I 、截面积A 及弹性模量E 均已知。
解:在杆上距下端为 x 处取一任意横 截面m-m ,则该截面轴力为 N (x )= qx , 根据此式可作出轴力图如图 2-6b 所示。
m-m 截面的应力为 (x ) = N (x )/A = qx/A 。
显然,悬挂端有最大轴力 N max = ql 及最 大正应力■- 'max =ql / A 。
材料力学例题

B
DC
1
3
2
A
B
DC
1
3
2
A
1 32
A
Δl1
Δl3
F
A'
A'
变形几何方程为 Δl1 Δl3 cos
物理方程为
Δl1
FN1l1 EA1
Δl3
FN3l cos
E3 A3
(3)补充方程
FN1
FN 3
EA E3 A3
cos2
(4)联立平衡方程与补充方程求解 B
DC
FN1 FN2
FN1 cos FN2 cos FN3 F 0
d
[] = 60MPa ,许用挤压应力为 [bs]= 200MPa .试校核销钉的
强度.
F
B
A
d1
d d1
F
解: (1)销钉受力如图b所示
F
剪切面
F
d
F
F
2
2
挤压面
d
B
A
d1
d d1
F
(2)校核剪切强度
剪切面
F
由截面法得两个面上的剪力
FS
F 2
d
剪切面积为 A d 2
4
FS 51MPa
3
2
1
l
a
a
B
C
A
F
解:(1) 平衡方程
Fx 0 Fx 0 l
3 a
2 a
1
Fy 0
B
C
A
FN1 FN2 FN3 F 0
MB 0
F FN3
FN2
FN1
3 a
2 a
1
材料力学课堂例题(湖南大学)-静力学.

40.4kN
由BC杆强度,可得
P NBC 2 A2
2
2
160106 600106 48103 N 2
48kN
综合考虑两杆的强度,整个结 构的许用荷载为:
P 40.4kN
当 P P 40.4kN时,AB杆将达到许用
应力,但BC却强度有余,即BC的面积可减小。
A
B DC
2m 1m 1m
1马力=745.7瓦
为简化计算,1马力取700瓦。
解:① 计算外力偶
m1
9550 Nk n
马力 9550 0.7
n
7000 300 N m 7 300 kN m 7kN m
300
300
m2
m3
7
150 300
3.5kN m
故可能危险截面为1截面和2截面
170 30 y2=139 y1=61
25kNm
+
1
M
2
10kNm
–
+
200
z
+
–
30
Iz 40.3106 m4 y
“ 1”
Lmax
M max Iz
y1
10103 40.3106
61103
15.1MPa [ L ]
Cmax
式中
Ip
(D4
32
d4)
(1004
32
804 ) 1012
5.79106 m4
m1
m2
m3
“ DC”轴
max
T DC max
工程力学材料力学-知识点-及典型例题
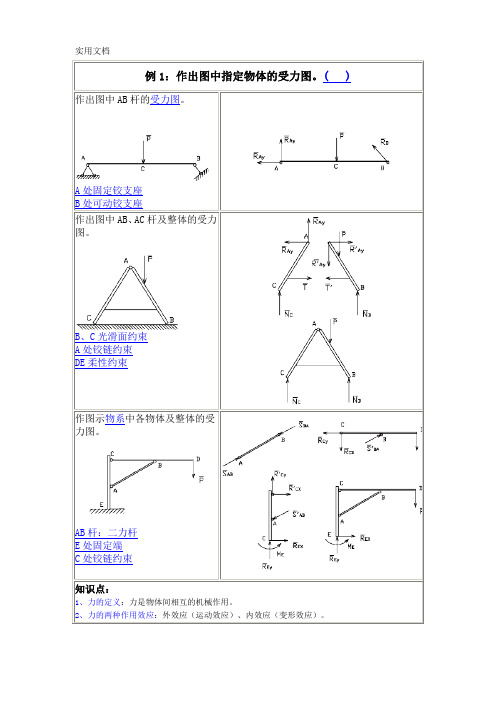
作出图中AB杆的受力图。
A处固定铰支座B处可动铰支座作出图中AB、AC杆及整体的受力图。
B、C光滑面约束A处铰链约束DE柔性约束作图示物系中各物体及整体的受力图。
AB杆:二力杆E处固定端C处铰链约束(1)运动效应:力使物体的机械运动状态发生变化的效应。
(2)变形效应:力使物体的形状发生和尺寸改变的效应。
3、力的三要素:力的大小、方向、作用点。
4、力的表示方法:(1)力是矢量,在图示力时,常用一带箭头的线段来表示力;(注意表明力的方向和力的作用点!)(2)在书写力时,力矢量用加黑的字母或大写字母上打一横线表示,如F、G、F1等等。
5、约束的概念:对物体的运动起限制作用的装置。
6、约束力(约束反力):约束作用于被约束物体上的力。
约束力的方向总是与约束所能限制的运动方向相反。
约束力的作用点,在约束与被约束物体的接处7、主动力:使物体产生运动或运动趋势的力。
作用于被约束物体上的除约束力以外的其它力。
8、柔性约束:如绳索、链条、胶带等。
(1)约束的特点:只能限制物体原柔索伸长方向的运动。
(2)约束反力的特点:约束反力沿柔索的中心线作用,离开被约束物体。
()9、光滑接触面:物体放置在光滑的地面或搁置在光滑的槽体内。
(1)约束的特点:两物体的接触表面上的摩擦力忽略不计,视为光滑接触面约束。
被约束的物体可以沿接触面滑动,但不能沿接触面的公法线方向压入接触面。
(2)约束反力的特点:光滑接触面的约束反力沿接触面的公法线,通过接触点,指向被约束物体。
()10、铰链约束:两个带有圆孔的物体,用光滑的圆柱型销钉相连接。
约束反力的特点:是方向未定的一个力;一般用一对正交的力来表示,指向假定。
()11、固定铰支座(1)约束的构造特点:把中间铰约束中的某一个构件换成支座,并与基础固定在一起,则构成了固定铰支座约束。
(2)约束反力的特点:固定铰支座的约束反力同中间铰的一样,也是方向未定的一个力;用一对正交的力来表示,指向假定。
()12、可动铰支座(1)约束的构造特点把固定铰支座的底部安放若干滚子,并与支撑连接则构成活动铰链支座约束,又称锟轴支座。
材料力学典型例题与详解(经典题目)
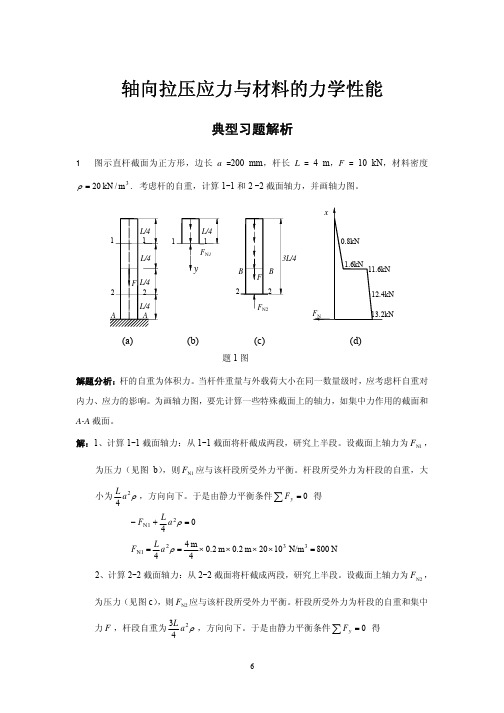
所以石柱体积为
V3
=
G ρ
=
[σ ]A(l) − ρ
F
= 1×106 Pa ×1.45 m 2 −1000 ×103 N = 18 m3 25 ×103 N/m3
三种情况下所需石料的体积比值为 24∶19.7∶18,或 1.33∶1.09∶1。 讨论:计算结果表明,采用等强度石柱时最节省材料,这是因为这种设计使得各截面的正应 力均达到许用应力,使材料得到充分利用。 3 滑轮结构如图,AB 杆为钢材,截面为圆形,直径 d = 20 mm ,许用应力 [σ ] = 160 MPa ,BC 杆为木材,截面为方形,边长 a = 60 mm ,许用应力 [σ c ] = 12 MPa 。试计算此结构的许用载
= 1.14 m 2
A
2=
F+ρ [σ ] −
A1 l1 ρ l2
=
1000 ×103 N + 25 ×103 N/m3 ×1.14 m 2 × 5 m 1×106 N/m 2 − 25×103 N/m3 × 5 m
= 1.31 m 2
A
3=
F
+ ρA1l1 + ρA2l2 [σ ] − ρ l3
= 1000 ×103 N + 25 ×103 N/m3 ×1.14 m 2 × 5 m + 25×103 N/m3 ×1.31 m 2 × 5 m = 1.49m 2 1×106 N/m 2 − 25 ×103 N/m3 × 5 m
解:1、计算 1-1 截面轴力:从 1-1 截面将杆截成两段,研究上半段。设截面上轴力为 FN1 ,
为压力(见图 b),则 FN1 应与该杆段所受外力平衡。杆段所受外力为杆段的自重,大
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
q/2
A
4
B C
wC 1
5(q 2)l 5ql 384 EI 768 EI (q 2)l ql 24 EI 48 EI
3 3
4
q/2 A C q/2 B
B1 A1
(2)反对称荷载作用下 在跨中C截面处,挠度 wC等于零,但 转角不等于零且该截面的 弯矩也等于零 可将AC段和BC段分别视为受均布线荷载作用且长度为l /2 的简支梁
解:将外伸梁沿B截面截成两段, 将AB 段看成B端固定的悬臂 A 梁,BC段看成简支梁.
B截面两侧的相互作用为:
2q q B a a D C
2qa
M B qa
2q
M B qa
2
2a
2
2qa
M B qa
2
q
A
B 2qa
B
D
C
简支梁BC的受力情况与 外伸梁AC 的BC段的受力情 2 M qa B 况相同
例7 下图为一空心圆杆,内外径分别为:d=40mm,D=80mm,杆的
E=210GPa,工程规定C点的[w/L]=0.00001,B点的[]=0.001弧度,试
校核此杆的刚度.
l=400mm A D B a=0.1m C B A D C
200mm F1=1kN
F2=2kN
F2
=
=
B
a
A
D
B
C
C
F2 M
第七章 弯曲变形 上课例题
例题1 图示一抗弯刚度为 EI 的悬臂梁, 在自由端受一集中力 F 作用.试求梁的挠曲线方程和转角方程, 并确定其最大挠度 wmax 和最大转角 max w
A
F
B x
l
解:
w
F
A B
x
(1) 弯矩方程为
x
M ( x ) F (l x )
(1)
(2) 挠曲线的近似微分方程为
最大转角和最大挠度分别为
FRA
FRB
在 x=0 和 x=l 处转角的绝对值相等且都是最大值,
max
ql 3 A B 24 EI
x l 2
在梁跨中点处有最大挠度值 wmax w
5ql 4 384 EI
例题3 图示一抗弯刚度为EI的简支梁, 在D点处受一集中力F的作 用.试求此梁的挠曲线方程和转角方程,并求其最大挠度和最大转 角. F
x 0, w 0
(4)
将边界条件代入(3)(4)两式中,可得 C1 0 梁的转角方程和挠曲线方程分别为
C2 0
Fx 2 EIw Flx 2
EIw Flx Fx 2 6
2
3
y A
F
B x
wmax
l
max
max 和 wmax都发生在自由端截面处
Fl 2 Fl 2 Fl 2 ( ) max | x l EI 2 EI 2 EI Pl 3 wmax w | x l ( ) 3 EI
l
EIw M ( x ) Fl Fx (2)
对挠曲线近似微分方程进行积分
Fx EIw Flx C1 (3) 2 2 3 Flx Fx EIw C 1x C 2 2 6
2
(4)
Fx 2 EIw Flx C1 (3) 2 2 3 Flx Fx EIw C 1x C 2 2 6 边界条件 x 0, w 0
I ( D4 d 4 ) 64 3.14 (804 404 ) 1012 64 188 108 m 4
2
3
2
+
C
+
F2 M
F2
图3 A
D
B
C
F1l F2 la 0.4 400 200 B ( ) 16 EI 3 EI 210 1880 16 3 -4 +0.423 10 (rad)
可得到: wC 2 0
q/2 A
θ A 2 θB 2
q l 3 ( )( ) 3 ql 2 2 24 EI 384 EI
A
4
C
q/2 q/2 C
B
将相应的位移进行叠加, 即得
B
5ql wC wC 1 wC 2 ( ) 768 EI 3 3 3 ql ql 3ql A A1 A 2 48 EI 384 EI 128 EI
例题2 图示一抗弯刚度为 EI 的简支梁,在全梁上受集度为q 的
均布荷载作用.试求此梁的挠曲线方程和转角方程,并确定其 max 和 wmax
q A l B
q
解:由对称性可知,梁的两 个支反力为
A x
B
FRA FRB
ql 2
FRA
l
FRB
此梁的弯矩方程及挠曲线微分方程分别为
ql q 2 M ( x) x x 2 2 ql q 2 EIw x x 2 2
Fab( l b ) A 1 | x 0 6lEI Fab( l a ) B 2 | x l 6lEI
当 a > b 时, 右支座处截面的转角绝对值为最大
max
Fab( l a ) B 6lEI
简支梁的最大挠度应在
w' 0 处
先研究第一段梁,令 w1 0 得
Fb 2 2 (l b 3 x 2) 0 1 w 1' 6lEI
l 2 b2 a (a 2b ) x1 3 3
当 a > b时, x1 < a 最大挠度确实在第一段梁中
2 Fb Pbl 2 2 3 w | ( l b ) 0.0642 w max x x1 EI 9 3lEI
两段梁的挠曲线方程分别为 (a)(0 x a)
b 挠曲线方程 EIw 1 M 1 F x l
转角方程
b x2 F EIw1 C1 l 2 b x3 EIw1 F C1 x D1 l 6
挠度方程
(b)( a x l )
b 挠曲线方程 EIw 2 M 2 F x F ( x a ) l
梁中点 C 处的挠度为
Fb Fbl 2 2 wC (3l 4b ) 0.0625 48 EI EI
2
2 Fb Fbl 2 2 3 y | ( l b ) 0.0642 w max x x1 EI 9 3lEI
结论:在简支梁中, 不论它受什么荷载作用, 只要挠曲线上无 拐点, 其最大挠度值都可用梁跨中点处的挠度值来代替, 其精确度 是能满足工程要求的.
2qa
q C
B
D
q
由简支梁BC求得的B,wD 就是外伸梁AC的 B,wD 简支梁BC的变形就是MB 和均布荷载q分别引起变形的 叠加.
B
C D
M B qa
2
B
C D
2qa
M B qa
2
q
(1)求 B ,wD
C
B
D
B
( B )q D ( w D )q
C
ql qa ( B )q 24 EI 3 EI 3 M Bl 2qa ( B ) M B 3 EI 3 EI 4 4 5ql 5qa ( w D )q 384 EI 24 EI 4 MB l2 qa ( wD )MB 16 EI 4 EI
A
B
( B ) M e
)
( A ) MC ( wC ) M
e
e
l
例题5 试利用叠加法,求图 所示抗弯刚度为EI的简支 梁跨中点的挠度 wC 和两端 截面的转角A , B .
q A C B
l/2 l
q/2
解:可视为正对称荷载
与反对称荷载两种情况的叠 加.
A C
B
q/2 A C q/2
B
(1)正对称荷载作用下
3
3
3
M B qa
2
由叠加原理得:
( B ) M B
(wD ) M B
B
D
C
qa B ( B )q ( B ) M B 3 EI 4 qa w D ( w D )q ( w D ) M B 24 EI
2q A
M B qa
2
2qa A
M B qa
F1l 2 16 EI
=
+ +
l=400mm
a=0.1m
(2)叠加求复杂载荷下的变形
C
A
D
B
200mm F1=1kN A D
F1l 2 F2la B F2=2kN 16 EI 3 EI
C
=
图1
F1=1kN
B 图2
F1l a F2a F2a l wC 16 EI 3 EI 3 EI
C
+
F1=1kN
A
B
F2
A
D B
+
C
F2=2kN
l=400mm A D B
a=0.1m C
解:(1)结构变换,查表求简 单载荷变形.
200mm F =1kN 1 图1
F2=2kN
1 B
D
C
F1=1kN
图2 B
C
F2
图3 A
F2
M
D
B
C
F1l 2a w1C 1 B a 16 EI 2B 0 F2a 3 w2C 3 EI Ml laF2 3B 3 EI 3 EI F2 la 2 w3 C 3 B a 3 EI
