福建省泉州市南安市2018-2019学年八年级上学期数学期中考试试卷及参考答案
2018-2019学年上学期期中考试八年级数学试卷及答案
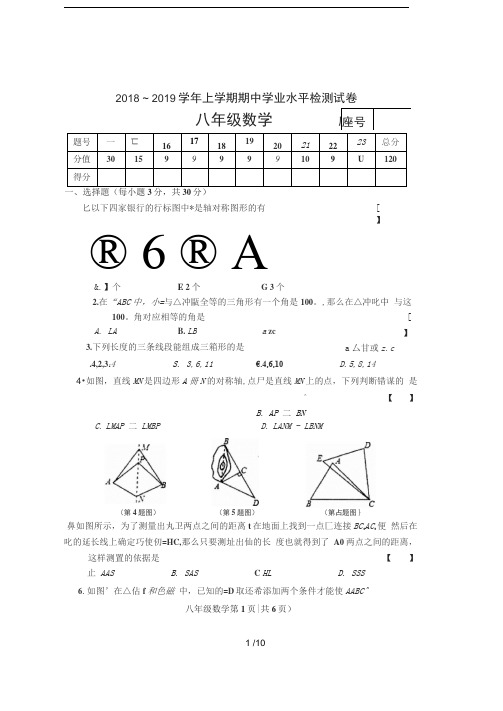
2018 ~ 2019学年上学期期中学业水平检测试卷题号一匸1617181920212223总分分值301599999109U120得分330匕以下四家银行的行标图中*是轴对称图形的有[】® 6 ® A.4,2,314 S. 3,6,11€.4,6,10 D.5,8,14 4•如图,直线MN是四边形A冊N的对称轴,点尸是直线MN上的点,下列判断错谋的是^ 【】B.AP二BN(第4题图)(第5題图)(第占题图}鼻如图所示,为了测量出丸卫两点之间的距离t在地面上找到一点匚连接BC t AC t便然后在叱的延长线上确定巧使仞=HC,那么只要测址出仙的长度也就得到了A0两点之间的距离,这样测置的依据是【】止AAS B. SAS C HL D. SSS6.如图’在△佔f和色磁中,已知的=D取还希添加两个条件才能使AABC^八年级数学第1页|共6页)八年级数学座号座号&.】个 E 2个G 3个2.在“ABC中,小=与△冲甌全等的三角形有一个角是100。
,那么在△冲叱中与这100。
角对应相等的角是[】a厶甘或z.cA. LAB. LB a zc3.下列长度的三条线段能组成三箱形的是C.LMAP二LMBPNM - LBNM1 /102/1012.如图危ABC 中“C 二呂卫C = 5,仙的垂直平分线加交血于点D,交边AC 于点E, _________________________ 则的周长为R 等腰三角形的两边检分别为4』,则它的周长为 __________八年级数学第2页(共6页)△ DEC*不能添加的一组条件是A. BC = EC r Z.F = Z.E R* SC - EC,AC = DC Q BC = DC, LA = LDD.AC = DC, LA = CD7. 一个多边形的内角和是外角和的2倍*这个多边形擡I乩四边形 E 五边形 C 六边形D •八边形8. 如图,已知0为A4BC 边佔的中点疋在边必上,将△肋C 折叠,使占点落在HC ]f 第g 题图)(第9題图)9.如图,冊//CD,BP 和CP 分别平分AABC 和Af )CH,AD 过点罠且与AB 垂直 若]AD 二肌则点F 到月f 的距离是 A. 8R6C4D.210.如图,正方形网格中,网格线的交点称为格点+已知沖上是两格点,如果C 也是图 中的格点,且使得^ABC 为等腰三角形,则点C 的个数有【】儿4个艮6个C 8亍D. 10个二、填空题(毎小题3分,共15分)11.如图,点。
福建省泉州一中2018-2019学年度第一学期八年级(上册)期中考试数学试卷(解析版)

福建省泉州一中2018-2019学年度第一学期八年级(上册)期中考试数学试卷一、选择题:(每小题4分,共40分)1.下列四个实数中,是无理数的是()A.0 B.﹣3 C.D.2.下列运算正确的是()A.3a+2b=5ab B.5a﹣2a=3aC.b2•b3=b6D.(x+y)2=x2+y23.一个数的立方根是它本身,则这个数是()A.1 B.0或1 C.﹣1或1 D.1,0或﹣1 4.如图,在△ABC中,AB=AD=DC,∠B=60°,则∠C的度数为()A.60°B.30°C.35°D.40°5.下列各式中,不能用平方差公式计算的是()A.(﹣x﹣y)(x﹣y)B.(﹣x+y)(﹣x﹣y)C.(x+y)(﹣x+y)D.(x﹣y)(﹣x+y)6.若x+y=3且xy=1,则代数式(1+x)(1+y)的值等于()A.5 B.﹣5 C.3 D.﹣37.对于命题“若a2>b2,则a>b”,下面四组关于a,b的值中,能说明这个命题是假命题的是()A.a=3,b=﹣2,B.a=﹣2,b=3,C.a=2,b=﹣3,D.a=﹣3,b=2,8.如图,在△ABC和△DEF中,∠B=∠DEF,AB=DE,添加下列一个条件后,仍然不能证明△ABC≌△DEF,这个条件是()A.∠A=∠D B.BC=EF C.∠ACB=∠F D.AC=DF9.如图,OC平分∠AOB,点P是射线OC上的一点,PD⊥OB于点D,且PD=3,动点Q在射线OA上运动,则线段PQ的长度不可能是()A.2 B.3 C.4 D.510.在△ABC中,高AD和BE所在的直线交于点H,且BH=AC,则∠ABC等于()A.45°B.120°C.45°或135°D.45°或120°二、填空题(每小题4分,共18分)11.2的平方根是.12.计算:(6y2﹣2xy)(﹣2y)=.13.把两根钢条AD,BC的中点连在一起,可以做成一个测量工件内槽宽的工具(卡钳),如图,若测得AB=8厘米,则槽宽为厘米.14.若2x=1,3y=2,则4x•27y=.15.如图,在△ABC中,AB的垂直平分线交AB于E,交BC于D,连结AD.若AC=4cm,△ADC的周长为11cm,则BC的长为cm.16.等腰直角三角形ABC,AB=AC,∠BAC=∠BDC=90°,(1)若∠DBA=20°,则∠ACD=°;(2)连接AD,则∠ADB=°.三、解答题:(17-21每题8分,22、23每题10分,24、25每题13分,共86分)17.(8分)计算:(1)+|1﹣|(2)20172﹣2016×201818.(8分)化简:(1)(4a﹣b)•(﹣2b)2(2)(x+2y﹣3)(x﹣2y+3)19.(8分)已知x2﹣2x=2,将下式先化简,再求值:(x﹣1)2+(x+3)(x﹣3)+(x﹣3)(x﹣1)20.(8分)如图,已知AD为△ABC的中线,延长AD,分别过点B,C作BE⊥AD,CF ⊥AD.求证:DF=DE.21.(8分)如图,点A是∠MON边OM上一点,AE∥ON.(1)尺规作图:作∠MON的角平分线OB,交AE于点B(保留作图痕迹,不写作法);(2)求证:△AOB是等腰三角形.。
18—19学年上学期八年级期中考试数学试题(附答案)(2)

2018~2019学年度上学期期中阶段质量检测试题八年级数学2018.11注意事项:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共6页,满分100分,考试时间90分钟.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、准考证号、座号填写在答题纸规定的位置.考试结束后,将本试卷和答题纸一并交回. 2.答题注意事项见答题纸,答在本试卷上不得分.第Ⅰ卷(选择题共36分)一、选择题(每小题3分,共12小题;共36分)在每小题所给的四个选项中,只有一项是符合题目要求的,请把正确答案涂在答题卡中.1.在以下回收、绿色食品、节能、中国民生银行四个标志中,是轴对称图形的是A .B .C .D .2.下列各式计算正确的是A .729()a a = B .7214a a a =C .235235a a a +=D .333()ab a b =3.在平面直角坐标系中,点(3,-2)关于y 轴对称的点的坐标是 A .(3,2) B .(3,-2) C .(-3,2) D .(-3,-2) 4.以下列各组长度的三条线段为边,能组成三角形的是 A .1cm ,2cm ,3cm B .8cm ,6cm ,4cm C .12cm ,5cm ,6cm D .2cm , 3cm ,6cm5.能把一个三角形分成面积相等的两部分的是该三角形的 A .角平分线 B .中线C .高D .一边的垂直平分线6.如图是跷跷板的示意图,支柱OC 与地面垂直,点O 是AB 的中点,AB 绕着点O 上下转动.当A 端落地时,∠OAC =20°,跷跷板上下可转动的最大角度(即'A OA ∠)是A .20°B .40°C .60°D .80°7.如图,△ABC 与'''A B C ∆关于直线MN 对称,P 为MN 上任一点(P 不与'AA 共线),下列结论中错误的是A .'AA P ∆是等腰三角形B .MN 垂直平分'AA ,'CC C .△ABC 与'''A B C ∆面积相等D .直线AB ,''A B 的交点不一定在MN 上8.如图,已知太阳光线AC 和DE 是平行的,在同一时刻两根高度相同的木杆竖直插在地面上,在太阳光照射下,其影子一样长.这里判断影长相等利用了全等图形的性质,其中判断ABC DFE ∆≅∆的依据是A .SASB .AASC.HL D.ASA9.如图,以点O为圆心,任意长为半径画弧,与射线OM交于点A,再以点A为圆心,AO 长为半径画弧,两弧交于点B,画出射线OB,则∠AOB=A.30°B.45°C.60°D.90°10.如图,在△ABC中,BE,CE分别是∠ABC和∠ACB的平分线,过点E作DF∥BC交AB于D,交AC于F,若AB=4,AC=3,则△ADF周长为A.6 B.7C.8 D.1011.如图,在等腰△ABC中,AB=AC,BD⊥AC,∠ABC=72°,则∠ABD等于A.18°B.36°C .54°D .64°12.如图,将正方形OABC 放在平面直角坐标系中,O 是原点,A 的坐标为(1,则点C 的坐标为A .(1)B .(-1C .1)D .(-1)第Ⅱ卷(非选择题 共64分)注意事项:1.第Ⅱ卷分填空题和解答题.2.第Ⅱ卷所有题目的答案,考生须用0.5毫米黑色签字笔答在答题纸规定的区域内,在试卷上答题不得分.二、填空题(每小题4分,共6小题;共24分) 13.计算:323()a a =________.14.已知一个多边形的内角和为540°,则这个多边形是________边形.15.如图1是一把园林剪刀,把它抽象为图2,其中OA =OB ,若剪刀张开的角为30°,则∠A =________度.16.如图,已知点A,D,C,F在同一条直线上,AB=DE,∠B=∠E,要使△ABC≌△DEF,还需要添加一个条件是________.17.如图,在Rt△ABC中,∠C=90°,AD是△ABC的角平分线,DC=3,则点D到AB的距离是________.18.如图,在△ABC中,∠C=90°,∠ABC=60°,BD平分∠ABC,若AD=6,则AC=________.三、解答题(共5小题;共40分)19.(本题满分5分)用圆规、直尺作图,不写作法,但要保留作图痕迹.如图所示,某汽车探险队要从A城穿越沙漠到B城,途中需要到河边为汽车加水,则汽车在河边哪一点加水,才能使行驶的总路程最短?请你在图上画出这一点.20.(本题满分7分)如图,点A,F,C,D在同一条直线上,已知AF=DC,∠A=∠D,BC∥EF.求证:AB=DE.21.(本题满分8分)如图,在△ABC中,AD,AE分别是△ABC的高和角平分线,若∠B=30°,∠C=50°,求∠DAE的度数.22.(本题满分9分)如图,△ABC是等腰三角形,AB=AC,∠A=36°.(1)尺规作图:作∠B的平分线BD,交AC于点D(保留作图痕迹,不写作法);(2)判断△DBC是否为等腰三角形,并说明理由.23.(本题满分11分)如图,△ABE和△ACD都是等边三角形,BD与CE相交于点O.(1)求证:△AEC≌△ABD;(2)求∠BOC的度数.参考答案一、选择题1.B2.D3.D4.B5.B6.B7.D8.B9.C10.B 11.C 12.A 二、填空题 13.9a 14.五 15.15.7516.BC =EF (答案不唯一) 17.3 18.9 三、解答题19.如下图所示,本题可以进行数学建模,即在直线l 上作一点C ,使它到同侧点A ,B 的距离之和最小.作法:作点A 关于直线l 的对称点A 1,连接A 1B ,则A 1B 与直线l 的交点C 即为所求的点.…………………………………………………………5分20.∵AF =CD ,∴AC =DF ,…………………………………………………………………………1分 ∵BC ∥EF ,∴∠ACB =∠DFE ,……………………………………………………………………3分 在△ABC 和△DEF 中,,,,A D AC DF ACB DFE ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△ABC ≌△DEF (ASA),……………………………………………………………………6分∴AB=DE.……………………………………………………………………………………7分21.∵∠B=30°,∠C=50°,…………………………………………………………1分∴∠BAC=180°-∠B-∠C=100°,……………………………………………………2分∵AE是△ABC的角平分线,∴111005022BAE BAC∠=∠=⨯︒=︒………………………………………………4分∵AD是△ABC的高,∴∠BAD=90°-∠B=90°-30°=60°,………………………………………………6分∴∠DAE=∠BAD-∠BAE=60°-50°=10°.………………………………………………8分22.(1)如图所示:BD即为所求.……………………………………………………………………3分(2)是等腰三角形,理由如下:∵AB=AC,∴∠ABC=∠C,…………………………………………………………4分∵∠A=36°,∴∠ABC=∠ACB=(180°-36°)÷2=72°,…………………………………………5分∵BD平分∠ABC,∴∠ABD=∠DBC=36°,…………………………………………………………6分∴∠BDC=36°+36°=72°,…………………………………………………………7分∴BD=BC,…………………………………………………………………………8分∴△DBC是等腰三角形.…………………………………………………………9分23.(1)∵△ABE和△ACD是等边三角形,∴AE=AB,AD=AC,∠EAB=60°,∠DAC=60°,…………………………1分∴∠EAB+∠BAC=∠DAC+∠BAC,即∠EAC=∠BAD,……………………………………………………………………2分在△AEC和△ABD中,,,,AE AB EAC BAD AC AD =⎧⎪∠=∠⎨⎪=⎩∴△AEC ≌△ABD .……………………………………………………………………5分 (2)由(1)得△AEC ≌△ABD ,…………………………………………………………6分 ∴∠AEC =∠ABD ,……………………………………………………………………7分 ∵∠AFE =∠BFO (对顶角),在△AEF 中,∠AEF +∠EF A +∠EAF =180°,…………………………8分在△BFO 中,∠FBO +∠BFO +∠FOB =180°,……………………………………9分 ∴∠EAB =∠EOB =60°,…………………………………………………………10分 ∴∠BOC =180°-∠EOB =120°.……………………………………………………11分。
2018-2019学年人教版上学期初二数学期中考试试卷及答案解析

2018-2019学年初二数学第一学期期中检测学校:___________姓名:___________班级:___________考号:___________一、选择题(每题3分,共30分)1.下列计算错误的是(▲ )A .a 2·a=a 3B .(ab )2=a 2b 2C .(a 2)3=a 5D .-a+2a=a2.下列四个图案中,是轴对称图形的是 (▲)3.下面各角能成为某多边形的内角和的是 (▲)A.430°B.4320°C. 4334°D.4360°4.如图,已知MB=ND,∠MBA=∠NDC ,下列条件中不能判定△ABM ≌△CDN 的是( ▲ )A .∠M=∠NB . AM ∥CNC .AB = CD D . AM=CN5.已知等腰三角形的两条边长分别是2和4,则它的周长是( ▲ )A .10B .8C .8或10D .无法确定6. 如图,点D 为△ABC 边AB 的中点,将△ABC 沿经过点D 的直线折叠,使点A 刚好落在BC 边上的点F 处,若∠B=48°,则∠BDF 的度数为( ▲ )A .88°B .86°C .84°D .82°7.如图,∠MON 内有一点P ,P 点关于OM 的轴对称点是G ,P 点关于ON 的轴对称点是H ,GH分别交OM 、ON 于A 、B 点,若GH 的长为10cm ,求△PAB 的周长为( ▲ )A .5cmB . 10cmC . 20cmD . 15cm8.如图,点B 、C 、E 在同一条直线上,△ABC 与△CDE 都是等边三角形,则下列结论不一定成立的是( ▲ )A .△ACE≌△BCDB.△BGC≌△AFC C .△ADB≌△CEAD.△DCG≌△ECF9.如图,在△ABC 中,AB =AC ,∠ABC 、∠ACB 的平分线BD ,CE 相交于O 点,且BD 交AC 于点D ,CE 交AB 于点E.某同学分析图形后得出以下结论: A B D C M N①△BCD≌△CBE;②△BAD≌△BCD;③△BDA≌△CEA;④△BOE≌△COD;⑤△ACE≌△BCE.上述结论一定正确的是( )A.①②③ B.②③④C.①③⑤ D.①③④10.如图所示,AD是△ABC的中线,∠ADC=45°,把△ADC沿AD对折,使点C落在点C´的位置,则图中的一个等腰直角三角形是()A. △ADCB. △BDC’C. △ADC´D. 不存在二、填空题(每题3分,共24分)11.实数4的平方根是.12.点A(-5,-6)与点B(5,-6)关于__________对称。
18—19学年上学期八年级期中考试数学试题(附答案)(6)

2018—2019年度上学期部分学校八年级期中考试数学试卷一、选择题(共10小题,每小题3分,共30分)1、下列长度的三条线段,其中能组成三角形的是()A、1、2、3B、3、4、5C、1、3、5D、2、4、62、五边形的内角和为()A、180°B、360°C、540°D、900°3.点M(3,﹣4)关于y轴的对称点的坐标是()A.(3,4)B.(﹣3,﹣4)C.(﹣3,4)D.(﹣4,3)4.下列图形中具有稳定性的是()A.六边形B.五边形C.平行四边形D.三角形5.已知图中的两个三角形全等,则∠1等于()A.70°B.68° C.58° D.52°6、如图,OP为∠AOB的角平分线,PC⊥OA于C,PD⊥OB于D,则下列结论中错误的是()A、∠COP=∠DOPB、PC=PDC、OC=ODD、∠CPD=2∠COD7.如图,直线a、b、c表示三条互相交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有()A.1处B.2处C.3处D.4处8.如图3,在△ABC中,若BC=6 cm,AC=4 cm,AB边的垂直平分线交AB于点E,交BC于点D,则△ADC的周长是()A.14 B.12 C. 10 D. 89.如图,在长方形网格中,每个小长方形的长为2,宽为1,A 、B 两点在网格格点上,以A 、B 、C 为顶点的三角形面积为2,则满足条件的格点C 的个数是( )A .7B .6C .5D .410如图所示,AB =AC =AD ,∠BAC=70° 则∠BDC 度数是( ) A 、18° B 、30° C 、35° D 、25°二、填空题(本大题共6个小题,每小题3分,共18分)11、直角三角形中,有一个锐角是40°,它的另一个锐角的度数为___________ 12、等腰三角形的两边长分别为2和5,则周长为___________13、如图,点O 在△ABC 内,且到三个顶点距离相等.若∠A =50°,则∠BOC =___________度14.如图,已知AB =CD ,请添加一个角的条件,使△ABC ≌△CDA ,这个条件是 .15.△ABC 的高BD 、CE 所在的直线交于点H ,若∠BHC =75°,则∠BAC的度数为E BNDM A CBDCA___________16.已知:如图AB =24,AC =12,且CA ⊥AB 于A ,射线BM ⊥AB 于B .一个动点E 从A 点出发沿射线AN 运动,点D 为射线BM 上的一个动点,且始终保持ED =CB .当AE= 时,△DBE 与△BCA 全等.17、(本题8分)等腰三角形周长为15,设腰长为x ,底边长为y (1) 用含x 的式子表示y(2) 若腰长是底边长的2倍,求此三角形三边长18、(本题8分)如图,已知AB =DE ,AC =DF ,BE =CF ,判断AC 与DF 的关系并证明。
2018-2019(含答案)八年级(上)期中数学试卷

2018-2019(含答案)八年级(上)期中数学试卷.................................................................................................................................................................2018.10.22一、选择题(每题3分,共18分)1.下列各式中互为有理化因式的是()A.a+b和a−bB.−x−1和x−1C.5−2和−5+2D.x a+y b和x a+y b2.下列各式中,在实数范围内不能分解因式的是()A.x2+4x+4B.x2−4x−4C.x2+x+1D.x2−x−13.已知a=7−5,b=5−3,c=3−7,则a、b、c三个数的大小关系是()A.b>c>aB.b>a>cC.a>b>cD.c>a>b4.已知一个两位数等于它个位上的数的平方,并且十位上的数字比个位上的数字小3,则这个两位数为()A.25B.25或36C.36D.−25或−365.关于x的方程(a−6)x2−8x+6=0有实数根,则整数a的最大值是()A.6B.7C.8D.96.若等腰△ABC的周长是50cm,底边长为xcm,一腰长为ycm,则y与x的函数关系式及自变量x的取值范围是()A.y=50−2x(0<x<50)B.y=50−2x(0<x<25)(50−2x)(0<x<50)C.y=12(50−x)(0<x<25)D.y=12二、填空题:(每题2分,共24分)7.如果(x+2)2=−x−2,则x的取值范围是________.8.已知20n是整数,则满足条件的最小正整数n为________.9.已知m=n−1−1−n+3,则m n+1=________.a−1是同类二次根式,则a=________,b=________.10.若最简根式4a−1和3b+511.关于x的一元二次方程(a−1)x2+x+(a2−1)=0的一个根是0,则a的值是________.12.已知(x2+y2)2+2(x2+y2)=15,则x2+y2=________.13.如果关于x的方程(a−1)x2−2x−1=0有两个不相等的实数根,那么a的取值范围是________.14.在实数范围内因式分解:2x2−8xy+5y2=________.15.某件商品原价100元,经过两次降价后,售价为64元,设平均每次降价的百分率为x,依题意可列方程________.16.已知点P(a, b)在第三象限,则直线y=(a+b)x经过第________象限,y随x的增大而________.17.反比例函数y=kx的图象经过点P(a, b),且a、b是一元二次方程x2−5x+4=0的两根,k的值是________,点P的坐标为________.18.如图,A、B两点在双曲线y=4x上,分别经过A、B两点向轴作垂线段,已知S阴影=1,则S1+S2=________.三、简答题(每题4分,共28分)19.计算:12−(3+1)2+434÷513.20.计算:xy2−1x8x3y+1y18xy3(x>0, y>0)21.解方程:(x+5)2−2(x+5)=8.22.解方程:2x2−5x+1=0(用配方法)23.如图,在宽为20米、长为30米的矩形地面上修建两条同样宽的道路,余下部分作为耕地.若耕地面积需要551米2,则修建的路宽应为多少米?24.已知y=y1−y2,y1与x成反比例,y2与(x−2)成正比例,并且当x=3时,y=5,当x=1时,y=−1;求y与x之间的函数关系式.25.小强骑车从家到学校要经过一段先上坡后下坡的路,在这段路上小强骑车的距离s(千米)与骑车的时间t(分钟)之间的函数关系如图所示,请根据图中信息回答下列问题:(1)小强去学校时下坡路长________千米;(2)小强下坡的速度为________千米/分钟;(3)若小强回家时按原路返回,且上坡的速度不变,下坡的速度也不变,那么回家骑车走这段路的时间是________分钟.四、综合题:(每题6分,共30分)26.已知关于x的方程x2−(2k+1)x+4k−2=0(1)求证:不论k取什么实数值,这个方程总有实数根;(2)若等腰△ABC的一边长为a=4,另两边的长b、c恰好是这个方程的两个根,求△ABC 的周长.27.如图,科技小组准备用材料围建一个面积为60m2的矩形科技园ABCD,其中一边AB靠墙,墙长为12m.设AD的长为xm,DC的长为ym.(1)求y与x之间的函数关系式;(2)若围成矩形科技园ABCD的三边材料总长不超过26m,材料AD和DC的长都是整米数,求出满足条件的所有围建方案.28.如图,在△ABC中,∠C=90∘,AC=6cm,BC=8cm,点P从点A出发沿边AC向点C以1cm/s的速度移动,点Q从C点出发沿CB边向点B以2cm/s的速度移动.(1)如果P、Q同时出发,几秒钟后,可使△PCQ的面积为8平方厘米?(2)点P、Q在移动过程中,是否存在某点时刻,使得△PCQ的面积等于△ABC的面积的一半?若存在,求出运动的时间;若不存在,说明理由.29.如图,正方形OAPB、ADFE的顶点A、D、B在坐标轴上,点E在AP上,点P、F在函数y=k的图x象上,已知正方形OAPB的面积为9.(1)求k的值和直线OP的解析式;(2)求正方形ADFE的边长.30.如图,在四边形ABCD中,AB=BC=1,∠ABC=90∘,且AB // CD,将一把三角尺的直角顶点P放在对角线AC上滑动,直角的一边始终经过点B,另一边与射线DC相交于点Q,探究:(1)如图,当点Q在边CD上时,线段PQ与BP有怎样的数量关系?并证明你的猜想.(2)当点Q在线段DC延长线上时,在备用图中画出符合要求的示意图,并判断(1)中的结论是否仍成立?(3)点P在线段AC上运动时,△PCQ是否可能为等腰三角形?若可能,求此时AP的值;若不可能,请说明理由.答案1. 【答案】B【解析】根据有理化因式的定义进行解答即可.【解答】解:A、∵⋅=(a+b)(a−b),∴两根式不互为有理化因式,故本选项错误;B、∵(−x−1)⋅x−1=1−x,∴两根式互为有理化因式,故本选项正确;C、∵(5−2)•(−5+2)=210−7,∴两根式不互为有理化因式,故本选项错误;D、∵(x a+y b)•(x a+y b)=(x a+y b)2,∴两根式不互为有理化因式,故本选项错误.故选B.2. 【答案】C【解析】先令二次三项式为0,若有实数根则能因式分解,否则不能.【解答】解:A、x2+4x+4=0有实数根,故本选项能在实数范围内因式分解;B、x2−4x−4=0有实数根,故本选项能在实数范围内因式分解;C、x2+x+1=0没有实数根,故本选项不能在实数范围内因式分解;D、x2−x−1=0有实数根,故本选项能在实数范围内因式分解;故选C.3. 【答案】B【解析】首先求出a,b,c的倒数,进而比较它们的大小,进而得出a、b、c三个数的大小关系.【解答】解:∵a=7−5,b=5−3,c=3−7,∴1 a =7−5=7+52,1 b =5−3=5+32,1 c =3−7=3+72,∵7>3,∴1 a >1b,∵3>5,∴1 a <1c,∴1 c >1a>1b,∴b>a>c.故选:B.4. 【答案】B【解析】设十位上的数字为x,则个位上的数字为(x+3),根据该两位数等于它个位上的数的平方,即可得出关于x的一元二次方程,解之即可得出x的值,进而即可得出该两位数.【解答】解:设十位上的数字为x,则个位上的数字为(x+3),根据题意得:10x+x+3=(x+3)2,整理得:x2−5x+6=0,解得:x=2或x=3,∴x+3=5或x+3=6,∴这个两位数为25或36.故选B.5. 【答案】C【解析】方程有实数根,应分方程是一元二次方程与不是一元二次方程,两种情况进行讨论,当不是一元二次方程时,a−6=0,即a=6;当是一元二次方程时,有实数根,则△≥0,求出a的取值范围,取最大整数即可.【解答】解:当a−6=0,即a=6时,方程是−8x+6=0,解得x=68=34;当a−6≠0,即a≠6时,△=(−8)2−4(a−6)×6=208−24a≥0,解上式,得a≤263≈8.6,取最大整数,即a=8.故选C.6. 【答案】D【解析】根据等腰三角形的腰长=(周长-底边长)×12,及底边长x>0,腰长>0得到.【解答】解:依题意有y=12(50−x).∵x>0,50−x>0,且x<2y,即x<2×12(50−x),得到0<x<25.故选D7. 【答案】x≤−2【解析】根据二次根式的性质,可得答案.【解答】解:由(x+2)2=(−x−2)2=−x−2,得x+2≤0,解得x≤−2,故答案为:x≤−2.8. 【答案】5【解析】因为20n是整数,且20n=4×5n=25n,则5n是完全平方数,满足条件的最小正整数n为5.【解答】解:∵20n=4×5n=25n,且20n是整数;∴25n是整数,即5n是完全平方数;∴n的最小正整数值为5.故答案为:5.9. 【答案】9【解析】根据二次根式中的被开方数必须是非负数列出不等式,求出n的值,得到m的值,代入代数式根据乘方法则计算即可.【解答】解:由题意得,n−1≥0,1−n≥0,解得,n=1,∴m=3,则m n+1=9,故答案为:9.10. 【答案】3,2【解析】根据最简二次根式与同类二次根式的定义列方程组求解.【解答】解:由题意,得a−1=24a−1=3b+5,解得a=3 b=2,故答案为:3,2.11. 【答案】−1【解析】根据一元二次方程的解的定义,将x=0代入已知方程就可以求得a的值.注意,二次项系数a −1≠0.【解答】解:∵关于x 的一元二次方程(a −1)x 2+x +(a 2−1)=0的一个根是0, ∴x =0满足该方程,且a −1≠0.∴a 2−1=0,且a ≠1.解得a =−1.故答案是:−1.12. 【答案】3【解析】首先设x 2+y 2=z ,然后将原方程转化为关于z 的一元二次方程,解该方程即可解决问题.【解答】解:设x 2+y 2=z ,(z ≥0)则原方程变为:z 2+2z −15=0,解得:z =3或−5(舍去).故答案为:3.13. 【答案】a >12且a ≠1【解析】根据方程有两个不相等的实数根利用根的判别式结合二次项系数非零即可得出关于a 的一元一次不等式组,解之即可得出结论.【解答】解:∵关于x 的方程(a −1)x 2− 2x −1=0有两个不相等的实数根,∴ a −1≠0△=(− 2)2+4(a −1)>0, 解得:a >12且a ≠1.故答案为:a >12且a ≠1.14. 【答案】( 2x −2 2y + 3y )( 2x −2 2y − 3y )【解析】首先把5y 2变为8y 2−3y 2,然后把前三项组合提公因式2,再利用完全平方分解,然后再次利用平方差分解因式即可.【解答】解:原式=2x 2−8xy +8y 2−3y 2,=2(x −2y )2−3y 2,=[ 2(x −2y )+ 3y ][ 2(x −2y )− 3y ],=( 2x −2 2y + 3y )( 2x −2 2y − 3y ),故答案为:( 2x −2 2y + 3y )( 2x −2 2y − 3y ).15. 【答案】100(1−x )2=64【解析】设平均每次降价的百分率为x ,根据某件商品原价100元,经过两次降价后,售价为64元,可列方程求解.【解答】解:设平均每次降价的百分率为x ,100(1−x )2=64.故答案为:100(1−x )2=64.16. 【答案】二、四,减小【解析】先根据第三象限点的坐标特征得到a <0,b <0,然后根据正比例函数与系数的关系判断直线y =(a +b )x 经过的象限.【解答】解:因为点P (a , b )在第三象限,所以a <0,b <0,可得a+b<0,所以直线y=(a+b)x经过第二、四象限,y随x的增大而减小;故答案为:二、四;减小17. 【答案】4,(1, 4)或(4, 1)的图象经过点P(a, b),把点P的坐标代入解析式,得到关【解析】先根据反比例函数y=kx于a、b、k的等式ab=k;又因为a、b是一元二次方程x2−5x+4=0的两根,得到a+b=5,ab=4,根据以上关系式求出a、b的值即可.得,ab=k,【解答】解:把点P(a, b)代入y=kx因为a、b是一元二次方程x2−5x+4=0的两根,根据根与系数的关系得:a+b=5,ab=4,解得a=1,b=4或a=4,b=1,所以k=4,点P的坐标是(1, 4)或(4, 1).故答案为4,(1, 4)或(4, 1).18. 【答案】6【解析】欲求S1+S2,只要求出过A、B两点向x轴、y轴作垂线段求出与坐标轴所形成的矩形的面积即可,而矩形面积为双曲线y=4的系数k,由此即可求出S1+S2.x上的点,分别经过A、B两点向x轴、y轴作垂线段,【解答】解:∵点A、B是双曲线y=4x则根据反比例函数的图象的性质得两个矩形的面积都等于|k|=4,∴S1+S2=4+4−1×2=6.故答案为6.19. 【答案】解:原式=23−(3+23+1)+23×343=23−(4+23)+5=−【解析】根据二次根式的运算性质即可求出答案.【解答】解:原式=2−(3+2+1)+2×343=23−(4+23)+5=−20. 【答案】解:原式=2xy−22xy+32xy2xy.=322【解析】根据二次根式性质与化简,可得同类二次根式,根据合并同类二次根式,可得答案.【解答】解:原式=2xy−22xy+32xy2=322xy.21. 【答案】解:∵(x+5)2−2(x+5)−8=0,∴(x+5+2)(x+5−4)=0,即(x+7)(x+1)=0,则x+7=0或x+1=0,解得:x=−7或x=−1.【解析】将x+5看做整体因式分解法求解可得.【解答】解:∵(x+5)2−2(x+5)−8=0,∴(x+5+2)(x+5−4)=0,即(x+7)(x+1)=0,则x+7=0或x+1=0,解得:x=−7或x=−1.22. 【答案】解:∵2x2−5x=−1,∴x2−52x=−12,∴x2−52x+2516=−12+2516,即(x−54)2=1716,则x−54=±174,∴x=5±174.【解析】将常数项移到右边后把二次项系数化为1,再两边配上一次项系数一半的平方求解可得.【解答】解:∵2x2−5x=−1,∴x2−52x=−12,∴x2−52x+2516=−12+2516,即(x−54)2=1716,则x−54=±174,∴x=5±174.23. 【答案】修建的道路宽为1米.【解析】设路宽为x,则道路面积为30x+20x−x2,所以所需耕地面积551=20×30−(30x+20x−x2),解方程即可.【解答】解:设修建的路宽为x米.则列方程为20×30−(30x+20x−x2)=551,解得x1=49(舍去),x2=1.24. 【答案】解:因为y1与x成反比例,y2与(x−2)成正比例,故可设y1=k1x,y2=k2(x−2),因为y=y1−y2,所以y=k1x−k2(x−2),把当x=3时,y=5;x=1时,y=−1,代入得k13−k2=5 k1+k2=−1,解得k1=3k2=−4,再代入y=k1x −k2(x−2)得,y=3x+4x−8.【解析】根据题意设出反比例函数与正比例函数的解析式,代入y=y1−y2,再把当x=3时,y=5,当x=1时,y=−1代入关于y的关系式,求出未知数的值,即可求出y与x之间的函数关系式.【解答】解:因为y1与x成反比例,y2与(x−2)成正比例,故可设y1=k1x,y2=k2(x−2),因为y=y1−y2,所以y=k1x−k2(x−2),把当x=3时,y=5;x=1时,y=−1,代入得k13−k2=5 k1+k2=−1,解得k1=3k2=−4,再代入y=k1x −k2(x−2)得,y=3x+4x−8.25. 【答案】2; 0.5; 14【解析】(1)根据题意和函数图象可以得到下坡路的长度;; (2)根据函数图象中的数据可以求的小强下坡的速度;; (3)根据题意可以求得小强上坡的速度,进而求得小强返回时需要的时间.【解答】解:(1)由题意和图象可得,小强去学校时下坡路为:3−1=2(千米),; (2)小强下坡的速度为:2÷(10−6)=0.5千米/分钟,; (3)小强上坡时的速度为:1÷6=16千米/分钟,故小强回家骑车走这段路的时间是:21+10.5=14(分钟),26. 【答案】(1)证明:∵在方程x2−(2k+1)x+4k−2=0中,△=[−(2k+1)]2−4(4k−2)=4k2−12k+9=(2k−3)2≥0,∴不论k取什么实数值,这个方程总有实数根;; (2)解:当a为底边时,b=c,∴△=(2k−3)2=0,解得:k=32,∴b+c=2k+1=4=a,∴此种情况不合适;当a为腰时,将x=4代入原方程得:16−4(2k+1)+4k−2=0,解得:k=52.∴b+c=2k+1=6,∴△ABC的周长=a+b+c=4+6=10.【解析】(1)根据方程的系数结合根的判别式即可得出△=(2k−3)2≥0,由此可得出:不论k取什么实数值,这个方程总有实数根;; (2)当a为底时,由根的判别式△=(2k−3)2= 0可求出k值,再根据根与系数的关系可得出b+c=4,由b+c=a可知此种情况不符合题意;当a为腰时,将x=4代入原方程求出k值,再根据根与系数的关系可得出b+c=6,套用三角形的周长公式即可求出结论.【解答】(1)证明:∵在方程x2−(2k+1)x+4k−2=0中,△=[−(2k+1)]2−4(4k−2)=4k2−12k+9=(2k−3)2≥0,∴不论k取什么实数值,这个方程总有实数根;; (2)解:当a为底边时,b=c,∴△=(2k−3)2=0,解得:k=32,∴b+c=2k+1=4=a,∴此种情况不合适;当a为腰时,将x=4代入原方程得:16−4(2k+1)+4k−2=0,解得:k=52.∴b+c=2k+1=6,∴△ABC的周长=a+b+c=4+6=10.27. 【答案】解:(1)由题意得,S矩形ABCD=AD×DC=xy,故y=60x .; (2)由y=60x,且x、y都是正整数,可得x可取1,2,3,4,5,6,10,12,15,20,30,60,∵2x+y≤26,0<y≤12,∴符合条件的围建方案为:AD=5m,DC=12m或AD=6m,DC=10m或AD=10m,DC=6m.【解析】(1)根据面积为60m2,可得出y与x之间的函数关系式;; (2)由(1)的关系式,结合x、y都是正整数,可得出x的可能值,再由三边材料总长不超过26m,DC的长<12,可得出x、y的值,继而得出可行的方案.【解答】解:(1)由题意得,S矩形ABCD=AD×DC=xy,故y=60x .; (2)由y=60x,且x、y都是正整数,可得x可取1,2,3,4,5,6,10,12,15,20,30,60,∵2x+y≤26,0<y≤12,∴符合条件的围建方案为:AD=5m,DC=12m或AD=6m,DC=10m或AD=10m,DC=6m.28. 【答案】解:(1)设x秒钟后,可使△PCQ的面积为8平方厘米,由题意得:12(6−x)⋅2x=8,x=2或x=4,当2秒或4秒时,面积可为8平方厘米;; (2)不存在.理由:设y秒时,△PCQ的面积等于△ABC的面积的一半,由题意得:1 2(6−y)⋅2y=12×12×6×8y2−6y+12=0.△=36−4×12<0.方程无解,所以不存在.【解析】(1)设x秒钟后,可使△PCQ的面积为8平方厘米,用x表示出△PCQ的边长,根据面积是8可列方程求解.; (2)假设y秒时,△PCQ的面积等于△ABC的面积的一半,列出方程看看解的情况,可知是否有解.【解答】解:(1)设x秒钟后,可使△PCQ的面积为8平方厘米,由题意得:12(6−x)⋅2x=8,x=2或x=4,当2秒或4秒时,面积可为8平方厘米;; (2)不存在.理由:设y秒时,△PCQ的面积等于△ABC的面积的一半,由题意得:1 2(6−y)⋅2y=12×12×6×8y2−6y+12=0.△=36−4×12<0.方程无解,所以不存在.29. 【答案】解:(1)∵正方形OAPB的面积为9,∴PA=PB=3,∴P点坐标为(3, 3),把P(3, 3)代入y=kx得,k=3×3=9,即y=9x;设直线OP的解析式为y=k1x,把P(3, 3)代入y=k1x得,k1=1,∴直线OP的解析式为y=x;; (2)设正方形ADFE的边长为a,则F点的坐标为(a+3, a),把F(a+3, a)代入y=9x 得,a(a+3)=9,解得a1=−3+352,a2=−3−352,∴正方形ADFE的边长为得−3+352.【解析】(1)利用正方形的性质得到P点坐标为(3, 3),再把P点坐标代入y=kx即可得到k的值;然后利用待定系数法求直线OP的解析式;; (2)设正方形ADFE的边长为a,利用正方形的性质易表示F点的坐标为(a+3, a),然后把F(a+3, a)代入y=9x,再解关于a的一元二次方程即可得到正方形ADFE的边长.【解答】解:(1)∵正方形OAPB的面积为9,∴PA=PB=3,∴P点坐标为(3, 3),把P(3, 3)代入y=kx得,k=3×3=9,即y=9x;设直线OP的解析式为y=k1x,把P(3, 3)代入y=k1x得,k1=1,∴直线OP的解析式为y=x;; (2)设正方形ADFE的边长为a,则F点的坐标为(a+3, a),把F(a+3, a)代入y=9x 得,a(a+3)=9,解得a1=−3+352,a2=−3−352,∴正方形ADFE的边长为得−3+352.30. 【答案】(1)证明:如图1,过点P作PF⊥BC于点F,PE⊥CD于点E,∵∠PCE=45∘,∠PEQ=90∘,∴PE=EC.∴四边形PFCE是正方形.∴PE=PF.∵∠BPF=∠QPE=90∘−∠FPQ,∠BFP=∠PEQ=90∘,在△BPF与△QPE中,∠BPF=∠QPEPF=PE∠BFP=∠QEP=90∘,∴△BPF≅△QPE(ASA),∴BP=PQ;; (2)成立.理由:如图2,过点P作PF⊥BC于点F,PE⊥CD于点E,∵∠PCE=45∘,∠PEC=90∘,∴PE=EC.∴四边形PFCE是正方形.∴PE=PF.∵∠BPF=∠QPE=90∘−∠FPQ,∠BFP=∠PEQ=90∘,在△BPF与△QPE中,∠BPF=∠QPEPF=PE∠BFP=∠QEP=90∘,∴△BPF≅△QPE(ASA),∴BP=PQ;; (3)能.证明:如图3,延长BP交DC于G,∵点Q在DC的延长线上,∴∠PCQ>90∘,∴等腰△PCQ中,PC=QC,∴∠1=∠2,∵∠BPQ=90∘,∴∠1+∠5=90∘,∠2+∠3=90∘,∵∠1=∠2,∴∠5=∠3,在正方形ABCD中,AB // DC,∴∠4=∠5,∴∠4=∠3,∴AP=AB=1.【解析】(1)可通过构建全等三角形来证PB=PQ,过点P作PF⊥BC于点F,PE⊥CD于点E,由于△PEC是等腰直角三角形,因此PE=EC,可得出四边形PECF是正方形,由此可得出PE=PF,根据同角的余角相等可得出∠FPB=∠QPE,这两个三角形中又有一组直角,因此构成了全等三角形判定条件中ASA的条件.根据全等三角形即可得出PB=PQ;; (2)根据题意画出图形,同(1)过点P作PF⊥BC于点F,PE⊥CD于点E可得出四边形PFCE是正方形,故PE=PF.由ASA定理得出△BPF≅△QPE,根据全等三角形的性质即可得出结论;; (3)延长BP交DC于G,可得出等腰△PCQ中,PC=QC,故可得出∠1=∠2,由直角三角形的性质得出∠5=∠3,在正方形ABCD中根据平行线的性质即可得出结论.【解答】(1)证明:如图1,过点P作PF⊥BC于点F,PE⊥CD于点E,∵∠PCE=45∘,∠PEQ=90∘,∴PE=EC.∴四边形PFCE是正方形.∴PE=PF.∵∠BPF=∠QPE=90∘−∠FPQ,∠BFP=∠PEQ=90∘,在△BPF与△QPE中,∠BPF=∠QPEPF=PE,∠BFP=∠QEP=90∘∴△BPF≅△QPE(ASA),∴BP=PQ;; (2)成立.理由:如图2,过点P作PF⊥BC于点F,PE⊥CD于点E,∵∠PCE=45∘,∠PEC=90∘,∴PE=EC.∴四边形PFCE是正方形.∴PE=PF.∵∠BPF=∠QPE=90∘−∠FPQ,∠BFP=∠PEQ=90∘,在△BPF与△QPE中,∠BPF=∠QPEPF=PE,∠BFP=∠QEP=90∘∴△BPF≅△QPE(ASA),∴BP=PQ;; (3)能.证明:如图3,延长BP交DC于G,∵点Q在DC的延长线上,∴∠PCQ>90∘,∴等腰△PCQ中,PC=QC,∴∠1=∠2,∵∠BPQ=90∘,∴∠1+∠5=90∘,∠2+∠3=90∘,∵∠1=∠2,∴∠5=∠3,在正方形ABCD中,AB // DC,∴∠4=∠5,∴∠4=∠3,∴AP=AB=1.。
19学年上学期八年级期中考试数学试题(附答案)

2018—2019学年第一学期期中学业检测八年级数学试题温馨提示:1. 本试卷分第Ⅰ卷和第Ⅱ卷两部分,共6页。
满分150分。
考试用时120分钟。
2.答卷前,考生务必用0.5毫米黑色签字笔将自己的学校、姓名、准考证号填写在答题卡中规定的位置上。
3.第Ⅰ卷每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案标号。
答案不能答在试题卷上。
4. 第Ⅱ卷必须用0.5毫米黑色签字笔作答,答案必须写在答题卡各题目指定区域内相应的位置,不能写在试题卷上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带。
不按以上要求作答的答案无效。
第Ⅰ卷(选择题共36分)一、选择题(本题共12个小题,在每小题的四个选项中只有一个是正确的,请把正确的选项选出来,每小题3分,满分36分)1.下列图形中,轴对称图形的个数有A.1个B.2个C.3个D.4个2.下列各组数中,能作为一个三角形三边边长的是A.2,2,4 B.1,3,4 C.2,3,4 D.2,3,53.若一个点到一个三角形三条边的距离都相等,则这个点是这个三角形的A.三条中线的交点B.三条角平分线的交点C.三条高的交点D.三条边的垂直平分线的交点4.如图,在△ABC和△DEF中,∠B=∠DEF,AB=DE,添加下列一个条件后,仍然不能证明△ABC≌△DEF,这个条件是A.∠A=∠D B.BC=EF C.∠ACB=∠F D.AC=DF5.下列说法正确的是A.位置相同的两个三角形全等B.完全重合的两个三角形全等C.面积相等的两个三角形全等D.所有的等边三角形全等6. 如果三角形的三个内角的度数比是2:3:5,则它是A.直角三角形 B. 钝角三角形 C.钝角或直角三角形D.锐角三角形7.如图所示,图中x的值是A.80 B.70 C.60 D.508.若等腰三角形的周长为30cm,一边为14cm,则腰长为A.2cm B.8cm C.8cm或2cm D.14cm或8cm9.如图,在△ABC中,AC=4 cm,线段AB的垂直平分线交AC于点N,△BCN的周长是7 cm,则BC的长为A.1 cm B.2 cm C.3 cm D.4 cm10.已知非直角三角形ABC中,∠A=45°,高BD与CE所在直线交于点H,则∠BHC的度数是A.45°B.45°或135°C.45°或125°D.135°11.如图,小莹和小华在棋盘中练习摆图案,小莹执圆子,小华执星子.已知棋盘中心圆子的位置用(-1,0)表示,右下角圆子的位置用(0,-1)表示.若小华将第4枚星子放入棋盘后,所有棋子构成一个轴对称图形,则他放的位置是A.(-2,1)B.(0,-2)C.(1,-2)D.(-1,1)12. 如图,将一张三角形纸片ABC的一角折叠,使点A落在△ABC外的A'处,折痕为DE.如果∠A=α,∠CEA′=β,∠BDA'=γ,那么下列式子中正确的是A.γ=2α+βB.γ=α+2βC.γ=α+βD.γ=180°﹣α﹣β第Ⅱ卷(非选择题共114分)二、填空题:(本大题共8个小题,每小题填对最后结果得5分,满分40分.)13.等边三角形是轴对称图形,它有条对称轴.14.已知点P(m+1,5)与Q(4,n+2)关于x轴对称,则m-n= .15.如图,小明家的凳子坏了,于是他给凳子加了两根木条,这样凳子就比较牢固了,他所应用的数学原理是.16.在△ABC中,∠ABC=90°,∠A=48°,DB∥AC,则∠CBD=______.17.等腰三角形的一个底角为35°,则顶角的度数是度.18.如图,∠ACB=90°,AC=BC,BE⊥CE,AD⊥CE,垂足分别为E,D,AC=13,BE=5,则DE=.19.在平面直角坐标系中,点A(2,0),B(0,1),当点C的坐标为_______ 时,△BOC与△ABO全等.20.如图,∠BAC的平分线与BC的垂直平分线相交于点P,PE⊥AB,PF⊥AC,垂足分别为E、F.若AB=8,AC=4,则AE= .三、解答题:(本大题共7个小题,满分74分.解答时请写出必要的演推过程.)21.(本小题满分10分)①如图21-1,已知∠AOB及M、N两点,求作:点P,使点P到∠AOB的两边距离相等且到M、N的两点也距离相等。
学18—19学年上学期八年级期中考试数学试题(附答案)

2018-2019学年南平三中第一学期期中质量检测八年级数学试题(满分:150分;考试时间:120分钟)★友情提示:①所有答案都必须填在答题卡相应的位置上,答在本试卷上一律无效;②试题未要求对结果取近似值的,不得采取近似计算.一、选择题(本大题共10小题,每小题4分,共40分.每小题只有一个正确的选项,请在答题卡...的相应位置填涂)1.如下图形中,不.是.轴对称图形的是()2.下列尺规作图,能判断AD是△ABC边上的高是()A.B.C.D.3.长度分别为2,7,x的三条线段能组成一个三角形,x的值可以是()A.9 B.5 C.6 D.44.小明不慎将一块三角形的玻璃摔碎成如图所示的四块(即图中标有1、2、3、4的四块),你认为将其中的哪一些块带去,就能配一块与原来一样大小的三角形?应该带()A.第1块B.第2块C.第3块D.第4块第4题第6题第7题第8题5.将点P(4,﹣5)关于y轴对称得P1,则P1的坐标为()A .(4,5)B .(﹣4,5)C .(4,﹣5)D .(﹣ 4,﹣5)6.如图,△ABC ≌△EBD ,AB=3cm ,BC=4cm ,AC=5cm,则BE 的长度为( )A .3cmB .4cmC .5cmD .1cm7. 如图,在△ABC 中,∠A=70°,点D 是BC 延长线上一点,∠ACD=150°,则∠B 等于( )A .60°B .70°C .80°D .90°8.如图,在△ABC 中,AD 平分∠BAC ,DE ⊥AB 于E ,DF ⊥AC 于F ,若DE=5,则DF 的值是( )A .5B .10C .2.5D .49.已知等腰三角形的一个内角是40°,则它的顶角是( )A .100°B .40°C .70°或50°D .40°或100°10.如图,在Rt △ABC 中,∠ACB=90°,AC=6,BC=8,AB=10,AD 是∠BAC 的平分线.若P ,Q 分别是AD 和AC 上的动点,则PC+PQ 的最小值( )A .2.4B .4C .5D .4.8二、填空题(本题共6小题,每小题4分,共24分.请将答案填入答题卡...的相应位置) 11.一个正多边形的一个外角都是36°,则这个多边形是________边形.12.如图,为了使木门不变形,木工师傅在木门上加钉了一根木条,这样是利用三角形的 .第10题 第12题 第13题13.如图所示,∠A+∠B +∠C +∠D +∠E +∠F =__________. 14.在Rt △ABC 和Rt △A′B′C′中,AB=A′B′,AC=A′C′,∠C=∠C′=90°,则Rt △ABC ≌Rt △A′B′C′的根据是 .第16题15.如果等腰三角形两边长是4cm 和8cm ,那么它的周长是 cm .16. 如图,△ABC 和△CDE 都是等边三角形,B 、C 、D 三点在一条直线上,AD 与BE 相交于点P ,AC 、BE 相交于点M ,AD 、CE 相交于点N ,则下列五个结论:①AD=BE ;②∠BMC=∠ANC ;③∠APM=60∘;④CP 平分∠MCN ;⑤△CMN 是等边三角形.其中,一定正确的是 (填序号)三、解答题(本大题共9小题,共86分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、单选题
1. 计算 的结果为( ) A. B. C. D. 2. 下列实数是无理数的是( ) A . B . C . 0 D . 5.53 3. 如图,数轴上点A表示的数可能是( )
A . 3的算术平方根 B . 4的算术平方根 C . 7的算术平方根 D . 9的算术平方根
三、解答题
17. 根据表中所给信息,完成表格:
被开方数
________
平方根
±1
算术平方根
1
立方根
1
2 ________
4 ±2 ________
64 ±8 8 ________
18. 计算:
.
19. 计算:14a8b4÷2a4b4-a3×a+(2a2)2
20. 把下列多项式分解因式:
(1)
(2)
12. 计算:
________.
13.
,则A=________.
14. 若x2+mx+16=(x+4)2 , 则m的值为________.
15. 计算:
=________.
16. 有两个正方形A,B,现将B放在A的内部得图甲,将A,B并列放置后构造新的正方形得图乙.若图甲和图乙中阴
影部分的面积分别为7和30,则图乙面积为________.
(2) 观察图3,写出图3中所表示的等式:=.
(3) 若
、
、
,且
,请利用(2)所得的结论求:
的值
25. 阅读下列文字与例题,并解答:
将一个多项式分组进行因式分解后,可用提公因式法或公式法继续分解的方法称作分组分解法.
例如:以下式子的分解因式的方法就称为分组分解法.
A2+2ab+b2+ac+bc 原式=(a2+2ab+b2)+ac+bc =(a+b)2+c(a+b)
8. 可以改写成( )
A. B.
C. D.
9. 如图,长方形的长、宽分别为a、b,且a比b大5,面积为10,则a2b–ab2的值为( )
A . 60 B . 50 C . 25 D . 15
10. 若
,
则
A . 4 B . 20182 C . 22018 D . 42018
的值是( )
二、填空题
11. 已知:一个正数的两个平方根分别是-5和a+1,则a的值是________.
21. 先化简,再求值:
,其中
.
22. 若x+y=5,xy=4..
(1) 求
的值
(2) 求x-y的值.
23. 已知
,
.(1Leabharlann 填空: =; =.(2) 求m与n的数量关系.
24. 我们知道,对于一个图形,通过两种不同的方法计算它的面积,可以得到一个等式.例
如图1可以得到
.请解答下列问题:
(1) 根据图2,完成数学等式: =;
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17.
18.
19.
20. 21. 22.
23. 24. 25.
=(a+b)(a+b+c)
(1) 试用“分组分解法”因式分解: (2) 已知四个实数a,b,c,d,满足a≠b,c≠d,并且aa+ac=12k,b2+bc=12k,c2+ac=24k,d2+ad=24k ,同时成立.
①当k=1时,求a+c的值;
②当k≠0时,用含a的代数式分别表示 、 、 (直接写出答案即可). 参考答案
4. 计算:
的结果是( )
A. B.- C. D.
5. 下列从左边到右边的变形,是因式分解的是( ).
A.
B.
C.
D.
6. 运用乘法公式计算(x+3)2的结果是( )
A . x2+9 B . x2–6x+9 C . x2+6x+9 D . x2+3x+9
7. 计算
结果正确的是( )
A. B. C. D.
