第7章习题答案
第7章_微型计算机存储器习题参考答案

第7章_微型计算机存储器习题参考答案计算机存储器7.1 ⼀个微机系统中通常有哪⼏级存储器?它们各起什么作⽤?性能上有什么特点?答:⼀个微机系统中通常有3级存储器结构:⾼速缓冲存储器、内存储器和辅助存储器。
⾼速缓冲存储器简称快存,是⼀种⾼速、⼩容量存储器,临时存放指令和数据,以提⾼处理速度。
内存存取速度快,CPU可直接对它进⾏访问,⽤来存放计算机运⾏期间的⼤量程序和数据。
辅存存储容量⼤,价格低,CPU不能直接进⾏访问,通常⽤来存放系统程序、⼤型⽂件及数据库等。
7.2 半导体存储器分为哪两⼤类?随机存取存储器由哪⼏个部分组成?答:根据存取⽅式的不同,半导体存储器可分为随机存取存储器RAM和只读存储器ROM 两类。
其中随机存取存储器主要由地址译码电路、存储体、三态数据缓冲器和控制逻辑组成。
7.3 什么是SRAM,DRAM,ROM,PROM,EPROM和EEPROM?答:SRAM:静态随机存取存储器;DRAM:动态随机存取存储器;ROM:掩膜只读存储器;PROM:可编程的只读存储器;EPROM:可擦除可编程只读存储器;EEPROM:⽤电可擦除可编程只读存储器。
7.4 常⽤的存储器⽚选控制⽅法有哪⼏种?它们各有什么优缺点?答:常⽤的存储器⽚选控制译码⽅法有线选法、全译码法和部分译码法。
线选法:当存储器容量不⼤、所使⽤的存储芯⽚数量不多、⽽CPU寻址空间远远⼤于存储器容量时,可⽤⾼位地址线直接作为存储芯⽚的⽚选信号,每⼀根地址线选通⼀块芯⽚,这种⽅法称为线选法。
直观简单,但存在地址空间重叠问题。
全译码法:除了将低位地址总线直接与各芯⽚的地址线相连接之外,其余⾼位地址总线全部经译码后作为各芯⽚的⽚选信号。
采⽤全译码法时,存储器的地址是连续的且唯⼀确定,即⽆地址间断和地址重叠现象。
部分译码法:将⾼位地址线中的⼀部分进⾏译码,产⽣⽚选信号。
该⽅法常⽤于不需要全部地址空间的寻址、采⽤线选法地址线⼜不够⽤的情况。
采⽤部分译码法存在地址空间重叠的问题。
离散习题(附答案) (7)

习题7.11.设Z是整数集合,Z上的二元运算*定义为:a*b=ab+2(a+b+1)。
证明代数系统<Z,*>是半群。
证明:由于任意两个整数经加、减、乘运算后,其结果仍然是整数。
所以运算*对于是封闭的。
现证*是可结合运算。
由于(a*b)*c=(ab+2(a+b+1))*c=(ab+2(a+b+1))c+2(ab+2(a+b+1)+c+1)=abc+2ac+2bc+2c+2ab+4a+4b+2c+6=abc+2(ab+bc+ca)+4(a+b+c)+6a*(b*c)=a*(bc+2(b+c+1))=a(bc+2(b+c+1))+2(a+bc+2(b+c+1)+1)=abc+2ab+2ac+2a+2a+2bc+4b+4c+6=abc+2(ab+bc+ca)+4(a+b+c)+6所以(a*b)*c=a*(b*c)。
由此证得*是可结合运算,<Z,*>是半群。
在证明*是可结合运算时,还可先把*的定义改写如下:a*b=ab+2(a+b+1)=ab+2a+2b+2=a(b+2)+2(b+2)−2=(a+2)(b+2)−2从而有(a*b)*c=((a +2)(b+2)−2)*c=(((a +2)(b+2)−2)+2)(c+2)−2=(a +2)(b+2)(c +2)−2a*(b*c)=a*((b +2)(c+2)−2)=(a +2)(((b +2)(c+2)−2)+2)−2=(a +2)(b+2)(c +2)−2于是(a*b)*c=a*(b*c)。
显然,上述证明方法,不仅简明清晰,而且可以对运算过程和运算结果有较好的把握和预测,避免了盲目性。
2.写出独异点<A,*>的所有子独异点,其中A=⎨1,2,3,4,5⎬,a*b=max(a,b)。
解:对于A中任意元素a,都有1*a=a*1=max(a,1)=a所以1是独异点<A,*>的幺元。
由于<A,*>的子独异点必须与<A,*>有相同的幺元,因此,<A,*>的所有子独异点分别为<⎨1⎬,*>,<⎨1,2⎬,*>,<⎨1,3⎬,*>,<⎨1,4⎬,*>,<⎨1,5⎬,*>,<⎨1,2,3⎬,*>,<⎨1,2,4⎬,*>,<⎨1,2,5⎬,*>,<⎨1,3,4⎬,*>,<⎨1,3,5⎬,*>,<⎨1,4,5⎬,*>,<⎨1,2,3,4⎬,*>,<⎨1,2,3,5⎬,*>,<⎨1,2,4,5⎬,*>,<⎨1,3,4,5⎬,*>,<A,*>。
第七章 习题答案
第七章动态电路的时域分析习题一、选择题1. 一阶电路的时间常数取决于: C(A) 电路的结构(B) 外施激励(C) 电路的结构和参数(D) 电路的参数2. 图示电路中I S = 5 A恒定,电路原已稳定,t = 0时开关S打开。
在求解过渡过程中,下列式子中正确的是: D(A) u(∞) = 125 V (B) τ = 0.4 s (C) u(0+) = 100 V (D) i(∞) = 5AL3.在电路换路后的最初瞬间( t = 0+ ),根据换路定律,电路元件可作如下等效: C(A) 无储能的电容可看做开路(B) 无储能的电感可看做短路(C) 电容可看作具有其初值电压的电压源(D) 电压源可看作短路,电流源可看作开路(0+)的值为:D4. 图示电路在开关S合上前电感L中无电流,合上开关的瞬间uL(A) 0 V (B) 63.2 V (C) ∞(D) 100 V5. 图示电路中电压源电压恒定,且电路原已稳定。
在开关S闭合瞬间,i(0+)的值为:C(A) 0.2 A (B) 0.6 A (C) 0 A (D) 0.3 A6. 表征一阶动态电路的电压、电流随时间变化快慢的参数是:D(A) 电感L(B) 电容C(C) 初始值(D) 时间常数τ7. 图示正弦脉冲信号的数学表达式为:B (A) sin ω t ⋅ ε (t ) + sin ω ( t - T ) ⋅ ε ( t - T ) (B) sin ω t ⋅ ε (t ) - sin ω t ⋅ ε ( t - T ) (C) sin ω t ⋅ ε (t ) - sin ω ( t - T ) ⋅ ε ( t - T ) (D) sin ω t ⋅ ε (t ) + sin ω t ⋅ ε ( t - T )8. 图示电路中,原已达稳态, t = 0开关 S 打开,电路的时间常数为:D (A)s 41 (B) s 61(C) s 4 (D)s 69. 示电路中,t = 0 时开关打开,则 u (0+)为:C(A) 0V (B) 3.75V (C) – 6V (D) 6V10.图示电路中,开关打开已久,在 t = 0 时开关闭合,i (0+) 为:D(A) 0A (B) 0.8A(C) 2A (D)1A11.R 、C 串联电路,已知全响应()()10C 83V,0t u t e t -=-≥,其零状态响应为:(A )(A) 1088V te-- (B) 1083V t e -- (C) 103V t e -- (D) 105V t e -12. .一阶电路的全响应()()10C 106V,0tu t et -=-≥若初始状态不变而输入增加一倍,则全响应u C (t)为 ( D ) (A) 20-12e -10t ; (B) 20-6e -10t ; (C) 10-12e -10t ; (D) 20-16 e -10t 。
数据结构课后习题答案第七章
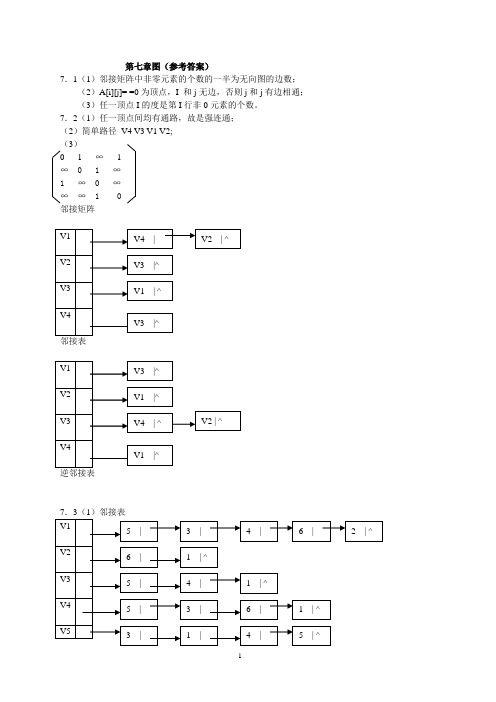
第七章图(参考答案)7.1(1)邻接矩阵中非零元素的个数的一半为无向图的边数;(2)A[i][j]= =0为顶点,I 和j无边,否则j和j有边相通;(3)任一顶点I的度是第I行非0元素的个数。
7.2(1)任一顶点间均有通路,故是强连通;(2)简单路径V4 V3 V1 V2;(3)0 1 ∞ 1∞ 0 1 ∞1 ∞ 0 ∞∞∞ 1 0邻接矩阵邻接表(2)从顶点4开始的DFS序列:V5,V3,V4,V6,V2,V1(3)从顶点4开始的BFS序列:V4,V5,V3,V6,V1,V27.4(1)①adjlisttp g; vtxptr i,j; //全程变量② void dfs(vtxptr x)//从顶点x开始深度优先遍历图g。
在遍历中若发现顶点j,则说明顶点i和j间有路径。
{ visited[x]=1; //置访问标记if (y= =j){ found=1;exit(0);}//有通路,退出else { p=g[x].firstarc;//找x的第一邻接点while (p!=null){ k=p->adjvex;if (!visited[k])dfs(k);p=p->nextarc;//下一邻接点}}③ void connect_DFS (adjlisttp g)//基于图的深度优先遍历策略,本算法判断一邻接表为存储结构的图g种,是否存在顶点i //到顶点j的路径。
设 1<=i ,j<=n,i<>j.{ visited[1..n]=0;found=0;scanf (&i,&j);dfs (i);if (found) printf (” 顶点”,i,”和顶点”,j,”有路径”);else printf (” 顶点”,i,”和顶点”,j,”无路径”);}// void connect_DFS(2)宽度优先遍历全程变量,调用函数与(1)相同,下面仅写宽度优先遍历部分。
第七章课后习题参考答案

2. 试简单说明下列协议的作用:IP、ARP、RARP和ICMP。
答:IP协议:实现网络互连。
使参与互连的性能各异的网络从用户看起来好像是一个统一的网络。
ARP协议:完成IP地址到MAC地址的映射。
RARP:使只知道自己硬件地址的主机能够知道其IP地址。
ICMP:允许主机或路由器报告差错情况和提供有关异常情况的报告。
5. 试说明IP 地址与硬件地址的区别。
为什么要使用这两种不同的地址?答:IP地址在IP数据报的首部,而硬件地址则放在MAC帧的首部。
在网络层以上使用的是IP地址,而链路层及以下使用的是硬件地址。
在IP层抽象的互连网上,我们看到的只是IP数据报,路由器根据目的站的IP地址进行选路。
在具体的物理网络的链路层,我们看到的只是 MAC 帧,IP 数据报被封装在 MAC 帧里面。
MAC帧在不同的网络上传送时,其MAC帧的首部是不同的。
这种变化,在上面的IP层上是看不到的。
每个路由器都有IP 地址和硬件地址。
使用IP地址与硬件地址,尽管连接在一起的网络的硬件地址体系各不相同,但IP层抽象的互连网却屏蔽了下层这些很复杂的细节,并使我们能够使用统一的、抽象的IP地址进行通信。
6.(1)子网掩码为255.255.255.0代表什么意思?(2)一网络的子网掩码为255.255.255.248,问该网络能够连接多少台主机?(1)一A类网络和一B类网络的子网号subnet-id分别为16bit的8bit,问这两个网络的子网掩码有何不同?(2)一个B类地址的子网掩码是255.255.240.0。
试问在其中每一个子网上的主机数最多是多少?(3)一个A类地址的子网掩码为255.255.0.255。
它是否为一个有效的子网掩码?(4)某个IP地址的十六进制表示是C22F1481,试将其转换为点分十进制的形式.这个地址是哪一类IP 地址?(5)C类网络使用子网掩码有无实际意义?为什么?答:(1)C类地址对应的子网掩码值。
第七章习题答案

第七章1.计算氢原子核外电子从第三能级跃迁到第二能级时产生的谱线H α的波长与频率。
解: ν = R H ⎪⎭⎫ ⎝⎛-222111n n= 3.289 ⨯ 1015⎪⎪⎭⎫⎝⎛-223121s -1= 4.57⨯1014s -1νλc= =11418s 1057.4s m 10998.2--⨯⋅⨯= 656⨯10-9m= 656nm2.计算基态氢原子的电离能为多少? 解: I = ∆E = h ν= 6.626⨯10-34 J ⋅s ⨯3.289⨯1015s -1(1/12 -1/∞)=2.179⨯10-18J3.下列各组量子数哪些是不合理的?为什么?n l m(1) 2 1 0(2) 2 2 -1(3) 2 3 +2解:(1)合理;(2) l 取值不合理,应小于n ;(3) l 、m 取值不合理,l 应小于n ,m 取值为0, ±1, ±2,⋯ ± l ;4.用合理的量子数表示:(1)3d 能级; (2)4s 1电子解:(1)3d 能级: n =3,l =2;(2)4s 1电子:n =4,l =0,m = 0;5.分别写出下列元素基态原子的电子分布式,并分别指出各元素在周期表中的位置。
9F 10Ne 25Mn 29Cu 24Cr 55Cs 71Lu解:9F 1s 22s 22p 5 第二周期VIIA 族 10Ne [He]2s 22p 6 第二周期VIIIA 族25Mn [Ar]3d 54s 2 第四周期VIIB 族 29Cu [Ar]3d 104s 1 第四周期I B 族24Cr [Ar]3d 54s 1 第四周期VI B 族 55Cs [Xe]6s 1 第六周期I A 族71Lu [Xe]4f 145d 16s 2 第六周期IIIB 族6.以(1)为例,完成下列(2)~(4)题。
(1)Na (Z = 11) [Ne]3s 1 ; (3 ) (Z =24) [ ? ] 3d 54s 1;(2) 1s 22s 22p 63s 23p 3 ; (4 ) Kr (Z = ) [ ? ] 3d 104s 24p 6;解:(1) Na (Z = 11) [Ne]3s 1 ; (3 ) Cr (Z =24) [Ar ] 3d 54s 1;(2) P(Z=15) 1s 22s 22p 63s 23p 3 ; (4 ) Kr (Z = 36 ) [Ar] 3d 104s 24p 6;7.写出下列离子的最外层电子分布式:S 2-K + Pb 2+ Ag + Mn 2+ Co 2+ 解:8.试完成下表。
第七章 练习题参考答案

V1 V3 V6
7. 对下图所示的有向图
(1) 画出它的邻接表 (2) 根据邻接表写出其拓扑排序序列
解:(1)邻接表为
0
2
5∧
2
3
4∧
2 3∧
4∧
1
2
3
6∧
1
4∧
(2)由邻接表可得拓朴排序序列:
1 5 2 3 64
8.已知n个顶点的有向图用邻接矩阵表示,编 写函数,计算每对顶点之间的最短路径。
4 18 ∧
2
1 12
32
5 22 ∧
3
1 16
22
44∧
4
1 18
34
5 10 ∧
5
2 22
4 10 ∧
解:(1) V1
12 V2
16 2
18
4 V3 22
V4
10 V5
(2)深度优先遍历的结点序列:v1,v2,v3,v4,v5
广度优先搜索的结点序列:v1,v2,v3,v4,v5
(3)最小生成树
CD CA CAB
CD CA CAB
CD CA CABΒιβλιοθήκη CD3DB
DB
DB DBC
DBCA DB DBC
DBCA DB DBC
10.对于如图所示的AOE网,求出各活动可能 的最早开始时间和允许的最晚开始时间, 哪些是关键活动?
a1=4
v2
v1
a3=2
a2=3
v3
a5=6 v4
a4=4
解:
顶点 Ve Vl V1 0 0 V2 4 4 V3 6 6 v4 10 10
if(length[i][k]+length[k][j]<length[i][j]) { length[i][j]=length[i][k]+length[k][j];
第7章图习题及参考答案

第7章-图习题及参考答案第7章习题一、单项选择题1.在无向图中定义顶点的度为与它相关联的()的数目。
A. 顶点B. 边C. 权D. 权值2.在无向图中定义顶点v i与v j之间的路径为从v i到达v j的一个()。
A. 顶点序列B. 边序列C. 权值总和D.边的条数3.图的简单路径是指()不重复的路径。
A. 权值B. 顶点C. 边D. 边与顶点均4.设无向图的顶点个数为n,则该图最多有()条边。
A. n-1B. n(n-1)/2C. n(n+1)/2D.n(n-1)5.n个顶点的连通图至少有()条边。
A. n-1B. nC. n+1D. 06.在一个无向图中,所有顶点的度数之和等于所有边数的( ) 倍。
A. 3B. 2C. 1D. 1/27.若采用邻接矩阵法存储一个n个顶点的无向图,则该邻接矩阵是一个( )。
A. 上三角矩阵B. 稀疏矩阵C. 对角矩阵D. 对称矩阵8.图的深度优先搜索类似于树的()次序遍历。
A. 先根B. 中根C. 后根D. 层次9.图的广度优先搜索类似于树的()次序遍历。
A. 先根B. 中根C. 后根D. 层次10.在用Kruskal算法求解带权连通图的最小(代价)生成树时,选择权值最小的边的原则是该边不能在图中构成()。
A. 重边B. 有向环C. 回路D. 权值重复的边11.在用Dijkstra算法求解带权有向图的最短路径问题时,要求图中每条边所带的权值必须是()。
A. 非零B. 非整C. 非负D. 非正12.设G1 = (V1, E1) 和G2 = (V2, E2) 为两个图,如果V1 ⊆ V2,E1 ⊆ E2,则称()。
A. G1是G2的子图B. G2是G1的子图C. G1是G2的连通分量D. G2是G1的连通分量13.有向图的一个顶点的度为该顶点的()。
A. 入度B. 出度C. 入度与出度之和D. (入度﹢出度))/214.一个连通图的生成树是包含图中所有顶点的一个()子图。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
7-11 Casio Merchants and Trust Bank, N.A., has a portfolio of loans and securities expected to generate cash inflows for the bank as follows:Expected Cash Receipts Period in Which Receipts Are Expected$1,385,421 Currentyear746,872 Two yearsfrom today341,555 Three yearsfrom today62,482 Four yearsfrom today9,871 Five yearsfrom todayDeposits and money market borrowings are expected to require the following cash outflows: Expected Cash Payments Period in Which Payments Will be Made$1,427,886 Currentyear831,454 Two yearsfrom today123,897 Three yearsfrom today1,005 Four yearsfrom today----- Five yearsfrom todayIf the discount rate applicable to the previous cash flows is 8 percent, what is the duration of the bank's portfolio of earning assets and of its deposits and money market borrowings? What will happen to the bank's total returns, assuming all other factors are held constant, if interest rates rise? If interest rates fall? Given the size of the duration gap you have calculated, in what type of hedging should Casio engage? Please be specific about the hedging transactions that are needed and their expected effects.Casio has asset duration of:$1,385,421 *1 + $746,872 * 2 + $341,555 * 3 + $62,482 * 4 + $9,871 * 5(1 + 0.08)1(1 + 0.08)2(1 + 0.08)3(1 + 0.08)4(1 +0.08)5D A = $1,385,421 + $746,872 + $341,555 + $62,482 + $9,871(1 + 0.08)1(1 + 0.08)2 (1 + 0.08)3(1 + 0.08)4(1 + 0.08)5= $3, 594, 1481 / $2,246,912 = 1.5996 years Casio has a liability duration of:$1,427,886 * 1 + $831,454 * 2 + $123,897 * 3 + $1,005 * 4(1 + 0.08)1 (1 + 0.08)2 (1 + 0.08)3 (1 + 0.08)4 D L = $1,427,886 + $831,454 + $123,897 + $1,005(1 + 0.08)1 (1 + 0.08)2 (1 + 0.08)3 (1 + 0.08)4= $3,045,808 / $2,134,047 = 1.4272 yearsCasio's Duration Gap = Asset Duration - Liability Duration = 1.5996 - 1.4272 = 0.1724 years.Because Casio's Asset Duration is greater than its Liability Duration, the bank has a positive duration gap, which means that the bank's total returns will decrease if interest rates rise because the value of the liabilities will decline by less than the value of the assets. On the other hand, if interest rates were to fall, this positive duration gap will result in the bank's total returnsincreasing. In this case, the value of the assets will rise by a greater amount than the value of the liabilities.Given the magnitude of the duration gap, the management of Casio Merchants and Trust Bank needs to do a combination of things to close its duration gap between assets and liabilities. It probably needs to try to shorten asset duration, lengthen liability duration, and use financialfutures or options to deal with whatever asset-liability gap exists at the moment. The bank may want to consider securitization or selling some of its assets, reinvesting the cash flows inmaturities that will more closely match its liabilities' maturities. The bank may also consider negotiating some interest-rate swaps to change the cash flow patterns of its liabilities to more closely match its asset maturities.7-12. Given the cash inflow and outflow figures in Problem 11 for Casio Merchants and Trust Bank, suppose interest rates began at a level of 8 percent and then suddenly rose to 9 percent. If the bank has total assets of $125 million and total liabilities of $110 million, by how much would the value of Casio’s net worth change as a result of this movement in interest rates? Suppose on the other hand, that interest rates decline from 8 percent to 7 percent. Whathappens to the value of Casio’s net worth in this case and by how many dollars does it change? What is the size of its duration gap?From Problem #11 we find that Casio's average asset duration is 1.5996 years and average liability duration is 1.4272 years. If total assets are $125 million and total liabilities are $110 million, then Casio has a duration gap of:Duration Gap = 1.5996 – 1.4272 * mill.$125mill. $110 = 1.5996 – 1.2559= 0.3437The change in Casio's net worth would be:Change in Value of Net Worth = [-D A * r)(1r +∆* A] – [- D L * r)(1r +∆* L]If interest rates rise from 8 percent to 9 percent,)]110$*)08.1(01.*4272.1()125$*.08)(1.01*[(-1.5996 Net Worth of Value in the Change +--+= = -1.8514 +1.4536= -.3978 millionIf interest rates fall from 8 percent to 7 percent,Change in NW = ⎥⎦⎤⎢⎣⎡+-⎥⎦⎤⎢⎣⎡+mill. $110x .08)(1(-.01) x 1.4272- $125x .08)(1(-.01) x 1.5996-= + 1.8514 – 1.4536= + 0.3978 million.7-13. Watson Thrift Association reports an average asset duration of 5 years, an average liability duration of 4.25 years. In its latest financial report, the association recorded assets of $1.8 billion and total liabilities of $1.5 billion. If interest rates began at 7 percent and thensuddenly climbed to 9 percent, what change will occur in the value of Watson’s net worth? By how much would Watson’s net worth change if, instead of rising, interest rates fell from 7 percent to 5 percent?The key formula is:Change in net worth = [-D A * ∆r (1r)+* A] - [- D L *Dr (1r)+* L]For the change in interest rates from 7 to 9 percent, Watson's net worth will change to:Change in Net Worth =⎥⎦⎤⎢⎣⎡++⎥⎦⎤⎢⎣⎡++mill. $1500x .07)(1.02)( x years $4.25- -mill. x$1800.07)(1.02)( x years 5-= -$168.22 million + $119.16 million= -$49.06 millionOn the other hand, if interest rates decline from 7 to 5 percent we have:Change in Net Worth =⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡+mill. x$1500.07)(1(-.02) x yrs 4.25--mill. x$1800.07)(1(-.02) x yrs 5-= + $168.22 mill. - $119.l6 mill.= + $49.06 million.7-14. A bank holds a bond in its investment portfolio whose duration is 13.5 years. Its current market price is $1020. While market interest rates are currently at 8 percent for comparable quality securities, a decrease to 7.25 percent is expected in the coming weeks. What changes (in percentage terms) will the bond’s price experience if market interest rates change as anticipated?Solution:percent 9.38or 09375.)08.1()0075.(5.13)1(+=--=+∆-≈∆x i i Dx P PThis bond’s price will increased by 9.38 percent or its price will rise to $1116.7-15. A savings bank’s dollar weighted asset duration is seven years. Its total liabilities amount to $900 million, while its assets total $1 billion. What is the dollar-weighted duration of the bank’s liability portfolio if the bank’s duration gap were zero?Given the bank has a duration gap equal to zero:Duration Gap = AssetsTotal s Liabilitie Total x D - D L Ayears 7.78 $900$1000 x 0) - (7 s Liabilitie T otal Assets T otal x Gap)Duration - (D D A L ===7-16 New Phase National Bank holds assets and liabilities whose average duration and dollar amount are as shown in this table:Asset and Liability ItemsDuration $ AmountInvestment Grade Bonds10 $50 Commercial Loans4 $400 Consumer Loans7 $250 Deposits1.1 $600 Nondeposit Borrowings 0.1 $20What is the weighted average duration of New Phase’s asset portfolio and liability portfolio. What is the leverage-adjusted duration gap?years 5.55.22857.27143.7*7002504*70040010*70050D *W D i i A =++=++==∑years 1.6773 0032.0645.11.*620201.1*620600 D *W D i i L =+=+==∑0144.4700620*6773.15.5TA TL *D D Gap Duration L A =-=-=7-17 A government bond currently carries a yield to maturity of 8 percent and a market price of $1080. If the bond promises to pay $100 in interest annually for five years, what is its current duration?years 20.4)08.1(1100$)08.1(100$)08.1(100$)08.1(100$)08.1(100$)08.1(1100$*5)08.1(100$*4)08.1(100$*3)08.1(100$*2.08)(1$100*1 D 5432154321=++++++++++++++++++=7-18 Dewey National Bank holds $15 million in government bonds having a duration of six years. If interest rates suddenly rise from 6 percent to 7 percent, what percentage change should occur in the bonds’ market price?0566..06)(1.01*-6r)(1r *P P -=+=+∆-=∆D or 5.66 percent。
