小学奥数行程问题-新希望杯
希望杯辅导资料_行程问题

小学四年级“希望杯”数学竞赛辅导讲义——《有趣的行程问题》刘强2009、3有趣的行程问题【探究新知】例1、甲、乙二人分别从相距30千米的两地同时出发相向而行,甲每小时走6千米,乙每小时走4千米,问:二人几小时后相遇?分析与解:出发时甲、乙二人相距30千米,以后两人的距离每小时都缩短6+4=10(千米),即两人的速度的和(简称速度和),所以30千米里有几个10千米就是几小时相遇.30÷(6+4)=30÷10=3(小时)答:3小时后两人相遇.本题是一个典型的相遇问题.在相遇问题中有这样一个基本数量关系:路程=速度和×时间.例2、如右下图有一条长方形跑道,甲从A点出发,乙从C点同时出发,都按顺时针方向奔跑,甲每秒跑5米,乙每秒跑4.5米。
当甲第一次追上乙时,甲跑了多少圈?(第二届希望杯试题)分析与解:这是一道环形路上追及问题。
在追及问题问题中有一个基本关系式:追击路程=速度差×追及时间。
追及路程:10+6=16(米)速度差:5-4.5=0.5(米)追击时间:16÷0.5=32(秒)甲跑了5×32÷[(10+6)×2]=5(圈)答:甲跑了5圈。
例3、一列货车早晨6时从甲地开往乙地,平均每小时行45千米,一列客车从乙地开往甲地,平均每小时比货车快15千米,已知客车比货车迟发2小时,中午12时两车同时经过途中某站,然后仍继续前进,问:当客车到达甲地时,货车离乙地还有多少千米?分析与解:货车每小时行45千米,客车每小时比货车快15千米,所以,客车速度为每小时(45+15)千米;中午12点两车相遇时,货车已行了(12—6)小时,而客车已行(12—6-2)小时,这样就可求出甲、乙两地之间的路程.最后,再来求当客车行完全程到达甲地时,货车离乙地的距离.解:①甲、乙两地之间的距离是:45×(12—6)+(45+15)×(12—6—2)=45×6+60×4=510(千米).②客车行完全程所需的时间是:510÷(45+15)=510÷60=8.5(小时).③客车到甲地时,货车离乙地的距离:510—45×(8.5+2)=510-472.5=37.5(千米).答:客车到甲地时,货车离乙地还有37.5千米.例4、两列火车相向而行,甲车每小时行36千米,乙车每小时行54千米.两车错车时,甲车上一乘客发现:从乙车车头经过他的车窗时开始到乙车车尾经过他的车窗共用了14秒,求乙车的车长?分析与解:首先应统一单位:甲车的速度是每秒钟36000÷3600=10(米),乙车的速度是每秒钟54000÷3600=15(米).本题中,甲车的运动实际上可以看作是甲车乘客以每秒钟10米的速度在运动,乙车的运动则可以看作是乙车车头的运动,因此,我们只需研究下面这样一个运动过程即可:从乙车车头经过甲车乘客的车窗这一时刻起,乙车车头和甲车乘客开始作反向运动14秒,每一秒钟,乙车车头与甲车乘客之间的距离都增大(10+15)米,因此,14秒结束时,车头与乘客之间的距离为(10+15)×14=350(米).又因为甲车乘客最后看到的是乙车车尾,所以,乙车车头与甲车乘客在这段时间内所走的路程之和应恰等于乙车车身的长度,即:乙车车长就等于甲、乙两车在14秒内所走的路程之和.解:(10+15)×14=350(米)答:乙车的车长为350米.例5、某列车通过250米长的隧道用25秒,通过210米长的隧道用23秒,若该列车与另一列长150米.时速为72千米的列车相遇,错车而过需要几秒钟?分析与解:解这类应用题,首先应明确几个概念:列车通过隧道指的是从车头进入隧道算起到车尾离开隧道为止.因此,这个过程中列车所走的路程等于车长加隧道长;两车相遇,错车而过指的是从两个列车的车头相遇算起到他们的车尾分开为止,这个过程实际上是一个以车头的相遇点为起点的相背运动问题,这两个列车在这段时间里所走的路程之和就等于他们的车长之和.因此,错车时间就等于车长之和除以速度之和。
2023江苏省三年级奥数“希望杯”争夺赛竞赛数学试卷含答案
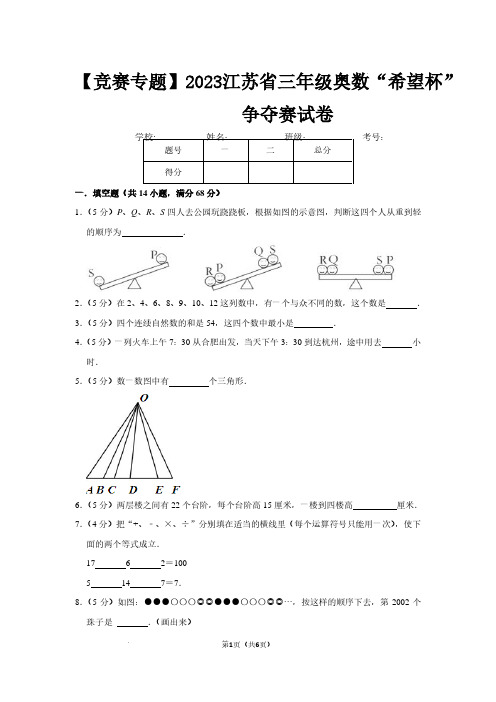
【竞赛专题】2023江苏省三年级奥数“希望杯”争夺赛试卷学校:___________姓名:___________班级:___________考号:___________题号一二总分得分一.填空题(共14小题,满分68分)1.(5分)P、Q、R、S四人去公园玩跷跷板,根据如图的示意图,判断这四个人从重到轻的顺序为.2.(5分)在2、4、6、8、9、10、12这列数中,有一个与众不同的数,这个数是.3.(5分)四个连续自然数的和是54,这四个数中最小是.4.(5分)一列火车上午7:30从合肥出发,当天下午3:30到达杭州,途中用去小时.5.(5分)数一数图中有个三角形.6.(5分)两层楼之间有22个台阶,每个台阶高15厘米,一楼到四楼高厘米.7.(4分)把“+、﹣、×、÷”分别填在适当的横线里(每个运算符号只能用一次),使下面的两个等式成立.1762=1005147=7.8.(5分)如图:●●●〇〇〇◎◎●●●〇〇〇◎◎…,按这样的顺序下去,第2002个珠子是.(画出来)9.(4分)已知:△=〇+2,□=△+△,☆=△+□+5,☆=〇+31问:△=〇=□=☆=.10.(5分)沿海5个省:广东、福建、浙江、江苏和山东,在地图上,隐去省名,用5个字母代替,请五个学生来辨认:甲答:A是福建,B是浙江乙答:C是浙江,D是山东丙答:D是广东,C是福建丁答:A是福建,E是江苏戊答:B是广东,E是江苏老师发现每人说对一个,说错一个,那么五个不同的字母各代表哪个省?A代表省;B代表省;C代表省;D代表省;E代表省.11.(5分)4个人参加乒乓球小组赛,每2个人比赛一场,一共要比赛场.12.(5分)在有余数的除法里,商是6,除数是7,余数是3,被除数是.13.(5分)被减数、减数、差相加得76,被减数是.14.(5分)一桶油连桶共重100千克,倒出半桶油后,连桶共重60千克,这桶油重千克.二.解答题(共4小题,满分32分,每小题8分)15.(8分)有两块一样长的木板,订成一块长1米30厘米的木板,中间订在一起的重叠部分是10厘米,这两块木板每块长多少厘米?16.(8分)有一堆木料,最下面一层是15根,每上一层减少1根,最上面一层是4根,这一堆木料一共有多少根?17.(8分)某炼钢厂在一周内炼了一批钢,前2天平均每天炼钢42吨,后5天平均每天炼钢49吨,这一周平均每天炼钢多少吨?18.(8分)两筐水果共重150千克,第一筐比第二筐多8千克,两筐水果各是多少千克?【竞赛专题】江苏省五年级奥数“希望杯”争夺赛试卷参考答案与试题解析一.填空题(共14小题,满分68分)1.(5分)P、Q、R、S四人去公园玩跷跷板,根据如图的示意图,判断这四个人从重到轻的顺序为R>S>P>Q.【答案】见试题解答内容2.(5分)在2、4、6、8、9、10、12这列数中,有一个与众不同的数,这个数是9.【答案】见试题解答内容3.(5分)四个连续自然数的和是54,这四个数中最小是12.【答案】见试题解答内容4.(5分)一列火车上午7:30从合肥出发,当天下午3:30到达杭州,途中用去8小时.【答案】见试题解答内容5.(5分)数一数图中有15个三角形.【答案】见试题解答内容6.(5分)两层楼之间有22个台阶,每个台阶高15厘米,一楼到四楼高990厘米.【答案】见试题解答内容7.(4分)把“+、﹣、×、÷”分别填在适当的横线里(每个运算符号只能用一次),使下面的两个等式成立.17×6﹣2=1005+14÷7=7.【答案】见试题解答内容8.(5分)如图:●●●〇〇〇◎◎●●●〇〇〇◎◎…,按这样的顺序下去,第2002个珠子是●.(画出来)【答案】见试题解答内容9.(4分)已知:△=〇+2,□=△+△,☆=△+□+5,☆=〇+31问:△=12〇=10□=24☆=41.【答案】见试题解答内容10.(5分)沿海5个省:广东、福建、浙江、江苏和山东,在地图上,隐去省名,用5个字母代替,请五个学生来辨认:甲答:A是福建,B是浙江乙答:C是浙江,D是山东丙答:D是广东,C是福建丁答:A是福建,E是江苏戊答:B是广东,E是江苏老师发现每人说对一个,说错一个,那么五个不同的字母各代表哪个省?A代表广东省;B代表浙江省;C代表福建省;D代表山东省;E代表江苏省.【答案】见试题解答内容11.(5分)4个人参加乒乓球小组赛,每2个人比赛一场,一共要比赛6场.【答案】见试题解答内容12.(5分)在有余数的除法里,商是6,除数是7,余数是3,被除数是45.【答案】见试题解答内容13.(5分)被减数、减数、差相加得76,被减数是38.【答案】见试题解答内容14.(5分)一桶油连桶共重100千克,倒出半桶油后,连桶共重60千克,这桶油重80千克.【答案】见试题解答内容二.解答题(共4小题,满分32分,每小题8分)15.(8分)有两块一样长的木板,订成一块长1米30厘米的木板,中间订在一起的重叠部分是10厘米,这两块木板每块长多少厘米?【答案】见试题解答内容16.(8分)有一堆木料,最下面一层是15根,每上一层减少1根,最上面一层是4根,这一堆木料一共有多少根?【答案】见试题解答内容17.(8分)某炼钢厂在一周内炼了一批钢,前2天平均每天炼钢42吨,后5天平均每天炼钢49吨,这一周平均每天炼钢多少吨?【答案】见试题解答内容18.(8分)两筐水果共重150千克,第一筐比第二筐多8千克,两筐水果各是多少千克?【答案】见试题解答内容。
五年级希望杯培训(四)(行程问题)

相遇与追及1、电气机车和磁悬浮列车各一列,从相距298千米的两地同时出发相向而行,磁悬浮列车的速度比电气机车速度的5倍还快20千米/时,半小时后两车相遇,则电气机车和磁悬浮列车的速度分别为。
2、甲、乙两个电动玩具车同时从轨道的两端相对而行,甲车每秒行5厘米,乙车每秒行1厘米,第二秒行2厘米,第三秒行3厘米……这样的两车相遇时,走的路程相同。
则轨道长厘米。
3、一条环形跑道长400米,甲骑自行车的速度是550米/分,乙跑步的速度是250米/分,若两人同时从同地反向而行,经过分钟两人首次相遇;若两人同时同地同向而行,经过分种两人首次相遇。
4、哥弟俩上学,弟弟先步行,离家16分钟后哥哥骑车追他,速度是弟弟的3倍,哥哥追上弟弟需要分钟。
5、李刚在儿子读书的学校工作。
一天,父子二人同时从家步行去学校,李刚每分钟比儿子多走20米,30分钟后李刚到学校,发现忘了带钥匙,就立即按原路返回。
在离校350米的地方遇上儿子。
则儿子从家到学校走分钟。
6\小明的爸爸开车从甲地到乙地,如果以80千米/时的速度行驶,将于下午2时到达乙地;如果以120千米/时的速度行驶,将于中午12时到达。
如果要求下午1时到达,他应以千米/时的速度行驶。
※7、北京、天津相距140千米,客车和货车同时从北京出发驶向天津。
客车每小时行70千米,货车每小时行50千米,客车到达天津后停留15分钟,又以原速度返回北京。
则两车首次相遇的地点距离北京千米。
(结果保留整数)※8、李经理的司机每天早上7点30分到达李经理家接他去公司。
有一天李经理7点从家里出发去公司,路上遇到从公司按时来接他的车,再乘车去公司,结果比平常早到5分钟。
则李经理乘车的速度是步行速度的倍。
(假设车速、步行速度保持不变,汽车掉头与上下车时间忽略不计)列车过桥问题1、列车通过300米的隧道需要15秒,通过180米长的桥用12秒,列车车身长米。
2、一列火车长240米,速度为60千米/时,一辆越野车的车速为80千米/时,当火车行进时,越野车与火车同向而行,越野车越过列车尾到车头,需要的时间为。
四年级寒假-希望杯复习—行程问题

四年级希望杯复习—行程问题【相遇问题】1.甲、乙两车同时从A 、B 两地出发,相向而行,4 小时后相遇,相遇后所有甲车继续行驶了 3 小时到达B 地,乙车每小时行60 千米,A 、B 两地相距多少千米?2. (走走停停问题)一列客车和一列货车同时从两地相向开出,经过18 小时两车在某处相遇,已知两地相距1488 千米,货车每小时比客车少行8 千米,货车每行驶3 小时要停驶1 小时,客车每小时行多少千米?3.(二次相遇问题)甲、乙两车同时从A、B 两地相向而行,第一次两车在距B地64 千米外相遇,相遇后两车仍以原速度继续行驶,并在到达对方车站后立即沿原路返回,途中两车在距A 地48 千米处第二次相遇,两次相遇后之间相距多少千米?【追及问题】1. 甲乙两车同时从相距30 千米的两地同时出发同向而行,乙车在前,每小时6千米,甲车在后行车,每小时12 千米,甲经过几小时才能追上乙?2.(中途休息问题)甲乙两车同时从A 地出发去B 地,甲车每小时行50 千米,乙车每小时行45 千米,途中甲车停车 3 小时,结果甲车比乙车晚一小时到达 B 地.AB 两地之间的距离几千米?3.(看到问题)乔家大院的长方形围墙,长边长120 米,短边长80 米,有甲、乙两个学生分从围墙的两个对角同时出发,都沿顺时针方向绕围墙行走,已知甲每分钟行100 米,乙每分钟行80 米,问甲看到乙至少要经过多少分钟?4.甲乙两人在相距12 千米的AB 两地同时出发,同向而行.甲步行每小时行4千米,车在后面,每小时速度是甲的3 倍.几小时后乙能追上甲?【练习】1.甲、乙两地相距471 千米,一辆客车和一辆货车同时分别从两地相对开出,经过3 小时相遇.已知客车每小时行82 千米,货车每小时行多少千米?2.客车和货车同时从A、B 两地相向开出,客车每小时行驶60 千米,货车每小时行驶80 千米,两车在距中点15 千米处相遇.求A、B 两地相距多少千米?3.甲乙二人同时同地同向出发,甲每小时骑行15 千米,乙每小时骑行10 千米,甲骑行25 千米后马上返回,甲出发后多少时间与乙相遇?4.甲乙两车相距20 千米,乙车在前,甲车在后,两车同时出发,2 小时后甲车追上乙车,已知乙车每小时行50 千米,甲车每小时行多少千米?5.甲、乙两人绕周长1000 米的环形广场竞走,已知甲每分钟走125 米,乙的速度是甲的2 倍.现在甲在乙后面250 米,乙追上甲需要多少分钟?6.兄妹二人同时离家去同一个学校,哥哥每分钟走80 米,妹妹每分钟走60 米。
名师串讲(行程)
名师串讲:七天搞定2014新希望杯之行程篇考点分析行程问题一直是各大比赛中填空题和解答题的必考问题!分值大,难度高,是大部分学生的薄弱环节,也是丢分较多的题目。
要学好行程问题,需要学生有完整的知识体系和严密的思维,熟知行程问题的分类特性,良好的画图做题习惯,深厚的计算功底以及灵活的应变能力。
对于新希望杯的行程模块的命题有如下特点:1、五年级初赛整体难度偏小,但有时会出现多个答案的情况,一般都可以用画图和方程结合的方式解答;六年级的行程问题相对较难,除了画图之外往往还需要用到比例的知识去解答。
2、比较倾向于将条件蕴含在坐标图中让学生去发现,贴近实际生活,这类问题在近两年的考试和训练题中已多次出现,符合现在的命题趋势。
3、新希望杯考试范围中五六年级的行程考点中这几类出现的十分频繁:流水行船,多人相遇追及,多次相遇追及,环形问题,比例行程,变速变道。
备考时可以重点向这几个知识点倾斜。
精选真题讲解【第8届“新希望杯”全国数学大赛五年级预赛(A 卷)·第7题】邮递员翻山送邮件,上坡用了1.2小时,平均每小时行5千米;下坡用了2小时,平均每小时行8.2千米,全程平均每小时行______千米。
【考点】平均速度 【答案】7【分析】要求平均速度,用总路程除以总时间。
()722.122.82.15=+÷⨯+⨯)((千米/小时)【第9届“新希望杯”全国数学大赛五年级预赛(A 卷)·第12题】五年级 考点 梯形难度 六年级考点题型难度第八届填空题第7题平均速度★解答题第1题 认识坐标图 平均速度 追及问题 ★★解答题第2题 环形问题 变道问题 ★★★★ 第九届解答题第2题多人相遇★★★解答题第2题环形问题 变速问题★★甲、乙从A 地出发,丙从B 地与甲、乙同时出发相向而行,A 、B 两地相距8640米,甲、乙、丙的速度分别为64米/分,56米/分,48米/分。
请问,出发后多长时间会出现其中一人与另外两人等距? 【考点】多人相遇 【答案】72,7177,80,13183,90 【分析】分以下情况讨论: (1)甲在乙、丙中间:7248728640=+÷)((分钟)(2)甲与丙相遇:717748648640=+÷)((分钟)(3)丙在甲、乙中间:8048608640=+÷)((分钟)(4)乙与丙相遇:1318348568640=+÷)((分钟) (5)乙在甲、丙中间:9048488640=+÷)((分钟)【第8届“新希望杯”全国数学大赛六年级预赛(A 卷)·第11题】航天城小学的一部分学生有幸参加了开仓仪式,同学们分成甲、乙两队,甲队先出发,两队均从学校出发去航天城,且从学校到航天城只有一条路,路程为24千米。
希望杯小学五年级数学竞赛《行程问题(一)》专题辅导培训资料导学讲义

行程问题(一)讨论有关物体运动的速度、时间、路程三者关系的应用题叫做行程应用题。
行程问题的主要数量关系是:路程=速度×时间如果用字母s表示路程,t表示时间,v表示速度,那么,上面的数量关系可用字母公式样表示为:s=vt。
行程问题内容丰富多彩、千变万化。
主要有一个物体的运动和两个或几物体的运动两大类。
两个或几个物体的运动又可以分为相遇问题、追及问题两类。
这一讲我们学习一个物体运动的问题的一些简单的相遇问题。
例题与方法例1.小明上学时坐车,回家时步行,在路上一共用了90分。
如果他往返都坐车,全部行程需30分。
如果他往返都步行,需多少分?例2.甲、乙两城相距280千米,一辆汽车原定用8小时从甲城开到乙城。
汽车行驶了一半路程,在中途停留30分。
如果汽车要按原定时间到达乙城,那么,在行驶后半段路程时,应比原来的时速加快多少?例3.一列火车于下午1时30分从甲站开出,每小时行60千米。
1小时后,另一列火车以同样的速度从乙站开出,当天下午6时两车相员。
甲、乙两站相距多少千米?例4.苏步青教授是我国著名的数学家。
一次出国访问,他在电车上碰到了一位外国数学家,这位外国数学家出了一道题目让苏步青做,题目是:甲、乙两人同时从两地出发,相向而行,距离是100千米。
甲每小时行6千米,乙每小时行4千米。
甲带着一只狗,狗每小时行10千米。
这只狗同甲一道出发,碰到乙的时候,它就掉头朝甲这边走,碰到甲时又往乙那边走,直到两人相遇。
这只狗一共走了多少千米?苏步青略加思索,就把正确答案告诉了这位外国数学家。
小朋友们,你能解答这道题吗?例5.甲、乙两辆汽车同时从东、西两地相向开出,甲车每小时行56千米,乙车每小时行48千米,两辆汽车在距中点32千米处相遇。
东、西两地相距多少千米?练习与思考1.小王、小李从相距50千米的两地相向而行,小王下午2时出发步行,每小时行4.5千米。
小李下午3时半骑自行车出发,、经过2.5小时两人相遇。
六年级下册数学试题-小升初数学专题训练——希望杯考前100题精讲(四)行程(无答案,全国通用)

希望杯考前100题精讲(四)行程------希望杯100题行程(1)例题1:(第48题)两只蜗牛由于耐不住阳光的照射,从井口逃向井底。
白天往下爬,两只蜗牛爬行的速度不同,每一个白天一只爬20分米,另一只爬15分米。
黑夜时,又往下滑,两只蜗牛滑行的速度相同。
结果一只蜗牛恰好用5个昼夜到达井底,另一只蜗牛恰好用6个昼夜到达井底,那么,井深_____米。
例题2:(第52题)早晨7点10分,妈妈叫醒小强,让他穿衣准备上学。
可小强看到镜子中的时钟的指针还没有指到起床的时刻。
小强认为当时是____点____分。
例题3:(第60题)甲乙丙三人同时从湖边同一地点出发绕湖行走,甲乙同向,速度分别为每小时5.4千米和4.2千米,丙与他们反向,30分钟后丙与甲第一次相遇,再过5分钟与乙相遇,则绕湖一周的行程是____千米。
例题4:(第61题)从A地到森林公园的路程为3000米。
小兔从A地出发去森林公园,每分钟向前跳36米,每跳3分钟就在原地玩耍,第1次玩耍0.5分钟,以后每次玩耍的时间都要比前一次多0.5分钟。
则小兔从A地到森林公园需要____分钟。
例题5:(第67题)6人在一环形路上散步,从同一点沿同一方向出发,各自速度保持不变。
经过30分钟后,6人均匀分布在环形路线上且速度最快的人未追上速度最慢的人。
当速度最快的人比速度最慢的人多走一圈时,又过了_____分钟。
希望杯考前100题精讲(四)行程------希望杯100题行程(2)例题1:(第68题)某人步行,走平路的速度是4千米/时,走下坡路的速度是6千米/时。
此人经过一段路,其中上坡和下坡的路程相等,平均速度依然是4千米/时,则此人走上坡路的速度是____千米/时。
例题2:(第69题)甲、乙两车分别同时从A、B两地相对开出,几小时后在距中点40千米处相遇。
已知甲车行驶全程用8小时,乙车行驶全程用10小时,则AB两地相距_____千米。
例题3:(第70题)甲乙两人在同一所学校读书,并且住同一栋楼。
小升初数学专题训练——希望杯六年级考前热身—历年真题精讲(三)行程(含答案,全国通用)

希望杯六年级考前热身—历年真题精讲(三)------行程(1)例题1:(07年·六年级1试第9题)甲、乙两车分别从A、B两地同时相向开出,甲车的速度是50千米/时,乙车的速度是40千米/时,当甲车驶过A、B距离的13多50千米时,与乙车相遇。
A、B两地相距____千米。
例题2:(08年·六年级1试第20题)甲、乙两人分别从相距35.8千米的两地出发,相向而行。
甲每小时行4千米,但每行30分钟就休息5分钟;乙每小时行12千米,则经过____小时____分的时候两人相遇。
例题3:(10年·六年级1试第20题)甲、乙两人分别从A、B两地同时出发,相向而行。
出发时他们的速度之比是3:2,相遇后,甲的速度提高20%,乙的速度提高13,这样当甲到达B地时,乙离A地还有41千米,那么A、B两地相距_____千米。
例题4:(11年·六年级1试第20题)小明从家出发去奶奶家,骑自行车每小时行12千米。
他走后2.5小时,爸爸发现小明忘带作业,便骑摩托车以每小时36千米的速度去追。
结果小明到奶奶家后半小时爸爸就到了。
小明家距离奶奶家_____千米。
例题5:(07年·六年级2试第12题)甲乙两车同时从A、B两地相对开出,两车第一次在距A地32千米处相遇。
相遇后两车继续行驶,各自达到B、A两地后,立即沿原路返回,第二次在距A地64千米处相遇,则A、B两地间的距离是______千米。
1、甲车每时行40千米,乙车每时行60千米,甲车从A地、乙车从B地同时出发相向而行,两车相遇后4.5时,甲车到达B地,A,B两地相距多少千米?2、甲、乙同时从A,B两地相向走来。
甲每时走5千米,两人相遇后,乙再走10千米到A地,甲再走1.6时到B地。
乙每时走多少千米?3、一列客车和一列货车同时从两地相向开出,经过18时两车在某处相遇,已知客车每时行50千米,货车每时比客车少行8千米,货车每行驶3时要停驶1时。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
六年级新希望杯模块检测题行程模块基础篇1. 甲乙两列火车同时从相距600千米的两地相对开出,5小时后相距50千米,已知甲车每小时行60千米,乙车每小时行多少千米?2. 在同一条公路上,毛毛和豆豆同向而行,毛毛在豆豆前面若干米。
如果豆豆的速度是60米/分,5分钟后可追上毛毛;如果豆豆的速度是70米/分,3分钟金可追上毛毛。
求毛毛的速度。
3. 客车、货车同时从相距360千米的两地相对开出,4.5小时后相遇。
货车速度比客车速度慢29,客、货两车每小时分别行驶多少千米?4. 如图,有一个圆,两只小虫分别从直径的两端A 与C 同时出发,绕圆周相向而行。
它们第一次相遇在离A 点8厘米处的B 点,第二次相遇在离C 点处6厘米的D 点,问,5. 小李步行前往少年宫,15分钟走了全程的四分之一,估计步行不能准时到达,于是改乘出租车前往,三分钟后共行全程的二分之一。
小李到达少年宫花的时间比一直步行提前了多少分钟?6. 小明从家出发去图书馆,然后回家,根据下面折线统计图回答:①小明在图书馆呆了多长时间?②如果在去图书馆的途中不休息,那么小明几时几分可以到达图书馆?③小明从图书馆回家的速度是多少?距离//小时7.图是一个边长100米的正方形,甲从A点出发,每分钟走70米,乙同时从B点出发,每分钟走85米,两人都按逆时针方向沿着正方形边行进,问:乙在何处首次追上甲?乙第二次追上甲时,距B点多远?8.某船往返于相距180千米的两港之间,顺水而下需用10小时,逆水而上需用15小时。
由于暴雨后水速增加,该船顺水而行只需9小时,那么逆水而行需要几小时?提高篇9.小明从家到学校,前一半路程步行,后一半路程乘车;他从学校回家,前23时间乘车,後13时间步行。
结果去学校比回家多用了10分钟。
已知小明步行60米/分钟,乘车180米/分钟,求小明家到到学校的路程是多少千米?10.某人徒步旅行,去时每走40分钟休息5分钟,到达目的地共花去4小时46分;回来时,他的速度为去时速度的2倍,所以每走30分钟休息10分钟,这样他走回原地要多少时间?11.某天早上8点甲从B地出发,同时乙从A地出发追甲,结果在距离B地9千米的地方追上,如果乙把速度提高一倍而甲的速度不变,或者乙提前40分钟出发,那么都将在距离B地2千米处追上,AB两地相距多少千米,乙的速度是多少?12.甲、乙两人沿400米环形跑道练习跑步,两人同时从跑道的同一地点向相反方向跑去。
相遇后甲比原来速度增加2米/秒,乙比原来速度减少2米/秒,结果都用24秒同时回到原地。
求甲原来的速度。
13.如图所示,甲、乙两人从长为400米的圆形跑道的A点背向出发跑步。
跑道右半部分(粗线部分)道路比较泥泞,所以两人的速度都将减慢,在正常的跑道上甲、乙速度均为每秒8米,而在泥泞道路上两人的速度均为每秒4米。
两人一直跑下去,问:他们第99次迎面相遇的地方距A点还有多少米?14.甲、乙两地相距100千米,张山骑摩托车从甲地出发,1小时后李强驾驶汽车也从甲地出发,二人同时到达乙地。
已知摩托车开始的速度是每小时50千米,中途减为每小时40千米;汽车的速度是每小时80千米,并在途中停留10分钟。
那么,张山骑摩托车在出发多少分钟后减速?15.李华登山,从山脚到途中A点的速度是83千米小时,从A点到山顶的速度是2千米/小时,他到达山顶后立即按原路下山的速度是4千米/小时,下山比上山少用了78小时,已知途中B点到山顶的路程比A点到山顶的路程少500米,且李华从A点开始上山至下山到达B点恰好用了1小时,问从山脚到山顶的路程是多少?16.某人沿公路前进,迎面来了一辆汽车,他问司机:“后面有骑自行车的人吗?”司机回答:“十分钟前我超过了一个骑自行车的人,”这人继续走了十分钟,遇到了这个骑自行车的人,如果自行车的速度是人步行的三倍,问汽车速度是人步行速度的多少倍?超越篇17.甲、乙两人同时从一个正方形小区ABCD一个顶点A同时出发,绕ABCD顺时针同向行走,甲绕一周需84分钟,乙绕一周需100分钟,甲在行走10周的过程中,乙能看见甲的背影多少分钟?18.等边三角形的边长为100米,甲从A点,乙从B点同时出发,按顺时针的方向沿三角形的边前进,每分钟甲行90米,乙行150米,在经过每个顶点时,两人都会因转弯而耽误10秒。
那么乙在出发多少秒后能追上甲?19.文文和强强同时从山脚沿同一条路开始登山,到达山顶后立即原路下山,他们下山的速度是各自上山速度的2倍。
文文到达山顶时,强强距山顶500米;文文回到山脚时,强强刚好下到半山腰。
求山脚到山顶的路程。
20.两条公路成十字交叉,甲从十字路口南1350米处向北直行,乙从十字路口处向东直行,二人同时出发10分钟后,二人距十字路口距离相等;二人仍保持原速继续直行,又过了80分钟,这时二人离十字路口的距离又相等;求甲、乙二人的速度。
六年级新希望杯模块检测题·答案行程模块基础篇1.【答案】50米/秒;70米/秒【分析】 相距可以是还没有相遇,还可以是相遇后相距。
若为还没有相遇,那么两车的路程和是60050550-=千米,那么速度和为5505110÷=米/秒,乙车速度即为1106050-=米/秒;若为相遇后相距,那么两车的路程和是60050650+=千米,那么速度和为6505130÷=米/秒,乙车速度即为1306070-=米/秒。
2. 【答案】45米/分【分析】 设毛毛的速度为x 米/分,有:()()560370x x ⨯-=⨯-,解得45x =米/分。
3. 【答案】45千米/小时;35千米/小时【分析】 根据题意速度和为360 4.580÷=千米/小时,货车速度是客车的79,因此客车速度为7801459⎛⎫÷+= ⎪⎝⎭千米/小时,货车速度为745359⨯=千米/小时。
4. 【答案】36厘米【分析】 第一次相遇,两只小虫共爬行了半个圆周,其中从A 点出发的小虫爬了8厘米,第二次相遇,两只小虫从出发共爬行了1个半圆周,其中从A 点出发的应爬行8324⨯=(厘米),比半个圆周多6厘米,半个圆周长为83618⨯-=(厘米),一个圆周长就是:()836236⨯-⨯=(厘米)。
5. 【答案】36分钟【分析】 因为15分钟走了全程的四分之一,所以走完全程需要115604÷=分钟,每分钟走全程的160。
三分钟汽车行驶了全部的:111244-=,所以,汽车每分钟走全程的:113412÷=,所以,还需要走:11161212⎛⎫-÷= ⎪⎝⎭分钟,一共走了:631524++=分钟。
而若一直步行则要60分钟,所以提前了602436-=分钟。
6. 【答案】12千米/小时【分析】 根据图意,小明在图书馆从2点待到2点半,因此呆了半个小时。
小明用20分钟就走了全程的一半,因此如果不休息那么1点40的时候就可以到达图书馆。
回家的时间是0.5小时,因此速度为60.512÷=千米/小时。
7. 【答案】1333米 【分析】 乙比甲快,第一次追及距离为300米,所用时间为:()300857020÷-=(分钟),此时甲走了70201400⨯=(米),因此首次追上时,甲、乙在C 点。
第二次追距离从C 点开始算是一圈400米,用时为:()24008570263÷-=(分钟),乙走的距离为:222685226633⨯=(米),因此乙第二次追上甲时在A 、B 之间距B 1333米处。
8. 【答案】18小时【分析】 解船在静水中的速度是:()181018015215÷+÷÷=(千米/小时)。
暴雨前水流的速度是:()180101801523÷-÷÷=(千米/小时)。
暴雨后水流的速度是:1809155÷-=(千米/小时)。
暴雨后船逆水而上需用的时间为:()18015518÷-=(小时)。
提高篇9. 【答案】2520米【分析】 设一半路程为x ,则上学时间为160180x x t =+;回家时间为:21060180x x t =+-。
则可得等式:222118060233t t x ⨯⨯+⨯⨯=,代入解得1260x =米。
所以总路程为2520米。
10. 【答案】2小时48分钟【分析】 因为去时每走40分钟就休息5分钟,合45分钟,到达目的地共花去4小时46分,即46046286⨯+=分。
28645616÷=,可见这人去时在路上休息6次,计30分,去时若不休息,则28630256-=分就可走完。
回来时他行走的速度为去时速度的2倍,所以若不休息,则只需2562128÷=分。
现每走30分钟休息10分钟,128中含有4个30,余8。
即要休息4次,计41040⨯=分钟。
所以他走回原地要用12840168+=分钟,即2小时48分钟。
11. 【答案】4.2千米/小时【分析】 如下图所示,画出线段图:乙乙乙设AB 两地相距x 千米,对比第二种和第三种情况,两次甲都走了2千米,即时间相同,两次乙的速度比为2:1,因此乙的路程比为1:2,AC 长2x +千米,那么EC 长112x +千米,EB 长112x -千米。
对比第一种和第三种情况,甲走的路程比为9:2,乙走的路程比也是9:2,AD 长9x +千米,所以EC 长229x +,EB 长29x 千米。
那么有12129x x -=,解之得 3.6x =。
乙40分钟走了全程的79,所以乙的速度为723.6 4.293⨯÷=千米/小时。
12. 【答案】173米/秒 【分析】 因为相遇前后甲,乙的速度和没有改变,如果相遇后两人和跑一圈用24秒,则相遇前两人和跑一圈也用24秒。
以甲为研究对象,甲以原速v 跑了24秒的路程与以2v +跑了24秒的路程之和等于400米,()24242400v v ++=,易得173v =米/秒。
13. 【答案】150米【分析】 本题中,由于甲、乙两人在正常道路和泥泞道路上的速度都相同,可以发现,如果甲、乙各自绕着圆形跑道跑一圈,两人在正常道路和泥泞道路上所用的时间分别相同,那么两人所用的总时间也就相同,所以,两人同时出发,跑一圈后同时回到A 点,即两人在A 点迎面相遇,然后再从A 点出发背向而行,可以发现,两人的行程是周期性的,且以一圈为周期.在第一个周期内,两人同时出发背行而行,所以在回到出发点前肯定有一次迎面相遇,这是两人第一次迎面相遇,然后回到出发点是第二次迎面相遇;然后再出发,又在同一个相遇点第三次相遇,再回到出发点是第四次相遇……可见奇数次相遇点都是途中相遇的地点,偶数次相遇点都是A 点.本题要求的是第99次迎面相遇的地点与A 点的距离,实际上要求的是第一次相遇点与A 点的距离.对于第一次相遇点的位置,需要分段进行考虑:由于在正常道路上的速度较快,所以甲从出发到跑完正常道路时,乙才跑了20084100÷⨯=米,此时两人相距100米,且之间全是泥泞道路,此时两人速度相同,所以再各跑50米可以相遇.所以第一次相遇时乙跑了10050150+=米,这就是第一次相遇点与A 点的距离,也是第99次迎面相遇的地点与A 点的距离.14. 【答案】20分钟【分析】 汽车行驶了:100806075÷⨯=(分);摩托车行驶了:756010145++=(分)设摩托车减速前行驶了x 分,则减速后行驶了()145x -分,列方程为:14550401006060x x -⨯+⨯=,解之得20x =,所以张山骑摩托车出发20分钟后减速。
