第三讲 MATLAB预测(1)回归分析
用MATLAB求解回归分析

估
F值、与F对应的概率p
计
相关系数 r2 越接近 1,说明回归方程越显著;
.
(
缺
省显
时著
为性
0
水 平
05
)
F > F1-α(k,n-k-1)时拒绝 H0,F 越大,说明回归方程越显著;
与 F 对应的概率 p 时拒绝 H0,回归模型成立.
3、画出残差及其置信区间: rcoplot(r,rint)
例1 解:1、输入数据:
stats = 0.9702 40.6656
0.0005
1、回归:
非线性回 归
是事先用m-文件定 义的非线性函数
(1)确定回归系数的命令: [beta,r,J]=nlinfit(x,y,’model’, beta0)
估计出的 回归系数
残差 Jacobian矩阵
输入数据x、y分别为 n m矩阵和n维列向 量,对一元非线性回 归,x为n维列向量。
r2=0.9282, F=180.9531, p=0.0000
p<0.05, 可知回归模型 y=-16.073+0.7194x 成立.
3、残差分析,作残差图: rcoplot(r,rint)
从残差图可以看出,除第二个数据外,其余数据的残
差离零点均较近,且残差的置信区间均包含零点,这说明 回归模型 y=-16.073+0.7194x能较好的符合原始数据,而第 二个数据可视为异常点.
2、预测和预测误差估计:
(1)Y=polyval(p,x)求polyfit所得的回归多项式在 x处 的预测值Y; (2)[Y,DELTA]=polyconf(p,x,S,alpha)求 polyfit所得的回归多项式在x处的预测值Y及预测值的 显著性为 1-alpha的置信区间Y DELTA;alpha缺省时为0.5
matlab回归分析

2019/9/8
返回
13
四、可线性化的一元非线性回归 (曲线回归)
例2 出钢时所用的盛钢水的钢包,由于钢水对耐火材料的侵蚀, 容积不断增大.我们希望知道使用次数与增大的容积之间的关 系.对一钢包作试验,测得的数据列于下表:
使用次数
解 得 估 计 值 ˆ X T X 1 X T Y注 意 : ˆ 服 从 p + 1 维 正 态 分
得 到 的 ˆ i代 入 回 归 平 面 方 程 得 :
y ˆ 0 ˆ 1 x 1 . . ˆ k x k .
布 , 且 为 的 无 偏 估
计 , 协 方 差 阵 为 2 C .
y 的 置 信 水 平 为 1 的 预 测 区 间 近 似 为
y ˆ ˆ e u 1 2 , y ˆ ˆ e u 1 2
2019/9/8
12
(2)控制
要 求 : y 0 1 x 的 值 以 1 的 概 率 落 在 指 定 区 间 y , y
yi ˆ0 ˆ1xi
2
n
(yi yˆi )2
i1
i1
称 Qe 为残差平方和或剩余平方和.
2 的无偏估计为
ˆ
2 e
Qe
(n 2)
称ˆ
2 e
为剩余方差(残差的方差), ˆ
2 e
分别与ˆ0 、ˆ1
独立 。
ˆe 称为剩余标准差.
2019/9/8
返回
7
三、检验、预测与控制
y 0 的 置 信 水 平 为 1 的 预 测 区 间 为
MATLAB回归分析工具箱使用方法

MATLAB回归分析工具箱使用方法1.数据准备在使用回归分析工具箱进行分析之前,首先需要准备好要使用的数据集。
数据集通常包含自变量和因变量,自变量是预测因变量的变量。
将数据集导入MATLAB中,并确保数据格式正确,可以使用MATLAB内置的导入工具或手动输入数据。
2.回归模型的选择在进行回归分析之前,需要选择适当的回归模型。
回归模型决定了如何拟合数据和生成预测。
常见的回归模型包括线性回归、多项式回归、逻辑回归等。
根据数据的特征和目的选择合适的回归模型。
3.拟合数据选择适当的回归模型后,可以使用回归分析工具箱中的函数来拟合数据。
常用的函数包括“fitlm”(线性回归)、“fitpoly”(多项式回归)、“fitglm”(逻辑回归)等。
将自变量和因变量传入对应的函数中,并得到拟合的模型。
例如,对于线性回归可以使用以下代码进行拟合:```mdl = fitlm(X,Y,'linear');```其中,X为自变量数据,Y为因变量数据,'linear'表示选择线性回归模型。
4.模型评估在拟合数据后,需要对模型进行评估以确定其拟合程度和预测性能。
可以使用回归分析工具箱中的函数来评估模型,如“plotResiduals”(绘制残差图)、“predict”(预测值)、“coefTest”(参数显著性检验)等。
通过观察残差图、计算R²值、进行参数显著性检验等方法,评估模型的拟合效果。
5.预测拟合好模型后,可以使用该模型进行预测未来的趋势。
使用“predict”函数可以生成预测值,并与实际值进行比较以评估模型的预测能力。
例如```Ypred = predict(mdl,Xnew);```其中,Xnew为新的自变量数据,Ypred为预测的因变量值。
6.结果可视化最后,可以使用MATLAB中的绘图工具来可视化回归分析的结果。
可以绘制拟合曲线、残差图、预测结果等,以便更直观地理解数据和模型。
用MATLAB求解回归分析讲解共28页文档

谢谢你的阅读
❖ 知识就是财富 ❖ 丰富你的人生
71、既然我已经踏上这条道路,那么,任何东西都不应妨碍我沿着这条路走下去。——康德 72、家庭ห้องสมุดไป่ตู้为快乐的种子在外也不致成为障碍物但在旅行之际却是夜间的伴侣。——西塞罗 73、坚持意志伟大的事业需要始终不渝的精神。——伏尔泰 74、路漫漫其修道远,吾将上下而求索。——屈原 75、内外相应,言行相称。——韩非
用MATLAB求解回归分析讲 解
31、别人笑我太疯癫,我笑他人看不 穿。(名 言网) 32、我不想听失意者的哭泣,抱怨者 的牢骚 ,这是 羊群中 的瘟疫 ,我不 能被它 传染。 我要尽 量避免 绝望, 辛勤耕 耘,忍 受苦楚 。我一 试再试 ,争取 每天的 成功, 避免以 失败收 常在别 人停滞 不前时 ,我继 续拼搏 。
33、如果惧怕前面跌宕的山岩,生命 就永远 只能是 死水一 潭。 34、当你眼泪忍不住要流出来的时候 ,睁大 眼睛, 千万别 眨眼!你会看到 世界由 清晰变 模糊的 全过程 ,心会 在你泪 水落下 的那一 刻变得 清澈明 晰。盐 。注定 要融化 的,也 许是用 眼泪的 方式。
35、不要以为自己成功一次就可以了 ,也不 要以为 过去的 光荣可 以被永 远肯定 。
利用Matlab进行线性回归分析

利用Matlab进行线性回归分析回归分析是处理两个及两个以上变量间线性依存关系的统计方法;可以通过软件Matlab实现;1.利用Matlab软件实现在Matlab中,可以直接调用命令实现回归分析,1b,bint,r,rint,stats=regressy,x,其中b是回归方程中的参数估计值,bint是b的置信区间,r和rint分别表示残差及残差对应的置信区间;stats 包含三个数字,分别是相关系数,F统计量及对应的概率p值;2recplotr,rint作残差分析图;3rstoolx,y一种交互式方式的句柄命令;以下通过具体的例子来说明;例现有多个样本的因变量和自变量的数据,下面我们利用Matlab,通过回归分析建立两者之间的回归方程;% 一元回归分析x=1097 1284 1502 1394 1303 1555 1917 2051 2111 2286 2311 2003 2435 2625 2948 3, 55 3372;%自变量序列数据y=698 872 988 807 738 1025 1316 1539 1561 1765 1762 1960 1902 2013 2446 2736 2825;%因变量序列数据X=onessizex',x',pauseb,bint,r,rint,stats=regressy',X,,pause%调用一元回归分析函数rcoplotr,rint%画出在置信度区间下误差分布;% 多元回归分析% 输入各种自变量数据x1= 8 3 3 8 9 4 5 6 5 8 6 4 7';x2=31 55 67 50 38 71 30 56 42 73 60 44 50 39 55 7040 50 62 59'; x3=10 8 12 7 8 12 12 5 8 5 11 12 6 10 10 6 11 11 9 9';x4=8 6 9 16 15 17 8 10 4 16 7 12 6 4 4 14 6 8 13 11';%输入因变量数据y= 160 155 195';X=onessizex1,x1,x2,x3,x4;b,bint,r,rint,stats=regressy,X%回归分析Q=r'rsigma=Q/18rcoplotr,rint;%逐步回归X1=x1,x2,x3,x4;stepwiseX1,y,1,2,3%逐步回归% X2=onessizex1,x2,x3;% X3=onessizex1,x1,x2,x3;% X4=onessizex1,x2,x3,x4;% b1,b1int,r1,r1int,stats1=regressy,X2% b2,b2int,r2,r2int,stats2=regressy,X3;% b3,b3int,r3,r3int,stats3=regressy,X4;。
利用MATLAB进行回归分析
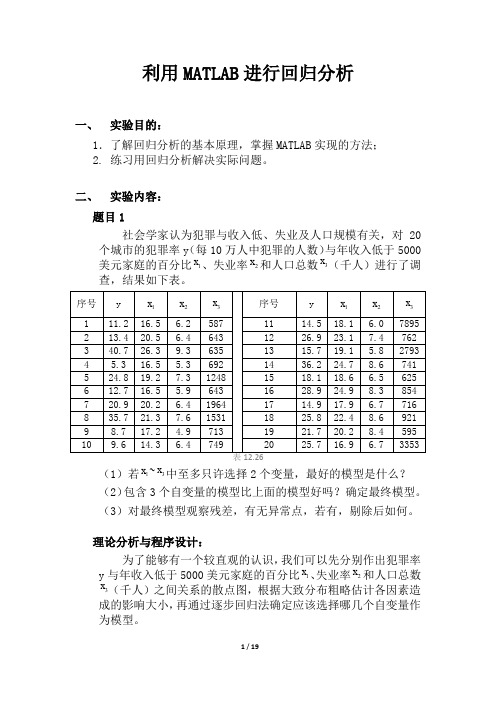
利用MATLAB进行回归分析一、实验目的:1.了解回归分析的基本原理,掌握MATLAB实现的方法;2. 练习用回归分析解决实际问题。
二、实验内容:题目1社会学家认为犯罪与收入低、失业及人口规模有关,对20个城市的犯罪率y(每10万人中犯罪的人数)与年收入低于5000美元家庭的百分比1x、失业率2x和人口总数3x(千人)进行了调查,结果如下表。
(1)若1x~3x中至多只许选择2个变量,最好的模型是什么?(2)包含3个自变量的模型比上面的模型好吗?确定最终模型。
(3)对最终模型观察残差,有无异常点,若有,剔除后如何。
理论分析与程序设计:为了能够有一个较直观的认识,我们可以先分别作出犯罪率y与年收入低于5000美元家庭的百分比1x、失业率2x和人口总数x(千人)之间关系的散点图,根据大致分布粗略估计各因素造3成的影响大小,再通过逐步回归法确定应该选择哪几个自变量作为模型。
编写程序如下:clc;clear all;y=[11.2 13.4 40.7 5.3 24.8 12.7 20.9 35.7 8.7 9.6 14.5 26.9 15.736.2 18.1 28.9 14.9 25.8 21.7 25.7];%犯罪率(人/十万人)x1=[16.5 20.5 26.3 16.5 19.2 16.5 20.2 21.3 17.2 14.3 18.1 23.1 19.124.7 18.6 24.9 17.9 22.4 20.2 16.9];%低收入家庭百分比x2=[6.2 6.4 9.3 5.3 7.3 5.9 6.4 7.6 4.9 6.4 6.0 7.4 5.8 8.6 6.5 8.36.7 8.6 8.4 6.7];%失业率x3=[587 643 635 692 1248 643 1964 1531 713 749 7895 762 2793 741 625 854 716 921 595 3353];%总人口数(千人)figure(1),plot(x1,y,'*');figure(2),plot(x2,y,'*');figure(3),plot(x3,y,'*');X1=[x1',x2',x3'];stepwise(X1,y)运行结果与结论:犯罪率与低收入散点图犯罪率与失业率散点图犯罪率与人口总数散点图低收入与失业率作为自变量低收入与人口总数作为自变量失业率与人口总数作为自变量在图中可以明显看出前两图的线性程度很好,而第三个图的线性程度较差,从这个角度来说我们应该以失业率和低收入为自变量建立模型。
第三讲 MATLAB预测(1)回归分析
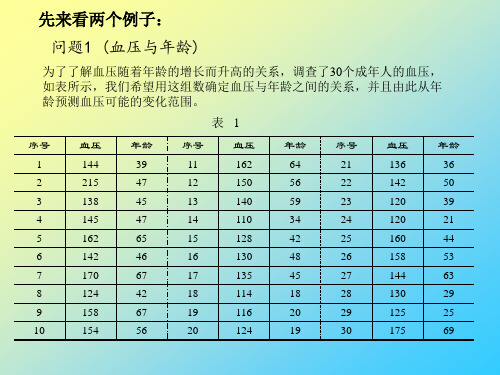
ˆ 489.2946 s t 2 65.8896 t 9.1329
方法二
化为多元线性回归:
t=1/30:1/30:14/30;
s=[11.86 15.67 20.60 26.69 33.71 41.93 51.13 61.49 72.90 85.44 99.08 113.77 129.54 146.48];
3
1
模型:记血压为 y ,年龄为 x1 ,体重指数为 x2 ,吸烟习惯为 x3 , 用Matlab将 y 与 x2 的数据做散点图,看出大致也呈线性关系,建立 模型: y 0 1 x1 2 x2 3 x3 由数据估计系数 0,2,3,4 ,也可看做曲面拟合(其实为 超平面)
T=[ones(14,1) t‘ (t.^2)'];
[b,bint,r,rint,stats]=regress(s',T); b,stats
得回归模型为 :
ˆ 9.1329 65.8896 s t 489.2946 t2
预测及作图
Y=polyconf(p,t,S) plot(t,s,'k+',t,Y,'r')
(二)多元二项式回归
命令:rstool(x,y,’model’, alpha)
nm矩阵
n维列向量
显著性水平
(缺省时为0.05)
由下列 4 个模型中选择 1 个(用字符串输入,缺省时为线性模型): linear(线性): y 0 1 x1 m xm purequadratic(纯二次): interaction(交叉): y
其中 x=(x1,x2,„,xn) ,y=(y1,y2 ,„,yn) ; m m-1 p=(a1,a2,„,am+1)是多项式 y=a1x +a2x +„+amx+am+1 的系数;S 是一个矩阵,用来估计预测误差.
利用 Matlab作回归分析

利用 Matlab 作回归分析一元线性回归模型:2,(0,)y x N αβεεσ=++求得经验回归方程:ˆˆˆyx αβ=+ 统计量: 总偏差平方和:21()n i i SST y y ==-∑,其自由度为1T f n =-; 回归平方和:21ˆ()n i i SSR y y ==-∑,其自由度为1R f =; 残差平方和:21ˆ()n i i i SSE y y ==-∑,其自由度为2E f n =-;它们之间有关系:SST=SSR+SSE 。
一元回归分析的相关数学理论可以参见《概率论与数理统计教程》,下面仅以示例说明如何利用Matlab 作回归分析。
【例1】为了了解百货商店销售额x 与流通费率(反映商业活动的一个质量指标,指每元商品流转额所分摊的流通费用)y 之间的关系,收集了九个商店的有关数据,见下表1.试建立流通费率y 与销售额x 的回归方程。
表1 销售额与流通费率数据【分析】:首先绘制散点图以直观地选择拟合曲线,这项工作可结合相关专业领域的知识和经验进行,有时可能需要多种尝试。
选定目标函数后进行线性化变换,针对变换后的线性目标函数进行回归建模与评价,然后还原为非线性回归方程。
【Matlab数据处理】:【Step1】:绘制散点图以直观地选择拟合曲线x=[1.5 4.5 7.5 10.5 13.5 16.5 19.5 22.5 25.5];y=[7.0 4.8 3.6 3.1 2.7 2.5 2.4 2.3 2.2];plot(x,y,'-o')输出图形见图1。
510152025图1 销售额与流通费率数据散点图根据图1,初步判断应以幂函数曲线为拟合目标,即选择非线性回归模型,目标函数为:(0)b y ax b =< 其线性化变换公式为:ln ,ln v y u x == 线性函数为:ln v a bu =+【Step2】:线性化变换即线性回归建模(若选择为非线性模型)与模型评价% 线性化变换u=log(x)';v=log(y)';% 构造资本论观测值矩阵mu=[ones(length(u),1) u];alpha=0.05;% 线性回归计算[b,bint,r,rint,states]=regress(v,mu,alpha)输出结果:b =[ 2.1421; -0.4259]表示线性回归模型ln=+中:lna=2.1421,b=-0.4259;v a bu即拟合的线性回归模型为=-;y x2.14210.4259bint =[ 2.0614 2.2228; -0.4583 -0.3934]表示拟合系数lna和b的100(1-alpha)%的置信区间分别为:[2.0614 2.2228]和[-0.4583 -0.3934];r =[ -0.0235 0.0671 -0.0030 -0.0093 -0.0404 -0.0319 -0.0016 0.0168 0.0257]表示模型拟合残差向量;rint =[ -0.0700 0.02300.0202 0.1140-0.0873 0.0813-0.0939 0.0754-0.1154 0.0347-0.1095 0.0457-0.0837 0.0805-0.0621 0.0958-0.0493 0.1007]表示模型拟合残差的100(1-alpha)%的置信区间;states =[0.9928 963.5572 0.0000 0.0012] 表示包含20.9928SSR R SST==、 方差分析的F 统计量/963.5572//(2)R E SSR f SSR F SSE f SSE n ===-、 方差分析的显著性概率((1,2))0p P F n F =->≈; 模型方差的估计值2ˆ0.00122SSE n σ==-。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
方法一
直接作二次多项式回归: t=1/30:1/30:14/30;
s=[11.86 15.67 20.60 26.69 33.71 41.93 51.13 61.49 72.90
85.44 99.08 113.77 129.54 146.48]; [p,S]=polyfit(t,s,2) 得回归模型为 :
ˆ 0 u s, y ˆ0 u s] ,可以得到其置信度为0.95 根据预测区间 [ y 1 1
2 2
的置信区间为:[125.7887,163.2708].
10
同样方法做问题二 第一次做多元回归结果: 回归系数 回归系数估计值 45.3636 0.3604 回归系数置信区间 [3.5537 87.1736] [-0.0758 0.7965]
0 1 2
3.0906
11.8246
[1.0530 5.1281]
[-0.1482 23.7973]
3
R2=0.6855
F=18.8906 p<0.0001 s2=169.7917
通过残差分析图可以得到第2个点和第10个点为异常点,删除后重 新进行回归分析,可以得到下面表:
11
回归系数
回归系数估计值
9
剔除第二个点后得到的结果: 回归系数 回归系数估计值
96.8665 0.9533 F=66.8358
回归系数置信区间
[85.4771, 108.2559] [0.7140, 1.1925]
0 1
R2=0.7123
p<0.0001 s2=91.4305
对50岁的人血压进行预测,得到结果为: ˆ ˆ x 96.8665 0.9533 x 144.5298 ˆ0 y 0 1 0 0
表 2
序号 血压 年龄 1 2 3 4 5 6 7 8 9 10 144 215 138 145 162 142 170 124 158 154 39 47 45 47 65 46 67 42 67 56 体重 吸烟 体重 吸烟 体重 吸烟 序号 血压 年龄 序号 血压 年龄 指数 习惯 指数 习惯 指数 习惯 24.2 0 11 162 64 28.0 1 21 136 36 25.0 0 31.1 22.6 24.0 25.9 25.1 29.5 19.7 27.2 19.3 1 0 1 1 0 1 0 1 0 12 13 14 15 16 17 18 19 20 150 140 110 128 130 135 114 116 124 56 59 34 42 48 45 18 20 19 25.8 27.3 20.1 21.7 22.2 27.4 18.8 22.6 21.5 0 0 0 0 1 0 0 0 0 22 23 24 25 26 27 28 29 30 142 120 120 160 158 144 130 125 175 50 39 21 44 53 63 29 25 69 26.2 23.5 20.3 27.1 28.6 28.3 22.0 25.3 27.4 1 0 0 1 1 0 1 0
先来看两个例子:
问题1 (血压与年龄)
为了了解血压随着年龄的增长而升高的关系,调查了30个成年人的血压, 如表所示,我们希望用这组数确定血压与年龄之间的关系,并且由此从年 龄预测血压可能的变化范围。 表 1
序号 1 2 3 4 5 6 7 8 9 10 血压 144 215 138 145 162 142 170 124 158 154 年龄 39 47 45 47 65 46 67 42 67 56 序号 11 12 13 14 15 16 17 18 19 20 血压 162 150 140 110 128 130 135 114 116 124 年龄 64 56 59 34 42 48 45 18 20 19 序号 21 22 23 24 25 26 27 28 29 30 血压 136 142 120 120 160 158 144 130 125 175 年龄 36 50 39 21 44 53 63 29 25 69
4
第三讲 MATLAB预测方法(1)回归分析
多元线性回归
y 0 1 x1 ... p x p
1、确定回归系数的点估计值:
b=regress( Y, X )
Y1 Y Y 2 ... Yn
ˆ 0 ˆ 1 b ... ˆ p
%已知的因变量数组
%已知的自变量数组 %已知的数据容量 %1与自变量组成的输入矩阵 %回归分析程序(显著性水平为0.05) %输出回归系数及其置信区间和统计量 %残差及其置信区间作图
输出结果为: b= 98.4084 0.9732 bint = s= 0.4540 23.2834 0.0000 273.7137
模型:记血压为y,年龄为x,可以做出如上图所示的散点图,从图形 上直观的可以看出,y与x大致呈线性关系,即有:
y 0 1 x ˆ , ˆ 。 需要由数据确定系数 0 , 1 的估计值 0 1
此函数为一元线性函数!!
2
问题2 (血压与年龄,体重指数,吸烟习惯)
世界卫生组织颁布的“体重指数”的定义是体重(kg)除以身高(m)的平 方,下表给出了30个人的体重指数等数据,其中,0表示不吸烟,1表示吸 烟,怎么考虑吸烟这个因素,此因素对于血压升高有影响吗,并对体重指 数为25,50岁的吸烟者的血压做出预测。
78.7484 118.0683
0.5601 1.3864
7
结果整理为下表: 回归系数 回归系数估计值
98.4084 0.9732 F=23.2834
回归系数置信区间
[74.7484, 118.0683] [0.5601 1.3864]
0 1
R2=0.4540
p<0.001 s2=273.7137
回 归 系 数 的 区 间 估 计 残 差 置 信 区 间 用于检验回归模型的统计量, 有三个数值:R2、F值、与F 对应的概率p、以及残差的方 差的估计值
R2 越接近 1,说明回归方程越显著;
( 缺 省显 时著 为性 水 平 )
F F1 (k , n k 1) 时,F 越大,说明回归方程越显著;
1 x11 1 x 21 X ... ... 1 x n1
x12 x 22 ... xn2
... x1 p ... x 2 p ... ... ... x np
对一元线性回归,取 p=1 即可
2、求回归系数的点估计和区间估计、并检验回归模型: [b, bint,r,rint,stats]=regress(Y,X,alpha)
3
1
模型:记血压为 y ,年龄为 x1 ,体重指数为 x2 ,吸烟习惯为 x3 , 用Matlab将 y 与 x2 的数据做散点图,看出大致也呈线性关系,建立 模型: y 0 1 x1 2 x2 3 x3 由数据估计系数 0,2,3,4 ,也可看做曲面拟合(其实为 超平面)
(二)多元二项式回归
命令:rstool(x,y,’model’, alpha)
nm矩阵
n维列向量
显著性水平
(缺省时为0.05)
由下列 4 个模型中选择 1 个(用字符串输入,缺省时为线性模型): linear(线性): y 0 1 x1 m xm purequadratic(纯二次): interaction(交叉): y
用上面的参数通过计算可以得到: 50岁,体重指数为25,吸烟的人的血压预测为:148.9525 置信度为0.95的置信区间为:[134.5951,163.3099]
12
多项式回归 (一)一元多项式回归 1、回归: y=a1xm+a2xm-1+…+amx+am+1
(1)确定多项式系数的命令:[p,S]=polyfit(x,y,m)
与 F 对应的概率 p 时回归模型成立,否则,则说明回归方程中 有多余的自变量,可以将这些多余的自变量从回归方程中剔除
0.05
3、画出残差及其置信区间:
rcoplot(r,rint)
6
问题1的求解:
y=[„„];
x=[„„]; n=„„; X=[ones(n,1),x’]; [b,bint,r,rint,s]=regress(y’,X); b, bint, s, rcoplot(r,rint)
从以下几点可以看出模型是有效的:参数的置信区间不含0 点;p小于显著性水平;用Matlab可以求出F1-α(1,n-2)=4.1960,显 然小于F值。 但是由于β1的置信区间过长,R2较小,说明模型的精度不 高!
8
残差图如图所示:
图中第二个点的残差置信区间中不包含0点,由于残差服从均值为0的正 态分布,因此可以认为这个点为异常数据,偏离数据整体的变化范围, 应该剔除,重新进行回归分析!! 残差与残差区间杠杆图,最好在0点线附近比较均匀的分布,而不呈现一 定的规律性,如果是这样,就说明回归分析做得比较理想。
T=[ones(14,1) t‘ (t.^2)'];
[b,bint,r,rint,stats]=regress(s',T); b,stats
得回归模型为 :
ˆ 9.1329 65.8896 s t 489.2946 t2
预测及作图
Y=polyconf(p,t,S) plot(t,s,'k+',t,Y,'r')
ˆ 489.2946 s t 2 65.8896 t 9.1329
方法二
化为多元线性回归:
t=1/30:1/30:14/30;
s=[11.86 15.67 20.60 26.69 33.71 41.93 51.13 61.49 72.90 85.44 99.08 113.77 129.54 146.48];
