matlab中回归分析实例分析
用MATLAB求解回归分析

估
F值、与F对应的概率p
计
相关系数 r2 越接近 1,说明回归方程越显著;
.
(
缺
省显
时著
为性
0
水 平
05
)
F > F1-α(k,n-k-1)时拒绝 H0,F 越大,说明回归方程越显著;
与 F 对应的概率 p 时拒绝 H0,回归模型成立.
3、画出残差及其置信区间: rcoplot(r,rint)
例1 解:1、输入数据:
stats = 0.9702 40.6656
0.0005
1、回归:
非线性回 归
是事先用m-文件定 义的非线性函数
(1)确定回归系数的命令: [beta,r,J]=nlinfit(x,y,’model’, beta0)
估计出的 回归系数
残差 Jacobian矩阵
输入数据x、y分别为 n m矩阵和n维列向 量,对一元非线性回 归,x为n维列向量。
r2=0.9282, F=180.9531, p=0.0000
p<0.05, 可知回归模型 y=-16.073+0.7194x 成立.
3、残差分析,作残差图: rcoplot(r,rint)
从残差图可以看出,除第二个数据外,其余数据的残
差离零点均较近,且残差的置信区间均包含零点,这说明 回归模型 y=-16.073+0.7194x能较好的符合原始数据,而第 二个数据可视为异常点.
2、预测和预测误差估计:
(1)Y=polyval(p,x)求polyfit所得的回归多项式在 x处 的预测值Y; (2)[Y,DELTA]=polyconf(p,x,S,alpha)求 polyfit所得的回归多项式在x处的预测值Y及预测值的 显著性为 1-alpha的置信区间Y DELTA;alpha缺省时为0.5
matlab多个因变量回归

matlab多个因变量回归Matlab是一种强大的科学计算软件,可以用于多个因变量回归分析。
多个因变量回归分析是一种统计方法,用于探究多个自变量对多个因变量的影响关系。
在本文中,将介绍如何使用Matlab进行多个因变量回归分析,并解释结果的含义。
我们需要准备一组数据,包括多个自变量和多个因变量。
假设我们想要研究一辆汽车的油耗情况,可能的自变量包括车速、引擎排量、重量等,而因变量则是油耗量和二氧化碳排放量。
在Matlab中,可以使用regress函数进行多个因变量回归分析。
该函数的语法如下:```[b,bint,r,rint,stats] = regress(y,X)```其中,y是因变量矩阵,每一列代表一个因变量;X是自变量矩阵,每一列代表一个自变量。
函数的输出包括回归系数b、回归系数的置信区间bint、残差r、残差的置信区间rint以及回归统计信息stats。
接下来,我们将使用一个具体的例子来说明多个因变量回归分析在Matlab中的应用。
假设我们有一组数据,包括100辆汽车的车速、引擎排量、重量以及油耗量和二氧化碳排放量。
我们的目标是探究车速、引擎排量和重量对油耗量和二氧化碳排放量的影响。
我们需要加载数据并将自变量和因变量分别存储在矩阵X和矩阵y 中。
假设数据存储在一个名为"car_data.csv"的文件中,我们可以使用readmatrix函数来读取数据:```data = readmatrix('car_data.csv');X = data(:, 1:3); % 车速、引擎排量、重量y = data(:, 4:5); % 油耗量和二氧化碳排放量```接下来,我们可以使用regress函数进行多个因变量回归分析,并获取回归系数、残差等信息:```[b,bint,r,rint,stats] = regress(y, X);```回归系数b代表了自变量对因变量的影响程度。
matlab回归分析一例
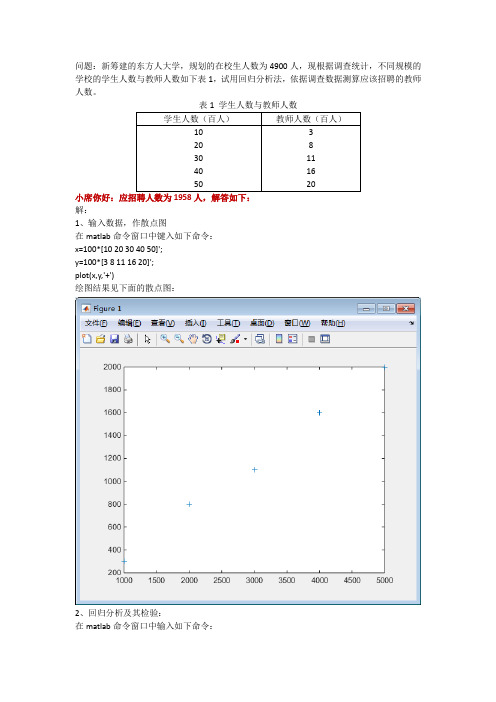
问题:新筹建的东方人大学,规划的在校生人数为4900人,现根据调查统计,不同规模的学校的学生人数与教师人数如下表1,试用回归分析法,依据调查数据测算应该招聘的教师人数。
表1 学生人数与教师人数小席你好:应招聘人数为1958人,解答如下:解:1、输入数据,作散点图在matlab命令窗口中键入如下命令:x=100*[10 20 30 40 50]';y=100*[3 8 11 16 20]';plot(x,y,'+')绘图结果见下面的散点图:2、回归分析及其检验:在matlab命令窗口中输入如下命令:X=[ ones(5,1) x];Y=y;[b,bint,r,rint,stats]=regress(Y ,X);b,bint,stats运行结果为:b =-100.00000.4200bint =-272.3621 72.36210.3680 0.4720stats =1.0e+03 *0.0010 0.6615 0.0000 2.6667即42.0ˆ,100ˆ10=-=ββ;0ˆβ的置信区间为[-272.3621,72.3621], 1ˆβ的置信区间为[0.3680,0.4720]; r 2=1, F=661.5, p=0.0000p<0.05, 可知回归模型 y=-100+0.42x 成立.3、残差分析,作残差图在matlab 命令窗口中键入如下命令:rcoplot(r,rint)残差图如下:从残差图可以看出,所有数据的残差离零点均较近,且残差的置信区间均包含零点,这说明回归模型y=-100+0.42x能较好地符合原始数据.4、预测及作图:z=b(1)+b(2)*xplot(x,Y,'k+',x,z,'r')上图再次直观地说明回归模型y=-100+0.42x能较好地符合原始数据.5、测算应该招聘的教师人数在matlab窗口中键入如下命令:zprs=b(1)+b(2)*4900运行结果为:zprs =1.9580e+03即应招聘人数为1958人.。
利用Matlab进行线性回归分析

利用Matlab进行线性回归分析回归分析是处理两个及两个以上变量间线性依存关系的统计方法;可以通过软件Matlab实现;1.利用Matlab软件实现在Matlab中,可以直接调用命令实现回归分析,1b,bint,r,rint,stats=regressy,x,其中b是回归方程中的参数估计值,bint是b的置信区间,r和rint分别表示残差及残差对应的置信区间;stats 包含三个数字,分别是相关系数,F统计量及对应的概率p值;2recplotr,rint作残差分析图;3rstoolx,y一种交互式方式的句柄命令;以下通过具体的例子来说明;例现有多个样本的因变量和自变量的数据,下面我们利用Matlab,通过回归分析建立两者之间的回归方程;% 一元回归分析x=1097 1284 1502 1394 1303 1555 1917 2051 2111 2286 2311 2003 2435 2625 2948 3, 55 3372;%自变量序列数据y=698 872 988 807 738 1025 1316 1539 1561 1765 1762 1960 1902 2013 2446 2736 2825;%因变量序列数据X=onessizex',x',pauseb,bint,r,rint,stats=regressy',X,,pause%调用一元回归分析函数rcoplotr,rint%画出在置信度区间下误差分布;% 多元回归分析% 输入各种自变量数据x1= 8 3 3 8 9 4 5 6 5 8 6 4 7';x2=31 55 67 50 38 71 30 56 42 73 60 44 50 39 55 7040 50 62 59'; x3=10 8 12 7 8 12 12 5 8 5 11 12 6 10 10 6 11 11 9 9';x4=8 6 9 16 15 17 8 10 4 16 7 12 6 4 4 14 6 8 13 11';%输入因变量数据y= 160 155 195';X=onessizex1,x1,x2,x3,x4;b,bint,r,rint,stats=regressy,X%回归分析Q=r'rsigma=Q/18rcoplotr,rint;%逐步回归X1=x1,x2,x3,x4;stepwiseX1,y,1,2,3%逐步回归% X2=onessizex1,x2,x3;% X3=onessizex1,x1,x2,x3;% X4=onessizex1,x2,x3,x4;% b1,b1int,r1,r1int,stats1=regressy,X2% b2,b2int,r2,r2int,stats2=regressy,X3;% b3,b3int,r3,r3int,stats3=regressy,X4;。
matlab中回归分析实例分析

1.研究科研人员的年工资与他的论文质量、工作年限、获得资助指标之间的关系.24位科研人员的调查数据(ex81.txt):设误差ε~(0,σ 2 ), 建立回归方程; 假定某位人员的观测值 , 预测年工资及置信度为95%的置信区间.程序为:A=load('ex81.txt')Y=A(:,1)X=A(1:24,2:4)xx=[ones(24,1) X]b = regress(Y,X)Y1=xx(:,1:4)*bx=[1 5.1 20 7.2]s=sum(x*b)调出Y 和X 后,运行可得:b =17.84691.10310.32151.2889010203(,,)(5.1,20,7.2)x x x =x =1.0000 5.1000 20.0000 7.2000s =39.1837所以,回归方程为:Y= 17.8469+1.1031X1+0.3215X2+1.2889X3+ε当 时,Y=39.18372、 54位肝病人术前数据与术后生存时间(ex82.txt,指标依次为凝血值,预后指数,酵素化验值,肝功能化验值,生存时间).(1) 若用线性回归模型拟合, 考察其各假设合理性;(2) 对生存是时间做对数变换,用线性回归模型拟合, 考察其各假设合理性;(3) 做变换 用线性回归模型拟合, 考察其各假设合理性; (4) 用变量的选择准则,选择最优回归方程010203(,,)(5.1,20,7.2)x x x =0.0710.07Y Z -=(5)用逐步回归法构建回归方程程序为:A=load('ex82.txt')Y=A(:,5)X=A(1:54,1:4)xx=[ones(54,1) X][b,bint,r,rint,stats]=regress(Y,xx) 运行结果为:b =-621.597633.16384.27194.125714.0916bint =-751.8189 -491.376219.0621 47.26563.1397 5.40403.0985 5.1530-11.0790 39.2622stats =1.0e+003 *0.0008 0.0628 0 3.7279由检验结果知,bi的置信区间分别为:[-751.8189 ,-491.3762][ 19.0621 47.2656][3.1397 5.4040][3.0985 5.1530][-11.0790 39.2622]R2 =8 f=0.0628 p=0 估计误差方差为3.7279所以可见这种拟合不合理。
MATLAB回归分析

MATLAB回归分析回归分析是统计学中常用的一种方法,用于建立一个依赖于自变量(独立变量)的因变量(依赖变量)的关系模型。
在MATLAB环境下,回归分析可以实现简单线性回归、多元线性回归以及非线性回归等。
简单线性回归是一种最简单的回归分析方法,它假设自变量和因变量之间存在线性关系。
在MATLAB中,可以通过`polyfit`函数进行简单线性回归分析。
该函数可以拟合一元数据点集和一维多项式,返回回归系数和截距。
例如:```matlabx=[1,2,3,4,5];y=[2,3,4,5,6];p = polyfit(x, y, 1);slope = p(1);intercept = p(2);```上述代码中,`x`是自变量的数据点,`y`是因变量的数据点。
函数`polyfit`的第三个参数指定了回归的阶数,这里是1,即一次线性回归。
返回的`p(1)`和`p(2)`分别是回归系数和截距。
返回的`p`可以通过`polyval`函数进行预测。
例如:```matlabx_new = 6;y_pred = polyval(p, x_new);```多元线性回归是在有多个自变量的情况下进行的回归分析。
在MATLAB中,可以使用`fitlm`函数进行多元线性回归分析。
例如:```matlabx1=[1,2,3,4,5];x2=[2,4,6,8,10];y=[2,5,7,8,10];X=[x1',x2'];model = fitlm(X, y);coefficients = model.Coefficients.Estimate;```上述代码中,`x1`和`x2`是两个自变量的数据点,`y`是因变量的数据点。
通过将两个自变量放在`X`矩阵中,可以利用`fitlm`函数进行多元线性回归分析。
返回值`model`是回归模型对象,可以通过`model.Coefficients.Estimate`获得回归系数。
多元回归分析报告matlab

回归分析MATLAB 工具箱一、多元线性回归多元线性回归:p p x x y βββ+++=...110 1、确定回归系数的点估计值: 命令为:b=regress(Y, X ) ①b 表示⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡=p b βββˆ...ˆˆ10②Y 表示⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=n Y Y Y Y (2)1③X 表示⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡=np n n p p x x x x x x x x x X (1)............ (1) (12)12222111211 2、求回归系数的点估计和区间估计、并检验回归模型: 命令为:[b, bint,r,rint,stats]=regress(Y,X,alpha) ①bint 表示回归系数的区间估计. ②r 表示残差. ③rint 表示置信区间.④stats 表示用于检验回归模型的统计量,有三个数值:相关系数r 2、F 值、与F 对应的概率p.说明:相关系数2r 越接近1,说明回归方程越显著;)1,(1-->-k n k F F α时拒绝0H ,F 越大,说明回归方程越显著;与F 对应的概率p α<时拒绝H 0,回归模型成立. ⑤alpha 表示显著性水平(缺省时为0.05)3、画出残差及其置信区间. 命令为:rcoplot(r,rint) 例1.如下程序. 解:(1)输入数据.x=[143 145 146 147 149 150 153 154 155 156 157 158 159 160 162 164]'; X=[ones(16,1) x];Y=[88 85 88 91 92 93 93 95 96 98 97 96 98 99 100 102]'; (2)回归分析及检验.[b,bint,r,rint,stats]=regress(Y,X) b,bint,stats得结果:b = bint =-16.0730 -33.7071 1.5612 0.7194 0.6047 0.8340 stats =0.9282 .9531 0.0000即7194.0ˆ,073.16ˆ10=-=ββ;0ˆβ的置信区间为[-33.7017,1.5612], 1ˆβ的置信区间为[0.6047,0.834]; r 2=0.9282, F=180.9531, p=0.0000,我们知道p<0.05就符合条件, 可知回归模型 y=-16.+0.7194x 成立. (3)残差分析,作残差图. rcoplot(r,rint)从残差图可以看出,除第二个数据外,其余数据的残差离零点均较近,且残差的置信区间均包含零点,这说明回归模型 y=-16.+0.7194x 能较好的符合原始数据,而第二个数据可视为异常点. (4)预测及作图.z=b(1)+b(2)*x plot(x,Y,'k+',x,z,'r')二、多项式回归 (一)一元多项式回归.1、一元多项式回归:1121...+-++++=m m m m a x a x a x a y (1)确定多项式系数的命令:[p,S]=polyfit(x,y,m)说明:x=(x 1,x 2,…,x n ),y=(y 1,y 2,…,y n );p=(a 1,a 2,…,a m+1)是多项式y=a 1x m +a 2x m-1+…+a m x+a m+1的系数;S 是一个矩阵,用来估计预测误差. (2)一元多项式回归命令:polytool(x,y,m) 2、预测和预测误差估计.(1)Y=polyval(p,x)求polyfit 所得的回归多项式在x 处的预测值Y ;(2)[Y,DELTA]=polyconf(p,x,S,alpha)求polyfit 所得的回归多项式在x 处的预测值Y 及预测值的显著性为1-alpha 的置信区间Y ±DELTA ;alpha 缺省时为0.5.例1. 观测物体降落的距离s 与时间t 的关系,得到数据如下表,求s. (关于t 的回归方程2ˆct bt a s++=)解法一:直接作二次多项式回归. t=1/30:1/30:14/30;s=[11.86 15.67 20.60 26.69 33.71 41.93 51.13 61.49 72.90 85.44 99.08 113.77 129.54 146.48]; [p,S]=polyfit(t,s,2) 得回归模型为:1329.98896.652946.489ˆ2++=t t s解法二:化为多元线性回归. t=1/30:1/30:14/30;s=[11.86 15.67 20.60 26.69 33.71 41.93 51.13 61.49 72.90 85.44 99.08 113.77 129.54 146.48];T=[ones(14,1) t' (t.^2)']; [b,bint,r,rint,stats]=regress(s',T);b,stats 得回归模型为:22946.4898896.651329.9ˆt t s++= 预测及作图: Y=polyconf(p,t,S) plot(t,s,'k+',t,Y,'r')(二)多元二项式回归多元二项式回归命令:rstool(x,y,’model ’, alpha)说明:x 表示n ⨯m 矩阵;Y 表示n 维列向量;alpha :显著性水平(缺省时为0.05);model 表示由下列4个模型中选择1个(用字符串输入,缺省时为线性模型):linear(线性):m m x x y βββ+++=Λ110purequadratic(纯二次):∑=++++=nj j jjm m x x x y 12110ββββΛinteraction(交叉):∑≤≠≤++++=mk j k j jkm m x x x x y 1110ββββΛquadratic(完全二次):∑≤≤++++=mk j k j jkm m x x x x y ,1110ββββΛ例1. 设某商品的需求量与消费者的平均收入、商品价格的统计数据如下,建立回归模型,预测平均收入为1000、价格为6时的商品需求量. 需求量 100 75 80 70 50 65 90 100 110 60 收入10006001200500300400130011001300300价格5766875439解法一:选择纯二次模型,即2222211122110x x x x y βββββ++++=.直接用多元二项式回归:x1=[1000 600 1200 500 300 400 1300 1100 1300 300]; x2=[5 7 6 6 8 7 5 4 3 9];y=[100 75 80 70 50 65 90 100 110 60]'; x=[x1' x2'];rstool(x,y,'purequadratic')在左边图形下方的方框中输入1000,右边图形下方的方框中输入6,则画面左边的“Predicted Y ”下方的数据变为88.47981,即预测出平均收入为1000、价格为6时的商品需求量为88.4791.在画面左下方的下拉式菜单中选”all ”, 则beta 、rmse 和residuals 都传送到Matlab 工作区中.在Matlab 工作区中输入命令:beta, rmse 得结果:beta = 110.5313 0.1464 -26.5709 -0.0001 1.8475 rmse = 4.5362故回归模型为:2221218475.10001.05709.261464.05313.110x x x x y +--+=剩余标准差为4.5362, 说明此回归模型的显著性较好.解法二:将2222211122110x x x x y βββββ++++=化为多元线性回归:X=[ones(10,1) x1' x2' (x1.^2)' (x2.^2)']; [b,bint,r,rint,stats]=regress(y,X); b,stats 结果为: b =110.5313 0.1464 -26.5709 -0.0001 1.8475 stats =0.9702 40.6656 0.0005三、非线性回归 1、非线性回归:(1)确定回归系数的命令:[beta,r,J]=nlinfit(x,y,’model ’, beta0)说明:beta 表示估计出的回归系数;r 表示残差;J 表示Jacobian 矩阵;x,y 表示输入数据x 、y 分别为矩阵和n 维列向量,对一元非线性回归,x 为n 维列向量;model 表示是事先用m-文件定义的非线性函数;beta0表示回归系数的初值. (2)非线性回归命令:nlintool(x,y,’model ’, beta0,alpha) 2、预测和预测误差估计:[Y,DELTA]=nlpredci(’model ’, x,beta,r,J)表示nlinfit 或nlintool 所得的回归函数在x 处的预测值Y 及预测值的显著性为1-alpha 的置信区间Y ±DELTA. 例1. 如下程序.解:(1)对将要拟合的非线性模型y=a x b e /,建立m-文件volum.m 如下: function yhat=volum(beta,x) yhat=beta(1)*exp(beta(2)./x); (2)输入数据: x=2:16;y=[6.42 8.20 9.58 9.5 9.7 10 9.93 9.99 10.49 10.59 10.60 10.80 10.60 10.90 10.76];beta0=[8 2]'; (3)求回归系数:[beta,r ,J]=nlinfit(x',y','volum',beta0); beta (4)运行结果:beta =11.6036 -1.0641 即得回归模型为:xey 10641.16036.11-=(5)预测及作图:[YY,delta]=nlpredci('volum',x',beta,r ,J);plot(x,y,'k+',x,YY,'r')四、逐步回归1、逐步回归的命令:stepwise(x,y,inmodel,alpha)n⨯阶矩阵;y表示因变量数据,1⨯n阶矩阵;inmodel表示矩说明:x表示自变量数据,m阵的列数的指标,给出初始模型中包括的子集(缺省时设定为全部自变量);alpha表示显著性水平(缺省时为0.5).2、运行stepwise命令时产生三个图形窗口:Stepwise Plot,Stepwise Table,Stepwise History.在Stepwise Plot窗口,显示出各项的回归系数及其置信区间.(1)Stepwise Table窗口中列出了一个统计表,包括回归系数及其置信区间,以及模型的统计量剩余标准差(RMSE)、相关系数(R-square)、F值、与F对应的概率P.例1. 水泥凝固时放出的热量y与水泥中4种化学成分x1、x2、x3、x4有关,今测得一组数据如下,试用逐步回归法确定一个线性模型.解:(1)数据输入:x1=[7 1 11 11 7 11 3 1 2 21 1 11 10]';x2=[26 29 56 31 52 55 71 31 54 47 40 66 68]';x3=[6 15 8 8 6 9 17 22 18 4 23 9 8]';x4=[60 52 20 47 33 22 6 44 22 26 34 12 12]';y=[78.5 74.3 104.3 87.6 95.9 109.2 102.7 72.5 93.1 115.9 83.8 113.3 109.4]'; x=[x1 x2 x3 x4];(2)逐步回归.①先在初始模型中取全部自变量:stepwise(x,y)得图Stepwise Plot 和表Stepwise Table.图Stepwise Plot中四条直线都是虚线,说明模型的显著性不好.从表Stepwise Table中看出变量x3和x4的显著性最差.②在图Stepwise Plot中点击直线3和直线4,移去变量x3和x4.移去变量x3和x4后模型具有显著性虽然剩余标准差(RMSE)没有太大的变化,但是统计量F的值明显增大,因此新的回归模型更好.(3)对变量y和x1、x2作线性回归.X=[ones(13,1) x1 x2];b=regress(y,X)得结果:b =52.57731.46830.6623故最终模型为:y=52.5773+1.4683x1+0.6623x2或这种方法4元二次线性回归clc;clear;y=[1.84099 9.67 23.00 38.12 1.848794 6.22 12.22 19.72 1.848794 5.19 10.09 15.31 ];X1=[60.36558 59.5376 58.89861 58.74706 60.59389 60.36558 59.2 58.2 60.36558 59.97068 59.41918 5 X2=[26.1636 26.35804 26.82438 26.91521 25.90346 25.9636 27.19256 27.42153 26.1636 26.07212 26.27.06063];X3=[0.991227 0.994944 0.981322 0.98374 1.011865 0.991227 1.074772 1.107678 0.991227 0.917904 1 1.1239];X4=[59.37436 58.54265 57.91729 57.69332 59.58203 59.37436 57.76722 57.42355 59.37436 59.05278 57.76687];format short gY=y'X11=[ones(1,length(y));X1;X2;X3;X4]'B1=regress(Y,X11)% 多元一次线性回归[m,n]=size(X11)X22=[];for i=2:nfor j=2:nif i<=jX22=([X22,X11(:,i).*X11(:,j)]);elsecontinueendendendX=[X11,X22];B2=regress(Y,X)% 多元二次线性回归[Y X*B2 Y-X*B2]plot(Y,X11*B1,'o',Y,X*B2,'*')hold on,line([min(y),max(y)],[min(y),max(y)]) axis([min(y) max(y) min(y) max(y)]) legend('一次线性回归','二次线性回归') xlabel('实际值');ylabel('计算值')运行结果:Y =1.8419.672338.121.84886.2212.2219.721.84885.1910.0915.31X11 =1 60.366 26.164 0.99123 59.3741 59.538 26.358 0.99494 58.5431 58.899 26.824 0.98132 57.9171 58.747 26.915 0.98374 57.6931 60.594 25.903 1.0119 59.5821 60.366 25.964 0.99123 59.3741 59.2 27.193 1.0748 57.7671 58.2 27.422 1.1077 57.4241 60.366 26.164 0.99123 59.3741 59.971 26.072 0.9179 59.1 59.419 26.587 1.0604 58.3591 58.891 27.061 1.1239 57.767 B1 =1488.9-4.3582-9.6345-61.514-15.359m =12n =5B2 =3120.4-7129.2-622.23-362.71-105.061388.1120.25.25379.58170.48-796.41ans =1.841 1.8449 -0.0039029.67 9.67 1.0058e-00923 23 1.397e-00938.12 38.12 3.539e-1.8488 1.8488 1.6394e-0096.22 6.227.2643e-12.22 12.22 2.6077e-19.72 19.72 -2.0489e-1.8488 1.8449 0.0039025.19 5.19 1.4529e-00910.09 10.09 1.0803e-00915.31 15.31 4.0978e-由图形可以看出,多元二次线性回归效果非常好,即,相当于Y=3120.4*X1 -7129.2 *X2 + 0*X3 + 0*X4 -622.23*X1*X1 -362.71*X1*X2 -105.06*X1*X3 + 1388 120.25*X2*X2+ .25 *X2*X3+ 379.58*X2*X4 + 170.48*X3*X3+ 0*X3*X4 -796.41*X4*X4。
Matlab中的回归分析与时间序列预测

Matlab中的回归分析与时间序列预测引言:在现代数据分析中,回归分析和时间序列预测是两个重要且广泛应用的领域。
Matlab作为一款功能强大的数学软件,在回归分析和时间序列预测方面提供了丰富的工具和函数,使得实现这些分析变得更加简单和高效。
本文将介绍Matlab中回归分析和时间序列预测的相关知识和方法,并结合实例进行说明。
一、回归分析回归分析是通过寻找自变量与因变量之间的关系,来推测未来观测值的一种分析方法。
在Matlab中,可以通过使用regress函数进行回归分析。
该函数可以拟合线性回归模型,并返回各个回归系数的估计值以及回归模型的统计信息。
下面我们以一个简单的例子来说明如何使用Matlab进行回归分析。
实例1:房价预测假设我们有一组数据,其中包含了房屋的面积和对应的售价。
我们希望通过房屋的面积来预测未来房价。
首先,我们需要导入数据并进行预处理。
```matlabdata = load('house_data.csv'); % 导入数据X = data(:, 1); % 提取面积作为自变量y = data(:, 2); % 提取房价作为因变量```接下来,我们可以使用regress函数进行回归分析,并得到回归系数的估计值。
```matlab[B, BINT, R, RINT, STATS] = regress(y, [ones(size(X)) X]); % 回归分析```其中,B为回归系数的估计值,BINT为回归系数的置信区间,R为残差,RINT为残差的置信区间,STATS为回归模型的统计信息。
我们可以打印出回归系数的估计值,以及回归模型的统计信息。
```matlabdisp('回归系数的估计值:');disp(B);disp('回归模型的统计信息:');disp(STATS);```运行以上代码,我们可以得到回归模型的结果。
通过回归系数的估计值,我们可以得到回归方程为y = B(1) + B(2) * X,其中B(1)为截距,B(2)为斜率。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.研究科研人员的年工资与他的论文质量、工作年限、获得资助指标之间的关系.24位科研人员的调查数据(ex81.txt):
设误差ε~(0,σ 2 ), 建立回归方程; 假定某位人员的观测值 , 预测年工资及置信度为
95%的置信区间.
程序为:A=load('ex81.txt')
Y=A(:,1)
X=A(1:24,2:4)
xx=[ones(24,1) X]
b = regress(Y,X)
Y1=xx(:,1:4)*b
x=[1 5.1 20 7.2]
s=sum(x*b)
调出Y 和X 后,运行可得:
b =
17.8469
1.1031
0.3215
1.2889
010203(,,)(5.1,20,7.2)x x x =
x =
1.0000 5.1000 20.0000 7.2000
s =
39.1837
所以,回归方程为:Y= 17.8469+1.1031X1+0.3215X2+1.2889X3+ε
当 时,Y=39.1837
2、 54位肝病人术前数据与术后生存时间(ex82.txt,指标依次为凝血值,预后指数,酵素化验值,肝功能化验值,生存时间).
(1) 若用线性回归模型拟合, 考察其各假设合理性;
(2) 对生存是时间做对数变换,用线性回归模型拟合, 考察其各假设合理性;
(3) 做变换 用线性回归模型拟合, 考察其各假设合理性; (4) 用变量的选择准则,选择最优回归方程
010203
(,,)(5.1,20,7.2)x x x =0.0710.07
Y Z -=
(5)用逐步回归法构建回归方程
程序为:A=load('ex82.txt')
Y=A(:,5)
X=A(1:54,1:4)
xx=[ones(54,1) X]
[b,bint,r,rint,stats]=regress(Y,xx) 运行结果为:
b =
-621.5976
33.1638
4.2719
4.1257
14.0916
bint =
-751.8189 -491.3762
19.0621 47.2656
3.1397 5.4040
3.0985 5.1530
-11.0790 39.2622
stats =
1.0e+003 *
0.0008 0.0628 0 3.7279
由检验结果知,bi的置信区间分别为:[-751.8189 ,-491.3762]
[ 19.0621 47.2656]
[3.1397 5.4040]
[3.0985 5.1530]
[-11.0790 39.2622]
R2 =8 f=0.0628 p=0 估计误差方差为3.7279
所以可见这种拟合不合理。
(2)程序为:
A=load('ex82.txt')
Y=A(:,5)
X=A(1:54,1:4)
xx=[ones(54,1) X]
y=log(Y)
[b,bint,r,rint,stats]=regress(y,xx)
b =
1.1254
0.1578
0.0213
0.0218
0.0044
bint =
0.8929 1.3578
0.1326 0.1830
0.0193 0.0233
0.0200 0.0236
-0.0405 0.0494
stats =
0.9724 430.9813 0 0.0119
可见R2 =0.9724 F=430.9813 p=0<0.05 估计误差方差较小
所以该拟合较显著
所以y= 1.1254+0.1578X1+0.0213X2+0.0218X3+0.0044X4
(3) 程序为:A=load('ex82.txt')
Y=A(:,5)
X=A(1:54,1:4)
xx=[ones(54,1) X]
Z=[(power(Y,0.07)-1)/0.07] [b,bint,r,rint,stats]=regress(Z,xx) 运行结果为:
b =
0.4525
0.2260
0.0305
0.0310
0.0149
bint =
0.1261 0.7788
0.1907 0.2613
0.0276 0.0333
0.0285 0.0336
-0.0482 0.0780
stats =
0.9736 451.8277 0 0.0234
所以可见拟合是合理的。
(4)。
