人教版七年级上册数学：工程问题(公开课课件)
合集下载
人教版七年级上册数学一元一次方程的应用——工程问题精品课件PPT
人教版七年级上册数学课件：3.4一元 一次方 程的应 用—— 工程问 题
➢
1、 在 困 境 中 时刻把 握好的 机遇的 才能。 我在想 ，假如 这个打 算是我 往履行 那结果 必定失 败，由 于我在 作决策 以前会 把患上 失的因 素斟酌 患上太 多。
➢
2、 人 物 作 为 支撑影 片的基 本骨架 ，在影 片中发 挥着不 可替代 的作用 ，也是 影片的 灵魂， 阿甘是 影片中 的主人 公，是 支撑起 整个故 事的重 要人物 ，也是 给人最 大启示 的人物 。
人教版七年级上册数学课件：3.4一元 一次方 程的应 用—— 工程问 题
7、运动场跑道400m,小红跑步的速度是爷爷的5/3倍,他们从 同一起点沿跑道的同一方向同时出发,5分钟后小红第一次追 上了爷爷.你知道他们的跑步速度吗？ （1）几分钟后小红与爷爷第二次相遇？ （2）如果小红追上爷爷后立即转身沿相反方向跑，几分钟 后小红又一次与爷爷相遇？
人教版七年级上册数学课件：3.4一元 一次方 程的应 用—— 工程问 题
6、为庆祝校运会开幕,初一(2)班学生接受了制作小旗的任务. 原计划一半同学参加制作,每天制作40面.完成了三分之一以 后,全班同学一起参加,结果比原计划提前一天半完成任务,假 设每人的制作效率相同,问共制作小旗多少面?
人教版七年级上册数学课件：3.4一元 一次方 程的应 用—— 工程问 题
练习题
1、一件工程，甲独做需15天完成，乙独做需12天宅成，现 先由甲、乙合作3天后，甲有其他任务，剩下工程由乙单独 完成，问共要几天完成全部工程？
人教版七年级上册数学课件：3.4一元 一次方 程的应 用—— 工程问 题
人教版七年级上册数学课件：3.4一元 一次方 程的应 用—— 工程问 题
➢
1、 在 困 境 中 时刻把 握好的 机遇的 才能。 我在想 ，假如 这个打 算是我 往履行 那结果 必定失 败，由 于我在 作决策 以前会 把患上 失的因 素斟酌 患上太 多。
➢
2、 人 物 作 为 支撑影 片的基 本骨架 ，在影 片中发 挥着不 可替代 的作用 ，也是 影片的 灵魂， 阿甘是 影片中 的主人 公，是 支撑起 整个故 事的重 要人物 ，也是 给人最 大启示 的人物 。
人教版七年级上册数学课件：3.4一元 一次方 程的应 用—— 工程问 题
7、运动场跑道400m,小红跑步的速度是爷爷的5/3倍,他们从 同一起点沿跑道的同一方向同时出发,5分钟后小红第一次追 上了爷爷.你知道他们的跑步速度吗？ （1）几分钟后小红与爷爷第二次相遇？ （2）如果小红追上爷爷后立即转身沿相反方向跑，几分钟 后小红又一次与爷爷相遇？
人教版七年级上册数学课件：3.4一元 一次方 程的应 用—— 工程问 题
6、为庆祝校运会开幕,初一(2)班学生接受了制作小旗的任务. 原计划一半同学参加制作,每天制作40面.完成了三分之一以 后,全班同学一起参加,结果比原计划提前一天半完成任务,假 设每人的制作效率相同,问共制作小旗多少面?
人教版七年级上册数学课件：3.4一元 一次方 程的应 用—— 工程问 题
练习题
1、一件工程，甲独做需15天完成，乙独做需12天宅成，现 先由甲、乙合作3天后，甲有其他任务，剩下工程由乙单独 完成，问共要几天完成全部工程？
人教版七年级上册数学课件：3.4一元 一次方 程的应 用—— 工程问 题
人教版七年级上册数学课件：3.4一元 一次方 程的应 用—— 工程问 题
初中数学人教版七年级上册《工程问题》优质课公开课比赛获奖课件面试试讲课件
5.工地上搬运一匹砖，牛牛单独完成需14天， 彬彬单独完成需18天，臣臣单独完成需12天， 前7天由牛牛、彬彬两人合作，但彬彬中途离 开了一段时间，后2天由彬彬、臣臣合作完成， 这项工作总共用了9天完成，问彬彬中途离开 了几天？
解：设彬彬中途离开了x天. 根据题意，得
7 7x2 2 1. 14 18 12
四、学以致用，及时反馈.
选一张你喜爱的图片，并解答对应的题
1．杨师傅和贾师傅安装学校教室的灯管，由
杨师傅单独完成需3小时，由贾师傅单独完成需 4小时，贾师傅单独干了1小时后，两位合作完 成剩下的工作，这项工作共用（ B ）
9 A. h 7
15 C. h 7
16 B. h 7
6 D. h 7
2.在一块地里种植牡丹，甲单独做4天完成，乙单独 做6天完成，若甲先做1天，然后甲、乙合作完成此项 工作，设甲一共做了x天，则所列方程为（ D）
阶段
人均效率
1 80 1 80
人数
x x+5
工作时间 工作总量
2 8
8( x 5) 8012Fra bibliotek2x 80
工作总量=工作效率×工作时间 =人均效率×人数×工作时间
工作总量=工作效率×工作时间 小试牛刀 =人均效率×人数×工作时 间 我校志愿者，整理一批捐赠给山区的衣物，由一个 同学做要80h完成.现计划由一部分同学先做3 2h,然后增加 5位同学与他们一起做8h，完成这项工作的 4 .假设这些 同学的工作效率相同，具体应先安排多少名同学工作？
五、课堂小结
本节课你有那些收获？
1.列方程解应用题的步骤：
设未知数 实际问题 列方程
→
数学问题 （一元一次方程） 解 方 程
5.3 第1课时 配套问题和工程问题 课件(共21张PPT) 人教版七年级数学上册
解：设用x m3钢材做A部件，则用(6－x)m3钢材做B部件．根据题意，得3×40x＝(6－x)×240，解得x＝4，所以6－x＝2，4×40＝160(套)．答：应该用4 m3钢材做A部件，用2 m3钢材做B部件，才能恰好配成这种仪器160套．
变式：用白铁皮做罐头盒，每张铁皮可制盒身16个或制盒底43个，一个盒身与两个盒底配成一套罐头盒．现有150张白铁皮，用多少张制盒身，多少张制盒底，可以正好制成整套罐头盒(全部用完，无浪费)?
问题导入
有一个很有意思的问题：巍巍古寺在山林，不知寺中几多僧.三百六十四只碗，众僧刚好都用尽.三人共食一碗饭，四人共吃一碗羹请问先生名算者，算来寺内几多僧？诗的意思：3个和尚吃一碗饭，4个和尚吃一碗羹，刚好用了364只碗，请问寺内有多少和尚？这是一个很经典的配套问题，我们需要给和尚们配上数量刚好的碗，才能让每个人都吃上饭，喝上汤.
18
【题型二】工程问题
变式：甲、乙两人想共同承包一项工程，甲单独做30天完成，乙单独做20天完成，合同规定15天内(含15天)完成，否则每超过1天罚款1 000元，甲、乙两人经协商后签订了该合同．(1)正常情况下，甲、乙两人能否履行该合同？为什么？(2)现两人合作了这项工程的75%，因特殊情况，必须调走1人，问调走谁更合适？为什么？
解：设用x张制盒身，则用(150－x)张制盒底．根据题意，得16x×2＝43×(150－x)，解得x＝86.所以150－x＝150－86＝64.答：用86张制盒身，64张制盒底，可以正好制成整套罐头盒．
例2：一批文稿，若由甲抄，30小时可以抄完，若由乙抄，20小时可以抄完，现由甲抄3小时后改由乙抄余下部分，则乙还需抄_______小时．
5.3 实际问题与一元一次方程
第1课时 配套问题和工程问题
变式：用白铁皮做罐头盒，每张铁皮可制盒身16个或制盒底43个，一个盒身与两个盒底配成一套罐头盒．现有150张白铁皮，用多少张制盒身，多少张制盒底，可以正好制成整套罐头盒(全部用完，无浪费)?
问题导入
有一个很有意思的问题：巍巍古寺在山林，不知寺中几多僧.三百六十四只碗，众僧刚好都用尽.三人共食一碗饭，四人共吃一碗羹请问先生名算者，算来寺内几多僧？诗的意思：3个和尚吃一碗饭，4个和尚吃一碗羹，刚好用了364只碗，请问寺内有多少和尚？这是一个很经典的配套问题，我们需要给和尚们配上数量刚好的碗，才能让每个人都吃上饭，喝上汤.
18
【题型二】工程问题
变式：甲、乙两人想共同承包一项工程，甲单独做30天完成，乙单独做20天完成，合同规定15天内(含15天)完成，否则每超过1天罚款1 000元，甲、乙两人经协商后签订了该合同．(1)正常情况下，甲、乙两人能否履行该合同？为什么？(2)现两人合作了这项工程的75%，因特殊情况，必须调走1人，问调走谁更合适？为什么？
解：设用x张制盒身，则用(150－x)张制盒底．根据题意，得16x×2＝43×(150－x)，解得x＝86.所以150－x＝150－86＝64.答：用86张制盒身，64张制盒底，可以正好制成整套罐头盒．
例2：一批文稿，若由甲抄，30小时可以抄完，若由乙抄，20小时可以抄完，现由甲抄3小时后改由乙抄余下部分，则乙还需抄_______小时．
5.3 实际问题与一元一次方程
第1课时 配套问题和工程问题
人教版七年级上册数学：工程问题(公开课课件)
例题改编——求进价
2.某商品标价是2200元， 按此标价的八折出售，利 润率为10%。求此商品的 进价。
退出 返回 上一张下一张
例题改编——求进价
2.某商品标价是2200元，按此标价 的八折出售，利润率为10%。求此 商品的进价。
解：设此商品进价为x元，根据题意， 得 2200×80%－x = 10% ×x 解这个方程，得 x =1600（元）
5．某商品的进价是1 000元，售 价为1 500元，由于情况不好，商 店决定降价出售，但又要保证利 润率为5%，那么商店可降多少 元出售此商品？
退出 返回 上一张下一张
6．某商场将某种产品按进价提 高35%，然后打出“九折酬宾， 外送50元打的费”的广告，结果 每台产品仍获利208元，则每台 产品的进价是多少元？
退出 返回 上一张下一张
学习目标：
1、学会用方程表示销售问题中的数量关系和 变化规律。 2、在实际生活问题中，感受到数学的价值， 形成建模思想、方程思想，培养学生运用数 学知识分析问题、解决实际问题意识和能力 重点：1.正确分析出实际问题中的已知数、 未知数 2.找出可以表示实际问题全部含义的相等关 系 难点：能够准确地找出实际问题的相等关系
退出 返回 上一张下一张
（1）如果某种商品打“八折”出售，是指按 原价的 80 %出售 。
（ 原价2）便商宜店40出元售，一打种--九录---音-折机出，售原的价? 400元。比
（3）列一元一次方程解应用题的一般步骤是 _审_题__找__相__等_关__系__、__设_未__知__数__、_列__方__程__、_解__方__程__、检验
退出 返回 上一张下一张
小结：通过本节课的学习
你有哪些收获。
退出 返回 上一张下一张
人教版七年级上册数学：工程问题(公开课课件)
x 10 3
布置作业 ☞
、
课本：1、P101 练习2 2、P106习题4
一部分人先做4小时完 成的工作量 +（一部分+2)人一起做8小时的工作量
等量关系:
一部分人先做4小时完成的工作量 +（一部分+2)人一起做8小时的工作量=1
解：设具体应先安排x人工作。
4x
分析：x人先做4小时完成的工作量= 40
（x+2)人一起做8小时的工作量= 8(x 2)
可列方程：4x 8( x 2) 1 40
40
40
4x+8(x+2x=40 – 16 12x=24 x=2
答：具体应先排2人工作
思考： 方程还有其他的列法吗？
整理一批图书，由一个人做要40小时完成。现在计划由一部分人先做4小时, 再增加2人和他们一起做8小时，完成这项工作。假设这些人的工作效率相同， 具体应先安排多少人工作?
若由甲队先做6小时，乙队再加入一起合作完成了这项工作， 问两人一起合作了多长时间？
尝试解决：
1. 分析：本题的等量关系是：
甲先做的工作量 + 甲、乙合做的工作量 = 1
2. 解：设两人合作的时间是x小时，依题意得：
1 ×6 + ( 1 1 )x = 1
24
24 12
课堂小结 ☞
实际问题 设未知数，列方程 一元一次方程
人数
1
1
3( 1 1 ) a
b
ab
(只列式)
等量关系是
先前工作量
后来工作量
3 10
1 4 ( 1 1 )x 1
20
20 12
天
(只列式)
解：设后来加进x人一起合作，依题意得：
布置作业 ☞
、
课本：1、P101 练习2 2、P106习题4
一部分人先做4小时完 成的工作量 +（一部分+2)人一起做8小时的工作量
等量关系:
一部分人先做4小时完成的工作量 +（一部分+2)人一起做8小时的工作量=1
解：设具体应先安排x人工作。
4x
分析：x人先做4小时完成的工作量= 40
（x+2)人一起做8小时的工作量= 8(x 2)
可列方程：4x 8( x 2) 1 40
40
40
4x+8(x+2x=40 – 16 12x=24 x=2
答：具体应先排2人工作
思考： 方程还有其他的列法吗？
整理一批图书，由一个人做要40小时完成。现在计划由一部分人先做4小时, 再增加2人和他们一起做8小时，完成这项工作。假设这些人的工作效率相同， 具体应先安排多少人工作?
若由甲队先做6小时，乙队再加入一起合作完成了这项工作， 问两人一起合作了多长时间？
尝试解决：
1. 分析：本题的等量关系是：
甲先做的工作量 + 甲、乙合做的工作量 = 1
2. 解：设两人合作的时间是x小时，依题意得：
1 ×6 + ( 1 1 )x = 1
24
24 12
课堂小结 ☞
实际问题 设未知数，列方程 一元一次方程
人数
1
1
3( 1 1 ) a
b
ab
(只列式)
等量关系是
先前工作量
后来工作量
3 10
1 4 ( 1 1 )x 1
20
20 12
天
(只列式)
解：设后来加进x人一起合作，依题意得：
工程问题初一ppt课件ppt课件
系统工程方法
系统工程方法是一种基于系统思 想的工程管理方法，将工程系统 视为一个整体，从全局的角度出
发进行优化和管理。
系统工程方法包括系统分析、系 统设计、系统综合、系统评价等 阶段，通过各阶段的迭代和优化
，实现工程系统的最优解。
系统工程方法广泛应用于航空航 天、交通运输、制造业等领域， 可以提高工程项目的效率和成功
计算机模拟是通过计算机程序模拟实际系统的运行过程，可以用于预测和优化系统 的性能。
计算机模拟可以模拟各种复杂的工程系统，如机械系统、控制系统、流体系统等， 通过模拟可以发现潜在的问题并进行优化。
计算机模拟常用的工具有MATLAB、Simulink、COMSOL Multiphysics等，可以 根据具体需求选择合适的工具进行模拟。
问题分析
总结词
深入理解问题背景和相关因素
详细描述
对问题进行分析，包括理解问题的背景、相关因素和限制条件，以及识别关键变 量和参数。
解决方案设计
总结词
提出可能的解决方案
详细描述
基于问题分析，设计可能的解决方案，并考虑各种可能性和可行性。这一步可能涉及创新思维和多学科知识。
实施解决方案
总结词
实施解决方案并监控进展
案例三：环保工程的可持续发展问题
要点一
总结词
要点二
详细描述
环保工程的可持续发展问题涉及到环境保护、资源利用和 经济发展等多个方面，是当前全球关注的热点问题。
随着人类活动的不断扩大，环境问题日益严重。为了实现 可持续发展，工程师需要在环保工程中采取一系列措施， 包括减少污染物排放、提高资源利用效率、开发可再生能 源等。同时，还需要加强环境监测和评估，确保各项环保 措施的有效性和可持续性。
人教版七年级上册数学：工程问题(公开课课件)
1
（1）甲每天完成全部工作的 20 ；
1
乙每天完成全部工作的
12 ；两人合作3
天完成全部工作的
3( 1 1 ) 12 20
；此时剩余的工作
量是
1
3( 1 12
210)。
工作总量看成单
位1
学习提高
❖ 例1、一件工程甲单独做需要20小时完成，乙单独做需要30 小时完成，现由甲、乙两人合作需要多少小时完成任务？
试试身手
▪ 3.整理一批数据，由一个人做需80小时完 成，现在计划由一些人做2小时，再增加5 人做8小时，完成这项工作的3/4，怎样安 排参与整理数据的具体人数？
思考:
4.已知某水池有进水管与出水管一根，进水管工作 15小时可以将空水池放满，出水管工作24小时可 以将满池的水放完： （1）如果单独打开进水管，每小时可以注入的水 占水池的几分之几？ （2）如果单独打开出水管，每小时可以放出的水 占水池的几分之几？ （3）如果将两管同时打开，每小时的效果如何？ 如何列式？ （4）对于空的水池，如果进水管先打开2小时， 再同时打开两管，问注满水池还需要多少时间？
❖ 若这件工程先由乙单独做10小时，再由甲、 乙合作，还需多少小时才能完成任务？
再登高峰
❖例2 整理一批图书,由一个人做要40小
时完成.现计划先由一部分人先做4小时 后,再增加2人和他们一起做8小时,完成 这项工作.假设这些人的工作效率相同, 具体应先安排多少人工作?
分析:这里可以把工作总量看作 1 请填空:
人教版七年级
再探实际问题与一元一次方程
——工程问题
学学习习目目标标
1、理解工程问题中的基本量之间的关系； 2、根据工程问题中的等量关系，建立一元一次方程。
3.4.2一元一次方程的应用工程问题课件人教版数学七年级上册
后5天甲生产 零件的个数
后5天乙生产 零件的个数
940个
例1 甲每天生产某种零件 80 个，甲生产 3天后，乙也加入 生产同一种零件，再经过 5天，两人共生产这种零件 940 个，问 乙每天生产这种零件多少个？
等量关系式：
前3天甲 后5天甲 后5天乙
生产零件 生产零件 生产零件
940
的个数 的个数 的个数
例2 某项工作，甲单独做需要 4 小时，乙单独做需要 6 小 时，甲先做 30分钟，然后甲、乙合作．甲、乙合作还需要多少 小时才能完成全部工作？
解法2：设甲、乙合作还需要x小时才能完成全部工作．
根据题意，得
1 4
1 2
1 4
1 6
x
1
．
解方程，得 x ＝ 2.1．
答：甲、乙合作还需要2.1小时才能完成全部工作．
2023—2024学年人教版数学七年级上册
一元一次方程的应用—— 工程问题
上节课，我们学习了如何运用一元一次方程来解决实际问 题中的配套问题，本节课，我们来探究一元一次方程与实际问 题——工程问题．
在学习新课之前，先完成下面的填空： 工作量＝__工__作__效__率__×__工__作__时__间__； 工作效率＝_工___作__量__÷__工__作__时__间__； 工作时间＝__工__作__量__÷__工__作__效__率__．
40 40 解方程，得4x＋8(x＋2)＝40，4x＋8x＋16＝40， 12x＝24，x＝2． 答：应安排 2人先做 4 h．
问题 组内交流，提炼解题思路．
安排先工作 设安排 x 人先做4 h 4x 8(x 2)＝1
的人数
找出等量关系，列方程 40 40
安排 2人先做4 h
人教版七年级上册3.4实际问题与一元一次方程工程问题课件优质课件PPT
解：（1）设需要 x 天铺好，依题意，得：
1 1 x 1 30 20
解得： x = 12
∴ 需要12天铺好。
（2）若单独由甲队施工，则需30天完成，花费 200×30=6000（元）； 若单独由乙队施工，则需20天完成，花费 280×20=5600（元）；
若由甲、乙队共同施工，则需12天完成， 花费200×12+280×12=5760（元）。
∴ 按照少花钱多办事的原则，应选择由乙 队单独施工完成。
例3：一条地下管线由甲工程队单独铺设 需要12天，由乙工程队单独铺设需要24天. 如果由这两个工程队从两端同时施工，要 多少天可以铺好这条管线？
解：设 x多少天可以铺好这条管线. 依题意得： x x 1 ，
12 24 解方程，得： x＝8.
3.4实际问题与一元一次方程
工程问题 学 科网
活动1.自主学习 难点强调
工程问题中的量及其关系：
1.工作效率：单位时间完成的工作量 2.工程问题中的基本关系：
工作量= 工作效率×工作时间 3.总工作量可看做“1” 4.合效率：各效率之和;
各部分工作量之和=工作总量
☞比一比,赛一赛.
看谁做得好,看谁做得快！
并用自己的语言概括出来. （2）设适当的未知数，将上述问题在表格中表示出来.
总工 每个 作量 人的
工作 效率
先安 排的 人数
增加 的人 数
先安排的 人的工作 时间
增加 的人 的工 作时 间
先安排的人 完成的工作 量
增加的人完 成的工作量
143;8） 8小时
小时
1 8 4x
40
1 28 40
的工作量为
mm xy
或
1 x
人教版七年级上册数学：工程问题(公开课课件)
1
30
成，乙只要20天就能完成任务，若要求二人16天完成
1
16天 20
x天
任务，乙先加工几天后，甲加入合作加工，恰好能如
16 20
+
1x 30
=1
期完成任务？
想一想：若要求二人在16天内完成任务，乙先加工几 天后，甲加入合作加工，恰好能如期完成任务？
效率 时间
工作量
甲
1 30
x
1x 30
乙
1
16
16
20
20
解：设甲加工x天，两人如期完成任务，则 在甲加入之前，乙先工作了(16-x)天。
依题意，得
1 x 16 1. 30 20
解得x=6，则16-x=10。
答：乙需加工10天后,甲加入合作加工才可 正好按期完成任务。
巩固提高
甲、乙两人共同承包一项工程,甲所带的队（简
称甲队）单做30天完成,乙所带的队（简称乙队）
∴不能如期完工
可知甲、乙队共同完成工程的 3/4 ，则需9天，
施工费：（0.6+0.8）×9=12.6（万元）。
剩下的由甲队完成所需8天，施工费:0.6 ×8=4.8（万元）
共需要时间：9+8=17（天） 超期2天，违约金:2万元； 全部费用：12.6+4.8+2=19.4（万元）＜ 20万元 所以甲、乙二人不会亏损
转化
（一元一次方程）
解 方 程
检验
问题答案
数学问题的解 （一元一次方程的解）
布荣置耀作殿业堂-课外探索：游戏中的数学
1、教科书 P101练习2，习题 3.4 第4、5题
2、补充作业，课后评测练习
人教荣版七耀年级殿初堂中数-学课上外册 探索：游戏中的数学
30
成，乙只要20天就能完成任务，若要求二人16天完成
1
16天 20
x天
任务，乙先加工几天后，甲加入合作加工，恰好能如
16 20
+
1x 30
=1
期完成任务？
想一想：若要求二人在16天内完成任务，乙先加工几 天后，甲加入合作加工，恰好能如期完成任务？
效率 时间
工作量
甲
1 30
x
1x 30
乙
1
16
16
20
20
解：设甲加工x天，两人如期完成任务，则 在甲加入之前，乙先工作了(16-x)天。
依题意，得
1 x 16 1. 30 20
解得x=6，则16-x=10。
答：乙需加工10天后,甲加入合作加工才可 正好按期完成任务。
巩固提高
甲、乙两人共同承包一项工程,甲所带的队（简
称甲队）单做30天完成,乙所带的队（简称乙队）
∴不能如期完工
可知甲、乙队共同完成工程的 3/4 ，则需9天，
施工费：（0.6+0.8）×9=12.6（万元）。
剩下的由甲队完成所需8天，施工费:0.6 ×8=4.8（万元）
共需要时间：9+8=17（天） 超期2天，违约金:2万元； 全部费用：12.6+4.8+2=19.4（万元）＜ 20万元 所以甲、乙二人不会亏损
转化
（一元一次方程）
解 方 程
检验
问题答案
数学问题的解 （一元一次方程的解）
布荣置耀作殿业堂-课外探索：游戏中的数学
1、教科书 P101练习2，习题 3.4 第4、5题
2、补充作业，课后评测练习
人教荣版七耀年级殿初堂中数-学课上外册 探索：游戏中的数学
实际问题与一元一次方程-工程问题(课件)七年级数学上册课件(人教版)
实际做了多少小时？
解：设甲队实际做了小时，
根据题意，得
1
(
10
+
1
20
+
解得 = 5.
答：甲队实际做5小时．
1
)
30
+
1
(
20
+
1
)
30
6 − = 1．
例4.为推进我国“碳达峰、碳中和”双碳目标的实现，各地大力推广分布式
光伏发电项目．某公司计划建设一座光伏发电站，若由甲工程队单独施工需
要3周，每周耗资8万元，若由乙工程队单独施工需要6周，每周耗资3万元．
答：写出答案 (包括单位)．
解决工程问题的基本思路：
1. 三个基本量：工作量、工作效率、工作时间.
它们之间的关系是：工作量=工作效率×工作时间.
2. 相等关系：工作总量=各部分工作量之和.
(1) 按工作时间，工作总量=各时间段的工作量之和；
(2) 按工作者，工作总量=各工作者的工作量之和.
3. 通常在没有具体数值的情况下，把工作总量看作“1”.
答：这批防护服原计划生产任为3100套．
5.某厂接到一所中学的冬季校服定做任务，计划用、两台大型设备进行
加工，如果单独用型设备，需要45天做完；如果单独用型设备，需要30
天做完；为了同学们能及时领到冬季校服，工厂决定由两台设备同时赶
制．
(1)填空：型设备的工作效率是_______，型设备的工作效率是_______；
(1)若甲、乙两工程队合作施工，需要几周完成?共需耗资多少万元?
(2)若需要最迟4周完成工程，请你设计一种方案，既保证按时完成任务，又
最大限度节省资金．（时间按整周计算）
解：设甲队实际做了小时，
根据题意，得
1
(
10
+
1
20
+
解得 = 5.
答：甲队实际做5小时．
1
)
30
+
1
(
20
+
1
)
30
6 − = 1．
例4.为推进我国“碳达峰、碳中和”双碳目标的实现，各地大力推广分布式
光伏发电项目．某公司计划建设一座光伏发电站，若由甲工程队单独施工需
要3周，每周耗资8万元，若由乙工程队单独施工需要6周，每周耗资3万元．
答：写出答案 (包括单位)．
解决工程问题的基本思路：
1. 三个基本量：工作量、工作效率、工作时间.
它们之间的关系是：工作量=工作效率×工作时间.
2. 相等关系：工作总量=各部分工作量之和.
(1) 按工作时间，工作总量=各时间段的工作量之和；
(2) 按工作者，工作总量=各工作者的工作量之和.
3. 通常在没有具体数值的情况下，把工作总量看作“1”.
答：这批防护服原计划生产任为3100套．
5.某厂接到一所中学的冬季校服定做任务，计划用、两台大型设备进行
加工，如果单独用型设备，需要45天做完；如果单独用型设备，需要30
天做完；为了同学们能及时领到冬季校服，工厂决定由两台设备同时赶
制．
(1)填空：型设备的工作效率是_______，型设备的工作效率是_______；
(1)若甲、乙两工程队合作施工，需要几周完成?共需耗资多少万元?
(2)若需要最迟4周完成工程，请你设计一种方案，既保证按时完成任务，又
最大限度节省资金．（时间按整周计算）
人教版七年级上册数学：工程问题(公开课课件)
个人做要40小时完成。现在计划由一部分人先做4 小时，再增加两人和他们一起做8小时，完成这项工作．假设这些人的工作 效率相同，具体应安排多少人工作？ 分析 （1）人均效率（一个人做1小时完成的工作量）为
（2）有x人先做4小时，完成的工作量为 再增加2人和前一部分人一起做8小时，完成的工作量为 （3）这项工作分两段完成，两段完成的工作量之和为
(4) 完成解题过程。
课堂小结 本节课你学习了什么？
课堂检测
1、一项工程，甲工程队单独做40天可以完成，乙工程队单独 做80天可以完成，现由甲先独做10天，然后与乙共同完成了 余下的工程，问甲工程队一共做了多少天？
2、一件工作由一个人做要500小时完成，现在计划由一部分 人先做5小时，再增加8人和他们一起做10小时，完成了这项 工作，问：先安排多少人工作？
人教版七年级上册第三章一元一次方程
实际问题与一元一次方程
---- 工程问题
新疆生产建设兵团第四师77团中学 魏红
知识再现
我们探究了含有分母的一元一次方 程的解法，谁能说一下解方程的一般步 骤？
自学指导
1、小学学过的工程问题中工作量、工作效 率、工作时间三者有什么关系？
自学指导
2、填空:
（1）一件工作需要x小时完成，那么平均每小时完成的工作量
时，如果甲先做30分钟，然后甲、乙合作，问甲、乙合作还
需要多久才能完成全部工作？
分析：1. 知识准备 （1）工作量=
×
(2)工作时间=
×
（3工作效率=
注意：通常设完成全部工作的总工作量为
2. 设甲、乙合作还需要
小时才能完成全部工作
3. 相等关系：
列方程:
合作探究
1.加工一批零件，甲单独做要12小时，乙单独做 要15小时，若甲、乙两人合作要x小时，依题意 可列方程 2．一个道路工程，甲队单独施工9天完成，乙队 单独做24天完成。现在甲乙两队共同施工3天， 因甲另有任务，剩下的工程有乙队完成，问乙队 还需几天才能完成？
（2）有x人先做4小时，完成的工作量为 再增加2人和前一部分人一起做8小时，完成的工作量为 （3）这项工作分两段完成，两段完成的工作量之和为
(4) 完成解题过程。
课堂小结 本节课你学习了什么？
课堂检测
1、一项工程，甲工程队单独做40天可以完成，乙工程队单独 做80天可以完成，现由甲先独做10天，然后与乙共同完成了 余下的工程，问甲工程队一共做了多少天？
2、一件工作由一个人做要500小时完成，现在计划由一部分 人先做5小时，再增加8人和他们一起做10小时，完成了这项 工作，问：先安排多少人工作？
人教版七年级上册第三章一元一次方程
实际问题与一元一次方程
---- 工程问题
新疆生产建设兵团第四师77团中学 魏红
知识再现
我们探究了含有分母的一元一次方 程的解法，谁能说一下解方程的一般步 骤？
自学指导
1、小学学过的工程问题中工作量、工作效 率、工作时间三者有什么关系？
自学指导
2、填空:
（1）一件工作需要x小时完成，那么平均每小时完成的工作量
时，如果甲先做30分钟，然后甲、乙合作，问甲、乙合作还
需要多久才能完成全部工作？
分析：1. 知识准备 （1）工作量=
×
(2)工作时间=
×
（3工作效率=
注意：通常设完成全部工作的总工作量为
2. 设甲、乙合作还需要
小时才能完成全部工作
3. 相等关系：
列方程:
合作探究
1.加工一批零件，甲单独做要12小时，乙单独做 要15小时，若甲、乙两人合作要x小时，依题意 可列方程 2．一个道路工程，甲队单独施工9天完成，乙队 单独做24天完成。现在甲乙两队共同施工3天， 因甲另有任务，剩下的工程有乙队完成，问乙队 还需几天才能完成？
人教版七年级上册数学：工程问题(公开课课件)
2x 乙2km/h
A
50
B
2、甲乙相遇时,两人所走的路程与AB两地的距离有 什么关系？
路程角度：甲的路程 ＋ 乙的路程 =AB的距离 甲的速度×甲的时间＋乙的速度×乙的时间=AB的距 离3、甲行走的时间与乙行走的时间有什么关系？
时间角度：甲行走的时间=乙行走的时间
练习1：西安站和武汉站相距1500km，一列慢车从 西安开出，速度为65km/h，一列快车从武汉开出， 速度为85km/h，两车同时相向而行，几小时相遇？
西安(慢车)
慢车路程
快车路程
（快车）武汉
慢车路程＋快车路程＝总路程 慢车行驶的时间＝快车行驶的时间
相遇问题
延伸拓展
西安站和武汉站相距1500km，一列慢车从西安开出，速度为 65km/h，一列快车从武汉开出，速度为85km/h，若两车相 向而行，慢车先开30分钟，快车再开，快车行驶几小时后两车 相遇？
西安(慢车) 慢车先行路程
慢车后行路程
（快车）武汉 快车路程
（慢车先行路程＋慢车后行路程）＋快车路程＝总路程 慢车后行的时间＝快车行驶的时间
例2：甲、乙从一点出发，同向而 行，甲每小时走3km，乙每小时走 2km，乙先出发3小时，甲再出发追 赶乙，问甲要多久才能追上乙？
1、画出示意图：
乙 23
2x
行程问题
行程问题行程问题
——相遇、追及问题
速度、路程、时间之间的关系?
路程＝ 速度×时间 速度＝ 路程÷时间 时间＝ 路程÷速度
例1：甲、乙两人分别从相距50km 的A、B两地同时出发，相向而行， 甲每小时走3km，乙每小时走2km， 问他俩几小时后可以相遇？
1、画出示意图：
3km/h甲 3x
人教版七年级数学上册3.4 《调配问题、工程问题》一等奖优秀课件
X=2
答：应安排2人先做4h.
练习
2、一条地下管线由甲工程队单独铺设需要12天， 由乙工程队单独铺设需要24天。如果由这两个 工程队从两端同时施工，要多少天可以铺好这 条管线？
分析：把乙工的作工量作看效作 率单为位：1“1‘”，则甲的工作效率为11：2 24
根据工作效率×工作时间=工作量，得方程。
3.4实际问题与一元一次方程
调配问题、工程问题
调配问题、工程问题
自主探究 合作交流 建构知识
例1、某车间有22名工人，每人每天可以生产1200个螺钉或2000个 螺母。1个螺钉需要配2个螺母，为使每天生产的螺钉和螺母刚好配 套，应安排生产螺钉和螺母的工人各多少名？ 分析：每天生产的螺母数量是螺钉数量的 （2倍）时，它们刚好配套。 解： 设应安排x名工人生产螺钉，（22-x)名工人生产螺母
（8 x+2） 40
这两个工作量之和等于总工作量
例2、 整理一批图书，一起做8h,完
成这项工作。假设这些人的工作效率相同，具体
应先安排多少人工作？ 分析：成如的果工把作总量工为作量440x设,增为加1，2人则后人再均做效8率h完为成41的0 ，工x作人量先为做84(hx4完+02)
分析： 根据题意知B部件的数量是A部件数量的3倍这一等量关系 式得方程。
解：设应用x立方米钢材做A部件，则应用（6-x)立方米做B部 件，根据 题意得方程：
40x×3=(6-x) ×240
解方程，得
X=(6-x) ×2
6-x=2
3x=12 答：应用4立方米钢材做A部件，应用2立方米钢
X=4
材做B部件
作业布置： 1、制作一张桌子要用一个桌面和4条桌腿，1 m3 木材可制作20个桌面，或者制作400条桌 腿，现有12 m3 木材，应怎样计划用料才能制 作尽可能多的桌子？
数学人教版(2024)七年级上册 5.3.1配套问题与工程问题课件(共20张PPT)
3
2
解得y=13.
所以15+6-y=15+6-13=8（人）．
答：应安排13名工人生产A型配件，8名工人生产B型配件．
课堂练习
1.制作一张桌子要用1个桌面和4条桌腿，1立方米木材可制作20个桌面 或者400条桌腿．现有12立方米的木材，则下列方案能制作尽可能多的 桌子的是（ A ）
A．2立方米木材制作桌腿，10立方米制作桌面 B．3立方米木材制作桌腿，9立方米制作桌面 C．4立方米木材制作桌腿，8立方米制作桌面 D．5立方米木材制作桌腿，7立方米制作桌面
工人各多少名？
解：(1)设前3天应先安排x名工人生产，每名工人的工作效率为a. 由题意得：150a=3ax+5a(x+6)， 即3x+5(x+6)=150， 解得x=15．
答：前3天应先安排15名工人生产. (2)设应安排y名工人生产A型配件，则安排(15+6-y)名工人生产B型配件.
由题意得：600y 650(15 6 y) ，
新课引入
生活中，有很多需要进行配套的问题，如课桌和凳子、螺钉 和螺母、电扇叶片和电机等等，大家能举出生活中配套问题的例 子吗？
获取新知
探究点1 配套问题
配套问题通常从各个量之间的倍、分关系入手寻找相等关 系，建立方程.
解决配套问题的思路： 1.利用配套问题中物品之间具有的数量关系作为列方程的依据； 2.利用配套问题中的套数不变作为列方程的依据.
然后增加6名工人与他们一起再生产5天就能完成这批订单的生产任务．假
设每名工人的工作效率相同．
（1）前3天应先安排多少名工人生产？
（2）增加6名工人一起工作后，若每人每天使用机器可以生产600个A型配
5.3工程问题 课件 2024-2025学年数学人教版(2024)七年级上册
用为3 000元，则完成此项工程需付给甲、乙两队共多少元？
解：甲队的费用为2 500×(20＋4)＝60 000(元)，
乙队的费用为3 000×20＝60 000(元)，
60 000＋60 000＝120 000(元).
答：完成此项工程需付给甲、乙两队共120 000元.
1
2
3
4
5
6
7
8
9
10
11
12
由题意，得(5＋4)(x＋2)＋4 x ＝200，
解得 x ＝14， x ＋2＝16，
答：甲每小时加工16个零件，乙每小时加工14个零件.
1
2
3
4
5
6
7
8
9
10
11
12
5.3
课堂学练
实际问题与一元一次方程(3)——工程问题
知识点2：工作总量为“1”
3. 【例】一项工程，甲单独做要10天完成，乙单独做要15天完成，两人
5.3
分层检测
实际问题与一元一次方程(3)——工程问题
C培优
11. 一项工作，一个工人需要16天才能完成.开始先安排几个工人做1天
后，又增加1人和他们一起做2天，结果完成了这项工作的一半，假设每
个工人的工作效率相同.
(1)开始安排了多少个工人？
解：设开始安排了 x 个工人，由题意得
(+)
单独完成需要20小时；先由女生去做4小时，剩下的部分由全班同学一
起完成，则剩下的部分还需要几个小时完成？
解：设剩下部分还需要 x 个小时完成，
+
由题意得 ＋
＝1，
Байду номын сангаас
解：甲队的费用为2 500×(20＋4)＝60 000(元)，
乙队的费用为3 000×20＝60 000(元)，
60 000＋60 000＝120 000(元).
答：完成此项工程需付给甲、乙两队共120 000元.
1
2
3
4
5
6
7
8
9
10
11
12
由题意，得(5＋4)(x＋2)＋4 x ＝200，
解得 x ＝14， x ＋2＝16，
答：甲每小时加工16个零件，乙每小时加工14个零件.
1
2
3
4
5
6
7
8
9
10
11
12
5.3
课堂学练
实际问题与一元一次方程(3)——工程问题
知识点2：工作总量为“1”
3. 【例】一项工程，甲单独做要10天完成，乙单独做要15天完成，两人
5.3
分层检测
实际问题与一元一次方程(3)——工程问题
C培优
11. 一项工作，一个工人需要16天才能完成.开始先安排几个工人做1天
后，又增加1人和他们一起做2天，结果完成了这项工作的一半，假设每
个工人的工作效率相同.
(1)开始安排了多少个工人？
解：设开始安排了 x 个工人，由题意得
(+)
单独完成需要20小时；先由女生去做4小时，剩下的部分由全班同学一
起完成，则剩下的部分还需要几个小时完成？
解：设剩下部分还需要 x 个小时完成，
+
由题意得 ＋
＝1，
Байду номын сангаас
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
4 人数？
感悟与反思 ☞
小试牛刀
1、现有一份稿件需要打印，小张5小时可以打完这份 稿件，小李3小时可以打完这份稿件，如果两人合打， 需几小时可以打完？
2、整理一批数据，由一个人做要80 h完成．现在计
划先由一部分人做2 h，再增加5人和他们一起做8 h， 完成这项工作的 3 ．怎样安排参与整理数据的具体
单位时间的工作量叫做工作效率 工作效率×工作时间 = 工作量
2、某公司安排甲工程队完成一项工程，甲工程队的工作 效率为 1 ，甲工程队工作了7天，则甲工程队已完成的
25 7
工作量为 25 ；
3、一项工作甲单独做5天完成，乙单独做10天完成，
1
那么甲的工作效率是 51 ，
乙的工作效率是 10 ，
两人合作1天完成的工作量是
实际问题与一元一次方程
第二课时 工程问题
学习目标： 1、能够理解工作效率的含义； 2、能够理解工作效率、工作时间、工作量之间 的关系； 3、能正确找到列方程的依据；
☞比一比,赛一赛.
看谁做得好,看谁做得快！
1、甲同学单独完成一项任务需要5小时，那么他一个小时完成
1
的工作量为 5 ；（总工作量看做单位“ 1 ”）
4、完成的工作量是多少？
第一段的工作量 + 第二段的工作量 = 总工作量
问题情境 2 整理一批图书，由一个人做要40 h完成．现在计划由一
部分人先做4 h，再增加2人和他们一起做8 h，完成这项工 作．假设这些人的工作效率相同，具体应安排多少人工作？
交流讨论：
5、x人的工作量是多少？
(x+2)人的工作量是多少？
1 1 5 10
，
1 1 3 9 或 1 3 1 3 9 两人合作3天完成的工作量是 5 10 10 5 10 1。0
问题情境 1
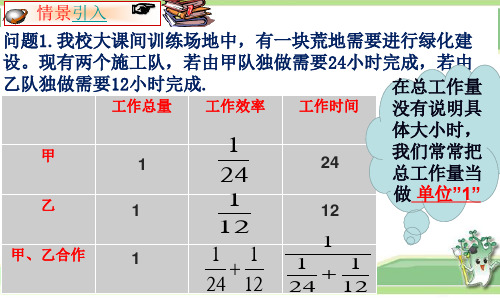
一条地下管线由甲工程队单独铺设需要12天，由乙工 程单独铺设需要24天，如果有这两个工程队从两端同时施 工，要多少天可以铺好这条管线？
思考并回答：
1、甲乙各自的工作效率是多少？
2、x个人合作的工作效率是多少？
问题情境 2
整理一批图书，由一个人做要40 h完成．现在计划由一 部分人先做4 h，再增加2人和他们一起做8 h，完成这项工 作．假设这些人的工作效率相同，具体应安排多少人工作？
交流讨论：
3、任务是如何完成的？ 第一段：①x人先一起工作4 h 第二段：②(x+2)人再一起工作8 h
4、工作量该如何计算？
5、x人的工作量是多少；(x+2)人的工作量是多少？
问题情境 2
整理一批图书，由一个人做要40 h完成．现在计划由一 部分人先做4 h，再增加2人和他们一起做8 h，完成这项工 作．假设这些人的工作效率相同，具体应安排多少人工作？
交流讨论：
1、每个人工作效率是多少？
即人均效率1 甲的工效×来自时 乙的工效×工时= = =
问题情境 2
整理一批图书，由一个人做要40 h完成．现在计划由一 部分人先做4 h，再增加2人和他们一起做8 h，完成这项工 作．假设这些人的工作效率相同，具体应安排多少人工作？
交流讨论：
1、每个人工作效率是多少？
2、 x个人合作的工作效率是多少？
3、任务是如何完成的？
甲的工作效率 = ，乙的工作效率 =
2、任务是如何完成的？
甲乙合作同时施工
问题情境 1 一条地下管线由甲工程队单独铺设需要12天，由乙工
程单独铺设需要24天，如果有这两个工程队从两端同时施 工，要多少天可以铺好这条管线？
思考并回答：
3、工作量该如何计算？
①工作量 = 合作工作效率×合作时间 ②工作量 = 甲的工作量 + 乙的工作量
感悟与反思 ☞
小试牛刀
1、现有一份稿件需要打印，小张5小时可以打完这份 稿件，小李3小时可以打完这份稿件，如果两人合打， 需几小时可以打完？
2、整理一批数据，由一个人做要80 h完成．现在计
划先由一部分人做2 h，再增加5人和他们一起做8 h， 完成这项工作的 3 ．怎样安排参与整理数据的具体
单位时间的工作量叫做工作效率 工作效率×工作时间 = 工作量
2、某公司安排甲工程队完成一项工程，甲工程队的工作 效率为 1 ，甲工程队工作了7天，则甲工程队已完成的
25 7
工作量为 25 ；
3、一项工作甲单独做5天完成，乙单独做10天完成，
1
那么甲的工作效率是 51 ，
乙的工作效率是 10 ，
两人合作1天完成的工作量是
实际问题与一元一次方程
第二课时 工程问题
学习目标： 1、能够理解工作效率的含义； 2、能够理解工作效率、工作时间、工作量之间 的关系； 3、能正确找到列方程的依据；
☞比一比,赛一赛.
看谁做得好,看谁做得快！
1、甲同学单独完成一项任务需要5小时，那么他一个小时完成
1
的工作量为 5 ；（总工作量看做单位“ 1 ”）
4、完成的工作量是多少？
第一段的工作量 + 第二段的工作量 = 总工作量
问题情境 2 整理一批图书，由一个人做要40 h完成．现在计划由一
部分人先做4 h，再增加2人和他们一起做8 h，完成这项工 作．假设这些人的工作效率相同，具体应安排多少人工作？
交流讨论：
5、x人的工作量是多少？
(x+2)人的工作量是多少？
1 1 5 10
，
1 1 3 9 或 1 3 1 3 9 两人合作3天完成的工作量是 5 10 10 5 10 1。0
问题情境 1
一条地下管线由甲工程队单独铺设需要12天，由乙工 程单独铺设需要24天，如果有这两个工程队从两端同时施 工，要多少天可以铺好这条管线？
思考并回答：
1、甲乙各自的工作效率是多少？
2、x个人合作的工作效率是多少？
问题情境 2
整理一批图书，由一个人做要40 h完成．现在计划由一 部分人先做4 h，再增加2人和他们一起做8 h，完成这项工 作．假设这些人的工作效率相同，具体应安排多少人工作？
交流讨论：
3、任务是如何完成的？ 第一段：①x人先一起工作4 h 第二段：②(x+2)人再一起工作8 h
4、工作量该如何计算？
5、x人的工作量是多少；(x+2)人的工作量是多少？
问题情境 2
整理一批图书，由一个人做要40 h完成．现在计划由一 部分人先做4 h，再增加2人和他们一起做8 h，完成这项工 作．假设这些人的工作效率相同，具体应安排多少人工作？
交流讨论：
1、每个人工作效率是多少？
即人均效率1 甲的工效×来自时 乙的工效×工时= = =
问题情境 2
整理一批图书，由一个人做要40 h完成．现在计划由一 部分人先做4 h，再增加2人和他们一起做8 h，完成这项工 作．假设这些人的工作效率相同，具体应安排多少人工作？
交流讨论：
1、每个人工作效率是多少？
2、 x个人合作的工作效率是多少？
3、任务是如何完成的？
甲的工作效率 = ，乙的工作效率 =
2、任务是如何完成的？
甲乙合作同时施工
问题情境 1 一条地下管线由甲工程队单独铺设需要12天，由乙工
程单独铺设需要24天，如果有这两个工程队从两端同时施 工，要多少天可以铺好这条管线？
思考并回答：
3、工作量该如何计算？
①工作量 = 合作工作效率×合作时间 ②工作量 = 甲的工作量 + 乙的工作量