多重自相关函数在微弱正弦信号检测中的应用_李一兵
微弱信号检测——基于自相关检测的微弱信号分析与仿真

器问世[5],锁相放大器在微弱信号的测领域中受到了广泛的重视与应用[5]。在过去的几十年 里, 锁相放大器的研究有了突飞猛进的发展, 锁相放大器由早期的模拟电路发展到现在的数 字电路,其性能有了很大的改善,提高了系统的精度和拓宽了动态范围。锁相放大器的原理 主要是应用相干检测完成对待测信号的频率迁移过程。 近些年来, 国内对于锁相放大器的研究有了很大的进展, 主要的研究公司有南京鸿宾微 弱信号检测有限公司等[5]。其对具有代表性的是 HB-211 精密双相锁相放大器,其输入信号 频率范围 5Hz〜lOOKHz,输出总动态范围大于 120dB。 相比与国内,国外对锁相放大器的研究比较成熟,国外代表性的锁相放大器有 SRS(sta nford Research System)公司的 SR8XX 系列[5], 日本 NF 公司的 LI5630/5640 锁相放大器和美 国 SIGNAL RECOVERY 公司的 Model7265 系列锁相放大器比较具代表性的锁相放大器 Mo del7265[5]。 Model7265 为数字双相锁相放大器,输入信号频率范围为 0.001Hz〜250KHz,最大动态 范围大于 100dB, 具有双参考模式。新一代的锁相放大器具有较为理想的动态范围和稳定性 。目前,相比于国内,国外的输入信号频率范围、稳定性等较好与国内,国内锁相放大器的 性能仍有很大的提升空间。 1.4 研究的内容 本文主要讲述了微弱信号检测中的相关检测法以及 MATLAB 的仿真。 第一节,相干检测的原理。简要说明了微弱信号检测的原理。详细说明了自相关检测和 互相关检测的原理,并简单的对两者进行了比较。 第二节,相干检测的 MATLAB 仿真。给出了 MATLAB 的仿真程序。 第三节,总结。总结了这学期的课程学习,以及对微弱信号检测这门课程的理解。
基于多重自相关算法的微弱正弦信号检测技术

基于多重自相关算法的微弱正弦信号检测技术
范晓志
【期刊名称】《机电产品开发与创新》
【年(卷),期】2015(0)6
【摘要】离散小波变换具有时频分析特性,可把信号的细微变化反应出来,可明显提高信号的信噪比,在用小波变换进行预处理的前提下,利用正弦信号的特殊性质,在信号未知的情况下通过多重自相关运算可检测出埋没于噪声中的微弱正弦信号.讨论了多重自相关法在白噪声背景下、有色噪声背景下等情况的检测效果,并给出仿真结果.
【总页数】3页(P107-108,125)
【作者】范晓志
【作者单位】北京工商大学材料与机械工程学院,北京102488
【正文语种】中文
【中图分类】TN911
【相关文献】
1.基于多重自相关微弱正弦信号的检测 [J], 陈明奎;刘正平
2.多重自相关函数在微弱正弦信号检测中的应用 [J], 李一兵;岳欣;杨莘元
3.用多重自相关法检测微弱正弦信号 [J], 陈明奎;刘正平
4.基于小波分析和多重自相关法的微弱信号检测技术 [J], 范晓志;王长广;黄晓红;宋学君
5.微弱正弦信号的互相关——混沌系统合成检测技术 [J], 路鹏;钟时;谭力
因版权原因,仅展示原文概要,查看原文内容请购买。
用多重自相关法检测微弱正弦信号

=
一
l ys ×fr i r( s+ a E r )( ) l f f
i (×( f Hr f ) r i ( )× ( ) f H r f
. .
+
3
上 , 分利用 此 软件 的特 点 , 建 虚 拟 仪器 , 充 构 实现 对 数据 的仿 真。实 验结 果表 明该方 法 可有效 提高 对信
z( )= s t + ( )= As ( t+ ) ( ) t () t i w + n t
摘 要 : L b E 平 台的基 础上 , 在 aVl W 研究 了利用多重 自相关来检测微弱正弦信号的方法 。此方法利用 正弦函 数的特性 , 通过 多重 自相关运算 , 再对信号进行频谱分析 , 就能准确检测 出湮没于 强大噪声 的微 弱正弦信号 的频率 信息和幅值信息 。 关键词 : 动与波 ;a VlW ; 振 L b E 弱信号检测 ; 多重 自相关 中 图分 类 号 : 9 16 T 6 . TN 1 . ; H15 3 文献标识码 : A
在工 程测 试 中 , 杂 噪声 的正 弦 信 号 是一 种 比 夹
较常见的信号 , 尤其是在旋转机械的故障诊断当中 ,
检 测 出湮 没 于强 噪 声 背景 的微 弱 正 弦信 号 , 进 一 对 步排查 故 障是 十分 必 要 的 。为 此 , 文 研 究 了多 重 本 自相关 函数 时域 检测 法 。鉴于 实际 的信号 分析 仪器
如下
相关 函数 可 以表 示为
1 r 丁
尺() 一r r
寺 (xt r Jxt (+ ) )
( 1 )
信号的自相关函数
假 设测量 过 程 具 备各 态 历 经性 , 可 以利 用 样 则 本 函数 的 自相 关 函数 来 代 替 随 机 过 程 的 自相 关 函 数 。设 待测 正 弦信号 为 s t =As (U + ) 噪声 () i c , n t 信号 为 ( )则 输入 信号 为 t,
基于MATLAB微弱信号的相关检测设计与仿真
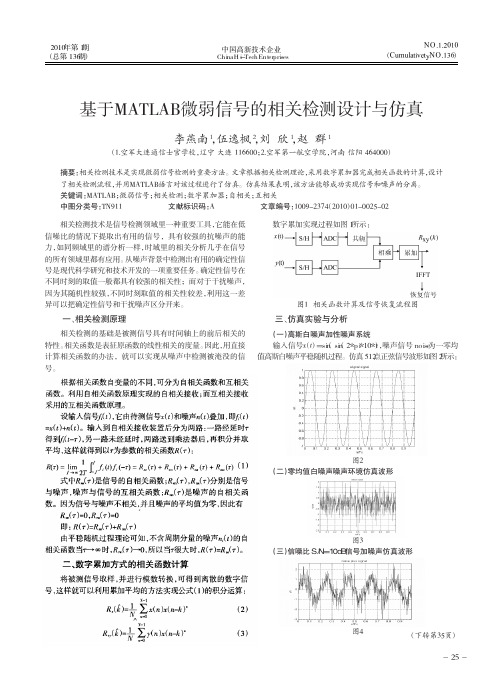
图2 (二)零均值白噪声噪声环境仿真波形
与噪声,噪声与信号的互相关函数;Rn(n τ)是噪声的自相关函
数。因为信号与噪声不相关,并且噪声的平均值为零,因此有
Rs(n τ)=0,Rn(s τ)=0
即:R(τ)=R(ss τ)+Rn(n τ)
由平稳随机过程理论可知,不含周期分量的噪声n(i t)的自 相关函数当τ→∞时,Rn(n τ)→0,所以当τ很大时,R(τ)=R(ss τ)。
中图分类号:TN911
文献标识码:A
文章编号:1009-2374(2010)01-0025-02
相关检测技术是信号检测领域里一种重要工具,它能在低 信噪比的情况下提取出有用的信号,具有较强的抗噪声的能 力,如同频域里的谱分析一样,时域里的相关分析几乎在信号 的所有领域里都有应用。从噪声背景中检测出有用的确定性信 号是现代科学研究和技术开发的一项重要任务。确定性信号在 不同时刻的取值一般都具有较强的相关性;而对于干扰噪声, 因为其随机性较强,不同时刻取值的相关性较差,利用这一差 异可以把确定性信号和干扰噪声区分开来。
数字累加实现过程如图1所示: 图1 相关函数计算及信号恢复流程图
一、相关检测原理
三、仿真实验与分析
相关检测的基础是被测信号具有时间轴上的前后相关的 特性。相关函数是表征原函数的线性相关的度量。因此,用直接 计算相关函数的办法,就可以实现从噪声中检测被淹没的信 号。
根据相关函数自变量的不同,可分为自相关函数和互相关 函数。利用自相关函数原理实现的自相关接收;而互相关接收 采用的互相关函数原理。
- 35 -
图3 (三)信噪比S/N=10dB信号加噪声仿真波形
二、数字累加方式的相关函数计算
将被测信号取样,并进行模数转换,可得到离散的数字信
一种认知无线电频谱检测新算法

t rs h e a g r h ,whc s s e e g e e t n a ig e n d ee t n meh d,t k s t e c a n lfd n n e .T lo t m n i ih u e n ry d tci s s l - o e d t ci t o o n o a e h h n e a ig a d
一ห้องสมุดไป่ตู้
种 认 知 无 线 电频 谱 检 测 新 算 法
李文生 , 李一兵
( 尔滨工程大 学 信息与通信工程学院 , 哈 黑龙 江 哈 尔滨 100 ) 50 1
摘
一
要: 认知无线 电(onterdo c 是一种革命性智能频谱共 享技术 , cgiv i, R) i a 可显著 提高频谱 使用率 . 该文 提出 种基于似然 比判决的协同频谱检测算 法用 于多用户认 知无线 电系统的主用户 检测. 算法特 别考虑 了主用 该
tu u i z to r m t iain.T sp p rp e e t i ei o d r t e tag rt m o h p c r m e i g o o n tv a i y — l hi a e r s n sa lk lh o a i t s lo h frt e s e tu s nsn fc g iie r d o s s o i
基于自相关函数和混沌理论的微弱正弦信号检测方法
图/ ・-・
万方数据
计量技术 )443 1+ 3
节后, 输入信号中的噪声已得到了充分的抑制, 因此整 个系统输出信噪比很高, 同时输入信噪比门限很低, 由 此而来, 我们可以得到信噪比改善非常高的系统, 更好 地实现了微弱正弦信号检测的目的。 五、 结论 本文首次提出了将上述两种方法相结合作弱信号 检测, 无论从理论上分析, 还是通过实验方法仿真, 都 证明了此方案是可行的、 有效的。此方法是相关检测 方法的一个突破。由于其具有很低的信噪 比 工 作 门 限, 且对噪声还有抑制能力 (对噪声有免疫力) , 除此之 外, 此方法还具有时域方法所具有的直观、 物理意义明 显、 硬件易实现等优点。因 此, 有望降低检测仪器成 本, 若将此理论应用到实际工程上一定具有很高的实
参考文献
[3]王冠宇等 8 混沌振子在具有强噪声背景的信号检测中的应用 8 仪器 ()) : 仪表学报, 3!!:, 3; )4! [)] <+(=5"838 #’>?8 @A=+B’* +&*’55=B+> =(" @CDD10 B+> &’6(=5 "EBE*B’+( ’( (+’&E E(F’>+(GE(B&8 HIII H(BE>(=B’+(=5 J+’(B @+(KE>E(*E +( (EL>=5 1EBM+>N&, 3!!)8 O+58)8;)3 9 ;;; [,] P8 @AE(8 Q8 @AE(8 =(" R8 S6GE(8 , H"E(B’KT’(6 @A=+B’* 0T&BEG F’= = M’E(E>U ( : BTVE *=&*="E G+"E5, HIII @+(B>+58 0T&BEG8 C=6=W’(6, 3!!:, ; ;) )! 9 ,/
基于自相关检测法和能量重心法的正弦信号频率估计算法

基于自相关检测法和能量重心法的正弦信号频率估计算法侯盼卫;杨录
【期刊名称】《科学技术与工程》
【年(卷),期】2014(014)003
【摘要】为了提高淹没在高斯白噪声中的实正弦信号的频率估计精度,提出了一种综合的结合自相关检测法和能量重心法的正弦信号频率估计算法.该算法首先通过多次自相关运算对输入信号进行预处理,可检测出淹没在噪声中的微弱正弦信号,来提高信噪比;然后对信号进行FFT(fast fourier transform)运算可得信号的功率谱,通过搜索最大值谱线的位置可粗估计出信号频率;最后运用离散频谱能量重心法,可精确估计出正弦信号的频率.仿真结果表明本算法在整个频段上频率估计性能比较稳定、频率估计的均方根误差更小,性能优于Rife算法、Quinn算法和能量重心法,并易于硬件实现,具有工程实用价值.
【总页数】6页(P97-102)
【作者】侯盼卫;杨录
【作者单位】中北大学电子测试技术国家重点实验室,太原030051;中北大学电子测试技术国家重点实验室,太原030051
【正文语种】中文
【中图分类】TP911.6
【相关文献】
1.基于LE和IIN算法的正弦信号频率估计算法 [J], 谭钏章;李宏伟;樊昌周;耿耿
2.基于自相关函数相位的正弦信号频率估计新算法 [J], 黄超;索继东;于亮
3.扩展自相关的正弦信号频率估计算法 [J], 黄超;索继东;于亮
4.基于快速傅里叶变换的正弦信号频率高精度估计算法 [J], 樊磊;齐国清
5.一种基于窄带自相关的实信号频率估计算法 [J], 曹燕; 王一歌; 李欣雯; 赵明剑; 丁泉龙
因版权原因,仅展示原文概要,查看原文内容请购买。
多重自相关函数在微弱正弦信号检测中的应用_李一兵

微弱信号检测的方法很多, 从噪声的角度来看, 可分为滤除噪声和添加噪声两类. 添加噪声的方法 利用了非线性系统的随机共振理论, 尽管其计算量 小, 检测速度快, 但目前只限于对微弱信号进行定性 的分析[ 1~ 4] . 与此相比, 滤除噪声是一种很传统的方 法, 但经过多年的研究, 其可行性是不容忽视的. 针 对微弱信号的时域处理, 自从 20 世纪 60 年代出现 Boxcar 积分 器以来, 一 直没有 特别有 效的 改进方 法[ 5, 6] . 为此, 提出了多 重自相关函数 时域检测法. 该方法在正弦信号频率未知的条件下可有效提高对 信号的检测能力.
摘 要: 研究了一种用于微弱正弦信号检测的新方 法, 该方法利用了正 弦函数的特 殊性质, 在信号未 知的情况 下, 通 过多次自相关运算成功的检测出埋没于强大噪声中的微弱正弦信号. 分别讨论 了多重自 相关法在白 噪声背景 下、有 色噪声背景下, 单一正弦信号、多个正弦信号等情况的检测效果, 并给出了具体 的仿真结 果. 此方 法在频率 测量中具 有极高 的准确性; 在幅度测量上, 精度略低, 但 通过多 次测量取 平均值, 仍 可达到 预期的精 度. 与以往 的弱信 号时域 处理方法比较, 多重自相关检测方法具有 理论推导简单、物理意义明确等特点, 应用前景广泛. 关键词: 信号检测; 自相关; 微弱信号; 有色噪声 中图分类号: T N 911. 711 文献标识码: A 文章编号: 1006- 7043( 2004) 04- 0525- 04
根据以上理论分析, 利用 MAT LAB 仿真可得
到如图 4 所示的结果.
从图 4 中可以 看到利用多重 相关可将淹没于
噪 声 中 的 信 号, 清 晰 的 提 取 出 来 ( 信 噪 比 为
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
哈 尔 滨 工 程 大 学学 报 Journal of H arbin Engineering Universit y
V ol. 25 . 4 Aug . 2004
多重自相关函数在微弱正弦信号检测中的应用
李一兵, 岳 欣, 杨莘元
( 哈尔滨工程大学 信息与通信工程学院, 黑龙江 哈尔滨 150001)
A2 2
cos(
).
( 5)
1. 2 信号与噪声的互相关函数
如果噪声为标准 的高斯白 噪声, 则 E[ n ( t ) ] 、
E[ n( t + ) ] 均为 0, 从而 E[ s ( t ) n ( t + ) ] 、E[ s( t +
) n( t) ] 也都为 0. 但在实际测量中, 由于观测时间有
限、噪 声 白 化 程 度 未 必 十 分 理 想, 从 而 导 致
E[ n( t ) ] 、E[ n ( t + ) ] 并不一定为零. 因此, 根据式
( 4) 信号与噪声的相关函数可写为
E[ s( t)
n( t +
)] =
1 T-
T-
s( t ) dt
0
1 T-
T-
n( t + ) dt. ( 6)
0
E[ s( t +
)
n( t) ] =
1 T-
T-
s( t + ) dt
0
1 T-
T-
n( t ) dt .
0
( 7)
1. 3 噪声的自相关函数
尽管在理论上高斯白噪声除 = 0 外, 其余值
均为 0. 但是在实际测量时, 噪声不可能达到理论所
设想的那样. 因此, RN ( ) ( 0) 总是存在的, 并且 是 的函数[ 9] . 但是其幅度与原噪声相比必然大幅
率或多次测量取平均来消除.
2. 2 双正弦信号的检测
对自相关运算的解法做了详细的推导后, 现在
图 4 单一信号检测结果 Fig. 4 T he result of a single signal
将在此基础上讨论双正弦信号的情况. 设输入信号为
y( t) = s( t) + n( t ) = s1( t) + s2( t) +
的叠 加. 如 果 忽 略 E [ s ( t + ) n ( t ) ] 和
A2 2T
T
cos[
0
( 2t +
) + 2 ] dt 的影响, 则 A 1 =
A2 2
.
利 用 这一 关 系 式,
可 推得 原 信 号 幅 度为
0 986, 与真实值 1 相 比, 误差 为 0. 014. 由于这一
误差是由噪声产生的, 因此, 可 以通过提高采样频
Estimation of sinusoidal parameters in powerful noise by multi_layer autocorrelation
L I Yi_bing, YU E Xin, YANG Xin_yuan
( Schoo l of Infor mation and Communication Eng ineering, Harbin Engineering U niversit y, Harbin 150001, China)
微弱信号检测的方法很多, 从噪声的角度来看, 可分为滤除噪声和添加噪声两类. 添加噪声的方法 利用了非线性系统的随机共振理论, 尽管其计算量 小, 检测速度快, 但目前只限于对微弱信号进行定性 的分析[ 1~ 4] . 与此相比, 滤除噪声是一种很传统的方 法, 但经过多年的研究, 其可行性是不容忽视的. 针 对微弱信号的时域处理, 自从 20 世纪 60 年代出现 Boxcar 积分 器以来, 一 直没有 特别有 效的 改进方 法[ 5, 6] . 为此, 提出了多 重自相关函数 时域检测法. 该方法在正弦信号频率未知的条件下可有效提高对 信号的检测能力.
) + n( t) . ( 1)
R Y( ) = E[ y( t) y( t + )] =
RS ( ) + E[ s( t) n ( t + ) ] +
E [ s ( t + ) n ( t ) ] + RN ( ) . ( 2) 对于具备各态历经性的过程, 可以利用样本函
5 26
哈尔滨工程大学学报
第 25 卷
数的时间自相关函数来代替随机 过程的自相关函
数. 此时, 自相关函数可以表示为
RX (
)=
lim
T
1 T
T
x( t) x ( t +
0
) dt .
( 3)
在实际测量中, 考虑到实际观测时间 T 总是有
限的, 因此, 通常按下式实现相关运算:
RX ( )
R^ X( t ) x ( t + ) dt.
骤多次, 过程如图 1. 自相关的次数越多, 信噪比提
高的就越多, 因此可检测出淹没于噪声中的微弱信 号.
图 1 多重相关检测法 Fig . 1 Multilay er autocorr elatio n
值得注意的是, 为了进一步化简式( 8) , 将积分 时间增加至 T , 从而必须得到 T - 之外的 s ( t + c) 和 n ( t + ) 的信息. 对于循环卷积, 不考虑噪声, 如果采样时间恰为信号周期的整数倍, 则可以用前 部分信息充当 s ( t + ) 从 T - 到 T 的信息, 如图 2 所示. 若采样时间不是信号周期的整数倍, 仍采用 这种信息替代, 则可能得到如图 3 所示的自相关图 形. 信号的幅度发生了巨大的变化, 无法继续计算. 为此, 提出了一种相关积分的新方法, 即将采样时间 改为 2T , 然后仅对 0~ T 积分, 从而有效的解决了 这一问题.
n( t) ] 的叠加; n1 ( t ) 是 E [ s ( t ) n ( t + ) ] 和
RN ( ) 的叠加.
对比式( 1) 和( 10) , 尽管两者信号的幅度和相位
不同, 频率却没有变化. 它通过相关运算增加了信噪
比, 但其改善程度是有限的, 因而限制了检测微弱信 号的能力.
多重自相关法将 y 1( t ) 当作 y ( t ) , 重复上述步
第4期
李一兵, 等: 多重自相关函数在微弱正弦信号检测中的 应用
5 27
图 2 信息转移 F ig. 2 T ransfo rm the sig nal
图 3 相关图形 Fig . 3 Autocor relation g raph
2 多重自相关函数在微弱信号检测中 的应用
2. 1 单一信号在高斯白噪声中的检测
T
cos[
0
( 2t +
)+
2
] dt +
1 T
T
s( t)dt
0
1 T
T
n( t+
0
) dt +
1 T
T
s( t + ) dt
0
1 T
T
n( t)dt+
0
RN (
).
( 9)
式( 2) 可改写为
y 1 ( t ) = A 1 cos( 1 t + 1 ) + n1 ( t ) . ( 10)
式中: A 1 cos( 1 t + 1 ) 是 R S ( ) 和 E [ s ( t + )
当 和 T 都很大时, 且噪声为标准的高斯白噪声, 式( 12) 可化简为[ 10]
根据以上理论分析, 利用 MAT LAB 仿真可得
到如图 4 所示的结果.
从图 4 中可以 看到利用多重 相关可将淹没于
噪 声 中 的 信 号, 清 晰 的 提 取 出 来 ( 信 噪 比 为
- 20 dB) . 在前面的理论分析中提到相关后的信号
A 1 cos( 1 t + 1 ) 是 R S ( ) 和 E[ s ( t + ) n ( t ) ]
摘 要: 研究了一种用于微弱正弦信号检测的新方 法, 该方法利用了正 弦函数的特 殊性质, 在信号未 知的情况 下, 通 过多次自相关运算成功的检测出埋没于强大噪声中的微弱正弦信号. 分别讨论 了多重自 相关法在白 噪声背景 下、有 色噪声背景下, 单一正弦信号、多个正弦信号等情况的检测效果, 并给出了具体 的仿真结 果. 此方 法在频率 测量中具 有极高 的准确性; 在幅度测量上, 精度略低, 但 通过多 次测量取 平均值, 仍 可达到 预期的精 度. 与以往 的弱信 号时域 处理方法比较, 多重自相关检测方法具有 理论推导简单、物理意义明确等特点, 应用前景广泛. 关键词: 信号检测; 自相关; 微弱信号; 有色噪声 中图分类号: T N 911. 711 文献标识码: A 文章编号: 1006- 7043( 2004) 04- 0525- 04
Abstract: A new method is int roduced t hat can be used in weak signal detect ion. Because t he sinusoidal sig nal has a particular aut ocorrelat ion t rait , it is possible t o detect the unknow n w eak signal in powerful noise. M ultiple st atuses are studied, such as sing le sine sig nal and m ulti_sine signal, w hich are disturbed by white noise or col ored noise. T hroug h t heory analysis and simulat ion, it is proved that t his method can obt ain ex act f requency measurements. It is less veracious in amplitude measurem ent , although t his problem can be solved by survey av erages. Compared w ith ot her means, this met hod can be widely used because it has many virt ues such as simple theoret ic deduction and ex plicit physical signif icat ion. Key words: w eak signal detection; auto correlat ion; sinusoidal signal; colored noise
