7.6 归纳-猜想-论证(含答案)
归纳、猜想、证明答案

1、xxxxn x x x x22221,41,31,21++++2、()()12121+-n n3、1+n n4、()1121111132222++<+++++n n n5、2211;815,47,23--n n6、21432112815,47,23,1--=====n n a a a a a 猜想下面用数学归纳法证明:(1) 当n=1时,由上述可知,显然成立(2) 假设n=k (k ∈N )时,命题成立,即2112--=k ka,那么()()()221111111111122122212212,1-++-++++++-=⇒+-=+=-+=+-∴-+=+=+=k k k k k k k k k k k k a a a a a a a a S S k k k k n 时∴φ4 ν=κ+1时,命题成立由(1)(2)知,对n ∈N ,命题成立7、解:猜想()()N n n a a a a aa n n ∈≥⎪⎪⎭⎫⎝⎛++++++22121111证明:n=1,1111≥⋅aa 显然,n=2,()42221121122121=+≥++=⎪⎪⎭⎫⎝⎛++a a a a a a a a 也成立,假设k a a ki i ki i 2111≥⎪⎪⎭⎫ ⎝⎛∙∑∑==,则当n=k+1时,()12212111111111111111111111212111111111+∑∑∑∑∑∑∑∑∑∑∑∑=++=++≥+⎪⎪⎭⎫ ⎝⎛++=+∙++⋅=⎪⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+=⋅==++===+=+==+=+=+=+=k k k a a a a a a a a a a a a a aa k k i ki k i i k ki ik i i k i i k k i i k k i i k i k k i i k k i i k i ik i i故n=k+1时,不等式也成立8、当n=1时,()12+n >3n当n=2时,()12+n =3n当n=3时,()12+n <3n9、()()N n n n n q ∈≥=,2下面用数学归纳法证明: 当N n n ∈≥,2时,等式()11321-=++++-a aa a a n n n 成立1︒当n=2时,()()121212121=⨯=-=aa q ,结论成立2︒假设当n=k (k=2)时结论成立,则()()()()()()()1111111111111321-+=⎪⎭⎫⎝⎛-+++=++-+=-+=+-=++++++-a a a a a a a a aa a k k k k k k k k k k k k k kk k即当n=k+1时结论成立由1︒、2︒可知,对于大于1的自然数n ,存在()n n q =,使等式()()1121-=+++-a aa a n n n q 恒成立10、n+111、(1)n2(2)()12221++-n n n n(3)()()()N k k n n k n n ∈⎪⎪⎩⎪⎪⎨⎧=--=+22122112、证明:设()522≥>k k k,则当n=k+1时,()()()()⎪⎭⎫ ⎝⎛>⋅>-+=--+++=⋅>⋅=-+-++2212122211112222222221k k k k k k k k k k k综上所述,n=1或n=5时,()2f>1122+-nn ;n=2或4时,()2f=1122+-nn;n=3时,()2f<1122+-nn.13、a a a a a a sin 3cos sin 2cos 32==猜想a na a n sin cos =以下用数学归纳法证明:1︒当n=1时,a aa sin cos 1=,猜想正确 2︒假设当n=k 时猜想正确,即a ka a k sin cos =,则()[]()a a k a a ka a ka ka a akaa k a a a kk sin 1cos sin sin sin cos cos sin cos sin cos 11sin cos 1+=-=-=-+-=+∴φ4 ν=κ+1时,猜想也正确据1︒、2︒可知,对任意的n ∈N ,猜想都正确14、(1)⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛3,3,2,221b a b a P P (2)猜想⎪⎭⎫ ⎝⎛++=1,1n b n aP n ,下面用数学归纳法证之: n=1时,已得;假设n=k 时,⎪⎭⎫ ⎝⎛++1,1k b k a P k ,通过(0,b ),⎪⎭⎫⎝⎛+0,1k a 的直线方程为()111=++y bx ak ,与x a b y =联立得⎪⎭⎫ ⎝⎛+++2,21k b k a P k ,也即当n=k+1时,猜想也真.15、(n-2)π16、()321-n n17、22+-n n18、n 219、()12221++-n n n n20、⎪⎪⎩⎪⎪⎨⎧=--=+k n n k n n 2,212,2121、证明:⇒=+=+++==++=++=⇒=⇒=++0111,0111110133654363232332S S zzzS S zzzz S zzz z z 猜想3=Sn。
2015届广东高考数学(理)一轮课件【7.6】数学归纳法

只要完成这两个步骤,就可以断定命题对从 n0 开始的所 有正整数 n 都成立.
基础知识 题型分类 思想方法 练出高分
基础知识·自主学习
夯基释疑
夯实基础 突破疑难
题号
1 2 3 4 5
答案
(1)× (2) × (3) × (4) × (5) √ (6) √
解析
C C
1 1 - 2n+1 2n+2
2k
(2n-1)(n∈N+).
- 1)(2k+ 1)· 2= 2k 1· 1· 3· 5· „· (2k-
+
1)(2k+ 1),
这就是说当 n=k+1 时等式也成立.
由①②可知,对所有 n ∈N+ 等式 成立.
基础知用数学归纳法证明等式
思维启迪 解析 思维升华
由(1)(2)可知,对一切 n∈N*等式都成立.
基础知识 题型分类 思想方法 练出高分
题型分类·深度剖析
题型二 用数学归纳法证明不等式
思维启迪 解析 思维升华
【例 2】 已知函数 f(x)=ax 3 2 1 - x 的最大值不大于 ,又 2 6 1 1 1 当 x∈[ , ]时,f(x)≥ . 4 2 8 (1)求 a 的值; 1 (2)设 0<a1< ,an+1=f(an), 2 1 * n∈N ,证明:an< . n+ 1
基础知识 题型分类
3 由题意,知 f(x)=ax- x2= 2 3 a 2 a2 - (x- ) + . 2 3 6 1 a a2 1 又 f(x)max≤6,所以 f(3)= 6 ≤6. (1)解
所以 a2≤1.
1 1 1 又 x∈[4,2]时,f(x)≥8, a 3 1 1 1 2-8≥8, f2≥8, 所以 即 1 1 f ≥ , a- 3 ≥1, 4 8 4 32 8
专题一---归纳猜想问题

专题一归纳猜想问题一.考点扫描:专题概述:归纳猜想问题也是探索规律型问题,这类问题一般给出一组具有某种有规律的数、式、图形,或是给出与图形有关的操作变化过程,或某一具体的问题情境,通过认真观察、分析推理,探究其中蕴含的规律,进而归纳或猜想出一般性的结论.考查学生的归纳、概括、类比能力.有利于培养学生思维的深刻性和创造性.思路分析:解决这类题的基本思路是“观察→归纳→猜想→证明(验证)”,具体做法:1.认真观察所给的一组数、式、图等,发现它们之间的关系;2.根据它们之间的关系分析、概括,归纳它们的共性和蕴含的变化规律,猜想得出一个一般性的结论;3.结合题目所给的材料情景证明或验证结论的正确性.二.典例精析:考点一:数式归纳猜想题:【例1】.(2013•淄博)如下表,从左到右在每个小格中都填入一个整数,使得任意三个相邻格子所填整数之和都相等,则第2013个格子中的整数是﹣2.﹣4 a b c 6 b ﹣2 …考点:规律型:数字的变化类.分析:根据三个相邻格子的整数的和相等列式求出a、c的值,再根据第9个数是﹣2可得b=﹣2,然后找出格子中的数每3个为一个循环组依次循环,在用2013除以3,根据余数的情况确定与第几个数相同即可得解.解答:解:∵任意三个相邻格子中所填整数之和都相等,∴﹣4+a+b=a+b+c,解得c=﹣4,a+b+c=b+c+6,解得a=6,所以,数据从左到右依次为﹣4、6、b、﹣4、6、b,第9个数与第三个数相同,即b=﹣2,所以,每3个数“﹣4、6、﹣2”为一个循环组依次循环,∵2013÷3=671,∴第2013个格子中的整数与第3个格子中的数相同,为﹣2.故答案为:﹣2.考点二:图形归纳猜想题:【例2】. (2012宁波)用同样大小的黑色棋子按如图所示的规律摆放:(1)第5个图形有多少颗黑色棋子?(2)第几个图形有2013颗黑色棋子?请说明理由。
考点三:数形结合归纳猜想题:【例3】.(2012益阳)观察图形,解答问题:考点四:类比归纳猜想题:【例4】.(2013江西)某数学活动小组在作三角形的拓展图形,研究其性质时,经历了如下过程:●操作发现:在等腰△ABC 中,AB=AC ,分别以AB 和AC 为斜边,向△ABC 的外侧作等腰直角三角形,如图1所示,其中DF ⊥AB 于点F ,EG ⊥AC 于点G ,M 是BC 的中点,连接MD 和ME ,则下列结论正确的是 ①②③④ (填序号即可) ①AF =AG =21AB ;②MD=ME ;③整个图形是轴对称图形;④∠DAB =∠DMB . ●数学思考:在任意△ABC 中,分别以AB 和AC 为斜边,向△ABC 的外侧..作等腰直角三角形,如图2所示,M 是BC 的中点,连接MD 和ME ,则MD 和ME 具有怎样的数量和位置yx关系?请给出证明过程; ●类比探索:在任意△ABC 中,仍分别以AB 和AC 为斜边,向△ABC 的内侧作等腰直角三角形,如图3所示,M 是BC 的中点,连接MD 和ME ,试判断△MED 的形状. 答: .三.专题精练:1.(2013东营)如图,已知直线l :y=33x ,过点A (0,1)作y 轴的垂线交直线l 于点B ,过点B 作直线l 的垂线交y 轴于点A 1;过点A 1作y 轴的垂线交直线l 于点B 1,过点B 1作直线l 的垂线交y 轴于点A 2;……按此作法继续下去,则点A 2013的坐标为 .2.如图,圆柱形容器中,高为1.2m ,底面周长为1m ,在容器内壁..离容器底部0.3m 的点B 处有一蚊子,此时一只壁虎正好在容器外壁..,离容器上沿0.3m 与蚊子相对..的点A 处,则壁虎捕捉蚊子的最短距离为 m (容器厚度忽略不计) 3.(2012•珠海)观察下列等式: 12×231=132×21, 13×341=143×31, 23×352=253×32,6030A CB D A B34×473=374×43,62×286=682×26,…以上每个等式中两边数字是分别对称的,且每个等式中组成两位数与三位数的数字之间具有相同规律,我们称这类等式为“数字对称等式”.(1)根据上述各式反映的规律填空,使式子称为“数字对称等式”:①52×= ×25;②×396=693×.(2)设这类等式左边两位数的十位数字为a,个位数字为b,且2≤a+b≤9,写出表示“数字对称等式”一般规律的式子(含a、b),并证明.解:(1)①∵5+2=7,∴左边的三位数是275,右边的三位数是572,∴52×275=572×25,②∵左边的三位数是396,∴左边的两位数是63,右边的两位数是36,63×369=693×36;故答案为:①275,572;②63,36.(2)∵左边两位数的十位数字为a,个位数字为b,∴左边的两位数是10a+b,三位数是100b+10(a+b)+a,右边的两位数是10b+a,三位数是100a+10(a+b)+b,∴一般规律的式子为:(10a+b)×[100b+10(a+b)+a]=[100a+10(a+b)+b]×(10b+a),证明:左边=(10a+b)×[100b+10(a+b)+a]=(10a+b)(100b+10a+10b+a)=(10a+b)(110b+11a)=11(10a+b)(10b+a)右边=[100a+10(a+b)+b]×(10b+a)=(100a+10a+10b+b)(10b+a)=(110a+11b)(10b+a)=11(10a+b)(10b+a),左边=右边,所以“数字对称等式”一般规律的式子为:(10a+b)×[100b+10(a+b)+a]=[100a+10(a+b)+b]×(10b+a).。
归纳—猜想—证明

归纳—猜想—证明归纳法是由一系列有限的特殊事例得出一般结论的推理方法。
归纳法分为不完全归纳法与完全归纳法,数学归纳法是“完全归纳”的一种科学方法,对于无穷尽的事例,常用不完全归纳法去发现规律,得出结论,并设法予以证明,这就是“归纳—猜想—证明”的思想方法,1.什么是归纳法在初中学习平面几何时,常会遇到如下推理:三角形内角和为180°,直角三角形是三角形,所以直角三角形内角和为180°。
这种由一般命题推出特殊命题的推理方法,我们称为演绎法。
但很多时候,往往需要从特殊的事例推出一般的原理,例如,一个人通过若干天的观察,看到“太阳从东方升起”, 就推出一般结论:“今后的每一天太阳都从东方升起”,这种推理方法叫做归纳法。
归纳法在科学发展和社会生活中起着重要作用,如气象工作者、水文工作者根据积累的历史资料作气象预测、水文预测,用的就是归纳法归纳法有什么特点?来看两个问题。
问题1:这里有一袋球共10个,要判断这袋球的颜色是白色,还是其他颜色,请问怎么办?学生:一个个拿出来看一看。
教师:这一袋球都是白色的。
问题2:数列的通项公式()2255n a n n =-+,计算1234,,,a a a a 的值,可以得到什么结论?学生:该数列的前四项都是1,猜测该数列的所有项都是1教师:这是错误的结论,该数列第五项是25。
解决以上两个问题用的都是归纳法——用一些特殊事例推出一般结论。
为什么问题1的结论正确,问题2的结论错误呢?这是因为问题1中,一共10个球,全部看了一遍,结论当然正确。
问题2中,根据前4 项为1,推测到所有项都是1,由于自然数有无数多个,因此得出的结论不一定正确。
实际上在这两个问题中运用的归纳法是有区别的,问题1中把研究对象都一一考察到了,这样推出结论的归纳法称为完全归纳法(通过验证一切可能的特殊事例,从而得出一般性结论,这种归纳推理称为完全归纳法)。
问题2中,根据部分事实推出了更加一般的事实,这种推理方法称为不完全归纳法(通过验证有限的特殊事例,从中推断出一般性的结论,这种归纳推理称为不完全归纳法)。
归纳-猜测-论证

a +2 (ii) 假设 ak = 4k − 2 , 则当 n = k + 1 时, k +1 = 2S k +1 . 2 ak + 2 又 2Sk = = 2k ⇒ S k = 2k 2 2 ak +1 + 2 ∴ = 2( Sk + ak +1 ) = 2(2k 2+1 + 2) 2 = 2(2k 2 + ak +1 ) 4 ⇒ ak +1 = 4k + 2 = 4(k + 1) − 2
3
1 1 1 1 + ⋯ 1 + 1 + b2 bk bk +1
3
3
3
3
(1 + bk +1 )3 1 > bk +1 1 + = b2 k +1 bk +1
(1 + bk +1 )3 (1 + bk +1 )3 − bk2+1bk + 2 9k + 5 又 − bk + 2 = = 2 >0 2 2 bk +1 bk +1 bk +1
9. 用天平称质量,若砝码只能放一边,求证:用1, 2 , 4 ,⋯ , 2 n −1 克的砝码,可以称出 1, 2 , 3 , ⋯ , 2 n − 1 克的质量。
证明: 当 n = 1 时,用1 克砝码可以称出1 克的质量,命题成立。 (i)
(ii) 假设 n = k 时,命题成立, 即用 1, 2, 4,⋯ , 2k −1 克的砝码,
∴不能被 5 整除, 命题也成立。
上海市崇明区横沙中学高二数学学案:7.6归纳——猜想——论证缺答案

7.6 归纳-—猜想——论证
一、概念
在数学问题的探索中,为了寻求一般的规律,往往先考察一些特例,进行归纳,形成猜想,然后再去证明这些猜想正确与否。
一些与正整数有关的等式也可以通过这样的途径得到。
这就是归纳-—猜想—-论证的原理.
二、举例
例1、依次计算数列 ,1234321,12321,121,1++++++++++++的前四项的值,由此猜想,123)1()1(321++++-++-++++= n n n a
n 的有限项表达式,并用数学归纳法加以证明。
例2、已知数列 )13)(23(1,,1071,741,411+-⨯⨯⨯n n ,设n S 为该数列的前n 项和,计算4321,,,S S S S 的值,根据计算结果猜测n S 关于n 的表达式,并用数
学归纳法加以证明.
三、课堂练习
1、(1)分别计算8642,642,42,2++++++的值.
(2)根据(1)的计算,猜想n 2642++++ 的表达式;
(3)用数学归纳法证明你的猜想。
2、(1)分别计算7531,531,31,1+-+--+-+--的值。
(2)根据(1)的计算,猜想)12()1(7531-+-+-+-=n a n n 的表达式;
(3)用数学归纳法证明你的猜想。
3、在数列}{n
a 中,*),2()1(22,111N n n n n n a a a n n ∈≥+++==- (1)求432,,a a a ;(2)猜想数列}{n a 的通项公式)(n f a n =,前用数学归纳法
证明你的猜想.
四、课外作业.
练习册15、16页,7。
6 归纳—-猜想-—论证A 组1、2、3、4及B
组1、2题。
高二数学上册 7.6《归纳-猜想-论证》沪教版
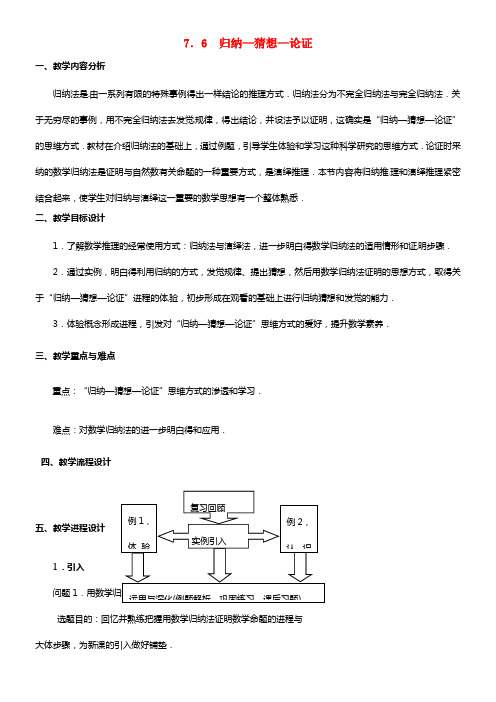
7.6 归纳—猜想—论证一、教学内容分析 归纳法是由一系列有限的特殊事例得出一样结论的推理方式.归纳法分为不完全归纳法与完全归纳法.关于无穷尽的事例,用不完全归纳法去发觉规律,得出结论,并设法予以证明,这确实是“归纳—猜想—论证”的思维方式.教材在介绍归纳法的基础上,通过例题,引导学生体验和学习这种科学研究的思维方式.论证时采纳的数学归纳法是证明与自然数有关命题的一种重要方式,是演绎推理.本节内容将归纳推理和演绎推理紧密结合起来,使学生对归纳与演绎这一重要的数学思想有一个整体熟悉.二、教学目标设计1.了解数学推理的经常使用方式:归纳法与演绎法,进一步明白得数学归纳法的适用情形和证明步骤.2.通过实例,明白得利用归纳的方式,发觉规律、提出猜想,然后用数学归纳法证明的思想方式,取得关于“归纳—猜想—论证”进程的体验,初步形成在观看的基础上进行归纳猜想和发觉的能力.3.体验概念形成进程,引发对“归纳—猜想—论证”思维方式的爱好,提升数学素养. 三、教学重点与难点重点:“归纳—猜想—论证”思维方式的渗透和学习.难点:对数学归纳法的进一步明白得和应用.四、教学流程设计五、教学进程设计 1.引入 问题1.用数学归纳法证明: 选题目的:回忆并熟练把握用数学归纳法证明数学命题的进程与大体步骤,为新课的引入做好铺垫.例1,体验复习回顾 实例引入 例2,认识运用与深化(例题解析、巩固练习、课后习题)2.归纳猜想咱们已经学习了用数学归纳法来证明一些等式,可是这些等式又是如何取得的呢?[说明] 引发学生试探,探求结论取得的可能方式:一是直接计算取得结论,二是归纳猜想.问题2.数列的通项公式22(55)n a n n =-+,计算1234,,,a a a a 的值,你能够取得什么结论?问题3.费马(Fermat )是17世纪法国闻名的数学家,他是解析几何的发明者之一,是对微积分的创建作出奉献最多的人之一,是概率论的开创者之一,他对数论也有许多奉献.费马以为,当n ∈N 时,221n+必然都是质数,这是他对n=0,1, 2,3,4作了验证后取得的.18世纪伟大的瑞士科学家欧拉(Euler )却证明了5221+=4 294 967 297=6 700 417×641,从而否定了费马的推测.问题4.设2()41f n n n =++,那么当n ∈N 时,()f n 是不是都为质数? (0)41f =,(1)43f =,(2)47f =,(3)53f =,(4)61f =,(5)71f =,(6)83f =,(7)97f =,(8)113f =,(9)131f =,(10)151f =,,(39)1601f =.可是(40)16814141f ==⨯是合数.找出运用归纳法犯错的缘故,并研究出计谋来!3.归纳猜想论证 在数学问题的探讨中,为了寻求一样规律,往往先考虑一些特例,进行归纳,形成猜想,这是归纳与猜想.但猜想的结论必然正确吗?不必然!通过归纳猜想的结论可能错误也可能正确,然后必然要去证明这些猜想的正确与否.证明一个命题为假命题只需要举出一个反例.证明一个命题为真命题需要逻辑推理.例1.依次计算数列1,1+2+1,1+2+3+2+1,1+2+3+4+3+2+1,…的前四项值,由此猜想123(1)(1)321n a n n n =++++-++-++++的有限项表达式,并加以证明.选题目的:(1)引导学生体验从特殊到一样的试探进程,形成归纳猜想的意识.(2)那个地址去掉了原题中“并用数学归纳法证明”的证明方式的要求,以期证明方式的开放性,引发学生更开阔的试探.如:(3)要证明2n a n =对一切正整数都成立,一个一个验证是不可能的.一些与正整数有关的命题能够用数学归纳法加以证明.例2.已知数列114⨯,147⨯,1710⨯,…,1(32)(31)n n -+,…,设n S 为该数列前n 项和,计算1234,,,S S S S 的值.依照计算结果猜想n S 关于n 的表达式,并用数学归纳法证明.选题目的:经历和体验“归纳—猜想—论证”的完整进程,明白得把握这一重要的思维方式.4.练习P36—1,2,35.小结本节课要紧学习用“归纳—猜想—论证”的方式分析和解决问题.归纳—猜想—论证是咱们分析和解决问题的经常使用方式,它经历三个进程:尝试,观看特例;体验,归纳猜想一样规律;理性,证明猜想.这也告知咱们在分析和解决问题时要“斗胆假设,警惕求证”.斗胆假设,也确实是斗胆猜想,这是探讨发觉真理的重要手腕,是制造的源泉;但对猜想要警惕求证,这是思维严谨的表现. 在证明进程中,咱们进一步学习了如何用数学归纳法进行演绎推理证明.6.作业P15—2,3 P16—4六、教学建议与说明1.以问题为中心.通过对问题1的分析与解决,追根溯源,提出疑惑.通过对问题2,3,4的感受体验,思维冲击,斗胆质疑.通过度析解决例题1,形成方式.2.以思维方式为主线.应切实让学生感受“归纳—猜想—论证”这一重要数学思维方式的进展进程和理性熟悉,将归纳推理和演绎推理紧密结合起来,使学生对归纳与演绎这一重要的数学思想有一个整体熟悉.。
7.6归纳—猜想——论证

2 2
∴由(1) (2)可知,等式对任何 n N 都成立。
1 1 1 1 , , , , , ,设 S n 为该数列前 n 项和,计算 2、已知数列 1 4 4 7 7 10 3n 2 3n 1
二、例题讲解:
测 an 1 2 3 4 n 1 n n 1 4 3 2 1 的表达式,并用数学 归纳法加以证明。
解: a1 1 1 , a2 1 2 1 2 , a3 1 2 3 2 1 3 ,
解: (1)当 n 1 时, f 1 1
1 3 , 2 2 4
1 1 3 8 2 4 1 2 , 22 3 4 9 3 6
(2)当 n 2 时, f 2 1
1 1 1 3 8 15 5 , (3)当 n 3 时, f 3 1 2 1 2 1 2 2 3 4 4 9 16 8
2
2
1、依次计算数列1,1 2 1,1 2 3 2 1,1 2 3 4 3 2 1,的前四项的值,由此猜
2
a4 1 2 3 4 3 2 1 42 ;
猜出: an 1 2 3 4 n 1 n n 1 3 2 1 n n N
S1 , S2 , S3 , S4 的值,根据计算结果猜测 S n 关于 n 的表达式,并用数学归纳法加以证明。
解一: S1
1 1 1 1 2 , S2 , 1 4 4 1 4 4 7 7 1 1 1 2 1 3 S3 , 1 4 4 7 7 10 7 70 10 1 1 1 1 3 1 4 S4 1 4 4 7 7 10 10 13 10 130 13
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【课堂例题】例1.计算并归纳出下列求和的一般公式,并证明.114=⨯ 111447+=⨯⨯ 1111447710++=⨯⨯⨯ 111114477101013+++=⨯⨯⨯⨯11111447710(32)(31)n n ++++=⨯⨯⨯-+例2.尝试推导正整数立方和公式3333123?n ++++=例3.在平面上画n 条直线,任何两条都相交,任意3条直线不共点,则这n 条直线将平面分成多少部分?【基础训练】1.观察下列数字:12343456745678910……猜想第n 行的各数之和n S =________________. 2= . 3任取一个正整数,反复进行下述两种运算:(1)若是奇数,就将该数乘3再加上1;(2)若是偶数,就将该数除以2.你能据此作出什么猜想?.4.已知数列{}n a 满足11a =,且*11429,n n n n a a a a n N ++-+=∈,通过计算若干项n a 后,可以猜想通项公式n a = .5.已知数列1111,,,,,,122334(1)n n ⨯⨯⨯+ 前n 项和为n S . (1)计算123,,S S S 的值; (2)推测计算n S 的公式并证明.6.在数列{}n a 中,*1121,2,2,(1)n n n a a a n n N n n -+==+≥∈+. (1)求234,,a a a ;(2)猜想数列{}n a 的通项公式()n a f n =,并用数学归纳法证明你的猜想.7.已知数列{}n a 满足:*2,n n S n a n N =-∈(*0,n a n N ≠∈)(1)求1234,,,a a a a .(2)猜想{}n a 的通项公式()n a f n =,并用数学归纳法加以证明.【巩固提高】8.是否存在常数,,a b c 使等式:222222421(1)2(2)()n n n n n an bn c ⋅-+⋅-++⋅-=++对于一切正整数n 都成立?证明你的结论.提示:先利用1,2,3n =求出一组,,a b c ,再…….9.是否存在大于1的正整数m 使得()(27)39n f n n =+⋅+对于任意正整数n 都能被m 整除?若存在,求出m 的最大值,并证明你的结论;若不存在,请说明理由.(选做)10.下面两题,任选1题完成:(1)如图,在圆内画2条相交弦,彼此分割成4条线段;画3条弦,彼此最多分割成9条线段;画4条弦,彼此最多分割成16条弦,那么①在圆内画5条弦,它们彼此最多分割成多少条线段?②在圆内画n 条弦,两两相交,彼此最多分割成多少条线段?用数学归纳法证明你的猜想.(2)证明:平面上的n 个圆,最多把平面分成22n n -+个区域.【温故知新】 11.已知函数()f x ,若(4)2f =,且对于任意*12,n n N ∈都有1212()()()f n n f n f n =+成立,猜想()f x 的表达式可以是 .【课堂例题答案】例1.1234,,,,47101331n n + 证:①当1n =时,等式显然成立;②假设当n k =时,等式成立,即11111447710(32)(31)31k k k k ++++=⨯⨯⨯-++ 当1n k =+时,111111447710(32)(31)(31)(34)1(34)1(31)(1)131(31)(34)(31)(34)(31)(34)34k k k k k k k k k k k k k k k k k k +++++⨯⨯⨯-++++++++=+===++++++++等式也成立;根据①②,对于任意*n N ∈,等式都成立. 证毕 例2.猜想:2233332(1)123(12)4n n n n +++++=+++= 证:①当1n =时,等式显然成立;②假设当n k =时,等式成立,即223333(1)1234k k k +++++= 当1n k =+时, 2222333333(1)(1)(44)123(1)(1)44k k k k k k k k ++++++++++=++= 22(1)(2)4k k ++= 等式也成立;根据①②,对于任意*n N ∈,等式都成立. 证毕例3.记n 条直线把平面分成n a 个部分.猜想:1(12)n a n =++++证:①当1n =时,结论显然成立;②假设当n k =时,结论成立,即 1(12)k a k =++++当1n k =+时,第1k +条直线与前面k 条直线都相交,有k 个交点,这k 个交点将这条直线分成1k +段,每段都将原有平面部分分成两个部分,因此1(1)1(12)11[12(1)]k k a a k k k k k +=++=++++++=++++++结论也成立;根据①②,对于任意*n N ∈,结论都成立. 证毕【习题答案】1.2(21)n -2.333n个 3.最终变为1(或者最终在1,2,4之间循环,这个就是著名的Collatz 猜想,尚未被证明)4.*65,21n n N n -∈- 5.(1)123123,,234S S S === (2)猜想:1n n S n =+. 证:①当1n =时,结论显然成立;②假设当n k =时,结论成立,即1k k S k =+ 当1n k =+时, 2111211(1)(2)1(1)(2)(1)(2)2k k k k k k S S k k k k k k k k ++++=+=+==++++++++ 结论也成立;根据①②,对于任意*n N ∈,结论都成立. 证毕 6.(1)234812315913,6,12334455a a a ==-==-==- (2)猜想:2*132,1n n a n N n -=⋅-∈+ 证:①当1n =时,结论显然成立;②假设当n k =时,结论成立,即21321k k a k -=⋅-+ 当1n k =+时,2111131322(32)(1)(2)1(1)(2)323(24)1323232(1)(2)1(1)(2)2k k k k k k k k a a k k k k k k k k k k k k k k -+---++=+=⋅-++++++++-+=⋅+-=⋅+=⋅-++++++ 结论也成立; 根据①②,对于任意*n N ∈,结论都成立. 证毕 7.(1)123437151,,,248a a a a ==== (2)猜想:*112,2n n a n N -=-∈ 证:①当1n =时,结论显然成立;②假设当n k =时,结论成立,即*112,2k k a n N -=-∈ 当1n k =+时,1112(1)2(1)k k k k a k S k S a +++=+-=+--,则112111(1)(1)1(2)222222k k k k k S k a a k k +--=+-=+-=+-=- 结论也成立;根据①②,对于任意*n N ∈,结论都成立. 证毕 8.存在11,,044a b c ==-= 提示:代入1,2,3n =得: 0164381918a b c a b c a b c ++=⎧⎪++=⎨⎪++=⎩解得:11,,044a b c ==-=,下面证明对于一切*n N ∈成立. 证:①当1n =时,等式显然成立;②假设当n k =时,等式成立,即22222242111(1)2(2)()44k k k k k k k ⋅-+⋅-++⋅-=- 当1n k =+时,222222221[(1)1]2[(1)2][(1)](1)[(1)(1)]k k k k k k k k ⋅+-+⋅+-++⋅+-++⋅+-+ 2222221(121)2(221)(21)0k k k k k k k k =⋅-+++⋅-++++⋅-+++222222[1(1)2(2)()][1(21)2(21)(21)]k k k k k k k k k =⋅-+⋅-++⋅-+⋅++⋅+++⋅+ 4222111(1)(21)(21)(12)(1)4442k k k k k k k k k ++=-++⋅+++=-+ 22(1)(1)(1)(2)[(1)2(21)](32)444k k k k k k k k k k k k ++++=-++=++= 242(1)[(1)1][(1)1](1)(1)444k k k k k ++-++++==- 等式也成立;根据①②,对于任意*n N ∈,等式都成立. 证毕9.max 36m =提示:(1)36,(2)108,(3)360f f f ===,因此猜测max 36m =证:①当1n =时,结论显然成立;②假设当n k =时,结论成立,即 ()(27)39k f k k =+⋅+能被36整除;当1n k =+时,1111(1)[2(1)7]39(27)39233[(27)39]63183()18(31)k k k k k k f k k k k f k +++-+=++⋅+=+⋅++⋅=+⋅++⋅-=+-显然131k --是偶数,因此118(31)k --也能被36整除,所以(1)f k +能被36整除;结论成立;根据①②,对于任意*n N ∈,结论都成立. 证毕10.(1)①如图,彼此最多分割成25条线段;②猜想:分割成2n 线段.证:①当2n =时,结论显然成立;②假设当(2)n k k =≥时,结论成立,即 k 条弦两两相交,彼此最多分割成2k 条弦当1n k =+时,第1k +条弦与原来k 条弦最多有k 个交点,因此第1k +条弦最多被分割成1k +段, 每一个交点又把原来的弦的某一段分割成两部分,因此总共比原来多了1k k ++条线段. 即1k +条弦两两相交,彼此最多分割成221(1)k k k k +++=+条弦结论也成立;根据①②,对于任意*,2n N n ∈≥,结论都成立. 证毕(2)①当1n =时,结论显然成立;②假设当n k =时,结论成立,即平面上的k 个圆,最多把平面分成22k k -+个区域;当1n k =+时,第1k +个圆与原来的每一个圆都交于2点,因此第1k +个圆上最多有2k 个交点, 第1k +个圆最多被分成2k 段,每一段都把原来平面区域分成两部分, 因此平面上的1k +个圆,最多把平面分成2222(1)(1)2k k k k k -++=+-++个区域, 结论也成立;根据①②,对于任意*n N ∈,结论都成立. 证毕11.2()log f x x =。
