管道沿程水头损失计算
沿程水头损失公式

沿程水头损失公式
1 沿程水头损失公式
沿程水头损失是将流体从一个管道节点流出一个节点又流回管道
的损耗,它是一个无穷小的能量量,沿着管道流动时会损耗一部分能量。
在这种情况下,Bernoulli定律可以用来估计沿程水头损失,它可以简单地通过压差和流量估算沿程水头损失。
Bernoulli定律给出了一个简单的沿程水头损失计算公式:hL= f
q2/2g。
在这个公式中,hL表示沿程水头损失,f表示运动阻力形象,q表示流量,g表示重力加速度。
例如,一个典型的气体管道中有一个从3000kPa到5000kPa的压
力变化,假设流量是2.5m3/s,重力加速度是9.8m/s2,那么管道的沿
程水头损失可由如上公式计算出来:hL= f q2/2g = 0.67m/s。
从上面的例子中可以看出,沿程水头损失是通过管道的压差和流
量之间的关系来计算的。
在实际的工程设计当中,应该根据管道的尺寸,材料,流速等条件来确定正确的沿程水头损失数值,以确保其管
道系统性能之间的有效比较和分析。
以上是关于沿程水头损失的介绍,它是一种由流体所造成的能量
损失,可以用Bernoulli定律来估算损失的数值,需要结合实际情况
来准确估算该系统的沿程水头损失。
管道沿程水头损失三种计算方法
铝合金管、镀锌钢管、锦塑软管
使用多年的旧钢管、铸铁管、离心浇筑
管长 L m
1280
管径 d mm
600
沿程水 头损 失 hf m m
17.15
0.600
152.4
100
0.100
5.98
1200
110
0.110
8.57
152.4
100
0.100
6.14
8.732615835
152.4
100
0.100
6.08
常用管材的C值表 管道种类 玻璃钢管 塑料管 石棉水泥管 C 160 150 140 130 120 110 100 90
管道的糙率n值表 管道种类 缸瓦管(带釉) 混凝土和钢筋混凝土管(雨水管) 混凝土和钢筋混凝土管(污水管) 石棉水泥管 铸铁管 钢管 玻璃钢管 n 0.013 0.013 0.014 0.012 0.013 0.012 0.0084
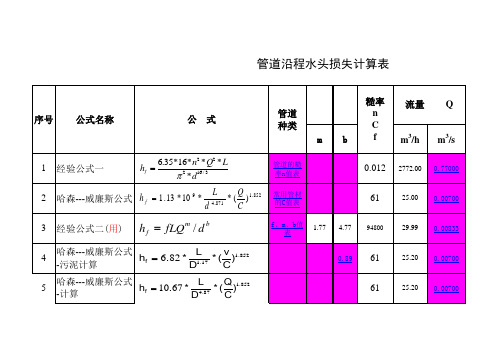
管道沿程水头损失计算表
糙率 n C f 0.012 61
1.77 4.77
94800
序号
公式名称
公
式
管道 种类 m b
பைடு நூலகம்
流量 m3/h
2772.00
Q m3/s
0.77000
1 2 3 4 5
经验公式一
6.35*16* n2 * Q2 * L hf 2 * d16 / 3
管道的糙 率n值表
哈森---威廉斯公式 h f 1 . 13 * 10 9 * 经验公式二(用)
0.948*105 0.861*10 5.65*10
5
1.77 1.74 1.85 1.85 1.9 2.0 2.0 2.0 2.0 2.0
管道沿程水头损失三种计算方法(自动计算)
混凝土和钢筋混凝土管(污水管) 石棉水泥管 铸铁管 钢管 玻璃钢管
0.014 0.012 0.013 0.012 0.0084
管、新(光滑)铸铁管
管、镀锌钢管、锦塑软管
半旧钢管、铸铁管 普通砼管
旧钢管、铸铁管、离心浇筑砼管
L d
4 . 871
*(
Q 1 .852 ) C
常用管材 的C值表 f、m、b值 表
2772.00
0.77000
h f fLQ m / d b
f、m、b值表 管道种类
29.99
0.00833
f
m
b
常用管材的C值表 管道种类 玻璃钢管
塑料硬管,玻璃钢管 铝管、铝合金管
0.948*105 0.861*105
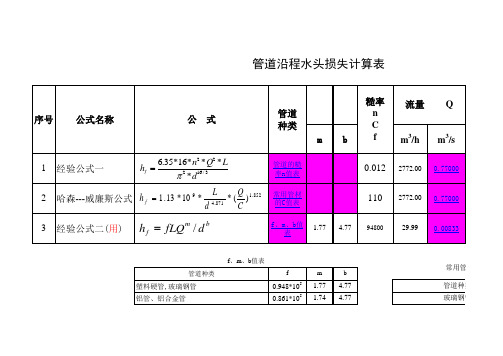
管道沿程水头损失计算表
糙率 n C f 0.012 110
1.77 4.77
94800
序 号
公式名称
公
式
管道 种类 m b
流量 m3/h
2772.00
Q m3/s
0.77000
1 2 3
经验公式一
6.35*16* n2 * Q2 * L hf 2 * d16 / 3
管道的糙 率n值表
哈森---威廉斯公式 h f 1 . 13 * 10 9 * 经验公式二(用)
管长 L m
1280
管径 d mm
600
沿程水 头损失 hf m m
17.15
0.600
1280
600
0.600
16.72
1200
110
0.110
8.57
常用管材的C值表 管道种类 玻璃钢管 C 160
管道沿程水头损失计算公式

管道沿程水头损失计算公式【最新版】目录1.管道沿程水头损失计算公式介绍2.公式中各参数的含义和计算方法3.计算实例及其分析4.结论正文一、管道沿程水头损失计算公式介绍管道沿程水头损失是指水流在管道中流动时所受到的阻力,它会影响管道系统的流动性能和效率。
管道沿程水头损失的常用计算公式为:H=(λ/d)×(L/d)+(u^2/2g)+Z1+Z2+...+Zn其中,H为沿程水头损失,λ为沿程阻力系数,d为管道直径,L为管道长度,u为管道平均流速,g为重力加速度,Z1、Z2、...Zn为管道中的各种压力损失。
二、公式中各参数的含义和计算方法1.沿程阻力系数(λ):沿程阻力系数是指水流在管道中流动时所受到的阻力大小,它与管道的形状、材质、粗糙度等因素有关。
在实际应用中,可以根据管道的尺寸和设计要求进行计算。
2.管道直径(d):管道直径是指管道横截面的直径,通常以毫米或英寸为单位。
3.管道长度(L):管道长度是指管道的长度,通常以米或英尺为单位。
4.管道平均流速(u):管道平均流速是指管道中水的平均流速,通常以米/秒或英尺/秒为单位。
平均流速可以根据管道直径和设计流量进行计算。
5.重力加速度(g):重力加速度是指物体受到的重力作用的大小,通常以米/秒或英尺/秒为单位。
6.压力损失(Z1、Z2、...Zn):压力损失是指水流在管道中流动时所受到的各种压力损失,通常包括沿程压力损失、局部压力损失、入口压力损失等。
这些压力损失的大小和种类可以根据具体设计要求进行计算。
三、计算实例及其分析假设有一段长度为100米、直径为0.1米的圆形管道,设计流量为10立方米/小时,管道材质为钢管,粗糙度为0.01毫米。
根据管道沿程水头损失计算公式,可以计算出沿程阻力系数为0.05,平均流速为0.5米/秒,各种压力损失的大小和种类可以根据具体设计要求进行计算。
根据计算结果,可以得出以下结论:1.沿程水头损失为5米。
这意味着水流在管道中流动时所受到的阻力大小为5米的水头。
管道水头损失核算

合计
9.520m
Hale Waihona Puke 蜗壳271-2002)、《水轮机基本技术条件》 (GB/T15468-2010) 《水力计算手册》(第二版)、《小型水电站 上》(天津大学水利系1976) 转轮D1= 主管管径 0.60 m 【据《DL/T5195》附录C1、C2】 支管径 0.40 m
水轮机 2 台 损失: hm=ξ*V^2/(2*g) 栅形系数β 1.83 湿周 X(m) 5.40 5.40
平均湿周 水力半径 谢才系数 沿程损失 沿损糙率n 局损系数ξ R(m) C X(m) hf(m) 3.64 0.231 46.08 0.017 0.05 0.000 湿周 X(m) 1.88 湿周 X(m) 1.88 湿周 X(m) 1.88 湿周 X(m) 1.88 湿周 X(m) 1.26 湿周 X(m) 2.51 沿程损失 水力半径 谢才系数 沿损糙率n 局损系数ξ R(m) C hf(m) 0.150 60.74 0.012 0.090 7.323 水力半径 谢才系数 沿损糙率n v支/v主= 局损系数ξ R(m) C 0.150 60.74 0.012 0.180 0.650 沿程损失 水力半径 谢才系数 沿损糙率n 局损系数ξ R(m) C hf(m) 0.150 60.74 0.012 0.108 0.571 沿程损失 水力半径 谢才系数 沿损糙率n 局损系数ξ R(m) C hf(m) 0.067 53.06 0.012 0.180 0.076 沿程损失 水力半径 谢才系数 沿损糙率n 局损系数ξ R(m) C hf(m) 0.100 56.77 0.012 0.180 0.106 沿程损失 水力半径 谢才系数 沿损糙率n 局损系数ξ R(m) C hf(m) 0.200 63.73 0.012 0.138 0.000
各种管道水头损失的简便计算公式

各种管道水头损失的简便计算公式各种管道水头损失的简便计算公式(879)摘要:从计算水头损失的最根本公式出发,将各种管道的计算公式加以推导,得出了计算水头损失的简便公式,使得管道工程设计人员从繁琐的计算中解脱出来,提高了工作效率。
关键词:水头损失塑料管钢管铸铁管混凝土管钢筋混凝土管在给水工程应用中经常要用到水头损失的计算公式,一般情况下计算水头损失都是从水力摩阻系数λ等基本参数出发,一步一步的代入计算。
其实各个公式之间是有一定的联系的,有的参数在计算当中可以抵消。
如果公式中只剩下流速、流量、管径这些基本参数,那么就会给计算者省去不少的麻烦。
在此我们充分利用了各参数之间以及水头损失与水温的关系,将公式整理简化,供大家参考。
1、PVC-U、PE的水头损失计算根据《埋地硬聚氯乙烯给水管道工程技术规程》规定,塑料管道沿程水头损失hf应按下式计算:(式1-1)式中λ—水力摩阻系数;L—管段长度(m);di—管道内径(m);v—平均流速(m/s);g—重力加速度,9.81m/s2。
因考虑到在通常的流速条件下,常用热塑性塑料给水管PVC-U、PE管一般处于水力光滑区,管壁绝对当量粗糙度对结果的影响非常小或没有影响,故水力摩阻系数λ可按下式计算:(式1-2)式中Re—雷诺数。
雷诺数Re应按下式计算:(式1-3)式中γ—水的运动粘滞度(m3/s),在不同温度时可按表1采用。
表1水在不同温度时的γ值(×10-6)水温℃0510********40γ(m3/s)1.78 1.52 1.31 1.14 1.000.890.800.66从前面的计算可知,若要计算水头损失,需将表1中的数据代入,并逐步计算,最少需要3个公式,计算较为繁琐。
为将公式和计算简化,以减少工作量,特推导如下:因具体工程水温的变化较大,水力计算中通常按照基准温度计算,然后根据具体情况,决定是否进行校正。
冷水管的基准温度多选择10℃。
当水温为10℃时的γ=1.31×10-6 m3/s,代入式1-3得(式1-4)将式1-4代入式1-2(式1-5)再将式1-5代入式1-1得(式1-6)取L为单位长度时,hf即等同于单位长度的水头损失i,所以(式1-7)又因为(式1-8)(式1-9)(式1-10)现可用式1-7或式1-10代替式式1-1、式1-2和式1-3,式1-7适用于流速为已知的条件下,式1-10适用于规定流量的条件下。
管道沿程水头损失三种计算方法

管道沿程水头损失三种计算方法管道沿程水头损失是指流体在管道中由于摩擦阻力和其他因素导致的能量损失。
在工程设计中,准确计算管道沿程水头损失十分重要。
下面将介绍三种常用的计算方法:Darcy-Weisbach法、Hazen-Williams法和Manning公式。
1. Darcy-Weisbach法:Darcy-Weisbach法是一种经验公式,被广泛用于计算流体在管道中的摩擦阻力。
根据该法,管道沿程水头损失可以通过以下公式计算:hf = f * (L/D) * (V^2/2g)其中,hf表示管道沿程水头损失,f为阻力系数,L为管道长度,D 为管道直径,V为流速,g为重力加速度。
阻力系数f可以通过Colebrook-White公式计算,但是该公式存在迭代过程,计算较为复杂。
因此,在实际工程中,一般使用基于Darcy-Weisbach法的Moody图或以f为参数的简化公式进行计算。
2. Hazen-Williams法:Hazen-Williams法是一种简化计算方法,适用于水力学设计中对于流速和水头损失的估算。
该方法假设水头损失仅与流速成线性关系,忽略了管道内的摩擦阻力。
根据该法,水头损失可以通过以下公式计算:hf = 10.67 * (Q/C)^1.852 * (L/D^4.87)其中,hf表示管道沿程水头损失,Q为流量,C为摩擦系数,L为管道长度,D为管道直径。
摩擦系数C是由管道材料和粗糙度等参数决定的,可以通过经验公式或实验数据查表获得。
Hazen-Williams法适用于流量变化较小的情况,具有计算简便的优点。
3. Manning公式:Manning公式是一种适用于自然河流和管道流动的方法,根据河床粗糙度和比水深等参数计算流体在河道或管道中的摩擦阻力。
hf = [(1.49/n^2) * (V^2/2g)] * (R^(4/3)) * (S^(1/2))其中,hf表示管道沿程水头损失,n为曼宁粗糙系数,V为流速,g 为重力加速度,R为水力半径,S为水力坡度。
管道水头损失计算公式总结

管道水头损失计算公式管道的水头损失主要分为:沿程水头损失 f和局部水头损失 j两类。
某管道的总水头损失 w为各分段的沿程水头损失和沿程各种局部水头损失的总和。
1.沿程水头损失计算公式1.1达西——魏斯巴赫公式达西——魏斯巴赫(Darcy-Weisbach)公式:f=λLdv2 2g式中: f—沿程水头损失(m);λ—沿程水头损失系数;L—管长(m);d—管径(m);v—管道水流速度(m/s)。
运用达西——魏斯巴赫(Darcy-Weisbach)公式,主要是确定沿程阻力系数λ,目前主要是一些经验公式:(1)根据尼古拉兹实验分区对沿程阻力系数λ进行计算①层流区层流区λ与相对粗糙度无关,只与雷诺数R e有关。
λ=64R e(R e<2000)②紊流水力光滑区紊流水力光滑区λ与相对粗糙度无关,只与雷诺数R e有关布拉休斯公式:λ=0.3164R e0.25(104<R e<105)普朗特—尼古拉兹公式(J.Nikuradse):λ=2lg(R eλ)-0.8(105<R e<3ⅹ106)③紊流水力粗糙过度区紊流水力粗糙过度区λ与相对粗糙度kd和雷诺数R e都有关柯列布鲁克—怀特(Colebrook-White)公式:1λ−2lg(2.51R eλk3.71d)公式中:R e—雷诺数;k—管道当量粗糙度(mm);d—管道直径一般适用于紊流光滑区、紊流过渡区和粗糙区,其适用范围较为宽泛、准确性高,④紊流水力粗糙区紊流水力粗糙过度区λ与雷诺数R e无关,只与相对粗糙度kd相关。
卡门(Karman)公式:1λ=−2lgk3.7d公式中:k—管道当量粗糙度(mm);d—管道直径(2)齐恩(jain,A.k)公式齐恩(jain,A.k)公式一般用于紊流过渡区λ=1.14-2lg(kd+21.25R e0.9)(5000<R e<108)(3)哈兰德公式λ=−1.8lg[k3.7d1.11+6.8R e)(4)阿尔特舒尔公式λ=0.11(kd+68R e)0.251.2谢才公式谢才公式只有谢才系数C一个影响参数,一般能适用于不同的流态区。
