五年级奥数平面图形面积(附答案)
小学五年级奥数练习及部分答案--8平面图形的面积(二)
奥数五年级上一、数列规律的应用--找规律(四) (1)二、等差数列求和的应用--数列(二) (7)三、包含与排除(二) (14)四、小数的巧算--巧算(四) (19)五、行程问题(三) (25)六、行程问题(四) (31)七、牛吃草问题 (36)八、平面图形的面积(二) (39)九、计数问题 (45)十、数的进位制(二) (50)十一、简单抽屉原理(一) (54)十二、简单的统筹规划问题 (60)部分答案 (68)八、平面图形的面积(二)等积变换：有的图形计算面积时，找不到面积公式需要的量，或分割、拼补较麻烦，可以把它们变形为面积相等(或面积具有倍数关系)易于求面积的图形后，再求面积。
规律一：等底等高(指相同或相等)的三角形(或平行四边形)面积相等。
规律二：如果两个三角形的底相等，而第一个三角形的高是第二个三角形的高的几倍，那么，第一个三角形的面积也是第二个三角形面积的几倍。
S△BCD=BC×ED÷2S△ABC=BC×EA÷2=BC×3ED÷2=(BC×ED÷2)×3所以，S△ABC=3S△BCD规律三：如果两个三角形的高相等，而第一个三角形的底是第二个三角形的底的几倍，那么，第一个三角形的面积也是第二个三角形面积的几倍。
例117、已知大、小正方形连长分别是10cm和7cm，求阴影部分BDCE面积(用多种方法解答)。
例118、如图，直角△ADE、直角△BDF、正方形EDFC正好组成一个大直角△ABDC。
如果AD=12cm、BD=10cm，那么图中阴影部分的面积是多少平方厘米？→例119、已知一个四边形ABCD的两条边的长度和三个角(如下图所示)，求四边形ABCD的面积是多少？例120、如图，已知△ABC、△ACD、△ADE、△AEF都是等腰直角三角形，且AB=2，求多边形ABCDEF的面积。
例121、等腰直角三角形的斜边长6cm，它的面积是多少平方厘米？例122、△ABC和△DEF是两个重叠在一起的等腰直角三角形，已知BC=10cm，CF=1cm，DE=7cm，求阴影部分的面积？例123、ABCD是4×7的长方形，AEFG是2×10的长方形，求△BCM与△GMF的面积之差。
五年级奥数培优《平面图形面积》(含答案)
平面图形的面积一（例题精讲）例1. 一个等腰直角三角形，最长的边是12厘米，这个三角形的面积是多少平方厘米？例2. 正图正方形中套着一个长方形，正方形的边长是12厘米，长方形的四个角的顶点把正方形的四条边各分成两段，其中长的一段是短的2倍。
求中间长方形的面积。
例3.图中两个正方形的边长分别是6厘米和4厘米，求阴影部分的面积。
例4.如图所示，一大一小两个正方形中，已知阴影部分的面积是7平方厘米。
甲的面积是多少平方厘米？例5.下图中两个完全一样的三角形重叠在一起，求阴影部分的面积。
（单位：厘米）例6. 图中ABCD 是长方形，S 1比S 2的面积大6平方厘米，求EC 的长。
平面图形的面积一（课堂小测）7.求四边形ABCD 的面积。
（单位：厘米）8. 如下图长方形ABCD 的面积是16平方厘米，E 、F 都是所在边的中点，求三角形AEF 的面积。
9.右图中，正方形的边长4厘米，求长方形的面积。
10.如图，平行四边形BCEF 中，BC=8厘米，直角三角形中，AC=10厘米，阴影部分面积比甲的面积小8平方厘米。
平行四边形的高是多少厘米？A BCD 345°CD F CB DS 1A 4 6 S 2EE11.一个正方形的对角线长5厘米，这个正方形的面积是多少平方厘米？12.已知大正方形的边长是12厘米，求中间最小正方形的面积。
13.下图中，甲三角形的面积比乙三角形的面积大多少平方厘米？14.如图（单位：厘米）是两个相同的直角梯形重叠在一起，求阴影部分的面积。
15.如图所示，长方形的长12厘米，宽8厘米，A 、B 两点是长方形长和宽的中点，那么阴影部分的面积是多少？AB94 3 84 6乙甲5平面图形的面积二（例题精讲）例1. 一个等腰直角三角形，最长的边是12厘米，这个三角形的面积是多少平方厘米？12×12＝144（平方厘米） 144÷4＝36（平方厘米）例2. 正图正方形中套着一个长方形，正方形的边长是12厘米，长方形的四个角的顶点把正方形的四条边各分成两段，其中长的一段是短的2倍。
五年级奥数题图形及面积含详细答案
五年级奥数题：图形与面积一、填空题〔共10小题，每题3分，总分值30分〕1．〔3分〕如图是由16个同样大小的正方形组成的，如果这个图形的面积是400平方厘米，则它的周长是_________ 厘米．2．〔3分〕第一届保良局亚洲区城市小学数学邀请赛在7月21日开幕，下面的图形中，每一小方格的面积是1．则7，2，1三个数字所占的面积之和是_________ ．3．〔3分〕如图中每一小方格的面积都是1平方厘米，则用粗线围成的图形面积是_________ 平方厘米．4．〔3分〕〔2014•模拟〕如图的两个正方形，边长分别为8厘米和4厘米，则阴影局部的面积是_________ 平方厘米．5．〔3分〕在△ABC中，BD=2DC，AE=BE，△ABC的面积是18平方厘米，则四边形AEDC的面积等于_________ 平方厘米．6．〔3分〕如图是边长为4厘米的正方形，AE=5厘米、OB是_________ 厘米．7．〔3分〕如图正方形ABCD的边长是4厘米，CG是3厘米，长方形DEFG的长DG是5厘米，则它的宽DE 是_________ 厘米．8．〔3分〕如图，一个矩形被分成10个小矩形，其中有6个小矩形的面积如下图，则这个大矩形的面积是_________ ．9．〔3分〕如图，正方形ABCD的边长为12，P是边AB上的任意一点，M、N、I、H分别是边BC、AD上的三等分点，E、F、G是边CD上的四等分点，图中阴影局部的面积是_________ ．10．〔3分〕图中的长方形的长和宽分别是6厘米和4厘米，阴影局部的总面积是10平方厘米，四边形ABCD 的面积是_________ 平方厘米．二、解答题〔共4小题，总分值0分〕11．图中正六边形ABCDEF的面积是54．AP=2PF，CQ=2BQ，求阴影四边形CEPQ的面积．12．如图，涂阴影局部的小正六角星形面积是16平方厘米．问：大正六角星形面积是多少平方厘米．13．一个周长是56厘米的大长方形，按图中〔1〕与〔2〕所示意那样，划分为四个小长方形．在〔1〕中小长方形面积的比是：A：B=1：2，B：C=1：2．而在〔2〕中相应的比例是A'：B'=1：3，B'：C'=1：3．又知，长方形D'的宽减去D的宽所得到的差，与D'的长减去在D的长所得到的差之比为1：3．求大长方形的面积．14．〔2012•模拟〕如图，CD=5，DE=7，EF=15，FG=6，直线AB将图形分成两局部，左边局部面积是38，右边局部面积是65，则三角形ADG的面积是_________ ．2010年五年级奥数题：图形与面积〔B〕参考答案与试题解析一、填空题〔共10小题，每题3分，总分值30分〕1．〔3分〕如图是由16个同样大小的正方形组成的，如果这个图形的面积是400平方厘米，则它的周长是170 厘米．考点：巧算周长．分析：要求该图形的周长，先求出每个小正方形的面积，根据正方形的面积公式，得出小正方形的边长，然后先算出该图形的外周的长，因为、外的长相等，再乘2即可得出结论．解答：解：400÷16=25〔平方厘米〕，因为5×5=25〔平方厘米〕，所以每个小正方形的边长为5厘米，周长为：〔5×4+5×4+5×3+5×2+5×3+5〕×2，=85×2，=170〔厘米〕；答：它的周长是170厘米．点评：此类题解答的关键是先求出每个小正方形的面积，根据正方形的面积公式，得出小正方形的边长，进而算出该图形的外周的长，因为、外的长相等，再乘2即可得出结论．2．〔3分〕第一届保良局亚洲区城市小学数学邀请赛在7月21日开幕，下面的图形中，每一小方格的面积是1．则7，2，1三个数字所占的面积之和是25 ．考点：组合图形的面积．分析：此题需要进展图形分解："7〞分成一个长方形、一个等腰直角三角形、一个平行四边形；"2〞分成一个梯形、一个平行四边形、一个长方形；"1〞分成一个梯形和两个长方形．然后进展图形转换，依据题目条件即可求出结果．解答：解："7〞所占的面积和=+3+4=，"2〞所占的面积和=3+4+3=10，"1〞所占的面积和=+7=，则7，2，1三个数字所占的面积之和=++10=25．故答案为：25．点评：此题关键是进展图形分解和转换．3．〔3分〕如图中每一小方格的面积都是1平方厘米，则用粗线围成的图形面积是 6.5 平方厘米．考点：组合图形的面积．分析：由图可以观察出：大正方形的面积减粗线以外的图形面积即为粗线围成的图形面积．解答：解：大正方形的面积为4×4=16〔平方厘米〕；粗线以外的图形面积为：整格有3个，左上，右上，右中，右下，左中，右中，共有3++5×=9.5〔平方厘米〕；所以粗线围成的图形面积为16﹣9.5=6.5〔平方厘米〕；答：粗线围成的图形面积是6.5平方厘米．故此题答案为：6.5．点评：此题关键是对图形进展合理地割补．4．〔3分〕〔2014•模拟〕如图的两个正方形，边长分别为8厘米和4厘米，则阴影局部的面积是24 平方厘米．考点：组合图形的面积．分析：两个正方形的面积减去两个空白三角形的面积．解答：解：4×4+8×8﹣×4×〔4+8〕﹣×8×8，=16+64﹣24﹣32，=24〔cm2〕；答：阴影的面积是24cm2．故答案为：24．点评：求组合图形面积的化为求常用图形面积的和与差求解．5．〔3分〕在△ABC中，BD=2DC，AE=BE，△ABC的面积是18平方厘米，则四边形AEDC的面积等于12 平方厘米．考点：相似三角形的性质〔份数、比例〕；三角形的周长和面积．分析：根据题意，连接AD，即可知道△ABD和△ADC的关系，△ADE和△BDE的关系，由此即可求出四边形AEDC的面积．解答：解：连接AD，因为BD=2DC，所以，S△ABD=2S△ADC，即，S△ABD=18×=12〔平方厘米〕，又因为，AE=BE，所以，S△ADE=S△BDE，即，S△BDE=12×=6〔平方厘米〕，所以AEDC的面积是：18﹣6=12〔平方厘米〕；故答案为：12．点评：解答此题的关键是，根据题意，添加辅助线，帮助我们找到三角形之间的关系，由此即可解答．6．〔3分〕如图是边长为4厘米的正方形，AE=5厘米、OB是 3.2 厘米．考点：组合图形的面积．分析：连接BE、AF可以看出，三角形ABE的面积是正方形面积的一半，再依据三角形面积公式就可以求出OB 的长度．解答：解：如图连接BE、AF，则BE与AF相交于D点S△ADE=S△BDF则S△ABE=S正方形=×〔4×4〕=8〔平方厘米〕；OB=8×2÷5=3.2〔厘米〕；答：OB是3.2厘米．故答案为：3.2．点评：此题主要考察三角形和正方形的面积公式，将数据代入公式即可．7．〔3分〕如图正方形ABCD的边长是4厘米，CG是3厘米，长方形DEFG的长DG是5厘米，则它的宽DE 是 3.2 厘米．考点：组合图形的面积．分析：连接AG，则可以依据题目条件求出三角形AGD的面积，因为DG，进而可以求三角形AGD的高，也就是长方形的宽，问题得解．解答：解：如图连接AGS△AGD=S正方形ABCD﹣S△CDG﹣S△ABG，=4×4﹣3×4÷2﹣1×4÷2=16﹣6﹣2=8〔平方厘米〕；8×2÷5=3.2〔厘米〕；答：长方形的宽是3.2厘米．故答案为：3.2．点评：依据题目条件做出适宜的辅助线，问题得解．8．〔3分〕如图，一个矩形被分成10个小矩形，其中有6个小矩形的面积如下图，则这个大矩形的面积是243 ．考点：组合图形的面积．分析：从图中可以看出每上、下两个小矩形的一个边是相邻的，也就是说长是相等的，则根据矩形的面积公式知，如果长一样，面积之比也就是宽之比，反之宽之比也就是面积之比；由中间面积20和16的矩形，可以算出空着的小矩形面积，最后把所有小矩形面积加起来就是大矩形的面积．解答：解：由图和题意知，中间上、下小矩形的面积比是：20：16=5：4，所以宽之比是5：4，则，A：36=5：4得A=45；25：B=5：4得B=20；30：C=5：4得C=24；D：12=5：4得D=15；所以大矩形的面积=45+36+25+20+20+16+30+24+15+12=243；故答案为：243．点评：此题考察了如果长方形的长一样，宽之比等于面积之比，还考察了比例的有关知识．9．〔3分〕如图，正方形ABCD的边长为12，P是边AB上的任意一点，M、N、I、H分别是边BC、AD上的三等分点，E、F、G是边CD上的四等分点，图中阴影局部的面积是60 ．考点：组合图形的面积．分析：根据题意：正方形ABCD的边长为12，P是边AB上的任意一点，M、N、I、H分别是边BC、AD上的三等分点，E、F、G是边CD上的四等分点，可连接DP，然后再利用三角形的面积公式进展计算即可得到答案．解答：解：阴影局部的面积=×DH×AP+×DG×AD+×EF×AD+×MN×BP=×4×AP+×3×12+×3×12+×4×BP=2AP+18+18+2BP=36+2×〔AP+BP〕=36+2×12=36+24=60．答：这个图形阴影局部的面积是60．点评：此题主要考察的是三角形的面积公式．10．〔3分〕图中的长方形的长和宽分别是6厘米和4厘米，阴影局部的总面积是10平方厘米，四边形ABCD 的面积是 4 平方厘米．考点：重叠问题；三角形的周长和面积．分析：因为S△EFC+S△GHC=四边形EFGH面积÷2=12，S△AEF+S△AGH=四边形EFGH面积÷2=12，所以S△ABE+S△ADH=S△BFC+S△DGC=四边形EFGH面积÷2﹣阴影局部的总面积是10平方厘米=2平方厘米．所以：四边形ABCD面积=S△ECH﹣〔S△ABE+S△ADH〕=四边形ABCD面积÷4﹣2=6﹣2=4平方厘米．解答：解：由题意推出：S△ABE+S△ADH=S△BFC+S△DGC=四边形EFGH面积÷2﹣阴影面积10平方厘米=2平方厘米．所以：四边形ABCD面积=S△ECH﹣〔S△ABE+S△ADH〕=四边形ABCD面积÷4﹣2=6﹣2=4平方厘米．故答案为：4．点评：此题在重叠问题中考察了三角形的周长和面积公式，此题设计的非常精彩．二、解答题〔共4小题，总分值0分〕11．图中正六边形ABCDEF的面积是54．AP=2PF，CQ=2BQ，求阴影四边形CEPQ的面积．考点：等积变形〔位移、割补〕．分析：如图，将正六边形ABCDEF等分为54个小正三角形，根据平行四边形对角线平分平行四边形面积，采用数小三角形的方法来计算面积．解答：解：如图，S△PEF=3，S△CDE=9，S四边形ABQP=11．上述三块面积之和为3+9+11=23．因此，阴影四边形CEPQ面积为54﹣23=31．点评：此题主要利用面积分割，用数根本小三角形面积来解决问题．12．如图，涂阴影局部的小正六角星形面积是16平方厘米．问：大正六角星形面积是多少平方厘米．考点：等积变形〔位移、割补〕．分析：由图及题意知，可把涂阴影局部小正六角星形等分成12个小三角形，且都与外围的6个空白小三角形面积相等，涂阴影局部的小正六角星形面积是16平方厘米，可求出大正六角星形中心正六边形的面积，而这个正六边形又可等分成6个小正三角形，且它们与外围六个大角的面积相等，进而可求出大正六角星形面积解答：解：如下列图所示，涂阴影局部小正六角星形可等分成12个小三角形，且都与外围的6个空白小三角形面积相等，所以正六边形ABCDEF的面积：16÷12×〔12+6〕=24〔平方厘米〕；又由于正六边形ABCDEF又可等分成6个小正三角形，且它们与外围六个大角的面积相等，所以大正六角星形面积：24×2=48〔平方厘米〕；答：大正六角星形面积是48平方厘米．点评：此题要借助求正六边形的面积来解答，它既可看作是18个小正三角形，又可看作是6个大点的正三角形组成．13．一个周长是56厘米的大长方形，按图中〔1〕与〔2〕所示意那样，划分为四个小长方形．在〔1〕中小长方形面积的比是：A：B=1：2，B：C=1：2．而在〔2〕中相应的比例是A'：B'=1：3，B'：C'=1：3．又知，长方形D'的宽减去D的宽所得到的差，与D'的长减去在D的长所得到的差之比为1：3．求大长方形的面积．考点：比的应用；图形划分．分析：要求大长方形的面积，需求出它的长和宽，由条件"在〔1〕中小长方形面积的比是：A：B=1：2，B：C=1：2．而在〔2〕中相应的比例是A'：B'=1：3，B'：C'=1：3．又知，长方形D'的宽减去D的宽所得到的差，与D'的长减去在D的长所得到的差之比为1：3〞可知：D的宽是大长方形宽的，D′的宽是大长方形宽的，D的长是×〔28﹣大长方形的宽〕，D′的长是×〔28﹣大长方形的宽〕，由此便可以列式计算．解答：解：设大长方形的宽为*，则长为28﹣*因为D的宽=*，D′的宽=*，所以，D′的宽﹣D的宽=．D长=×〔28﹣*〕，D′长=×〔28﹣*〕，D′长﹣D长=×〔28﹣*〕，由题设可知：=即=，于是=，*=8．于是，大长方形的长=28﹣8=20，从而大长方形的面积为8×20=160平方厘米．答：大长方形的面积是160平方米．点评：此题比拟复杂，主要考察比的关系，应利用比的意义，找清数量见的比，再利用题目条件，就可以进展计算求得结果．14．〔2012•模拟〕如图，CD=5，DE=7，EF=15，FG=6，直线AB将图形分成两局部，左边局部面积是38，右边局部面积是65，则三角形ADG的面积是40 ．考点：三角形的周长和面积．分析：可以把S△ADE看成是一个整体，根据各线段的关系和左右两局部面积的关系，可以列出一个方程，求出S△ADE的面积，然后再根据所求三角形与S△ADE的关系求出答案．解答：解：由题意知，S=3S△ADE，S△BFE=S△BEC，△AEG设S△ADE=*，则S△AEG=3*，S△BFE=〔38﹣*〕，可列出方程：〔38﹣*〕+3*=65，解方程，得：*=10，所以S△ADG=10×〔1+3〕=40．故答案为：40．点评：此题考察了如何利用边的关系求三角形的面积．。
五年级奥数题：图形与面积含详细答案汇总
五年级奥数题：图形与面积一、填空题(共10小题,每小题3分,满分30分）1．（3分)如图是由16个同样大小的正方形组成的，如果这个图形的面积是400平方厘米,那么它的周长是_________厘米．2．(3分)第一届保良局亚洲区城市小学数学邀请赛在7月21日开幕，下面的图形中，每一小方格的面积是1．那么7，2,1三个数字所占的面积之和是_________．3．(3分) 如图中每一小方格的面积都是1平方厘米,那么用粗线围成的图形面积是_________平方厘米．4．（3分）(2014•长沙模拟）如图的两个正方形，边长分别为8厘米和4厘米，那么阴影部分的面积是_________平方厘米．5．（3分）在△ABC中,BD=2DC,AE=BE，已知△ABC的面积是18平方厘米，则四边形AEDC的面积等于_________平方厘米．6．(3分）如图是边长为4厘米的正方形，AE=5厘米、OB是_________厘米．7．（3分）如图正方形ABCD的边长是4厘米，CG是3厘米,长方形DEFG的长DG是5厘米,那么它的宽DE是_________厘米．8．(3分）如图，一个矩形被分成10个小矩形，其中有6个小矩形的面积如图所示，那么这个大矩形的面积是_________．9．(3分)如图，正方形ABCD的边长为12，P是边AB上的任意一点,M、N、I、H分别是边BC、AD上的三等分点,E、F、G是边CD上的四等分点,图中阴影部分的面积是_________．10．（3分) 图中的长方形的长和宽分别是6厘米和4厘米,阴影部分的总面积是10平方厘米，四边形ABCD的面积是_________平方厘米．二、解答题（共4小题，满分0分）11．图中正六边形ABCDEF的面积是54．AP=2PF，CQ=2BQ，求阴影四边形CEPQ的面积．12．如图，涂阴影部分的小正六角星形面积是16平方厘米．问:大正六角星形面积是多少平方厘米．13．一个周长是56厘米的大长方形，按图中（1）与（2）所示意那样，划分为四个小长方形．在（1)中小长方形面积的比是:A：B=1：2，B：C=1：2．而在（2)中相应的比例是A'：B’=1：3,B’：C’=1:3．又知，长方形D'的宽减去D的宽所得到的差,与D’的长减去在D的长所得到的差之比为1：3．求大长方形的面积．14．(2012•武汉模拟）如图，已知CD=5，DE=7，EF=15,FG=6，直线AB将图形分成两部分,左边部分面积是38，右边部分面积是65，那么三角形ADG的面积是_________．2010年五年级奥数题：图形与面积（B)参考答案与试题解析一、填空题(共10小题,每小题3分,满分30分)1．（3分)如图是由16个同样大小的正方形组成的，如果这个图形的面积是400平方厘米,那么它的周长是170厘米．考点：巧算周长．分析：要求该图形的周长，先求出每个小正方形的面积，根据正方形的面积公式,得出小正方形的边长，然后先算出该图形的外周的长，因为内、外的长相等，再乘2即可得出结论．解答：解:400÷16=25（平方厘米），因为5×5=25（平方厘米），所以每个小正方形的边长为5厘米，周长为：（5×4+5×4+5×3+5×2+5×3+5）×2，=85×2，=170(厘米)；答：它的周长是170厘米．点评：此类题解答的关键是先求出每个小正方形的面积，根据正方形的面积公式，得出小正方形的边长，进而算出该图形的外周的长，因为内、外的长相等，再乘2即可得出结论．2．（3分)第一届保良局亚洲区城市小学数学邀请赛在7月21日开幕，下面的图形中，每一小方格的面积是1．那么7,2，1三个数字所占的面积之和是25．考点：组合图形的面积．分析:此题需要进行图形分解：“7"分成一个长方形、一个等腰直角三角形、一个平行四边形；“2"分成一个梯形、一个平行四边形、一个长方形;“1”分成一个梯形和两个长方形．然后进行图形转换，依据题目条件即可求出结果．解答:解：“7”所占的面积和=+3+4=,“2”所占的面积和=3+4+3=10,“1”所占的面积和=+7=，那么7，2,1三个数字所占的面积之和=++10=25．故答案为：25．点评：此题关键是进行图形分解和转换．3．（3分）如图中每一小方格的面积都是1平方厘米，那么用粗线围成的图形面积是6。
五年级奥数平面几何图形的面积计算
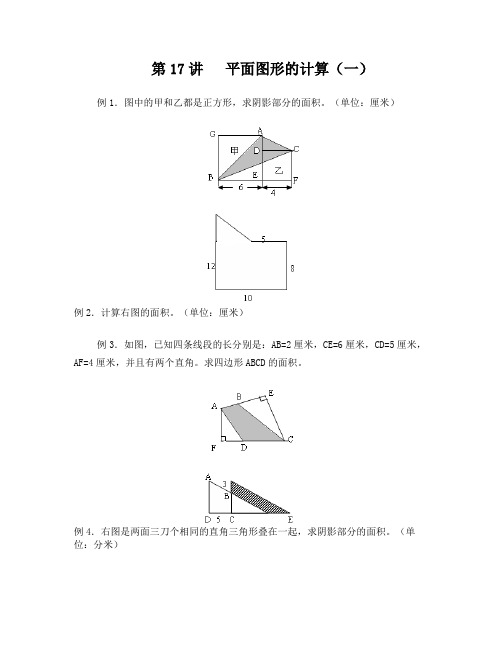
第17讲平面图形的计算（一）例1．图中的甲和乙都是正方形，求阴影部分的面积。
（单位：厘米）例2．计算右图的面积。
（单位：厘米）例3．如图，已知四条线段的长分别是：AB=2厘米，CE=6厘米，CD=5厘米，AF=4厘米，并且有两个直角。
求四边形ABCD的面积。
例4．右图是两面三刀个相同的直角三角形叠在一起，求阴影部分的面积。
（单位：分米）例5．下页左图是一块长方形草地，长方形的长是16，宽是10，中间有两条道路，一条是长方形，一条是平行四边形，那么，有草部分（阴影部分）的面积有多大？（单位：米）练习与思考1．求图中阴影部分的面积。
2．求图中阴影部分的面积。
3．下左图的长方形中，三角形ADE与四边形DEBF和三角形CDF的面积分别相等，求三角形DEF的面积。
4．四中平等四边形ABCD的边BC长10厘米，直角三角形BCE的直角边EC长8厘米，已知阴影部分的面积比三角形EFG的面积大10平方厘米，求CF的长。
5．图中三角形的高为4，面积为16；长方形的宽为6，长方形的面积是三角形面积的多少倍？6．如图，长方形的长是8，宽是6，A和B是宽的中点，求长方形内阴影部分的面积。
7．如图，BC长为5，求画斜线的两个三角形的面积之和。
8．上右图是两个一样的直角三角形重叠在一起，按照图上标出的数，计算阴影部分的面积。
9．右图是一块长方形草地，长方形长为16，宽为12，中间有一条宽为2的道路，求草地（阴影部分）的面积。
简便计算作业（12月23日）：1.996+19.97+199.82.894.68+4.686.11+4.68 754.7+15.925平均数问题作业（12月23日）：1.已知九个数的平均数是72.去掉一个数之后，余下的数的平均数是78。
去掉的数是多少？2.甲、乙、丙三个小组的同学去植树，甲、乙两组平均每组植树18棵，甲、丙两组平均每组植树17棵，乙、丙两组平均每组植树19棵。
三个小组各植树多少棵？3.五一班同学数学考试平均成绩91.5分，事后复查发现计算成绩时将一位同学的98分误作89分计算了。
小学五年奥数-平面图形的面积
平面图形的面积【试金石】例1如右图，已知一个四边形ABCD的两条边的长度AD=7，BC=3，三个角的度数：角B和角D是直角，角A是45°，求这个四边形的面积。
（单位；厘米）【针对性训练】如右图，已知一个四边形ABCD的两条边的长度AD=14厘米，BC=6厘米，三个角的度数：角B和角D是直角，角A是45°，求这个四边形的面积。
【试金石】例2右图中长方形的长是20厘米，宽是12厘米，求它的内部阴影部分的面积。
答：阴影部分的面积是120平方厘米。
【针对性训练】图中长方形的长是8米，宽是6米，A和B是宽的中点，求长方形内部阴影部分的面积。
【试金石】例3右图中，有四条线段的长度已经知道，还有两个角是直角，那么四边形ABCD（阴影部分）的面积是多少？（单位：分米）【针对性训练】右图中，有四条线段的长度已经知道，还有两个角是直角，那么四边形ABCD（阴影部分）的面积是多少？【试金石】例4如右图，甲、乙两图形都是正方形，它们的边长分别是10厘米和12厘米，求阴影部分的面积。
【针对性训练】如右图，甲、乙两图形都是正方形，它们的边长分别是6厘米和8厘米，求阴影部分的面积。
【试金石】例5【针对性训练】【试金石】【针对性训练】【智能提速训练营】1、如图，已知BD长是2厘米，DC长是3厘米，E是AD的中点，如果三角形ABD的面积是5平方厘米，那么三角形DEC的面积是多少？2、如图，已知平行四边形ABCD的面积是60平方分米，E、F分别是AB、AD边上的中点，图中阴影部分的面积是多少平方分米？3、如图，在平行四边形ABCD中，AE=ED，BF=FC，CG=GD，平行四边形ABCD的面积是阴影三角形EFG的多少倍？4、如图，BD=6厘米，BC=15厘米，△ABD的面积是24平方厘米，△ADC 的面积是多少平方厘米？5、右图中，有四条线段的长度已经知道，还有两个角是直角，那么四边形ABCD（阴影部分）的面积是多少？（单位：厘米）6、如图，梯形的面积是70平方厘米，上底8厘米，下底12厘米，阴影部分的面积是多少平方厘米？7、如图，四边形ABCD是平行四边形，DC=CE，如果△BCE的面积是15平方厘米，那么梯形ABED的面积是多少平方厘米？8、如图，平行四边形的面积是60平方厘米，阴影三角形的面积是多少平方厘米？9、如图，正方形ABCD的边长是4厘米，CG=3厘米，长方形DEFG的长DG=5厘米，那么它的宽DE是多少厘米？10、如图，四边形ABCD内有一点O，O点到四条边的垂线长都是4厘米，已知四边形的周长是36厘米，四边形ABCD的面积是多少平方厘米？11、如图，已知ABFE是平行四边形，ABCD是长方形，且AD=6厘米，AB=3厘米，CO=2厘米，阴影部分的面积是多少平方厘米？12、一个长方形被两条直线分成四个长方形，其中三个的面积分别是20平方米、25平方米和30平方米，阴影部分的面积是多少平方米？13、如右图，已知正方形ABCD和正方形CEFG，且正方形ABCD每边长为10厘米，求图中阴影（三角形BFD）部分的面积。
【人教版】五年级上册奥数试题：平面图形面积
平面图形1、 和差法：分割、合并、倍数比2、 运动法：3、 等积变换法：等底、等高则等积；等积、等高则等底；等积、等底则等高。
例1、求阴影部分的面积。
例2、大、小两个正方形的边长分别是8厘米和6厘米， 求阴影部分的面积。
例3、两个相同的直角三角形如图重叠在一起， 求阴影部分的面积。
例4、求阴影部分面积。
例5、图中长方形ABCD 中AB=5厘米，BC=8厘米。
三角形DEF （甲）的面积 比三角形ABF （乙）的面积大8平方厘米。
求DE 的长。
3cm4cm6cm5cm2cm12cm甲ABCDEF乙AD B C 10cm 10cm24cm45° E5cm例6、在三角形ABC 中，DC=2BD ，CE=3AE ，三角形ADE 的面积是 8平方厘米。
求三角形ABC 的面积。
例7、四边形ABCD 中，AC 和BD 互相垂直，AC=20厘米，BD=15厘米。
求四边形的面积。
例8、在四边形ABCD 中，∠C=45°，∠B=90°，∠D=90°， AD=4cm ，BC=12cm 。
求四边形ABCD 的面积。
例9、AF=2cm,AB=4cm,CD=5cm,DE=8cm,∠B=∠E=90°。
求四边形ACDF 的面积。
例10、已知大正方形比小正方形边长多2厘米，大正方形比小正方形的面积大10平方厘米。
求大、小正方形的面积各数多少平方厘米。
ABCDC45°AB CDABCDEF 4cm8cm2cm练习1、图中两个正方形的边长是10厘米和7厘米，求阴影部分的面积（如图）练习2、如下图，在三角形ABC中，AD=BD,CE=3BE。
若三角形BED的面积是1平方厘米，则三角形ABC的面积是多少平方厘米？练习3、三角形ABC是直角三角形,阴影部分①的面积比阴影部分②的面积小28平方厘米. A B长40厘米, BC长多少厘米.练习4、在右图中(单位:厘米),两个阴影部分面积的和是平方厘米.练习5、ABC是等腰直角三角形. D是半圆周的中点,BC是半圆的直径,已知:AB=BC=10,那么阴影部分的面积是多少?练习6、已知右图中大正方形边长是6厘米,中间小正方形边长是4厘米.求阴影部分的面积. C②①A B121520A10DCB练习7、右图中三角形是等腰直角三角形, 阴影部分的面积是 (平方厘米).练习8、如右图,阴影部分的面积是 .练习9、如图所求,圆的周长是16.4厘米,圆的面积与长方形的面积正好相等.图中阴影部分的周长是 厘米.)14.3(=π练习10、ABC 是等腰直角三角形. D 是半圆周的中点, BC 是半圆的直径,已知: AB =BC =10,那么阴影部分的面积是多少?练习11、在四边形ABCD 中，∠C=135°，∠D=90°。
小学五年级奥数第13课《面积计算》试题附答案
小学五年级上册数学奥数知识点讲解第13课《面积计算》试题附答案第十四讲面积计算在小学阶段学习的各种平面图形之间有着密切的联系.我们把平面图形之间的转化方法及它们的面积、周长公式归纳如下图：计算图形的面积要用面积公式，对于一些复杂的图形有意识地运用运动变化的观点，将平面图形简单地变动位置，可以化繁为简，化难为易，从而获得最佳解法。
例1己知三角形ABC的面积为1, BE=2AB, BC=CD,求三角形BDE的面积? （下页图）例2求右图中阴影部分的面积.（大圆直径为2,单位：厘米）。
例3如下图在图中三角形ABE、ADF和四边形AECF的面积相等，求三角形AEF 的面积。
S，幺=&J&AEH — 3、§ △娅D - gQ^ABD同理，CGF =§S&BCD22因此3AAEH +Q&CGF = §(3&ABD + 二&BCD)=d、CLABCD2同理^ABFE +3&DHG =§、CJABCD，、4所以S&AEH +Q&CGF + ：&BFE += '^^□ABCD所以S[JEFGH = (1g) ScJABCD =□此CD即四边形EFGH的面积：四边形ABCD面积=5 ：9。
例8如右图，己知三角形ABC的三条高必定交于一点，如记成P点, 请你讲明黑+北+福=1为什么成立？AJJ b 匕Cr分析与解答从右图中可以看出APBC和AABC是同底的两个三角形, 它们的面积之比等于它们对应高的比，所以2=黑•.同理可得：L 右图是一个圆心角为45°的扇形，其中直角三角形B0C 的直角边为6厘 米，求阴影部分面积。
2 .在右图中，阴影部分A 的面积比阴影部分B 的面积大10. 5平方厘米，求线 段BC 的长度？sQ&PCA=PE $&PAB二西=PF CF'所以 s s s“△PBC 十 2&PCA 十 2 APABQ AAB CJ AAB C° AAB CPD PE PF = + + ——。
五年级奥数第14讲——平面图形面积计算
学生课程讲义课程名称五年级奥数上课时间任课老师沈老师第14 讲，本讲课题：平面图形面积计算内容概要如何将一般多边形及组合图形转化为基本图形。
本讲所指平面图形面积计算主要指多边形及其组合图形面积的计算，这些图形面积计算一般都可以转化成三角形、长方形、平行四边形和梯形的面积计算，后者的计算公式都是我们在课内已经学过并且应该熟记的。
主要的技巧在于如何将一般多边形及其组合图形“转化”为基本图形。
【例1】在梯形中阴影部分面积是150平方厘米，求梯形面积。
随堂练习11.已知平行四边形的的面积是28平方厘米，求阴影图形的面积。
2.如果用铁丝围成如下图一样的平行四边形，需要用多少厘米铁丝？（单位：厘米）【例2】如图，两个完全相同的直角三角形叠在一起，求阴影部分的面积。
（单位分米）随堂练习21.下图中两个完全一样的三角形重叠在一起，求阴影部分的面积。
（单位：厘米）2.图中两个正方形的边长分别是6厘米和4厘米，求阴影部分的面积。
【例3】如图，将长为9厘米，宽为6厘米的长方形划分成四个三角形，其面积分别为S 1、S 2、S 3、S 4、，且S 1＝S 2＝S 3＋S 4，求S 4 。
随堂练习31.如图，四边形ABCD 是直角梯形，其中AD ＝12厘米，AB ＝8厘米，BC ＝15厘米，且△ADE 、四边形DEBF 及△CDF 的面积相等，求三角形EBF 的面积。
2. 已知大正方形的边长是5厘米，小正方形的边长是4厘米，求阴影部分的面积。
3. 正方形的边长分别是10厘米、6厘米，阴影部分的面积是多少平方厘米？ABC EFDG【例4】如图，ABCD 是边长为4分米的正方形，长方形DEFG 的长是5分米，求长方形DEFG 的宽。
随堂练习4如图，ABCD 是正方形，EDGF 是长方形，CD=6厘米，DG=8厘米，求宽ED=?FA B GCD E 86【例5】如图，已知四边形ABCD 被它的两条对角线分成四个三角形，其中甲的面积是1，乙的面积是2，丙的面积是3，求丁的面积。
五年级奥数题图形与面积含详细答案
五年级奥数题：图形与面积一、填空题（共10小题，每小题3分，满分30分）1．（3分）如图是由16个同样大小的正方形组成的，如果这个图形的面积是400平方厘米，那么它的周长是_________ 厘米．2．（3分）第一届保良局亚洲区城市小学数学邀请赛在7月21日开幕，下面的图形中，每一小方格的面积是1．那么7，2，1三个数字所占的面积之和是_________ ．3．（3分）如图中每一小方格的面积都是1平方厘米，那么用粗线围成的图形面积是_________ 平方厘米．4．（3分）（2014•长沙模拟）如图的两个正方形，边长分别为8厘米和4厘米，那么阴影部分的面积是_________ 平方厘米．5．（3分）在△ABC中，BD=2DC，AE=BE，已知△ABC的面积是18平方厘米，则四边形AEDC的面积等于_________ 平方厘米．6．（3分）如图是边长为4厘米的正方形，AE=5厘米、OB是_________ 厘米．7．（3分）如图正方形ABCD的边长是4厘米，CG是3厘米，长方形DEFG的长DG是5厘米，那么它的宽DE是_________ 厘米．8．（3分）如图，一个矩形被分成10个小矩形，其中有6个小矩形的面积如图所示，那么这个大矩形的面积是_________ ．9．（3分）如图，正方形ABCD的边长为12，P是边AB上的任意一点，M、N、I、H分别是边BC、AD 上的三等分点，E、F、G是边CD上的四等分点，图中阴影部分的面积是_________ ．10．（3分）图中的长方形的长和宽分别是6厘米和4厘米，阴影部分的总面积是10平方厘米，四边形ABCD的面积是_________ 平方厘米．二、解答题（共4小题，满分0分）11．图中正六边形ABCDEF的面积是54．AP=2PF，CQ=2BQ，求阴影四边形CEPQ的面积．12．如图，涂阴影部分的小正六角星形面积是16平方厘米．问：大正六角星形面积是多少平方厘米．13．一个周长是56厘米的大长方形，按图中（1）与（2）所示意那样，划分为四个小长方形．在（1）中小长方形面积的比是：A：B=1：2，B：C=1：2．而在（2）中相应的比例是A'：B'=1：3，B'：C'=1：3．又知，长方形D'的宽减去D的宽所得到的差，与D'的长减去在D的长所得到的差之比为1：3．求大长方形的面积．14．（2012•武汉模拟）如图，已知CD=5，DE=7，EF=15，FG=6，直线AB将图形分成两部分，左边部分面积是38，右边部分面积是65，那么三角形ADG的面积是_________ ．2010年五年级奥数题：图形与面积（B）参考答案与试题解析一、填空题（共10小题，每小题3分，满分30分）1．（3分）如图是由16个同样大小的正方形组成的，如果这个图形的面积是400平方厘米，那么它的周长是170 厘米．考点：巧算周长．菁优网版权所有分析：要求该图形的周长，先求出每个小正方形的面积，根据正方形的面积公式，得出小正方形的边长，然后先算出该图形的外周的长，因为内、外的长相等，再乘2即可得出结论．解答：解：400÷16=25（平方厘米），因为5×5=25（平方厘米），所以每个小正方形的边长为5厘米，周长为：（5×4+5×4+5×3+5×2+5×3+5）×2，=85×2，=170（厘米）；答：它的周长是170厘米．点评：此类题解答的关键是先求出每个小正方形的面积，根据正方形的面积公式，得出小正方形的边长，进而算出该图形的外周的长，因为内、外的长相等，再乘2即可得出结论．2．（3分）第一届保良局亚洲区城市小学数学邀请赛在7月21日开幕，下面的图形中，每一小方格的面积是1．那么7，2，1三个数字所占的面积之和是25 ．考点：组合图形的面积．菁优网版权所有分析：此题需要进行图形分解：“7”分成一个长方形、一个等腰直角三角形、一个平行四边形；“2”分成一个梯形、一个平行四边形、一个长方形；“1”分成一个梯形和两个长方形．然后进行图形转换，依据题目条件即可求出结果．解答：解：“7”所占的面积和=+3+4=，“2”所占的面积和=3+4+3=10，“1”所占的面积和=+7=，那么7，2，1三个数字所占的面积之和=++10=25．3．（3分）如图中每一小方格的面积都是1平方厘米，那么用粗线围成的图形面积是 6.5 平方厘米．，右上，，右下，右中3++5×=9.54．（3分）（2014•长沙模拟）如图的两个正方形，边长分别为8厘米和4厘米，那么阴影部分的面积是24平方厘米．﹣××5．（3分）在△ABC中，BD=2DC，AE=BE，已知△ABC的面积是18平方厘米，则四边形AEDC的面积等于12 平方厘米．考点：相似三角形的性质（份数、比例）；三角形的周长和面积．菁优网版权所有分析：根据题意，连接AD，即可知道△ABD和△ADC的关系，△ADE和△BDE的关系，由此即可求出四边形AEDC 的面积．解答：解：连接AD，因为BD=2DC，所以，S△ABD=2S△ADC，即，S△ABD=18×=12（平方厘米），又因为，AE=BE，所以，S△ADE=S△BDE，即，S△BDE=12×=6（平方厘米），所以AEDC的面积是：18﹣6=12（平方厘米）；故答案为：12．点评：解答此题的关键是，根据题意，添加辅助线，帮助我们找到三角形之间的关系，由此即可解答．6．（3分）如图是边长为4厘米的正方形，AE=5厘米、OB是 3.2 厘米．考点：组合图形的面积．菁优网版权所有分析：连接BE、AF可以看出，三角形ABE的面积是正方形面积的一半，再依据三角形面积公式就可以求出OB 的长度．解答：解：如图连接BE、AF，则BE与AF相交于D点S△ADE=S△BDF则S△ABE=S正方形=×（4×4）=8（平方厘米）；OB=8×2÷5=3.2（厘米）；答：OB是3.2厘米．故答案为：3.2．点评：此题主要考查三角形和正方形的面积公式，将数据代入公式即可．7．（3分）如图正方形ABCD的边长是4厘米，CG是3厘米，长方形DEFG的长DG是5厘米，那么它的宽DE是 3.2 厘米．考点：组合图形的面积．菁优网版权所有分析：连接AG，则可以依据题目条件求出三角形AGD的面积，因为DG已知，进而可以求三角形AGD的高，也就是长方形的宽，问题得解．解答：解：如图连接AGS△AGD=S正方形ABCD﹣S△CDG﹣S△ABG，=4×4﹣3×4÷2﹣1×4÷2=16﹣6﹣2=8（平方厘米）；8×2÷5=3.2（厘米）；答：长方形的宽是3.2厘米．故答案为：3.2．点评：依据题目条件做出合适的辅助线，问题得解．8．（3分）如图，一个矩形被分成10个小矩形，其中有6个小矩形的面积如图所示，那么这个大矩形的面积是243 ．考点：组合图形的面积．菁优网版权所有分析：从图中可以看出每上、下两个小矩形的一个边是相邻的，也就是说长是相等的，那么根据矩形的面积公式知，如果长相同，面积之比也就是宽之比，反之宽之比也就是面积之比；由中间面积20和16的矩形，可以算出空着的小矩形面积，最后把所有小矩形面积加起来就是大矩形的面积．解答：解：由图和题意知，中间上、下小矩形的面积比是：20：16=5：4，所以宽之比是5：4，那么，A：36=5：4得A=45；25：B=5：4得B=20；30：C=5：4得C=24；D：12=5：4得D=15；所以大矩形的面积=45+36+25+20+20+16+30+24+15+12=243；故答案为：243．点评：此题考查了如果长方形的长相同，宽之比等于面积之比，还考查了比例的有关知识．9．（3分）如图，正方形ABCD的边长为12，P是边AB上的任意一点，M、N、I、H分别是边BC、AD上的三等分点，E、F、G是边CD上的四等分点，图中阴影部分的面积是60 ．考点：组合图形的面积．菁优网版权所有分析：根据题意：正方形ABCD的边长为12，P是边AB上的任意一点，M、N、I、H分别是边BC、AD上的三等分点，E、F、G是边CD上的四等分点，可连接DP，然后再利用三角形的面积公式进行计算即可得到答案．解答：解：阴影部分的面积=×DH×AP+×DG×AD+×EF×AD+×MN×BP=×4×AP+×3×12+×3×12+×4×BP=2AP+18+18+2BP=36+2×（AP+BP）=36+2×12=36+24=60．答：这个图形阴影部分的面积是60．点评：此题主要考查的是三角形的面积公式．10．（3分）图中的长方形的长和宽分别是6厘米和4厘米，阴影部分的总面积是10平方厘米，四边形ABCD的面积是 4 平方厘米．二、解答题（共4小题，满分0分）11．图中正六边形ABCDEF的面积是54．AP=2PF，CQ=2BQ，求阴影四边形CEPQ的面积．数小三角形的办法来计算面积．12．如图，涂阴影部分的小正六角星形面积是16平方厘米．问：大正六角星形面积是多少平方厘米．13．一个周长是56厘米的大长方形，按图中（1）与（2）所示意那样，划分为四个小长方形．在（1）中小长方形面积的比是：A：B=1：2，B：C=1：2．而在（2）中相应的比例是A'：B'=1：3，B'：C'=1：3．又知，长方形D'的宽减去D的宽所得到的差，与D'的长减去在D的长所得到的差之比为1：3．求大长方形的面积．比的应用；图形划分．菁优网版权所有，′的宽是大长方形宽的D的长是×（28﹣大长方形的宽），D′的长是×（28﹣大长方形的宽），由此便可以列式计算．因为D的宽=x，D′的宽=x，所以，D′的宽﹣D的宽=．=×（=×（D′长﹣D长=×（28﹣x），：==，于是=14．（2012•武汉模拟）如图，已知CD=5，DE=7，EF=15，FG=6，直线AB将图形分成两部分，左边部分面积是38，右边部分面积是65，那么三角形ADG的面积是40 ．S△ADE的面积，然后再根据所求三角形与S△ADE的关系求出答案．解：由题意知，S△AEG=3S△ADE，S△BFE=S△BEC，BFE=（可列出方程：（38﹣X）+3X=65，。
五年级奥数平面图形的面积计算
12 CF= S△DEF ×2÷DE
=24×2÷8
=6（厘米）
求下面组合图形的面积：
单位：厘米
求下图中阴影部分的面积：
单位：厘米
求下图中阴影部分的面积：
单位：厘米
应用题：
1. 一块梯形木板面 积为9.2平方米,中 位线长2.3米,求梯 形木板的高是多少
应用题：
6.在下图中,梯形的面积是60平 方厘米,周长是36厘米,两腰长度 之和是16厘米.求梯形的高.
7.如下图,梯形ABCD的面积等于72平 方厘米,AB=4厘米,DC=8厘米.求三角 形ABD的面积.
8.在下图中,阴影部分的面积是 21平方厘米,直角梯形的面积是 多少平方厘米
单位：厘米
观赏
五年级第学1期
△ADE
5．正方形ABCD的边长是12厘米,已知DE是EC长度的2倍,求： （1）三角形的DEF的面积．（2）CF的长．
DE是EC长度的2Байду номын сангаас
倍,DC=12厘米. 12÷3=4（厘米）
EC=4（厘米）DE=4×2=8（厘米）12
12 8
S△DEF = S△ADF － S△ADE
S△DEF =12×12÷2 －8×12÷2
2. 一个梯形的上底为6 厘米,下底为9厘米,面 积为45平方厘米,它的 高是多少厘米
应用题：
3. 已知梯形的面积是 21平方米,高6米,下底 长4米,求上底长多少
应用题：
4. 某梯形上底与下 底的和为100米,面积 为1500平方米,它的 高是多少米
应用题：
5. 一座拦河大坝横截面
是梯形,面积是30平方米, 它的高是8米,下底比上底 多1.5米,梯形的下底是多 少
五年级奥数第4讲平面图形面积计算
同学个性化教学设计年级：教师: 科目：
班主任：日期: 时段:
【例 1】 在梯形中阴影部分面积是150平方厘米，求梯形面积。
【巩固】如图，已知平行四边形面积是48平方厘米，求阴影部分面积。
【例 2】 如图，是两个完全相同的直角三角形叠在一起，求阴影部分的面积。
（单位：分米）
【例 3】 如图，将长为9厘米、宽为6厘米的长方形划分成四个三角形，其面积分别为1S 、2S 、3S 、
4S ，且4321S S S S +==,求4S 。
【巩固】如图，四年级ABCD是直角三角形，其中AD=12厘米，AB=8厘米，BC=15厘米，且△ADE 四边形DEBF及△CDF的面积相等，求三角形EBF的面积。
【例 4】如图，AE=5厘米，CF=2厘米，AB=6厘米，CD=4厘米，∠B=∠D=90°。
求四边形AFCE 的面积。
【巩固】如图，四边形ABCD中，AE=5厘米，AB=10厘米，FC=12厘米，∠B=∠D=90°，求四边形AFCE的面积。
【例 5】如图，求图示长方形中阴影部分的面积。
（单位：厘米）
【例 6】如图，平行四边形ABCD的边长BC=10厘米，直角三角形BCE的直角边CE长8厘米。
已知阴影部分的面积比三角形FEG的面积大10平方厘米。
求CF的长。
【巩固】如图，正方形ABCD的边长是12厘米，已知DE是EC的长度的2倍。
求（1）△DEF的面积；(2)CF的长。
学生签字：__________
教研组长签字：____
_______。
小学五年级奥数-平面图形面积
五年级思维第三讲基础知识：ah1.三角形面积公式：S=122.平行四边形（含正方形，长方形）面积公式：S=ah3.等底等高的三角形面积相等，等底等高的平行四边形面积相等4.解题思路：将难以求解的图形进行拆分，利用等积变换化为可求解图形求解例题：例1.如图1，每一个小方格的面积都是1平方厘米，那么粗线围成的图形的面积是多少平方厘米？例2.每个小方格面积是1平方厘米，那么下面三张图的面积之和是多少平方厘米？例3.如图，如果每一个小三角形的面积是1平方厘米，那么三角形ABC的面积是多少平方厘米？例4.如图2，如果每一个三角形的面积都是1平方厘米，那么四边形ABCD的面积是多少平方厘米？例5.把同一个三角形的三条边分别五等分，七等分，适当连接这些分点，便得到了若干个面积相等的小三角形。
已知下方左图中粗线围成的面积为294，那么下方右图粗线围成的面积是多少平方分米？例6.如图，三角形ABC 和DEF 是两个完全相同的等腰直角三角形，其中DF 长9厘米，CF 长3厘米，那么阴影部分的面积是多少平方厘米？例7．如图，大正方形的边长是10厘米。
连接大正方形的各边中点得小正方形，将小正方形每边三等分，再将三等分点和正方形中心和一个顶点相连，那么图中阴影部分面积总和等于多少平方厘米？例8.已知一个四边形的两条边长度和三个角，那么这个四边形的面积是多少？B E例9.如图，两个形状和大小都一样的直角三角形ABC 与DEF 如图放置，它们的面积都是2011平方厘米，而每一个直角三角形直角的顶点都恰好落在另一个直角三角形的斜边上。
这两个直角三角形的重叠部分是一个长方形，那么四边形ADEC 的面积是多少平方厘米？例10.如图所示，在任意凸四边形ABCD 中取各边的中点，并与它相对的一个顶点连结，那么所围成的中央四边形面积与周围那四个阴影三角形的面积总和相等吗？为什么？作业题：1.在面积为1平方米的正六边形中，连结相隔一个顶点的各对顶点，则阴影部分的面积是多少平方米？2.如图的大正方形由三十六个面积为1平方分米的小正方形拼成。
五年级数学 平面几何图形的面积训练题 带详细答案
平面几何图形的面积板块一：基础巩固1、一个三角形的面积比与他等底等高的平行四边形的面积少12平方分米，则平行四边形的面积是（）平方分米，三角形的面积是（）平方分米。
2、李叔叔在院子里靠着墙边围城了一个鸡笼，围鸡笼的网子长20.5米，求这个鸡笼的占地面积是多少平方米？3、有一个长方形，如果宽减少2米，或长减少3米，则面积均减少24平方米，求这个长方形的是是多少平方米？324、如图是由边长分别为4厘米、8厘米的两个正方形组成的图形，求阴影部分面积。
5、如图是由边长分别为4、8、6厘米的三个正方形组成的图形，求阴影部分面积。
板块二：拓展提高【例题1】下图(单位：厘米)是两个相同的直角梯形重叠在一起，求阴影部分的面积.【例题2】右图中甲的面积比乙的面积大__________平方厘米．6厘米8厘米4厘米【例3】右图中，矩形ABCD 的边AB 为4厘米，BC 为6厘米，三角形ABF 比三角形EDF 的面积大9平方厘米，求ED 的长．A BC DEF【巩固】如图所示，CA=AB=4厘米，△ABE 比△CDE 的面积小2平方厘米，求CD 的长为多少厘米？A BECD【例4】一块长方形铁板，长15分米，宽12分米，如果长和宽各减少2分米，面积比原来减少多少平方分米？1215222【巩固】一个长方形，如果长减少5厘米，宽减少2厘米，那么面积就减少66平方厘米，这时剩下的部分恰好成为一个正方形，求原来长方形的面积？5×225【例5】下面图形中，长方形ABCD的面积是32平方厘米，EF都是所在边的中点，求三角形AEF的面积。
【例6】四边形ABCD是直角梯形，AD=12厘米，AB=8厘米，BC=15厘米，且三角形ADE，四边形DEBF，三角形CDF的面积相等，求阴影三角形的面积是多少平方厘米？【例7】一块长方形，用垂直于长和宽的两条线分成四块，其中三块面积分别为15、18、30平方米。
第四块面积是多少平方米？【巩固】如图有9个小长方形，其中的5个小长方形的面积分别为4、8、12、16、20平方米，其余4个长方形的面积分别是多少平方米？【例8】如下图，在一个之间三角形铁皮上剪下一个正方形，并且使正方形的面积尽可能的大，正方形的面积最大是多少？【巩固】如图，直角三角形ABC套住了一个正方形CDEF，E恰好在AB边上，直角边AC长40厘米，BC长12厘米，求正方形的边长是多少？【例9】如图，长方形ABCD 长是8厘米，宽是7厘米，点E 、F 、G 分别是长方形ABCD 边上的中点，H 为AD 边上的任意一点，求阴影部分的面积．E【巩固】如图，三角形ABC 的面积是24，D 、E 和F 分别是BC 、AC 和AD 的中点．求三角形DEF 的面积．FE DC BA【例10】如图，三角形ABC 中，DC=2BD ，CE=3AE ，三角形ADE 的面积是20平方厘米，三角形ABC 的面积是多少？ED CB A【巩固】图中三角形ABC 的面积是180平方厘米，D 是BC 的中点，AD 的长是AE 长的3倍，EF 的长是BF 长的3倍．那么三角形AEF 的面积是多少平方厘米？C B【答案】板块一：1、24 122、上底+下底=20.5-8.5=12（米）梯形面积=12×8.5÷2=51（平方米）3、原长方形的长：24÷2=12（米）原长方形的宽：24÷3=8（米）原来长方形的面积：12×8=96（平方米）4、方法一：可以分割成两个钝角三角形第一个钝角三角形的底是4，高是4，第二个钝角三角形的高是8，底是8-4=4，所以总共的面积是：4×4÷2+8×（8-4）÷2=24（平方厘米）方法二：两个正方形的面积-2处空白的面积=4×4+8×8-8×8÷2-4×（4+8）÷2=24（平方厘米）方法一：可以分割成三个钝角三角形第一个钝角三角形的底是4，高是4，面积是：4×4÷2=8（平方厘米）第二个钝角三角形的高是8，底是（8-4），面积：8×（8-4）÷2=16（平方厘米）第三个钝角三角形的高是8，底是6，面积是：6×8÷2=24（平方厘米）一共的面积：8+16+24=48（平方厘米）方法二：把右上角补起来阴影面积=三个正方形的面积+小长方形面积-两处空白的面积=4×4+8×8+6×6+6×（8-6）-（8+4）×4÷2-8×（6+8）÷2=48（平方厘米）板块二：拓展提高【例题1】、阴影部分+中间空白=中间空白+下面空白所以阴影部分=下面空白20-5=15（厘米）（15+20）×8÷2=140（平方厘米）【例题2】、利用同增同减差不变甲-乙=（甲+空白）-（乙+空白）=大三角形面积-小三角形面积=6×8÷2-4×8÷2=24-16=8（平方厘米）【例题3】、利用同增同减差不变三角形ABF-三角形EDF的面积=9平方厘米同时增加梯形BCDF的面积，则：长方形ABCD-三角形BCE=9长方形ABCD的面积=4×6=24（平方厘米）则三角形BCE的面积=24-9=15（平方厘米）EC=15×2÷6=5（厘米）ED=5-4=1（厘米）【巩固】、利用同增同减差不变三角形CDE-三角形ABE的面积=2平方厘米同时增加三角形BCE的面积，则：三角形BCD-三角形ABC=2三角形ABC的面积=4×4÷2=8（平方厘米）则三角形BCD的面积=8+2=10（平方厘米）CD=10×2÷4=5(厘米)【例题4】原来的面积=15×12=180（平方分米）现在的的面积=（15-2）×（12-2）=130（平方厘米）减少的面积：180-130=50（平方厘米）【巩固】66-2×5=56（平方厘米）设剩下的部分正方形的边长为x厘米5x+2x=56X=8原来长方形的长：8+5=13（厘米）原来长方形的宽：8+2=10（厘米）原来长方形的面积：13×10=130（平方厘米）【例题5】三角形ADF的面积：32÷2÷2=8（平方厘米）三角形ABE的面积：32÷2÷2=8（平方厘米）三角形CEF的面积：32÷2÷2÷2=4（平方厘米）三角形AEF的面积：32-8-8-4=12（平方厘米）【例题6】梯形的面积：（12+15）×8÷2=108（平方厘米）三角形ADE的面积：108÷3=36（平方厘米）AE 的长：36×2÷12=6（厘米）三角形ACF 的面积：108÷3=36（平方厘米）CF 的长：36×2÷8=9（厘米）BE 的长：8-6=2（厘米）BF 的长：15-9=6（厘米）阴影部分面积=2×6÷2=6（平方厘米）【例题7】15×30÷18=25（平方米）【巩固】A 面积：4×16÷8=8（平方米）B 面积：16×12÷8=24（平方米）D 面积：20×24÷16=30（平方米）C 面积：8×20÷16=10（平方米）【例题8】连接DB ，把大三角形分成两个小三角形，正方形的边长就是这两个三角形的高大三角形ABC 的面积是：40×10÷2=200（平方厘米）设正方形的边长为x 厘米40x÷2+10x÷2=20025x=200 X=8正方形面积=8×8=64（平方厘米）【巩固】连接CE ，把大三角形分成两个小三角形，正方形的边长就是这两个三角形的高大三角形ABC 的面积是：40×12÷2=240（平方厘米）设正方形的边长为x 厘米40x÷2+12x÷2=24026x=240X=120/13【例题9】长方形的面积：8×7=56（平方厘米） A B C D阴影部分面积：56÷2=28（平方厘米）【巩固】24÷2÷2÷2=3【例题10】三角形CDE的面积：20×3=60（平方厘米）三角形ADC的面积：20+60=80（平方厘米）三角形ABD的面积：80÷2=40（平方厘米）三角形ABC的面积：40+80=120（平方厘米）【巩固】三角形ABD的面积：180÷2=90（平方厘米）三角形ABE的面积：90÷3=30（平方厘米）三角形AEF的面积：30÷4×3=22.5（平方厘米）。
五年级奥数平面图形面积(附答案)
平面图形的面积计算例1：已知平行四边形的的面积是28平方厘米，求阴影图形的面积。
模仿练习如果用铁丝围成如下图一样的平行四边形，需要用多少厘米铁丝？（单位：厘米）例2：已知大正方形的边长是5厘米，小正方形的边长是4厘米，求阴影部分的面积。
模仿练习正方形的边长分别是10厘米、6厘米，阴影部分的面积是 平方厘米。
ABC EFD GA B CED G例3：如图，ABCD 是边长为4分米的正方形，长方形DEFG 的长是5分米，求长方形DEFG 的宽。
模仿练习如图，ABCD 是正方形，EDGF 是长方形，CD=6厘米，DG=8厘米，求宽ED=?FA B GCD E 86例4：如图，已知四边形ABCD 被它的两条对角线分成四个三角形，其中甲的面积是1，乙的面积是2，丙的面积是3，求丁的面积。
模仿练习两条对角线把梯形ABCD 分割成四个三角形，已知两个三角形的面积，求另两个三角形的面积。
FA EDCBABC DE 甲丁乙丙A BCDO4812 108铜牌练习（1）右面图形的面积是多少平方厘米。
（单位：厘米）（2）如右图，长方形ABCD 中，BE=4厘米，CE=3厘米，长方形的面积是多少平方厘米。
（3） 一个等腰直角三角形，最长的边是20厘米，这个三角形的面积是多少平方厘米。
（4）一个正方形的对角线长5厘米，这个正方形的面积是 平方厘米C D银牌练习（1）已知右面的两个正方形边长分别为6分米和4分米，求图中阴影部分的面积。
（2）如下图，是一块长方形草地，长方形的长是16米，宽是10米，中间有两条宽2米的道路，一条是长方形，一条是平行四边形，那么有草部分（阴影部分）的面积有多大(3)如图，求四边形的面积是是 平方厘米。
（单位：厘米）(4)如图所示，梯形中的两个小三角形的面积为3、9平方厘米，梯形ABCD 的面积是 平方厘米。
金牌练习如右图，在直角三角形ABC 内画一个最大的正方形BEFD ， AB=4厘米，BC=6厘米，正方形的面积最大是 平方厘米。
五年级奥数平面图形的面积计算
7.如下图，梯形ABCD的面积等于72平 方厘米，AB=4厘米，DC=8厘米。求三 角形ABD的面积。
五年级奥数平面图形的面积计算
8.在下图中，阴影部分的面积是 21平方厘米，直角梯形的面积是 多少平方厘米？
五年级奥数平面图形的面积计算
ห้องสมุดไป่ตู้
单位：厘米
谢谢观赏
五年级奥数平面图形的面积计算
此课件下载可自行编辑修改，供参考！ 感谢你的支持，我们会努力做得更好！
谢谢
五年级奥数平面图形的面积计算
五年级奥数平面图形的面积计算
求下面组合图形的面积：
单位：厘米
五年级奥数平面图形的面积计算
求下图中阴影部分的面积：
五年级奥数平面图形的面积计算
单位：厘米
求下图中阴影部分的面积：
五年级奥数平面图形的面积计算
单位：厘米
应用题：
1. 一块梯形木板面 积为9.2平方米，中 位线长2.3米，求梯 形木板的高是多少？
五年级奥数平面图形的面积计算
应用题：
2. 一个梯形的上底为6 厘米,下底为9厘米,面 积为45平方厘米,它的 高是多少厘米？
五年级奥数平面图形的面积计算
应用题：
3. 已知梯形的面积是 21平方米,高6米,下底 长4米,求上底长多少？
五年级奥数平面图形的面积计算
应用题：
4. 某梯形上底与下 底的和为100米,面积 为1500平方米,它的 高是多少米？
五年级第学1期
五年级奥数平面图形的面积计算
五年级奥数平面图形的面积计算
△ADE 五年级奥数平面图形的面积计算
五年级奥数平面图形的面积计算
5．正方形ABCD的边长是12厘米，已知DE是EC长度的2倍， 求：（1）三角形的DEF的面积．（2）CF的长．
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
平面图形的面积计算
例1：已知平行四边形的的面积是28平方厘米，求阴影图形的面积。
模仿练习
如果用铁丝围成如下图一样的平行四边形，需要用多少厘米铁丝？（单位：厘米）
例2：已知大正方形的边长是5厘米，小正方形的边长是4厘米，求阴影部分
的面积。
模仿练习
正方形的边长分别是10厘米、6厘米，阴影部分的面积是 平方厘米。
A
B
C E
F
D G
A B C
E
D G
例3：如图，ABCD 是边长为4分米的正方形，长方形DEFG 的长是5分米，求
长方形DEFG 的宽。
模仿练习
如图，ABCD 是正方形，EDGF 是长方形，CD=6厘米，DG=8厘米，求宽ED=?
F
A B G
C
D E 8
6
例4：如图，已知四边形ABCD 被它的两条对角线分成四个三角形，其中甲的面
积是1，乙的面积是2，丙的面积是3，求丁的面积。
模仿练习
两条对角线把梯形ABCD 分割成四个三角形，已知两个三角形的面积，求另两个三角形的面积。
F
A E
D
C
B
A
B
C D
E 甲丁乙
丙
A B
C
D
O
48
12 10
8
铜牌练习
（1）右面图形的面积是多少平方厘米。
（单位：厘米）
（2）如右图，长方形ABCD 中，BE=4厘米，CE=3厘米，长方形的面积是多少平方厘米。
（3） 一个等腰直角三角形，最长的边是20厘米，这个三角形的面积是多少平
方厘米。
（4）一个正方形的对角线长5厘米，这个正方形的面积是 平方厘米
C D
银牌练习
（1）已知右面的两个正方形边长分别为6分米和4分米，求图中阴影部分的面积。
（2）如下图，是一块长方形草地，长方形的长是16米，宽是10米，中间有两条宽2米的道路，一条是长方形，一条是平行四边形，那么有草部分（阴影部分）的面积有多大
(3)如图，求四边形的面积是是 平方厘米。
（单位：厘米）
(4)如图所示，梯形中的两个小三角形的面积为3、9平方厘米，梯形ABCD 的面积是 平方厘米。
金牌练习
如右图，在直角三角形ABC 内画一个最大的正方形BEFD ， AB=4厘米，BC=6厘米，正方形的面积最大是 平方厘米。
45°
3
7
3 9
A
B
C
┐ D E
F
平面图形的面积计算
例1：已知平行四边形的的面积是28平方厘米，求阴影图形的面积。
4
模仿练习
如果用铁丝围成如下图一样的平行四边形，需要用多少厘米铁丝？（单位：厘米）
40
例2：已知大正方形的边长是5厘米，小正方形的边长是4厘米，求阴影部分
的面积。
8
模仿练习
正方形的边长分别是10厘米、6厘米，阴影部分的面积是 平方厘米。
50
A
B
C E
F
D G
A B
C E
D
G
例3：如图，ABCD 是边长为4分米的正方形，长方形DEFG 的长是5分米，求
长方形DEFG 的宽。
3.2
模仿练习
如图，ABCD 是正方形，EDGF 是长方形，CD=6厘米，DG=8厘米，求宽ED=?
F
A B G
C
D E 8
6 4.5
例4：如图，已知四边形ABCD 被它的两条对角线分成四个三角形，其中甲的面
积是1，乙的面积是2，丙的面积是3，求丁的面积。
1.5
模仿练习
两条对角线把梯形ABCD 分割成四个三角形，已知两个三角形的面积，求另两个三角形的面积。
36
F
A E D
C B
A
B
C D
E 甲丁乙
丙
A
B
C
D
O
48
12 10
8 铜牌练习
（1）右面图形的面积是多少平方厘米。
（单位：厘米）
90
（2）如右图，长方形ABCD 中，BE=4厘米，CE=3厘米，长方形的面积是多少平方厘米。
12
（4） 一个等腰直角三角形，最长的边是20厘米，这个三角形的面积是多少平
方厘米。
100
（4）一个正方形的对角线长5厘米，这个正方形的面积是 平方厘米 12.5
C
D
银牌练习
（1）已知右面的两个正方形边长分别为6分米和4分米，求图中阴影部分的面积。
14
（2）如下图，是一块长方形草地，长方形的长是16米，宽是10米，中间有两条宽2米的道路，一条是长方形，一条是平行四边形，那么有草部分（阴影部分）的面积有多大
112
(3)如图，求四边形的面积是是 平方厘米。
（单位：厘米）
20
(4)如图所示，梯形中的两个小三角形的面积为3、9平方厘米，梯形ABCD 的面积是 平方厘米。
16
金牌练习
如右图，在直角三角形ABC 内画一个最大的正方形BEFD ， AB=4厘米，BC=6厘米，正方形的面积最大是 平方厘米。
5.76
45°
3
7
3 9
A
B
C
┐ D E
F。