第6章图像编码与压缩
第六章图像编码技术()
6.3 基础理论
信息量 概率为P(E)的随机事件 E 的信息量
1 I ( E ) log logP ( E ) P( E )
I(E )称为E的自信息（随概率增加而减少） 特例：P(E ) = 1（即事件总发生），那么I(E ) = 0 信息的单位：比特（log以2为底）
产生单个信源符号的自信息：I (aj) = –logP(aj)
2
峰值信噪比（PSNR）
2 PSNR 10 lg MN f max f max max{f ( x, y )}
M 1 N 1 x 0 y 0
ˆ ( x, y ) f ( x, y ) 2 f
2. 主观保真度准则 观察者对图像综合评价的平均 P151 例6.2.1 电视图像质量评价
SNRms
g x, y
2
g x, y f x, y
2
将 SNRms 归一化信噪比并用分贝（dB）表示.令
1 M 1 f MN x 0
N 1 y 0
f ( x, y )
则有
M 1 N 1 2 f ( x, y ) f x 0 y 0 SNR 10 lg M 1 N 1 ˆ f ( x, y ) f ( x, y ) x 0 y 0
哈夫曼的编法并不惟一 （2）
例：单符号离散无记忆信源
X x1 , x2 , x3 , x4 , x5 , P( X ) 0.4 0.2 0.2 0.1 0.1 ，用
两种不同的方法对其编二进制哈夫曼码。
方法一：合并后的新符号排在其它相同概率符号的后面。
数字图像处理要点简述详述
第一.二章.采样，量化，数字图像的表示 基本的数字图像处理系统系统的层次结构I 应用程序 I 开发工具 操作系统 设备驱动程序I硬件I图像处理的主要任务： 图像获取与数字化 图像增强 图像恢复 图像重建 图像变换 图像编码与压缩 图像分割 特点：(1) 处理精度高。
(2) 重现性能好。
(3) 灵活性髙1•图像的数字化包括两个主要步骤：离散和量化2. 在数字图像领域，将图像看成是许多大小相同、形状一致的像素组成3. 为便于数字存储和计算机处理可以通过数模转换(A/D)将连续图像变为数字图像。
4•数字化包括取样和量化两个过程：取样：对空间连续坐标(x,y)的离散化量化：幅值f(x,y)的离散化(使连续信号的幅度用有限级的数码表示的过程。
)5.数字化图像所需的主要硬件：♦采样孔、图像扫描机构、光传感器、量化器、输岀存储体6•取样和量化的结果是一个矩阵 7.其中矩阵中的每个元素代表一个邃塞8•存储一幅图像的数据量又空间分辨率和幅度分辨率决定 9•灵敏度、分辨率、信噪比是三大指标第三章，傅里叶变换，DCT变换，WHT•余弦型变换：•傅里叶变换(DFT)和余弦变换(DCT)O•方波型变换：•沃尔什•哈达玛变换(DWT)1•二维连续傅里叶正反变换:F(u,v)= I f f(x.y)eJ_oc J_ocf g y)= \f F(u, v)ej27r(nA+vv)dwdvJ —oo J —oo二维离散傅里叶变换：M — 1 N — I=乏疋 Fgg 宀SS)if=o v=O。
F(u, v)即为f (x, y)的频谱。
频谱的直流成分说明在频谱原点的傅里叶变换尸(0,0)等于图像的平均灰度级 卷积定理：/(x,y)*^(x, y)= ss /O, n)g(x 一 m, y~n)/?/=() n=02•二维离散余弦变换(DCT)一维离散余弦变换：EO)=%)岳gfg 芈严 其中 c®=怜 ""DCT 逆变换为F(u.v)=1~MN A =0 y=02 A r -1/(«)=咅 C(0) + \1三工 F (gsn(2n +1)« ~~2N3•—维沃尔什变换核g （W ）：1 X_JL£（乂申）=丄口（一 1）®（”）為一】一心）＜N i=o• 厂、Cn 7V--1 ^T-l码3》=卡吝 /G 〉耳(—1)635—一 3«JC> =牙中 O )n (—O务i二维：•正变换: 1 N —l. N —!■H —1护(“*) = —X X /X%」)口( — 1)4(5—373$一_W] N 宜 U • JO■逆变换二1 AT-l JV-l 片_]/（X.y ）=丄 £ 乞 疗（心巧 口弟-i -心）JN 為 v=o ~。
语音压缩编码与图像压缩编码
语音压缩编码与图像压缩编码语音压缩编码语音压缩编码可分为三类：波形编码、参量编码和混合编码。
这些都属于有损压缩编码。
1．波形编码（1）波形编码的定义波形编码是指对利用调制信号的波形对语音信号进行调制编码的方式。
（2）波形编码的性能要求保持语音波形不变，或使波形失真尽量小。
2．语音参量编码（1）语音参量编码的定义语音参量编码是将语音的主要参量提取出来编码的方式。
（2）语音参量编码的基本原理首先分析语音的短时频谱特性，提取出语音的频谱参量，然后再用这些参量合成语音波形。
（3）语音参量编码的性能要求保持语音的可懂度和清晰度尽量高。
3．混合编码（1）混合编码的定义混合编码是既采用了语音参量又包括了部分语音波形信息的编码方式。
（2）混合编码的基本原理混合编码除了采用时变线性滤波器作为核心外，还在激励源中加入了语音波形的某种信息，从而改进其合成语音的质量。
（3）混合编码的性能要求保持语音的可懂度和清晰度尽量高。
图像压缩编码图像压缩按照图像是否有失真，可分为有损压缩和无损压缩；按照静止图像和动态图像，又可分为静止图像压缩和动态图像压缩。
1．静止图像压缩编码的特点（1）静止数字图像信号是由二维的许多像素构成的；（2）在各邻近像素之间都有相关性；（3）所以可以用差分编码（DPCM）或其他预测方法，仅传输预测误差从而压缩数据率。
2．动态图像压缩编码的特点（1）动态数字图像是由许多帧静止图像构成的，可看成是三维的图像；（2）在邻近帧的像素之间有相关性；（3）动态图像的压缩可看作是在静止图像压缩基础上再设法减小邻近帧之间的相关性。
《数字图像处理》习题参考答案
《数字图像处理》习题参考答案第1 章概述连续图像和数字图像如何相互转换答：数字图像将图像看成是许多大小相同、形状一致的像素组成。
这样，数字图像可以用二维矩阵表示。
将自然界的图像通过光学系统成像并由电子器件或系统转化为模拟图像（连续图像）信号，再由模拟/数字转化器（ADC）得到原始的数字图像信号。
图像的数字化包括离散和量化两个主要步骤。
在空间将连续坐标过程称为离散化，而进一步将图像的幅度值（可能是灰度或色彩）整数化的过程称为量化。
#采用数字图像处理有何优点答：数字图像处理与光学等模拟方式相比具有以下鲜明的特点：1．具有数字信号处理技术共有的特点。
（1）处理精度高。
（2）重现性能好。
（3）灵活性高。
2．数字图像处理后的图像是供人观察和评价的，也可能作为机器视觉的预处理结果。
3．数字图像处理技术适用面宽。
4．数字图像处理技术综合性强。
数字图像处理主要包括哪些研究内容答：图像处理的任务是将客观世界的景象进行获取并转化为数字图像、进行增强、变换、编码、恢复、重建、编码和压缩、分割等处理，它将一幅图像转化为另一幅具有新的意义的图像。
]讨论数字图像处理系统的组成。
列举你熟悉的图像处理系统并分析它们的组成和功能。
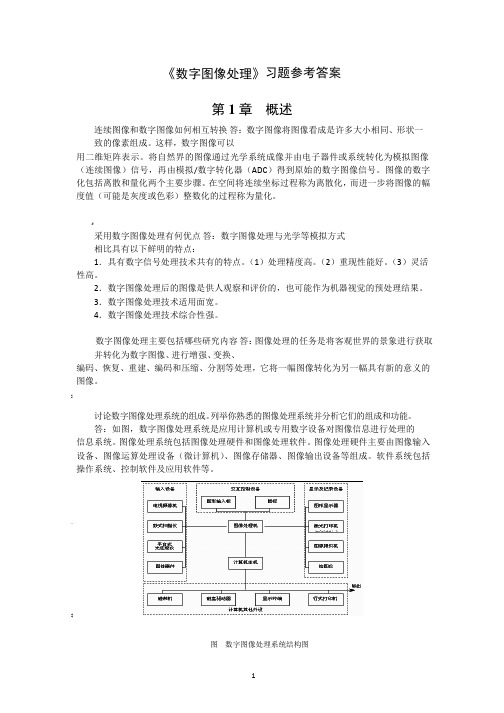
答：如图，数字图像处理系统是应用计算机或专用数字设备对图像信息进行处理的信息系统。
图像处理系统包括图像处理硬件和图像处理软件。
图像处理硬件主要由图像输入设备、图像运算处理设备（微计算机）、图像存储器、图像输出设备等组成。
软件系统包括操作系统、控制软件及应用软件等。
$图数字图像处理系统结构图1常见的数字图像处理开发工具有哪些各有什么特点答．目前图像处理系统开发的主流工具为Visual C++（面向对象可视化集成工具）和MATLAB 的图像处理工具箱（Image Processing Tool box）。
两种开发工具各有所长且有相互间的软件接口。
Microsoft 公司的VC++是一种具有高度综合性能的面向对象可视化集成工具，用它开发出来的Win 32 程序有着运行速度快、可移植能力强等优点。
图像编码与压缩
LZW编码
LZW编码是由Lemple和Ziv提出并经 Welch扩充而形成的无损压缩专利技术。在 对文件进行编码时，需要生成特定字符序列 的表以及对应的代码。每当表中没有的字符 串出现时，就把它与其代码一道存储起来。 这以后当该串再次出现时，只存储其代码。 实际上，字符串表是在压缩过程中动态生成 的，而且由于解压缩算法可以从压缩文件中 重构字符串表，因而字符串表也不必存储。
5
差
图像质量很差，妨碍观看的干扰始终存在，几乎无法观看。
6
不能用 图像质量极差，不能使用尺度
进行评价。如果观察者将 和f(x,y)逐个进行对照，则
可以得到相对的质量分。例如可用
来代
表主观评价{很差，较差，稍差，相同，稍好，较好，很
好}。
四、霍夫曼编码
DCT编码 DCT变换是图像压缩标准中常用的变换方法，
如JPEG标准中将图像按照8x8分块利用DCT变换 编码实现压缩。
Lena.bmp(原图)
Lenna.jpg (压缩率9.2)
Lenna.jpg (压缩率18.4)
Lenna.jpg (压缩率51.6)
其它变换编码
变换方法是实现图像数据压缩的主要手段，其基本原 理是首先通过变换将图像数据投影到另一特征空间，降低 数据的相关性，使有效数据集中分布；再采用量化方法离 散化，最后通过Huffman等无损压缩编码进一步压缩数据 的存储量。DCT是一种常用的变换域压缩方法，是 JPEG,MPEGI-II等图像及视频信号压缩标准的算法基础。 在实际采用DCT编码时，需要分块处理，各块单独变换编 码，整体图像编码后再解压会出现块状人工效应，特别是 当压缩比较大时非常明显，使图像失真。因此，为了获得 更高的图像压缩比，人们提出了一些其它方法，如基于小 波变换的图像压缩算法和基于分形的图像压缩算法等。
数字图像处理图像压缩与编码
数字图像处理
28
#include <stdio.h> #include <stdlib.h> #include <string.h> const char *o = ""; int main() {
char *d = malloc(2*strlen(o)); char *oc = malloc(strlen(o)); int rl = rle_encode(d, o, strlen(o)); int ocl = rle_decode(oc, d, rl); fwrite(oc, 1, ocl, stdout); free(d); free(oc); return 0; }
无损压缩的格式可以很容易的转换为其它有损压缩格式， 而不存在多次有损压缩所带来的更大失真问题
当然，无损压缩的缺点也是明显的，包括：
占用空间大，压缩比有限
解码无损压缩格式需要更大的计算量，所以对解码硬件 具有更高的要求
数字图像处理
18
游程编码
差分脉冲编码调 制
熵编码
LZW字典算法
Huffman编码
小波分析是把一个信号分解成由原始小波经过移位 和缩放后的一系列小波，因此小波是小波变换的基 函数，即小波可用作表示一些函数的基函数。
经过多年的努力，小波理论基础已经基本建立并成为应 用数学的一个新领域，引起了众多数学家和工程技术人 员的极大关注。
数字图像处理
9
压缩的完成主要依靠，一是使用线性变换来剔 除图像数据的相关性，二是对所得到的变换系 数进行量化，三是对不同类型的数据分配比特 位，四是对量化后的结果进行熵编码。
return dl;
}
数字图像处理
数字图像处理复习资料(11春季)
数字图像处理课程复习大纲——————上大（11春季）已扩展第1章绪论要求：掌握《数字图像处理》理论及技术的基础性概念；掌握数字图像处理这门学科的基本理论及技术架构；熟悉其应用领域，硬件系统及设备1.1.数字图像及应用数字图像，各种电磁波谱及各种图像成像技术，以及图像处理在各种行业当中的应用，不同波段的图像，图像类型，图像应用领域1.信息是事物存在的一种形式，数据是信息的“符号”载体；2.图像：用各种观测系统①以不同的形式和手段观测世界②而获得的，可以直接或间接作用于人眼③并进而产生视知觉的实体④3.图像在计算机里的表示形式就是所谓的“数字图像”。
4.数字图像处理的应用主要有三方面的因素需要考虑：存储器的容量，计算速度，传输带宽。
5.图像的分类：按灰度分：二值图像和多灰度图像；按色彩分：单色图像和彩色图像；按运动分类：静态图像和动态图像；按时空分布分类：二维图像，三维图像和多维图像。
6.图像处理的基本内容：图像信息的获取，图像的存储，图像的传输，图像处理。
1.2.图像工程概述图像处理3层次，数字图像处理于其他学科的关系1.图像工程的三个层次：图像理解，图像分析，图像处理；2.图像：主要特点为由一系列的具有不同灰度值的像素所组成；图形：主要特点为由一组数学公式描述。
1.3.图像表示和显示图像与函数，像素，图像的矩阵表示，图像的解析表示，图像输出设备1.一幅图像一般可以用一个2-D函数f(x, y)来表示（计算机中为一个2-D数组）。
2.一幅图像可分解为许多个单元。
每个基本单元叫做图像元素，简称像素。
3.将一个区域分成3*3个单元以输出10种不同的灰度。
用“区域”来代替“像素”。
4.抖动技术：通过调节或变动图像的幅度值来改善量化过粗图像的显示质量。
1.4.数字图像存储格式存储器件，图像文件格式主题词：不同波段的图像，数字图像，数字图像处理系统，图像成像技术；3-D图像，彩色图像，多光谱图像，立体图像，序列图像，深度图像，纹理图像，投影重建图像，合成图像；图像处理，图像分析，图像理解；图像的矩阵表示，半调输出，抖动技术，BMP，GIF，TIFF，JPEG1.图像文件格式：一种是矢量形式，另一种是光栅形式。
JPEG图像压缩与编码解析
JPEG图像压缩与编码解析
JPEG（Joint Photographic Experts Group）压缩格式，以其易于使用、压缩率高而著称，是应用最为广泛的一种图像压缩格式。
JPEG压缩
算法把图像分为内容和质量两个维度来进行压缩。
下面将详细论述JPEG
图像编码与解码的基本原理。
1.JPEG图像编码过程
（1）空间域转换
空间域转换是将原始图像由空间域变换成更加节省存储空间的频域。
JPEG压缩采用的是离散余弦变换（DCT）这种空间域转换方法，它可以把
图像表示成一系列正交基函数的线性组合，每一个函数表示的是对应的图
像量化值。
利用DCT将一幅图像分成8×8（也有可能是16×16）大小的块，每一个块由64（或者256）个相互独立的像素构成，被称为DCT子块。
（2）频段选择
JPEG图像压缩算法采用频段选择的原则，根据图像中的特征，把空
间域转换之后的低频分量即低频信息传��有损，而只把高频分量即高频
信息传递以达到保留重要信息的目的，在JPEG中，特征的保留按照“从
重要的到不重要的”的顺序进行。
（3）变换。
图像无损压缩算法研究
图像无损压缩算法研究第一章：引言图像压缩技术的发展使得图像在存储和传输方面更加高效。
无损压缩算法通过减少图像文件的大小，同时保持图像质量不受影响，从而实现对图像的高效压缩。
无损压缩算法广泛应用于数字图像处理、电视广播、远程监控、医学图像存储和互联网传输等领域。
本文旨在探讨图像无损压缩算法的研究现状和发展趋势。
第二章：图像无损压缩算法综述本章首先介绍图像压缩的基本原理和目标，然后综述了当前常用的图像无损压缩算法。
其中包括哈夫曼编码、算术编码、预测编码、差分编码和自适应编码等。
对每种算法的原理、优点和缺点进行了详细的分析和比较。
第三章：小波变换与图像无损压缩算法小波变换是一种重要的数学工具，在图像无损压缩算法中得到了广泛的应用。
本章介绍了小波变换的基本概念和原理，并详细介绍了小波变换在图像压缩中的应用。
重点讨论了小波系数的编码方法和解码方法，以及小波变换在图像无损压缩中的优化算法。
第四章：自适应编码在图像无损压缩中的应用自适应编码是一种基于概率统计的编码方法，具有较好的压缩效果和灵活性。
本章介绍了自适应编码的基本原理和常见的算法，如算术编码、自适应霍夫曼编码和自适应等长编码等。
特别说明了自适应编码在图像无损压缩中的应用，包括颜色映射编码、熵编码和像素值编码等。
第五章：基于预测的图像无损压缩算法预测编码是一种基于差值的编码方法，通过对图像中的像素进行预测，将预测误差进行编码，从而实现图像的高效压缩。
本章介绍了常见的预测编码算法，如差分编码和预测误差编码等。
详细讨论了这些算法的原理、优点和局限性，并提出了一些改进方法和思路。
第六章：图像无损压缩算法的性能评估和比较本章分析了图像无损压缩算法的性能评估指标和方法，并对常见的图像无损压缩算法进行了性能比较。
主要包括压缩比、失真度和计算复杂度等方面的评估标准。
通过对比实验和分析，得出了各种算法在不同场景下的适用性和优劣势。
第七章：图像无损压缩算法的发展趋势本章展望了图像无损压缩算法的发展趋势，并提出了一些可能的研究方向。
图像编码的原理与流程详解
图像编码是一种将图像数据转换为更紧凑表示的过程，它在数字图像处理和传输中起着至关重要的作用。
本文将详细解析图像编码的原理和流程，从数据压缩到图像还原，逐步揭示其工作机制。
一、图像编码的基本原理图像编码的基本原理是基于人眼的视觉特性和图像的空间相关性。
人眼对图像的敏感度不均匀，对细节和变化较大的区域更敏感。
因此，图像编码可以通过降低对细节和变化较小的区域的精度来实现压缩。
此外，图像中的相邻像素之间存在一定的相关性，这种相关性可以通过差分编码来利用。
二、图像编码的流程图像编码一般包括以下几个主要的步骤：预处理、变换、量化、编码和解码。
1. 预处理预处理是对原始图像进行一些基本操作，以准备好数据进行后续处理。
常见的预处理操作包括图像去噪、颜色空间转换和亮度调整等。
2. 变换变换是将图像从空间域转换到频域的过程。
常用的变换方法包括离散余弦变换（DCT）和小波变换。
变换的目的是将图像的能量集中在少数重要的频率成分上，减小冗余信息。
3. 量化量化是将变换后的频域系数映射到有限数量的离散级别，以减小数据表示的精度。
量化通常使用固定或自适应的量化表，对不同频率的系数施加不同的量化步长。
4. 编码编码是将量化后的系数进行压缩表示的过程。
常用的编码方法有霍夫曼编码、算术编码和熵编码等。
这些编码方法利用了频率统计和冗余信息的特性，实现了高效的数据压缩。
5. 解码解码是编码的逆过程，将压缩表示的图像数据恢复为原始的图像信息。
解码过程包括解码器的反量化和反变换操作，以及任何必要的后处理步骤。
三、图像编码的应用和发展图像编码技术在图像和视频传输、存储和处理中得到了广泛的应用。
随着网络宽带的提升和存储设备的发展，人们对图像质量和数据压缩比的要求越来越高，图像编码技术也在不断进步。
目前，主流的图像编码标准有JPEG、JPEG 2000和HEVC等。
JPEG 是最常用的静态图像编码标准，它利用了DCT、量化和霍夫曼编码等技术，实现了相对较高的压缩比。
图像压缩编码原理I
图像压缩编码的发展
第一代，着重于图像信息冗余度的压缩方 法，如预测编码、变换编码、矢量量化编 码、小波编码等 第二代，着重于图像视觉冗余信息的压缩 方法，如基于方向滤波的图像编码、基于 图像轮廓——纹理的编码法等 第三代基于模型的图像压缩方法，如分形 编码法、基于模型的编码方法等
有关图像压IF是图形交换格式(Graphics Interchange Format)的英文缩 写，是由CompuServe公司于80年代推出的一种高压缩比的彩色 图像文件格式 GIF图像格式采用无损数据压缩方法中压缩效率较高的LZW算法， 主要用于图像文件的网络传输。 考虑到网络传输中的实际情况，GIF图像格式还增加了渐显方式， 即在图像传输过程中，用户先看到图像的大致轮廓，然后随着传输 过程的继续而逐渐看清图像的细节部分，从而适应了用户的观赏心 理，这种方式以后也被其他图像格式所采用 最初，GIF只是用来存储单幅静止图像，后来，又进一步发展成为 可以同时存储若干幅静止图像并进而形成连续的动画，目前 Internet上大量采用的彩色动画文件多为这种格式的GIF文件。 GIF通常用来表示由计算机生成的动画序列，其图像相对而言比较 简单，因此可以得到比较高的无损压缩率，文件尺寸也不大。然而， 对于来自外部世界的真实而复杂的影像信息而言，无损压缩便显得 无能为力
图像编码中的数据重排与压缩技巧(五)
图像编码是将图像信号转化为二进制编码的过程，通过压缩和重排图像数据，可以有效减小图像文件的大小，并提高其在传输和存储过程中的效率。
在图像编码中，数据重排和压缩技巧起着至关重要的作用。
一、数据重排技巧数据重排是指通过重新排列图像数据的存储方式，使得图像压缩的效果更好。
其中，最常用的技巧是行程长度编码（Run-length Encoding，RLE）和熵编码。
1. 行程长度编码（Run-length Encoding，RLE）RLE是一种简单有效的数据重排技巧，它通过统计连续采样值的个数，将相同的像素值序列编码为次数和数值的对应关系。
例如，对于一副宽度为8个像素，高度为8个像素的图像，其中的一个行程长度编码可以表示为：(5, 2)，即出现5次的像素值为2。
通过这种方式，可以将重复出现的像素值有效地压缩成更短的编码，减小图像文件的大小。
2. 熵编码熵编码是一种通过统计图像数据的频次分布来进行数据重排的技巧，其中包括哈夫曼编码和算术编码。
哈夫曼编码通过构建一颗二叉树，根据各个像素值的频次来确定唯一的二进制编码，从而实现数据的高效压缩。
算术编码则是通过将符号（像素值）映射到某个数值区间，根据像素值出现概率的大小来确定区间范围，从而实现数据的有损压缩。
二、压缩技巧在图像编码过程中，压缩技巧是将图像数据转化为更紧凑、高效的形式，以减小图像文件的大小。
常用的压缩技巧包括离散余弦变换（Discrete Cosine Transform，DCT）和小波变换。
1. 离散余弦变换（Discrete Cosine Transform，DCT）DCT是一种将空域信号转换为频域信号的技术，通过将图像数据分解为不同频率的分量，将高频分量的系数置为0，从而实现数据的压缩。
DCT压缩技巧广泛应用于JPEG图像编码中，它可以对图像进行有损压缩，保留图像较重要的细节信息，同时达到较好的压缩比。
2. 小波变换小波变换是一种基于多尺度分析的信号处理技术，通过将图像数据进行分解和重组，实现对图像数据的压缩和重构。
数字图像处理教学大纲
《数字图像处理》课程教学大纲课程代码：030742025课程英文名称：Digital Image Processing课程总学时：40 讲课：32 实验：8 上机：0适用专业：电子信息科学与技术大纲编写（修订）时间：2017.5一、大纲使用说明（一）课程的地位及教学目标数字图像处理是电子信息科学与技术专业开设的一门培养学生具有数字图像处理能力的选修的专业课之一，通过本课程的学习，要求学生掌握有关数字图像处理的基本概念、方法、原理及应用，培养和增强学生数字图像处理技能的创新意识和创新思维，提高实际动手能力和创新能力，为学生进一步学习专业课程奠定基础。
通过本课程的学习，学生将达到以下要求：1．牢固掌握图像数字化理论、图像直方图及其应用、傅立叶变换、图像增强的基本算法、图像分割、影像纹理的基本分析法、二值图像处理等内容；；2．掌握空间滤波的卷积算法、几何校正和灰度内插法等；；3．了解图像复原与重建、数据压缩、模板匹配、分类、图像处理与分析的发展趋势。
（二）知识、能力及技能方面的基本要求1.基本知识：数字图像处理的基本概念和算法2.基本理论和方法：数字图像与图像数字化的概念；灰度直方图；图像处理算法形式；傅立叶变换、图像空间域、频率域增强；图像分割的边缘检测；纹理分析；二值图像处理与分析等。
3.基本技能: 能较为熟练地用Matlab或VC++语言编写常用的数字图像处理算法。
（三）实施说明1．教学方法：本课程在讲解上着重数学公式物理含义的阐述，对于难点内容，可以结合实际的图像矩阵来解释。
力求做到重点突出，由浅入深，便于学生理解和掌握。
在应用方面，主要结合自己和他人的研究成果，介绍一些图像处理方法的应用实例，增强学生的直观体验，培养学生的学习兴趣。
2．教学手段：在教学中采用电子教案、CAI课件及多媒体教学系统等先进教学手段，这样可以达到图文并茂的效果，有利于学生理解掌握各种算法。
（四）对先修课的要求先修课：MATLAB程序设计；概率论与数理统计；线性代数；数值分析；数字信号处理。
数字图像处理第6章_图像编码与压缩技术.
霍夫曼编码
例 假设一个文件中出现了8种符号S0、S1、S2、S3、S4、S5、S6、 S7，那么每种符号编码至少需要3bit S0=000, S1=001, S2=010, S3=011, S4=100, S5=101, S6=110, S7=111 那么，符号序列S0 S1 S7 S0 S1 S6 S2 S2 S3 S4 S5 S0 S0 S1编码后 000 001 111 000 001 110 010 010 011 100 101 000 000 001 （共42bit） 和等长编码不同的一种方法是可变长编码。在这种编码方法中， 表示符号的码字的长度不是固定不变的，而是随着符号出现的概率 而变化，对于那些出现概率大的信息符号编以较短的字长的码，而 对于那些出现概率小的信息符号编以较长的字长的码。
6.3.3 霍夫曼编码
霍夫曼(Huffman)编码是根据可变长最佳编码定理，应用霍夫曼算
1．
对于每个符号，例如经过量化后的图像数据，如果对它们每 个值都是以相同长度的二进制码表示的，则称为等长编码或均匀 编码。采用等长编码的优点是编码过程和解码过程简单，但由于 这种编码方法没有考虑各个符号出现的概率，实际上就是将它们 当作等概率事件处理的，因而它的编码效率比较低。例6.3给出了 一个等长编码的例子。
6.1.1 图像的信息冗余
图像数据的压缩是基于图像存在冗余这种特性。压缩就是去掉 信息中的冗余，即保留不确定的信息，去掉确定的信息（可推知 的）；也就是用一种更接近信息本身的描述代替原有冗余的描述。 8 （1） 空间冗余。在同一幅图像中，规则物体或规则背景的物理表 面特性具有的相关性，这种相关性会使它们的图像结构趋于有序和 平滑，表现出空间数据的冗余。邻近像素灰度分布的相关性很强。 （2） 频间冗余。多谱段图像中各谱段图像对应像素之间灰度相关 （3） 时间冗余。对于动画或电视图像所形成的图像序列（帧序 列），相邻两帧图像之间有较大的相关性，其中有很多局部甚至完
图像编码与压缩技术
下一页
home
上一页
熵是无失真图像编码的下界。
设变长编码所用的码进元制为D，第i个符号出现的概率p为i 与其对应的码字长度N为i，则变长最佳编码的均平编码长度 R的范围为：
H 1 R H
log2D
log2 D
下一页
home
上一页
四.图像编码新技术
图像编码已经发展了几十年，人们不断提出新 的压缩方法。如，利用人工神经网络（Artificial Neural Network，ANN）的压缩编码、分形编码 （Fractal Coding）、小波编码（Wavelet Coding）、 基于对象的压缩编码（Object Based Coding）和基 于模型的压缩编码（Model Based Coding）等等。
下一页
home
上一页
图 分形图像
下一页
home
上一页
给出一个稍微复杂的树模型：
设图形 T 0 为一条单位长直线
段，在第一个三等分点上各向两
边45角的方向延伸出两条 1
2
L0
长的
线段，在中点处向左以 30 延伸
出分线点段12 L 0处。长向得的右到线方图段以形，T3再10。 在延将第伸T二出n 个的13 L三每0 的等5
下一页
home
上一页
4)算法的复杂度 • 算法的复杂度即指完成图像压缩和解压缩所需的
运算量和硬件实现该算法的难易程度。
优秀的压缩算法要求有较高的压缩比，压缩 和解压缩快，算法简单，易于硬件实现，还要求 解压缩后的图像质量较好。选用编码方法时一定 要考虑图像信源本身的统计特性、多媒体系统(硬 件和软件产品)的适应能力、应用环境以及技术标 准。
数字图像处理复习题
第一章绪论一.选择题1. 一幅数字图像是：( )A、一个观测系统B、一个有许多像素排列而成的实体C、一个2-D数组中的元素D、一个3-D空间的场景。
提示：考虑图像和数字图像的定义2. 半调输出技术可以：( )A、改善图像的空间分辨率B、改善图像的幅度分辨率C、利用抖动技术实现D、消除虚假轮廓现象。
提示：半调输出技术牺牲空间分辨率以提高幅度分辨率3. 一幅256*256的图像，若灰度级数为16，则存储它所需的比特数是：( )A、256KB、512KC、1M C、2M提示：表达图像所需的比特数是图像的长乘宽再乘灰度级数对应的比特数。
4. 图像中虚假轮廓的出现就其本质而言是由于：( )A、图像的灰度级数不够多造成的B、图像的空间分辨率不够高造成C、图像的灰度级数过多造成的D、图像的空间分辨率过高造成。
提示：平滑区域内灰度应缓慢变化，但当图像的灰度级数不够多时会产生阶跃，图像中的虚假轮廓最易在平滑区域内产生。
5. 数字图像木刻画效果的出现是由于下列原因所产生的：（）A、图像的幅度分辨率过小B、图像的幅度分辨率过大C、图像的空间分辨率过小D、图像的空间分辨率过大提示：图像中的木刻效果指图像中的灰度级数很少6. 以下图像技术中属于图像处理技术的是：（）（图像合成输入是数据，图像分类输出是类别数据）A、图像编码B、图像合成C、图像增强D、图像分类。
提示：对比较狭义的图像处理技术，输入输出都是图像。
解答：1.B 2.B 3.A 4.A 5.A 6.AC二.简答题1. 数字图像处理的主要研究内容包含很多方面，请列出并简述其中的4种。
2. 什么是图像识别与理解？3. 简述数字图像处理的至少3种主要研究内容。
4. 简述数字图像处理的至少4种应用。
5. 简述图像几何变换与图像变换的区别。
解答:1. ①图像数字化：将一幅图像以数字的形式表示。
主要包括采样和量化两个过程。
②图像增强：将一幅图像中的有用信息进行增强，同时对其无用信息进行抑制，提高图像的可观察性。
图像压缩
其中，p(ai|bk)表示信源编码输出为bk，估计信 源输入为ai的条件概率。I(ai|bk)称为条件自信 息量，表示在发现信源编码输出为bk，对信源 输入为ai的不确定性的猜测或知道bk后ai还保 留的信息量。I(ai)表示ai的不确定性。两者值 差即为bk解除的ai不确定性的多少。
无损压缩编码
3、平均码字长 • 借助熵的概念可以定义量度任何特定码的 性能的准则，即平均码字长度。
N i p(d i )
m
• 其中βi为灰度级di所对应的码字长度。的单 位也是比特/字符。
i 1
4、编码效率 编码符号是在字母集合A={a1,a2,a3,…am}中选取的。如果编 码后形成一个新的等概率的无记忆信源，字母数为n，则 它的最大熵应为logn比特/符号。因此这是一个极限值。如 果H(d)/ =logn，则可以认为编码效率已经达到100%，如 果H(d)/ <logn，则可认为编码效率较低。
信源熵为：
H=-∑Pilog2Pi =-(0.4log20.4+0.3log20.3
+2*0.1log20.1+0.06log20.06+0.04log20.04)
=2.14比特/符号
码字 长度
平均码字长度：R=∑βiPi R= ∑βiPi =0.4×1+0.3 × 2+0.1 × 3+0.1 × 4+0.06 × 5+0.04 × 5=2.2比特/符号
• 哈夫曼编码 • 游程编码 • 无损预测编码
哈夫曼编码
• 50年代提出，一种无损的统计编码方法 • 用变长的码使冗余量达到最小，用一棵 二叉树来编码，使常出现的字符用较短 的码表示，不常出现的字符用较长的码 表示。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
算术编码示例
编码来自1个4-符号信源{a1, a2, a3, a4}的由5个符号组成 的符号序列：b1b2b3b4b5 = a1a2a3a3a4
信源符号 概率 0.2 0.2 0.4 0.2 初始子区间 [0 , 0.2] [0.2 , 0.4] [0.4 , 0.8] [0.8 , 1.0]
a1 a2
解码过程
0.068
(1)0.068 在区间[0 ,0.2] ，可知第一个源符号为a1 (2) (3) (4) (5)
0.068 0 0.34 0.2
30 10 20 40 20 40 0 20
20 20 30 30 20 40 40 20
霍夫曼编码的特点：
(1) 霍夫曼编码构造出来的编码值不是唯一的。（在编码时， 可以大概率为’1’，小概率为’0’，也可相反） (2) 当图像灰度值分布很不均匀时，霍夫曼编码的效率就高， 反之，编码效率低。 (3) 霍夫曼编码必须先计算出图像数据的概率特性形成编码 后，才能对数据进行编码，必须通过查表方法建立对应关 系。
6.1 概述 6.1.1 图像数据压缩的必要性与可能性 数据压缩的研究内容包括数据的表示、传输、 变换和编码方法，目的是减少存储数据所需的空 间和传输所用的时间。 图像编码与压缩就是对图像数据按一定的规 则进行变换和组合，达到以尽可能少的代码（符 号）来表示尽可能多的图像信息。
6.1.2 图像的数据冗余
霍夫曼编码 费诺.仙侬编码 行程编码 算术编码
预测编码 变换编码 其它编码
6.2 图像保真度准则
描述解码图像相对原始图像偏离程度的测度一般称为 保真度。常用的保真度准则可分为两大类：客观保真度准 则和主观保真度准则。 6.2.1 客观保真度准则 最常用的客观保真度准则是原图像和解码图像之间的 均方根误差和均方根信噪比两种。 6.2.2 主观保真度准则 很多解压图最终是供人观看的，一种常用的方法是让 一组（不少于20人）观察者观察图像并给该图像评分，将 他们对该图像的评分取平均，作为这幅图像的质量。
W w1 , w2 , w3 , w4 , w5 , w6
霍夫曼编码算法基于一种称为“编码树”（coding tree） 的技术。算法步骤如下： （1）初始化，根据符号概率的大小按由大到小顺序对符号 进行排序。 （2）把概率最小的两个符号组成一个新符号（节点），即 新符号的概率等于这两个符号概率之和。 （3）重复第2步，直到形成一个符号为止（树），其概率 最后等于1。 （4）从编码树的根开始回溯到原始的符号，并将每一下分 枝赋值为1，上分枝赋值为0。 在上述工作完毕之后，从最后两个概率开始逐步向前 进行编码。对于概率大的消息赋予0，小的赋予1。
a3
a4
a1a2a3a3a4
a1 [0,0.2]
a1a2
StartN=Start+but×L EndN=Start+top×L
[0.2*0.2, 0.2*0.4 ]=[0.04, 0.08]
a1a2a3
a1a2a3a3
[0.04+0.04*0.4, 0.04+0.04*0.8 ]=[0.056, 0.072]
s6
S5
1101
s7
S6
1110
S0
00
S1
01
S2
100
S3
101
S7
1111
6.3.4 算术编码
使用霍夫曼编码方式进行编码时，很多 时候不能得到最佳的压缩效果。 与前述的变长编码不同，算术编码生 的是非块码。算术编码给整个信源符号序 列分配一个单一的算术码字。这个码字本 身定义了一个介于0和1之间的实数间隔。
• 费诺.仙侬编码与Huffman编码相反，采用从上到 下的方法。香农-范诺编码算法步骤： • （1）按照符号出现的概率减少的顺序将待编码的 符号排成序列。 • （2）将符号分成两组，使这两组符号概率和相等 或几乎相等。 • （3）将第一组赋值为0，第二组赋值为1。
• （4）对每一组，重复步骤2的操作。
图象质量非常好，如同人能想象出的最好质量。 图象质量高，观看舒服，有干扰但不影响观看。 图象质量可接受，有干扰但不太影响观看。 图象质量差，干扰有些妨碍观看，观察者希望改进。 图象质量很差，妨碍观看的干扰始终存在，几乎无法观看。 图象质量极差，不能使用。
6.2.3 图像冗余度和编码效率
根据Shannon无干扰信息保持编码定理，若对原始 图像数据的信息进行无失真图像编码，压缩后平均码 长存在一个下限，这个下限是图像信息熵H。理论上最 佳信息保持编码的平均码长可以无限接近图像信息熵H。 但总是大于或等于图像的熵H。信息熵定义：
霍夫曼码 01 10 11 001 0001 00000 000010 000011
b3
b4
b5 b6 b7 b8
1100 00000 1101 00001 1110 00010 1111 00011 2.73 2.73
11001 000001 2.78 2.75
熵 平均长度
2.65 2.7
6.3.2费诺.仙侬编码（Fano-Shannon）
1/8
11 111 S1 00 0 S4 11 111
110 10
30 10 20 40
霍夫曼编码举例二
20 40 0
20
20 20 30 30 20 40 40 20
(1)统计出每级灰度出现的频率：
灰度值 出现频率 20 7/16
1
40 4/16
30 3/16
10 1/16
0 1/16
1
9/16 7/16 5/16 4/16 2/16 3/16
• 霍夫曼编码举例一 • 输入数据流:S1 S2 S1 S3 S2 S1 S1 S4
符号 S1 S2 S3 S4
出现概率
等长编码 霍夫曼 数据流源 等长编码 霍夫曼 S1 00 0
1/2
00 0 S2 01 10
1/4
01 10 S1 00 0 S3 10
1/8
10 110 S2 01 S1 00 0
数字化后的图像信息数据量非常大，图像压缩 利用图像数据存在冗余信息，去掉这些冗余信息 后可以有效压缩图像。常见图像的冗余类型主要 表现在： 1）空间冗余 2）视觉冗余（心理视觉冗余） 3）编码冗余 与灰度布的概率特性有关
减少/消除其中的一种/多种冗余，就能取得数 据压缩的效果
11.5.1 位平面的分解
ቤተ መጻሕፍቲ ባይዱ
块号 第一块
信源符号
b1 b2
概率 0.25 0.21 0.19 0.16 0.08 0.06 0.03 0.02
截断霍夫曼码 01 10 000 001 01 10 11 001
平移霍夫曼码 01 10 000 001 1101 1110 11000 01 10 11 001 00001 00010 00011
S6 0.05
S7 0.04
s0,s1,s2,s3,s4,s5,s6,s7
1 0.22 1 0.13 1 0 0.09 1
s0,s1
0 1 0
s2,s3,s4,s5,s6,s7 s1
0
s0
s2,s3 s2 s3
s4,s5,s6,s7 s4,s5
0 1 0
s6,s7
1
s4
灰度值 香浓-范诺码
s5
S4
1100
例：设一副灰度级为8的图象中，各灰度所对应的概率分别为0.04，0.05， 0.06，0.07，0.10，0.10，0.18，0.40，现在对其进行二分法费诺.仙侬编码？
灰度值 出现频率 S0 0.40 S1 0.18
0.58 0 0.20
S2 0.10
0.42
S3 0.10
S4 0.07
S5 0.06
H pi log 2 pi
i 0
L 1
平均码长定义 B
i
i 0
L 1
i
pi
是灰度值为i的编码长度，pi为灰度值为 i 的概率
冗余度为
B r 1 H
H 1 编码效率为 B 1 r
6.3 统计编码方法
6.3.1 霍夫曼编码 Huffman编码是1952年由Huffman提出的一种编码方法。 这种编码方法是根据信源数据符号发生的概率进行编码的。 思想：在信源数据中出现概率越大的符号，编码以后相应 的码长越短；出现概率越小的符号，其码长越长。 （理论最佳）。 设输入编码为 ，其频率分 布分别为P(x1)=0.4 X x2)=0.3，P(x35 , x6 ，P(x 1 , x2 , x3 , x4 , x )=0.1，P(x4) =0.1，P(x5)=0.06，P(x6)=0.04。求其最佳霍夫曼编码
[0.056+0.016*0.4, 0.056+0.016*0.8 ]=[0.0624, 0.0688]
a1a2a3a3a4
编码序列 b 1= a 1 1 a4 a3 a2 0 a1
[0.0624+0.0064*0.8, 0.056+0.0064*1 ]=[0.06752, 0.0688]
b2= a 2 0.2 a4 a3 a2 0 a1 0.04 b3 = a 3 0.08 a4 a3 a2 a1 0.056 b4 = a 3 0.072 a4 a3 a2 a1 0.062 4 b 5= a4 0.068 8 0.067 52 a4 a3 a2 a1
1. 客观保真度准则
（归一化）信噪比：令
1 f MN
M 1 N 1 x 0 y 0
f ( x, y )
M 1 N 1 2 f ( x, y ) f 单位：分贝（dB） x 0 y 0 SNR 10 lg M 1 N 1 ˆ f ( x, y ) f ( x, y ) x 0 y 0