大学物理第11章习题解答
大学物理习题答案第十一章

[习题解答]11-7 在磁感应强度大小为B = 0.50 T 的匀强磁场中,有一长度为l = 1.5 m 的导体棒垂直于磁场方向放置,如图11-11所示。
如果让此导体棒以既垂直于自身的长度又垂直于磁场的速度v 向右运动,则在导体棒中将产生动生电动势。
若棒的运动速率v = 4.0 m ⋅s -1 ,试求:(1)导体棒内的非静电性电场K ;(2)导体棒内的静电场E ;(3)导体棒内的动生电动势ε的大小和方向;(4)导体棒两端的电势差。
解(1)根据动生电动势的表达式,由于()的方向沿棒向上,所以上式的积分可取沿棒向上的方向,也就是d l 的方向取沿棒向上的方向。
于是可得.另外,动生电动势可以用非静电性电场表示为.以上两式联立可解得导体棒内的非静电性电场,为,方向沿棒由下向上。
图11-11(2)在不形成电流的情况下,导体棒内的静电场与非静电性电场相平衡,即,所以,E 的方向沿棒由上向下,大小为.(3)上面已经得到,方向沿棒由下向上。
(4)上述导体棒就相当一个外电路不通的电源,所以导体棒两端的电势差就等于棒的动生电动势,即,棒的上端为正,下端为负。
11-8 如图11-12所表示,处于匀强磁场中的导体回路ABCD ,其边AB 可以滑动。
若磁感应强度的大小为B = 0.5 T ,电阻为R = 0.2 Ω,AB 边长为 l = 0.5 m ,AB 边向右平移的速率为v = 4 m ⋅s -1 ,求:(1)作用于AB 边上的外力;(2)外力所消耗的功率;(3)感应电流消耗在电阻R 上的功率。
解(1)当将AB 向右拉动时,AB 中会有电流通过,流向为从B 到A 。
AB 中一旦出现电流,就将受到安培力F 的作用,安培力的方向为由右向左。
所以,要使AB 向右移动,必须对AB施加由左向右图11-12的力的作用,这就是外力F外。
在被拉动时,AB中产生的动生电动势为,电流为.AB所受安培力的大小为,安培力的方向为由右向左。
外力的大小为,外力的方向为由左向右。
大学物理第11章习题答案(供参考)

因此
即
又
表明 中电动势方向为 .
所以半圆环内电动势 方向沿 方向,
大小为
点电势高于 点电势,即
例2如图所示,长直导线通以电流 =5A,在其右方放一长方形线圈,两者共面.线圈长 =0.06m,宽 =0.04m,线圈以速度 =0.03m·s-1垂直于直线平移远离.求: =0.05m时线圈中感应电动势的大小和方向.
.
解: 设给两导线中通一电流 ,左侧导线中电流向上,右侧导线中电流向下.
在两导线所在的平面内取垂直于导线的坐标轴 ,并设其原点在左导线的中心,如图所示,由此可以计算通过两导线间长度为 的面积的磁通量.
两导线间的磁感强度大小为
取面积元 ,通过面积元的磁通量为
则穿过两导线间长度为 的矩形面积的磁通量为
故
2动生电动势:仅由导体或导体回路在磁场中的运动而产生的感应电动势。
3感生电场 :变化的磁场在其周围所激发的电场。与静电场不同,感生电场的电
场线是闭合的,所以感生电场也称有旋电场。
4感生电动势:仅由磁场变化而产生的感应电动势。
5自感:有使回路保持原有电流不变的性质,是回路本身的“电磁惯性”的量度。
自感系数 :
第11章 电磁感应
11.1 基本要求
1理解电动势的概念。
2掌握法拉第电磁感应定律和楞次定律,能熟练地应用它们来计算感应电动势的大小,判别感应电动势的方向。
3理解动生电动势的概念及规律,会计算一些简单问题中的动生电动势。
4理解感生电场、感生电动势的概念及规律,会计算一些简单问题中的感生电动势。
5理解自感现象和自感系数的定义及物理意义,会计算简单回路中的自感系数。
大学物理题库通用版-第11章-波动光学--光的干涉(含答案解析)
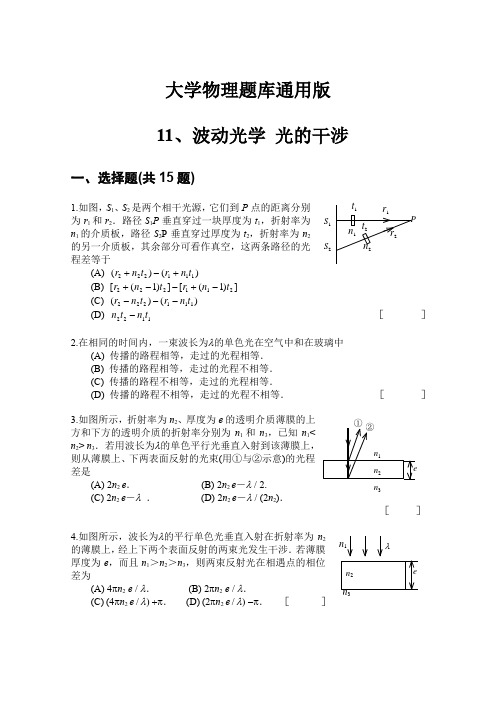
大学物理题库通用版11、波动光学 光的干涉一、选择题(共15题)1.如图,S 1、S 2是两个相干光源,它们到P 点的距离分别为r 1和r 2.路径S 1P 垂直穿过一块厚度为t 1,折射率为n 1的介质板,路径S 2P 垂直穿过厚度为t 2,折射率为n 2的另一介质板,其余部分可看作真空,这两条路径的光程差等于 (A) )()(111222t n r t n r +-+(B) ])1([])1([211222t n r t n r -+--+(C) )()(111222t n r t n r ---(D) 1122t n t n - [ ]2.在相同的时间内,一束波长为λ的单色光在空气中和在玻璃中(A) 传播的路程相等,走过的光程相等.(B) 传播的路程相等,走过的光程不相等.(C) 传播的路程不相等,走过的光程相等.(D) 传播的路程不相等,走过的光程不相等. [ ]3.如图所示,折射率为n 2、厚度为e 的透明介质薄膜的上方和下方的透明介质的折射率分别为n 1和n 3,已知n 1<n 2> n 3.若用波长为λ的单色平行光垂直入射到该薄膜上,则从薄膜上、下两表面反射的光束(用①与②示意)的光程差是(A) 2n 2 e . (B) 2n 2 e -λ / 2. (C) 2n 2 e -λ . (D) 2n 2 e -λ / (2n 2).[ ]4.如图所示,波长为λ的平行单色光垂直入射在折射率为n 2的薄膜上,经上下两个表面反射的两束光发生干涉.若薄膜厚度为e ,而且n 1>n 2>n 3,则两束反射光在相遇点的相位差为(A) 4πn 2 e / λ. (B) 2πn 2 e / λ. (C) (4πn 2 e / λ) +π. (D) (2πn 2 e / λ) -π. [ ]P S 1S 2 r 1 n 1 n 2 t 2 r 2 t 1n 3n 1 λ5.如图所示,平行单色光垂直照射到薄膜上,经上下两表面反射的两束光发生干涉,若薄膜的厚度为e ,并且n 1<n 2>n 3,λ1为入射光在折射率为n 1的媒质中的波长,则两束反射光在相遇点的相位差为 (A) 2πn 2e / ( n 1 λ1). (B)[4πn 1e / ( n 2 λ1)] + π. (C) [4πn 2e / (n 1 λ1) ]+ π. (D) 4πn 2e / ( n 1 λ1). [ ]6.一束波长为λ的单色光由空气垂直入射到折射率为n 的透明薄膜上,透明薄膜放在空气中,要使反射光得到干涉加强,则薄膜最小的厚度为(A) λ / 4 . (B) λ / (4n ).(C) λ / 2 . (D) λ / (2n ). [ ]7. 两块平玻璃构成空气劈形膜,左边为棱边,用单色平行光垂直入射.若上面的平玻璃以棱边为轴,沿逆时针方向作微小转动,则干涉条纹的(A) 间隔变小,并向棱边方向平移.(B) 间隔变大,并向远离棱边方向平移.(C) 间隔不变,向棱边方向平移.(D) 间隔变小,并向远离棱边方向平移. [ ]8.用白光光源进行双缝实验,若用一个纯红色的滤光片遮盖一条缝,用一个纯蓝色的滤光片遮盖另一条缝,则(A) 干涉条纹的宽度将发生改变.(B) 产生红光和蓝光的两套彩色干涉条纹.(C) 干涉条纹的亮度将发生改变.(D) 不产生干涉条纹. [ ]9.把双缝干涉实验装置放在折射率为n 的水中,两缝间距离为d ,双缝到屏的距离为D (D >>d ),所用单色光在真空中的波长为λ,则屏上干涉条纹中相邻的明纹之间的距离是(A) λD / (nd ) (B) n λD /d .(C) λd / (nD ). (D) λD / (2nd ). [ ]10.在双缝干涉实验中,若单色光源S 到两缝S 1、S 2距离相等,则观察屏上中央明条纹位于图中O 处.现将光源S 向下移动到示意图中的S '位置,则 (A) 中央明条纹也向下移动,且条纹间距不变.(B) 中央明条纹向上移动,且条纹间距不变. (C) 中央明条纹向下移动,且条纹间距增大. (D) 中央明条纹向上移动,且条纹间距增大. [ ]11.在双缝干涉实验中,入射光的波长为λ,用玻璃纸遮住双缝中的一个缝,若玻璃n 1λ1 S S '纸中光程比相同厚度的空气的光程大2.5 λ,则屏上原来的明纹处(A) 仍为明条纹;(B) 变为暗条纹;(C) 既非明纹也非暗纹;(D) 无法确定是明纹,还是暗纹.[]12.在牛顿环实验装置中,曲率半径为R的平凸透镜与平玻璃扳在中心恰好接触,它们之间充满折射率为n的透明介质,垂直入射到牛顿环装置上的平行单色光在真空中的波长为λ,则反射光形成的干涉条纹中暗环半径r k的表达式为(A) r k =Rkλ.(B) r k =nRk/λ.(C) r k =Rknλ.(D) r k =()nRk/λ.[]13.把一平凸透镜放在平玻璃上,构成牛顿环装置.当平凸透镜慢慢地向上平移时,由反射光形成的牛顿环(A)向中心收缩,条纹间隔变小.(B)向中心收缩,环心呈明暗交替变化.(C)向外扩张,环心呈明暗交替变化.(D)向外扩张,条纹间隔变大.[]14.如图a所示,一光学平板玻璃A与待测工件B之间形成空气劈尖,用波长λ=500 nm (1 nm=10-9 m)的单色光垂直照射.看到的反射光的干涉条纹如图b所示.有些条纹弯曲部分的顶点恰好与其右边条纹的直线部分的连线相切.则工件的上表面缺陷是(A) 不平处为凸起纹,最大高度为500 nm.(B) 不平处为凸起纹,最大高度为250 nm.(C) 不平处为凹槽,最大深度为500 nm.(D) 不平处为凹槽,最大深度为250 nm.[]15.在迈克耳孙干涉仪的一条光路中,放入一折射率为n,厚度为d的透明薄片,放入后,这条光路的光程改变了(A) 2 ( n-1 ) d.(B) 2nd.(C) 2 ( n-1 ) d+λ / 2.(D) nd.(E) ( n-1 ) d.[]二、填空题(共15题)1. 在双缝干涉实验中,两缝分别被折射率为n1和n2的透明薄膜遮盖,二者的厚度均为e.波长为λ的平行单色光垂直照射到双缝上,在屏中央处,两束相干光的相位差∆φ=________.图b2. 如图所示,假设有两个同相的相干点光源S 1和S 2,发出波长为λ的光.A 是它们连线的中垂线上的一点.若在S 1与A 之间插入厚度为e 、折射率为n 的薄玻璃片,则两光源发出的光在A 点的相位差∆φ=_2π (n -1) e / λ_.若已知λ=500 nm ,n =1.5,A 点恰为第四级明纹中心,则e =_____nm .(1 nm =10-9 m)3. 如图所示,两缝S 1和S 2之间的距离为d ,媒质的折射率为n =1,平行单色光斜入射到双缝上,入射角为θ,则屏幕上P 处,两相干光的光程差为___ ______.4.在双缝干涉实验中,所用光波波长λ=5.461×10–4 mm ,双缝与屏间的距离D =300 mm ,双缝间距为d =0.134 mm ,则中央明条纹两侧的两个第三级明条纹之间的距离为________ _______.5.用波长为λ的单色光垂直照射折射率为n 的劈形膜形成等厚干涉条纹,若测得相邻明条纹的间距为l ,则劈尖角θ=________.6.把双缝干涉实验装置放在折射率为n 的媒质中,双缝到观察屏的距离为D ,两缝之间的距离为d (d <<D ),入射光在真空中的波长为λ,则屏上干涉条纹中相 邻明纹的间距是_____________.7.用λ=600 nm 的单色光垂直照射牛顿环装置时,从中央向外数第4个(不计中 央暗斑)暗环对应的空气膜厚度为____________.(1 nm=10-9 m)8.用波长为λ的单色光垂直照射折射率为n 2的劈形膜(如图)图中各部分折射率的关系是n 1<n 2<n 3.观察反射光的干涉条纹,从劈形膜顶开始向右数第5条暗条纹中心所对应的厚度e =____________.9.波长为λ的平行单色光,垂直照射到劈形膜上,劈尖角为θ,劈形膜的折射率为n ,第三条暗纹与第六条暗之间的距离是______.10. 一束波长为λ=600 nm (1 nm=10-9 m)的平行单色光垂直入射到折射率为n =1.33的透明薄膜上,该薄膜是放在空气中的.要使反射光得到最大限度的加强,薄膜最小厚度应为________________nm .11.波长为λ的平行单色光垂直照射到劈形膜上,劈尖角为θ,劈形膜的折射率为n ,第k 级明条纹与第k +5级明纹的间距是__________.12.波长λ=600 nm 的单色光垂直照射到牛顿环装置上,第二个明环与第五个明环所对应的空气膜厚度之差为____nm .(1 nm=10-9 m)n 1n 2n 313.折射率分别为n 1和n 2的两块平板玻璃构成空气劈尖,用波长为λ的单色光垂直照射.如果将该劈尖装置浸入折射率为n 的透明液体中,且n 2>n >n 1,则劈尖厚度为e 的地方两反射光的光程差的改变量是_______.14.如图所示,在双缝干涉实验中SS 1=SS 2,用波长为λ的光照射双缝S 1和S 2,通过空气后在屏幕E 上形成干涉条纹.已知P 点处为第三级明条纹,则S 1和S 2到P 点的光程差为___3λ ____.若将整个装置放于某种透明液体中,P 点为第四级明条纹,则该液体的折射率n =________.15.已知在迈克耳孙干涉仪中使用波长为λ的单色光.在干涉仪的可动反射镜移动距离d 的过程中,干涉条纹将移动__________条. 三、计算题(共5题)1.白色平行光垂直入射到间距为a =0.25 mm 的双缝上,距D =50 cm 处放置屏幕,分别求第一级和第五级明纹彩色带的宽度.(设白光的波长范围是从400nm 到760nm .这里说的“彩色带宽度” 指两个极端波长的同级明纹中心之间的距离.) (1 nm=10-9 m)2.在双缝干涉实验中,波长λ=550 nm 的单色平行光垂直入射到缝间距a =2×10-4 m 的双缝上,屏到双缝的距离D =2 m .求:(1) 中央明纹两侧的两条第10级明纹中心的间距;(2) 用一厚度为e =6.6×10-5 m 、折射率为n =1.58的玻璃片覆盖一缝后,零级明纹将移到原来的第几级明纹处?(1 nm = 10-9 m)3.用波长为500 nm (1 nm=10-9 m)的单色光垂直照射到由两块光学平玻璃构成的空气劈形膜上.在观察反射光的干涉现象中,距劈形膜棱边l = 1.56 cm 的A 处是从棱边算起的第四条暗条纹中心.(1) 求此空气劈形膜的劈尖角θ;(2) 改用600 nm 的单色光垂直照射到此劈尖上仍观察反射光的干涉条纹,A 处是明条纹还是暗条纹?(3) 在第(2)问的情形从棱边到A 处的范围内共有几条明纹?几条暗纹?2分4.图示一牛顿环装置,设平凸透镜中心恰好和平玻璃接触,透镜凸表面的曲率半径是R =400 cm .用某单色平行光垂直入射,观察反射光形成的牛顿环,测得第5个明环的半径是0.30 cm . (1) 求入射光的波长. (2) 设图中OA =1.00 cm ,求在半径为OA 的范围内可观察到的明环数目.5.用波长λ=500 nm 的平行光垂直照射折射率n =1.33的劈形膜,观察反射光的等厚干涉条纹.从劈形膜的棱算起,第5条明纹中心对应的膜厚度是多少? P E光的干涉习题答案一、选择题1、B ;2、C ;3、B ;4、A ;5、C ;6、B ;7、A ;8、D ;9、A ;10、B ;11、B ;12、B ;13、B ;14、B ;15、A二、填空题1、 2π(n 1 – n 2) e / λ2、4×103 nm3、d sin θ +(r 1-r 2)4、7.33 mm5、nl 2λ6、D λ / (dn )7、1.2=2λ μm8、249n λ9、3λ / (2n θ)10、113nm11、5λ / (2n θ)12、900 nm13、2 ( n – 1) e – λ /214、1.3315、2d /λ三、计算题1解:由公式x =kD λ / a 可知波长范围为∆λ时,明纹彩色宽度为∆x k =kD ∆λ / a2分 由 k =1可得,第一级明纹彩色带宽度为∆x 1=500×(760-400)×10-6 / 0.25=0.72 mm2分 k =5可得,第五级明纹彩色带的宽度为∆x 5=5·∆x 1=3.6 mm1分2解:(1) ∆x =20 D λ / a2分 =0.11 m2分 (2) 覆盖云玻璃后,零级明纹应满足(n -1)e +r 1=r 22分 设不盖玻璃片时,此点为第k 级明纹,则应有r 2-r 1=k λ 2分所以 (n -1)e = k λ k =(n -1) e / λ=6.96≈7 零级明纹移到原第7级明纹处 2分3解:(1) 棱边处是第一条暗纹中心,在膜厚度为e 2=21λ处是第二条暗纹中心,依此可知第四条暗纹中心处,即A 处膜厚度 e 4=λ23 ∴ ()l l e 2/3/4λθ===4.8×10-5 rad 5分(2) 由上问可知A 处膜厚为 e 4=3×500 / 2 nm =750 nm对于λ'=600 nm 的光,连同附加光程差,在A 处两反射光的光程差为λ'+2124e ,它与波长λ'之比为0.321/24=+'λe .所以A 处是明纹 3分 (3) 棱边处仍是暗纹,A 处是第三条明纹,所以共有三条明纹,三条暗纹.4解:(1) 明环半径 ()2/12λ⋅-=R k r 2分()Rk r 1222-=λ=5×10-5 cm (或500 nm) 2分 (2) (2k -1)=2 r 2 / (R λ) 对于r =1.00 cm , k =r 2 / (R λ)+0.5=50.5 3分 故在OA 范围内可观察到的明环数目为50个. 1分5解: 明纹, 2ne +λ21=k λ (k =1,2,…) 3分 第五条,k =5,ne 2215λ⎪⎭⎫ ⎝⎛-==8.46×10-4 mm 2分。
赵近芳大学物理学第五版第十一章课后习题答案

习题1111.1选择题(1)一圆形线圈在均匀磁场中作下列运动时,哪些情况会产生感应电流()(A )沿垂直磁场方向平移;(B )以直径为轴转动,轴跟磁场垂直;(C )沿平行磁场方向平移;(D )以直径为轴转动,轴跟磁场平行。
[答案:B](2)下列哪些矢量场为保守力场()(A )静电场;(B )稳恒磁场;(C )感生电场;(D )变化的磁场。
[答案:A](3)用线圈的自感系数L 来表示载流线圈磁场能量的公式221LI W m=()(A )只适用于无限长密绕线管;(B )只适用于一个匝数很多,且密绕的螺线环;(C )只适用于单匝圆线圈;(D )适用于自感系数L 一定的任意线圈。
[答案:D](4)对于涡旋电场,下列说法不正确的是():(A )涡旋电场对电荷有作用力;(B )涡旋电场由变化的磁场产生;(C )涡旋场由电荷激发;(D )涡旋电场的电力线闭合的。
[答案:C]11.2填空题(1)将金属圆环从磁极间沿与磁感应强度垂直的方向抽出时,圆环将受到。
[答案:磁力](2)产生动生电动势的非静电场力是,产生感生电动势的非静电场力是,激发感生电场的场源是。
[答案:洛伦兹力,涡旋电场力,变化的磁场](3)长为l 的金属直导线在垂直于均匀的平面内以角速度ω转动,如果转轴的位置在,这个导线上的电动势最大,数值为;如果转轴的位置在,整个导线上的电动势最小,数值为。
[答案:端点,221l B ω;中点,0]11.3一半径r =10cm 的圆形回路放在B =0.8T的均匀磁场中.回路平面与B垂直.当回路半径以恒定速率trd d =80cm/s 收缩时,求回路中感应电动势的大小.解:回路磁通2πr B BS m ==Φ感应电动势大小40.0d d π2)π(d d d d 2====trr B r B t t m ΦεV 11.4一对互相垂直的相等的半圆形导线构成回路,半径R =5cm,如题11.4图所示.均匀磁场B =80×10-3T,B 的方向与两半圆的公共直径(在Oz 轴上)垂直,且与两个半圆构成相等的角α当磁场在5ms内均匀降为零时,求回路中的感应电动势的大小及方向.解:取半圆形cba 法向为i,题11.4图则αΦcos 2π21B R m=同理,半圆形adc 法向为j,则αΦcos 2π22B R m=∵B 与i 夹角和B 与j夹角相等,∴︒=45α则αΦcos π2R B m =221089.8d d cos πd d -⨯-=-=Φ-=tBR t m αεV 方向与cbadc 相反,即顺时针方向.题11.5图11.5如题11.5图所示,载有电流I 的长直导线附近,放一导体半圆环MeN 与长直导线共面,且端点MN 的连线与长直导线垂直.半圆环的半径为b ,环心O 与导线相距a .设半圆环以速度v 平行导线平移.求半圆环内感应电动势的大小和方向及MN 两端的电压N M U U -.解:作辅助线MN ,则在MeNM 回路中,沿v方向运动时0d =m Φ∴0=MeNM ε即MNMeN εε=又∵⎰+-<+-==ba ba MN ba ba Iv l vB 0ln 2dcos 0πμπε所以MeN ε沿NeM 方向,大小为ba ba Iv -+ln 20πμM 点电势高于N 点电势,即ba ba Iv U U N M -+=-ln 20πμ题11.6图11.6如题11.6所示,在两平行载流的无限长直导线的平面内有一矩形线圈.两导线中的电流方向相反、大小相等,且电流以tId d 的变化率增大,求:(1)任一时刻线圈内所通过的磁通量;(2)线圈中的感应电动势.解:以向外磁通为正则(1)]ln [ln π2d π2d π2000da db a b Il r l r I r l r I ab b a d d m +-+=-=⎰⎰++μμμΦ(2)tI b a b d a d l t d d ]ln [ln π2d d 0+-+=-=μΦε11.7如题11.7图所示,用一根硬导线弯成半径为r 的一个半圆.令这半圆形导线在磁场中以频率f 绕图中半圆的直径旋转.整个电路的电阻为R .求:感应电流的最大值.题11.7图解:)cos(2π02ϕωΦ+=⋅=t r B S B m∴Bfr f r B r B t r B t m m i 222202ππ22π2π)sin(2πd d ===+=-=ωεϕωωΦε∴RBf r R I m 22π==ε11.8如题11.8图所示,长直导线通以电流I =5A,在其右方放一长方形线圈,两者共面.线圈长b =0.06m,宽a =0.04m,线圈以速度v =0.03m/s垂直于直线平移远离.求:d =0.05m时线圈中感应电动势的大小和方向.题11.8图解:AB 、CD 运动速度v方向与磁力线平行,不产生感应电动势.DA 产生电动势⎰==⋅⨯=AD I vb vBb l B v d2d )(01πμεBC 产生电动势)(π2d )(02d a I vbl B v CB+-=⋅⨯=⎰με∴回路中总感应电动势8021106.111(π2-⨯=+-=+=ad d Ibv μεεεV 方向沿顺时针.11.9长度为l 的金属杆ab 以速率v在导电轨道abcd 上平行移动.已知导轨处于均匀磁场B中,B 的方向与回路的法线成60°角(如题11.9图所示),B的大小为B =kt (k 为正常).设t =0时杆位于cd 处,求:任一时刻t 导线回路中感应电动势的大小和方向.解:⎰==︒=⋅=22212160cos d klvt lv kt Blvt S B m Φ∴klvt tm-=-=d d Φε即沿abcd 方向顺时针方向.题11.9图11.10一矩形导线框以恒定的加速度向右穿过一均匀磁场区,B的方向如题11.10图所示.取逆时针方向为电流正方向,画出线框中电流与时间的关系(设导线框刚进入磁场区时t =0).解:如图逆时针为矩形导线框正向,则进入时0d d <Φt,0>ε;题11.10图(a)题11.10图(b)在磁场中时0d d =tΦ,0=ε;出场时0d d >tΦ,0<ε,故t I -曲线如题10-9图(b)所示.题11.11图11.11导线ab 长为l ,绕过O 点的垂直轴以匀角速ω转动,aO =3l磁感应强度B 平行于转轴,如图11.11所示.试求:(1)ab 两端的电势差;(2)b a ,两端哪一点电势高?解:(1)在Ob 上取dr r r +→一小段则⎰==320292d l Ob l B r rB ωωε同理⎰==302181d l Oa l B r rB ωωε∴2261)92181(l B l B Ob aO ab ωωεεε=+-=+=(2)∵0>ab ε即0<-b a U U ∴b 点电势高.题11.12图11.12如题11.12图所示,长度为b 2的金属杆位于两无限长直导线所在平面的正中间,并以速度v平行于两直导线运动.两直导线通以大小相等、方向相反的电流I ,两导线相距2a .试求:金属杆两端的电势差及其方向.解:在金属杆上取r d 距左边直导线为r ,则ba b a Iv r r a r Iv l B v b a b a B A AB -+-=-+-=⋅⨯=⎰⎰+-lnd 211(2d )(00πμπμε ∵<AB ε∴实际上感应电动势方向从A B →,即从图中从右向左,∴ba ba Iv U AB -+=ln 0πμ题11.13图11.13磁感应强度为B的均匀磁场充满一半径为R 的圆柱形空间,一金属杆放在题11.13图中位置,杆长为2R ,其中一半位于磁场内、另一半在磁场外.当tBd d >0时,求:杆两端的感应电动势的大小和方向.解:∵bcab ac εεε+=tBR B R t t ab d d 43]43[d d d d 21=--=-=Φε=-=tabd d 2Φεt BR B R t d d 12π]12π[d d 22=--∴tB R acd d ]12π43[22+=ε∵0d d >tB∴0>ac ε即ε从ca →11.14半径为R的直螺线管中,有dtdB>0的磁场,一任意闭合导线abca ,一部分在螺线管内绷直成ab 弦,a ,b 两点与螺线管绝缘,如题11.14图所示.设ab =R ,试求:闭合导线中的感应电动势.解:如图,闭合导线abca 内磁通量436π(22R R B S B m -=⋅= Φ∴tBR R i d d )436π(22--=ε∵0d d >tB∴0<i ε,即感应电动势沿acba ,逆时针方向.题11.14图题11.15图11.15如题11.15图所示,在垂直于直螺线管管轴的平面上放置导体ab 于直径位置,另一导体cd 在一弦上,导体均与螺线管绝缘.当螺线管接通电源的一瞬间管内磁场如题11.15图示方向.试求:(1)ab 两端的电势差;(2)cd 两点电势高低的情况.解:由⎰⎰⋅-=⋅l S tB l Ed d d d 旋知,此时旋E 以O 为中心沿逆时针方向.(1)∵ab 是直径,在ab 上处处旋E与ab 垂直∴⎰=⋅ll 0d 旋∴0=ab ε,有b a U U =(2)同理,0d >⋅=⎰l E cddc旋ε∴0<-c d U U 即dc U U >题11.16图11.16一无限长的直导线和一正方形的线圈如题11.16图所示放置(导线与线圈接触处绝缘).求:线圈与导线间的互感系数.解:设长直电流为I ,其磁场通过正方形线圈的互感磁通为⎰==32300122ln π2d π2a a Iar r Ia μμΦ∴2ln π2012aI M μΦ==11.17两线圈顺串联后总自感为1.0H,在它们的形状和位置都不变的情况下,反串联后总自感为0.4H.试求:它们之间的互感.解:∵顺串时M L L L 221++=反串联时M L L L 221-+='∴M L L 4='-15.04='-=L L M H题11.18图11.18一矩形截面的螺绕环如题11.18图所示,共有N匝.试求:(1)此螺线环的自感系数;(2)若导线内通有电流I ,环内磁能为多少?解:如题11.18图示(1)通过横截面的磁通为⎰==baabNIh r h r NI ln π2d π200μμΦ磁链abIh N N lnπ220μΦψ==∴ab h N I L lnπ220μψ==(2)∵221LI W m =∴ab h I N W m lnπ4220μ=11.19一无限长圆柱形直导线,其截面各处的电流密度相等,总电流为I .求:导线内部单位长度上所储存的磁能.解:在R r <时20π2R I B r μ=∴4222002π82R r I B w m μμ==取r r V d π2d =(∵导线长1=l )则⎰⎰===RR m I R r r I r r w W 00204320π16π4d d 2μμπ。
大学物理课本答案习题 第十一章习题解答

则 在O点产生的 的大小为
而 在O点产生的 的大小为
和 方向相反,大小相等.即
。
直导线 在O点产生的
。
直导线 在O点产生的
,方向垂直纸面向外。
则O点总的磁感强度大小为
方向垂直纸面向外
11-8一载有电流 的长导线弯折成如题图11-8所示的形状,CD为1/4圆弧,半径为R,圆心O在AC,EF的延长线上.求O点处磁场的场强。
原点O处的电流元 在(a,0,0)点产生的 为:
在(0,a,0)点产生的 为:
在(a, 为
11-7用两根彼此平行的长直导线将半径为R的均匀导体圆环联到电源上,如题图11-7所示,b点为切点,求O点的磁感应强度。
解:先看导体圆环,由于 和 并联,设大圆弧有电流 ,小圆弧有电流 ,必有:
任取半径,宽为d的电流环,该电流环共有电流为
该电流环在线圈中心产生的磁感强度大小为
圆心处总磁感强度大小
方向垂直纸面向外。
11-13如题图11-13所示,在顶角为 的圆锥台上密绕以线圈,共N匝,通以电流 ,绕有线圈部分的上下底半径分别为 和 .求圆锥顶O处的磁感应强度的大小.
解:只要将题11-12中的均匀密绕平面线圈沿通过中心的轴垂直上提,便与本题条件相一致,故解题思路也相似。
答:稳恒电场与静电场有相同之处,即是它们都不随时间的变化而变化,基本规律相同,并且都是位场。但稳恒电场由分布不随时间变化的电荷产生,电荷本身却在移动。
正因为建立稳恒电场的电荷分布不随时间变化,因此静电场的两条基本定理,即高斯定理和环路定理仍然适用,所以仍可引入电势的概念。
11-3一根铜导线表面涂以银层,当两端加上电压后,在铜线和银层中,电场强度是否相同?电流密度是否相同?电流强度是否相同?为什么?
大学物理课答案11章

习题1111-1.测量星体表面温度的方法之一是将其看作黑体,测量它的峰值波长m λ,利用维恩定律便可求出T 。
已知太阳、北极星和天狼星的m λ分别为60.5010m -⨯,60.4310m -⨯和60.2910m -⨯,试计算它们的表面温度。
解:由维恩定律:m T b λ=,其中:310898.2-⨯=b ,那么:太阳:362.8981057960.510m bT K λ--⨯===⨯; 北极星:362.8981067400.4310m bT K λ--⨯===⨯;天狼星:362.8981099930.2910m bT K λ--⨯===⨯。
11-2.宇宙大爆炸遗留在宇宙空间的均匀背景辐射相当于温度为K 3的黑体辐射,试计算: (1)此辐射的单色辐出度的峰值波长; (2)地球表面接收到此辐射的功率。
解:(1)由m T b λ=,有342.898109.66103m b m T λ--⨯===⨯; (2)由4M T σ=,有:424P T R σπ=⨯地,那么:328494(637010) 5.67103 2.3410P W π-=⨯⨯⨯⨯⨯=⨯。
11-3.在加热黑体过程中,其单色辐出度对应的峰值波长由0.69μm 变化到0.50μm ,求总辐出度改变为原来的多少倍?解:由 b T m =λ 和 4T M σ=可得,63.3)5.069.0()()(440400====m m T T M M λλ11-4.已知000K 2时钨的辐出度与黑体的辐出度之比为259.0。
设灯泡的钨丝面积为2cm 10,其他能量损失不计,求维持灯丝温度所消耗的电功率。
解:∵4P T S σ=⋅黑体,消耗的功率等于钨丝的幅出度,所以,44840.2591010 5.67102000235P S T W ησ--==⨯⨯⨯⨯⨯=。
11-5.天文学中常用热辐射定律估算恒星的半径。
现观测到某恒星热辐射的峰值波长为m λ;辐射到地面上单位面积的功率为W 。
攀枝花学院大学物理第11章题库答案(最新修改)

第十一章一、填空题易:1、光学仪器的分辨率R= 。
(R= 1.22a λ) 易:2、若波长为625nm 的单色光垂直入射到一个每毫米有800条刻线的光栅上时,则第一级谱线的衍射角为 。
(6π) 易:3、在单缝的夫琅和费衍射实验中,屏上第三级暗纹对应的单缝处波面可划分为个半波带。
(6)易:4、在单缝夫琅和费衍射实验中波长为λ的单色光垂直入射在宽度为a =2λ的单缝上,对应于衍射角为30°方向,单缝处的波面可分成的半波带数目为 个。
(2)易:5、干涉相长的条件是两列波的相位差为π的 (填奇数或偶数)倍。
(偶数)易:6、如图(6题)所示,1S 和2S ,是初相和振幅均相同的相干波源,相距4.5λ,设两波沿1S 2S 连线传播的强度不随距离变化,则在连线上1S 左侧各点和2S 右侧各点是 (填相长或相消)。
(相消)易:7、在麦克耳逊干涉仪的一条光路中,插入一块折射率为n ,厚度为d 的透明薄片,插入薄片使这条光路的光程改变了 ; 2(n-1)d易:8、波长为λ的单色光垂直照射在由两块平玻璃板构成的空气劈尖上,测得相邻明条纹间距为L ‘若将劈尖角增大至原来的2倍,则相邻条纹的间距变为 。
(2L ) 易:9、单缝衍射中狭缝愈窄,条纹间距愈 。
(宽)易:10、在单缝夫琅和费衍射实验中,第一级暗纹发生在衍射角300的方向上,所用单色光波长为500nm λ=,则缝宽为: 。
(1000nm )易:11、用波长为λ的单色光垂直照射置于空气中的厚度为e 的折射率为1.5的透明薄膜,两束反射光的光程差为 ;(23λ+e )易:12、光学仪器的分辨率与 和 有关,且越小,仪器的分辨率越高。
(入射波长λ,透光孔经a ,λ)易:13、由马吕斯定律,当一束自然光通过两片偏振化方向成30o 的偏振片后,其出射光与入射光的光强之比为 。
(3:8)易:14、当光由光疏介质进入光密介质时,在交界面处的反射光与入射光有相位相反的现象,这种现象我们称之为 。
大学物理第十一章波动光学习题答案

第十一章 波动光学习题11-1 在杨氏双缝实验中,双缝间距d =0.20 mm ,缝屏间距D =1.0 m ,若第2级明条纹离屏中心的距离为6.0 mm ,试求:(1)入射光的波长;(2)相邻两明条纹间的距离。
解:(1)由λk d D x =明知, λ22.01010.63⨯⨯= 30.610m m 600n m λ-=⨯= (2)3106.02.010133=⨯⨯⨯==∆-λd D x mm 11-2 在双缝装置中,用一很薄的云母片(n =1.58)覆盖其中的一条缝,结果使屏幕上的第7级明条纹恰好移到屏幕中央原零级明纹的位置。
若入射光的波长为550 nm ,求此云母片的厚度。
解:设云母片厚度为e ,则由云母片引起的光程差为e n e ne )1(-=-=δ 按题意 λδ7= ∴610106.6158.1105500717--⨯=-⨯⨯=-=n e λm 6.6=m μ 11-3 在折射率n 1=1.52的镜头表面涂有一层折射率n 2=1.38的MgF 2增透膜,如果此膜适用于波长λ=550 nm 的光,问膜的最小厚度应取何值?解:设光垂直入射增透膜,欲透射增强,则膜上、下两表面反射光应满足干涉相消条件,即λ)21(22+=k e n ),2,1,0(⋅⋅⋅=k 222422)21(n n k n k e λλλ+=+=)9961993(38.14550038.125500+=⨯+⨯=k k o A令0=k ,得膜的最薄厚度为996o A 。
11-4 白光垂直照射在空气中厚度为0.4μm 的玻璃片上,玻璃的折射率为1.50。
试问在可见光范围内(λ= 400~700nm ),哪些波长的光在反射中增强?哪些波长的光在透射中增强?解:(1)222n d j λδλ=+= 24 3,480n m 21n d j j λλ===- (2)22(21) 22n d j λλδ=+=+ 22n d j λ= 2,600n m j λ==;3,400nm j λ== 11-5 白光垂直照射到空气中一厚度为380 nm 的肥皂膜上,设肥皂膜的折射率为1.33,试问该膜的正面呈现什么颜色?背面呈现什么颜色? 解:由反射干涉相长公式有42221ne ne k k λδλλ=+==-, ),2,1(⋅⋅⋅=k 得4 1.3338002674nm 2214 1.3338003404nm 231k k λλ⨯⨯===⨯-⨯⨯===⨯-,红色,紫色所以肥皂膜正面呈现紫红色。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
习题111. 选择题(1) 一圆形线圈在均匀磁场中作下列运动时, 哪些情况会产生感应电流( ) A. 沿垂直磁场方向平移B. 以直径为轴转动, 轴跟磁场垂直C. 沿平行磁场方向平移D. 以直径为轴转动, 轴跟磁场平行(2) 尺寸相同的铁环与铜环所包围的面积中, 通以相同变化率的磁通量, 环中( ) A. 感应电动势相同, 感应电流不同. B. 感应电动势相同, 感应电流相同. C. 感应电动势不同, 感应电流相同. D. 感应电动势不同.(3) 对于涡旋电场, 下列说法不正确的是( ) A. 涡旋电场对电荷有作用力. B. 涡旋电场由变化的磁场产生. C. 涡旋电场由电荷激发.D. 涡旋电场的电场线是闭合的.(4) 用线圈的自感系数L 来表示载流线圈磁场能量的公式212m W LI =( ) A. 只适用于单匝圆线圈.B. 只适用于一个匝数很多, 且密绕的螺线环.C. 适用于自感系数L 一定的任意线圈.D. 只适用于无限长密绕螺线管.(5) 有两个长直密绕螺线管, 长度及线圈匝数均相同, 半径分别为1r 和2r . 管内充满均匀介质, 其磁导率分别为1μ和2μ. 设1212r r =, 1221μμ=, 当将两只螺线管串联在电路中通电稳定后, 其自感系数之比12L L 与磁能之比12m m W W 分别为( ) A. 1211L L =, 1211m m W W =. B. 1212L L =, 1211m m W W =. C. 1212L L =, 1212m m W W =. D. 1221L L =, 1221m m W W =.答案:B A C D C2. 填空题(1) 电阻2R =Ω的闭合导体回路置于变化磁场中, 通过回路包围面的磁通量与时间的关系为23(582)10()m t t Wb -Φ=+-⨯, 则在2t s =至3t s =的时间内, 流过回路导体横截面的感应电荷等于______________C .(2) 长为l 的金属直导线在垂直于均匀磁场的平面内以角速度ω转动. 如果转轴在导线上的位置是在_______, 整个导线上的电动势为最大, 其值为_________; 如果转轴位置是在___________, 整个导线上的电动势为最小, 其值为____________.(3) 半径为a 的无限长密绕螺线管, 单位长度上的匝数为n , 通以交变电流sin m i I t ω=, 则围在管外的同轴圆形回路(半径为r )上的感生电动势为______________.(4) 一自感系数为0.25H 的线圈, 当线圈中的电流在0.01s 内由2A 均匀地减小到零. 线圈中的自感电动势的大小为______________.(5) 产生动生电动势的非静电力是______________, 产生感生电动势的非静电力是______________, 激发感生电场的场源是______________. 答案:(1) 21065.1-⨯ (2) 端点,2B lω;中点,0。
(3) ()200 cos n r I t V μπωω- (4) 50V (5)洛伦兹力,感生电场力(或涡旋电场力),变化的磁场。
3. 计算题(1)面积为S 的单匝平面线圈,以恒定角速度ω在磁感强度k t B Bωsin 0=的均匀外磁场中转动,转轴与线圈共面且与B 垂直( k 为沿z 轴的单位矢量).设t =0时线圈的正法向与k同方向,求线圈中的感应电动势.解: 0cos sin cos m BS t B S t t ωωωΦ==220/(sin cos )m d dt B S t t ωωωΦ=-+)2cos(0t S B ωω=0cos(2)B S t εωω=-(2)电量Q 均匀分布在半径为a 、长为L( a L >>)的绝缘薄壁长圆筒表面上,圆筒以角速度ω绕中心轴线旋转, 一半径为2a 、电阻为R 的单匝圆形线圈套在圆筒上(如图10.22所示). 若圆筒转速按照ω=ω0(1-t/t 0)的规律(ω0和t 0是已知常数)随时间线性地减小, 求圆形线圈中感应电流的大小和流向.解:筒以ω旋转时,相当于表面单位长度上有环形电流π⋅2ωL Q ,它和通电流螺线管的nI 等效.按长螺线管产生磁场的公式,筒内均匀磁场磁感强度为:LQ B π=20ωμ (方向沿筒的轴向)筒外磁场为零.穿过线圈的磁通量为:2202m Q aa B LμωπΦ==在单匝线圈中产生感生电动势为m d dt εΦ=-=)d d (220t L Qa ωμ-20002Qa Lt μω= 感应电流i 为 2002Qa i RRLt μωε==a⊗ Bri 的流向与圆筒转向一致.(3)如图11.23所示, 一长圆柱状磁场,磁场方向沿轴线并垂直图面向里,磁场大小既随到轴线的距离r 成正比而变化,又随时间t 作正弦变化,即B =B 0r sin ωt ,B 0、ω均为常数.若在磁场内放一半径为a 的金属圆环,环心在圆柱状磁场的轴线上,求金属环中的感生电动势,并讨论其方向.解:取回路正向顺时针,则 20022sin am B rdr B r tdr ππωΦ==⎰⎰t a B ωsin )3/2(30π=30/(2/3)cos m d dt B a t επωω=-Φ=-当 0ε>时,电动势沿顺时针方向;当0ε<时,电动势沿逆时针方向.(4)两根平行无限长直导线相距为d, 载有大小相等方向相反的电流I, 电流变化率dI/dt=α且α>0. 一个边长为d 的正方形线圈位于导线平面内与一根导线相距d ,如图11.24所示.求线圈中的感应电动势ε,并说明线圈中的感应电流是顺时针还是逆时针方向. 解1:穿过面元d S 的磁通量为0012d d d d 2()2m IIΦB dS B S B dS d x x x d xμμππ=⋅=⋅+⋅=-+ 因此穿过线圈的磁通量为 220003d d d ln 2()224d d m m ddIdId Id ΦΦx x x d x μμμπππ==-=+⎰⎰⎰再由法拉第电磁感应定律,有0d 3d ln d 24d m Φd It t μεπ⎛⎫=-= ⎪⎝⎭ 解2:当两长直导线有电流I 通过时,穿过线圈的磁通量为03ln 24m Id Φμπ=线圈与两长直导线间的互感为03ln 24m Φd M I μπ== 当电流以tId d 变化时,线圈中的互感电动势为0d 3d ln d 24d d I I Mt tμεπ⎛⎫=-= ⎪⎝⎭(5)一内外半径分别为R 1, R 2的均匀带电平面圆环, 电荷面密度为σ, 其中心有一半径为r 的导体小环(R 1>>r ),二者同心共面如图11.25所示. 设带电圆环以变角速度ω(t )绕垂直于环面的中心轴旋转,导体小环中的感应电流i 等于多少?方向如何(已知小环的电阻为R ')? 解:带电平面圆环的旋转相当于圆环中通有电流I ,在R 1与R 2之间取半径为R 、宽度为dRR 1 R 2 rσω (t )的环带,环带内有电流 ()dI R t dR σω=,dI 在圆心处O 产生的磁场0011/()22B dI R t dR μμσω== 由于整个带电圆环面旋转,在中心产生的磁感应强度的大小为0211())2B t R R μσω=-( 选逆时针方向为小环回路的正方向,则小环中20211())2m t R R r μσωπΦ=-( 2021())2m L d r d t R R dt dtμπωεσΦ=-=--( 2021()()2'r R R d t i RR dtμσεω-==-方向,当d ω(t)/dt >0时,i 与选定的正方向相反;当d ω(t)/dt <0时,i 与选定的正方向相同。
(6)如图11.26所示,一根长为L 的金属细杆ab 绕竖直轴O 1O 2以角速度ω在水平面内旋转,O 1O 2在离细杆a 端L/5处. 若已知地磁场 在竖直方向的分量为B. 求ab 两端间的电势差U a -U b .解: (1)在Ob 上取dr r r +→一小段 则425016d 50l Ob rB r B l εωω==⎰同理2501d 50l Oa rB r B l εωω==⎰∴221613()505010ab aO Ob B l B l εεεωω=+=-= (2)∵0>ab ε 即0<-b a U U∴b 点电势高.(7)如图11.27所示, 一长直导线通有电流I, 其旁共面地放置一匀质金属梯形线框a b c d a, 已知:da=ab=bc=L, 两斜边与下底边夹角均为60°,d 点与导线相距为 l. 今线框从静止开始自由下落H 高度, 且保持线框平面与长直导线始终共面, 求: ①下落H 高度后瞬间,线框中的感应电流为多少?r②该瞬时线框中电势最高处与电势最低处之间的电势差为多少?解:①由于线框垂直下落,线框所包围面积内的磁通量无变化,故感应电流I i =0②设dc 边长为l′,则由图可见 l′=L+2Lcos60°=2L 取d→c 的方向为dc 边内感应电动势的正向,则()002()'2ln2c cdc ddl v B dl vBdlu Idrr l l lgH l l Llεπ=⨯⋅==++=+=⎰⎰⎰cd 段内电动势ε的方向d→c 由于回路内无电流,llL gH I u U U V dc d c cd +==-=2ln220πε 因为c 点电势最高,d 点电势最低,故V 为电势最高处与电势最低处之间的电势差。
(8)如图11.28所示, 一长直导线载有电流I ,在它的旁边有一段直导线AB(AB=L),长直载流导线与直导线在同一平面内, 夹角为θ. 直导线AB 以速度v (v 的方向垂直于载流导线)运动. 已知: I=100A, v=5.0m/s, θ=30°, a=2cm, AB=16cm. 求: ①在图示位置AB 导线中的感应电动势ε. ②A 和B 哪端电势高.解:① AB 中的感应电动势为动生电动势,如图所示,d l 所在处的磁感强度为 )2/(0r I B π=μ d l 与d r 的关系为 d l = d r /sin θ令 b = a + L sin θ,AB 中的感应电动势为00()cos cos 22sin bL aI Iv drv B dl v dl r r μμεθθππθ=⨯==⋅⎰⎰⎰40sin cot ln 2.79102Iv L a aμθθπ-+==⨯ V ② B 端电势高.(9)载有恒定电流I 的长直导线旁有一半圆环导线cd,半圆环半径为b, 环面与直导线垂直,且半圆环两端点连线的延长线与直导线相交, 如图11.29所示. 当半圆环以速度v沿平行于直导线的方向平移时, 求半圆环上的感应电动势 解:由于无限长直导线所产生的磁场方向与半圆形导线所在平面平行,因此当导线回路运动时,通过它的磁通量不随时间改变,导线回路中感应电动势0ε=。
