matlab算法G-S
控制系统MATLAB仿真基础

系统仿真§ 4.1控制系统的数学模型1、传递函数模型(tranfer function)2、零极点增益模型(zero-pole-gain)3、状态空间模型(state-space)4、动态结构图(Simulink结构图)一、传递函数模型(transfer fcn-----tf)1、传递函数模型的形式传函定义:在零初始条件下,系统输出量的拉氏变换C(S)与输入量的拉氏变换R(S)之比。
C(S) b1S m+b2S m-1+…+b mG(S)=----------- =- --------------------------------R(S) a1S n + a2S n-1 +…+ a nnum(S)= ------------den(S)2、在MATLAB命令中的输入形式在MATLAB环境中,可直接用分子分母多项式系数构成的两个向量num、den表示系统: num = [b1, b2, ..., b m];den = [a1, a2, ..., a n];注:1)将系统的分子分母多项式的系数按降幂的方式以向量的形式输入两个变量,中间缺项的用0补齐,不能遗漏。
2)num、den是任意两个变量名,用户可以用其他任意的变量名来输入系数向量。
3)当系统种含有几个传函时,输入MATLAB命令状态下可用n1,d1;n2,d2…….。
4)给变量num,den赋值时用的是方括号;方括号内每个系数分隔开用空格或逗号;num,den方括号间用的是分号。
3、函数命令tf( )在MATLAB中,用函数命令tf( )来建立控制系统的传函模型,或者将零极点增益模型、状态空间模型转换为传函模型。
tf( )函数命令的调用格式为:圆括号中的逗号不能用空格来代替sys = tf ( num, den ) [G= tf ( num, den )]其中,函数的返回变量sys或G 为连续系统的传函模型;函数输入参量num和den分别为系统的分子分母多项式的系数向量。
基于Matlab方法确定VG模型参数

V 由美 国 学 者 vn nct G模 型 a G uh n于 18 e e 90提 出}, ’ 其表达式 为 : 〕
土壤水分特征曲线的测定在室内采用“ 张力计称 重法”用张力计( , 负压计 ) 测定土壤负压 h 用称重法 , 测定相应的含水率 0 试验装置如图 1 , 所示。为了保 证装土的初始含水率均匀、 密度一致 , 土样经过粉碎和
2 6
水文地质工程地质
20 年第 6 06 期
各个土样的实测按照早期每天早 8 点测一次、 后期一 天测 2 3 至 个数据的频率进行 , 测得的数据见表 2 0
2 2. 8 6 4
0.9 30
0. 7 33 0. 5 3 1 0. 2 37
0. 8 46
0. 7 46
0 3 2 1 7. 6 .8 5 7
0. 6 35
9 .0 2 5
1 0.0 9 4
0 3 8 10 1 .7 1 .6 0 3 2 16 0 .6 3 .0 03 .5 1 9 以) 4 .
046 .6 042 .5 0.4 42 0. 2 49 0 43 .1
0. () 4洲
0. 51 2 4.0 3 4 8 0. 3 2 8 4 3 5 5 .0 0. 1 2 9.0 32 9 2 0. 8 3 7 2 27 3 .8 0. 71 3 8. 6 2 6 5 0. 6 3 3.4 2 1 9 0 0. 5 4 9 7 2 3 2 .6
收稿 日期: 051 2 ;修订日期 : 06 6 0 20- - 04 20- - 02
11自动控制原理MATLAB实验指导书

实验一 典型环节的MATLAB 仿真一、实验目的1.熟悉MATLAB 桌面和命令窗口,初步了解SIMULINK 功能模块的使用方法。
2.通过观察典型环节在单位阶跃信号作用下的动态特性,加深对各典型环节响应曲线的理解。
3.定性了解各参数变化对典型环节动态特性的影响。
二、SIMULINK 的使用MATLAB 中SIMULINK 是一个用来对动态系统进行建模、仿真和分析的软件包。
利用SIMULINK 功能模块可以快速的建立控制系统的模型,进行仿真和调试。
1.运行MATLAB 软件,在命令窗口栏“>>”提示符下键入simulink 命令,按Enter 键或在工具栏单击按钮,即可进入如图1-1所示的SIMULINK 仿真环境下。
2.选择File 菜单下New 下的Model 命令,新建一个simulink 仿真环境常规模板。
3.在simulink 仿真环境下,创建所需要的系统。
以图1-2所示的系统为例,说明基本设计步骤如下:1)进入线性系统模块库,构建传递函数。
点击simulink 下的“Continuous ”,再将右边窗口中“Transfer Fen ”的图标用左键拖至新建的“untitled ”窗口。
2)改变模块参数。
在simulink 仿真环境“untitled ”窗口中双击该图标,即可改变传递函数。
其中方括号内的数字分别为传递函数的分子、分母各次幂由高到低的系数,数字之间用空格隔开;设置完成后,选择OK ,即完成该模块的设置。
图1-1 SIMULINK 仿真界面 图1-2 系统方框图3)建立其它传递函数模块。
按照上述方法,在不同的simulink 的模块库中,建立系统所需的传递函数模块。
例:比例环节用“Math ”右边窗口“Gain ”的图标。
4)选取阶跃信号输入函数。
用鼠标点击simulink 下的“Source ”,将右边窗口中“Step ”图标用左键拖至新建的“untitled ”窗口,形成一个阶跃函数输入模块。
应用MATLAB进行时域响应与稳定性分析

>>t=[0:0.1:10];num=[1];
>>den=[1,1,1];
>>[y,x,t]=impulse(num,den,t);
>>plot (t,y);grid on;
>>xlabel (‘t’); ylabel (‘y’);
其响应结果如图1-25所示。
图1-25 例1-15的单位脉冲响应曲线
1.4 判别系统稳定性
例1-17 试利用MATLAB判断下列系统的 稳定性。
s3 7s2 24s 24 G(s) s4 10s3 35s2 50s 24
解 MATLAB程序如下 num = [0,1,7,24,24]; den = [1,10,35,50,24]; [z, p] = tf2zp(num, den);
响应曲线如图1-23所示。
图1-23 例1-13的单位阶跃响应曲线
1.2 单位脉冲响应
当输入信号为单位脉冲函数 (t) 时,系统 输出为单位脉冲响应。MATLAB中求取脉 冲响应的函数为impulse( ),调用格式为:
[y,x,t]=impulse(num,den,t) 或impulse(num,den)
C(s) R(s)
G(s)
s2
1 0.3s
1
对单位斜坡输入 位斜坡响应。
1 r(t) t, R(s) s2
,求取其单
解 把单位斜坡输出函数转化为
C(s)
1
1
1
1
s2 0.3s 1 s2 (s2 0.3s 1) s s
系统单位斜坡响应的MATLAB命令:
>>num=[1]; >>den=[1,0.3,1,0]; >>t=[0:0.1:10]; >>c=step (num,den,t); >>plot (t,c); >>grid on; >>xlabel ('t sec'); >>ylabel (‘Input and Output’);
MatLab讲义五:Root-locus Design
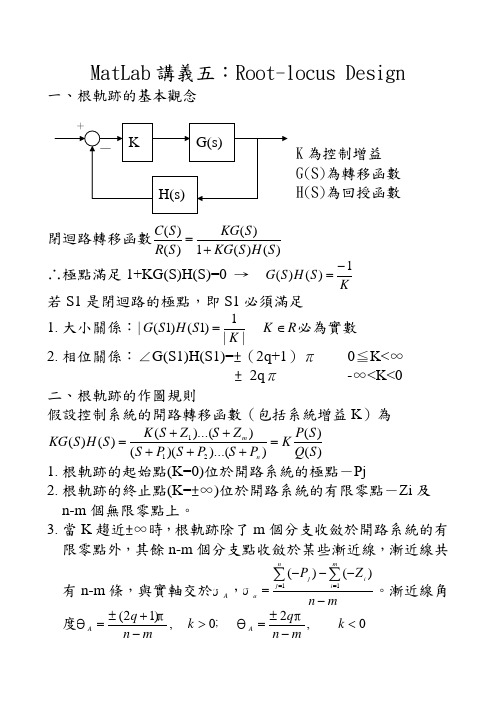
MatLab 講義五:Root-locus Design一、根軌跡的基本觀念K 為控制增益 G(S)為轉移函數H(S)為回授函數閉迴路轉移函數)()(1)()()(S H S KG S KG S R S C +=∴極點滿足1+KG(S)H(S)=0 → KS H S G 1)()(-=若S1是閉迴路的極點,即S1必須滿足1. 大小關係:||1)1()1(|K S H S G = R K ∈必為實數2. 相位關係:∠G(S1)H(S1)=±(2q+1)π 0≦K<∞ ± 2q π -∞<K<0 二、根軌跡的作圖規則假設控制系統的開路轉移函數(包括系統增益K )為)()())...()(())...(()()(211S Q S P KP S P S P S Z S Z S K S H S KG n m =+++++= 1. 根軌跡的起始點(K=0)位於開路系統的極點-Pj 2. 根軌跡的終止點(K=±∞)位於開路系統的有限零點-Zi 及n-m 個無限零點上。
3. 當K 趨近±∞時,根軌跡除了m 個分支收斂於開路系統的有限零點外,其餘n-m 個分支點收斂於某些漸近線,漸近線共有n-m 條,與實軸交於A σ,mn Z P nj mi i j a ----=∑∑==11)()(σ。
漸近線角度0,20,)12(<-±=>-+±=k mn q k m n q A A π; θ πθ 4. 根軌跡兩分支或兩分支以上相交的點稱為分離點。
分離點滿足0)()(=dSS H S dG 5. 根軌跡與S 平面上虛軸的交點,可由系統閉迴路方程式)()()(S KP S Q S +=∆建立羅斯表,令某列為零為K ,代入輔助方程解得純虛根即為所求。
二、根軌跡的推廣觀念與變化型1. 由特性方程式→改寫為1+KG(S)=0,定義G(S)為單位開迴路轉移函數,利用此來做根軌跡。
Matlab语言基本知识

Matlab 语言基本知识 (三 )
1.了解图形窗口与坐标系的概念 MATLAB 图形窗口如下:
窗口的设置: >>axis([0,2,0,4])
>>axis square
2.二维图形的绘制 (1)plot 函数的多种调用方法: plot(y) y 为向量 plot(t,y) t 为向量、y 为矩阵 plot(t,y) t、y 为矩阵 例:y=[0 0.6 2.3 5 8.3 11.7 15 17.7 19.4 20]; plot(y)
含义
产生正态分布随机数组 产生 (0,1)均匀分布随机数组 产生 (-1,1)均匀分布随机数组 产生全0数组 返回指定矩阵的最大长度
poly(p,A) ——按数组运算规则求多项式p在自变量A的值 polym(p,A) ——按矩阵运算规则求多项式p在自变量A的值 7. MATLAB的其他常用函数的使用练习 (1) sin cos asin acos tan atan 等 exp log log10 log2 pow sqrt 等 abs angle real imag fix floor ceil rem sign round sum min max (2) all any find isempty isinf 各函数的用法不清楚时,请使用 help 命令。
matlab的常用函数表8标准数组生成函数指令含义diag产生对角形数组对高维不适用eye产生单位数组对高维不适用magic产生魔方数组对高维不适用ones产生全1数组size返回指定矩阵的行数和列数指令randnrandrandszeroslength返回指定矩阵的最大长度含义产生正态分布随机数组产生01均匀分布随机数组产生11均匀分布随机数组产生全0数组表9数组操作函数指令含义diagflipudfliplrreshape提取对角线元素或生成对角阵以数组水平中线为对称轴交换上下对称位置上的数组元素以数组垂直中线为对称轴交换左右对称位置上的数组元素在总元素数不变的前提下改变数组的行数列数rot90det矩阵逆时针旋转90度方阵的行列式值rankinveig矩阵的秩矩阵求逆矩阵的特征值矩阵转置6
传递函数、零极点增益与状态空间转换的matlab算法实现
传递函数、零极点增益与状态空间三种模型转换的MATLAB算法实现一、引言微分方程是自控控制系统最原始的数学模型,它反映系统动态运行规律。
时域分析中要用拉普拉斯变换定义传递函数,再做其它转化。
为了方便我们对自动控制理论的理解和学习,本人总结了传递函数、零极点增益与状态空间三种模型转换的MATLAB算法,用处多多。
二、状态空间模型转换为传递函数、零极点增益模型1、MATLAB算法%将状态空间模型x(t)=Ax(t)+Bu(t),y(t)=Cx(t)+Du(t)转化成传递函数G(s)=num(s)/den(s)%或零极点模型G(s)=k(s+z1)(s+z2)...(s+zm)/(s+p1)(s+p2)...(s+pn)的函数ssto2.m%调用格式G=ssto2(key,A,B,C,D),其中输入参数A,B,C,D为状态空间四个矩阵,输出参数当key=1%时为传递函数;当key=2时,为状态空间模型function G=ssto2(key,A,B,C,D)if key==1sys=ss(A,B,C,D);G=tf(sys),elseif key==2sys=ss(A,B,C,D);G=zpk(sys),end2、例题分析【例1】已知一加压液流箱系统,该系统的状态变量是液位h(t)与料浆总压H(t),输入变量是料浆流入量u1(t)与空气流入量u2(t),输出变量就是状态变量H(t)与h(t)本身,系统状态空间模型为H(H)−0.39120.01234H(H)0.033440.01234H1(H)=+ℎ(H)ℎ(H)H2(H)−0.02200.0008960H1(H)H(H)H1(H)=11+00H2(H)ℎ(H)H2(H)求多个输入到输出的传递函数模型与多个输入到输出的零极点增益模型。
>> clear;A=[-0.3912,0.01234;-0.022,0];B=[0.03344,0.01234;0.000896,0];C=[1,1];D=[0,0];key=1;G=ssto2(key,A,B,C,D);key=2;G=ssto2(key,A,B,C,D);G =From input 1 to output:0.03434 s - 0.0003741--------------------------s^2 + 0.3912 s + 0.0002715From input 2 to output:0.01234 s - 0.0002715--------------------------s^2 + 0.3912 s + 0.0002715 Continuous-time transfer function.G =From input 1 to output:0.034336 (s-0.0109)------------------------(s+0.3905) (s+0.0006952)From input 2 to output:0.01234 (s-0.022)------------------------(s+0.3905) (s+0.0006952) Continuous-time zero/pole/gain model.三、传递函数模型转换为状态空间、零极点增益模型1、MATLAB算法%将传递函数模型G(s)=num(s)/den(s)转换成零极点模型%G(s)=k(s+z1)(s+z2)...(s+zm)/(s+p1)(s+p2)...(s+pn)%或状态空间模型x(t)=Ax(t)+Bu(t),y(t)=Cx(t)+Du(t)的函数%tfto2.m,函数的调用格式为G=tfto2(key,n,d)%其中输入参数n与d为传递函数分子、分母均按s的降幂排列的两个向量%输出参数key=1时,为零极点模型;key=2时,为状态空间模型%sys = tf(num,den)命令可以建立一个传递函数,其中分子和分母分别为num和den。
Matlab中的传递函数
SISO系统(1/7)
(1) SISO系统
线性定常连续系统一般以常系数线性常微分方程来描述。 ➢ 对于一个SISO线性定常连续系统,其常微分方程描述为:
a0 y(n) a1 y(n1)
an y b0u(m) b1u(m1) bmu (a0 0,b0 0, n m)
对应的经拉氏变换得到的传递函数模型为
对已建立好的SISO系统传递函数模型变量sys,其传递函数的 分子和分母多项式可分别由sys.num{1}和sys.den{1}获得。 ➢ 如在Matlab程序m2-1执行后有 sys_1.num{1}=[1 2 1]; sys_1.den{1}=[1 5 6];
MIMO系统(1/7)
(2) MIMO系统
对已建立好的传递函数模型阵变量sys,传递函数模型阵G(s) 的各元素的分子和分母多项式可分别由sys.num{i,j}和 sys.den{i,j}获得。
➢ 如在Matlab程序执行后有
sys.num{2,1}=[0 0 2 3]; sys.den{2,1}=[1 6 11 6];
分别表示
G21 (S )
由状态空间模型求解传递函数模型问题的调用格式 为: 连续系统: con_tf=tf(con_ss) 离散系统: dis_tf=tf(dis_ss)
其中,con_ss和dis_ss分别为已赋值的连续和离散系统状 态空间模型, ➢ con_tf和dis_tf就分别为求得的连续和离散系统 传递函数模型。
s3
2s 6s2
3 11s
6
的分子和分母多项式。
➢ 这里Matlab内部的分子多项式表示[0 0 2 3]是因为要与分 母多项式表示为同阶的多项式,由于分子的阶次低,故高 次项补0。
匹配算法MATLAB
求二部图G 的最大匹配的算法(匈牙利算法), 其基本思想是:从G 的任意匹配M 开始,对X 中所有M 的非饱和点, 寻找M -增广路. 若不存在M -增广路, 则M 为最大匹配; 若存在M -增广路P, 则将P 中M 与非M 的边互换得到比M 多一边的匹配M1 , 再对M1 重复上述过程.设G = ( X, Y, E )为二部图, 其中X = {x1, x2, ⋯, xn }, Y = { y1, y2, ⋯, yn}. 任取G 的一初始匹配M (如任取e∈E, 则M = {e}是一个匹配).①令S = f , T = f , 转向②.②若M 饱和X \ S 的所有点, 则M 是二部图G 的最大匹配. 否则, 任取M 的非饱和点u∈X \ S , 令S = S ∪{ u }, 转向③.③记N (S ) = {v | u∈S, uv∈E }. 若N (S ) = T, 转向②. 否则取y∈N (S ) \ T. 若y 是M的饱和点, 转向④, 否则转向⑤.④设x y∈M, 则令S = S ∪{ x }, T = T ∪{ y }, 转向③.⑤u - y 路是M-增广路, 设为P, 并令M = M⊕P, 转向①. 这里M⊕P = M∪P\ M∩P, 是对称差.由于计算M-增广路P 比较麻烦, 因此将迭代步骤改为:①将X 中M 的所有非饱和点(不是M 中某条边的端点)都给以标号0 和标记*, 转向②.②若X 中所有有标号的点都已去掉了标记*, 则M 是G 的最大匹配. 否则任取X 中一个既有标号又有标记*的点xi , 去掉xi 的标记*, 转向③.③找出在G 中所有与xi 邻接的点yj (即xi yj∈E ), 若所有这样的yj 都已有标号, 则转向②, 否则转向④.④对与xi 邻接且尚未给标号的yj 都给定标号i. 若所有的yj 都是M的饱和点, 则转向⑤,否则逆向返回. 即由其中M的任一个非饱和点yj的标号i 找到xi, 再由xi的标号k找到yk , ⋯,最后由yt 的标号s 找到标号为0 的xs 时结束, 获得M -增广路xs yt ⋯xi yj, 记P = {xs yt, ⋯,xi yj }, 重新记M 为M⊕P, 转向①.⑤将yj在M 中与之邻接的点xk (即xk yj∈M), 给以标号j 和标记*, 转向②.例1 求图6-9 中所示的二部图G 的最大匹配.匈牙利算法的MATLAB 程序代码如下:m=5;n=5;A=[0 1 1 0 01 1 0 1 10 1 1 0 00 1 1 0 00 0 0 1 1];M(m,n)=0;for(i=1:m)for(j=1:n)if(A(i,j))M(i,j)=1;break;end;end %求初始匹配Mif(M(i,j))break;end;end %获得仅含一条边的初始匹配Mwhile(1)for(i=1:m)x(i)=0;end %将记录X中点的标号和标记*for(i=1:n)y(i)=0;end %将记录Y中点的标号和标记*for(i=1:m)pd=1; %寻找X中M的所有非饱和点for(j=1:n)if(M(i,j))pd=0;end;endif(pd)x(i)=-n-1;end;end %将X中M的所有非饱和点都给以标号0 和标记*, 程序中用n+1 表示0 标号, 标号为负数时表示标记*pd=0;while(1)xi=0;for(i=1:m)if(x(i)<0)xi=i;break;end;end %假如X 中存在一个既有标号又有标记*的点, 则任取X中一个既有标号又有标记*的点xiif(xi==0)pd=1;break;end %假如X中所有有标号的点都已去掉了标记*, 算法终止x(xi)=x(xi)*(-1); %去掉xi 的标记*k=1;for(j=1:n)if(A(xi,j)&y(j)==0)y(j)=xi;yy(k)=j;k=k+1;end;end %对与xi 邻接且尚未给标号的yj 都给以标号iif(k>1)k=k-1;for(j=1:k)pdd=1;for(i=1:m)if(M(i,yy(j)))x(i)=-yy(j);pdd=0;break;end;end %将yj 在M中与之邻接的点xk (即xkyj∈M), 给以标号j 和标记*if(pdd)break;end;endif(pdd)k=1;j=yy(j); %yj 不是M的饱和点while(1)P(k,2)=j;P(k,1)=y(j);j=abs(x(y(j))); %任取M的一个非饱和点yj, 逆向返回if (j==n+1)break ;end %找到X 中标号为0 的点时结束, 获得M-增广路P k=k+1;endfor (i=1:k)if (M(P(i,1),P(i,2)))M(P(i,1),P(i,2))=0; %将匹配M 在增广路P 中出现的边去掉else M(P(i,1),P(i,2))=1;end ;end %将增广路P 中没有在匹配M 中出现的边加入 到匹配M 中break ;end ;end ;endif (pd)break ;end ;end %假如X 中所有有标号的点都已去掉了标记*, 算法终止 M %显示最大匹配M, 程序结束图 6-9利用可行点标记求最佳匹配的算法步骤如下:设 G = ( X , Y , E , F )为完备的二部赋权图, L 是其一个初始可行点标记, 通常取 (){}()max |,()0,L L x F xy y Y x X M G L y y Y ⎧=∈∈⎪⎨=∈⎪⎩是的一个匹配 ① 若X 的每个点都是M 的饱和点, 则M 是最佳匹配. 否则取 M 的非饱和点u ∈X , 令S= {u }, T = f , 转向②.② 记NL (S ) = {v | u ∈S , uv ∈EL }. 若NL ( S ) = T , 则GL 没有完美匹配, 转向③. 否则转向④.③ 调整可行点标记, 计算aL = min { L ( x ) + L ( y ) - F (x y ) | x ∈S , y ∈Y \T }.由此得新的可行顶点标记(),,(),,(),L L L a S L v a v T L v νν-∈⎧⎪+∈⎨⎪⎩否则令 L = H , GL = GH , 重新给出GL 的一个匹配M , 转向①.④ 取 y ∈NL ( S ) \T , 若y 是M 的饱和点, 转向⑤. 否则, 转向⑥.⑤ 设 x y ∈M , 则令S = S ∪{ x }, T =T ∪{ y }, 转向②.⑥ 在 GL 中的u - y 路是M -增广路, 记为P , 并令M = M ⊕P , 转向①. 利用可行点标记求最佳匹配算法的 MATLAB 程序代码如下:n=4;A=[4 5 5 12 2 4 64 2 3 35 0 2 1];for (i=1:n)L(i,1)=0;L(i,2)=0;endfor (i=1:n)for (j=1:n)if (L(i,1)<A(i,j))L(i,1)=A(i,j);end ; %初始可行点标记L M(i,j)=0;end ;endfor (i=1:n)for (j=1:n) %生成子图Glif (L(i,1)+L(j,2)==A(i,j))Gl(i,j)=1;else Gl(i,j)=0;end;end;endii=0;jj=0;for(i=1:n)for(j=1:n)if(Gl(i,j))ii=i;jj=j;break;end;endif(ii)break;end;end %获得仅含Gl 的一条边的初始匹配MM(ii,jj)=1;for(i=1:n)S(i)=0;T(i)=0;NlS(i)=0;endwhile(1)for(i=1:n)k=1;否则.for(j=1:n)if(M(i,j))k=0;break;end;endif(k)break;end;endif(k==0)break;end %获得最佳匹配M, 算法终止S(1)=i;jss=1;jst=0; %S={xi}, T=while(1)jsn=0;for(i=1:jss)for(j=1:n)if(Gl(S(i),j))jsn=jsn+1;NlS(jsn)=j; %NL(S)={v|u∈S,uv∈EL} for(k=1:jsn-1)if(NlS(k)==j)jsn=jsn-1;end;end;end;end;endif(jsn==jst)pd=1; %判断NL(S)=T?for(j=1:jsn)if(NlS(j)~=T(j))pd=0;break;end;end;endif(jsn==jst&pd)al=Inf;%如果NL(S)=T, 计算al, Inf 为∞for(i=1:jss)for(j=1:n)pd=1;for(k=1:jst)if(T(k)==j)pd=0;break;end;endif(pd&al>L(S(i),1)+L(j,2)-A(S(i),j))al=L(S(i),1)+L(j,2)-A(S(i),j);end;end;endfor(i=1:jss)L(S(i),1)=L(S(i),1)-al;end %调整可行点标记for(j=1:jst)L(T(j),2)=L(T(j),2)+al;end %调整可行点标记for(i=1:n)for(j=1:n) %生成子图GLif(L(i,1)+L(j,2)==A(i,j))Gl(i,j)=1;else Gl(i,j)=0;endM(i,j)=0;k=0;end;endii=0;jj=0;for(i=1:n)for(j=1:n)if(Gl(i,j))ii=i;jj=j;break;end;endif(ii)break;end;end %获得仅含Gl 的一条边的初始匹配MM(ii,jj)=1;breakelse %NL(S)≠Tfor(j=1:jsn)pd=1; %取y∈NL(S)\Tfor(k=1:jst)if(T(k)==NlS(j))pd=0;break;end;endif(pd)jj=j;break;end;endpd=0; %判断y 是否为M的饱和点for(i=1:n)if(M(i,NlS(jj)))pd=1;ii=i;break;end;endif(pd)jss=jss+1;S(jss)=ii;jst=jst+1;T(jst)=NlS(jj); %S=S∪{x}, T=T∪{y}else %获得Gl 的一条M-增广路, 调整匹配Mfor(k=1:jst)M(S(k),T(k))=1;M(S(k+1),T(k))=0;endif(jst==0)k=0;endM(S(k+1),NlS(jj))=1;break;end;end;end;endMaxZjpp=0;for(i=1:n)for(j=1:n)if(M(i,j))MaxZjpp=MaxZjpp+A(i,j);end;end;end M %显示最佳匹配MMaxZjpp %显示最佳匹配M的权, 程序结束。
优化方法MATLAB编程——大连理工大学
优化方法上机大作业学院:姓名:学号:指导老师:肖现涛第一题源程序如下:function zy_x = di1ti(x)%di1ti是用来求解优化作业第一题的函数。
x0=x; yimuxulong=0.000001;g0=g(x0);s0=-g0;A=2*ones(100,100);k=0;while k<100lanmed=-(g0)'*s0/(s0'*A*s0);x=x0+lanmed*s0;g=g(x);k=k+1;if norm(g)<yimuxulongzy_x=x;fprintf('After %d iterations,obtain the optimal solution.\n \n The optimal solution is \n %f.\n\nThe optimal "x" is "ans".',k,f(x) )break;endmiu=norm(g)^2/norm(g0)^2;s=-g+miu*s0;g0=g; s0=s;x0=x;endfunction f=f(x)f=(x'*ones(100,1))^2-x'*ones(100,1);function g=g(x)g=(2*x'*ones(100,1))*ones(100,1)-ones(100,1);代入x0,运行结果如下:>> x=zeros(100,1);>> di1ti(x)After 1 iterations,obtain the optimal solution.The optimal solution is-0.250000.The optimal "x" is "ans".ans =0.005*ones(100,1).第二题1.最速下降法。
