立体几何题型与方法总结(理科)
立体几何知识点与例题讲解、题型、方法技巧(理科)

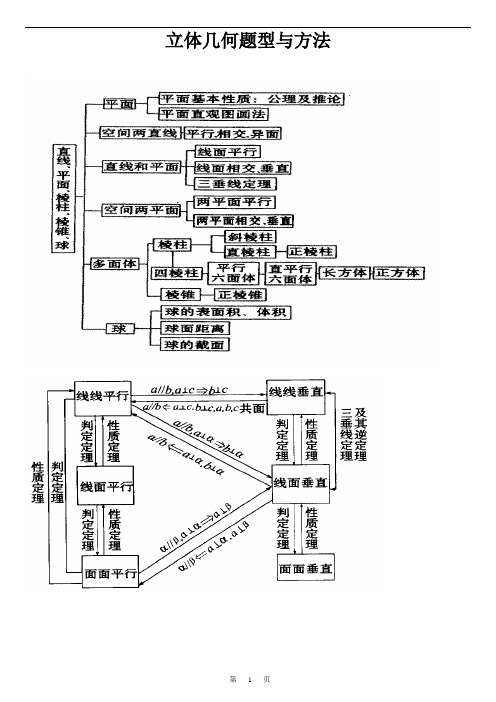
啊没立体几何知识点和例题讲解一、知识点<一>常用结论1.证明直线与直线的平行的思考途径:(1)转化为判定共面二直线无交点;(2)转化为二直线同与第三条直线平行;(3)转化为线面平行;(4)转化为线面垂直;(5)转化为面面平行. 2.证明直线与平面的平行的思考途径:(1)转化为直线与平面无公共点;(2)转化为线线平行;(3)转化为面面平行.3.证明平面与平面平行的思考途径:(1)转化为判定二平面无公共点;(2)转化为线面平行;(3)转化为线面垂直.4.证明直线与直线的垂直的思考途径:(1)转化为相交垂直;(2)转化为线面垂直;(3)转化为线与另一线的射影垂直;(4)转化为线与形成射影的斜线垂直. 5.证明直线与平面垂直的思考途径:(1)转化为该直线与平面内任一直线垂直;(2)转化为该直线与平面内相交二直线垂直;(3)转化为该直线与平面的一条垂线平行;(4)转化为该直线垂直于另一个平行平面;(5)转化为该直线与两个垂直平面的交线垂直. 6.证明平面与平面的垂直的思考途径:(1)转化为判断二面角是直二面角;(2)转化为线面垂直. 7.夹角公式 :设a =123(,,)a a a ,b =123(,,)b b b ,则cos 〈a ,b 〉.8.异面直线所成角:cos |cos ,|a b θ==21||||||a b a b x ⋅=⋅+(其中θ(090θ<≤)为异面直线a b ,所成角,,a b 分别表示异面直线a b ,的方向向量) 9.直线AB 与平面所成角:sin||||AB marc AB m β⋅=(m 为平面α的法向量).10、空间四点A 、B 、C 、P 共面OC z OB y OA x OP ++=⇔,且 x + y + z = 1 11.二面角l αβ--的平面角cos||||m n arc m n θ⋅=或cos ||||m narc m n π⋅-(m ,n 为平面α,β的法向量).12.三余弦定理:设AC 是α内的任一条直线,且BC ⊥AC ,垂足为C ,又设AO 与AB 所成的角为1θ,AB 与AC 所成的角为2θ,AO 与AC 所成的角为θ.则12cos cos cos θθθ=. 13.空间两点间的距离公式 若A 111(,,)x y z ,B 222(,,)x y z ,则,A B d =||AB AB AB =⋅221()x x =-+14.异面直线间的距离: ||||CD n d n ⋅=(12,l l 是两异面直线,其公垂向量为n ,C D 、分别是12,l l 上任一点,d 为12,l l 间的距离).15.点B 到平面α的距离:||||AB n d n ⋅=(n 为平面α的法向量,AB 是经过面α的一条斜线,A α∈). 16.三个向量和的平方公式:2222()222a b c a b c a b b c c a ++=+++⋅+⋅+⋅2222||||cos ,2||||cos ,2||||cos ,a b c a b a b b c b c c a c a =+++⋅+⋅+⋅17. 长度为l 的线段在三条两两互相垂直的直线上的射影长分别为123l l l 、、,夹角分别为123θθθ、、,则有2222123l l l l =++222123cos cos cos 1θθθ⇔++=222123sin sin sin 2θθθ⇔++=.(立体几何中长方体对角线长的公式是其特例).18. 面积射影定理 'cos S S θ=.(平面多边形及其射影的面积分别是S 、'S ,它们所在平面所成锐二面角的θ).19. 球的组合体(1)球与长方体的组合体: 长方体的外接球的直径是长方体的体对角线长.(2)球与正方体的组合体:正方体的内切球的直径是正方体的棱长, 正方体的棱切球的直径是正方体的面对角线长, 正方体的外接球的直径是正方体的体对角线长.(3) 球与正四面体的组合体: 棱长为a 的正四面体的内切球的半径为6a ,外接球的半径为6a . 20. 求点到面的距离的常规方法是什么?(直接法、体积法)21. 求多面体体积的常规方法是什么?(割补法、等积变换法) 〈二〉温馨提示:1.直线的倾斜角、两条异面直线所成的角等时它们各自的取值范围? ① 异面直线所成的角、直线与平面所成的角、二面角的取值范围依次.② 直线的倾斜角、到的角、与的夹角的取值范围依次是.〈三〉解题思路:1、平行垂直的证明主要利用线面关系的转化:线∥线线∥面面∥面判定线⊥线线⊥面面⊥面性质线∥线线⊥面面∥面←→−←→−−→−−←→−←→−←−−−←→−←→− 线面平行的判定: a b b a a ∥,面,∥面⊂⊄⇒αααabα线面平行的性质:αααβαβ∥面,面,∥⊂=⇒ b a b三垂线定理(及逆定理):P A A O P O ⊥面,为在内射影,面,则αααa ⊂a OA a PO a PO a AO⊥⊥;⊥⊥⇒⇒αaPO线面垂直:a b a c b c b c O a ⊥,⊥,,,⊥⊂=⇒ααaO α b c面面垂直:a a ⊥面,面⊥αββα⊂⇒ 面⊥面,,,⊥⊥αβαβαβ =⊂⇒l l aaaα alβa b a b⊥面,⊥面∥αα⇒ 面⊥,面⊥∥αβαβa a ⇒ a bα2、三类角的定义及求法(1)异面直线所成的角θ,0°<θ≤90°(2)直线与平面所成的角θ,0°≤θ≤90°θαα=时,∥或0b ob ⊂()二面角:二面角的平面角,30180αβθθ--<≤l o o(三垂线定理法:A ∈α作或证AB ⊥β于B ,作BO ⊥棱于O ,连AO ,则AO ⊥棱l ,∴∠AOB 为所求。
立体几何题型及解题方法

立体几何题型及解题方法
立体几何是数学中研究三维空间几何图形的学科。
以下是一些常见的立体几何题型及其解题方法:
1. 计算体积和表面积:这类题目通常涉及到三维空间中的几何形状,如长方体、圆柱体、圆锥体等。
解题方法包括使用体积和表面积的公式,以及根据题目描述建立数学模型。
2. 证明定理和性质:这类题目通常涉及到几何图形的性质和定理,如平行线性质、勾股定理等。
解题方法包括使用已知定理和性质进行推导,以及通过构造辅助线或辅助图形来证明。
3. 求解最值问题:这类题目通常涉及到求几何图形中的最值,如最短路径、最大面积等。
解题方法包括使用不等式、极值定理和优化方法等。
4. 判定和性质应用:这类题目通常涉及到判定几何图形是否满足某个性质,或应用某个性质到实际场景中。
解题方法包括根据性质进行推导和判断,以及根据实际场景建立数学模型。
以上是一些常见的立体几何题型及其解题方法,当然还有其他的题型和解题方法。
在解决立体几何问题时,需要灵活运用几何知识和方法,多做练习,提高自己的解题能力。
高考理科立体几何大题常考题型

高考理科立体几何大题常考题型
高考理科立体几何大题常考题型包括以下几个方面:
1. 空间位置关系的证明:这类问题主要涉及线线、线面、面面的平行和垂直关系的证明。
解决这类问题需要熟练掌握相关的判定定理和性质定理,并能够灵活运用。
2. 空间角的计算:这类问题主要涉及异面直线所成的角、直线与平面所成的角、二面角的计算等。
解决这类问题需要熟练掌握相关的计算公式,并能够准确建立空间直角坐标系。
3. 空间几何体的体积和表面积计算:这类问题主要涉及圆锥、圆柱、棱锥、棱柱等基本几何体的体积和表面积的计算,以及一些组合体的体积和表面积的计算。
解决这类问题需要熟练掌握相关的计算公式,并能够根据题目要求选择合适的计算方法。
4. 投影与直观图:这类问题主要涉及根据几何体的直观图求其三视图,以及根据三视图还原几何体的直观图。
解决这类问题需要熟练掌握三视图的形成原理,并能够准确判断出几何体的各个面在三视图中的投影。
综上所述,高考理科立体几何大题常考题型多样,需要考生具备扎实的数学基础和灵活的解题能力。
建议考生在复习时注重对基础知识的理解和掌握,多做练习题,培养自己的空间想象能力和逻辑思维能力。
立体几何题型与方法(理科)
立体几何题型与方法2.如图,已知矩形ABCD和矩形ADEF所在平面互相垂直,点M,N分别在对角线BD,AE上,且13BM BD=,13AN AE=.求证://MN平面CDE.解析:要证明//MN平面CDE,只要证明向量NM可以用平面CDE内的两个不共线的向量DE和DC线性表示.例题:已知ABCD,从平面AC外一点O引向量,,,OE kOA OF kOB OG kOC OH kOD====,(1)求证:四点,,,E F G H共面;(2)平面AC//平面EG.例题:已知正方体1111ABCD A B C D-中,E,F分别为11D C,11C B的中点,AC BD P=,11AC EF Q=.求证:(1)D,B,F,E四点共面;(2)若1A C交平面DBFE于R点,则P,Q,R三点共线.例题:如图,O1是正方体ABCD—A1B1C1D1的上底面的中心,G是对角线A1C和截面B1D1A的交点,求证:O1、G、A三点共线。
OA BCDHFE1AADE1CQ1BRPBCF考点二 证明空间线面平行与垂直3. 如图, 在直三棱柱ABC -A 1B 1C 1中,AC =3,BC =4,AA 1=4,点D 是AB 的中点, (I )求证:AC ⊥BC 1; (II )求证:AC 1//平面CDB 1;解析:(1)证明线线垂直方法有两类:一是通过三垂线定理或逆定理证明,二是通过线面垂直来证明线线垂直;(2)证明线面平行也有两类:一是通过线线平行得到线面平行,二是通过面面平行得到线面平行.4. (2007武汉3月)如图所示,四棱锥P —ABCD 中,AB ⊥AD ,CD ⊥AD ,PA ⊥底面ABCD ,PA=AD=CD=2AB=2,M 为PC 的中点。
(1)求证:BM ∥平面PAD ;(2)在侧面PAD 内找一点N ,使MN ⊥平面PBD ;(3)求直线PC 与平面PBD 所成角的正弦。
解析:本小题考查直线与平面平行,直线与平面垂直,二面角等基础知识,考查空间想象能力和推理论证能力.点评:(1)证明线面平行只需证明直线与平面内一条直线平行即可;(2)求斜线与平面所成的角只需在斜线上找一点作已知平面的垂线,斜线和射影所成的角,即为所求角;(3)证明线面垂直只需证此直线与平面内两条相交直线垂直变可.这些从证法中都能十分明显地体现出来例题:如图,已知P 是平行四边形ABCD 所在平面外一点,M 、N 分别是AB 、PC 的中点(1)求证:MN //平面PAD ;(2)若4M N BC ==,PA =PA 与MN 所成的角的大小例题:如右图,在正方体ABCD —A 1B 1C 1D 1中,M 、N 、P 分别是C 1C 、B 1C 1、C 1D 1的中点,求证:平面MNP ∥平面A 1BD.例题:已知四棱锥P-ABCD 中, 底面ABCD 为平行四边形. 点M 、N 、Q 分别在PA 、BD 、PD 上, 且PM :MA =BN :ND =PQ :QD . 求证:平面MNQ ∥平面PBC .例题:如图,在正方体1111ABCD A B C D -中,E 是1CC 的中点,F 是AC ,BD 的交点,求证:1A F BED ⊥平面.GFE DCB AD 1C 1B 1A 1例题:如图, 在空间四边形ABCD 中,,,AB BC CD DA == ,,E F G 分别是,,CD DA AC 的中点,求证:平面BEF ⊥平面BGD .异面直线夹角3.S 是正三角形ABC 所在平面外的一点,如图SA =SB =SC ,且∠ASB =∠BSC =∠CSA =2π,M 、N 分别是AB和SC 的中点.求异面直线SM 与BN 所成的角的余弦值.BM AN CS5 ,A 1B 1C 1—ABC 是直三棱柱,∠BCA=90°,点D 1、F 1 分别是A 1B 1、A 1C 1BC=CA=CC 1,求BD 1与AF 1所成角的余弦值是9.如图,四面体ABCD 中,AB ⊥BC ,AB ⊥BD ,BC ⊥CD ,且AB =BC =6,BD =8,E 是AD 中点,求BE 与CD 所成角的余弦值57点到平面的距离例1、如图,在梯形ABCD 中,AD ∥BC, ∠ABC =90°,AB =BC =1∕3AD =a,PA ⊥平面ABCD,且PA =a,点F 在AD 上,且CF ⊥PC.求点A 到平面PCF 的距离;求AD 与平面PBC 间的距离。
立体几何知识、方法、问题总结

立体几何知识、方法、问题总结一、基本知识与方法:1、 位置和符号 ①空间两直线:平行、相交、异面;判定异面直线用定义或反证法②直线与平面: a ∥α、a ∩α=A (a ⊄α) 、a ⊂α ③平面与平面:α∥β、α∩β=a2、常用定理: 4个公理,3个推论①⇒线线平行:b a b a a ////⇒⎪⎭⎪⎬⎫=⋂⊂βαβα;b a b a ////⇒⎪⎭⎪⎬⎫=⋂=⋂γβγαβα;bc c a b a //////⇒⎭⎬⎫ ;b a b a //⇒⎭⎬⎫⊥⊥αα②⇒线面平行:ααα////a a b b a ⇒⎪⎭⎪⎬⎫⊄⊂;αββα////a a ⇒⎭⎬⎫⊂; ③⇒面面平行:βαββαα////,//,⇒⎪⎭⎪⎬⎫=⋂⊂⊂b a O b a b a ;βαβα//⇒⎭⎬⎫⊥⊥a a ;④⇒线线垂直:b a b a ⊥⇒⎭⎬⎫⊂⊥αα;直线b a ,所成角︒90;c b c a b a ⊥⇒⎭⎬⎫⊥// ⑤⇒线面垂直:ααα⊥⇒⎪⎭⎪⎬⎫⊥⊥=⋂⊂⊂l b l a l Ob a b a ,,;βαβαβα⊥⇒⎪⎭⎪⎬⎫⊥⊂=⋂⊥a l a a l ,;βαβα⊥⇒⎭⎬⎫⊥a a //;αα⊥⇒⎭⎬⎫⊥b a ba //⑥⇒面面垂直:二面角成︒90;βααβ⊥⇒⎭⎬⎫⊥⊂a a ;3、求空间角①异面直线所成角θ的求法:(1)范围:(0,]2πθ∈; (2)求法:平移以及补形法、向量法。
如: (1)正四棱锥ABCD P -的所有棱长相等,E 是PC 的中点,那么异面直线BE与PA 所成的角的余弦值等于____(答:33); (2)在正方体AC 1中,M 是侧棱DD 1的中点,O 是底面ABCD 的中心,P 是棱A 1B 1上的一点,则OP 与AM 所成的角的大小为___ _(答:90°); ②直线和平面所成的角: (1)范围[0,90] ;(2)斜线与平面中所有直线所成角中最小的角。
:APBCFED(3)求法:作垂线找射影或求点线距离 (向量法);如:(1)在正三棱柱ABC-A 1B 1C 1中,已知AB=1,D 在棱BB 1上,BD=1,则AD 与平面AA 1C 1C 所成的角正弦值为______(答:46); (2)正方体ABCD-A 1B 1C 1D 1中,E 、F 分别是AB 、C 1D 1的中点,则棱 A 1B 1 与截面A 1ECF所成的角的余弦值是______(答:13);③ 二面角的平面角:(1)范围:[0,]π, (2)求法4、平行六面体→直平行六面体→长方体→正四棱柱→正方体间联系三棱锥中:侧棱长相等(侧棱与底面所成角相等)⇔顶点在底面射影为底面外心;侧棱两两垂直(两对对棱垂直)⇔顶点在底面射影为底面垂心;斜高相等(侧面与底面所成相等)⇔顶点在底面射影为底面内心;正三角形四心(内心、外心、垂心、重心)? 内切、外接圆半径? 正三棱锥与正四面体的关系5、平面图形翻折(展开):注意翻折(展开)后在同一平面图形中角度、长度不变; 如:如图甲,在直角梯形PBCD 中,//PB CD ,CD BC ⊥,2BC PB CD ==,A 是PB的中点. 现沿AD 把平面PAD 折起,使得PA AB ⊥(如图乙所示),E 、F 分别为BC 、AB 边的中点. (Ⅰ)求证:PA ⊥平面ABCD ; (Ⅱ)求证:平面PAE ⊥平面PDE ;(Ⅲ)在PA 上找一点G ,使得//FG 平面PDE .6、等积法⇒关键是要找到与面垂直的直线,即底面上的高如:如图, ABCD 为矩形,CF ⊥平面ABCD ,DE ⊥平面ABCD ,AB =4a ,BC = CF =2a , P 为AB 的中点.(1)求证:平面PCF ⊥平面PDE ;图甲图乙左视图主视图(2)求四面体PCEF的体积.7、三视图:长对正,宽相等,高平齐⇒以两两互相垂直的光线去投影,在三个投影面上留下的影子即为三视图如:(1)如图,一个空间几何体的主视图、左视图、俯视图为全等的等腰直角三角形,如果直角三角形的直角边长为1,那么这个几何体的表面积为 . (答:233+)(2)已知球O点面上四点A、B、C、D,DA⊥平面ABC,AB⊥BC,DA=AB=BC=3,则球O体积等于___________. (π29)注:三棱锥是长方体或正方体的一部分(2222cbaR++=)8、常用转化思想: ①构造四边形、三角形把问题化为平面问题②将空间图展开为平面图③割补法④等体积转化⑤线线平行⇔线面平行⇔面面平行⑥线线垂直⇔线面垂直⇔面面垂直⑦有中点等特殊点线,用“中位线、重心”转化.二、基本问题与方法:1、三垂线定理注重推导过程。
立体几何怪难题-理科

立体几何提升训练【例1】如图,在四棱锥ABCD P -中,底面为直角梯形,//,90AD BC BAD ︒∠=,PA 垂直于底面ABCD ,N M BC AB AD PA ,,22====分别为PB PC ,的中点。
(1)求证:DM PB ⊥;(2)求BD 与平面ADMN 所成的角;(3)求截面ADMN 的面积。
解:(1)证明:因为N 是PB 的中点,AB PA =, 所以PB AN ⊥。
由PA ⊥底面ABCD ,得PA AD ⊥, 又90BAD ︒∠=,即BA AD ⊥,∴ ⊥AD 平面PAB ,所以PB AD ⊥ , ∴ ⊥PB 平面ADMN , ∴DM PB ⊥。
(2)连结DN ,因为⊥BP 平面ADMN ,即⊥BN 平面ADMN , 所以BDN ∠是BD 与平面ADMN 所成的角,在Rt ABD ∆中,2222BD BA AD =+=,在Rt PAB ∆中,2222PB PA AB =+=,故122BN PB ==,在Rt BDN ∆中, 21sin ==∠BD BN BDN ,又π≤∠≤BDN 0, 故BD 与平面ADMN 所成的角是6π。
(3)由,M N 分别为PB PC ,的中点,得//MN BC ,且1122MN BC ==, 又//AD BC ,故//MN AD ,由(1)得⊥AD 平面PAB ,又AN ⊂平面PAB ,故AD AN ⊥,∴四边形ADMN 是直角梯形,在Rt PAB ∆中,2222PB PA AB =+=,122AN PB ==, ∴ 截面ADMN 的面积11152()(2)22224S MN AD AN =+⨯=+⨯=。
(1)以A 点为坐标原点建立空间直角坐标系A xyz -,如图所示(图略)由22====BC AB AD PA ,得(0,0,0)A ,1(0,0,2),(2,0,0),(1,,1),(0,2,0)2P B M DABC DA 1B 1C 1D 1PEPD 1A 1DC BA因为3(2,0,2)(1,,1)2PB DM ⋅=-- 0= ,所以DM PB ⊥。
第四讲-立体几何题型归类总结
第四讲-立体几何题型归类总结高中数学-立体几何第四讲立体几何题型归类总结一、考点分析基本图形1.棱柱——有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的几何体叫做棱柱。
斜棱柱底面是正多边形的棱柱正棱柱直棱柱其他棱柱2.棱锥——有一个面是多边形,其余各面是有一个公共顶点的三角形,由这些面所围成的几何体叫做棱锥。
正棱锥——如果有一个棱锥的底面是正多边形,并且顶点在底面的垂线上,这样的棱锥叫做正棱锥。
3.球球的性质:球心与截面圆心的连线垂直于截面;r=R2-d2(其中,球心到截面的距离为d、球的半径为R、截面的半径为r)球与多面体的组合体:球与正四面体、长方体、正方体等的内接与外切。
注:球的有关问题转化为圆的问题解决。
球面积、体积公式:S球=4πR,V球=4/3πR³(其中R为球的半径)二、平行垂直基础知识网络平行与垂直关系可互相转化平行关系a⊥α,b⊥α⇒a//ba⊥α,a//b⇒b⊥αa⊥α,a⊥β⇒α//βα//β,a⊥α⇒a⊥βα//β,γ⊥α⇒γ⊥β垂直关系线线平行判定线线垂直性质判定性质判定面面垂直定义面面垂直线面平行面面平行线面垂直异面直线所成的角,线面角,二面角的求法1.求异面直线所成的角θ∈(0°,90°):解题步骤:找(作):利用平移法找出异面直线所成的角;(1)可固定一条直线平移另一条与其相交;(2)可将两条一面直线同时平移至某一特殊位置。
常用中位线平移法证:证明所找(作)的角就是异面直线所成的角(或其补角)。
常需要证明线线平行;计算:通过解三角形,求出异面直线所成的角;2求直线与平面所成的角度$\theta\in[0^\circ,90^\circ]$:关键在于找到“两足”:垂足和斜足。
解题步骤:1.找到斜线与其在平面内的射影的夹角(注意三垂线定理的应用);2.证明所找到的角度就是直线与平面所成的角度(或其补角)(常常需要证明线面垂直);3.通过解直角三角形,计算线面角度。
2020年高考数学 专题四 立体几何题型分析 理
2020专题四:立体几何题型分析考点一三视图、直观图与表面积、体积1.直观图(1)画法:常用斜二测画法.(2)规则:①原图形中x轴、y轴、z轴两两垂直,直观图中,x′轴、y′轴的夹角为45°(或135°),z′轴与x′轴和y′轴所在平面垂直.②原图形中平行于坐标轴的线段,直观图中仍平行于坐标轴.平行于x轴和z轴的线段在直观图中保持原长度不变,平行于y轴的线段长度在直观图中变为原来的一半.按照斜二测画法得到的平面图形的直观图,其面积与原图形的面积有以下关系S直观图=24S原图形,S原图形=22S直观图.2.三视图(1)几何体的三视图包括正(主)视图、侧(左)视图、俯视图,分别是从几何体的正前方、正左方、正上方观察几何体画出的轮廓线.(2)三视图的画法①基本要求:长对正,高平齐,宽相等.②画法规则:正侧一样高,正俯一样长,侧俯一样宽;看不到的线画虚线1.圆柱、圆锥、圆台的侧面展开图及侧面积公式圆柱圆锥圆台侧面展开图侧面积公式S圆柱侧=2πrl S圆锥侧=πrlS圆台侧=π(r+r′)l2名称几何体表面积体积柱体(棱柱和圆柱)S表面积=S侧+2S底V=Sh锥体(棱锥和圆锥)S表面积=S侧+S底V=13Sh台体(棱台和圆台)S表面积=S侧+S上+S下V=13(S上+S下+S上S下)h球S =4πR 2 V =43πR 3例1.等腰梯形ABCD ,上底CD =1,腰AD =CB =2,下底AB =3,以下底所在直线为x 轴,则由斜二测画法画出的直观图A ′B ′C ′D ′的面积为________.例2.(2020·重庆高考)某几何体的三视图如图所示,则该几何体的表面积为( )A .180B .200C .220D .240例3.(1)如图所示,已知三棱柱ABC A 1B 1C 1的所有棱长均为1,且AA 1⊥底面ABC ,则三棱锥B 1 ABC 1的体积为( )A.312 B.34 C.612D.64(2)(2020·新课标Ⅰ)某几何体的三视图如图所示,则该几何体的体积为( )A .16+8πB .8+8πC .16+16πD .8+16π考点二 球与空间几何体的“切”“接”问题 方法主要是“补体”和“找球心” 方法一:直接法例1、一个长方体的各顶点均在同一球面上,且一个顶点上的三条棱长分别为1,2,3 ,则此球的表面积为 .练习:已知各顶点都在一个球面上的正四棱柱高为4,体积为16,则这个球的表面积为( ) A. 16π B. 20π C. 24π D. 32π 方法二:构造法(构造正方体或长方体)例2(2020年福建高考题)若三棱锥的三条侧棱两两垂直,且侧棱长均为3,则其外接球的表面积是 练习 (2020年全国卷)一个四面体的所有棱长都为2,四个顶点在同一球面上,则此球的表面积为( ) A. 3π B. 4π C. 33π D. 6π 三、确定球心位置法例3、在矩形ABCD 中,AB=4,BC=3,AC 沿将矩形ABCD 折成一个直二面角B-AC-D ,则四面体ABCD 的外接球的体积为( )四、构造直角三角形例4、正四面体的棱长为a ,则其内切球和外接球的半径是多少,体积是多少?练习: 角度一 直三棱柱的外接球1.(2020·辽宁高考)已知直三棱柱ABC A 1B 1C 1的6个顶点都在球O 的球面上,若AB =3,AC =4,AB ⊥AC ,AA 1=12,则球O 的半径为( )A.3172 B .210 C.132D .310角度二 正方体的外接球2.(2020·合肥模拟)一个正方体削去一个角所得到的几何体的三视图如图所示 (图中三个四边形都是边长为2的正方形),则该几何体外接球的体积为________. 角度三 正四面体的内切球3.(2020·长春模拟)若一个正四面体的表面积为S 1,其内切球的表面积为S 2,则S 1S 2=________. 角度四 四棱锥的外接球4.四棱锥P ABCD 的五个顶点都在一个球面上,该四棱锥的三视图如图所示,E ,F 分别是棱AB ,CD 的中点,直线EF 被球面所截得的线段长为22,则该球的表面积为( ) A .9π B .3π C .22π D .12π考点三 利用空间向量求角和距离 1.两条异面直线所成角的求法π12125.A π9125.B π6125.C π3125.D设两条异面直线a ,b 的方向向量为a ,b ,其夹角为θ,则cos φ=|cos θ|=|a·b||a||b|(其中φ为异面直线a ,b 所成的角).2.直线和平面所成的角的求法如图所示,设直线l 的方向向量为e ,平面α的法向量为n ,直线l 与平面α所成的角为φ,两向量e 与n 的夹角为θ,则有sin φ=|cos θ|=|n·e||n||e|.3.求二面角的大小(1)如图①,AB ,CD 是二面角α l β的两个面内与棱l 垂直的直线,则二面角的大小θ=〈AB u u u r ,CD u u ur 〉.(2)如图②③,n 1,n 2分别是二面角α l β的两个半平面α,β的法向量,则二面角的大小θ=〈n 1,n 2〉(或π-〈n 1,n 2〉).4.点到平面的距离的求法设n r 是平面α的法向量,在α内取一点B, 则 A 到α的距离|||||cos |||AB n d AB n θ==u u u r r u u u r g r 易错点:1.求异面直线所成角时,易求出余弦值为负值而盲目得出答案而忽视了夹角为⎝⎛⎦⎥⎤0,π2.2.求直线与平面所成角时,注意求出夹角的余弦值的绝对值应为线面角的正弦值.3.利用平面的法向量求二面角的大小时,二面角是锐角或钝角由图形决定.由图形知二面角是锐角时cosθ=|n 1·n 2||n 1||n 2|;由图形知二面角是钝角时,cos θ=-|n 1·n 2||n 1||n 2|.当图形不能确定时,要根据向量坐标在图形中观察法向量的方向,从而确定二面角与向量n 1,n 2的夹角是相等(一个平面的法向量指向二面角的内部,另一个平面的法向量指向二面角的外部),还是互补(两个法向量同时指向二面角的内部或外部),这是利用向量求二面角的难点、易错点.一、线线角问题1.(2020·沈阳调研)在直三棱柱A 1B 1C 1 ABC 中,∠BCA =90°,点D 1,F 1分别是A 1B 1,A 1C 1的中点,BC =CA =CC 1,则BD 1与AF 1所成角的余弦值是( )A.3010 B.12 C.3015D.15102.如图,在棱长为1的正方体ABCD A 1B 1C 1D 1中,M 和N 分别是A 1B 1和BB 1的中点,那么直线AM 与CN 所成角的余弦值为________.二、线面角的问题3、(2020·湖南高考)如图,在直棱柱ABCD A 1B 1C 1D 1中,AD ∥BC ,∠BAD =90°,AC ⊥BD ,BC =1,AD =AA 1=3.(1)证明:AC ⊥B 1D ;(2)求直线B 1C 1与平面ACD 1所成角的正弦值.[针对训练](2020·福建高考改编)如图,在四棱柱ABCD A 1B 1C 1D 1中,侧棱AA 1⊥底面ABCD ,AB ∥DC ,AA 1=1,AB =3k ,AD =4k ,BC =5k ,DC =6k (k >0).若直线AA 1与平面AB 1C 所成角的正弦值为67,求k 的值.三、二面角问题4、(2020·新课标卷Ⅱ)如图,直三棱柱ABC A 1B 1C 1中,D ,E 分别是AB ,BB 1的中点,AA 1=AC =CB =22AB . (1)证明:BC 1//平面A 1CD ; (2)求二面角D A 1C E 的正弦值.[针对训练](2020·杭州模拟)如图,已知平面QBC 与直线PA 均垂直于Rt△ABC 所在平面, 且PA =AB =AC .(1)求证:PA ∥平面QBC ;(2)若PQ ⊥平面QBC ,求二面角Q PB A 的余弦值.四、 利用空间向量解决探索性问题.(2020·江西模拟)如图,四边形ABCD 是边长为3的正方形,DE ⊥平面ABCD ,AF ∥DE ,DE =3AF ,BE 与平面ABCD 所成的角为60°.(1)求证:AC ⊥平面BDE ; (2)求二面角F BE D 的余弦值;(3)设点M 是线段BD 上一个动点,试确定点M 的位置,使得AM ∥平面BEF ,并证明你的结论.[针对训练]已知正方体ABCD A 1B 1C 1D 1的棱长为1,点P 在线段BD 1上.当∠APC 最大时,三棱锥P ABC 的体积为________.五、近三年新课标高考试题立体几何(三视图1小+1小1大:(1)三视图(2)线面关系(3)与球有关的组合体(4)证明、求体积与表面积(注意规范性),作辅助线的思路(5)探索性问题的思考方法)(11)(6)在一个几何体的三视图中,正视图和俯视图如右图所示,则相应的侧视图可以为(15)已知矩形ABCD 的顶点都在半径为4的球O 的球面上,且6,23AB BC ==,则棱锥O ABCD -的体积为(18)(本小题满分12分)如图,四棱锥P-ABCD 中,底面ABCD 为平行四 边形,∠DAB=60°,AB=2AD ,PD ⊥底面ABCD . (Ⅰ)证明:PA ⊥BD ;(Ⅱ)若PD =AD ,求二面角A-PB-C 的余弦值。
高中数学立体几何的相关题型及解题思路
高中数学立体几何的相关题型及解题思路在高中数学中,立体几何是一个重要的考点,也是许多学生感到困惑和头疼的地方。
本文将介绍一些常见的立体几何题型,并给出相应的解题思路和技巧,希望能够帮助高中学生和他们的父母更好地应对这一考点。
一、体积计算题体积计算题是立体几何中最基础的题型之一,常见的题目有计算立方体、长方体、圆柱体、圆锥体、球体等的体积。
解决这类题目的关键在于熟练掌握各种几何体的体积公式,并能够根据题目给出的条件灵活运用。
例如,某题给出一个长方体的底面积为12平方厘米,高为5厘米,要求计算其体积。
我们可以直接应用长方体的体积公式V=底面积×高,代入已知数据计算得出答案为60立方厘米。
二、表面积计算题表面积计算题也是立体几何中常见的题型之一,常见的题目有计算立方体、长方体、圆柱体、圆锥体、球体等的表面积。
解决这类题目的关键在于熟练掌握各种几何体的表面积公式,并能够根据题目给出的条件灵活运用。
例如,某题给出一个正方体的边长为3厘米,要求计算其表面积。
我们可以直接应用正方体的表面积公式S=6a^2,其中a为边长,代入已知数据计算得出答案为54平方厘米。
三、立体图形的相似题立体图形的相似题是立体几何中较为复杂的题型之一,常见的题目有判断两个立体图形是否相似、计算相似立体图形的比例等。
解决这类题目的关键在于观察立体图形的形状和比例关系,并能够利用相似三角形的性质进行推理。
例如,某题给出一个正方体ABCDA'B'C'D',另一个正方体EFGHE'F'G'与之相似,要求计算两个正方体的体积比。
我们可以观察到两个正方体的边长比为AE/AA'=EF/EE'=FG/FF'=...=1/2,而体积与边长的关系为V=k^3,其中k为边长的比值。
因此,两个正方体的体积比为(1/2)^3=1/8。
四、立体图形的投影题立体图形的投影题是立体几何中较为抽象的题型之一,常见的题目有计算某个立体图形在某个平面上的投影面积或投影长度等。
立体几何大题题型总结
立体几何大题题型总结一、立体几何大题题型概述立体几何大题是高中数学中的重要内容之一,主要考察学生对于立体几何基本概念的掌握和应用能力。
在解答这类题目时,需要学生熟练掌握空间图形的性质、计算表达式的推导和运用等方面的知识。
二、常见的立体几何大题题型1. 空间图形计算此类题目主要考察学生对于空间图形面积和体积计算公式的掌握以及运用能力。
常见的空间图形包括球、圆锥、圆柱、棱锥、棱柱等。
2. 空间坐标系与向量此类题目主要考察学生对于三维空间坐标系和向量的理解和应用能力。
常见的问题包括平面方程、直线方程、点到直线距离等。
3. 空间解析几何此类题目主要考察学生对于空间解析几何基本概念的掌握和应用能力。
常见问题包括点与直线位置关系、两条直线位置关系等。
4. 立体几何证明此类题目主要考察学生对于立体几何基本定理的理解和应用能力。
常见问题包括等腰三角形的高垂线定理、平行四边形对角线互相平分定理等。
5. 空间向量证明此类题目主要考察学生对于向量基本定理的掌握和应用能力。
常见问题包括向量共线、垂直等性质。
三、解答立体几何大题的技巧1. 熟练掌握公式在解答立体几何大题时,需要熟练掌握空间图形面积和体积计算公式,以便快速准确地计算。
2. 善于化简表达式在解答立体几何大题时,需要善于化简表达式,以便更好地发现规律和思路。
3. 注意空间图形的性质在解答立体几何大题时,需要注意空间图形的性质,如平行关系、相交关系等,以便更好地推导出结论。
4. 善于利用画图辅助在解答立体几何大题时,需要善于利用画图辅助来更好地理解问题和推导出结论。
四、总结立体几何大题是高中数学中的重要内容之一,需要学生熟练掌握空间图形的性质、计算表达式的推导和运用等方面的知识。
常见的立体几何大题题型包括空间图形计算、空间坐标系与向量、空间解析几何、立体几何证明和空间向量证明等。
在解答这类题目时,需要注意熟练掌握公式、善于化简表达式、注意空间图形的性质以及善于利用画图辅助等技巧。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
立体几何题型与方法(理科)1.平面平面的基本性质:掌握三个公理及推论,会说明共点、共线、共面问题。
(1).证明点共线的问题,一般转化为证明这些点是某两个平面的公共点(依据:由点在线上,线在面内 ,推出点在面内), 这样可根据公理2证明这些点都在这两个平面的公共直线上。
(2).证明共点问题,一般是先证明两条直线交于一点,再证明这点在第三条直线上,而这一点是两个平面的公共点,这第三条直线是这两个平面的交线。
(3).证共面问题一般先根据一部分条件确定一个平面,然后再证明其余的也在这个平面内,或者用同一法证明两平面重合 2. 空间直线.(1). 空间直线位置关系三种:相交、平行、异面. 相交直线:共面有且仅有一个公共点;平行直线:共面没有公共点;异面直线:不同在任一平面内,无公共点[注]:①两条异面直线在同一平面内射影一定是相交的两条直线.(×)(也可能两条直线平行,也可能是点和直线等)②直线在平面外,指的位置关系是平行或相交③若直线a 、b 异面,a 平行于平面α,b 与α的关系是相交、平行、在平面α内. ④两条平行线在同一平面内的射影图形是一条直线或两条平行线或两点.⑤在平面内射影是直线的图形一定是直线.(×)(射影不一定只有直线,也可以是其他图形) ⑥在同一平面内的射影长相等,则斜线长相等.(×)(并非是从平面外一点..向这个平面所引的垂线段和斜线段)⑦b a ,是夹在两平行平面间的线段,若b a =,则b a ,的位置关系为相交或平行或异面.⑧异面直线判定定理:过平面外一点与平面内一点的直线和平面内不经过该点的直线是异面直线.(不在任何一个平面内的两条直线)(2). 平行公理:平行于同一条直线的两条直线互相平行. 等角定理:如果一个角的两边和另一个角的两边分别平行并且方向相同,那么这两个角相等(如右图). (直线与直线所成角]90,0[︒︒∈θ)(向量与向量所成角])180,0[ ∈θ推论:如果两条相交直线和另两条相交直线分别平行,那么这两组直线所成锐角(或直角)相等.(3). 两异面直线的距离:公垂线段的长度.空间两条直线垂直的情况:相交(共面)垂直和异面垂直.[注]:21,l l 是异面直线,则过21,l l 外一点P ,过点P 且与21,l l 都平行平面有一个或没有,但与21,l l距离相等的点在同一平面内. (1L 或2L 在这个做出的平面内不能叫1L 与2L 平行的平面) 3. 直线与平面平行、直线与平面垂直.(1). 空间直线与平面位置分三种:相交、平行、在平面内.(2). 直线与平面平行判定定理:如果平面外一条直线和这个平面内一条直线平行,那么这条直线和这个平面平行.(“线线平行⇒线面平行”)[注]:①直线a 与平面α内一条直线平行,则a ∥α. (×)(平面外一条直线) ②直线a 与平面α内一条直线相交,则a 与平面α相交. (×)(平面外一条直线)③若直线a 与平面α平行,则α内必存在无数条直线与a 平行. (√)(不是任意一条直线,可利用平行的传递性证之)④两条平行线中一条平行于一个平面,那么另一条也平行于这个平面. (×)(可能在此平面内) ⑤平行于同一个平面的两直线平行.(×)(两直线可能相交或者异面) ⑥直线l 与平面α、β所成角相等,则α∥β.(×)(α、β可能相交)(3). 直线和平面平行性质定理:如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行.(“线面平行⇒线线平行”)(4). 直线与平面垂直是指直线与平面任何一条直线垂直,过一点有且只有一条直线和一个平面垂直,过一点有且只有一个平面和一条直线垂直.● 若PA ⊥α,a ⊥AO ,得a ⊥PO (三垂线定理), ● 三垂线定理的逆定理亦成立.直线与平面垂直的判定定理一:如果一条直线和一个平面内的两条相交直线都垂直,那么这两条直线垂直于这个平面.(“线线垂直⇒线面垂直”)直线与平面垂直的判定定理二:如果平行线中一条直线垂直于一个平面,那么另一条也垂直于这个平面.性质:如果两条直线同垂直于一个平面,那么这两条直线平行.(5).a.垂线段和斜线段长定理:从平面外一点..向这个平面所引的垂线段和斜线段中,①射影相等的两条斜线段相等,射影较长的斜线段较长;②相等的斜线段的射影相等,较长的斜线段射影较长;③垂线段比任何一条斜线段短.[注]:垂线在平面的射影为一个点. [一条直线在平面内的射影是一条直线.(×)]b.射影定理推论:如果一个角所在平面外一点到角的两边的距离相等,那么这点在平面内的射影在这个角的平分线上。
4. 平面平行与平面垂直.(1). 空间两个平面的位置关系:相交、平行.(2). 平面平行判定定理:如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行.(“线面平行⇒面面平行”)推论:垂直于同一条直线的两个平面互相平行;平行于同一平面的两个平面平行.POAa[注]:一平面内的任一直线平行于另一平面.(3). 两个平面平行的性质定理:如果两个平面平行同时和第三个平面相交,那么它们交线平行.(“面面平行⇒线线平行”)(4). 两个平面垂直判定一:两个平面所成的二面角是直二面角,则两个平面垂直.两个平面垂直判定二:如果一条直线与一个平面垂直,那么经过这条直线的平面垂直于这个平面.(“线面垂直⇒面面垂直”)注:如果两个二面角的平面分别对应互相垂直,则两个二面角没有什么关系.(5). 两个平面垂直性质定理:如果两个平面垂直,那么在一个平面内垂直于它们交线的直线也垂直于另一个平面.推论:如果两个相交平面都垂直于第三平面,则它们交线垂直于第三平面. 简证:如图,在平面内过O 作OA 、OB 分别垂直于21,l l ,因为ααββ⊥⊂⊥⊂OB PM OA PM ,,,则OB PM OA PM ⊥⊥,.所以结论成立 (6). 两异面直线任意两点间的距离公式:θcos 2222mn d n m l -++=(θ为锐角取减,θ为钝角取加,综上,都取减则必有⎥⎦⎤⎝⎛∈2,0πθ)(1). a.最小角定理:21cos cos cos θθθ=(1θ为最小角,如图) b.最小角定理的应用(∠PBN 为最小角)简记为:成角比交线夹角一半大,且又比交线夹角补角一半长,一定有4条. 成角比交线夹角一半大,又比交线夹角补角小,一定有2条. 成角比交线夹角一半大,又与交线夹角相等,一定有3条或者2条. 成角比交线夹角一半小,又与交线夹角一半小,一定有1条或者没有. 5. 棱柱. 棱锥(1). 棱柱.a.①直棱柱侧面积:Ch S =(C 为底面周长,h 是高)该公式是利用直棱柱的侧面展开图为矩形得出的. ②斜棱住侧面积:l C S 1=(1C 是斜棱柱直截面周长,l 是斜棱柱的侧棱长)该公式是利用斜棱柱的侧面展开图为平行四边形得出的.b.{四棱柱}⊃{平行六面体}⊃{直平行六面体}⊃{长方体}⊃{正四棱柱}⊃{正方体}. {直四棱柱} {平行六面体}={直平行六面体}.四棱柱直平行六面体长方体正四棱柱底面是平行四边形侧棱垂直底面底面是矩形底面是正方形c.棱柱具有的性质:①棱柱的各个侧面都是平行四边形,所有的侧棱都相等;直棱柱的各个侧面都是矩形........;正棱柱的各个侧面都是全等的矩形...... ②棱柱的两个底面与平行于底面的截面是对应边互相平行的全等..多边形. PαβθM AB O图1θθ1θ2图2③过棱柱不相邻的两条侧棱的截面都是平行四边形.注:①棱柱有一个侧面和底面的一条边垂直可推测是直棱柱. (×) (直棱柱不能保证底面是矩形,可如图) ②(直棱柱定义)棱柱有一条侧棱和底面垂直. d.平行六面体:定理一:平行六面体的对角线交于一点.............,并且在交点处互相平分. [注]:四棱柱的对角线不一定相交于一点.定理二:长方体的一条对角线长的平方等于一个顶点上三条棱长的平方和.推论一:长方体一条对角线与同一个顶点的三条棱所成的角为γβα,,,则 1cos cos cos 222=++γβα. 推论二:长方体一条对角线与同一个顶点的三各侧面所成的角为γβα,,,则2cos cos cos 222=++γβα. [注]:①有两个侧面是矩形的棱柱是直棱柱.(×)(斜四棱柱的两个平行的平面可以为矩形) ②各侧面都是正方形的棱柱一定是正棱柱.(×)(应是各侧面都是正方形的直.棱柱才行) ③对角面都是全等的矩形的直四棱柱一定是长方体.(×)(只能推出对角线相等,推不出底面为矩形) ④棱柱成为直棱柱的一个必要不充分条件是棱柱有一条侧棱与底面的两条边垂直. (两条边可能相交,可能不相交,若两条边相交,则应是充要条件)(2). 棱锥:棱锥是一个面为多边形,其余各面是有一个公共顶点的三角形. [注]:①一个三棱锥四个面可以都为直角三角形.②一个棱柱可以分成等体积的三个三棱锥;所以棱柱棱柱3V S h V ==.a.①正棱锥定义:底面是正多边形;顶点在底面的射影为底面正多边形的中心. [注]:i. 正四棱锥的各个侧面都是全等的等腰三角形.(不是等边三角形) ii. 正四面体是各棱相等,而正三棱锥是底面为正三角形,侧棱与底棱不一定相等iii. 正棱锥定义的推论:若一个棱锥的各个侧面都是全等的等腰三角形(即侧棱相等);底面为正多边形. ②正棱锥的侧面积:'Ch 21S =(底面周长为C ,斜高为'h ) ③棱锥的侧面积与底面积的射影公式:αcos 底侧S S =(侧面与底面成的二面角为α)附:以知c ⊥l ,b a =⋅αcos ,α为二面角b l a --. 则l a S ⋅=211①,b l S ⋅=212②,b a =⋅αcos ③ ⇒①②③得αcos 底侧S S =. 注:S 为任意多边形的面积(可分别求多个三角形面积和的方法).b.棱锥具有的性质:①正棱锥各侧棱相等,各侧面都是全等的等腰三角形,各等腰三角形底边上的高相等(它叫做正棱锥的斜高).②正棱锥的高、斜高和斜高在底面内的射影组成一个直角三角形,正棱锥的高、侧棱、侧棱在底面内的射影也组成一个直角三角形.labcc.特殊棱锥的顶点在底面的射影位置:①棱锥的侧棱长均相等,则顶点在底面上的射影为底面多边形的外心.②棱锥的侧棱与底面所成的角均相等,则顶点在底面上的射影为底面多边形的外心. ③棱锥的各侧面与底面所成角均相等,则顶点在底面上的射影为底面多边形内心. ④棱锥的顶点到底面各边距离相等,则顶点在底面上的射影为底面多边形内心. ⑤三棱锥有两组对棱垂直,则顶点在底面的射影为三角形垂心. ⑥三棱锥的三条侧棱两两垂直,则顶点在底面上的射影为三角形的垂心.⑦每个四面体都有外接球,球心0是各条棱的中垂面的交点,此点到各顶点的距离等于球半径; ⑧每个四面体都有内切球,球心I 是四面体各个二面角的平分面的交点,到各面的距离等于半径.[注]:i. 各个侧面都是等腰三角形,且底面是正方形的棱锥是正四棱锥.(×)(各个侧面的等腰三角形不知是否全等)ii. 若一个三棱锥,两条相对棱互相垂直,则第三组相对棱必然垂直简证:AB ⊥CD ,AC ⊥BD ⇒ BC ⊥AD. 令b AC c AD a AB ===,, 得c a c b AD BC c AD a b AB AC BC -=⋅⇒=-=-=,,已知()()0,0=-⋅=-⋅c a b b c a0=-⇒c b c a 则0=⋅AD BC .iii. 空间四边形OABC 且四边长相等,则顺次连结各边的中点的四边形一定是矩形. iv. 若是四边长与对角线分别相等,则顺次连结各边的中点的四边是一定是正方形.简证:取AC 中点'O ,则⊥⇒⊥'⊥'AC AC O B AC o o ,平面=∠⇒⊥⇒'FGH BO AC B O O 90°易知EFGH 为平行四边形⇒EFGH 为长方形.若对角线等,则EFGH FG EF ⇒=为正方形.(3). 球:a.球的截面是一个圆面.①球的表面积公式:24R S π=.②球的体积公式:334R V π=.b.纬度、经度:①纬度:地球上一点P 的纬度是指经过P 点的球半径与赤道面所成的角的度数.②经度:地球上B A ,两点的经度差,是指分别经过这两点的经线与地轴所确定的二个半平面的二面角的度数,特别地,当经过点A 的经线是本初子午线时,这个二面角的度数就是B 点的经度.附:①圆柱体积:h r V 2π=(r 为半径,h 为高)②圆锥体积:h r V 231π=(r 为半径,h 为高)③锥体体积:Sh V 31=(S 为底面积,h 为高)B CFEHGBCDAO'O r(1). ①内切球:当四面体为正四面体时,设边长为a ,a h 36=,243a S =底,243a S =侧,得R a R a a a ⋅⋅+⋅=⋅2224331433643a a a R 46342334/42=⋅==⇒. 注:球内切于四面体:h S R S 313R S 31V 底底侧ACD B ⋅=⋅+⋅⋅⋅=-。
