竞赛课 公开课课件单项式乘多项式
合集下载
单项式乘多项式课件

注意事项
分配律是单项式乘多项式 的基础,必须熟练掌握。
乘法结合律的应用
乘法结合律定义
在单项式与多项式相乘时 ,先乘哪两项并不影响结 果。
运算示例
$(x + y) times (2x + 3) = x times 2x + x times 3 + y times 2x + y times 3$
注意事项
解决实际问题
总结词
单项式乘多项式的运算在解决实际问题中具有广泛的应用,如物理、工程和经济学等领域。
详细描述
在物理学中,单项式乘多项式的运算常用于解决力学、电磁学和量子力学等领域的问题。在工程学中,这种运算 用于分析结构、流体和热传导等问题。在经济学中,单项式乘多项式的运算用于研究市场供需关系、生产成本和 效用函数等。
多项式的表示方法
通常用数学符号和括号来表示,如f(x) = 3x^2 + 2x - 5、p(x) = x^3 + 2x^2 - x等。
02
单项式乘多项式的运算规则
分配律的应用
01
02
03
分配律定义
单项式与多项式相乘时, 单项式中的每一项分别与 多项式中的每一项相乘, 再将所得的积相加。
运算示例
$(x + y) times 2x = 2x^2 + 2xy$
问题3
一个圆柱体的底面半径为 $3x$ ,高为 $4y$,求这个圆柱体的
体积。
THANKS
感谢观看
练习2
化简代数式 $5xy(x + y) - 2y(x^2 - y^2)$
练习3
化简代数式 $4x(x^2 - y) + y(x^2 - y)$
单项式乘以多项式课件

运算示例
$(a+b) times x = ax + bx$
注意事项
乘法交换律在单项式乘以多项式的运算中可以简 化计算,但需要注意符号的变化。
03
单项式乘以多项式的实例 解析
实例一:单项式与二项式相乘
01
02
总结词:简单易懂
详细描述:通过具体的单项式与二项式相乘的例子,展示乘法的基本 规则和运算步骤,帮助学生理解单项式乘以多项式的计算方法。
单项式乘以多项式课件
目录
• 单项式与多项式的定义 • 单项式乘以多项式的运算规则 • 单项式乘以多项式的实例解析
目录
• 单项式乘以多项式的运算技巧 • 单项式乘以多项式的应用
01
单项式与多项式的定义
单项式的定义
总结词
单项式是数学中基本的代数表达式之一,由数字、变量和它们的幂次通过乘法运算连接 而成。
在物理中的应用
力学分析
在力学分析中,单项式乘 以多项式可以用于计算物 体的运动轨迹、速度和加 速度等物理量。
电磁学
在电磁学中,单项式乘以 多项式可以用于计算电场 、磁场等物理量的分布和 变化规律。
热力学
在热力学中,单项式乘以 多项式可以用于计算温度 、压力等物理量的变化规 律。
在日常生活中的应用
详细描述
单项式和多项式通常用数学符号表示,其中幂次表示变量的次数。单项式的表示方法为数字系数与变 量及其幂次的乘积,如 $ax^n$ 表示 $a$ 与 $x$ 的 $n$ 次幂的乘积。多项式的表示方法为若干个单 项式的和,如 $ax^n + bx^m + c$ 表示一个多项式,其中 $a$、$b$ 和 $c$ 是系数,$x^n$、 $x^m$ 是幂次。
$(a+b) times x = ax + bx$
注意事项
乘法交换律在单项式乘以多项式的运算中可以简 化计算,但需要注意符号的变化。
03
单项式乘以多项式的实例 解析
实例一:单项式与二项式相乘
01
02
总结词:简单易懂
详细描述:通过具体的单项式与二项式相乘的例子,展示乘法的基本 规则和运算步骤,帮助学生理解单项式乘以多项式的计算方法。
单项式乘以多项式课件
目录
• 单项式与多项式的定义 • 单项式乘以多项式的运算规则 • 单项式乘以多项式的实例解析
目录
• 单项式乘以多项式的运算技巧 • 单项式乘以多项式的应用
01
单项式与多项式的定义
单项式的定义
总结词
单项式是数学中基本的代数表达式之一,由数字、变量和它们的幂次通过乘法运算连接 而成。
在物理中的应用
力学分析
在力学分析中,单项式乘 以多项式可以用于计算物 体的运动轨迹、速度和加 速度等物理量。
电磁学
在电磁学中,单项式乘以 多项式可以用于计算电场 、磁场等物理量的分布和 变化规律。
热力学
在热力学中,单项式乘以 多项式可以用于计算温度 、压力等物理量的变化规 律。
在日常生活中的应用
详细描述
单项式和多项式通常用数学符号表示,其中幂次表示变量的次数。单项式的表示方法为数字系数与变 量及其幂次的乘积,如 $ax^n$ 表示 $a$ 与 $x$ 的 $n$ 次幂的乘积。多项式的表示方法为若干个单 项式的和,如 $ax^n + bx^m + c$ 表示一个多项式,其中 $a$、$b$ 和 $c$ 是系数,$x^n$、 $x^m$ 是幂次。
单项式乘以多项式PPT课件
= a2bc+ab2c+abc2
法则:单项式与多项式相乘,只要将单项式分别乘 以多项式的各项,再将所得的积相加。
例题教学
计算:(-2a2)· (3ab2-5ab3) 解:原式= (-2a2)· (-5ab3) (3ab2) + (-2a2) · = -6a3b2+l0a3b3 2、(3a2-5b)· 2a2 2a2 + (-5b)·2a2 解:原式= 3a2 · = -6a4-l0a2b
练习反馈
x(x-1)+2x(x+1)-3x(2x-5)
小
结
1、注意不要漏乘任何一项。 2、注意“-”的问题。 3、在几个单项式乘以多项的混合运算 中,要注意运算顺序,完成乘法后, 要合并同类项,得出最简结果。
知识拓展
(m+a)(n+b) = m(n+b)+a(n+b) = n(m+a)+b(m+a) = mn+mb+na+ab 它们之间有什么关系? 如果m=n,a=b,它们 之间又有什么关系?
mLeabharlann 这个图形的面 积该怎么表示
b
a n
作
业
1、 177
P
4
2、预习:多项式乘以多项式
练习反馈
1、3a(5a-2b) 2、(x-3y)(-6x)
例题教学
计算:-2a2(ab+b2)-5a(a2b-ab2) 解:原式= -2a2· ab +(-2a2· b2)+(-5a)· (a2b) (-ab2) + (-5a)· = -2a3b + (-2a2b2 ) + (-5a3b) + 5a2b2 = -7a3b + 3a2b2
单项式乘以多项式课件PPT课件

2.单项式与多项式相乘,其积仍是多 项式,项数与原多项式的项数相同,注 意不要漏乘项.
3.积的每一项的符号由原多项式各项 符号和单项式的符号来决定,注意运用 去括号法则.
知识延伸
1.已知:xy2=-2,求-xy(x3y7-3x2y5-y)
2.思考: 若 5x3 x2 ax 5 的结果中不含
x 4 项,则 a 等于多少?
知识延伸
3.已知A=-3xy2,B=2xy(x-y),求A·B 4.已知M,N分别表示不同的单项式,且3
x(M-5x)=6x2y3+N,求M、N的值.
学海无涯
驶向成功的 彼岸
再 见
直长 挂风 云破 帆浪 济会 沧有海时
感谢下 载
单项式乘以多项式
单项式的乘法法则
单项式与单项式相乘,把它们的系数、相同字 母的幂分别相乘,对于只在一个单项式里含有的字 母,则连同它的指数作为积的一个因式.
单项式的乘法法则包括以下三部分:
有理
((12))积相的同系字数母等相于乘各 ; 因式系数(同的底积数; 幂的乘数 乘法的 法)
(3)只在一个单项式里含有的字母,
单项式的乘法法则adab解答abacad结论单项式与多项式相乘用单项式乘单项式与多项式相乘用单项式乘多项式的每一项再把所得的积相加多项式的每一项再把所得的积相加ababab住宅用地人民广场商业用地3a2b2abab18单项式与多项式相乘的依据是乘法对加法的单项式与多项式相乘其积仍是项数与原多项式的积的每一项的符号由原多项式各项符号和单项式的符号来决定注意运用去括号法则
要连同它的指数写在积里.(注意 不要把这个因式丢掉)
1.根据单项式乘单项式的法则填空:
1 3xy 12x2 y
22ab 6a2bc
3.积的每一项的符号由原多项式各项 符号和单项式的符号来决定,注意运用 去括号法则.
知识延伸
1.已知:xy2=-2,求-xy(x3y7-3x2y5-y)
2.思考: 若 5x3 x2 ax 5 的结果中不含
x 4 项,则 a 等于多少?
知识延伸
3.已知A=-3xy2,B=2xy(x-y),求A·B 4.已知M,N分别表示不同的单项式,且3
x(M-5x)=6x2y3+N,求M、N的值.
学海无涯
驶向成功的 彼岸
再 见
直长 挂风 云破 帆浪 济会 沧有海时
感谢下 载
单项式乘以多项式
单项式的乘法法则
单项式与单项式相乘,把它们的系数、相同字 母的幂分别相乘,对于只在一个单项式里含有的字 母,则连同它的指数作为积的一个因式.
单项式的乘法法则包括以下三部分:
有理
((12))积相的同系字数母等相于乘各 ; 因式系数(同的底积数; 幂的乘数 乘法的 法)
(3)只在一个单项式里含有的字母,
单项式的乘法法则adab解答abacad结论单项式与多项式相乘用单项式乘单项式与多项式相乘用单项式乘多项式的每一项再把所得的积相加多项式的每一项再把所得的积相加ababab住宅用地人民广场商业用地3a2b2abab18单项式与多项式相乘的依据是乘法对加法的单项式与多项式相乘其积仍是项数与原多项式的积的每一项的符号由原多项式各项符号和单项式的符号来决定注意运用去括号法则
要连同它的指数写在积里.(注意 不要把这个因式丢掉)
1.根据单项式乘单项式的法则填空:
1 3xy 12x2 y
22ab 6a2bc
《单项式乘多项式》课件

《单项式乘多项式》ppt课件
• 引言 • 单项式乘多项式的定义与性质 • 单项式乘多项式的计算方法 • 单项式乘多项式的应用 • 练习与巩固 • 总结与回顾
01
引言
主题介绍
01
02
03
单项式乘多项式
理解单项式与多项式相乘 的规则和步骤。
数学表达式的简化
掌握如何将单项式与多项 式相乘后的结果进行简化 。
。
计算步骤与示例
列出多项式中的每一项,并确定单项 式的系数、字母因数和常数因数。
将相乘的结果按多项式的排列顺序组 合,得到最终的乘积。
将单项式的系数、字母因数和常数因 数分别与多项式的每一项相乘。
示例:计算2x^2y(x+3y),首先将 2x^2y分别与x和3y相乘,得到 2x^3y和6x^2y^2,然后将两项相加 得到2x^3y + 6x^2y^2。
实际应用
了解单项式乘多项式在日 常生活和科学计算中的应 用。
学习目标
01
02
03
04
掌握单项式与多项式相乘的基 本规则。
能够正确计算单项式与多项式 相乘的结果。
理解简化数学表达式的意义和 方法。
能够在实际问题中运用单项式 乘多项式的知识。
02
单项式乘多项式的定义与性质
单项式的定义与性质
定义
单项式是只包含一个项的代数式 ,通常表示为字母、数字和字母 的积。
ห้องสมุดไป่ตู้
通过练习和巩固,提 高了自己的计算能力 和数学思维能力。
理解了单项式乘多项 式的实际应用,如代 数式求值、解方程等 。
下节课预告
主题
《多项式乘多项式》
内容提要
掌握多项式乘多项式的计算方法,理解其实际应 用,如代数式求值、解方程等。
• 引言 • 单项式乘多项式的定义与性质 • 单项式乘多项式的计算方法 • 单项式乘多项式的应用 • 练习与巩固 • 总结与回顾
01
引言
主题介绍
01
02
03
单项式乘多项式
理解单项式与多项式相乘 的规则和步骤。
数学表达式的简化
掌握如何将单项式与多项 式相乘后的结果进行简化 。
。
计算步骤与示例
列出多项式中的每一项,并确定单项 式的系数、字母因数和常数因数。
将相乘的结果按多项式的排列顺序组 合,得到最终的乘积。
将单项式的系数、字母因数和常数因 数分别与多项式的每一项相乘。
示例:计算2x^2y(x+3y),首先将 2x^2y分别与x和3y相乘,得到 2x^3y和6x^2y^2,然后将两项相加 得到2x^3y + 6x^2y^2。
实际应用
了解单项式乘多项式在日 常生活和科学计算中的应 用。
学习目标
01
02
03
04
掌握单项式与多项式相乘的基 本规则。
能够正确计算单项式与多项式 相乘的结果。
理解简化数学表达式的意义和 方法。
能够在实际问题中运用单项式 乘多项式的知识。
02
单项式乘多项式的定义与性质
单项式的定义与性质
定义
单项式是只包含一个项的代数式 ,通常表示为字母、数字和字母 的积。
ห้องสมุดไป่ตู้
通过练习和巩固,提 高了自己的计算能力 和数学思维能力。
理解了单项式乘多项 式的实际应用,如代 数式求值、解方程等 。
下节课预告
主题
《多项式乘多项式》
内容提要
掌握多项式乘多项式的计算方法,理解其实际应 用,如代数式求值、解方程等。
单项式与多项式相乘公开课课件

乘法分配律的运用
乘法分配律是数学中的一个基本定律,它指出一个数乘以 两个数的和等于这个数分别乘以这两个数再求和。在单项 式与多项式相乘时,乘法分配律是非常重要的。
例如,单项式$a^3$与多项式$b + c$相乘时,可以运用 乘法分配律进行计算:$(a^3)(b+c) = a^3b + a^3c$。 这样可以简化计算过程,提高计算效率。
单项式与多项式相乘公开课课件
contents
目录
• 单项式与多项式简介 • 单项式与多项式相乘的法则 • 单项式与多项式相乘的运算实例 • 单项式与多项式相乘的注意事项 • 习题与解答
01
单项式与多项式简介
单项式的定义与性质
定义
单项式是只包含一个项的代数式 ,通常表示为数字、字母的积。
性质
单项式具有加法封闭性、乘法交 换律和结合律等基本性质。
单项式的几何意义
在数轴上,单项式可以表示一个点或一个单位长度。例如,$3x$表示在x轴上, 每移动一个单位长度,坐标增加3。
多项式的几何意义
多项式可以表示一条曲线或曲面。例如,$y = x^2$表示一个开口向上的抛物线 。
02
单项式与多项式相乘的法则
单项式乘以多项式的法则
单项式乘以多项式的运算法则,是将单项式中的每一个因子 与多项式中的每一个项分别相乘,然后将所得的积相加。
多项式的定义与性质
定义
多项式是由有限个单项式通过加法运 算组成的代数式,表示为$P(x) = a_n x^n + a_{n-1} x^{n-1} + cdots + a_1换律 和结合律等基本性质,还具有分配律 和幂的运算法则等特殊性质。
单项式与多项式的几何意义
单项式乘多项式ppt课件

课堂小结
同学们,对于数学这种思维性的学科来说,我们要保持一 种求真、严谨的态度,它不仅仅是一门学科,更是在考验 我们的耐心、细心和认真的程度,所以当我们学习数学的 时候应该打起十二万分的精神.
课堂小结
教材习题:完成课本100页练习. 作业本作业:完成对应练习.
3.你能尝试归纳单项式与多项式的乘法运算法则吗? 单项式与多项式相乘,就是用单项式去乘多项式的每一项, 再把所得的积相加
4.你能归纳出单项式与多项式相乘的步骤吗? ①用单项式乘多项式的每一项;②转化为单项式 与单项式的乘法运算;③把所得的积相加 5.请同学们完成课本100页例5.
小组讨论
1.请同学们分析课本100页例5中的两个计算题,指出其中的单 项式是什么,多项式是什么,转化为单项式乘单项式后是哪 些式子相乘.
例4:先化简,再求值: 1 (12a2-16a)-5(a2-3a+2),其中a2+7a- 2
7=0.
解:原式=6a2-8a-5a2+15a-10=a2+7ቤተ መጻሕፍቲ ባይዱ-10. ∵a2+7a-7=0, ∴a2+7a=7, ∴原式=7-10=-3.
【题型三】单项式乘多项式的应用 例5:如图,请计算阴影部分的面积.
注:(1)不为0的单项式与多项式相乘,结果是多项式, 其项数与因式中多项式的项数相同,可以用来检验在运 算中是否漏乘某些项; (2)计算时要注意符号问题,多项式中的每一项都包括它 前面的符号; (3)对于混合运算,要注意运算顺序,有同类项必须合并 同类项,从而得到最简结果.
典例精讲
【题型一】单项式与多项式乘法的计算 例1:计算:(1)3x(2x+y)-2x(x-y);(2)2(2x2-xy)+x(x-y); (3) -3a2+32a-53 (-6a);(4)ab(2ab2-a2b)-(2ab)2+a3b2. 解:(1)原式=6x2+3xy-2x2+2xy=4x2+5xy.
《单项式乘单项式和单项式乘多项式》课件

6.用科学记数法表示(2×102)(16×106)的结果应为_3_.2_×__1_0_9_. 7.若□×6xy=3x3y2,则□内应填的单项式是__12_x_2_y__.
8.一个三角形的底为 4a,高为12a2,它的面积为__a_3_.
9.计算: (1)(-5x2y)(-4x3y2); 解:原式=20x5y3
4.下列计算中,不正确的是( D ) A.(-3a2b)(-2ab2)=6a3b3 B.(2×10n)(25×10n)=45×102n C.(-2×102)(-8×103)=1.6×106 D.(-3x)·2xy+x2y=7x2y 5.计算:(2x2y)(-xy3)=_-__2_x_3_y_4__; (-12x2y)3·(-3xy2)2=__-__98_x_8y_7___.
方法技能: 1.单项式乘以单项式的结果仍然是单项式. 2.积的系数等于各项系数的积,先确定积的符号,再计算积的绝对 值. 3.相同字母相乘,按同底数幂的乘法计算. 4.只在一个单项式里含有的字母,连同它的指数写在积里,注意不 要遗漏. 5.对于三个及以上的单项式相乘,此法则同样适用. 易错提示: 对单项式的乘法法则理解不透而出错.
知识点:单项式与多项式相乘 1.计算2x(3x2+1)的结果是( C ) A.5x3+2x B.6x3+1 C.6x3+2x D.6x2+2x 2.计算x(2x-1)-x2(2-x)的结果是( B ) A.-x3-x B.x3-x C.-x2-1 D.x3-1 3.下列计算正确的是( D ) A.(-4x)(2x2+3x-1)=-8x3-12x2-4x B.(6xy2-4x2y)·3xy=6xy2-12x3y2 C.(-x)(2x+x2-1)=-x3-2x2+1 D.(-3x2y)(-2xy+3yz+1)=6x3y2-9x2y2z-3x2y
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
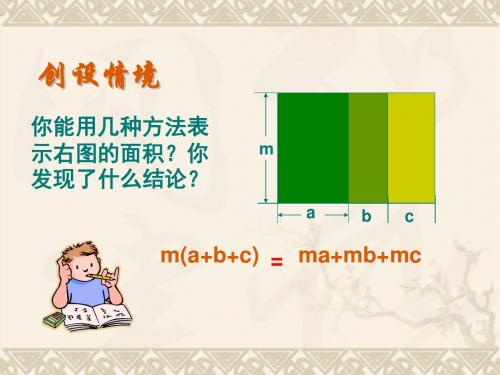
p(a + b + c)=pa + pb + pc
类似的
其实这就是单项式乘多项式你能总结出计算规 律吗?
=
=
归纳
p(a + b + c)= pa + pb + pc 单项式乘以多项式的法则
先用单项式乘以多项式的每一项,再把所得的积相加
. 思路: 单×
易错题 下面的计算对不对?如果不对,怎样改正?
补充题 答案:-98.
补充题
结果不含某项
提示:不含某项,化简后那项的系数就是 0
整体代入求值
整体代入求值
整体代入求值 求值:
答案:(1)-24.
(2)-78.
整体代入求值
已知m,n互为相反数,先化简再求值 :
提示:相反数的和为 0 答案:0
总结
这节课我们学会了什么?
p(a + b + c)= pa+ pb+ pc 单项式乘以多项式的法则
方法1:直接用扩大后的长乘宽 p(a+b+c) 方法2:先算出每个小长方形的面积再求和 pa+pb+pc
探究
这两个式子表示的都是扩大后绿地的面积,它们有什么关系呢
?
p(a+b+c)= pa+pb+pc
你能用乘法分配律解释这个等式吗?
探究 乘法分配律
先用单项式乘以多项式的每一项, 再把所得的积相加.
注意:各项符号的确定 ! 防止漏项哦!
注意事项
1.单项式乘多项式的结果是多项式,积的项数与原多项式的项 数相同. 2.单项式分别与多项式的每一项相乘时,要注意积的符号的 确定:同号相乘得正,异号相乘得负.
3.不要出现漏乘现象,运算要有顺序.
易错题
下列计算对吗?若不对,应该怎样改 ?
练习
练习 计算下列各式:
不变
相加
不变 不变
相乘
分配给 每个因式
知识回顾
单项式乘单项式的法则 相同字母的指数的和作 为积里这个字母的指数
= -12
b
各因式系数的积 作为积的系数
只在一个单项式里含有的字母连 同它的指数作为积的一个因式
知识回顾 计算:
思考 为了扩大绿地的面积,要把街心花园的一块长 p 米,宽 b 米的 长方形绿地,向两边分别加宽 a 米和 c 米,你能用几种方法表 示扩大后的绿地的面积?
先用单项式乘以多项式的每一项,再把所得的积相加.
转化
思路:单×多
单×单
分配律
单项式乘多项式
教学目标
理解单项式与多项式相乘的法则,能运用单项式与多项 式相乘的法则进行计算.
理解算理,发展学生的运算能力和“几何直观” 观念, 体会转化、数形结合和程序化思想.
教学重点 单项式与多项式相乘的法则的运用. 教学难点 单项式与多项式相乘去括号法则的应用.
知识回顾
幂的运算法则
乘法 乘方 乘方
练习 计算:
例题 计算:
混合运算怎么办呢?
先算乘法 再合并
总结:对于这类混合运算,一定要先算乘法,再合并.
练习 计算:
练习 计算:
练习 化简:
练习 化简:
练习 1.计算:
练习
补充题
化简求值: 当x=5时,计算下式的值 :
提示:先化简,再求值 .
补充题 化简求值
提示:先化简,再求值 .
