大学物理光的衍射一
合集下载
《大学物理》光的衍射(一)

放映结束 感谢各位的批评指导!
谢 谢!
让我们共同进步
③影响衍射图样的a和
由暗纹条件: asin k 若λ 一定时,
sin 1 : 缝越窄,衍射越显著,但a不能小于(a小于时 也有衍射,a但此时半波带理论不成立);缝越宽,衍射越不明显, 条纹向中心靠近,逐渐变成直线传播。
由暗纹条件: asin k 若a一定时, sin λ 越大,衍射越显著,
20 2sin0 2 / a 1.092102 rad
易得中央明条纹的线宽度为
x=2 f tan0 2 f sin0 5.46103 m
(2)浸入水中,折射率改变,设折射率为n,则波长改变为
=/n 2
an
n , ,即中央明条纹的角宽度减小
大学物理 习题练习 光的衍射
光的衍射
• 什么是光的衍射?
波在传播中遇到障碍物,使波面受到限制时,能够绕过障碍物 继续前进的现象。
光通过宽缝时,是沿直线传播的,若将缝的宽度减小到约104m及更 小时,缝后几何阴影区的光屏上将出现衍射条纹。
菲涅耳衍射
衍射屏、光源和接收屏之间(或 二者之一)均为有限远
夫琅禾费衍射
衍射屏与光源和接收屏三者之间 均为无限远。
单缝夫琅禾费衍射
衍射屏 透镜L
透镜L
B
S
*
a
Aδ f
f
观察屏
·p
0
衍射角:
①衍射图样中明、暗纹公式:
亮纹条件: a sin (2k 1)
2
(近似值)
暗纹条件: a sin 2k k
2
②单缝衍射条纹特点—条纹宽度
对K级暗纹有
大学物理101光的衍射(1)
解 :(1) x0
2 f
a
4.0m m
(2) 单缝衍射明纹的角位置由a
sin
(2k
1)
2
确定,得:sin 2
5 ,
2a
x2
f
tan 2
f
sin 2
5
2a
f
5.0mm
(3) 由ain (2k 1) 知: 相应于第二级、三级衍射明纹, k分别为2、3,
2
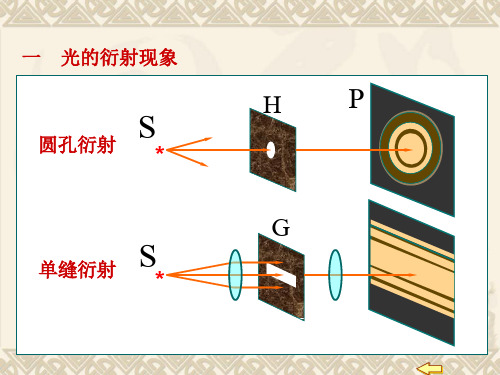
一 光的衍射现象
圆孔衍射
S
*
单缝衍射
S
*
HP
G
衍射 光在传播过程中绕过障碍物的边缘而偏离直线传 播的现象
说明
衍射现象是否明显取决于障碍物线度与波长的对 比,波长越大,障碍物越小,衍射越明显。
二 惠更斯 — 菲涅尔原理
n
S
rP *
S
t S : 时刻波阵面
S :波阵面上面元
(子波波源)
子波在 P点引起的振动振幅 s 并与 有关 .
当k=1时,λ=5000A0
当k=2时,λ=3000 A0
(3)中央明纹宽度为
x 2 f
a
5000 1010 2 1 0.5 103
在可见光范围内,入射光波长为λ=5000A0。 2 103 m
解:(1)对P点,由
(2)P点为第一级
tg x 1.5103 1.5103
f
1
明纹,k=1
sin 3 1.5103rad
2a
当θ很小, tgθ=sinθ=θ
半波带数为: 2k+1=3
由单缝衍射公式可知 2a sin 2atg 2k 1 2k
大学物理第15章a光的衍射课件

(a+b)sin0
(a+b)(sin sin0 )=k k=0,±1, ±2, ±3 ···
2、暗纹条件 暗条纹是由各缝射出的衍射光因干涉相消形成的。
( a b ) sin ( k n )
N
k 0,1,2,
k — 主极大级数 N — 光栅缝总数
n为正整数 n 1,2,N 1
在两个相邻主极大之间, 分布着N-1条暗条纹和N-2条次级明条纹。
缺级条件:
光栅衍射加强条件:
(a b)sin k
单缝衍射极小条件: a sin k '
两式相比得
缺级条件: a b k (式中k和k必须为整数) a k'
缺级级数为: k a b k a
(k 1, 2,3 )
当 a b k 4时 a k'
谱线中的第 –8、 – 4、4、8级条纹缺级。
b a
不透光缝宽度 b
d
光栅常数:
d a b
f
单缝的夫琅和费衍射图样,不随缝的上下移动而变化。 衍射角相同的光线,会聚在接收屏的相同位置上。
如果让平行光照射整个光栅,那么每个单缝在 屏上所产生的振幅情况是完全一样的。在单缝的情 况下振幅为零的地方迭加起来的合振幅仍为零。但 振幅不为零的地方,其位置仍没有变,但振幅变大 了,光强变大了。
个单缝上。如果所用的单缝的宽度a=1mm,缝后紧挨
着的薄透镜焦距f=100cm,求:(a)第一级暗纹到衍
射图样中心的距离;(b)中央明条纹的角宽度;
(c)中央亮纹的线宽度。
解: (a)
a sin0
atg0
a
x f
一级暗纹条件
x f 10010 5000107 mm 0.5mm
(a+b)(sin sin0 )=k k=0,±1, ±2, ±3 ···
2、暗纹条件 暗条纹是由各缝射出的衍射光因干涉相消形成的。
( a b ) sin ( k n )
N
k 0,1,2,
k — 主极大级数 N — 光栅缝总数
n为正整数 n 1,2,N 1
在两个相邻主极大之间, 分布着N-1条暗条纹和N-2条次级明条纹。
缺级条件:
光栅衍射加强条件:
(a b)sin k
单缝衍射极小条件: a sin k '
两式相比得
缺级条件: a b k (式中k和k必须为整数) a k'
缺级级数为: k a b k a
(k 1, 2,3 )
当 a b k 4时 a k'
谱线中的第 –8、 – 4、4、8级条纹缺级。
b a
不透光缝宽度 b
d
光栅常数:
d a b
f
单缝的夫琅和费衍射图样,不随缝的上下移动而变化。 衍射角相同的光线,会聚在接收屏的相同位置上。
如果让平行光照射整个光栅,那么每个单缝在 屏上所产生的振幅情况是完全一样的。在单缝的情 况下振幅为零的地方迭加起来的合振幅仍为零。但 振幅不为零的地方,其位置仍没有变,但振幅变大 了,光强变大了。
个单缝上。如果所用的单缝的宽度a=1mm,缝后紧挨
着的薄透镜焦距f=100cm,求:(a)第一级暗纹到衍
射图样中心的距离;(b)中央明条纹的角宽度;
(c)中央亮纹的线宽度。
解: (a)
a sin0
atg0
a
x f
一级暗纹条件
x f 10010 5000107 mm 0.5mm
浙江大学《大学物理》课件光的衍射1

这是具体的白光单缝夫琅禾费衍射
光的衍射
单缝夫琅禾费衍射图样特征的讨论: ③衍射效应还与缝宽 a、入射光的波长 密切相关。 只有 a~ 才有明显的衍射效应
分析书上P49页例17.1,注意各种物理量单位的统一
【例题】用单色平行光垂直照射到宽度为 a=0.5mm的单缝上, 在缝后放置一个焦距为 f=100cm的透镜,则在焦平面的屏幕 上形成衍射条纹,若在离屏上中央明纹中心距离为1.5mm处 的P点为一亮纹,试求: ①入射光的波长;②P点条纹的级数和该条纹对应的衍射角; ③狭缝处波面可分为几个半波带;④中央明纹的宽度。
②原中央明纹变为3 个小明纹,相当于 插入二条暗纹
光的衍射
2.振幅矢量叠加法:(只须了解其基本原理)
sinu u I A2 sin 2u 2 2 I 0 A0 u A A0
光的衍射
四、光栅衍射:
任何能周期性地分割波阵面的衍射屏------衍射光栅,相邻 两缝(或刻痕)中心间距称为光栅常数-----d
光的衍射
光栅衍射的整个过程是平行光先经各个单缝衍射后,再 进行多光束干涉! 对光栅的每一条缝而言,单缝衍射的结论完全适用,故 光栅的衍射条纹应看作单缝衍射和多光束干涉的综合结果。
光的衍射
多缝衍射的明暗情况:
相邻的两个主 极大之间均有 N 1个极小 N 2个次极大
光的衍射
光的衍射
光栅衍射条纹的明暗条件为: dsin k k 0,1, 2,...主极大 k dsin k 1, 2,..., N 1, N 1,...极小 N
光的衍射
三、单缝夫琅禾费衍射:
原来垂直入射的平行光经过衍射能出射各种角度的平行光, 到达观察屏的光的强度是各个平行衍射光的相干叠加。
《大学物理》光的衍射(一)ppt课件

通过测量星光经过望远镜后的衍射斑大小,可以 推算出望远镜的分辨率,进而评估其观测能力。
2 3
显微镜的分辨率
利用光的衍射现象,显微镜能够分辨出非常微小 的物体或结构,其分辨率受到光源波长和物镜数 值孔径的限制。
摄影镜头的分辨率
摄影镜头通过控制光的衍射,可以在底片上形成 清晰的像,镜头的分辨率决定了照片的清晰度。
2024/1/24
激光全息技术在光学信息存储、三维显示和防伪等领域的应用
利用全息技术实现高密度光学信息存储、真彩色三维显示以及高级防伪措施等。
22
06
总结与展望
Chapter
2024/1/24
23
本节内容回顾与总结
光的衍射现象及其分类
介绍了光的衍射现象,包括菲涅尔衍射和夫 琅禾费衍射等,以及它们的特点和应用。
8
衍射图样分析
01
02
03
中央明纹
在屏幕中心形成的最亮区 域,宽度约为其他明纹的 两倍。
2024/1/24
明暗相间条纹
在中央明纹两侧形成一系 列明暗相间的条纹,离中 心越远,明纹亮度越低, 暗纹越暗。
条纹间距
相邻明纹或暗纹之间的距 离,与波长、缝宽和观察 距离有关。
9
缝宽对衍射图样的影响
缝宽增加
明暗条纹的间距减小,且离中央 明纹越远的明纹亮度越低。
2024/1/24
双缝间距减小
明暗条纹的间距增大,且离中央明 纹较远的明纹亮度也有所提高。
极限情况
当双缝间距趋近于零时,双缝衍射 图样趋近于单缝衍射图样。
14
04
光的衍射在生活中的应用
Chapter
2024//24
15
光学仪器的分辨率
2 3
显微镜的分辨率
利用光的衍射现象,显微镜能够分辨出非常微小 的物体或结构,其分辨率受到光源波长和物镜数 值孔径的限制。
摄影镜头的分辨率
摄影镜头通过控制光的衍射,可以在底片上形成 清晰的像,镜头的分辨率决定了照片的清晰度。
2024/1/24
激光全息技术在光学信息存储、三维显示和防伪等领域的应用
利用全息技术实现高密度光学信息存储、真彩色三维显示以及高级防伪措施等。
22
06
总结与展望
Chapter
2024/1/24
23
本节内容回顾与总结
光的衍射现象及其分类
介绍了光的衍射现象,包括菲涅尔衍射和夫 琅禾费衍射等,以及它们的特点和应用。
8
衍射图样分析
01
02
03
中央明纹
在屏幕中心形成的最亮区 域,宽度约为其他明纹的 两倍。
2024/1/24
明暗相间条纹
在中央明纹两侧形成一系 列明暗相间的条纹,离中 心越远,明纹亮度越低, 暗纹越暗。
条纹间距
相邻明纹或暗纹之间的距 离,与波长、缝宽和观察 距离有关。
9
缝宽对衍射图样的影响
缝宽增加
明暗条纹的间距减小,且离中央 明纹越远的明纹亮度越低。
2024/1/24
双缝间距减小
明暗条纹的间距增大,且离中央明 纹较远的明纹亮度也有所提高。
极限情况
当双缝间距趋近于零时,双缝衍射 图样趋近于单缝衍射图样。
14
04
光的衍射在生活中的应用
Chapter
2024//24
15
光学仪器的分辨率
光的衍射第一讲概述

x ·
S
*
f
§4-5-1
0
f
光单缝夫琅禾费衍射
大学 物理
条件:1)狭缝非常窄(10 λ ~ 1000λ ) 2)满足夫琅禾费衍射条件 x
z
L1
a
y
l
L2
狭缝
点光源照射下 的单缝衍射条纹
§4-5-1
光单缝夫琅禾费衍射
大学 物理
现象: (1)衍射条纹呈明暗相间、对称的稳态分布。 (2)中央明纹最宽、最亮,其余条纹依次减弱;
§4-5-1
光单缝夫琅禾费衍射
大学 物理
1、单缝夫琅禾费衍射的明、暗纹条件
0 中央明纹中心
a sin
2k 1
2
(k 1,2) 近似明纹中心
(k 1,2) 暗纹中心
k
2、几个重要结论
(1) Δθ0 2θ1 2 λ a λ↑,a↓,条纹宽度越宽。 (2) λ a 0 Δθ0 0 波动光学退化到几何光学。
1、菲涅耳半波带法
2)其他各级明纹 思考(1):
A
若 a sinθ λ
相消 相消 明or 暗? P ——明条纹 且属于中央明纹区。 思考(2):
半波带 θ a
2
O
B
C1
C
f
§4-5-1
a sinθ λ,且 θ P点的位置与亮度? P O,亮度增加
光单缝夫琅禾费衍射
大学 物理
结 论
1.50λ, 2.50λ, 3.50λ,…
光单缝夫琅禾费衍射
大学 物理
sinα 光强公式: I I 0 α
2
其中
π a sinθ α λ
S
*
f
§4-5-1
0
f
光单缝夫琅禾费衍射
大学 物理
条件:1)狭缝非常窄(10 λ ~ 1000λ ) 2)满足夫琅禾费衍射条件 x
z
L1
a
y
l
L2
狭缝
点光源照射下 的单缝衍射条纹
§4-5-1
光单缝夫琅禾费衍射
大学 物理
现象: (1)衍射条纹呈明暗相间、对称的稳态分布。 (2)中央明纹最宽、最亮,其余条纹依次减弱;
§4-5-1
光单缝夫琅禾费衍射
大学 物理
1、单缝夫琅禾费衍射的明、暗纹条件
0 中央明纹中心
a sin
2k 1
2
(k 1,2) 近似明纹中心
(k 1,2) 暗纹中心
k
2、几个重要结论
(1) Δθ0 2θ1 2 λ a λ↑,a↓,条纹宽度越宽。 (2) λ a 0 Δθ0 0 波动光学退化到几何光学。
1、菲涅耳半波带法
2)其他各级明纹 思考(1):
A
若 a sinθ λ
相消 相消 明or 暗? P ——明条纹 且属于中央明纹区。 思考(2):
半波带 θ a
2
O
B
C1
C
f
§4-5-1
a sinθ λ,且 θ P点的位置与亮度? P O,亮度增加
光单缝夫琅禾费衍射
大学 物理
结 论
1.50λ, 2.50λ, 3.50λ,…
光单缝夫琅禾费衍射
大学 物理
sinα 光强公式: I I 0 α
2
其中
π a sinθ α λ
(大学物理ppt)光的衍射

ax 1 k 3 f 2
0
Δx
(b)当k=3时,光程差 a sin ( 2k 1 ) 7 2 2 狭缝处波阵面可分成7个半波带。
I / I0
相对光强曲线
1
明纹宽度 中央明条纹的角宽 为中央两侧第一暗条 纹之间的区域:
0.017 0.047 0 0.047
0.017
sin
-2(/a) -(/a)
/a
2(/a)
由a sin k
令k=1 半角宽
a
a
衍射屏 透镜
λ
观测屏 x2 x1 Δx Δx
Huygens-Fresnel’s principle
(1) 惠更斯原理:在波的传播过程中,波阵面(波面)(相位 相同的点构成的面)上的每一点都可看作是发射子波(次波)的 波源,在其后的任一时刻,这些子波的包迹就成为新的波阵面。
t 时刻波面
· · · · ·
t+t时刻波面
波传播方向
t + t
· ·· · · · · t · · · ·· · ·
一、衍射现象、惠更斯-菲涅耳原理 圆孔衍射
菲涅尔圆孔衍射
一、衍射现象、惠更斯-菲涅耳原理 各种孔径的夫琅禾费衍射图样 正三 边形 孔 正四 边形 孔
正六 边形 孔
正八 边形 孔
一、衍射现象、惠更斯-菲涅耳原理 圆屏衍射 R S 直边衍射 rk
P
菲涅尔圆屏衍射
直边衍射
2、惠更斯—菲涅耳原理
第 4 章 光的衍射
一、衍射现象、惠更斯-菲涅耳原理
二、单缝的夫琅禾费衍射
三、光学仪器的分辨本领
四、光栅衍射
五、光栅光谱
六、X 射线衍射
0
Δx
(b)当k=3时,光程差 a sin ( 2k 1 ) 7 2 2 狭缝处波阵面可分成7个半波带。
I / I0
相对光强曲线
1
明纹宽度 中央明条纹的角宽 为中央两侧第一暗条 纹之间的区域:
0.017 0.047 0 0.047
0.017
sin
-2(/a) -(/a)
/a
2(/a)
由a sin k
令k=1 半角宽
a
a
衍射屏 透镜
λ
观测屏 x2 x1 Δx Δx
Huygens-Fresnel’s principle
(1) 惠更斯原理:在波的传播过程中,波阵面(波面)(相位 相同的点构成的面)上的每一点都可看作是发射子波(次波)的 波源,在其后的任一时刻,这些子波的包迹就成为新的波阵面。
t 时刻波面
· · · · ·
t+t时刻波面
波传播方向
t + t
· ·· · · · · t · · · ·· · ·
一、衍射现象、惠更斯-菲涅耳原理 圆孔衍射
菲涅尔圆孔衍射
一、衍射现象、惠更斯-菲涅耳原理 各种孔径的夫琅禾费衍射图样 正三 边形 孔 正四 边形 孔
正六 边形 孔
正八 边形 孔
一、衍射现象、惠更斯-菲涅耳原理 圆屏衍射 R S 直边衍射 rk
P
菲涅尔圆屏衍射
直边衍射
2、惠更斯—菲涅耳原理
第 4 章 光的衍射
一、衍射现象、惠更斯-菲涅耳原理
二、单缝的夫琅禾费衍射
三、光学仪器的分辨本领
四、光栅衍射
五、光栅光谱
六、X 射线衍射
大学物理光的衍射

k1bsin
2
b213000A &
对于 , k1是明纹
则 bsin(2k1)
2
b s in 3 0 0 3, 4 3 3 ( 0A & )是 紫 光
2
.
例1:如图,波长为
的单色平行光垂直照 A
射单缝,若由单缝边
缘发出的光波到达屏
上P、Q、R三点的光
o
程差分别为2、2.5
P
3.5 ,比较P、Q、 R B
.
离得远 可分辨
瑞利判据 刚能分辨
离得太近 不能分辨 小孔(直径D)对两个靠近的遥远的点光源的分辨
.
S1
D
*
0
*
I
S2
最小分辨角
分辨本领
1
1.22 D
R 1 D
1.22
.
D
R
望远镜: 不可选择,可D R
▲ 世界上最大的光学望远镜: D=8m
建在了夏威夷山顶。 ▲世界上最大的射电望远镜:
f
Q
三点的亮度。
R
解题思路:2=22 第二级暗纹
2.5(221)
2
第二级明纹
2
3.5(231) 第三级明纹
2.
例:在单缝夫朗和费衍射实验中,屏上第3级暗纹 对应的单缝处波面可划分为——6 —个半波带?若 将缝宽缩小一半,原来第3级暗纹处将是明——纹。
例:波长为600nm的单色平行光,垂直入射 到缝宽为b=0.60mm的单缝上,缝后有一焦 距f=60cm的透镜。在透镜焦平面上观察衍射 图样. 则中央明纹宽度为—1— .2m—m。两个第3级暗纹之 间的距离为—3.6—m—m 。
sb
显 示
几何
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(2k 1) / 2 k 2 2.5 5
2
4.在单缝的夫琅禾费衍射实验中,屏上第三级暗纹对应的
单缝处波面可划分为 6 个半波带,若将缝宽缩小一半,
原来第三级暗纹处将是 第一级明 纹。
单缝衍射明暗条纹满足:
k 暗条纹 k 1, 2,3...
a
sin
(2k
1)
2
明条纹 k 0,1, 2,3...
an
n , ,即中央明条纹的角宽度减小
(A)P点最亮、Q点次之、R点最暗; (B)Q、R两点亮度相同,P点最暗; (C)P、Q、R三点亮度均相同; (D)Q点最亮、R点次之、P点最暗。
分析:垂直入射,单缝衍射明暗条纹条件
k 暗条纹 k 1, 2,3...
a
sin
(2k
1)
2
明条纹 k 0,1, 2,3...
则光程差满足
k 暗条纹 (2k 1) / 2 明条纹 P点:P 2 暗条纹,且k 2 Q点:Q 2.5 明条纹,且k=2 R点:R 3.5 明条纹,且k=3
f (k 1) f k f
a
a
a
x f
a
可见中央明纹约为其他各级明纹宽度的两倍。
❖ ③影响衍射图样的a和
由暗纹条件: asin k 若λ一定时,
sin 1 : 缝越窄,衍射越显著,但a不能小于(a小于时 也有衍射,a但此时半波带理论不成立);缝越宽,衍射越不明显, 条纹向中心靠近,逐渐变成直线传播。
影响衍射图样的有:a和 此题中,两者均没有改变,故衍射条纹 没有变化。
答案选:D
3.用波长为 的单色平行光垂直照射单缝,若屏上的P点
为第2级明条纹位置,则有单缝两边缘发出的光到P点处 的光程差为 2.5 ,从P点看来,对该光波而言,狭缝处的 波阵面可分成的半波带数为 5 个 .
明条纹光程差满足:
衍射屏与光源和接收屏三者之间 均为无限远。
❖单缝夫琅禾费衍射
衍射屏 透镜L
透镜L
B
S
*
a
Aδ f
f
观察屏
·p
0
Байду номын сангаас衍射角:
①衍射图样中明、暗纹公式:
亮纹条件: a sin (2k 1)
2
(近似值)
暗纹条件: a sin 2k k
2
❖ ②单缝衍射条纹特点—条纹宽度
当a 时,1 级暗纹对应的衍射
由暗纹条件: asin k 若a一定时, sin λ越大,衍射越显著,
当白光入射时,中央明纹仍为白色,其他各级由紫至红,一 般第2、3级即开始重叠。
练习35 光的衍射(1)
1.如图所示波长为 的单色平行光垂直照射单缝,若由单缝
边缘发出的光波到达光屏上 P、Q、R三点的光程差分别
为 2, 2.5, 3.5,比较 P、Q、R 三点的亮度,则有:
大学物理 习题练习 光的衍射
光的衍射
• 什么是光的衍射?
波在传播中遇到障碍物,使波面受到限制时,能够绕过障碍物 继续前进的现象。
光通过宽缝时,是沿直线传播的,若将缝的宽度减小到约104m及更 小时,缝后几何阴影区的光屏上将出现衍射条纹。
菲涅耳衍射
衍射屏、光源和接收屏之间(或 二者之一)均为有限远
夫琅禾费衍射
又各级明条纹的光强随级数增大而减小 Q点最亮,R点次之,P点最暗
答案:(D)
❖ 2. 在单缝夫琅和费衍射实验中,将单缝K沿垂直于光的入 射方向稍微平移(但仍未超出凸透镜),则
(A)衍射条纹移动,条纹宽度不变; (B)衍射条纹移动,条纹宽度变动; (C)衍射条纹中心不动,条纹变宽; (D)衍射条纹不动,条纹宽度不变; (E)衍射条纹中心不动,条纹变窄。
第一级暗条纹对应的衍射角0为:sin0 = / a 因sin0很小,可知中央明条纹的角宽度为
20 2sin0 2 / a 1.092102 rad
易得中央明条纹的线宽度为
x=2 f tan0 2 f sin0 5.46103 m
(2)浸入水中,折射率改变,设折射率为n,则波长改变为
=/n 2
f ax 0.25m
6
6.有一单缝宽 a=0.10 mm ,在缝0 后放一焦距为50cm的会
聚透镜,用平行绿光 ( 5460 ) 垂直照射单缝。求位于
透镜焦平面处屏上的中央明条纹的宽度,如果把此装置放 入水中,并设透镜焦距不变,则中央明条纹的角宽度如何 变化?
解:(1)由单缝衍射暗纹条件:asin= k k 1, 2,3...
(1)第三级即k 3,则a sin 3 6
2
(2)a2 0.5a a2 sin 1.5,明条纹,且k 1
5.用波长为5000A°的单色光垂直照射在缝宽为0.25mm 的单缝上,在位于透镜焦平面的屏上,测得中央明条纹 的两侧第3级暗纹之间间距为3.0mm,试求透镜的焦距。
解:由题意,暗条纹满足:asin=k (1) 条纹位置与衍射角满足:xk =f tan (2) 比较小时,有sin tan,此时由(1)(2)式 xk =kf / a 由题意,x=x3 x3 6 f / a
观测屏
角
衍射屏透镜
x2
由
1 sin1
a sin k
得: 1 a
λ
x1
1
0
0
Δx Δx0
I
A. 中央明纹
f
角宽度为
线宽度为
0
21
2
a
x0
2
f
tg1
2
f 1
2
f
a
a
B.其他各级明纹的宽度为相邻暗纹间距
对K级暗纹有
sin k
a
角宽度
s in k
s in k 1
a
a
x xk1 xk f sink1 f sink
2
4.在单缝的夫琅禾费衍射实验中,屏上第三级暗纹对应的
单缝处波面可划分为 6 个半波带,若将缝宽缩小一半,
原来第三级暗纹处将是 第一级明 纹。
单缝衍射明暗条纹满足:
k 暗条纹 k 1, 2,3...
a
sin
(2k
1)
2
明条纹 k 0,1, 2,3...
an
n , ,即中央明条纹的角宽度减小
(A)P点最亮、Q点次之、R点最暗; (B)Q、R两点亮度相同,P点最暗; (C)P、Q、R三点亮度均相同; (D)Q点最亮、R点次之、P点最暗。
分析:垂直入射,单缝衍射明暗条纹条件
k 暗条纹 k 1, 2,3...
a
sin
(2k
1)
2
明条纹 k 0,1, 2,3...
则光程差满足
k 暗条纹 (2k 1) / 2 明条纹 P点:P 2 暗条纹,且k 2 Q点:Q 2.5 明条纹,且k=2 R点:R 3.5 明条纹,且k=3
f (k 1) f k f
a
a
a
x f
a
可见中央明纹约为其他各级明纹宽度的两倍。
❖ ③影响衍射图样的a和
由暗纹条件: asin k 若λ一定时,
sin 1 : 缝越窄,衍射越显著,但a不能小于(a小于时 也有衍射,a但此时半波带理论不成立);缝越宽,衍射越不明显, 条纹向中心靠近,逐渐变成直线传播。
影响衍射图样的有:a和 此题中,两者均没有改变,故衍射条纹 没有变化。
答案选:D
3.用波长为 的单色平行光垂直照射单缝,若屏上的P点
为第2级明条纹位置,则有单缝两边缘发出的光到P点处 的光程差为 2.5 ,从P点看来,对该光波而言,狭缝处的 波阵面可分成的半波带数为 5 个 .
明条纹光程差满足:
衍射屏与光源和接收屏三者之间 均为无限远。
❖单缝夫琅禾费衍射
衍射屏 透镜L
透镜L
B
S
*
a
Aδ f
f
观察屏
·p
0
Байду номын сангаас衍射角:
①衍射图样中明、暗纹公式:
亮纹条件: a sin (2k 1)
2
(近似值)
暗纹条件: a sin 2k k
2
❖ ②单缝衍射条纹特点—条纹宽度
当a 时,1 级暗纹对应的衍射
由暗纹条件: asin k 若a一定时, sin λ越大,衍射越显著,
当白光入射时,中央明纹仍为白色,其他各级由紫至红,一 般第2、3级即开始重叠。
练习35 光的衍射(1)
1.如图所示波长为 的单色平行光垂直照射单缝,若由单缝
边缘发出的光波到达光屏上 P、Q、R三点的光程差分别
为 2, 2.5, 3.5,比较 P、Q、R 三点的亮度,则有:
大学物理 习题练习 光的衍射
光的衍射
• 什么是光的衍射?
波在传播中遇到障碍物,使波面受到限制时,能够绕过障碍物 继续前进的现象。
光通过宽缝时,是沿直线传播的,若将缝的宽度减小到约104m及更 小时,缝后几何阴影区的光屏上将出现衍射条纹。
菲涅耳衍射
衍射屏、光源和接收屏之间(或 二者之一)均为有限远
夫琅禾费衍射
又各级明条纹的光强随级数增大而减小 Q点最亮,R点次之,P点最暗
答案:(D)
❖ 2. 在单缝夫琅和费衍射实验中,将单缝K沿垂直于光的入 射方向稍微平移(但仍未超出凸透镜),则
(A)衍射条纹移动,条纹宽度不变; (B)衍射条纹移动,条纹宽度变动; (C)衍射条纹中心不动,条纹变宽; (D)衍射条纹不动,条纹宽度不变; (E)衍射条纹中心不动,条纹变窄。
第一级暗条纹对应的衍射角0为:sin0 = / a 因sin0很小,可知中央明条纹的角宽度为
20 2sin0 2 / a 1.092102 rad
易得中央明条纹的线宽度为
x=2 f tan0 2 f sin0 5.46103 m
(2)浸入水中,折射率改变,设折射率为n,则波长改变为
=/n 2
f ax 0.25m
6
6.有一单缝宽 a=0.10 mm ,在缝0 后放一焦距为50cm的会
聚透镜,用平行绿光 ( 5460 ) 垂直照射单缝。求位于
透镜焦平面处屏上的中央明条纹的宽度,如果把此装置放 入水中,并设透镜焦距不变,则中央明条纹的角宽度如何 变化?
解:(1)由单缝衍射暗纹条件:asin= k k 1, 2,3...
(1)第三级即k 3,则a sin 3 6
2
(2)a2 0.5a a2 sin 1.5,明条纹,且k 1
5.用波长为5000A°的单色光垂直照射在缝宽为0.25mm 的单缝上,在位于透镜焦平面的屏上,测得中央明条纹 的两侧第3级暗纹之间间距为3.0mm,试求透镜的焦距。
解:由题意,暗条纹满足:asin=k (1) 条纹位置与衍射角满足:xk =f tan (2) 比较小时,有sin tan,此时由(1)(2)式 xk =kf / a 由题意,x=x3 x3 6 f / a
观测屏
角
衍射屏透镜
x2
由
1 sin1
a sin k
得: 1 a
λ
x1
1
0
0
Δx Δx0
I
A. 中央明纹
f
角宽度为
线宽度为
0
21
2
a
x0
2
f
tg1
2
f 1
2
f
a
a
B.其他各级明纹的宽度为相邻暗纹间距
对K级暗纹有
sin k
a
角宽度
s in k
s in k 1
a
a
x xk1 xk f sink1 f sink
