第二章 分子动力学理论的平衡态理论
平衡态分子动力学

平衡态分子动力学平衡态分子动力学(Equilibrium Molecular Dynamics,EMD)是一种计算分子系统在平衡态下的热力学性质的方法。
它是分子动力学(Molecular Dynamics,MD)的一种特殊形式,它通过模拟分子之间的相互作用来计算温度、压力、能量等热力学性质。
下面将对EMD的原理、应用和发展进行详细介绍。
一、原理EMD是基于牛顿力学的,它通过模拟分子之间的相互作用来计算热力学性质。
在EMD中,分子之间的相互作用力可以用势函数来描述,通常采用的是Lennard-Jones势函数和Coulomb势函数。
分子的运动状态可以通过牛顿运动方程来描述,即F=ma,其中F是分子所受的力,m是分子的质量,a是分子的加速度。
通过求解牛顿运动方程,可以得到分子的位置和速度随时间的变化规律。
EMD的核心是模拟分子之间的相互作用,这需要用到分子间的相互作用势函数。
Lennard-Jones势函数是一种常用的分子间相互作用势函数,它可以描述分子之间的范德华力和排斥力。
Coulomb势函数则是描述分子之间的电荷相互作用。
在EMD中,这两种势函数通常被组合起来使用,以模拟分子间的相互作用。
二、应用EMD在材料科学、化学、生物学等领域都有广泛的应用。
其中,最常见的应用是研究材料的热力学性质,如热容、热导率、热膨胀系数等。
EMD也可以用来研究分子的结构和动力学性质,如溶剂分子的扩散、蛋白质的折叠等。
此外,EMD 还可以用来研究分子间的相互作用,如氢键、离子对等。
三、发展EMD是分子动力学的一种特殊形式,它的发展与分子动力学的发展密切相关。
随着计算机技术的不断进步,EMD的模拟规模和时间尺度得到了不断扩大,从而使得EMD在材料科学、化学、生物学等领域的应用得到了广泛的推广。
同时,EMD的理论基础也得到了不断加强,如基于密度泛函理论的EMD方法、基于量子力学的EMD方法等。
总之,EMD是一种计算分子系统在平衡态下的热力学性质的方法,它通过模拟分子之间的相互作用来计算温度、压力、能量等热力学性质。
第二章 分子动理学理论的平衡态理论 5

z H z H
) )
⑴ 单位: 长度单位(高度单位)
H RT Mm g
(J
⑵ 取高度z=H,则有:
P ( H ) P (0)e
1
m ol K N m ol
)K
J N
N m N
m
n( H ) n(0)e
1
高度为大气标高H处的压强及分子数密度是海平面处的 1/e ⑶ 大气标高H的物理意义: 大气标高是决定重力场中气体分子数密度随高度增加而衰 减得快慢程度的物理量; 是决定等温大气压强随高度增加而衰减得快慢程度的物理量。
麦氏速率分布:
f (v ) 4 ( m 2 kT
3 )2
exp(
mv
2
)v
2
2kT
麦氏速度分布:
dN ( v x , v y , v z ) N ( m 2 kT ) exp[
3 2
m(v x v y v z ) 2kT
2
2
2
] dv x d v y d v z
其中:
exp( mv
(
m 2 kT
exp(
Ek kT
)dv x dv ydv z
定义: 玻尔兹曼因子:exp(
kT
)
其中 k (或 p)
n ( r ) n 0 exp(
E p (r ) kT E p(z)
)
n ( z ) n ( 0 ) exp( n ( z ) n ( 0 ) exp(
RT
解: 设:地面大气压强为P0,气球体积为V0; 在高度h处的大气压强为P,气球体积为V 地球大气层等温,则:
P0V 0 PV
分子动力学基本知识

分子动力学基本知识分子动力学模拟基本步骤起始构型:进行分子动力学模拟的第一步是确定起始构型,一个能量较低的起始构型是进行分子模拟的基础,一般分子的起始构型主要来自实验数据或量子化学计算。
分子动力学在确定起始构型之后要赋予构成分子的各个原子速度,这一速度是根据波尔兹曼分布随机生成的,由于速度的分布符合波尔兹曼统计,因此在这个阶段,体系的温度是恒定的。
另外,在随机生成各个原子的运动速度之后须进行调整,使得体系总体在各个方向上的动量之和为零,即保证体系没有平动位移。
平衡相:由上一步确定的分子组建平衡相,在构建平衡相的时候会对构型、温度等参数加以监控。
生产相:在这个过程中,体系总能量不变,但分子内部势能和动能不断相互转化,从而体系的温度也不断变化请大家注意:温度是体系中分子动能的宏观体现关于势能函数:在计算宏观体积和微观成分关系的时候主要采用刚球模型的二体势,计算系统能量,熵等关系时早期多采用Lennard-Jones、morse势等双体势模型,对于金属计算,主要采用morse势,但是由于通过实验拟合的对势容易导致柯西关系,与实验不符,因此在后来的模拟中有人提出采用EAM等多体势模型,或者采用第一性原理计算结果通过一定的物理方法来拟合二体势函数。
但是相对于二体势模型,多体势往往缺乏明确的表达式,参量很多,模拟收敛速度很慢,给应用带来很大的困难,因此在一般应用中,通过第一性原理计算结果拟合势函数的L-J,morse等势模型的应用仍然非常广泛。
时间步长:就是抽样的间隔,因而时间步长的选取对动力学模拟非常重要。
太长的时间步长会造成分子间的激烈碰撞,体系数据溢出;太短的时间步长会降低模拟过程搜索相空间的能力,因此一般选取的时间步长为体系各个自由度中最短运动周期的十分之一。
但是通常情况下,体系各自由度中运动周期最短的是各个化学键的振动.分子动力学模拟应用很广泛,也正应为如此我们在使用的时候需要根据自己的特殊状况,对模拟中的很多状况加以选取与约束。
分子动理学理论的平衡态理论

思考:
v 2 vf
v1
(v )dv
是否表示在v1
~v2 区间内的平均速率
?
2. 方均根速率
v 2 v 2 f (v)dv 3kT
0
m
vrms
v2
3kT m
3RT 1.73 RT
Mm
Mm
p
2 3
n
t
2 n(1 mv 2 ) 32
2 n 1 m 3kT 32 m
nkT
理想气体 状态方程
x2 x1
f (x)dx 位置处于x1到x2范围内的概率
f (x)dx 1
(归一条件)
类似地可求出 f (y) N 并
N y
令 y 0 可得到黑点处于y~y+dy 范围内的概率为f(y)dy。
黑点处于x~x+dx,y~y+dy范围内的概
率就是图中打上斜线的范围内的黑点 数与总黑点数之比。
f(v) T
f (v)dv 1
O
0
(归一化条件)
vp
( 速率分布曲线 )
v
(5) 最概然速率v p f(v) 出现极大值时, 所对应的速率称为最概然速率
df (v ) 0 dv v v p
vp
2kT m
2RT 1.41 RT
Mm
Mm
(6) 不同气体, 不同温度下的速率分布曲线的关系 由于曲线下的面积不变,由此可见
第二章: 分子动(理学)理论的平衡态理论
§2.1 分子动理论与统计物理学 §2.2 概率论的基本知识 §2.3 麦克斯韦速率分布 §2.4 麦克斯韦速度分布 §2.5 气体分子碰壁数及其应用 §2.6 外力场中自由粒子的分布. 玻尔兹曼分布 §2.7 能量均分定理
分子动理学理论的平衡态理论

若氢气瓶为一绝热容器,情况又如何?
(2)平均速率
0 f ()d
8kT
m
8RT 1.60
M
RT M
(3)方均根速率
2
2
f
()d
3kT
0
m
rms
2
3kT m
3RT 1.73 M
RT M
(4)三种速率的比较 适用条件: 理想气体分子
则p所在区间内的分子数占分子总数的百分比最大。
f ()
O
p
f (v)
T1 300K T2 1200K
o vp1 vp2
v
N2 分子在不同 温度下的速率分布
思考:
② 温度T升高,p , f(υ ) 曲 线 , f(p) 如 何 变
化??为什么?
f ()
f (v)
O2 H2
o vp0 vpH
热物理学的微观理论由分子动理学理论、统 计物理学与非平衡态统计三部分组成。
(三)学习建议
重点掌握基本物理概念、处理问题的物理思 想及基本物理方法,熟悉物理理论的重要基础— —基本实验事实。
暂不去追求理论的十分严密与结果的十分精 确。
§2.2 概率论的基本知识
A、在一定的宏观条件下,大量偶然事件,在整体 上表现出确定的规律---统计规律
例题2: P102 习题2.3.1
例题3:
3. 导体中自由电子的运动可以看作类似气体分子
的运动,故称为电子气。设导体中共有N个自
由电子,这些电子的最大速率为vF,称为费米速 率。导体中的自由电子速率分布函数f(v)满
足以下关系式(式中A为常数):
第二章 分子动理学理论的平衡态理论

配情况,我们称为一种分布。
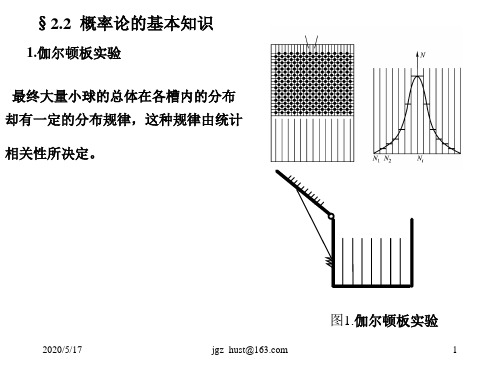
实验指出,只要小球的总数足够 大,则每次所得的分布几乎相等, 也即每个槽内的小球的数目与小球 总数之比
N1, N2, N3,,Ni , NNN N
几乎是完全确定的,即具有稳定的特性,只略有一些偏差。
§2.2 概率论的基本知识
由此可见,大量小球 在各槽内的一组分布决不 是偶然的,而是一个必然 规律。这种由大量偶然事 件的总体所服从的规律称
f (v) dN Ndv
f (v)
o
v
§2.3 麦克斯韦速率分布
2、三种统计速率
(1)、最概然速率v p
令
df (v) 0 dv vvp
f (v)
f max
根据分布函数求得
o vp
v
vp
2kT m
2RT Mm
物理意义
气体在一定温度下分布在最概然速
率 附v p近单位速率间隔内的相对分子
数最多。
二、麦克斯韦速率分布
1、麦克斯韦速率分布
麦克斯韦利用理想气体分子在三个方向上作独立运 动的假设,导出了理想气体分子在平衡态时按速度分布规 律,然后得到理想气体分子按速率分布规律。
在平衡态下,当气体分子间的相互作用可以忽略
时,分布在任意速率区间 v vdv分子数的比率
为
dN f(v )d v4 π ( m) e vd 32 m 2k v2T2 v
T130K0
f (v)
T2120K0
O2
H2
o v p1 vp2
v
N2 分子在不同温度下的 速率分布
o v p 0 v pH
v
同一温度下不同气体的速 率分布
§2.3 麦克斯韦速率分布
分子动理理论的平衡态理论PPT
那七个小矩形的上方轮廓线上下起伏,如该图虚线所示,且十四个小矩形的面
积之和为92%。
2018/11/10 jgz_hust@ 9
2018/11/10
jgz_hust@
10
当速率间隔取得足够小时, ,一排细窄矩形的上轮 廓线将趋于一条光滑曲线,上图所示 这条曲线就代表了分布在附近、单位速率间隔内的分子数 dN 比率 Nd 随 的变化情况,称这曲线为速率分布曲线, 其 对应的函数记为 :
3
3 平均值及其运算法则
统计分布的最直接的应用是求平均值。以求平均年龄为例,N人的年龄平均 值就是N人的年龄之和除以总人数N。求年龄之和可以将人按年龄分组,设ui
为随机变量(例如年龄),其中出现(年龄)u1值的次(或人)数为N1,u2
值的次(或人)数为N2……,则该随机变量(年龄)的平均值为
N u N 2u2 u 1 1 P Ni
f(v)
d ,
N dN N Nd
0
v
速率分布曲线
2018/11/10
jgz_hust@
11
• 分布函数与概率问题之间的关系:
• (1).气体中任意分子其速率在 →+ 区间内的概率应等于N个分子中 速率介于此区间内的分子数比率dN/N,此概率就是f()d; • (2).任意分子其速率落在附近的单位速率间隔内的概率则是
概率的基本性质 A. 任意一事件的概率PA, 必有0≤ PA≤ 1. B. PA=1意味着A事件在给定的条件下一定发生,是必然事件; C. PA=0则是A事件在给定的条件下根本不可能发生,这是不可能 事件。
D. 基本随机事件组中各事件的概率归一 . (概率的归一化条件 )
2018/11/10
第二节分子动理学理论的平衡态理论2

因而理论上必须使之应用于大数粒子 。
f (v) 4 (
m
)
3 2
exp(
mv
2
)
v
2
2 kT
2kT
但实际上可以用于处于平衡态的一切宏观容器中的理想气体。
5. 公式可以采用量纲来帮助记忆。
6. 混合气体的分子没有统一的速率分布。
但组成混合气体的各组分分别遵守各自的麦氏分布率:
dN1 N1
f (v1)dv1
N
(总分子数 )
N
则在总分子中分子速率介于
(v~vv的分子数 )
v ~ v+∆v 的分子的概率为:
Pv v v
N N
当∆v→0 时,即得分子速率分布的概率密度函数:
F (v) dN N dv
相应地,分子速率介于v ~ v+dv的概率即为:
dPvvdv F(v)dv
dN dv N dv
2. 三种速率各有用处:
vp 讨论速率分布时用到
v 讨论分子平均自由程、 时用到
vrms 讨论分子平均平动动能时用到
3. 若所给速率分布不是麦克斯韦速率分布,则 v p v vrms 不一定成立
但由前面 u2 u2 知,vrms v 总成立
例1.速率分布函数 f 的v 物理意义为:
(A)具有速率v 的分子占总分子数的百分比.
分布率的密勒·库士的铊蒸汽原子束实验。
这里仅介绍朗缪尔的实验
1. 分子束 又称分子射线。A平源自态真空SS1
S2
由于气体分子热运动,会有少部分气体分子从S 缝中逸出, 但因数量较少,并不影响A中气体分子所处的平衡态。 逸出气体分子带有容器中气体分子运动性质的信息。
测出逸出分子的速率分布,即可得到容器内气体分子随速 率的分布情况。但二者不相等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
少数分子无规律性
大量分子的统计分布
7
二、等概率性与概率的基本性质 1、概率的定义
概率:在总次数趋于无限大时,某事件出现次数对总次数的比率。
离散变量xi
P
( xi )
lim
N
Ni N
连续变量x , x-x+dx区间P(x) lim f (x)x f (x)dx lim dN(x)
P(A,B) = PA • PB
3>.概率的归一化条件:
P1+P2+P3+•••+Pi=1
三、平均值
离散变量xi
连续变量x
n
xi Ni xN
i1
x N1x1 N2x2
i
Ni xi ,当N 时:
Ni
N
i
x
xi Ni N
xi P(xi )
分布曲线 x
分布函数 f(x): x处的概率密度 ( x附近的单位区间内的概率)。
处于x1 x2范围内的概率:NN
x2 x1
f (x)dx
9
3、等概率性 在没有理由说明哪一事件出现的概率更大些(或
更小些)的情况下,每一事件出现的概率都应相等; 如:抛硬币、掷骰子中各面出现的等概率性。
第二章 分子动理学 理论的平衡态理论
本章目录
§2.1 分子动理学理论与统计物理学 §2.2 概率论的基本知识 §2.3 麦克斯韦速率分布 §2.4 麦克斯韦速度分布 §2.5 气体分子碰壁数及其应用 §2.6 外力场中自由粒子的分布 §2.7 能量均分定理
§2.1 分子动理学与统计物理
一、分子动理学理论包括: ▲ 理想气体的压强由大数分子碰撞器壁而产生,温度是
4).两个随机变量函数乘积的平均值
f (x) g(x) f (x) g(x)
五、均方偏差
回顾:涨落现象
若任一随机变量M 的平均值为M
附近M的偏 (差M M )
M ,M 显然
方均偏差不等于零
其相对方均根偏差称为涨落
,M则M 在
=0 ,但
相对方均根偏差表示了随机变量在平均值附近散开分 布的程度
x0
N N
分布函数 f(x): x处的概率密度( x附近的单位区间内的概率)
8
2、概率分布函数
f(x)
N (x)
lim f (x)
x0 N x
连续变量x 在 x-x+dx区间概
率
dN ( x)
P(x) lim f (x)x f (x)dx lim
x0
N N
麦克斯韦(James Clerk Maxwell 1831——1879)
•他提出了有旋电场和位移电流概念, 建立了经典电磁理论,预言了以光速传 播的电磁波的存在。
19世纪伟大的英 国物理学家、数 学家。经典电磁 理论的奠基人, 气体动理论的创 始人之一。
•1873年,他的《电磁学通论》问世, 这是一本划时代巨著,它与牛顿时代的 《自然哲学的数学原理》并驾齐驱,它 是人类探索电磁规律的一个里程碑。
平衡态的理想气体分子,其热运动速率出现在不同 速率间隔区间的几率有无规律性?
一、分子射线束实验
实验装置
接抽气泵
金属蒸汽 狭缝
L
显 示 屏
19
二 . 麦克斯韦速率分布函数
1859年麦克斯韦导出了理想气体在无外场的平衡态下, 分子速率分布函数为:
f (v) 4 ( m )3/ 2 em2v/ 2kT v2
▲ 它的最高目标是描述气体由非平衡态转入平衡态的 过程,这个过程是热力学中的不可逆过程;
▲ 我们将讨论:泻流,粘滞现象,热传导,扩散,悬 浮粒子运动,化学反应等。
三、统计物理学:
▲ 广义上讲:是从对物质的微观结构和相互作用的认识 出发,采用概率统计的方法来说明或预言由大量粒子组成 的宏观物体的物理性质;
x xf (x)dx
四、平均值的运算法则
1) x 的某一函数的平均值
n
F (x) F (xi )Pi (xi ) i 1
F(x) F(x) f (x)dx
12
2).随机变量函数和的平均值
c f (x) c f (x)
3).常数与随机变量函数的平均值
f (x) g(x) f (x) g(x)
分子热运动剧烈程度的量度和宏观描述;
▲ 单个分子遵循力学规律,集体运动遵循统计规律;
▲ 处于平衡态的气体分子速率有一个确定的分布,能量 也有一个分布--按自由度分布;
二、分子动理学的主要特点:
▲ 考虑分子之间,分子与器壁之间频繁的碰撞,考虑 分子之间的相互基本假定:如果对于系统 各种可能的状态没有更多的知识,可 暂时假定一切状态出现的概率相等。
原因:系统由大数粒子组成。统计对象越多,其 涨落越小,统计平均越正确。
4、概率的基本性质
1>.概率相加法则:n个互相排斥事件发生的总概率是每 个事件发生概率之和
PAorB=PA+PB
2>.概率相乘法则:同时或依次发生的,互不相关的事件 发生的概率等于各个事件概率之乘积
•在气体动理论方面,1859年提出气体 分子按速率分布的统计规律。
§2.3 麦克斯韦速率分布
要深入研究气体的性质,不能
光是研究一些平均值, 如 t ,V2
等,还应该进一步弄清分子按速率 和按能量等的分布情况。
个别分子的运动是杂乱无章的, 但大量分子运动的集体表现存在着 一定的统计规律。
统计物理关心两件事:
▲ 它认为物质的宏观性质是大量微观粒子运动的集体表 现,宏观量是微观量的统计平均值。
▲ 分子动理学理论和统计物理学都是热物理学的微观理 论的组成部分,它们都作一些假设或近似假设,其理论都 要受到实验的检验。
§2.2 概率论的基本知识
一、伽尔顿板实验
随机事件:若某一事件或现象可能发生也可能不发生。
伽尔顿板实 验是有关概率统 计的最直观的演 示。
1. 平均值; 2. 分布;
几个要用的积分公式
高斯积分
Q xneax2 dx, 0 n0 n 1 n2 n 3 n4
(a 0,n 0,1,2,3, )
Q 2a1/ 2
Q 1 2a
Q 4a3/ 2
Q
1 2a 2
Q
3
8a 5 / 2
由于分子受到频繁的碰撞,每个分子热运动的 速率是变化的,说某一分子具有多大的运动速 率没有意义,所以只能估计在某个速率间隔内 出现的概率。
