动量守恒(人船模型专题)
人船模型(学生版)-动量守恒的十种模型
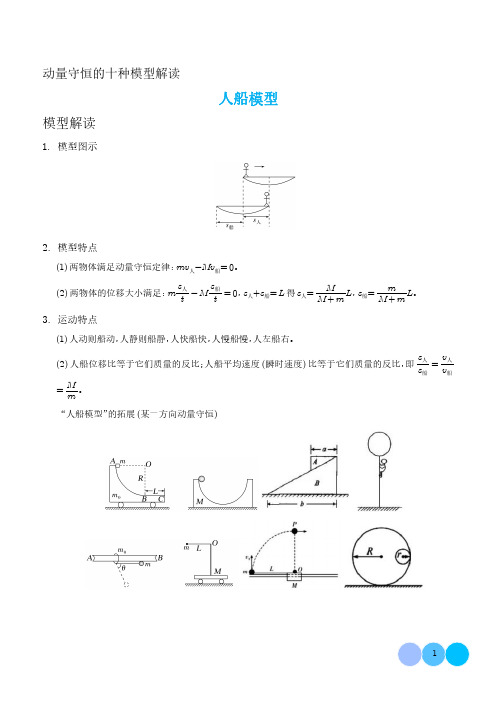
动量守恒的十种模型解读人船模型模型解读1.模型图示2.模型特点(1)两物体满足动量守恒定律:mv 人-Mv 船=0。
(2)两物体的位移大小满足:m s 人t -M s 船t =0,s 人+s 船=L 得s 人=M M +m L ,s 船=m M +mL 。
3.运动特点(1)人动则船动,人静则船静,人快船快,人慢船慢,人左船右。
(2)人船位移比等于它们质量的反比;人船平均速度(瞬时速度)比等于它们质量的反比,即s 人s 船=v 人v 船=M m 。
“人船模型”的拓展(某一方向动量守恒)【典例分析】1如图,质量为M 的匀质凹槽放在光滑水平地面上,凹槽内有一个半椭圆形的光滑轨道,椭圆的半长轴和半短轴分别为a 和b ,长轴水平,短轴竖直。
质量为m 的小球,初始时刻从椭圆轨道长轴的右端点由静止开始下滑。
以初始时刻椭圆中心的位置为坐标原点,在竖直平面内建立固定于地面的直角坐标系xOy ,椭圆长轴位于x 轴上。
整个过程凹槽不翻转,重力加速度为g 。
(1)小球第一次运动到轨道最低点时,求凹槽的速度大小;(2)凹槽相对于初始时刻运动的距离。
【针对性训练】1(2024河南名校联考).如图,棱长为a 、大小形状相同的立方体木块和铁块,质量为m 的木块在上、质量为M 的铁块在下,正对用极短细绳连结悬浮在平静的池中某处,木块上表面距离水面的竖直距离为h 。
当细绳断裂后,木块与铁块均在竖直方向上运动,木块刚浮出水面时,铁块恰好同时到达池底。
仅考虑浮力,不计其他阻力,则池深为()A.M +m M hB.M +m m (h +2a )C.M +m M (h +2a )D.M +m Mh +2a 2(2024全国高考模拟)一小船停靠在湖边码头,小船又窄又长(估计重一吨左右)。
一位同学想用一个卷尺粗略测定它的质量,他进行了如下操作:首先将船平行于码头自由停泊,轻轻从船尾上船,走到船头停下,而后轻轻下船。
用卷尺测出船后退的距离d ,然后用卷尺测出船长L 。
3.人船模型 专题练习-高二物理人教版选修3-5《动量守恒定律》

人船模型1.人船模型两个原来静止的物体发生相互作用时,若所受外力的矢量和为0,则系统动量守恒。
在相互作用的过程中,任一时刻两物体的速度大小之比等于质量的反比。
2.模型分析【问题】如图所示,长为L ,质量为m 船的小船停在静水中,一个质量为m 人的人站在船头,若不计水的阻力,当人从船头走到船尾的过程中,船和人对地的位移各是多少? 【分析】由动量守恒定律,得 0=-人人船船v m v m 由于在全过程动量都守恒,所以有0=-人人船船v m v m 同乘以时间t ,得 0=-t v m t v m 人人船船 即 人人船船x m x m = 由图知 L x x =+人船 解得两物体位移分别为 L m m m x 人船人船+=, Lm m m x 人船船人+=3.模型特点(1)“人船模型”适用于由两物体组成的系统,当满足动量守恒条件(含某一方向动量守恒)时,若其中一个物体向某一方向运动,则另一物体在其作用力的作用下向相反方向运动。
)两物体满足动量守恒定律:m 1v 1-m 2v 2=0。
(2)运动特点:人动船动,人停船停,人快船快,人慢船慢;人船位移比等于它们质量的反比;人船平均速度(瞬时速度)比等于它们质量的反比,即x 1x 2=v 1v 2=m 2m 1。
解题时要画出两物体的位移关系草图,找出各位移间的关系。
注意,公式v 1、v 2和x 一般都是相对地面的速度。
4.真题示例【2019·江苏卷】质量为M 的小孩站在质量为m 的滑板上,小孩和滑板均处于静止状态,忽略滑板与地面间的摩擦.小孩沿水平方向跃离滑板,离开滑板时的速度大小为v ,此时滑板的速度大小为( ) A .m v M B .M v m C .mv m M+ D .Mv m M+ 【答案】B【解析】u 0mu Mv =-Mu v m=设滑板的速度为,小孩和滑板动量守恒得:,解得:,故B 正确。
5.例题精选【例题1】如图所示,一个倾角为α的直角斜面体静置于光滑水平面上,斜面体质量为M ,顶端高度为h ,今有一质量为m 的小物体,沿光滑斜面下滑,当小物体从斜面顶端自由下滑到底端时,斜面体在水平面上移动的距离是( ) A .mh M +m B .Mh M +mC .αtan )(m M mh + D .αtan )(m M Mh+【答案】C【解析】此题属“人船模型”问题。
动量守恒 四 人船模型

动量守恒(四)——人船模型——两个原来静止的物体(人和船)发生相互作用时,不受其它外力,对这两个物体组成的系统来说,动量守恒,且任一时刻的总动量均为零,由动量守恒定律,有mv = MV (注意:几何关系)基本题型:如图所示,长为L,质量为M的船停在静火中,一个质量为的人站在船头,若不计火的阻力,当人从船头走到船尾的过程中,船和人对地面的位移各是多少?则mv2-Mv1=0,在人从船头走到船尾的过程中每一时刻系统的动量均守恒,故mv2t-Mv1t=0,即ms2-Ms1=0,而几何关系满足:s1+s2=L变化1:某人在一只静止的小船上练习射击,船、人连同枪(不包括子弹)及靶的总质量为M,枪内有n颗子弹,每颗子弹的质量为m,枪口到靶的距离为L,子弹水平射出枪口相对于地的速度为v0,在发射后一发子弹时,前一发子弹已射入靶中,在射完n颗子弹时,小船后退的距离为多少?变化2:一个质量为M,底面边长为 b 的劈静止在光滑的水平面上,如图,有一质量为 m 的物块由斜面顶部无初速滑到底部时,劈移动的距离是多少?变化3:一只载人的热气球原来静止于空中,热气球本身的质量是M,人的质量是m ,已知气球原来离地高H,若人想沿软梯着地,这软梯至少应为多长。
变化4:如图所示,质量为M,半径为R的光滑圆环静止在光滑水平面上,有一质量为 m 的小滑块从与环心O等高处开始无初速下滑到达最低点时,圆环发生的位移为多少?变化5:如图所示,一质量为ml的半圆槽体A,A槽内外皆光滑,将A置于光滑水平面上,槽半径为R.现有一质量为m2的光滑小球B由静止沿槽顶滑下,设A 和B均为弹性体,且不计空气阻力,求槽体A向一侧滑动的最大距离.参考答案:基本题型:s1=ML/(M+m) s2=mL/(M+m)变化1:s2=nmL/(M+m)变化2:s2=mb/(M+m)变化3:L=(M+m)H/M变化4:s2=mR/(M+m)变化5:系统在水平方向上动量守恒,当小球运动到糟的最右端时,糟向左运动的最大距离设为s1,则m1s1=m2s2,2R /(m1+m2)又因为s1+s2=2R,所以s1=m2。
动量守恒的条件 爆炸、反冲运动 人船模型(附精品解析)

动量守恒的条件爆炸、反冲运动人船模型考点一动量守恒的条件考点二爆炸、反冲运动考点三人船模型考点四连续射击问题1.动量守恒定律内容:如果一个系统不受外力,或者所受外力的矢量和为0,这个系统的总动量保持不变。
2.动量守恒定律常用表达式:m1v1+m2v2=m1v1′+m2v2′.1)p=p′:相互作用前系统的总动量p等于相互作用后的总动量p′.2)m1v1+m2v2=m1v1′+m2v2′:相互作用的两个物体组成的系统,作用前动量的矢量和等于作用后动量的矢量和.3)Δp1=-Δp2:相互作用的两个物体组成的系统,一个物体的动量变化量与另一个物体的动量变化量大小相等、方向相反.4)Δp=0:系统总动量增量为零.考点一动量守恒的条件⑴系统不受外力或者所受外力之和为零;⑵系统受外力,但外力远小于内力,可以忽略不计;⑶系统在某一个方向上所受的合外力为零,则该方向上动量守恒。
⑷全过程的某一阶段系统受的合外力为零,则该阶段系统动量守恒。
附:机械能守恒的条件:只有重力、系统内弹力做功.1.下列四幅图所反映的物理过程中,说法正确的是()A.甲图中子弹射入木块过程中,子弹和木块组成系统动量守恒,能量不守恒B.乙图中M、N两木块放在光滑水平面上,剪断束缚M、N的细线,在弹簧从压缩状态恢复原长过程中,M、N与弹簧组成的系统动量不守恒,机械能守恒C.丙图中细线断裂后,木球和铁球在水中运动的过程,两球组成的系统动量不守恒,机械能守恒D.丁图中木块沿光滑固定斜面下滑,木块和斜面组成的系统动量守恒,机械能守恒2.如图所反映的物理过程中,以物体A和物体B为一个系统符合系统机械能守恒且水平方向动量守恒的是()A.甲图中,在光滑水平面上,物块B以初速度v0滑上上表面粗糙的静止长木板AB.乙图中,在光滑水平面上,物块B以初速度v0滑下靠在墙边的表面光滑的斜面AC.丙图中,在光滑水平上面有两个带正电的小球A、B相距一定的距离,从静止开始释放D.丁图中,在光滑水平面上物体A以初速度v0滑上表面光滑的圆弧轨道B3.(多选)如图所示,A、B两物体质量之比为m A∶m B=3∶2,原来静止在足够长的平板小车C上,A、B间有一根被压缩的弹簧,地面光滑.当两物体被同时释放后,则( )A.若A、B与平板车上表面间的动摩擦因数相同,则A、B组成系统的动量守恒B.若A、B与平板车上表面间的动摩擦因数相同,则A、B、C组成系统的动量守恒C.若A、B所受的摩擦力大小相等,则A、B组成系统的动量守恒D.若A、B所受的摩擦力大小相等,则A、B、C组成系统的动量守恒4. (2021·全国乙卷·T14)如图,光滑水平地面上有一小车,一轻弹簧的一端与车厢的挡板相连,另一端与滑块相连,滑块与车厢的水平底板间有摩擦。
动量中的人船模型资料

人有悲欢离合,月有阴晴圆缺。对于离开的人,不必折磨自己脆弱的生命,虚度了美好的朝夕;不必让心灵痛苦不堪,弄丢了快乐的自己。擦汗眼泪,告诉自己, 日子还得继续,谁都不是谁的唯一,相信最美的风景一直在路上。
人生,就是一场修行。你路过我,我忘记你;你有情,他无意。谁都希望在正确的时间遇见对的人,然而事与愿违时,你越渴望的东西,也许越是无情无义地弃你 而去。所以美好的愿望,就会像肥皂泡一样破灭,只能在错误的时间遇到错的人。
动量守恒定律的应用
人船模型及应用
作者:孙广志
长为l ,质量为M的船停在静水中,一个质量为m的人 (可视为质点)站在船的左端,当人从船的左端以速 度v走到船的右端的过程中,船的速度是多少?船与人 相对于地的位移分别是多少?(忽略水对船的阻力)
m人S人=M船S船
S人+S船=L
人对地位移:s1=ML/(m+M)船对地位移:s2= mL/(m+M)
“不能。” “它能滋润你的干渴?”
“不能。”
其实,世上最温暖的语言,“ 不是我爱你,而是在一起。” 所以懂得才是最美的相遇!只有彼此以诚相待,彼此尊重,相互包容,相互懂得,才能走的更远。
相遇是缘,相守是爱。缘是多么的妙不可言,而懂得又是多么的难能可贵。否则就会错过一时,错过一世!
择一人深爱,陪一人到老。一路相扶相持,一路心手相牵,一路笑对风雨。在平凡的世界,不求爱的轰轰烈烈;不求誓言多么美丽;唯愿简单的相处,真心地付出, 平淡地相守,才不负最美的人生;不负善良的自己。
高中物理选修5—动量守恒(人船模型)

角色交换图2中,轻弹簧的一端固定,另一端与滑块B 相连,B 静止在水平直导轨上,弹簧处在原长状态。
另一质量与B 相同滑块A ,从导轨上的P 点以某一初速度向B 滑行,当A 滑过距离l 1时,与B 相碰,碰撞时间极短,碰后A 、B 紧贴在一起运动,但互不粘连。
已知最后A 恰好返回出发点P 并停止,滑块A 和B 与导轨的滑动摩擦因数都为μ,运动过程中弹簧最大形变量为l 2,重力加速度为g ,求A 从P 出发时的初速度v 0。
图2解析:令A 、B 质量皆为m ,A 刚接触B 时速度为v 1(碰前) 由功能关系,有121202121mgl mv mv μ=- A 、B 碰撞过程中动量守恒,令碰后A 、B 共同运动的速度为v 2 有212mv mv =碰后A 、B 先一起向左运动,接着A 、B 一起被弹回,在弹簧恢复到原长时,设A 、B 的共同速度为v 3,在这一过程中,弹簧势能始末状态都为零,利用功能关系,有)2()2()2(21)2(2122322l g m v m v m μ=- 此后A 、B 开始分离,A 单独向右滑到P 点停下,由功能关系有12321mgl mv μ= 由以上各式,解得)1610(210l l g v +=μ用轻弹簧相连的质量均为2kg 的A 、B 两物块都以s m v /6=的速度在光滑的水平地面上运动,弹簧处于原长,质量为4kg 的物体C 静止在前方,如图3所示,B 与C 碰撞后二者粘在一起运动。
求:在以后的运动中,图3(1)当弹簧的弹性势能最大时物体A 的速度多大? (2)弹性势能的最大值是多大? (3)A 的速度有可能向左吗?为什么?解析:(1)当A 、B 、C 三者的速度相等时弹簧的弹性势能最大,由于A 、B 、C 三者组成的系统动量守恒,有A CB A B A v )m m m (v )m m (++=+解得:s m v A /3=(2)B 、C 碰撞时B 、C 组成的系统动量守恒,设碰后瞬间B 、C 两者速度为'v ,则s m v v m m v m C B B /2'')(=+=,设物块A 速度为v A 时弹簧的弹性势能最大为E P ,根据能量守恒J v m m m v m v m m E A C B A A C B P 12)(2121')(21222=++-++=(3)由系统动量守恒得B C B A A B A v m m v m v m v m )(++=+设A 的速度方向向左,0<A v ,则s m v B /4> 则作用后A 、B 、C 动能之和J v m m v m E B C B A A k 48)(212122>++=实际上系统的机械能J v m m m E E A C B A P 48)(21'2=+++=根据能量守恒定律,'E E k >是不可能的。
人船模型的经典例题讲解

人船模型的经典例题讲解
人船模型是一种物理模型,用于描述两个物体在相互作用下各自的运动情况,其中物体所受的合外力为零,总动量守恒。
下面通过一个例题来讲解人船模型的运用。
题目:在平静的湖面上停泊着一条长为L,质量为M的船。
如果有一质量
为m的人从船的一端走到另一端,求船和人相对水面的位移各为多少?
解析:
1. 设人从船的一端走到另一端所用时间为t,人、船的速度分别为v和u。
2. 由人和船组成的系统在水平方向上满足动量守恒,则mv=Mu。
3. 由于人在走动过程中任意时刻人和船的速度v和u均满足上述关系,所
以运动过程中,人和船平均速度大小也应满足相似的关系,即mv=Mu。
而v=x/t,u=y/t,所以上式可以转化为:mx=My。
4. 又因为x+y=L,得:x=[M/(m+M)]L,y=[m/(m+M)]L。
综上,人和船相对于水面的位移只与人和船的质量有关,与运动情况无关。
以上就是运用人船模型解决的一个经典例题。
如需更多信息,建议查阅相关文献或咨询专业物理老师。
人船模型

地面
( M m) L h h M
一、人船模型(水平方向) 二、劈和物块(水平方向) 三、气球和人(竖直方向)
一、“人船模型”专题
在静水上浮着一只长为L=3m、质量为m船 =300kg的小船,船尾站着一质量m人=60kg的 人,开始时人和船都静止。若人匀速从船尾 走到船头,不计水的阻力。则船将
(
A
) (B)后退0.6m
(A)后退0.5m
(C)后退0.75m
(D)一直匀速后退
S人=L-S船
S船
应用动量守恒处理问题的方法
例1: 湖面上静止的一条小船(如图 所示),长l=4m, 质量M=20kg,质量为
m =60kg的人从船头走到船尾, 求此过
程中人和船相对于地面的位移s1、s2.
例1: 湖面上静止的一条小船(如图 所示),长l=4m, 质量M=20kg,质量为
m =60kg的人从船头走到船尾, 求此过
程中人和船相对于地面的位移s1、s2.
弹片飞行的轨迹可能正确的是(B)
←返回目录
思考1: 在光滑的水平面上有一辆平
板车,一个人站在车上用大锤敲打车
的左端。在连续的敲打下,这辆车能
持续地向右运动吗? 说明理由。
2. 质量为m的小球从光滑的半径为R 的半圆槽顶部A由静止滑下,如图所示. 设槽与桌面无摩擦,则: A. 小球不可能滑到右边最高点B; B. 小球到达槽底时的动能小于mgR; C. 小球升到最大高度时, 槽速度为零; A B D. 若球与槽有摩擦,则 系统水平方向动量不 守恒.
1、若系统在全过程中动量守恒,系统是由两个物 体组成,且相互作用前均静止,相互作用后均发 生运动,则由
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
返回
设人和船的质量分别为m1和m2,速度位移各为
v1和v2,s1和s2,船长为L,不计水的阻力
(1) 选取人和船组成的系统为研究对象,由于系统水 平方向不受外力作用,选取人前进方向为正方向,根据动 量守恒定律有: 0 = m1v1- m2v2 即得:m1v1=m2v2 ① (2) 由于人和船运动的时间 t 相同,所以有:
解析 A、R B、R/2 C、R/3 D、R/4
小结
分析:滑块下滑产生弹力,与 大球组成相互作用的系统,由于水 平面光滑,故该系统水平方向动量 守恒。
SB
SA
2R
解 设大球的位移为sB,则由图可知, 小球在水平方向上对地的位移为sA= (2R-sB),取大球的运动方向为正, 由动量守恒定律得
SA 3m = SB m
于相对位移的关系,即
S1+S2=S相对 [条件] 1、系统满足动量守恒定律 2、物体相互作用前均静止 [解题关键] 确定两物体的相对位移和绝对位移
之间的关系
[练习]水平面
如图所示,质量为M=200kg,长为b=10m的平板车静止在光 滑的水平面上,车上有一个质量为m=50kg的人,人由静止 开始从平板车左端走到右端,求此过程中,车相对地面的 位移大小?
头走向船尾,不计水的阻力。
[现象] 在人向船尾走的同时,船向人走的反方向
运动。人走船走,人快船快,人慢船慢,人停船停。
[问题] 1、为什么会发生这样的现象,这种运动遵
循什么规律? 2、 在人和船运动的过程中,二者的运动速 度、位移各有什么关系? 3、二者的位移与船长又有什么关系?
演示1
问题2
问题3
结论
[变式4]曲面
如图所示,一滑块B静止在光滑水平面上, 其上一部分为半径是R的1/4光滑圆轨道, 此滑块总质量为m2,一个质量为m1的小 球A(可视为质点)由静止从最高点释放,当 小球从最低点水平飞出时,小球和滑块对 地的位移S1,S2分别为多大?
A
B
SA R SB
解:由题意,m1,m2组成的系统水平方向 m2 1 动量守恒,所以根据动量守恒定律得: s — =— s m 2 1 又由几何关系知:S1+S2=R
m2 ___ 联立上式解得: S1= R m1+m2
m1 ___ SB= R m1+m2
[思考题]曲面 如图所示,质量为3m,半径为R 的大空心球B(内壁光滑)静止在 光滑水平面上,有一质量为 m 的 小球A(可视为质点)从与大球球 心等高处开始无初速下滑,滚到另 一侧相同高度时,大球移动的距离 为( )
m1 解:以人和车组成的系统为研究对象, m2 设人和车的位移分别为S1, S2。 由题
意,根据动量守恒定律可得
b
S1 M —— = —— S2 m 又由几何关系可知:S1+S2=b
代入数据联立解得:S1=8m, M=200kg,长为b=10m的平板车静止在光滑的水平面 上,车上有一个质量为m=50kg的人,人由静止开始从平板车左端走到 右端,求此过程中,车相对地面的位移大小?
一个质量为M,底面边长为 b 的劈静止在光滑的水平面上, 见左图,有一质量为m 的物 块由斜面顶部无初速滑到底部 时,劈移动的距离是S2多少?
可得
ms1=Ms2
由几何关系可得:s1=b-s2 联立上式得 s2=mb/(M+m) 即为M发生的位移。 可见,处理此类题,除熟记动量守恒定律外,关键是 确定位移关系。
联立解得SB=R/2
[小结]
人船模型规律
—— = ——
1、两物体绝对位移大小之比等于它们各自质量的 S1 m2 反比,即:
S2
m1
2、两物体的绝对位移之和等于相对位移, 即 S1+S2=S相对 [条件] 1、系统满足动量守恒定律 2、物体相互作用前均静止
[解题关键] 画出草图,找到两物体的相对位移和 绝对位移之间的关系
动量守恒定律的应用Ⅰ
人船模型及应用
制作:朱正泽
复习
动量守恒定律的要点:
1、内容: 如果一个系统不受外力或所受外力之和 为零,则这个系统的总动量保持不变.
2、矢量表达式:
m1v1+m2v2=m1v1′+m2v2′
3、条件: 系统不受外力或所受外力之和为零。
[演示1]一只小船,停在静水中,船头有一个人从船
a [变式练习1]若将此题中的人换成相同 质量,长为a=2m的小车 m (如图所示),结果又如何? M
解:由题意仍有:
1 = —— ——
b
S S2
M m
S1
S2
此时,小车不能视为质点 由几何关系知相对位移为(b-a),所以有
S1+S2=(b-a)
代入数据联立解得:S1=6.4m, S2=1.6m
[变式2]竖直方向 载人气球原来静止在空中(如图所示), 质量为M,下面拖一条质量不计的软梯, 质量为m的人(可视为质点)站在软梯上 端距地面高度为H,若人要沿轻绳梯返回 地面,则绳梯的长度L至少为多长? h
m1v1△t = m2v2 △ t m1v1′△t′= m2v2′ △ t ′ m1v1″△t″=m2v2″ △ t ″ m1s1=m2s2
……
累加即得:
② ③
(3) 由几何关系可知:S1+S2 = L 结论
返回
[解题规律]:
1、首先根据动量守恒确定两物体绝对位移大小之比等于 m2 它们各自质量的反比关系,即: S1 —— = —— S2 m1 2、其次由几何关系确定两物体的绝对位移大小之和等
解:取人和气球为对象,系统开始静止 且同时开始运动,可知系统所受外力之 和为零。人到地面时,人对地的位移为 H,设气球对地位移h(如图所示), 则根据动量守恒定律
m h 得 =— M H 因此绳的长度至少为 L=H+h=
H
(M+m)H
M
地面
[变式3]斜面
M
S2 S1
m
b 分析和解答:劈和小物块组成的系统水平方向不受外力, 故水平方向动量守恒,且初始时两物均静止,设物块的水平 位移为s1,故由动量守恒定律
