大学物理第4章 狭义相对论时空观习题解答改
狭义相对论习题和答案

作业6狭义相对论基础研究:惯性系中得物理规律;惯性系间物理规律得变换。
揭示:时间、空间与运动得关系.知识点一:爱因斯坦相对性原理与光速不变K 相对性原理:物理规律对所有惯性系都就是一样得,不存在任何一个特殊(如“绝对静止”)惯性系。
2s 光速不变原理:任何惯性系中,光在真空中得速率都相等。
(A )1(基础训练1)、宇宙飞船相对于地面以速度v 作匀速直线飞行,某一时刻飞船头部得宇航员 向飞船尾部发出一个光讯号,经过K 飞船上得钟)时间后,被尾部得接收器收到,则由此可知飞船得固 有长度为(c 表示真空中光速)(A) c ・t (B) V/ (C) (D)【解答】飞船得固有长度为飞船上得宇航员测得得长度,即为°知识点二:洛伦兹变换由牛顿得绝对时空观=> 伽利略变换,由爱因斯坦相对论时空观=> 洛仑兹变换。
(1) 在相对论中,时、空密切联系在一起(在X 得式子中含有t,t 式中含X)。
(2) 当u « c 时,洛仑兹变换=> 伽利略变换。
(3) 若UAC , P 式等将无意义1(自测与提髙5)、地而上得观察者测得两艘宇宙飞船相对于地而以速度v = 0. 90c 逆向飞行.其中一 艘飞船测得另一艘飞船速度得大小【解答】知识点三:时间膨胀(1) 固有时间:相对事件发生地静止得参照系中所观测得时间。
(2) 运动时间:相对事件发生地运动得参照系中所观测得时间。
(B )1 (基础训练2)、在某地发生两件事,静止位于该地得甲测得时间间隔为4 s,若相对于甲作匀速直线 运动得乙测得时间间隔为5 s,则乙相对于甲得运动速度就是(c 表示真空中光速)(A) (4/5) c. (B) (3/5) c ・ (C) (2/5) c ・ (D) ("5)c.【解答】飞行•当两飞船即将相遇时飞船在自己得天窗处相隔2s 发射两颗信号弹•在飞船得观测者测得两颗信 号弹相隔得时间间隔为多少?° 【解答】以地而为K 系,飞船A 为/T 系,以正东为x 轴正向侧飞船B 相对于飞船A 得相对速度-0.6c-0.8c0.8c 1一一^(一0・6。
狭义相对论作业习题及解答.doc

4-7.某飞船自地球出发,相对地球以速率v=0.30c匀速飞向月球,在地球测得该旅程的距离为Zo=3.84xl()8m, 在地球测得该旅程的时间间隔为多少?在飞船测得该旅程的距离Z=?利用此距离求出:在飞船测得该旅程的时间间隔为多少?解:取地球为K惯性系、飞船为K,惯性系。
在地球测得该旅程的时间间隔为:Az = L Q/V M4.27(S)在地球地球测得的£o=3.84xlO8 (m),为地球〜月球的固有距离。
则在飞船测得该旅程的距离为在飞船观测,地球与月球共同以速率v=0.30c匀速运行,先是地球、随后是月球掠过飞船,则在飞船测得该旅程的时间间隔为:Ar = Z/v^4.07(s)说明:显然,飞船测自身旅程的时间间隔宜为固有时,在地球测得该旅程的&为观测时。
△t与显然满足狭义相对论时间膨胀效应,即4-8.在K惯性系测两个同时发生相距Im的事件(该两事件皆在X、X,轴)。
在K,惯性系测该两事件间距为2m, 问:在K,惯性系测该两事件发生的时间间隔为多少?解:在K系测两事件相距Ax=lm;同时发生则&=0.在K,系测两事件相距Ax,=2m;两事件发生的时间间隔为由洛伦兹变换,有Ax —M A/A X 1 Ax' ~ V3-/ = = -/ —/ = — 2 u —Jl-("/c)2 Jl-(“/c)2Jl-("/c)2 Ax 24-10.测得不稳定粒子广介子的固有寿命平均值TO=2.6X1O8S,(1)当它相对某实验室以0.80c的速度运动时,所测的平均寿命z应是多少?(2)在实验室测该介子在衰变前运行距离L应是多少?解:取花+介子、实验室为K,和K惯性系,沿该介子运行方向取为X、X,轴,在K,系中观测:也,=宣=2.6*10%, Ax,=0在K系中观测:也与皆为待求量。
由时间膨胀效应关系式,有T = M MI Jl-(v/c)2 =T J J1-(0.80C/C)2| 1~。
大学物理 第四章练习及答案

洛伦兹坐标变换x '=;y y '=;z z '=;2v t x t -'=一、判断题1. 狭义相对论的相对性原理是伽利略相对性原理的推广。
………………………………[√]2. 物理定律在一切惯性参考系中都具有相同的数学表达式。
……………………………[√]3. 伽利略变换是对高速运动和低速运动都成立的变换。
…………………………………[×]4. 在一惯性系中同时发生的两个事件,在另一相对它运动的惯性系中,并不一定同时发生。
… …………………………………………………………………………………………[√]5. K '系相对K 系运动,在K '中测量相对K 系静止的尺的长度,测量时必须同时测量。
[√]6. 信息与能量的传播速度不可以超过光速。
………………………………………………[√]7. 人的眼睛可以直接观测到“动尺缩短”效应。
…………………………………………[×] 二、填空题8. 狭义相对论的两条基本原理是:1、物理定律在一切惯性参考系中都具有相同的数学表达式;2、在彼此相对作匀速直线运动的任一惯性参考系中,所测得的光在真空中的传播速度都是相等的。
9. 静止的细菌能存活4分钟,若它以速率0.6c 运动,存活的时间为5分钟。
10. 静止时边长为a 的正立方体,当它以速率v 沿与它的一个边平行的方向相对于S 系运动时,在S系中测得它的体积等于a11. 静止质量为0m ,以速率为v2;动220m c -。
三、计算题12. 在惯性系K 中观测到两事件同时发生,空间距离相隔1m ,惯性系K '沿两事件连线的方向相对于K 的运动,在K '系中观测到两事件之间的距离为3m ,求K '系相对于K 的速度和在其中测得两事件之间的时间间隔。
解:依题意1m;0;3m x t x '∆=∆=∆=。
由洛伦兹变换x '∆==,得v =t c '∆== 13. 在S 系中观察到在同一地点发生两个事件,第二事件发生在第一事件之后2s 。
狭义相对论习题和答案

作业6 狭义相对论基础研究:惯性系中得物理规律;惯性系间物理规律得变换。
揭示:时间、空间与运动得关系.知识点一:爱因斯坦相对性原理与光速不变1。
相对性原理:物理规律对所有惯性系都就是一样得,不存在任何一个特殊 (如“绝对静止”)惯性系。
2。
光速不变原理:任何惯性系中,光在真空中得速率都相等。
( A )1(基础训练1)、宇宙飞船相对于地面以速度v 作匀速直线飞行,某一时刻飞船头部得宇航员向飞船尾部发出一个光讯号,经过t (飞船上得钟)时间后,被尾部得接收器收到,则由此可知飞船得固有长度为(c表示真空中光速)(A) c·t (B) v·t (C) (D) 【解答】飞船得固有长度为飞船上得宇航员测得得长度,即为c ·∆t 。
知识点二:洛伦兹变换由牛顿得绝对时空观⇒伽利略变换,由爱因斯坦相对论时空观⇒洛仑兹变换。
(1)在相对论中,时、空密切联系在一起(在x 得式子中含有t,t 式中含x)。
(2)当u 〈< c时,洛仑兹变换 ⇒ 伽利略变换。
(3)若u ≥ c, x '式等将无意义1(自测与提高5)、地面上得观察者测得两艘宇宙飞船相对于地面以速度 v = 0、90c 逆向飞行.其中一艘飞船测得另一艘飞船速度得大小v ′=__、 【解答】知识点三:时间膨胀(1)固有时间:相对事件发生地静止得参照系中所观测得时间。
(2)运动时间:相对事件发生地运动得参照系中所观测得时间。
(B )1(基础训练2)、在某地发生两件事,静止位于该地得甲测得时间间隔为4 s,若相对于甲作匀速直线运动得乙测得时间间隔为5 s,则乙相对于甲得运动速度就是(c 表示真空中光速)(A) (4/5) c. (B) (3/5) c. (C) (2/5) c 。
(D) (1/5) c 、 【解答】()2220024311551/t v t v c c c t v c ∆⎛⎫⎛⎫⎛⎫∆=⇒=-⇒=-= ⎪ ⎪ ⎪∆⎝⎭⎝⎭⎝⎭-2(自测与提高12)、飞船以0。
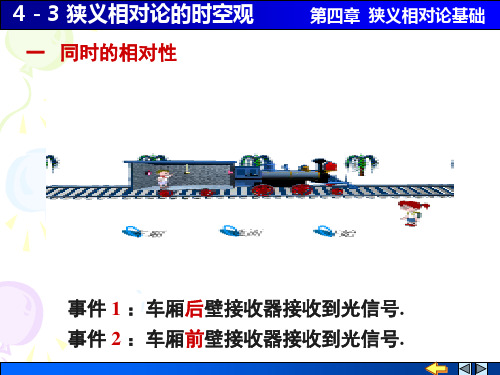
4-3 狭义相对论的时空观
6
2
12 x' x 9 3
6
S 系 ( 地面参考系 ) S' 系 (车厢参考系 )
事件 1 (x1, y1, z1,t1) (x'1 , y'1 , z'1 ,t'1 )
事件 2 (x2 , y2 , z2 ,t2 ) (x'2 , y'2 , z'2 ,t'2 )
同时 不同地
t' t'2 t'1 0
当 v c时 l l0 .
4 - 3 狭义相对论的时空观
第四章 狭义相对论基础
例2 设想有一光子火箭, 相对于地球以速率
v 0.95c 飞行,若以火箭为参考系测得火箭长度为
15 m,问以地球为参考系,此火箭有多长?
y y'
l0 15m
o o'
s'
v x' s
x
火箭参照系 地面参照系
解 :固有长度
S系(宇航员)观察,船身通过观测站的时间间隔为
t
x v
l0 v
3.75107 s
是否是原时?
S系(观测站): x1 x2 x
同一地点!
t t 1 (v)2 c
( t 为原时)
t t 1 ( v)2 2.25107 s c
4 - 3 狭义相对论的时空观
第四章 狭义相对论基础
方法三:洛仑兹变换
固有长度:物体相对静止时所测得的长度 .(最长)
4 - 3 狭义相对论的时空观
第四章 狭义相对论基础
注意
长度缩短纯粹是一种相对论效应,与物体内部结 构无关 . 长度测量值与被测物体相对于观测者的运动有关, 相对静止时最长 .
狭义相对论习题、答案与解法(2010.11.22)

狭义相对论习题、答案与解答一. 选择题 1. 有下列几种说法:(1) 真空中,光速与光的频率、光源的运动、观察者的运动无关; (2) 在所有惯性系中光在真空中沿任何方向的传播速率都相同; (3) 所有惯性系对物理基本规律都是等价的。
请在以下选择中选出正确的答案(C )A 、 只有(1)、(2)正确;B 、 只有(1)、(3)正确;C 、 只有(2)、(3)正确;D 、 3种说法都不正确。
2.(1)对某观察者来说,发生在某惯性系同一地点、同一时刻两个事件,对于相对该惯性系做匀速直线运动的其他惯性系中的观察者来说,它们是否同时发生?(2)在某惯性系不同地点、同一时刻的两个事件,它们在其他惯性系中是否同时发生?(A )A 、(1)同时,(2)不同时;B 、(1)不同时,(2)同时;C 、(1)同时,(2)同时;D 、(1)不同时,(2)不同时。
参考答案:(1) ⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎨⎧=∆=∆-∆-∆='∆001222x t c v x c v t t 0='∆t(2) ⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎨⎧≠'∆='∆-''∆+'∆=∆001222x t c v x cv t t 2221c v x c v t -'∆=∆3.K 系中沿x 轴方向相距3m 远的两处同时发生两事件,在K '系中上述两事件相距5m 远,则两惯性系间的相对速度为(A ) A 、c )54( ; B 、c )53(; C 、c )52(; D 、c )51(。
参考答案:221cv vt x x --=' 221cv t v x x -∆-∆='∆ c c x x c v 54531122=⎪⎭⎫⎝⎛-=⎪⎭⎫ ⎝⎛'∆∆-=4.两个惯性系K 和K ',沿x x '轴方向作相对运动,相对速度为v ,设在K '系中某点先后发生两个事件,用固定于该系的钟测出两事件的时间间隔为0t ∆,而用固定在K 系的钟测出这两个事件的时间间隔为t ∆。
第四章 狭义相对论习题以及答案

第4章狭义相对论习题及答案一 选择题1.下列几中说法:(1) 所有惯性系对物理基本规律都是等价的。
(2) 在真空中,光的速度与光的频率、光源的运动状态无关。
(3) 在任何惯性系中,光在真空中沿任何方向的传播速度都相同。
其中哪些说法是正确的?(A) 只有(1)、(2)是正确的。
(B) 只有(1)、(3)是正确的。
(C) 只有(2)、(3)是正确的。
(D) 三种说法都是正确的。
2.边长为a 的正方形薄板静止于惯性系K 的XOY 平面内,且两边分别与X ,Y 轴平行。
今有惯系K ′以0.8c(c 为真空中的光速)的速度相对于K 系沿X 轴作匀速直线运动,则从K ′系测得薄板的面积为(A)a ². (B)0.6a ² (C)0.8a ² (D)a ²/0.63.在某地发生两件事,静止位于该地的甲测得时间间隔为4s ,若相对于甲作匀速直线运动的乙测得时间间隔为5s ,测乙相对于甲的运动速度是(C 表示真空中光速)(A )(4/5)C (B )(3/5)C (C )(1/5)C (D )(2/5)C4.α粒子在加速器中被加速,其质量为静止质量的3倍时,动能为静止能量的(A)2倍 (B)3倍 (C)4倍 (D)5倍5.把一个静止质量为m 0的粒子,由静止加速到v=0.6c(c 为真空中光速)需作的功等于(A)0.18m 0c2 (B)0.25m 0c 2 (C)0.36m 0c 2 (D)1.25m 0c 2二 填空题1.狭义相对论的两条基本原理中,相对性原理说的是 __;光速不变原理说的是__________________________________.2.已知惯性系S ′相对于惯性系S 系以0.5c 的匀速度沿X轴的负方向运动,若从S ′系的坐标原点O′沿X轴正方向发出一光波,则S 系中测得此光波的波速为_____ ____.3.π+介子是不稳定的粒子,在它自己的参照系中测得平均寿命是2.6×10-8s ,如果它相对实验以0.8c (c 为真空中光速)的速度运动,那么实验坐标系中测得π+介子的寿命是____s.4.一门宽为 a.今有一固有长度为l 0(l 0>a)的水平细杆,在门外贴近门的平面内沿其长度方向匀速运动。
《大学物理》课后解答题 第四章狭义相对论基础

第四章 狭义相对论基础一、思考讨论题1、根据相对论问答下列问题: (1)在一个惯性系中同时、同地点发生的两事件,在另一惯性系中是否也是同时同地点发生? (2)在一个惯性系中同地点、不同时发生的两事件,可否在另一惯性系中为同时、同地点发生?(3)在一惯性系中的不同地点发生的两事件,应满足什么条件才可找另一惯性系,使它们成为同地点发生的事件?(4)在一惯性系中的不同时刻发生的两事件,应满足什么条件才可找到另一惯性系,使它们成为同时的事件?答:依据洛仑兹时空坐标变换)(ut x x -='γ )(2c ux t t -='γ (其中2211c u -=γ)得 )(t u x x ∆-∆='∆γ )(2c x u t t ∆-∆='∆γ(其中12x x x -=∆,'-'='∆12x x x ,12t t t -=∆,'-'='∆12t t t ) 所以有 (1)是。
(2)不能。
(3)若0≠∆x ,而欲0='∆x 应有0=∆-∆t u xxu c t∆∴=<∆ (4)若0≠∆t 而欲0='∆t ,应有02=∆-∆x u t2x c c t u∆∴=>∆ 2、一个光源沿相反方向放出两个光子(以光速c 运动),问两光子的相对速度的大小是多少?答:由相对论速度变换式易算得,相对速度大小仍为c 。
3、一发射台向东西两侧距离均为L 0的两个接收站发射光讯号,今有一飞机自西向东匀速飞行,在飞机上观察,两个接收站是否同时接到讯号?哪个先接到?如飞机在水平内向其它方向运动,又如何?解:以地面为S 系,飞机为S '系,设飞机相对于地面的速度为u 。
西、东两接收站接到光信号的时刻分别为:系中)(和系)(和S t t S t t '''2121S显然 021=∆⇒=t t t 0111222022222212<---=-∆-=-∆-∆='-'cu c L u cu c x u cu c x u t t t'<'∴12t t 即东边的接收台先接到。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
习 题4-1 一辆高速车以0.8c 的速率运动。
地上有一系列的同步钟,当经过地面上的一台钟时,驾驶员注意到它的指针在0=t ,她即刻把自己的钟拨到0'=t 。
行驶了一段距离后,她自己的钟指到6 us 时,驾驶员瞧地面上另一台钟。
问这个钟的读数就是多少? 【解】s)(10)/8.0(16/12220μ=-μ=-∆=∆c c s cu t t所以地面上第二个钟的读数为)(10's t t t μ=∆+=4-2 在某惯性参考系S 中,两事件发生在同一地点而时间间隔为4 s,另一惯性参考系S′ 以速度c u 6.0=相对于S 系运动,问在S′ 系中测得的两个事件的时间间隔与空间间隔各就是多少?【解】已知原时(s)4=∆t ,则测时(s)56.014/1'222=-=-∆=∆s cu t t由洛伦兹坐标变换22/1'c u ut x x --=,得:)(100.9/1/1/1'''8222220221012m c u t u c u ut x c u ut x x x x ⨯=-∆=-----=-=∆4-3 S 系中测得两个事件的时空坐标就是x 1=6×104 m,y 1=z 1=0,t 1=2×10-4 s 与x 2=12×104 m,y 2=z 2=0,t 2=1×10-4 s 。
如果S′ 系测得这两个事件同时发生,则S′ 系相对于S 系的速度u 就是多少?S′ 系测得这两个事件的空间间隔就是多少? 【解】(m)1064⨯=∆x ,0=∆=∆z y ,(s)1014-⨯-=∆t ,0'=∆t0)('2=∆-∆γ=∆cxu t t 2cxu t ∆=∆⇒ (m/s)105.182⨯-=∆∆=⇒x t c u (m )102.5)('4⨯=∆-∆γ=∆t u x x4-4 一列车与山底隧道静止时等长。
列车高速穿过隧道时,山顶上一观察者瞧到当列车完全进入隧道时,在隧道的进口与出口处同时发生了雷击,但并未击中列车。
试按相对论理论定性分析列车上的旅客应观察到什么现象?这现象就是如何发生的? 【解】S 系(山顶观察者)瞧雷击同时发生,但车厢长度短于山洞长度,故未被击中。
'S 系(列车观察者)瞧雷击不同时发生。
虽然车厢长度长于山洞长度,但出洞处先遭雷击,入洞处后遭雷击,此时车尾已经进入山洞。
故未被击中。
4-5 一飞船以0.99c 的速率平行于地面飞行,宇航员测得此飞船的长度为400 m 。
(1)地面上的观察者测得飞船长度就是多少?(2)为了测得飞船的长度,地面上需要有两位观察者携带着两只同步钟同时站在飞船首尾两端处。
那么这两位观察者相距多远?(3)宇航员测得两位观察者相距多远?【解】(1))(4.5699.01400/12220m c u l l =-=-=(2)这两位观察者需同时测量飞船首尾的坐标,相减得到飞船长度,所以两位观察者相距就是56.4 m 。
(3)上的两位观察者相距56.4 m,这一距离在地面参考系中就是原长,宇航员瞧地面就是运动的,她测得地面上两位观察者相距为)(96.799.014.56/12220m c u l l =-=-=所以宇航员测得两位观察者相距7.96 m 。
4-6 一艘飞船原长为l 0,以速度v 相对于地面作匀速直线飞行。
飞船内一小球从尾部运动到头部,宇航员测得小球运动速度为u ,求地面观察者测得小球运动的时间。
【解】宇航员测得小球离开尾部的时空坐标为)','11t x (,小球到达头部的时空坐标为)','22t x (。
地面上测得小球运动的时间为:)''(/11)''(/11)''(/11222211222222212c x v t c v c vx t cv c vx t c v t t t ∆+∆-=+--+-=-=∆012''l x x =- ,u l t t /''012=-2220222/1)/1()''(/11cv u c uv l c x u t c u t -+=∆+∆-=∆∴4-7 在实验室中测得两个粒子均以0.75c 的速度沿同一方向飞行,它们先后击中同一静止靶子的时间间隔为5×10-8 s 。
求击中靶子前两个粒子相互间的距离。
【解】(m)25.11=∆=∆t u x4-8 在参考系S 中,一粒子沿x 轴做直线运动,从坐标原点O 运动到x =1、50×108 m 处,经历时间Δt =1 s 。
试计算粒子运动所经历的原时就是多少? 【解】粒子在S 系中的速度为)(105.1018-⋅⨯=∆-=s m tx u 原时为:)(866.0/1220s c u t t =-∆=∆4-9 一个在实验室中以0.8c 的速度运动的粒子飞行了3 m 后衰变。
实验室中的观察者测量该粒子存在了多少时间?与粒子一起运动的观察者测得该粒子在衰变前存在了多少时间?【解】实验室中的观察者测得粒子的存在时间为:(s)1025.18-⨯=∆=∆uxt 与粒子一起运动的观察者测得粒子的存在时间为原时(s)101/18220-⨯=-∆=∆c u t t4-10 远方的一颗星体以0.8c 的速率离开我们。
我们接收到它辐射出来的闪光周期就是5昼夜,求固定在星体上的参考系测得的闪光周期。
【解】我们接收的闪光周期就是测时,固定在星体上的参考系测得的闪光周期为原时,即原时为:)(3/1'22昼夜=-∆=∆c u t t4-11 一星体与地球之间的距离就是16光年。
一观察者乘坐以0.8c 速度飞行的飞船从地球出发向着星体飞去。
该观察者测得飞船到达星体所花的时间就是多少?试解释计算结果。
【解】星体与地球之间的距离就是原长,飞船上的观察者测得的距离就是测长,测长为:)(6.98.01/1L '02220光年=-=-=L c u L)(128.0''年==∆cL t 地球上的观察者测得飞船到达星体所花的时间为:)(208.00年==∆cLt飞船上的观察者测得的时间就是原时,地球上的观察者测得飞船到达星体所花的时间为测时,这正就是时间膨胀的一种表现。
4-12 一根固有长度为1 m 的尺子静止在S′系中,与O ′x′轴成30°角。
如果在S 系中测得该尺与Ox 轴成45°角,则S′ 系相对于S 系的速度u 就是多少?S 系测得该尺的长度就是多少?【解】在'S 系中,米尺在x′ 轴方向的投影长度为:(m)2330cos '0==L x在y ′ 轴方向的投影长度为:(m)5.030sin '0==L y在S 系中,米尺在y 轴方向的投影长度不变,)(5.0'm y y ==由于米尺在S 系中测得该尺与Ox 轴的夹角为45°,则在x 轴方向的投影长度为:)(5.0m x =,即2222/1235.0'/1c u x c u x -=⇒-= S′ 系相对于S 系的速度为:c u 32=S 系中测得该尺的长度为:(m)707.05.02=⨯=L4-13 一立方体的质量与体积分别为m 0与V 0。
求立方体沿其一棱的方向以速速u 运动时的体积与密度。
【解】 设立方体沿x 方向运动,立方体的一条棱边平行于x 轴。
立方体的原边长为300V a =运动时,沿x 轴方向边长为:022/1'a c u a -=因此物体的体积为:22000022/1/1'c u V a a a c u V -=⨯⨯-= 运动时,物体的质量为:022/11m cu m -=因此运动时物体的密度为:12200220022)/1(/1/11''--=--==c u V mc u V m c u V m ρ4-14 直杆纵向平行于S 系的Ox 轴匀速运动,在S 系中同时标出该杆两端的位置,并测得两端坐标差Δx 1=4 m 。
若在固定于杆上的S′ 系中同时标出该杆两端的位置,则在S′ 系中测得两端坐标差Δx 2=9 m 。
求杆本身的长度与杆相对于S 系的运动速度。
【解】根据题意可知,在S′ 系中测得杆的长度即为原长0L 。
029()L x m =∆=根据长度收缩关系式2210/1cu x L -∆=1x ∆就是在s 系中测得杆的长度21221x u c x ∆⇒-=∆ 3u c ∴=【解】(邱雄习题答案)设直杆的原长为0L ,根据题意可知,在S′ 系中测得杆的长度即为原长。
了)这个题目的Δx 2=9 m 就是在S 系中的两个坐标之差,不就是原长。
如果用洛仑兹变换解这题的第二次测量,会更容易理解。
以下就是我的解法。
【解】在S′ 系中,不管就是否同时测量,杆两端坐标差都就是原长,设直杆的原长为0L 。
第一次测量,Δx 1=4 m 就是动长,可以直接用长度收缩公式,有以下关系:2210/1cu x L -∆=(1)第二次测量,Δt 2′ =0 Δx 2=9 m Δx 2′ =L 0 由洛仑兹变换)'t u 'x (c u 1x 22222∆∆∆+-=1 得到下面式子2220/1c u x L -∆= (2)由(1)(2)得到2122x x c u ∆∆=-1 c u 35=⇒ )(69519220m L =-=4-15 从地球上测得地球到最近的恒星半人马座α星的距离就是4、3×1016 m,设一宇宙飞船以速度0.99c 从地球飞向该星。
(1)飞船中的观察者测得地球与该星间距离就是多少?(2)按照地球上的时钟计算,飞船往返一次需要多少时间?若以飞船上的时钟计算,往返一次的时间又为多少?【解】(1)设地球为S 系,飞船为S’系。
地球上测得地球到半人马座α星的距离为原长,飞船测得的距离为测长。
则:)(1092.1999.01103.4/1'15216220m c u l l ⨯=-⨯⨯=-=(2)地球上的时钟计算飞船往返一次)2(0l 所需的时间为年)(1.9)(87.2103999.0103.4228160==⨯⨯⨯⨯==∆s u l t地球上的时钟计算飞船往返一次所需的时间为测时,以飞船时钟计为原时,则年)(41.0999.01.19/1'222=-⨯=-∆=∆c u t t4-16 天津与北京相距120 km 。
在北京于某日上午9时整有一工厂因过载而断电。
同日在天津于9时0分0、0003秒有一自行车与卡车相撞。
试求在以c 8.0沿北京到天津方向飞行的飞船中的观察者瞧来,这两个事件相距多远?这两个事件之间的时间间隔就是多少?哪一事件发生的更早?【解】(1)设飞船为'S 系,地球为S 系,北京发生事件1,天津发生事件2。
