九年级(上)数学期末复习题(一)
2021-2022学年北师大版九年级数学第一学期期末复习综合训练题1(附答案)

2021-2022学年北师大版九年级数学第一学期期末复习综合训练题1(附答案)1.若一元二次方程(k﹣1)x2+3x+k2﹣1=0的一个根为0,则k的值为()A.k=0B.k=1C.k=﹣1D.k=1或k=﹣1 2.菱形ABCD的周长是8cm,∠ABC=60°,那么这个菱形的对角线BD的长是()A.cm B.2cm C.1cm D.2cm3.如图,在菱形ABCD中,P是对角线AC上一动点,过点P作PE⊥BC于点E.PF⊥AB 于点F.若菱形ABCD的周长为24,面积为24,则PE+PF的值为()A.4B.C.6D.4.在一个不透明的袋子里,装有6枚白色棋子和若干枚黑色棋子,这些棋子除颜色外都相同.将袋子里的棋子摇匀,随机摸出一枚棋子,记下它的颜色后再放回袋子里.不断重复这一过程,统计发现,摸到白色棋子的频率稳定在0.1,由此估计袋子里黑色棋子的个数为()A.60B.56C.54D.525.已知反比例函数y=(k≠0)与正比例函数y=﹣2x没有交点,且双曲线图象上有三点A(﹣1,a)、B(﹣3,b)、C(4,c),则a、b、c的大小关系为()A.a>b>c B.b>a>c C.c>b>a D.c>a>b6.某广场有一块正方形的空地正中间修建一个圆形喷泉,在四个角修建四个四分之一圆形的水池,其余部分种植花草.若喷泉和水池的半径都相同,喷泉边缘到空地边界的距离为3m,种植花草的区域的面积为100m2,设水池半径为xm,可列出方程()A.(2x+3)2﹣πx2=100B.(x+6)2﹣πx2=100C.(2x+3)2﹣2x2=100D.(2x+6)2﹣2πx2=1007.如图,已知AB∥CD∥EF,它们依次交直线l1,l2于点A、D、F和点B、C、E,如果AD:DF=3:1,BE=12,那么CE等于()A.9B.4C.6D.38.矩形的正投影不可能是()A.矩形B.梯形C.正方形D.线段9.下列四个三角形,与图中的三角形相似的是()A.B.C.D.10.把图1中的菱形沿对角线分成四个全等的直角三角形,将这四个直角三角形分别拼成如图2,图3所示的正方形,则图1中菱形的面积为()A.6B.24C.26D.1211.下列关于比例线段和相似的叙述,不正确的是()A.若a:b=c:d,则ac=bdB.相似三角形的面积比等于相似比的平方C.点C是线段AB的黄金分割点,且AC>BC,则D.经过位似多边形对应顶点的直线一定交于同一点12.一个长方体的三视图如图所示,若其俯视图为正方形,则这个长方体的体积为()A.48cm3B.72cm3C.144cm3D.288cm313.x2=﹣x方程的根是.14.如图,在△ABC中,AB=6,AC=4,D是AB边上的一点,当AD=时,△ABC ∽△ACD.15.点(m+3,2)和点(3,)是同一个反比例函数图象上的点,则m的值为.16.如图,在边长为4cm的正方形ABCD中,点Q是边CD的中点,点P是边BC上的一点,连接AP,PQ,且∠APQ=∠P AD,则线段PQ的长为cm.17.如图,利用一面墙(墙长25米),用总长度49米的栅栏(图中实线部分)围成一个矩形围栏ABCD,且中间共留两个1米的小门,设栅栏BC长为x米.(1)若矩形围栏ABCD面积为210平方米,求栅栏BC的长;(2)矩形围栏ABCD面积是否有可能达到240平方米?若有可能,求出相应x的值,若不可能,请说明理由.18.新冠肺炎疫情期间,口罩需求量大幅上升.某工厂接到任务紧急生产一批口罩,下面是每时生产口罩的数量与完成任务总共需要的时间的关系.每时生产口罩的数量/万只2346时间/时72483624(1)每时生产口罩的数量与时间有什么关系?(2)如果每时生产8万只口罩,那么完成这项任务一共需要多少时?19.如图,转盘黑色扇形和白色扇形的圆心角分别为120°和240°.(1)让转盘自由转动一次,指针落在白色区域的概率是多少?(2)让转盘自由转动两次,请用树状图或者列表法求出两次指针都落在白色区域的概率.(注:当指针恰好指在分界线上时,无效重转)20.如图,在△ABC中,AB=AC,点D是BC中点,点E是AD中点,延长BE至F,使EF=BE,连接AF,CF,BF与AC交于点G.(1)求证:四边形ADCF是矩形.(2)若AB=5,BC=6,线段CG的长为.21.某一广告墙PQ旁有两根直立的木杆AB和CD,某一时刻在太阳光下,木杆CD的影子刚好不落在广告墙PQ上,(1)你在图中画出此时的太阳光线CE及木杆AB的影子BF;(2)若AB=6米,CD=3米,CD到PQ的距离DQ的长为4米,求此时木杆AB的影长.22.如图,在正方形ABCD中,E是边AD上的点,点F在边CD上,且CF=3FD,∠BEF =90°.(1)求证:△ABE∽△DEF;(2)若AB=6,延长EF交BC的延长线于点G,求CG的长.23.如图,在平面直角坐标系中,点B在x轴上,∠ABO=90°,AB=BO,直线y=kx﹣4与反比例函数y=(x>0)的图象交于点A,与y轴分别交于点C.(1)求k的值;(2)点D与点O关于AB对称,连接AD,CD.证明:△ACD是直角三角形;(3)在(2)的条件下,点E在反比例函数的图象上,若S△ECD=S△OCD,直接写出点E 的坐标.参考答案1.解:把x=0代入一元二次方程(k﹣1)x2+3x+k2﹣1=0,得k2﹣1=0,解得k=﹣1或1;又k﹣1≠0,即k≠1;所以k=﹣1.故选:C.2.解:∵菱形ABCD的周长为8cm,∴AB=BC=2(cm),OA=OC,OB=OD,AC⊥BD,∵∠ABC=60°,∴△ABC是等边三角形,∴AC=AB=2cm,∴OA=1(cm),在Rt△AOB中,由勾股定理得:OB===(cm),∴BD=2OB=2(cm),故选:B.3.解:连接BP,如图,∵四边形ABCD为菱形,菱形ABCD的周长为24,面积为24,∴BA=BC=6,S△ABC=S菱形ABCD=12,∵S△ABC=S△P AB+S△PBC,∴×6×PE+×6×PF=12,∴PE+PF=4,故选:A.4.解:设袋子里黑色棋子的个数为x个,根据题意得:=0.1,解得:x=54,经检验:x=54是分式方程的解,估计袋子里黑色棋子的个数为54个.故选:C.5.解:∵反比例函数y=(k≠0)与正比例函数y=﹣2x没有交点,∴函数y=﹣2x在二、四象限,则反比例函数y=(k≠0)图象在一、三象限,∵﹣3<﹣1<0,∴点A(﹣1,a)、B(﹣3,b)在第三象限,∴a<b<0,∵4>0,∴C(4,c)在第一象限,∴c>0,∴a、b、c的大小关系是c>b>a,故选:C.6.解:设水池半径为xm,则正方形的边长为(2x+6)m,根据题意得:(2x+6)2﹣2πx2=100,故选:D.7.解:∵AB∥CD∥EF,∴=3,∴BC=3CE,∵BC+CE=BE,∴3CE+CE=12,∴CE=3.故选:D.8.解:用平行光线对矩形从不同的方向,不同的角度正投影,可以得到矩形、正方形、线段,不可能是梯形,故选:B.9.解:根据勾股定理,所给图形的两直角边为=,=2,所以,夹直角的两边的比为=,观各选项,只有B选项三角形符合,与所给图形的三角形相似.故选:B.10.解:设图1中分成的直角三角形的长直角边为a,短直角边为b,,得,∴图1中菱形的面积为:×4=12,故选:D.11.解:若a:b=c:d,则ad=bc,A不正确;相似三角形的面积比等于相似比的平方,B正确;点C是线段AB的黄金分割点,且AC>BC,则,C正确;经过位似多边形对应顶点的直线一定交于同一点,D正确.故选:A.12.解:∵俯视图为正方形,根据主视图可得:正方形对角线为6cm,长方体的高为8cm,∴长方体的体积为:6×6÷2×8=144(cm3).故选:C.13.解:x2=﹣x,x2+x=0,x(x+1)=0,∴x=0或x+1=0,∴x1=0,x2=﹣1.14.解:∵△ABC∽△ACD,AB=6,AC=4,∴,即,解得AD=.故答案为:.15.解:∵点(m+3,2)和点(3,)是同一个反比例函数图象上的点,∴2(m+3)=3×,∴m=﹣6.故答案为:﹣6.16.解:如图,延长AD,PQ交于点H,设PC=xcm,∵四边形ABCD是正方形,∴AD=CD=BC=4cm,AD∥BC,∵点Q是边CD的中点,∴DQ=CQ=2cm,∵AD∥BC,∴∠H=∠QPC,又∵∠DQH=∠CQP,∴△DQH≌△CQP(AAS),∴PC=DH=xcm,PQ=QH,∴AH=AD+DH=(4+x)cm,∵∠APQ=∠P AD,∴AH=PH=(4+x)cm,∴PQ=QH=()cm,∵PQ2=CQ2+PC2,∴()2=4+x2,∴x=或x=0(舍),∴PQ=cm,故答案为:.17.解:若设BC=x米,则AB=(49+1+1﹣3x)=(51﹣3x)米.(1)依题意得:x(51﹣3x)=210,整理得:x2﹣17x+70=0,解得:x1=7,x2=10.当x=7时,51﹣3x=51﹣3×7=30>25,不合题意,舍去;当x=10时,51﹣3x=51﹣3×10=21<25,符合题意.答:栅栏BC的长为10米.(2)矩形围栏ABCD的面积不可能达到240平方米,理由如下:依题意得:x(51﹣3x)=240,整理得:x2﹣17x+80=0.∵Δ=(﹣17)2﹣4×1×80=﹣31<0,∴原方程没有实数根,∴矩形围栏ABCD的面积不可能达到240平方米.18.解:(1)因为每时生产口罩的数量与时间的积一定,所以每时生产口罩的数量与时间成反比例;(2)设反比例函数解析式为:y=,把(2,72)代入得:k=144,故反比例函数解析式为:y=,∴y==18(时),答:完成这项任务一共需要18小时.19.解:(1)∵转盘黑色扇形和白色扇形的圆心角分别为120°和240°,∴白色扇形是黑色扇形的2倍,∴让转盘自由转动一次,指针落在白色区域的概率是;(2)画树状图如下:共有9种等可能的结果,两次指针都落在白色区域的结果有4种,∴两次指针都落在白色区域的概率为.20.(1)证明:∵点E是AD中点,∴AE=DE,在△AEF和△DEB中,,∴△AEF≌△DEB(SAS),∴AF=DB,∠AFE=∠DBE,∴AF∥DB,∵AB=AC,点D是BC中点,∴DB=DC,AD⊥BC,∴AF=DC,∠ADC=90°,∴四边形ADCF是平行四边形,∵∠ADC=90°,∴平行四边形ADCF是矩形;(2)解:过G作GH⊥CD于H,如图所示:则GH∥AD,∵AB=AC=5,点D是BC中点,∴AD⊥BC,BD=CD=BC=3,∴AD===4,由(1)得:AF=DC=BD=3=BC,AF∥BC,∴△AGF∽△CGB,∴==,∴AG=CG,∴AG=AC=,∴CG=AC﹣AG=5﹣=,故答案为:.21.解:(1)如图所示:(2)设木杆AB的影长BF为x米,由题意,得=,解得x=8.答:木杆AB的影长是8米.22.(1)证明:∵四边形ABCD是正方形,∴∠A=∠D=90°,∵∠BEF=90°,∴∠AEB+∠DEF=90°,又∵∠ABE+∠AEB=90°,∴∠ABE=∠DEF,∴△ABE∽△DEF;(2)解:∵四边形ABCD是正方形,∴AB=AD=CD=6,AD∥BG,∵CF=3FD,∴DF=1.5,设DE=x,∵△ABE∽△DEF,∴,即,解得x=3,∴DE=3,∵DE∥CG,∴△DEF∽△CGF,∴,∵CF=3FD,∴,∴CG=9,23.(1)解:令AB=BO=m,∵∠ABO=90°,∴AB⊥x轴,则设点A的坐标为(m,m),∵反比例函数y=(x>0)的图象交于点A,∴=m,解得m=±2,∵m>0,∴m=2,∵点A(2,2)在直线y=kx﹣4上,∴2=2k﹣4,∴k=3;(2)证明:由(1)可知B(2,0),AB=2,∵AB⊥BO,点D与点O关于AB对称,∴D(4,0),BD=2,∴AD2=AB2+BD2=22+22=8,过点A作AE⊥y轴,垂足为E,则点E(0,2),AE=2,∵直线y=3x﹣4与y轴交于点C,∴C(0,﹣4)则CE=6,∴AC2=AE2+CE2=22+62=40,∵∠OCD=90°,OD=4,OC=4,∴CD2=OD2+OC2=42+42=32,∵8+32=40,∴AD2+CD2=AC2,∴△ACD是直角三角形;(3)解:①当点E在CD上方时,如下图,过点O、A作直线m,由点O、A的坐标知,直线OA的表达式为y=x,由点C、D的坐标知,直线CD的表达式为y=x﹣4,则直线CD∥m,即OA∥CD,∵S△ECD=S△OCD,即两个三角形同底,则点E与点A重合,故点E的坐标为(2,2);②当点E(E′)在CD下方时,在y轴负半轴取CH=OC=4,则点H(0,﹣8),∵则S△ECD=S△OCD,∴过点H作直线m′∥CD,则直线m′与反比例函数的交点即为点E,∴直线m′的表达式为y=x﹣8,联立y=x﹣8和y=并解得(不合题意值已舍去),故点E的坐标为(4+2,2﹣4),综上,点E的坐标为(4+2,2﹣4)或(2,2).。
竹中2009—2010学年九年级上数学期末复习试题(一)

竹中2009—2010学年上九年级数学期末试题一、选择题:(每小题3分,共30 分)1、一直角三角形的两直角边分别为,那么这个直角三角形的面积是( ) A .8..2、下列图形中既是轴对称又是中心对称图形的是( )A 、三角形B 、平行四边形C 、圆D 、正五边形 3、方程x 2-4=0的解是 ( )A 、4B 、±2C 、2D 、-2 4题4、如图,四边形ABCD 内接于⊙O ,BC 是直径,AD =DC ,∠ADB =20º,则∠ACB ,∠DBC 分别为( )A .15º与30ºB .20º与35ºC .20º与40ºD .30º与35º5、在一个不透明的塑料袋中装有红色、白色球共40,除颜色外其它都相同,小明通过多次摸球试验后发现,其中摸到红色球的频率稳定在15%左右,则口袋中红色球可能有( ) A 、4个 B 、6个 C 、34个 D 、36个 6、⊙o 1与⊙o 2的半径分别是3、4,圆心距为1,则两圆的位置关系是( ) A 、相交 B 、外切 C 、内切 D 、外离 7、如图,⊙O 是△ABC 的内切圆,切点分别是D 、E 、F ,已知 ∠A=100°,∠C=30°,则∠DFE 的度数是( )A.55°B.60°C.65°D.70°7题8、平面直角坐标系内一点p(-2,3)关于原点对称点的坐标是( ) A 、(3,-2) B 、(2,3) C 、(-2,-3) D 、(2,-3) 9、下列根式中,是最简二次根式的是( )A.a a3 B.35a C.ba ab D.522b b a + 10、⊙o 的半径是13,弦 AB ∥C D, AB=24, C D=10,则 AB 与C D 的距离是 ( )A 、 7B 、 17C 、7或17D 、34二、填空题:(每小题3分,共30 分)11、有人为了强调一件事情很难办,常说“除非太阳从西边出来”,你认为这个事件是 。
九年级数学第一学期期末考试综合复习测试题(含答案)

九年级数学第一学期期末考试综合复习测试题(含答案)一.选择题(共10小题,每小题3分,共30分) 1.2022的相反数是( )A .2022B .2022-C .12022D .2022± 2.若代数式3125m x y -与822m nx y +-是同类项,则( )A .73m =,83n =-B .3m =,4n =C .73m =,4n =- D .3m =,4n =-3.下列四组线段中,能组成直角三角形的是( ) A .1a =,3b =,3c = B .2a =,3b =,4c = C .2a =,4b =,5c =D .3a =,4b =,5c = 4.如图所示,直线//a b ,231∠=︒,28A ∠=︒,则1(∠= )A .61︒B .60︒C .59︒D .58︒5.下列关于事件发生可能性的表述,正确的是( )A .“在地面向上抛石子后落在地上”是随机事件B .掷两枚硬币,朝上面是一正面一反面的概率为13C .在同批次10000件产品中抽取100件发现有5件次品,则这批产品中大约有500件左右的次品D .彩票的中奖率为10%,则买100张彩票必有10张中奖6.某校10名学生参加课外实践活动的时间分别为:3,3,6,4,3,7,5,7,4,9(单位:小时),这组数据的众数和中位数分别为( ) A .9和7 B .3和3 C .3和4.5 D .3和5 7.一个正多边形的每一个内角都是150︒,则它的边数为( ) A .6 B .9 C .12 D .158.若不等式组841x x x m +<-⎧⎨>⎩的解集是3x >,则m 的取值范围是( )A .3m <B .3mC .3m >D .3m9.已知关于x 的一元二次方程22(21)0x m x m --+=有实数根,则m 的取值范围是( ) A .14m 且0m ≠ B .14m C .14m < D .14m >10.如图1,一个扇形纸片的圆心角为90︒,半径为6.如图2,将这张扇形纸片折叠,使点A 与点O 恰好重合,折痕为CD ,图中阴影为重合部分,则阴影部分的面积为( )A .9632π-B .693π-C .91232π-D .94π二.填空题(共5小题,每小题3分,共15分) 11.将数据2022万用科学记数法表示为 .12.已知当3x =时,代数式35ax bx +-的值为20,则当3x =-时,代数式35ax bx +-的值是 .13.将抛物线229y x x =-+-向左平移2个单位,再向上平移1个单位后,得到的抛物线的解析式为 .14.已知ABC ∆中,点O 是ABC ∆的外心,140BOC ∠=︒,那么BAC ∠的度数为 .15.如图,在正方形ABCD 中,顶点(5,0)A -,(5,10)C ,点F 是BC 的中点,CD 与y 轴交于点E ,AF 与BE 交于点G ,将正方形ABCD 绕点O 顺时针旋转,每次旋转90︒,则第2023次旋转结束时,点G 的坐标为 .三.解答题(一)(共3小题,每小题8分,共24分) 16.计算(1)2()(2)x y x y x +--;(2)2219(1)244a a a a --÷--+.17.如图,90ACB ∠=︒,AC AD =.(1)过点D 作AB 的垂线DE 交BC 与点E ,连接AE .(尺规作图,并保留作图痕迹) (2)如果8BD =,10BE =,求BC 的长.18.如图,在四边形ABCD 中,AC 与BD 交于点O ,BE AC ⊥,DF AC ⊥,垂足分别为点E ,F ,且BE DF =,ABD BDC ∠=∠.求证:四边形ABCD 是平行四边形.四.解答题(二)(共3小题,每小题9分,共27分) 19.阳光中学为了丰富学生的课余生活,计划购买围棋和中国象棋供棋类兴趣小组活动使用,若购买3副围棋和5副中国象棋需要98元;若购买1副围棋和2副中国象棋需要36元.(1)求每副围棋和每副中国象棋各多少元;(2)阳光中学决定购买围棋和中国象棋共40副,总费用不超过538元,且围棋的副数不低于象棋的副数,问阳光中学有几种购买方案;(3)请求出最省钱的方案需要多少钱?20.我市某中学举行“中国梦⋅我的梦”的演讲比赛,赛后整理参赛学生的成绩,将学生的成绩分为A,B,C,D四个等级,并将结果绘制成如图所示的条形统计图和扇形统计图,但均不完整,请你根据统计图解答下列问题.(1)参加比赛的学生人数共有名,在扇形统计图中,表示“D等级”的扇形的圆心角为度,图中m的值为;(2)补全条形统计图;(3)组委会决定从本次比赛中获得A等级的学生中,选出两名去参加市中学生演讲比赛,已知A等级中男生只有1名,请用画树状图或列表的方法求出所选学生恰是一男一女的概率.21.22.某网店专售一款新型钢笔,其成本为20元/支,销售中发现,该商品每天的销售量y与销售单价x(元/支)之间存在如下关系:10400y x=-+,自武汉爆发了“新型冠状病毒”疫情该网店店主决定从每天获得的利润中抽出200元捐赠给武汉,同时又让顾客得到实惠,当销售单价定位多少元时,捐款后每天剩余利润为550元?五.解答题(三)(共2小题,每小题12分,共24分)22.如图,以点O为圆心,AB长为直径作圆,在O上取一点C,延长AB至点D,连接DC,过点A作O的切线交DC的延长线于点E,且DCB DAC∠=∠.(1)求证:CD是O的切线;(2)若6AD=,2:3BC CA=,求AE的长.23.如图,在平面直角坐标系中,直线33y x =--与x 轴交于点A ,与y 轴交于点C .抛物线2y x bx c =++经过A 、C 两点,且与x 轴交于另一点B (点B 在点A 右侧). (1)求抛物线的解析式;(2)若点M 是线段BC 上一动点,过点M 的直线ED 平行y 轴交x 轴于点D ,交抛物线于点E ,求ME 长的最大值及此时点M 的坐标; (3)在(2)的条件下:当ME 取得最大值时,在x 轴上是否存在这样的点P ,使得以点M 、点B 、点P 为顶点的三角形是等腰三角形?若存在,请直接写出所有点P 的坐标;若不存在,请说明理由.答案一.选择题1. B .2. D .3. D .4. C .5. C .6. C .7. C .8. B .9. B .10. C . 二.填空题11. 72.02210⨯.12. 30-.13. 228y x x =---.14. 70︒或110︒.15. (4,3)-. 三.解答题16.解:(1)2()(2)x y x y x +--22222x xy y xy x =++-- 2y =;(2)2219(1)244a a a a --÷--+ 23(3)(3)2(2)a a a a a ---+=÷-- 23(2)2(3)(3)a a a a a --=⋅---+ 23a a -=--. 17.解:(1)如图所示即为所求作的图形. (2)ED 垂直AB , 90ADE EDB ∴∠=∠=︒,在Rt BDE ∆中,22221086DE BE BD =-=-=, 在Rt ADE ∆和Rt ACE ∆中, AC ADAE AE =⎧⎨=⎩, Rt ADE Rt ACE(HL)∴∆≅∆, 6EC ED ∴==, 16BC BE EC ∴=+=.18.证明:ABD BDC ∠=∠, //AB CD ∴.BAE DCF ∴∠=∠.在ABE ∆与CDF ∆中, 90BAE DCF AEB CFD BE DF ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩. ()ABE CDF AAS ∴∆≅∆. AB CD ∴=.∴四边形ABCD 是平行四边形.19.解:(1)设每副围棋x 元,每副中国象棋y 元,根据题意得:3598236x y x y +=⎧⎨+=⎩,∴1610x y =⎧⎨=⎩,∴每副围棋16元,每副中国象棋10元;(2)设购买围棋z 副,则购买象棋(40)z -副, 根据题意得:1610(40)538m m +-,40m z -,2023m ∴,m 可以取20、21、22、23则有:方案一:购买围棋20副,购买中国象棋20副方案二:购买围棋21副,购买中国象棋19副方案:购买围棋22副,购买中国象棋18副方案四:购买围棋23副,购买中国象棋17副由4种方案;(3)由上一问可知共有四种方案:方案一:购买围棋20副,购买中国象棋20副;方案二:购买围棋21副,购买中国象棋19副;方案三:购买围棋22副,购买中国象棋18副;方案四:购买围棋23副,购买中国象棋17副;方案一需要20162010520x x +=; 方案二需要21161910526x x +=; 方案三需要22161810532x x +=; 方案四需要23161710538x x +=; 所以最省钱是方案一,需要520元.20.(1)解:根据题意得:总人数为:315%20÷=(人), 表示“D 等级”的扇形的圆心角为43607220⨯︒=︒;C等级所占的百分比为8100%40% 20⨯=,所以40m=,故答案为:20,72,40.(2)解:等级B的人数为20(384)5-++=(人),补全统计图,如图所示:(3)解:根据题意,列出表格,如下:男女1女2男女1、男女2、男女1男、女1女2、女1女2男、女2女1、女2共有6种等可能结果,其中恰是一男一女的有4种,所以恰是一男一女的概率为42 63 =.21.解:由题意可得(20)(10400)200550x x--+-=解得125x=,235x=因为要让顾客得到实惠,所以25x=答:当销售单价定为25元时,捐款后每天剩余利润为550元.22.(1)证明:连接OC,OE,如图,AB为直径,90ACB∴∠=︒,即190BCO∠+∠=︒,又DCB CAD∠=∠,1CAD∠=∠,1DCB∴∠=∠,90DCB BCO ∴∠+∠=︒,即90DCO ∠=︒, CD ∴是O 的切线;(2)解:EC ,EA 为O 的切线, EC EA ∴=,AE AD ⊥, OC OA =, OE AC ∴⊥,90BAC EAC ∴∠+∠=︒,90AEO EAC ∠+∠=︒, BAC AEO ∴∠=∠, tan tan BAC AEO ∴∠=∠,∴23BC AO AC AE ==, Rt DCO Rt DAE ∆∆∽,∴23CD OC OA DA AE AE ===, 2643CD ∴=⨯=, 在Rt DAE ∆中,设AE x =,222(4)6x x ∴+=+, 解得52x =. 即AE 的长为52.23.解:(1)直线33y x =--与x 轴、y 轴分别交于点A 、C , (1,0)A ∴-,(0,3)C -抛物线2y x bx c =++经过点(1,0)A -,(0,3)C -, ∴103b c c -+=⎧⎨=-⎩,解得23b c =-⎧⎨=-⎩,∴抛物线的解析式为223y x x =--.(2)设(E x ,223)(03)x x x --<<,则(,3)M x x -, 222393(23)3()24ME x x x x x x ∴=----=-+=--+,∴当32x =时,94ME =最大,此时3(2M ,3)2-. (3)存在.如图3,由(2)得,当ME 最大时,则3(2D ,0),3(2M ,3)2-,32DO DB DM ∴===; 90BDM ∠=︒,223332()()222OM BM ∴==+=. 点1P 、2P 、3P 、4P 在x 轴上, 当点1P 与原点O 重合时,则1322PM BM ==,1(0,0)P ; 当2322BP BM ==时,则232632322OP -=-=, 2632(2P -∴,0); 当点3P 与点D 重合时,则3332P M P B ==,33(2P ,0); 当4322BP BM ==时,则432632322OP +=+=, 4632(2P +∴,0). 综上所述,1(0,0)P ,2632(2P -,0),33(2P ,0),4632(2P +,0).。
人教版初中数学-学年九年级上学期期末专题复习 专题1:一元二次方程 解析版

人教版初中数学2019-2020学年九年级上学期期末专题复习专题1:一元二次方程一、单选题1.下列方程中,关于x的一元二次方程是()A. x2+2y=1B. ﹣2=0C. ax2+bx+c=0D. x2+2x=12.一元二次方程x2-x-4=0的一次项系数和常数项分别是()A. 1,-1B. 1,-4C. -1,-4D. -1,43.将一元二次方程化为一般形式,正确的是()A. B. C. D.4.方程的解是()A. B. C. , D.5.关于x的一元二次方程kx2-2x-1=0有实数根,则k的取值范围是( )A. k>-1或k≠0B. k≥-1C. k≤-1或k≠0D. k≥-1且k≠06.一元二次方程x2+4x+2=0的根的判别式的值为()A. 8B. 24C.D.7.已知x1、x2、是一元二次方程x2+x-2=0的两个根,则x1+x2+x1x2的值为()A. 1B. -3C. 3D. -2二、填空题8.方程x2-2ax+3=0有一个根是1,a的值是________。
9.若代数式可化为,则=________,=________.10.定义符号min{a,b}的含义为:当a≥b时,min{a,b}=b;当a<b时,min{a,b}=a,如:min{1,-2)=-2,min{-3,-2)=-3,则方程min{x,-x}=x2-1的解是________.三、计算题11.解下列方程。
(1)x2-5x+6=0(2)(2x+1)(x-4)=5.12.(1)先化简,再求值:(x-2y)2-x(x+3y)-4y2,其中x=-4,y= .(2)已知:x+y=6,xy=4,求下列各式的值x2+y213.按要求解一元二次方程(1)4x2﹣8x+1=0(配方法)(2)7x(5x+2)=6(5x+2)(因式分解法)(3)3x2+5(2x+1)=0(公式法)(4)x2﹣2x﹣8=0.(5)(6x-1)2=25;四、解答题14.如图,在宽为20m,长为27m的矩形地面上修筑同样宽的道路(图中阴影部分),余下的部分种上草坪.要使草坪的面积为450 ,求道路的宽.15.要组织一次篮球邀请比赛,参赛的队伍每两个队都要比赛一场.赛程安排7天,每天比赛4场,问组织者应该邀请多少个队参赛?五、综合题16.已知关于x的一元二次方程x2+x+m﹣1=0.(1)当m=0时,求方程的实数根.(2)若方程有两个不相等的实数根,求实数m的取值范围.17.在一次聚会上,规定每两个人见面必须握手,且握手1次.(1)若参加聚会的人数为3,则共握手________次;若参加聚会的人数为5,则共握手________次;(2)若参加聚会的人数为n(n为正整数),则共握手________次;(3)若参加聚会的人共握手28次,请求出参加聚会的人数.(4)嘉嘉由握手问题想到了一个数学问题:若线段AB上共有m个点(不含端点A,B),线段总数为多少呢?请直接写出结论.答案解析部分一、单选题1. D解:A、含有两个未知数,不是一元二次方程,故本选项不符合题意;B、分母中含有未知数,是分式方程,故本选项不符合题意;C、当a=0时不是一元二次方程,故本选项不符合题意;D、是一元二次方程,故本选项符合题意;故答案为:D.【分析】一元二次方程是指含有一个未知数,并且所含未知数的项的最高次数是2次的整式方程,根据定义判断即可.2. C解:一元二次方程x2-x-4=0的一次项系数时-1,常数项是-4,故C正确。
华东师大版九年级上册数学期末复习试卷1(有答案)

2020-2021学年华东师大版九年级上册数学期末复习试卷1 一.选择题(共10小题,满分40分,每小题4分)1.已知关于x的一元二次方程(a﹣1)x2+2(a+2b)x+4b+2=0根的情况是()A.有两个不相等的实数根B.有两个相等的实数根C.没有实数根D.以上都可能2.若双曲线y=过两点(﹣1,y1),(﹣3,y2),则y1与y2的大小关系为()A.y1>y2B.y1<y2C.y1=y2D.y1与y2大小无法确定3.如图,l1∥l2∥l3,直线a,b与l1、l2、l3分别相交于A、B、C和点D、E、F.若,DE=4.2,则DF的长是()A.B.6C.6.3D.10.54.如图,线段AB两个端点的坐标分别为A(2,2)、B(3,1),以原点O为位似中心,在第一象限内将线段AB扩大为原来的2倍后得到线段CD,则端点C的坐标分别为()A.(3,1)B.(3,3)C.(4,4)D.(4,1)5.若一组数据x1+1,x2+1,…,x n+1的平均数为16,方差为2,则另一组数据x1+2,x2+2,…x n+2的平均数和方差分别为()A.17,2B.17,3C.16,2D.16,36.下列各式中,从左边到右边的变形是因式分解的是()A.(x+2y)(x﹣2y)=x2﹣4y2B.x2y﹣xy2﹣1=xy(x﹣y)﹣1C.a2﹣4ab+4b2=(a﹣2b)2D.ax+ay+a=a(x+y)7.在比例尺为1:n的某市地图上,A,B两地相距5cm,则A、B之间的实际距离为()A.B.C.5ncm D.25n2cm8.一次围棋比赛,要求参赛的每两位棋手之间都要比赛一场,根据赛程计划共安排45场比赛,设本次比赛共有x个参赛棋手,则可列方程为()A.x(x﹣1)=45B.x(x+1)=45C.x(x﹣1)=45D.x(x+1)=459.如图,∠1=∠2,要使△ABC∽△ADE,只需要添加一个条件即可,这个条件不可能是()A.∠B=∠D B.∠C=∠E C.D.10.如图,直线y=x+1与两坐标轴分别交于A,B两点,点C是OB的中点,点D,E分别是直线AB,y轴上的动点,则△CDE的周长的最小值是()A.B.C.D.二.填空题(共8小题,满分32分,每小题4分)11.若,则=.12.方程2(x+2)=x(x+2)的解为.13.已知y是x的反比例函数,当x>0时,y随x的增大而减小.请写出一个满足以上条件的函数表达式.14.如果关于x的一元二次方程ax2+bx﹣1=0的一个解是x=1,则2021﹣a﹣b=.15.如果两个相似三角形的周长的比等于1:3,那么它们的面积的比等于.16.生物工作者为了估计一片山林中麻雀的数量,设计了如下方案:先捕捉200只麻雀,给它们做上标记后放回山林,一段时间后,再从中随机捕捉300只,其中有标记的麻雀有8只,请帮助工作人员估计这片山林中麻雀的数量约为只.17.已知点A(m,﹣2)和点B(3,n),若直线AB∥x轴,且AB=4,则m+n的值.18.如图,E,F分别为矩形ABCD的边AD,BC的中点,且矩形ABCD与矩形EABF相似,AB=1,则BC的长为.三.解答题(共8小题,满分78分)19.计算:(1﹣)0+|﹣|﹣2cos45°+()﹣120.解方程:2x2﹣3x=1﹣2x.21.如图,▱OABC的边OA在x轴的正半轴上,OA=5,反比例函数(x>0)的图象经过点C(1,4).(1)求反比例函数的关系式和点B的坐标;(2)过AB的中点D作DP∥x轴交反比例函数图象于点P,连接CP,OP.求△COP 的面积.22.某一特殊路段规定:汽车行驶速度不超过36千米/时.一辆汽车在该路段上由东向西行驶,如图所示,在距离路边10米O处有一“车速检测仪”,测得该车从北偏东60°的A 点行驶到北偏东30°的B点,所用时间为1秒.(1)试求该车从A点到B点的平均速度.(2)试说明该车是否超速.(、)23.某校为了解九年级学生新冠疫情防控期间每天居家体育活动的时间(单位:h),在网上随机调查了该校九年级部分学生.根据调查结果.绘制出如下的统计图1和图2.请根据相关信息,解答下列问题:(1)本次接受调查的初中学生人数为,图1中m的值为;(2)这组数据的平均数是,众数是,中位数是.(3)根据统计的这组每天居家体育活动时间的样本数据,估计该校500名九年级学生居家期间每天体育活动时间大于1h的学生人数.24.又到了西瓜成熟的季节,重庆某水果超市7月初购进黑美人西瓜和无籽西瓜共3000千克,其中黑美人西瓜进价为每千克3元,以每千克8元的价格出售;无籽西瓜进价为每千克3元,以每千克5元的价格出售.(1)若该超市7月底售完全部的两种西瓜,总利润不低于9600元,则黑美人西瓜至少购进多少千克?(2)8月初,由于受到其他水果的冲击,该水果超市决定结合实际情况调整进货计划和销售方案.在进价均不发生变化的情况下,黑美人西瓜售价每千克降低a元(售价不低于进价),无籽西瓜售价保持不变;同时,黑美人西瓜以(1)中利润最低时销售量的基础上减少a%购进;无籽西瓜以(1)中利润最低时销售量的基础上增加2a%购进,但无籽西瓜在运输、卸货等过程中损坏购进量的5%.超市决定将损坏的无籽西瓜不出售.如果该月两种西瓜全部出售完毕,所获总利润比7月底的最低总利润少1500元,求a的值.25.如图,正方形ABCD的顶点A在等腰直角三角形DEF的斜边EF上,EF与BC相交于点G,连接CF.(1)求证:△DAE≌△DCF;(2)求证:△ABG∽△CFG;(3)若正方形ABCD的的边长为2,G为BC的中点,求EF的长.26.如图,矩形ABCD中,点E在边CD上,将△BCE沿BE折叠,点C落在AD边上的点F处,过点F作FG∥CD交BE于点G,连接CG.(1)求证:四边形CEFG是菱形;(2)若BC=10,cos∠ABF=,求菱形CEFG的边长.参考答案与试题解析一.选择题(共10小题,满分40分,每小题4分)1.解:∵(a﹣1)x2+2(a+2b)x+4b+2=0,∴a﹣1≠0,解得a≠1,∵关于x的一元二次方程(a﹣1)x2+2(a+2b)x+2(a+2b)=0的二次项系数是a﹣1,一次项系数是2(a+2b),常数项是4b+2,∴△=4(a+2b)2﹣4(a﹣1)(4b+2)=4a2+16ab+16b2﹣16ab﹣8a+16b+8=4(a﹣1)2+4(2b+1)2>0,∴方程有两个不相等的实数根.故选:A.2.解:∵双曲线y=过两点(﹣1,y1),(﹣3,y2),∴﹣1•y1=2,﹣3•y2=2,∴y1=﹣2,y2=﹣,∴y1<y2.故选:B.3.解:∵l1∥l2∥l3,∴=,即=,解得,EF=6.3,∴DF=DE+EF=10.5,故选:D.4.解:∵以原点O为位似中心,在第一象限内将线段AB扩大为原来的2倍后得到线段CD,∴A点与C点是对应点,∵C点的对应点A的坐标为(2,2),位似比为:1:2,∴点C的坐标为:(4,4)故选:C.5.解:∵数据x1+1,x2+1,…,x n+1的平均数是16,∴数据x1+2,x2+2,…x n+2与原数据相比,每一个数据都增加1,因此平均数就比原平均数增加1,即16+1=17;∵数据x1+1,x2+1,…,x n+1的方差是2,∴数x1+2,x2+2,…x n+2的方差不变,还是2;故选:A.6.解:根据因式分解的意义:把一个多项式化成几个整式积的形式,A、右边不是积的形式,故本选项错误;B、右边最后不是积的形式,故本选项错误;C、右边是(a﹣2b)(a﹣2b),故本选项正确;D、结果是a(x+y+1),故本选项错误.故选:C.7.解:设A、B之间的实际距离为x,则1:n=5:x,解得x=5n,故选:C.8.解:本次比赛共有x个参赛棋手,所以可列方程为:x(x﹣1)=45.故选:A.9.解:∵∠1=∠2,∴∠1+∠BAE=∠2+∠BAE,∴∠DAE=∠BAC,A、添加∠B=∠D可利用两角法:有两组角对应相等的两个三角形相似可得△ABC∽△ADE,故此选项不合题意;B、添加∠C=∠E可利用两角法:有两组角对应相等的两个三角形相似可得△ABC∽△ADE,故此选项不合题意;C、添加可利用两边对应成比例且夹角相等的两个三角形相似可得△ABC∽△ADE,故此选项不合题意;D、添加不能证明△ABC∽△ADE,故此选项符合题意;故选:D.10.解:如图,作点C关于AB的对称点F,关于AO的对称点G,连接FG分别交AB、OA于点D、E,此时三角形CDE的周长最小,∵直线y=x+1与两坐标轴分别交于A、B两点,点C是OB的中点,∴B(﹣1,0),C(﹣,0),∴BO=1,OG=,BG=,易得∠ABC=45°,∴△BCF是等腰直角三角形,∴BF=BC=,由轴对称的性质,可得DF=DC,EC=EG,△CDE的周长=CD+DE+CE=DF+DE+EG=FG,此时△DEC周长最小,∵Rt△BFG中,FG===,∴△CDE周长的最小值是.故选:B.二.填空题(共8小题,满分32分,每小题4分)11.解:∵,∴=,∴=1﹣=1﹣=.故答案为:.12.解:原方程可化为:x(x+2)﹣2(x+2)=0;(x+2)(x﹣2)=0;x+2=0或x﹣2=0;解得:x1=2,x2=﹣2.故答案是:x1=2,x2=﹣2.13.解:只要使反比例系数大于0即可.如y=(x>0),答案不唯一.故答案为:y=(x>0),答案不唯一.14.解:把x=1代入方程ax2+bx﹣1=0得a+b﹣1=0,所以a+b=1,所以2021﹣a﹣b=2021﹣(a+b)=2021﹣1=2020.故答案为:2020.15.解:∵两个相似三角形的周长的比等于1:3,∴它们的相似比为1:3,∴它们的面积的比等于1:9.故答案为:1:9.16.解:200÷=7500(只),即这片山林中麻雀的数量约为7500只,故答案为:7500.17.解:∵点A(m,﹣2)和点B(3,n)且直线AB∥x轴,∴n=﹣2,∵AB=4,∴m=3+4=7或m=3﹣4=﹣1,当m=7时,m+n=7﹣2=5;当m=﹣1时,m+n=﹣1﹣2=﹣3;综上,m+n=5或﹣3;故答案为:5或﹣3.18.解:∵矩形ABCD与矩形EABF相似,∴=,即=,解得,AD=,∴BC=AD=,故答案为:.三.解答题(共8小题,满分78分)19.解:原式=1+﹣2×+4=1+﹣+4=5.20.解:原方程化为2x2﹣x﹣1=0,∵a=2,b=﹣1,c=﹣1,∴△=b2﹣4ac=(﹣1)2﹣4×2×(﹣1)=9,∴x==,∴x1=1,x2=﹣.21.解:(1)∵反比例函数y=(x>0)的图象经过点C(1,4).∴m=1×4=4,∴反比例函数的关系式为y=(x>0).∵四边形OABC为平行四边形,且点O(0,0),OA=5,点C(1,4),∴点A(5,0),∴点B(6,4).(2)延长DP交OC于点E,如图所示.∵点D为线段BA的中点,点A(5,0)、B(6,4),∴点D(,2).令y=中y=2,则x=2,∴点P(2,2),∴PD=﹣2=,EP=ED﹣PD=,∴S=EP•(y C﹣y O)=××(4﹣0)=3.△COP22.解:(1)据题意,得∠AOC=60°,∠BOC=30°在Rt△AOC中,∠AOC=60°∴∠OAC=30°∵∠AOB=∠AOC﹣∠BOC=60°﹣30°=30°∴∠AOB=∠OAC∴AB=OB在Rt△BOC中OB=OC÷cos∠BOC=10=(米)∴AB=(米)∴V=÷1=(米/秒).(2)∵36千米/时=10米/秒又∵,∴,∴小汽车超速了.23.解:(1)本次接受调查的初中学生人数为:4÷10%=40人,m%==25%,则m=25;故答案为:40,25.(2)由条形统计图得,4个0.9,8个1.2,15个1.5,10个1.8,3个2.1,平均数是:=1.5(h),∵1.5h出现了15次,出现的次数最多,∴众数是1.5h,∵第20个数和第21个数都是1.5h,∴中位数是1.5h;故答案为:1.5,1.5,1.5;(3)根据题意得:500×0.9=450(人),答:该校每天在校体育活动时间大于1h的学生有450人.24.解:(1)设购进x千克黑美人西瓜,则购进(3000﹣x)千克无籽西瓜,依题意,得:(8﹣3)x+(5﹣3)(3000﹣x)≥9600,解得:x≥1200.答:黑美人西瓜至少购进1200千克.(2)依题意,得:(8﹣a﹣3)×1200(1﹣a%)+5×(3000﹣1200)×(1+2a%)×(1﹣5%)﹣3×(3000﹣1200)×(1+2a%)=9600﹣1500,整理,得:2a2﹣195a+1750=0,解得:a1=10,a2=.当a=10时,8﹣a=7>3,符合题意;当a=时,8﹣a=﹣<3,不合题意,舍去.答:a的值为10.25.证明:(1)∵正方形ABCD,等腰直角三角形EDF,∴∠ADC=∠EDF=90°,AD=CD,DE=DF,∴∠ADE+∠ADF=∠ADF+∠CDF,∴∠ADE=∠CDF,在△ADE和△CDF中,∴△ADE≌△CDF(SAS);(2)延长BA到M,交ED于点M,∵△ADE≌△CDF,∴∠EAD=∠FCD,即∠EAM+∠MAD=∠BCD+∠BCF,∵∠MAD=∠BCD=90°,∴∠EAM=∠BCF,∵∠EAM=∠BAG,∴∠BAG=∠BCF,∵∠AGB=∠CGF,∴△ABG∽△CFG.(3)∵正方形ABCD的的边长为2,G为BC的中点,∴BG=CG=1,AG=,∵△ABG∽△CFG,∴,CF=2FG,∵CF2+FG2=CG2,(2FG)2+FG2=12,∴GF=,CF=,∵△DAE≌△DCF,∴AE=CF,∴EF=EA+AG+GF=CF+AG+GF=++=.26.(1)证明:由题意可得,△BCE≌△BFE,∴∠BEC=∠BEF,FE=CE,∵FG∥CE,∴∠FGE=∠CEB,∴∠FGE=∠FEG,∴FG=FE,∴FG=EC,∴四边形CEFG是平行四边形,又∵CE=FE,∴四边形CEFG是菱形;(2)∵矩形ABCD中,BC=10,cos∠ABF==,由翻折可知:BF=BC=10,∴AB=8,AD=10,∴∠BAF=90°,AD=BC=BF=10,∴AF=6,∴DF=4,设EF=x,则CE=x,DE=8﹣x,∵∠FDE=90°,∴42+(8﹣x)2=x2,解得,x=5.∴CE=5.。
华师大九年级数学(上)期末大复习及答案

华师大九年级数学(上)期末大复习第Ⅰ卷(满分48分)一、选择题:(每小题3分,共48分)1、下列条件中,不一定能使两个三角形全等的条件是( ) (A )两边一角对应相等 (B )两角一边对应相等 (C )三边对应相等 (D )两边和它们的夹角对应相等2、计算:21424m m ++-的结果是( ) A 、m+2 B 、m -2 C 、12m + D 、12m - 3、方程(a+2)|a|+3ax+1=0是关于x 的一元二次方程,则a 的值为( )A 、a =±2B 、a=2C 、a=-2D 、a ≠-2 4、若x <2,则2|2|x x --的值为( ) A 、-1 B 、0 C 、1 D 、2 5、如图1,AC 是⊙O 的直径,BD 是⊙O 的弦,EC ∥AB 交⊙O于E ,则图中与12∠BOC 相等的角共有( ) A 、2个 B 、3个 C 、4个 D 、5个6、如果关于x 的一元二次方程Kx 2-6x+9=0有两个不相等的实数根,那么K 的取值范围是( )A 、K <1B 、K ≠0C 、K <1且K ≠0D 、K >1 7、如图2,O为ABCD 的对角线AC 、BD 的交点,过O 的直线与边AD 、BC 分别交于点E 、F,则图中全等的三角形共有( )A 、2对B 、3对C 、5对D 、6对 8、圆心都在x 轴上的两圆有一个公共点是(1,2),那么这两圆的关系是( ) A 、内切 B 、外切 C 、相交 D 、外离9、如果圆锥的底面半径为3cm ,母线长为4cm ,那么它的侧面积等于( ) A 、24πcm 2 B 、12πcm 2 C 、12cm 2 D 、6πcm 2 10、下面是赵明同学在一次测验中解答的填空题,其中,正确的是( )A 、若x 2 =4,则x=2B 、方程x(2x -1)=2x -1的解为x =1C 、关于x 的方程x 2-3x +m=0的一个根是1, 那么m = 2图1D图2F EDCABOD 、若分式2321x x x -+-的值为零,则x = 1或x = 211、下列命题中,真命题是( )A 、有两边相等的平行四边形是菱形。
苏教版九年级数学期末复习测试卷(一)含答案

苏教版九年级数学期末复习测试卷(一)含答案(满分:100分时间:90分钟)一、选择题(本大题共8小题,每小题2分,共16分)1.在统计中,样本的方差可以反映这组数据的( )A.集中程度B.分布规律C.离散程度D.数值大小2.方程x2=2x的解是( )A.x=2 B.x2x2=0 C.x1=2,x2=0 D.x=03.若关于x的方程x2-4x+m=0没有实数根,则实数m的取值范围是( ) A.m<-4 B.m>-4 C.m<4 D.m>44.如图,点A,B,C是⊙O上的三点,若∠OBC=50°,则∠A的度数是( ) A.40°B.50°C.80°D.100°5.若扇形的半径为4,圆心角为90°,则此扇形的弧长是( )A.πB.2πC.4πD.8π6.如图,AB是⊙O的直径,弦CD交AB于点E,若AE=CD=8,∠BAC=12∠BOD,则⊙O的半径为( )A.4 B.5 C.4,D.37.国家实施惠农政策后,某镇农民人均收入经过两年由1万元提高到1.44万元.这两年该镇农民人均收入的平均增长率是( )A.20% B.22% C.10% D.11%8.如图,两圆相交于A,B两点,小圆经过大圆的圆心O,点C,D分别在两圆上,若∠ADB=100°,则∠ACB的度数为( )A.35°B.40°C.50°D.80°二、填空题(本大题共10小题,每小题2分,共20分)9.一组数据-3,-5,9,12,6,0的极差是_______.10.如果圆锥的母线长为6cm,侧面积为12πcm2,那么它的底面圆的半径为_______cm.11.若关于x的一元二次方程(a-1)x2+x+a-1=0的一个根是0,则实数a的值是_______.12.如图,若⊙O的半径为13cm,点P是弦AB上一动点,若到圆心的最短距离为5cm,则弦AB的长为_______cm.13.如图,在△ABC中,AB=AC=5,BC=6,点D为边BC上一动点(不与点B重合),以点D为圆心、DC的长为半径作⊙D.当⊙D与边AB相切时,BD的长为_______.14.随机从甲、乙两块试验田中各抽取100株麦苗测量高度(单位:cm),若计算平均数和方差的结果为x甲=13,x乙=13,s2甲=3.6,s2乙=15.8,则小麦长势比较整齐的试验田是_______.15.若x=1是一元二次方程x2-mx+n=0的一个根,则m2-2mn+n2的值为_______.16.在一个不透明的口袋中有三个完全相同的小球,他们的标号分别是2,3,4.若从袋中随机地摸出一个小球然后放回,再随机地摸出一个小球,则两次摸出的小球的标号之和为5的概率是_______.17.在学校组织的实践活动中,小明同学用纸板制作了一个如图所示的圆锥模型,若它的底面半径为1,高为2,则这个圆锥的侧面积为_______(结果保留π)18.如图,在边长为1的小正方形构成的网格中,若⊙O的半径为1,则图中阴影部分两个小扇形的面积之和为_______.(结果保留π)三、解答题(本大题共10题,共64分)19.(8分)(1)解下列方程.①x2-4x-1=0;②(x-5)2=5-x.(2)已知关于x的一元二次方程x2+kx-3=0.①求证:不论k为何实数,方程总有两个不相等的实数根;②当k=2时,用配方法解此一元二次方程.20.(6分)某单位招聘员工,采取笔试与面试相结合的方式进行,两项成绩的原始分均为100分.前6名选手的得分如下:根据规定,笔试成绩和面试成绩分别按一定的百分比折合成综合成绩(综合成绩的满分仍为100分).(1)这6名选手笔试成绩的中位数是_______分,众数是_______分;(2)现得知1号选手的综合成绩为88分,求笔试成绩和面试成绩各占的百分比;(3)求出其余5名选手的综合成绩,并以综合成绩排序确定前两名人选.21.(9分)如图1,在⊙O中,AB为⊙O的直径,AC是弦,OC=4,∠OAC=60°.(1)求∠AOC的度数;(2)在图1中,P为直径BA延长线上的一点,当CP与⊙O相切时,求PO的长;(3)如图2,一动点M从点A出发,在⊙O上按逆时针方向运动,当S△MAO=S△CAO时,求动点M所经过的弧长.22.(9分)一个不透明的口袋里,装有红、黄、蓝三种颜色的小球(除颜色外其余都相同),其中有红球2个、蓝球1个、黄球若干个,现从中任意摸出1个球是红球的概率为12.(1)求口袋中黄球的个数;(2)甲同学先随机摸出1个小球(不放回),再随机摸出1个小球,请用“树状图法”或“列表法”求两次摸出的都是红球的概率;(3)现规定:摸到红球得5分,摸到黄球得3分,摸到蓝球得2分(每次摸后放回),乙同学在一次摸球游戏中,第一次随机摸到1个红球第二次又随机摸到1个蓝球,若随机再摸一次,求乙同学三次摸球所得分数之和不低于10分的概率.23.(8分)商场某种商品进价为70元,当售价定为每件100元时,平均每天可销售20件.经调查发现,每件商品每降价1元,商场平均每天可多售出2件,若商场规定每件商品的利润率不低于30%,设每件商品降价x元.(1)商场日销售量增加_______件,每件商品盈利_______元;(用含x的代数式表示)(2)在上述条件不变、销售正常的情况下,每件商品降价多少元时,日盈利可达到750元?24.(6分)如图,AB是⊙O的直径,弦DE垂直平分半径OA,垂足为点C,DE=3,连接DB,过点E作FM∥BD,交BA的延长线于点M.(1)求⊙O的半径;(2)求证:EM是⊙O的切线;(3)若弦DF与直径AB相交予点P,当∠APD=45°时,求图中阴影部分的面积.25.(8分)如图1,已知在△ABC中,AB=AC,以边AB为直径的⊙O交BC于点D,交AC于点E,连接DE.(1)求证:DE=DC;(2)如图2,连接OE,将∠EDC绕点D按逆时针方向旋转,使∠EDC的两边分别交OE的延长线于点F、AC的延长线于点G,试探究线段DF与DG的数量关系.26.(8分)若x1,x2是关于x的方程x2+bx+c=0的两个实数根,且122x x k+=(k是整数),则称方程x2+bx+c=0为“偶系二次方程”,如方程x2-6x-27=0,x2-2x-8=0,x2+6x-27=0,x2+4x+4=0都是“偶系二次方程”.(1)判断方程x2+x-12=0是否是“偶系二次方程”,并说明理由;(2)对于任意一个整数b,是否存在实数c使得关于x的方程x2+bx+c=0是“偶系二次方程”,请说明理由.27.(8分)如图1,Rt△ABC两直角边的长为AC=3,BC=4.(1)如图2,⊙O与Rt△ABC的边AB相切于点X,与边BC相切于点Y.请你在图2中作出并标明⊙O的圆心(用尺规作图,保留作图痕迹,不写作法和证明).(2)P是这个Rt△ABC上和其内部的动点,以点P为圆心的⊙P与Rt△ABC的两条边相切.设⊙P的面积为S,你认为能否确定S的最大值?若能,请你求出S的最大值;若不能,请你说明不能确定S的最大值的理由.28.(9分)某中学有一块长为am、宽为bm的矩形场地,计划在该场地上修筑两条宽都为2m的互相垂直的道路,余下的四块矩形小场地建成草坪.(1)如图,请分别写出每条道路的面积(用含a或b的代数式表示);(2)已知a:b=2:1,并且四块草坪的面积之和为312m2,试求原来矩形场地的长与宽的值;(3)在(2)的条件下,为进一步美化校园,根据实际情况,学校决定对整个矩形场地作如下设计(要求同时符合下述两个条件):条件①:在每块草坪上各修建一个面积尽可能大的菱形花圃(花圃各边必须分别与所在草坪的对角线平行),并且其中有两个花圃的面积之差为13m2;条件②:整个矩形场地(包括道路、草坪、花圃)为轴对称图形.请你画出符合上述设计方案的一种草图(不必说明画法与根据),并求出每个菱形花圃的面积.参考答案1.C2.C3.D4.A5.B6.B7.A8.B9.1710.211.-112.2413.10 314.甲15.116.2 917.3π18.4π19.(1)①x1=2x2=2②x2=5,x2=4 (2)②x1=1,x2=-320.(1) 84.5 84 (2)40%,60% (3) 4号和2号21.(1)60°(2)8 (3)①43π②83π22.(1)1 (2)16(3)3423.(1)2x 30-x (2)每件商品降价5元时,日盈利可达到750元24.(2)略(3)36 4π-25.略26.(1)不是.(2)存在.27.(1)由∠B的角平分线、平角∠BXA的角平分线、平角∠BYC的角平分线中的任意两条所得交点即为所求圆的圆心O (2)144 49π28.(1)这两条道路的面积分别是2am2和2bm2.(2)长为28m,宽为14m (3)32.5m2。
最新人教版九年级上期数学期末复习考试题(一)
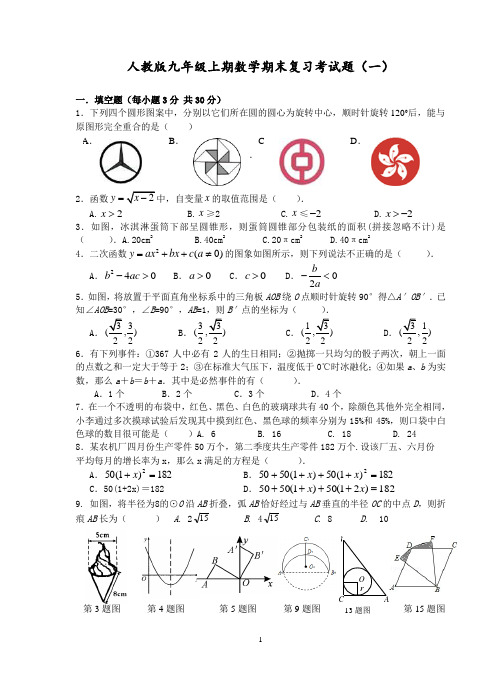
13题图rBAC O第5题图第3题图第4题图 第9题图第15题图人教版九年级上期数学期末复习考试题(一)一.填空题(每小题3分 共30分)1.下列四个圆形图案中,分别以它们所在圆的圆心为旋转中心,顺时针旋转120°后,能与CA.2x >B.x ≥2C.x ≤2-D.2x >-3.如图,冰淇淋蛋筒下部呈圆锥形,则蛋筒圆锥部分包装纸的面积(拼接忽略不计)是( ).A.20cm 2 B.40cm 2 C.20πcm 2 D.40πcm 24.二次函数2(0)y ax bx c a =++≠的图象如图所示,则下列说法不正确的是( ).A.240b ac -> B .0a > C .0c > D .02ba-< 5.如图,将放置于平面直角坐标系中的三角板AOB 绕O 点顺时针旋转90°得△A′OB′.已知∠AOB =30°,∠B =90°,AB =1,则B′点的坐标为( ).A .3)22B .3(22C .1(22D .1)226.有下列事件:①367人中必有2人的生日相同;②抛掷一只均匀的骰子两次,朝上一面的点数之和一定大于等于2;③在标准大气压下,温度低于0℃时冰融化;④如果a 、b 为实数,那么a +b =b +a .其中是必然事件的有( ).A .1个B .2个C .3个D .4个7.在一个不透明的布袋中,红色、黑色、白色的玻璃球共有40个,除颜色其他外完全相同,小李通过多次摸球试验后发现其中摸到红色、黑色球的频率分别为15%和45%,则口袋中白色球的数目很可能是( )A. 6 B. 16 C. 18 D. 24 8.某农机厂四月份生产零件50万个,第二季度共生产零件182万个.设该厂五、六月份 平均每月的增长率为x ,那么x 满足的方程是( ).A .182)1(502=+xB .182)1(50)1(50502=++++x x C .50(1+2x)=182 D .182)21(50)1(5050=++++x x9. 如图,将半径为8的⊙O 沿AB 折叠,弧AB 恰好经过与AB 垂直的半径OC 的中点D ,则折痕AB 长为( ) A. 215 B . 415 C . 8 D. 1010.矩形ABCD 中,AD =8cm ,AB =6cm .动点E 从点C 开始沿边CB 向点B 以2cm /s 的速度运动至点B 停止,动点F 从点C 同时出发沿边CD 向点D 以1cm /s 的速度运动至点D 停止.如图可得到矩形CFHE ,设运动时间为x (单位:s ),此时矩形ABCD 去掉矩形CFHE 后剩余部分的面积为y (单位:cm 2),则y 与x 之间的函数关系用图象表示大致是下图中的( )。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
竹中—上九年级数学期末试题
一、选择题:(每小题3分,共30 分)
1、一直角三角形的两直角边分别为a=2,b=3,那么这个直角三角形的面积是( ) A .8 B .7 C .9 D .
2、下列图形中既是轴对称又是中心对称图形的是( )
A 、三角形
B 、平行四边形
C 、圆
D 、正五边形 3、方程x 2
-4=0的解是 ( )
A 、4
B 、±2
C 、2
D 、-2 4题
4、如图,四边形ABCD 内接于⊙O ,BC 是直径,AD =DC ,∠ADB =20º,则∠ACB ,∠DBC 分别为( )
A .15º与30º
B .20º与35º
C .20º与40º
D .30º与35º 5、在一个不透明的塑料袋中装有红色、白色球共40,除颜色外其它都相同,小明通过多次摸球试验后发现,其中摸到红色球的频率稳定在15%左右,则口袋中红色球可能有( ) A 、4个 B 、6个 C 、34个 D 、36个 6、⊙o 1与⊙o 2的半径分别是3、4,圆心距为1,则两圆的位置关系是( ) A 、相交 B 、外切 C 、内切 D 、外离 7、如图,⊙O 是△ABC 的内切圆,切点分别是D 、
E 、
F ,已知 ∠A=100°,∠C=30°,则∠DFE 的度数是( )
A.55°
B.60°
C.65°
D.70°
7题
8、平面直角坐标系内一点p(-2,3)关于原点对称点的坐标是( ) A 、(3,-2) B 、(2,3) C 、(-2,-3) D 、(2,-3) 9、下列根式中,是最简二次根式的是( )
A.
a a 3 B.3
5a C.
b
a a
b D.5
22b b a + 10、⊙o 的半径是13,弦 AB ∥C D, AB=24, C D=10,则 AB 与C D 的距离是 ( )
A 、 7
B 、 17
C 、7或17
D 、34
二、填空题:(每小题3分,共30 分)
11、有人为了强调一件事情很难办,常说“除非太阳从西边出来”,你认为这个事件是 。
12、当x 时,
2
1
-+x x 在实数范围内有意义。
13、.一条弦把圆分为2﹕3的两部分, 则这条弦所对的圆周角的度数为 14、已知圆锥的母线长5,底面半径为3,则圆锥的侧面积为
15.如图,△ABC 绕点B 逆时针方向旋转到△EBD 的位置,若∠A=15°,∠C=10°,E,B,C 在一条直线
上,旋转角是 度。
20题 16、关于x 的一元二次方程0433)12222=-+++-m m x m x m (有一个根为0,则m 的值为 。
17、已知方程x 2 -3x+k=0有两个相等的实数根,则k= 18、在周长相等的正三角形,正方形,圆中,面积最大的是 。
19、掷3枚质地均匀的硬币,两枚正面朝上的概率是 。
20、在纸上剪下一个圆形和一个扇形的纸片,使之恰好能围成一个圆锥模型,若圆的半径为r,扇形的半
径为R ,扇形的圆心角等于90°,则r 与R 之间的关系是 。
三、 解答题(共25分) 21.(1)(5分)计算: 81
22-+ (2)(5分)解方程:0432
=--x x
362222O D
C
B A
22、(5分)不透明的袋中装有3个大小相同的小球,其中两个为白色,一个为红色,随机地从袋中摸取一个小球后放回,再随机地摸取一个小球,(用列表或树形图求下列事件的概率)
(1)两次取的小球都是红球的概率;(2)两次取的小球是一红一白的概率.
23、(5分)如图,有一面积是150平方米的长方形鸡场,鸡场的一边靠墙(墙长18米),墙对面有一个2米宽的门,另三边用竹篱笆围城,篱笆总长33米,求:鸡场的长和宽各为多少米?
24、(5分)如图,AB是⊙O的直径,∠BAC=45°,AB=BC.
(1)、求证:BC是⊙O的切线;
(2)、设阴影部分的面积为a,b, ⊙O的面积为S,请写出S与a,b的关系式。
四、解答题
25(7分)如图,在△ABC中,∠C=90°, AD是∠BAC的平分线,O是AB上一点, 以OA为半径的⊙O经过点D。
(1)求证: BC是⊙O切线;
(2)若BD=5, DC=3, 求AC的长。
五、(8分)26、在△ABC中,∠BAC=90°,
AB=AC=22,⊙A的半径为1,若点O在BC上运动(与B,C不重合)设OB=X,△AOC的面积为Y。
(1)求Y与X的函数关系式,指出自变量X的取值范围;
(2)以点O为圆心,OB长为半径作⊙O,当⊙O 与⊙A相切时△AOC的面积
O
A
C
D
B。
