快速绘制M图的一些规律
m序列快速生成算法

m序列快速生成算法摘要:1.m 序列的概述2.m 序列快速生成算法的原理3.m 序列快速生成算法的具体步骤4.m 序列快速生成算法的应用案例5.m 序列快速生成算法的优缺点分析正文:一、m 序列的概述m 序列,也被称为m 序列数列,是一种在数学和计算机科学中经常出现的数列。
它的定义是:从1 开始,每个数都是前两个数之和。
例如,前几个m 序列数为:1, 1, 2, 3, 5, 8, 13, 21, 34, 55,...。
m 序列具有很多有趣的性质,如斐波那契数列、卢卡斯数列等,因此在各个领域都有广泛的应用。
二、m 序列快速生成算法的原理m 序列快速生成算法是一种高效生成m 序列的方法,其原理是利用数学递推关系式,通过迭代计算来快速生成m 序列。
m 序列的递推关系式为:F(n) = F(n-1) + F(n-2),其中F(n) 表示第n 个m 序列数。
通过这个递推关系式,我们可以从已知的前两个m 序列数开始,逐步计算出后续的m 序列数。
三、m 序列快速生成算法的具体步骤1.初始化两个变量a 和b,分别表示m 序列的前两个数。
2.使用递推关系式F(n) = F(n-1) + F(n-2),计算出第n 个m 序列数。
3.将计算出的第n 个m 序列数赋值给变量a,并将变量b 的值赋给变量a。
4.重复步骤2 和3,直到计算出所需的m 序列数。
四、m 序列快速生成算法的应用案例m 序列快速生成算法在很多领域都有应用,如计算机图形学、数据压缩、金融分析等。
以计算机图形学为例,m 序列可以用来生成光滑的曲线和曲面,提高图形的质量。
在数据压缩中,m 序列可以用来压缩数据,减少存储空间。
在金融分析中,m 序列可以用来预测股票价格等。
五、m 序列快速生成算法的优缺点分析优点:1.m 序列快速生成算法计算速度快,能够高效地生成m 序列。
2.m 序列具有很多有趣的性质,因此在各个领域都有广泛的应用。
缺点:1.m 序列快速生成算法的计算过程较为复杂,需要处理递推关系式。
m顶的特征

m顶的特征说实话m顶这个东西,特征挺有意思的。
让我想想这个特征,我观察了好久呢。
首先呢,m顶的第一个特征就是有两个高点,这两个高点就像是两座小山峰一样,一左一右,或者一先一后吧。
不过要判断这两个高点可不容易呢,有时候我就看错了,把一些小波动也当成是高点了。
例如我之前观察一只股票的价格走势,感觉好像是要形成m顶了,结果仔细一看,那只不过是短期的正常波动。
再来,这两个高点之间还会有个小小的低谷,这个低谷就像是两座山峰中间的山谷一样。
这个低谷的深度也是有讲究的,把这两个高点连成一条线,低谷距离这条线的深度有时候能反映出很多东西。
我就发现如果这个低谷比较浅呢,可能这个m顶后面的走势就不会太剧烈的反转。
但如果这个低谷很深,就像深不见底的小峡谷,那可能后面的跌势就会比较猛。
从左右两边的走势来看,自左边高点下降再到低谷的斜率和右边高点下来的斜率有时候会不一样。
我发现有些时候左边下来的坡度比较缓,就像人慢慢走着下坡路,而右边呢则是像坐滑梯一样,一下子就滑下去了,这种情况往往预示着情况很危急哦。
不过我也不确定每次都会这样精确的发生,毕竟市场或者说各种情况影响因素太多了。
而且m顶的形成过程不是瞬间的,它需要一定的时间。
这就像是炖一锅汤,得慢慢熬制才能有这个形状的形成。
我观察股票走势就发现,有时候得好多交易日,甚至好几个月才能说m顶完整地呈现出来。
如果这个过程中突然有个很大的外力干扰,比如重大政策发布或者公司重大事件,那这m顶可能就半途而废了,这个时候我就很困惑到底还会不会形成m顶呢。
还有就是m顶两个高点的成交量也是个特征,通常在左边高点的时候成交量会比较大,不过这也不是绝对的啦,有时候右边高点的成交量也会很大,这时候就像是两个大汉在拔河,谁对市场的影响力更大就不好说了。
我还发现有时候m顶看起来并不那么对称,就像人的两只手一样,虽然都是手但是大小形状会有差异。
一个高点会比另一个高点略高一点或者略低一点,这个时候就很难判断到底是不是m顶了。
简述m样作用

简述m样作用m样(M样式)是一种用于描述数据分布和趋势的统计图表样式。
它是一种直观、简洁且易于理解的方式,可以帮助人们更好地理解和分析数据。
m样可以用于展示数据的分布情况。
通过绘制频率分布直方图,可以清晰地看出数据的分布情况。
直方图的x轴表示数据的取值范围,y轴表示频率或者百分比。
直方图的每个柱子代表了该区间内数据的频数或者频率。
通过观察直方图的形状,可以得出数据的分布特点,比如是否对称、是否呈现峰态等。
m样还可以用于展示数据的趋势情况。
通过绘制折线图,可以清晰地反映数据随时间变化的趋势。
折线图的x轴表示时间,y轴表示数据的取值。
通过观察折线的走势,可以判断数据是增长、下降还是保持稳定。
同时,折线图还可以用于比较不同组别或者不同条件下的数据变化趋势,帮助人们找出规律或者趋势。
m样还可以用于展示数据的关系。
通过绘制散点图,可以清晰地显示出两个变量之间的关系。
散点图的x轴表示一个变量,y轴表示另一个变量。
每个点代表了一个数据点,通过观察点的分布情况,可以判断出两个变量之间是否存在线性关系、正相关还是负相关。
除了以上几种常见的m样,还有其他一些特殊的m样。
比如地图可以用于展示地理数据的分布情况,热力图可以用于展示数据的密度情况,雷达图可以用于展示多个变量之间的关系等等。
不同的m样适用于不同的数据类型和分析目的,选择合适的m样可以更好地展示数据并得出结论。
需要注意的是,在使用m样时需要注意数据的准确性和合理性。
数据的准确性可以通过数据来源的可靠性和数据收集的方法来保证,而数据的合理性则需要根据具体情况来判断。
同时,在绘制m样时也要注意选择合适的图表类型和参数设置,以确保图表能够准确地传达数据的含义。
m样是一种用于描述数据分布和趋势的统计图表样式,可以帮助人们更好地理解和分析数据。
通过绘制直方图、折线图、散点图等不同类型的m样,可以清晰地展示数据的分布情况、趋势情况和关系情况。
在使用m样时,需要注意数据的准确性和合理性,选择合适的图表类型和参数设置,以确保图表能够准确地传达数据的含义。
找规律画图知识点总结

找规律画图知识点总结一、图形的形状1.1 点、线、面在找规律画图中,最基本的图形包括了点、线和面。
点是最基本的图形,它没有长度和宽度,只有位置;线由一连续的无限个点组成,具有长度但没有宽度;面由一条闭合的线组成,它有长度和宽度。
1.2 圆、三角形、矩形等几何形状几何形状是找规律画图中常见的图形,如圆、三角形、矩形等。
它们具有具体的形状和特征,通过观察和比较这些形状的变化,可以发现规律和趋势。
二、变化趋势2.1 增长、减少和不变在找规律画图中,常常需要观察图形的变化趋势,包括增长、减少和不变。
这些变化趋势反映了图形中的规律和关系,是问题解决和预测的重要依据。
2.2 正比例和反比例找规律画图中常常需要观察变量之间的关系,包括正比例和反比例关系。
正比例关系是指两个变量之间的比值保持不变,反比例关系是指一个变量的增加导致另一个变量的减少。
2.3 周期性变化在找规律画图中,有些图形呈现出周期性变化,如正弦曲线、余弦曲线等。
这种周期性变化反映了图形中的规律和规律,是问题解决和预测的重要依据。
三、数学关系3.1 等差数列和等比数列在找规律画图中,常常需要观察数列的变化规律,包括等差数列和等比数列。
等差数列是指数列中相邻两项的差保持不变,等比数列是指数列中相邻两项的比保持不变。
3.2 函数和方程在找规律画图中,常常需要通过函数和方程来描述图形的规律和趋势。
函数是一种数学关系,它描述了变量之间的对应关系;方程是一种数学表达式,它描述了方程中的未知数满足的条件。
3.3 图形表达式在找规律画图中,常常需要通过图形表达式来描述图形的形状和特征。
图形表达式包括了方程、不等式、函数等,它们可以用来描述图形的数学关系和规律。
四、应用找规律画图在数学、科学和工程等领域有广泛的应用。
在数学中,它常常用来发现数列的规律和趋势,解决代数和几何等问题;在科学中,它常常用来分析数据和趋势,推断和预测实验结果;在工程中,它常常用来设计模型和方案,优化生产和工艺等。
画Nyquist图的一些方法
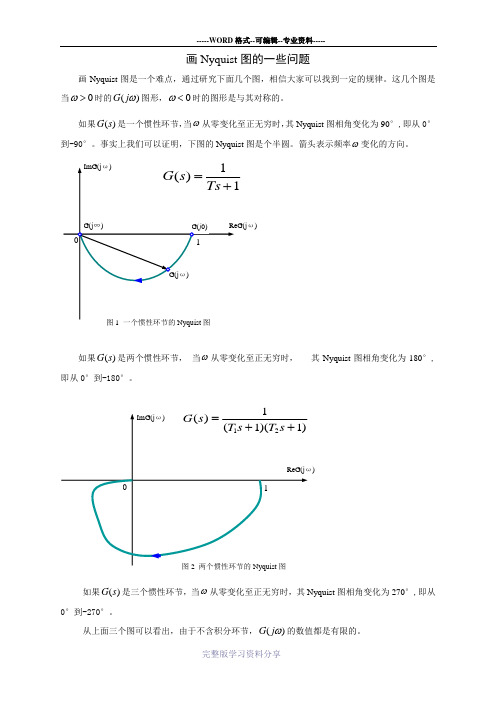
画Nyquist 图的一些问题画Nyquist 图是一个难点,通过研究下面几个图,相信大家可以找到一定的规律。
这几个图是当0ω>时的()G j ω图形,0ω<时的图形是与其对称的。
如果()G s 是一个惯性环节,当ω从零变化至正无穷时,其Nyquist 图相角变化为90°,即从0°到-90°。
事实上我们可以证明,下图的Nyquist 图是个半圆。
箭头表示频率ω变化的方向。
如果()G s 是两个惯性环节, 当ω从零变化至正无穷时, 其Nyquist 图相角变化为180°,即从0°到-180°。
如果()G s 是三个惯性环节,当ω从零变化至正无穷时,其Nyquist 图相角变化为270°,即从0°到-270°。
从上面三个图可以看出,由于不含积分环节,()G j ω的数值都是有限的。
当()G s 存在积分环节时,ω接近零时的()G j ω会趋于无穷大。
如果有一个积分环节,0()90G j ωω=+∠=-。
其Nyquist 图相角变化为90°,即从-90°到-180°。
如果()G s 有两个积分环节,0()180G j ωω=+∠=-。
其Nyquist 图相角变化为90°,即从-180°到-270°。
如果()G s 有三个积分环节,0()270G j ωω=+∠=-。
其Nyquist 图相角变化为90°,即从-270°到-360°。
如果()G j ω包含积分环节,我们在选择Nyquist 路径时,会沿着一个足够小的半圆从s 平面原点的右边绕过。
见下图。
此时 ,所以0r ≈,θ是从-90°到90°我们记Nyquist 路径的一部分(无穷小半圆)为C 0,则有一个积分环节且系统是非最小相位时,C 0的映射为()j j K G s e Re rθϕ-≈=,其中R 等于无穷大,ϕ是从90°顺时针变化到-90°。
弯矩图绘制方法汇总
D
M图
A
E FPa
FPa
a F
B
D
FPa
FPa
a
C
a
a
a
a
FPa MA =FPa A
a
FP B
C
D
FRAy =FP
M图
M图
精选课件
第17页
3-5 静定结构的特性
.4 荷载等效特性
当静定结构的内部几何 不变局部上的荷载作静 力等效变换时,只有该 部分的内力发生变化, 而其余部分的内力保持 不变。
A
C
P
P
4. 受集中力偶 m 作用时,在m作用点处M有跳跃(突变),跳 跃量为m,且左右直线均平行。
m
平行
m
精选课件
第3页
二. 铰处 M = 0
三. 刚结点力矩平衡
40
20
20
M0
M=0
M =?0
10
30
M0
20
20
精选课件
第4页
四. 集中力 P 与某些杆轴线重合时,M为零
P
M=0
P M=0
剪力Q为零时, M图为直线。
精选课件
FP
第23页
静定结构
M
FP 解除约束,单
自由度体系
Mα
FP 体系发生虚 Δ 位移
刚体虚位移原理的虚功方程
FP Δ - M α=0 可唯一地求得 M= FP Δ/α
精选课件
第24页
静定结构派生性质
支座微小位移、温度改变不产生反力和内力
若取出的结构部分(不管其可变性)能够平衡外荷载,则 其他部分将不受力
A
B
C t2
A
相似基本图形-M型

FED AC B 相似基本图形——M 型一、一般M 型基本条件:①∠PMQ=∠B=∠C .基本结论: ①相似结论:△BEM ∽___________; ②等积式:BM·CM=_______________.二、中点M 型基本条件:①∠PMQ=∠B=∠C ;②M 是BC 的中点.基本结论:①相似结论:△EMF ∽___________∽___________;②平分线结论:EM 平分___________,______________________; ③等积式:EM 2=EB·EF ,______________________,______________________三、常见特例 特例一:条件:①等边△ABC ;②∠MPN=60°,③P 是BC 的中点.特例二:条件:①等腰直角△ABC ,AC=BC ,∠C=90°;②∠EDF=45°;③点D 是AB 的中点.特例三:条件:①AB=AC ;②∠BAC=120°,③∠EDF=30°,D 是BC 的中点.FE DABCMD E P C AB N B B特例四:条件:①矩形ABC D ; ②∠GEF=90°;③E 是AB 的中点.特例五:条件:①直角梯形ABCD 中,AB ∥CD ,∠A=90°;②E 是AD 的中点;③∠BEC=90°.巩固训练:1.已知:如图,梯形ABCD 中,AD ∥BC ,∠A=90°,E 为AB 的中点,若AD=2,BC=4,∠CED=90°,则CD 的长为_____________.2.如图,在正方形ABCD 中,点E 、F 在边BC 、CD 上,若AE=2,EF=1,则正方形的边长为__________第1题 第2题3.已知正方形ABCD 的对角线相交于点Q ,点E 为射线AC 上的一个动点(不与A 、O 、C 重合),连结DE ,作EF ⊥DE 交直线AB 于点F.(1)当点在线段OA 上时(如图①),求证:CE -∙AF. (2)若AB=4,,连结DF 交AE 于点M ,求线段DM 的长; (3)连接FC 并延长交DE 于点N ,求DN 的长.E A BFA D G F EBC AD DEB C A图①图②已知E为△ABC内部一点,AE延长线交边BC于点D,连接BE、CE,∠BED=∠BAC=2∠DEC.(1)如图①,若AC=AB,求证:BE=2AE;(2)如图②,在(1)的条件下,将∠ABC沿BC翻折得到∠FBC,AE延长线经过点F,M为DF的中点,连接CM并延长交BF于点G.若CG=AE=2DE,求BD的长.AB CEDFGMDECBA图①图②FGMDECBA。
快速绘制M图的一些规律

3-4 快速绘制M图的一些规律一. 利用 q、Q、M 之间的微分关系以及一些 推论1.无荷载区段,M为直线直线12.受匀布荷载 q 作用时,M为抛物线,且凸向与 q 方 向一致ql 2 8 ql 2 823. 受集中荷载P作用时,M为折线,折点在集中力 作用点处,且凸向与P方向一致。
P P4. 受集中力偶 m 作用时,在m作用点处M有跳跃 (突变),跳跃量为m,且左右直线均平行。
mm平行二. 铰处 M = 0M=0 M=03?三. 刚结点力矩平衡40 20 20 10 30 20 20∑M =0∑M =0四. 集中力 P 与某些杆轴线重合 时,M 为零4P P M=0 M=0五. 剪力Q为常值时,M图为斜线; 剪力 Q为零时, M为常值, M图为直线。
5PP剪力Q为零时, M图为直线。
剪力Q为常值 时,M图为斜线六. 平衡力系的影响6当由平衡力系组成的荷载作用在静定结构的某 一本身为几何不变的部分上时,则只有此部分受 力,其余部分的反力内力皆为零。
P PP平衡力系P七、利用对称性作弯矩图结构对称,荷载对称 结构对称,荷载反对称Pa/2 P Pa/27内力对称 内力反对称mm0 0a a a a判断下列结构弯矩图形状是否正确,错的请改正。
8√q↓↓↓↓↓↓↓↓↓↓√ql2/8 l 0 lP9PP↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓P P√示例试作图示刚架的弯矩图。
各杆杆长均为l。
P P Pl Q= 0,M为一直线 M=0 2Pl P 2Pl P Q= P,M为一斜线10示例试作图示刚架的弯矩图。
各杆杆长均为l。
m m m m m11在m作用点处M 有跳跃 (突变),跳跃量为 m,且左右直线均平行。
Q= 0,M为一直线示例122Pa2Pa 2Pa 3Pa P铰处的M为零,且梁上无 集中荷载作用,M图为一 无斜率变化的斜直线。
Q= P,M 为一斜线P Q= 0,M为一直线 3Pa示例3qa 2q(2a)2 = 2qa 2 213qa ⋅ 2a = qa 2 2 qa 2 8例 作图示多跨静定梁的弯矩图4kN 4kN.m 1kN/m14铰处的M为零,且梁上无集中荷载作用, M图为一无斜率变化的斜直线。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3-4 快速绘制M图的一些规律
一. 利用 q、Q、M 之间的微分关系以及一些 推论
1.无荷载区段,M为直线
直线
1
2.受匀布荷载 q 作用时,M为抛物线,且凸向与 q 方 向一致
ql 2 8 ql 2 8
2
3. 受集中荷载P作用时,M为折线,折点在集中力 作用点处,且凸向与P方向一致。
P P
4. 受集中力偶 m 作用时,在m作用点处M有跳跃 (突变),跳跃量为m,且左右直线均平行。
m
m
平行
二. 铰处 M = 0
M=0 M=0
3
?
三. 刚结点力矩平衡
40 20 20 10 30 20 20
∑M =0
∑M =0
四. 集中力 P 与某些杆轴线重合 时,M 为零
4
P P M=0 M=0
五. 剪力Q为常值时,M图为斜线; 剪力 Q为零时, M为常值, M图为直线。
5
P
剪力Q为零时, M图为直线。
P
剪力Q为常值 时,M图为斜线
六. 平衡力系的影响
6
当由平衡力系组成的荷载作用在静定结构的某 一本身为几何不变的部分上时,则只有此部分受 力,其余部分的反力内力皆为零。
P P
P
平衡力系
P
七、利用对称性作弯矩图
结构对称,荷载对称 结构对称,荷载反对称
Pa/2 P Pa/2
7
内力对称 内力反对称
m
m
0 0
a a a a
示例1
试作图示刚架的弯矩图。
各杆杆长均为l。
P P Pl Q= 0,M为一直线 M=0 2Pl P 2Pl P Q= P,M为一斜线
8
例2 试作图示刚架的M图
ql 2 2 ql 2 2
9
ql 2 8
ql ql
(各杆杆长均为l)
示例 3
10
试作图示刚架的弯矩图。
各杆杆长均为l = 4m。
20kN/m 80 80 40kN 80 40
40
示例 4
试作图示刚架的弯矩图。
P P P
11
三根竖杆均为悬 臂,其M图可先 绘出。
Pa
Pa Pa Pa
Pa Pa
属悬臂部分,相应的 M图为水平线。
两段的剪力相等铰处 的M为零,M图的坡 度(斜率)相等,两 条线平行。
铰处的M为零,相应 的M图为一斜直线。
示例 5
试作图示刚架的弯矩图。
各杆杆长均为l。
m m m m m
12
在m作用点处M 有跳跃 (突变),跳跃量为 m,且左右直线均平 行。
Q= 0,M为一直线
示例 6
13
2Pa
2Pa 2Pa 3Pa P
铰处的M为零,且梁上无 集中荷载作用,M图为一 无斜率变化的斜直线。
Q= P,M 为一斜线
P Q= 0,M为一直线 3Pa
示例 7
试作图示刚架的弯矩图。
各杆杆长均为l。
ql 2 2 ql 2 2
14
ql ql
ql 2
ql
示例 8
3qa 2
15
q(2a)2 = 2qa 2 2
qa ⋅ 2a = qa 2 2 qa 2 8
例9 作图示多跨静定梁的弯矩图
4kN 4kN.m 1kN/m
16
铰处的M为零,且梁上无集中荷载作用, M图为一无斜率变化的斜直线。
4 8 2 2
ql 2 =2 2
4 2
ql 2 =2 8
2
4
2
示例 10
试作图示刚架弯矩图的形状。
ql 2 2
17
m
m
mm
P
m Q=0,M为一直线 P
示例11
2qa 2
18
4qa
2
4qa 2
2qa
4qa 2 2qa 4qa 2 4qa
2
2qa 2
2qa 2
4 qa 3 4qa
2 qa 3
示例12
19
18P 6P 6P
20 判断下列结构弯矩图形状是否正确,错的请改正。
√
q
↓↓↓↓↓↓↓↓↓↓
√
ql2/8 l 0 l
21P P P
↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓P P √。
