图像平滑的MATLAB实现
图像平滑的MATLAB实现

图像平滑的MATLAB实现摘要:图像平滑技术用于平滑图像的噪声,本文对均值滤波、中值滤波、维纳滤波等三种平滑滤波器进行理论学习,并通过MATLAB对滤波效果进行仿真。
关键词:图像平滑均值滤波中值滤波维纳滤波实际获得的图像一般都因受到某种干扰而含有噪声。
引起噪声的原因有敏感元器件的内部噪声、照相底片上感光材料的颗粒、传输通道的干扰及量化噪声等。
噪声产生的原因决定了噪声的分布特性及它和图像信号的关系。
根据噪声服从的分布,可以分为高斯噪声、泊松噪声和颗粒噪声等。
平滑技术用于平滑图像的噪声,平滑噪声可以在空间域中进行,基本方法是求像素灰度的平均值或中值。
为了既平滑噪声又保护图像信号,也有一些改进的技术,比如在频域中运用低通滤波器。
MATLAB图像处理工具箱提供了模拟噪声生成的函数imnoise和去除噪声的方法。
函数imnoise可以对图像添加一些典型的噪声。
由于噪声的随机性,它们对某一像点的影响使其灰度和邻点的灰度显著不同,因此可以利用这种不同来消除噪声。
去除噪声的方法有线性滤波、中值滤波、自适应滤波。
本文就针对上述三种平滑滤波进行MATLAB仿真。
1 图像平滑的MATLAB实现1.1 均值滤波[1]1.1.1理论基础邻域平均法是空间域平滑噪声技术,其均值滤波器对于扫描得到的图像中的颗粒噪声非常适用,理论依据如下:对于给定的图像f(i,j)中的每个像点(m,n),取其邻域S。
设S含有M个像素,取其平均值作为处理后所得图像像点(m,n)处的灰度。
用一像素邻域内各像素灰度平均值来代替该像素原来的灰度,即是邻域平均技术。
邻域S的形状和大小根据图像特点确定。
一般取的形状是正方形、矩形及十字形等,S的形状和大小可以在全图处理过程中保持不变,也可根据图像的局部统计特性而变化,点(m,n)一般位于S的中心。
如S为3×3邻域,点(m,n)位于S中心,则:假设噪声n是加性噪声,在空间各点互不相关,且期望为0,方差δ2,g是未受污染的图像,含有噪声的图像f经过邻域平均后为由上式可知,经邻域平均后,噪声的均值不变,方差,即噪声方差变小,说明噪声强度减弱了,即抑制了噪声。
利用Matlab进行图像处理的常用方法

利用Matlab进行图像处理的常用方法概述:图像处理是数字信号处理的一个重要分支,也是计算机视觉领域的核心内容之一。
随着计算机技术的不断发展,利用Matlab进行图像处理的方法变得越来越重要。
本文将介绍一些常用的Matlab图像处理方法,包括图像的读取与显示、图像的预处理、图像的滤波处理、基本的图像增强方法以及图像的分割与检测等。
一、图像的读取与显示在Matlab中,可以使用imread函数直接读取图像。
通过指定图像的路径,我们可以将图像读取为一个矩阵,并且可以选择性地将其转换为灰度图像或彩色图像。
对于灰度图像,可以使用imshow函数将其显示出来,也可以使用imwrite函数将其保存为指定格式的图像文件。
对于彩色图像,可以使用imshow函数直接显示,也可以使用imwrite函数保存为指定格式的图像文件。
此外,还可以使用impixel函数获取图像中指定像素点的RGB值。
二、图像的预处理图像的预处理是指在进一步处理之前对图像进行调整和修复以消除图像中的噪声和不良的影响。
常用的图像预处理方法包括图像的平滑处理、图像增强和图像修复等。
1. 图像平滑处理:常用的图像平滑方法有均值滤波、中值滤波和高斯滤波等。
其中,均值滤波将每个像素点的值替换为其周围像素点的平均值,中值滤波将每个像素点的值替换为其周围像素点的中值,高斯滤波则通过加权平均的方式平滑图像。
2. 图像增强:图像增强是指通过一些方法提高图像的质量和信息内容。
常用的图像增强方法包括直方图均衡化、对比度拉伸和锐化等。
直方图均衡化通过调整图像的灰度分布,以提高图像的对比度和细节。
对比度拉伸是通过将图像的像素值线性拉伸到整个灰度范围内,以增强图像的对比度。
锐化则是通过增强图像的边缘和细节,使图像更加清晰。
三、图像的滤波处理图像的滤波处理是指通过对图像进行一系列滤波操作,来提取图像中的特征和信息。
常用的图像滤波方法包括模板滤波、频域滤波和小波变换等。
1. 模板滤波:模板滤波是基于局部像素邻域的滤波方法,通过定义一个滤波模板,将其与图像进行卷积操作,从而实现图像的滤波。
图像处理与matlab实例之图像平滑(一)

图像处理与matlab实例之图像平滑(⼀) ⼀、何为图像噪声?噪声是妨碍⼈的感觉器官所接受信源信息理解的因素,是不可预测只能⽤概率统计⽅法认识的随机误差。
举个例⼦: 从这个图中,我们可以观察到噪声的特点:1>位置随机 2>⼤⼩不规则。
我们将这种噪声称为随机噪声(random noise),这是⼀种⾮常常见的噪声类型。
⼆、噪声的类型 噪声可以借⽤随机过程以及概率密度函数(Probability Density Function,PDF)来描述,通常可采⽤其数组特征,即均值,⽅差,相关函数等。
按照概率密度函数分为⾼斯噪声、瑞利噪声、伽马噪声、指数分布噪声、均匀分布噪声、脉冲噪声、泊松噪声等。
有的噪声与图像信号的强度不相关,如图像传输过程引⼊的信道噪声、摄像机扫描噪声等,这种噪声称为加性噪声(additive noise)。
常见的加性噪声按照概率密度函数特征分为短拖尾加性噪声(如均匀分布噪声)、中拖尾加性噪声(⾼斯分布噪声)、长拖尾加性噪声(如指数分布噪声)、脉冲噪声(如椒盐噪声、随机数脉冲噪声等)。
有的噪声与图像信号有关,往往随着图像信号的变化⽽变化,如光照变化引起的噪声、飞机扫描图像中的噪声、电视扫描光栅中的相⼲噪声、斑点噪声等。
这种噪声称为乘性噪声(multiplicative noise)。
matlab向图中添加噪声的指令: I1=imnoise(I,type,parameters); 其中,当type为gaussian,所加⼊噪声是parameters为m(均值)、v(⽅差)的⾼斯噪声,这是最普通的噪声。
当type为localvar时,所加⼊噪声是parameters为0(均衡)、v(⽅差)的⾼斯噪声。
当type为poission时,所加⼊的是⽆参数的泊松噪声,在照度⾮常⼩时出现,或在⾼倍电⼦放⼤线路中出现。
当type为salt&pepper时,所加⼊的噪声是parameters为d(密度)的椒盐噪声。
图像边沿平滑处理的matlab实现

图像边沿平滑处理的matlab实现完成图像处理的算法:1、读⼊⽂件通过matlab读取图像⽂件。
2、获取蒙版对图像进⾏逐点扫描,当点的三个通道值⾄少有⼀个⼩于阈值时让这个点变为纯⿊⾊。
如图,可见此时的蒙版中⼼有空缺,且边缘有噪声⽽且有粘连⼩块。
为了消除这些噪声和⼩块,我们对图像的蒙版进⾏腐蚀和扩张操作。
3、对蒙版进⾏腐蚀应⽤matlab的腐蚀函数,选择腐蚀的结构元素为11*11的全1矩阵,对图像进⾏腐蚀操作,腐蚀后,图像缩⼩,边缘变得平滑。
腐蚀后效果如图:4、对图像进⾏扩张操作将图像复原到原始蒙版,该扩张或丢失边缘信息,正好删除掉噪声和多余的⼩块。
进⾏扩张所⽤的结构元素和腐蚀所⽤的结构元素相同。
可以明显看到边缘得到改善。
扩张后效果如图:5、⽤蒙版遮罩⽣成图像利⽤蒙版的遮罩⽅式,通过原图⽣成新的图像。
能明显看出边沿的噪声和多余⼩块被去除。
产⽣的图像如下图:6、调整图像⼤⼩⾸先通过getFrame函数得到图像的边框,该函数的原理是从上下左右四个⽅向对图像进⾏逼近,记录四个边缘的位置,以便计算缩放的⼤⼩。
原理如下图:在获得了边框后,将框内的图像进⾏⼀个缩放,使该⼦图像的长或宽和原图⼀致,再⽤空⽩补齐另外⼀个⽅向。
最后达到缩放后的图像如下:附matlab程序:附1:main.minputFilePrefix = 'datacache\\';outFilePrefix = 'output\\';fileNamePrefix = 'dst_';picNum = 79;pxmin = 10000000;pdxmax = 0;pymin = 10000000;pdymax = 0;for p = 0:picNum-1if(p<10)fileName = sprintf('%s0%d.jpg',fileNamePrefix,p);else fileName = sprintf('%s%d.jpg',fileNamePrefix,p);end;inputFilePath = [inputFilePrefix fileName];outputFilePath = [outFilePrefix fileName];BW = imread(inputFilePath);[BW1 mask] = getSmoothImage(BW,230);[px py pdx pdy] = getFrame(mask);pxmin = min(pxmin,px);pdxmax = max(pdxmax,pdx);pymin = min(pymin,py);pdymax = max(pdymax,pdy);imwrite(BW1,outputFilePath,'jpg');pend%重新调整⼤⼩for p = 0:picNum-1if(p<10)fileName = sprintf('%s0%d.jpg',fileNamePrefix,p);else fileName = sprintf('%s%d.jpg',fileNamePrefix,p);end;inputFilePath = [outFilePrefix fileName];outputFilePath = [outFilePrefix fileName];I = imread(inputFilePath);INew = reScale(I,pxmin,pdxmax,pymin,pdymax);imwrite(INew,outputFilePath,'jpg');imshow(INew);pEnd附2:getSmoothImage.mfunction [ BW1 mask ] = getSmoothImage( BW,threshold )%GETSMOOTHIMAGE Summary of this function goes here% Detailed explanation goes here% 该函数⾸先得到图形的蒙版,然后对蒙版进⾏腐蚀和扩张,最后利⽤蒙版收缩和扩张 HEIGHT = size(BW,1);WIDTH = size(BW,2);mask = zeros(HEIGHT,WIDTH,'uint8');%得到蒙版threshold = 230;for i = 1:HEIGHTfor j = 1:WIDTHif(BW(i,j,1)>threshold&&BW(i,j,2)>threshold&&BW(i,j,3)>threshold)mask(i,j) = 255;endendend%腐蚀扩张蒙版SE = strel('square',11);mask = imdilate(mask,SE);mask = imerode(mask,SE);%利⽤蒙版遮罩获取图像BW1 = BW;for i = 1:HEIGHTfor j = 1:WIDTHif(mask(i,j) == 255)BW1(i,j,1) = 255;BW1(i,j,2) = 255;BW1(i,j,3) = 255;endendendend附3:getFrame.mfunction [ x,y,dx,dy ] = getFrame( mask )%GETFRAME Summary of this function goes here % Detailed explanation goes here获取图像外框backGroundColor = 255;found = false;for i = 1:size(mask,1)for j = 1:size(mask,2)if(mask(i,j) ~= backGroundColor)y = i;found = true;break;endendif foundbreak;endendfound = false;for i = 1:size(mask,1)for j = 1:size(mask,2)if(mask(size(mask,1)-i+1,j) ~= backGroundColor) dy = size(mask,1)-i+1-y;found = true;break;endendif foundbreak;endendfound = false;for i = 1:size(mask,2)for j = 1:size(mask,1)if(mask(j,i) ~= backGroundColor)x = i;found = true;break;endendif foundbreak;endendfound = false;for i = 1:size(mask,2)for j = 1:size(mask,1)if(mask(j,size(mask,2)-i+1) ~= backGroundColor)dx = size(mask,2)-i+1-x;found = true;break;endendif foundbreak;endendend附4:reScale.mfunction [ INew ] = reScale(I,pxmin,pdxmax,pymin,pdymax) %RESCALE Summary of this function goes here% Detailed explanation goes hereglobal WIDTH;global HEIGHT;ISub = I(pymin:pymin+pdymax,pxmin:pxmin+pdxmax,:);ISubScaled = imresize(ISub,min(WIDTH/pdxmax,HEIGHT/pdymax));INew = 255*ones(HEIGHT,WIDTH,3,'uint8');copyWidth = min(size(ISubScaled,2),WIDTH);copyHeight = min(size(ISubScaled,1),HEIGHT);if(copyWidth==WIDTH)pstarty = max(1,floor((HEIGHT-copyHeight)/2));pstartx = 1;elsepstartx = max(1,floor((WIDTH-copyWidth)/2));pstarty = 1;endt = ISubScaled(1:copyHeight,1:copyWidth,1);%INew(pstarty:pstarty+copyHeight-1,pstartx:pstartx+copyWidth-1,3) = t;for i = 1:copyHeightfor j = 1:copyWidthINew(pstarty+i-1,pstartx+j-1,:) = ISubScaled(i,j,:);endendend附:5:在探索过程中所写的⼀些函数:1、获取主体中的像素点:通过getRect函数,通过逐⾏扫描,依次查找不是纯⽩⾊的点,在找到这个点之后,搜索以这个点为左上定点以estimateLength为边长的矩形,统计出纯⽩点和⾮纯⽩点的⽐例,让这个⽐例达到⼀个阈值时,我们认为这个点就是主体中的⼀个点,可以根据这个点采⽤floodfill算法。
matlab让二维矩阵数据变平滑的方法

matlab让二维矩阵数据变平滑的方法MATLAB中有多种方法可以用来使二维矩阵数据变得平滑。
本文将介绍其中的两种常用方法:平均滤波和高斯滤波。
平均滤波是一种简单且直观的方法,通过计算每个像素周围的邻域像素的平均值来实现平滑。
在MATLAB中,可以使用imfilter函数来实现平均滤波。
以下是具体的步骤:1. 加载图像并转换为灰度图像。
你可以使用imread函数加载图像,并用rgb2gray函数将其转换为灰度图像。
2. 定义滤波器。
平均滤波器是一个具有相同权重的n×n大小的方形内核,其中n是奇数。
你可以使用fspecial函数来定义平均滤波器。
例如,h = fspecial('average', [3 3]) 将创建一个3×3的平均滤波器。
3. 对图像进行滤波。
使用imfilter函数将滤波器应用于图像。
例如,filtered = imfilter(image, h) 将对图像进行平均滤波,并将结果保存到filtered变量中。
通过改变滤波器的大小,你可以调整平滑的程度。
较小的滤波器将产生较弱的平滑效果,而较大的滤波器则会产生更明显的平滑效果。
然而,使用较大的滤波器也可能导致图像细节的丢失。
高斯滤波是一种基于高斯函数的平滑方法,它在平滑过程中考虑了像素之间的距离。
与平均滤波相比,高斯滤波可以更好地保留图像细节。
以下是使用MATLAB进行高斯滤波的步骤:1. 加载图像并转换为灰度图像,同样使用imread和rgb2gray函数。
2. 定义高斯滤波器。
与平均滤波器不同,高斯滤波器将在内核中应用不同的权重。
你可以使用fspecial函数来定义高斯滤波器。
例如,h = fspecial('gaussian', [5 5], 2) 将创建一个5×5的高斯滤波器,标准差为2。
3. 对图像进行滤波,同样使用imfilter函数。
例如,filtered= imfilter(image, h) 将对图像进行高斯滤波,并将结果保存到filtered变量中。
Matlab中的图像重建与图像恢复技术

Matlab中的图像重建与图像恢复技术深入研究和掌握图像重建与图像恢复技术对于图像处理和计算机视觉领域的研究人员来说至关重要。
在现实生活中,图像可能因传感器噪声、数据传输损失或其他因素而受损,导致图像出现模糊、噪声等问题。
为了改善这些问题,我们需要使用图像重建和恢复技术,将受损的图像还原到原始清晰的状态。
Matlab作为一种功能强大的科学计算软件,提供了丰富的工具和函数,可以帮助我们实现图像重建和恢复的任务。
在本文中,我们将探讨几种常用的图像重建和恢复技术,并介绍如何使用Matlab来实现它们。
第一部分:图像去噪与平滑图像中的噪声往往是由电子设备、图像采集过程或传输过程中引入的。
去除这些噪声对于提高图像质量非常重要。
在Matlab中,我们可以使用均值滤波、中值滤波、高斯滤波等方法进行图像去噪和平滑。
均值滤波是一种常用的线性滤波方法,它通过计算图像周围像素的平均值来减小噪声。
中值滤波则取邻域像素的中值作为当前像素的值,可以有效地去除脉冲噪声和椒盐噪声。
高斯滤波则使用高斯核函数对图像进行平滑,可以在平滑图像的同时保留图像的细节信息。
第二部分:图像复原与去模糊当图像受到模糊因素的影响时,如相机抖动、运动模糊等,我们可以使用图像复原和去模糊技术来提高图像的清晰度。
在Matlab中,我们可以使用逆滤波、维纳滤波等方法进行图像复原和去模糊。
逆滤波是一种经典的图像复原方法,通过将图像的频谱进行逆变换,消除因模糊而引入的相位延迟和衰减。
然而,逆滤波在存在噪声的情况下容易引入放大噪声的问题。
为了解决这个问题,可以使用维纳滤波器,它通过权衡图像信号和噪声的功率谱来恢复原始图像。
第三部分:图像超分辨率重建超分辨率重建是一种在低分辨率图像的基础上提高图像分辨率的技术。
它在很多应用中都非常有用,如视频监控、医学图像分析等。
在Matlab中,我们可以使用插值方法、重建方法等技术进行图像超分辨率重建。
插值方法是一种常用的图像超分辨率技术,它通过对像素进行重新采样来增加图像的分辨率。
MATLAB绘制平滑曲线
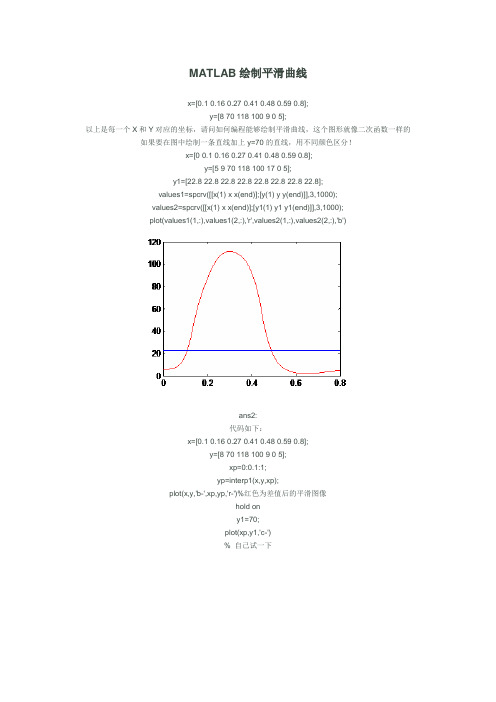
MATLAB绘制平滑曲线x=[0.1 0.16 0.27 0.41 0.48 0.59 0.8];y=[8 70 118 100 9 0 5];以上是每一个X和Y对应的坐标,请问如何编程能够绘制平滑曲线,这个图形就像二次函数一样的如果要在图中绘制一条直线加上y=70的直线,用不同颜色区分!x=[0 0.1 0.16 0.27 0.41 0.48 0.59 0.8];y=[5 9 70 118 100 17 0 5];y1=[22.8 22.8 22.8 22.8 22.8 22.8 22.8 22.8];values1=spcrv([[x(1) x x(end)];[y(1) y y(end)]],3,1000);values2=spcrv([[x(1) x x(end)];[y1(1) y1 y1(end)]],3,1000);plot(values1(1,:),values1(2,:),'r',values2(1,:),values2(2,:),'b')ans2:代码如下:x=[0.1 0.16 0.27 0.41 0.48 0.59 0.8];y=[8 70 118 100 9 0 5];xp=0:0.1:1;yp=interp1(x,y,xp);plot(x,y,'b-',xp,yp,'r-')%红色为差值后的平滑图像hold ony1=70;plot(xp,y1,'c-')% 自己试一下ans3:x=[0.1 0.16 0.27 0.41 0.48 0.59 0.8];y=[8 70 118 100 9 0 5];X=linspace(0,.9);Y=spline(x,y,X);plot(x,y,'ro',X,Y,X,70+0*X)another file:>help smooth自己查一下帮助another question:x有90个值,Y也有90个值,一一对应,用PLOT(x,y)后是折线,请问怎样把它改为平滑曲线,谢谢!ans:平滑曲线的话,建议你用样条插值。
Matlab中的插值和平滑方法

Matlab中的插值和平滑方法1. 引言在数值分析和数据处理中,插值和平滑是常用的技术手段,可以用于填补数据的空缺以及降低数据中的噪声。
Matlab作为一种强大的数值计算和数据处理软件,提供了丰富的插值和平滑方法,本文将介绍其中的一些常用方法及其应用。
2. 插值方法2.1 线性插值线性插值是最简单的一种插值方法,它假设待插值函数在相邻数据点之间是线性变化的。
Matlab中提供了interp1函数实现线性插值,可以通过设定插值点的横坐标向量和已知数据点的横坐标向量,以及对应的纵坐标向量,得到插值结果。
2.2 分段插值分段插值是一种更精确的插值方法,它假设待插值函数在相邻数据点之间是分段线性变化的。
Matlab中的interp1函数也可以实现分段插值,通过指定'linear'插值方法和 'pchip'插值方法,可以得到不同的插值结果,前者得到的结果比较平滑,而后者更接近原始数据的形状。
2.3 样条插值样条插值是一种更高阶的插值方法,它假设待插值函数在相邻数据点之间是多项式变化的。
Matlab中的spline函数可以实现三次样条插值,它通过计算每个数据点处的二阶导数,得到一个以每个数据点为节点的三次多项式函数。
样条插值可以更加精确地还原数据,但也容易受到离群点的干扰。
3. 平滑方法3.1 移动平均移动平均是一种常用的平滑方法,它通过计算数据点周围一定范围内的平均值,得到平滑后的结果。
Matlab中的smoothdata函数提供了不同的平滑方法,包括简单移动平均、指数移动平均和加权移动平均等,可以根据具体需求选择适当的方法。
3.2 Savitzky-Golay滤波Savitzky-Golay滤波是一种基于最小二乘法的平滑方法,它通过拟合多项式曲线来实现数据的平滑。
Matlab中的sgolay函数可以实现Savitzky-Golay滤波,通过指定不同的拟合阶数和窗口大小,可以得到不同程度的平滑结果。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
图像平滑的MATLAB实现
摘要:图像平滑技术用于平滑图像的噪声,本文对均值滤波、中值滤波、维纳滤波等三种平滑滤波器
进行理论学习,并通过MATLAB对滤波效果进行仿真。
关键词:图像平滑均值滤波中值滤波维纳滤波
实际获得的图像一般都因受到某种干扰而含有噪声。
引起噪声的原因有敏感元器件的内部噪声、照相底片上感光材料的颗粒、传输通道的干扰及量化噪声等。
噪声产生的原因决定了噪声的分布特性及它和图像信号的关系。
根据噪声服从的分布,可以分为高斯噪声、泊松噪声和颗粒噪声等。
平滑技术用于平滑图像的噪声,平滑噪声可以在空间域中进行,基本方法是求像素灰度的平均值或中值。
为了既平滑噪声又保护图像信号,也有一些改进的技术,比如在频域中运用低通滤波器。
MATLAB图像处理工具箱提供了模拟噪声生成的函数imnoise和去除噪声的方法。
函数imnoise可以对图像添加一些典型的噪声。
由于噪声的随机性,它们对某一像点的影响使其灰度和邻点的灰度显著不同,因此可以利用这种不同来消除噪声。
去除噪声的方法有线性滤波、中值滤波、自适应滤波。
本文就针对上述三种平滑滤波进行MATLAB仿真。
1 图像平滑的MATLAB实现
1.1 均值滤波[1]
1.1.1理论基础
邻域平均法是空间域平滑噪声技术,其均值滤波器对于扫描得到的图像中的颗粒噪声非常适用,理论依据如下:
对于给定的图像f(i,j)中的每个像点(m,n),取其邻域S。
设S含有M个像素,取其平均值作为处理后所得图像像点(m,n)处的灰度。
用一像素邻域内各像素灰度平均值来代替该像素原来的灰度,即是邻域平均技术。
邻域S的形状和大小根据图像特点确定。
一般取的形状是正方形、矩形及十字形等,S的形状和大小可以在全图处理过程中保持不变,也可根据图像的局部统计特性而变化,点(m,n)一般位于S的中心。
如S为3×3邻域,点(m,n)位于S中心,则:
假设噪声n是加性噪声,在空间各点互不相关,且期望为0,方差δ2,g是未受污染的图像,含有噪声的图像f经过邻域平均后为
由上式可知,经邻域平均后,噪声的均值不变,方差,即噪声方差变小,说明噪声强度减弱了,即抑制了噪声。
同时,邻域平均法也平滑了图像信号,特别是可能使图像目标区域的边界变得模糊。
可以证明,对图像进行邻域平均处理相当于图像信号通过一低通滤波器。
1.1.2 均值滤波的MATLAB程序
I=imread('E:/flower.jpg');
I=imnoise(I,'gaussian',0,0.02); %添加均值为0,方差为0.02的高斯噪声。
imshow(I);
h=[ 1 1 1
1 1 1
1 1 1 ]; %产生滤波模板。
h=h/9; %对滤波模板进行归一化。
J=conv2(I,h); %用均值模板对图像滤波。
figure,imshow(J,[])
1.1.3 均值滤波结果
Fig1 对图像进行均值滤波的结果
1.2 中值滤波
1.2.1 理论基础
中值滤波是抑制噪声的非线性处理方法。
对于给定的n个数值{a1, a 2 …a n},将它们按大小有序排列。
当n为奇数时,位于中间位置的那个数值称为这n个数值的中值。
当n为偶数时,位于中间位置的两个数值的平均值称为这n个数值的中值,记作med(a1, a 2 …a n)。
中值滤波就是这样的一个变换,图像中滤波后某像素的输出等于该像素邻域中
各像素灰度的中值。
中值滤波的方法运算简单,易于实现,而且能较好地保护边界,但有时会失掉图像的细线和小块的目标区域。
邻域的大小决定在多少个数值中求中值,窗口的形状决定在什么样的几何空间中取元素计算中值。
对二维图像,窗口A的形状可以使矩形、圆形及十字形等,它的中心一般位于被处理点上。
窗口的大小及形状有时对滤波效果影响很大。
在MATLAB图像处理工具箱中,提供了medfilt2函数用于实现中值滤波。
1.2.2 中值滤波的MATLAB程序
I=imread('F:/man.jpg');
K=medfilt2(I);
subplot(1,2,1),imshow(I)
subplot(1,2,2),imshow(K)
1.2.3 中值滤波结果
Fig2 对图像进行中值滤波的结果
3 维纳滤波器
1.3 维纳滤波器[2]
1.3.1理论基础
维纳滤波器也是经典的线性降噪滤波器,维纳滤波是一种在平稳条件下采用最小均误差准则得出的最佳滤波器,使得方均误差最小。
其实质是解维纳-霍夫方程。
维纳滤波器首先估计出像素的局部矩阵均值和方差:
η是图像中每个像素N×M的领域,利用维纳滤波器估计出其灰度值:
式中,v2是整幅图像的方差。
它根据图像的局部方差来调整滤波器的输出,当局部方差大时,滤波器的效果较弱,反之滤波器的效果较强,是一种自适应滤波器。
1.3.2 维纳滤波的MATLAB程序代码
I=imread(‘F:man.jpg’);
Figure,imshow(I);
K1=wiener2(J,[3,3];
K2=wiener2(J,[5,5];
K3=wiener2(J,[7,7];
figure,imshow(K1);
figure,imshow(K2);
figure,imshow(K3);
1.3.3 维纳滤波的结果
Fig3 原始图像
Fig3 3×3 维纳滤波的结果
Fig4 5×5维纳滤波的结果
Fig5 7×7维纳滤波的结果
2 总结
均值滤波器于高斯噪声滤波有比较好的滤波效果,中值滤波器对于椒盐噪声有比较好的滤波效果,维纳滤波器通常对于含有白色噪声的图像滤波效果较好,本文限于作者能力和时间,未能对各种噪声的去除方法进行逐一比较。
通过这次课程论文的撰写,本人对数字图像处理的研究内容和图像处理的实现方法有了初步的了解,感谢老师的严谨授课!在撰写过程中本人态度不积极,遇到问题未能积极思考解决方法,一直拖延,深感惭愧,在接下来的学习过程中定将努力改进,谢谢!
3 参考文献:
[1]孙兆林.MATLAB 6.x图像处理[M].北京:清华大学出版社,2002.
[2]张德丰.MATLAB数字图像处理[M].北京:机械工业出版社,2009.
[3]/downloads68/245557/6.ppt 2006-6-1
[4]朱虹.数字图像处理基础[M].北京:科学出版社,2011.。
