位移法表——常用形常数、载常数
形常数和载常数

位移法是计算超静定结构的基本方法之一
图1
如图1所示结构,力法计算,9个基本未知量
位移法计算,1个基本未知量
单跨超静定梁的形常数与载常数
1. 杆端力的正、负号规定
杆端弯矩:对杆件而言,当杆端弯矩绕杆件顺时针方向旋转为正,反之为负。
对结点而言,当杆端弯矩绕结点(或支座)逆时针方向旋转为正,反之为负。
杆端剪力:使所研究的分离体有顺时针转动趋势为正,有逆时针转动趋势为负。
2. 杆端位移的正、负号规定
杆端转角(角位移):以顺时针方向转动为正,反之为负。
杆端相对线位移:指杆件两端垂直于杆轴线方向的相对线位移,正负号则以使整个杆件顺时针方向转动规定为正,反之为负。
3. 等截面梁的形常数
杆端单位位移引起的杆端内力称为形常数•
i=EI/l——线刚度
4. 等截面梁的载常数
荷载引起的杆端内力称为载常数.
下图是在不同支承条件下的载常数和形常数
一端固定一端定向滑动的单跨超静定梁的载常数和形常数。
形常数和载常数

位移法是计算超静定结构的基本方法之一.
图1
如图1所示结构,力法计算,9个基本未知量
位移法计算, 1个基本未知量
单跨超静定梁的形常数与载常数
1. 杆端力的正、负号规定
杆端弯矩:对杆件而言,当杆端弯矩绕杆件顺时针方向旋转为正,反之为负。
对结点而言,当杆端弯矩绕结点(或支座)逆时针方向旋转为正,反之为负。
杆端剪力:使所研究的分离体有顺时针转动趋势为正,有逆时针转动趋势为负。
2. 杆端位移的正、负号规定
杆端转角(角位移):以顺时针方向转动为正,反之为负。
杆端相对线位移:指杆件两端垂直于杆轴线方向的相对线位移,正负号则以使整个杆件顺时针方向转动规定为正,反之为负。
3. 等截面梁的形常数
杆端单位位移引起的杆端内力称为形常数.
i=EI/l----线刚度
4. 等截面梁的载常数
荷载引起的杆端内力称为载常数.
下图是在不同支承条件下的载常数和形常数。
载常数和形常数表 单跨超静定梁PPT演示文稿

BA
A
B
l
BA
↓↓↓↓↓↓↓↓
Δ
MAB QAB
β θA
θB
转角位移方程
QBA MBA
4、已知杆端弯矩求剪力:取杆 件为分离体建立矩平衡方程:
QABMAB l MBAQA FB
MAB QAB
MAB
Q’‘ AB
P
MBA
+
P
QBA MBA
Q’‘ BA
Q0 AB
Q0 BA
单跨超静定梁 载常数和形常数表
1、形常数:由单位杆端位移引起的杆端力 (只 与截面尺寸和材料性质有关的常数)。 2、载常数:由荷载引起的杆端力 (只与荷载形 式有关的常数)
1
2
A
ql 2 12
ql 2
A
FPl 8
FP 2
两端固定的单跨超静定梁的载常数和形常数
q
i, l
B
A 1
B
i, l
6i
ql 2
3i
5FP l
16
3i
3i l2
16
l2
4
一端固定一端定向滑动的单跨超静定梁的载常数和形常数
q
A i, l
i, l
B
A
1
ql 2
3
ql 2
ql
6 0
i
0
B
i
0
A
FPl 2
FP
FP
i, l
B
FPl 2 0
5
3、转角位移方程:杆端弯矩的一般公式:
M 4i 2i 6i M F
AB
A
B
lHale Waihona Puke ABM 2i 4i 6i M F
结构力学-形常数和载常数表

FQAB
FQBA
19
(↓)
(↑)
20√
(↓)
(↑)
21√
(↓)
(↑)
22
0
0
23√
0
0
24
(↑)
0
25
(↑)
0
26
(↑)
(↑)
表1—载常数表(固端弯矩以顺时针方向为正;固端剪力以使杆件顺时针转动为正)
序号
计算简图及挠度图
弯矩图及固端弯矩
固端剪力
FQAB
FQBA
27
(↑)
(↑)
28
(↑)
0
29
表1—载常数表(固端弯矩以顺时针方向为正;固端剪力以使杆件顺时针转动为正)
序号
计算简图及挠度图
弯矩图及固端弯矩
固端剪力
FQAB
FQBA
1
√
(↑)
(↑)
2
(↑)
(↑)
3
(↑)
(↑)
4
√
(↑)
(↑)
5
√
0
0
6
√
(↑)
(↑)
7
(↑)
(↑)
8
(↑)
(↑)
9
(↑)
(↑)
表1—载常数表(固端弯矩以顺时针方向为正;固端剪力以使杆件顺时针转动为正)
(↑)
(↑)
30
(↑)
(↑)
31
(↑)
(↑)
32
(↑)
(↑)
33
(↑)
(↑)
34
(↑)
(↑)
表2—形常数表(固端弯矩以顺时针方向为正;固端剪力以使杆件顺时针转动为正)
位移法方程

MP
r11
3i
Z1=1 3i
M1
பைடு நூலகம்
Z1
M
位移法基本未知数 ----结点位移.
位移法的基本结构 ----单跨梁系. 位移法的基本方程 ----平衡方程.
位移法求解过程:
1)确定基本体系和基本未知量 2)建立位移法方程 3)作单位弯矩图和荷载弯矩图 4)求系数和自由项 5)解方程 6)作弯矩图
4.3 位移法
(Displacement Method)
位移法是计算超静定 结构的基本方法之一.
P
力法计算,9个基本未知量
位移法计算, 1个基本未知量
4.3 位移法
一.单跨超静定梁的形常数与载常数
1.等截面梁的形常数 杆端位移引起的杆端内力称为形常数. i=EI/l----线刚度
2.等截面梁的载常数
r
11
Z1
q
EI
EI
Z1
Z1=1
=
Z1
q
Z1
Z1
q
=
+
Z1
q
----刚臂,限制转动的约束
EI
Z1
EI
R1=0 R1=r11 Z1+ R1P =0
R1
q
r11
3i 3i
ql 8
2
r
11
=6i
EI
R1P
EI
ql 2 / 8
q
R1P
R1 P ql 2 / 8
Z1 ql 2 / 48i
M M 1 Z1 M P
练习: 作M图
EI
q
2 EI
l l
q
Z1
位移法典型方程
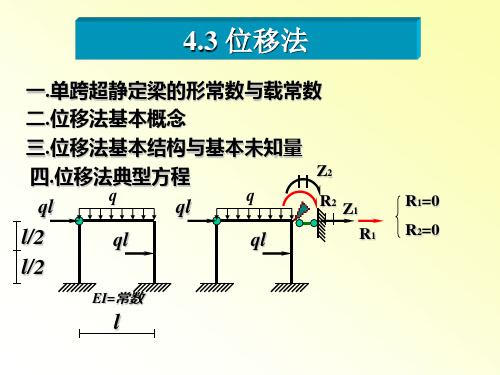
Z1=1
lq ql2 / 8 q
Z1
MP
6i / l 2 r11
3ql / 8 R1 P
练习4:
1)建立位移法基本 体系,列出典型方程
q
EI=常数
2) 求出典型方程中
系数r14, r32,R4P。
l
l
Z1
q
r11Z1 r12 Z2 r13 Z3 r14 Z4 R1P 0 r21Z1 r22 Z2 r23 Z3 r24 Z4 R2P 0 r31Z1 r32 Z2 r33 Z3 r34 Z4 R3P 0 r41Z1 r42 Z2 r43 Z3 r44 Z4 R4P 0
3i / l 2 3i / l 2
r22
12i / l 2 12i / l 2
练习1:
q
作M图,EI=常数
ql2 l
R1=0 r11Z1 R1P 0
r11 8i R1P 3ql 2 / 2 Z1 3ql 2 / 16i
M M1Z1 MP
l
l
l
Z1=1
i
r11
4i M1
r11
i 4i
3i
R2 r21Z1 r22Z2 R2P 0
r22
r11 30i / l 2 r12 r21 9i / l r21
R1P P
r22 11i
R2P 0
r22
Z1 0.044Pl 2 / i
8i
3i / l
12i / l
3i
4i
3i / l 2
3i
24i / l 2
8i
3i / l
Z2 0.036Pl / i R2P
17Pl 2 Z2 414i
EA
形常数和载常数

位移法是计算超静定结构的基本方法之一
图1
如图1所示结构,力法计算,9个基本未知量
位移法计算,1个基本未知量
单跨超静定梁的形常数与载常数
1. 杆端力的正、负号规定
杆端弯矩:对杆件而言,当杆端弯矩绕杆件顺时针方向旋转为正,反之为负。
对结点而言,当杆端弯矩绕结点(或支座)逆时针方向旋转为正,反之为负。
杆端剪力:使所研究的分离体有顺时针转动趋势为正,有逆时针转动趋势为负。
2. 杆端位移的正、负号规定
杆端转角(角位移):以顺时针方向转动为正,反之为负。
杆端相对线位移:指杆件两端垂直于杆轴线方向的相对线位移,正负号则以使整个杆件顺时针方向转动规定为正,反之为负。
3. 等截面梁的形常数
杆端单位位移引起的杆端内力称为形常数•
i=EI/l——线刚度
4. 等截面梁的载常数
荷载引起的杆端内力称为载常数.
下图是在不同支承条件下的载常数和形常数
一端固定一端定向滑动的单跨超静定梁的载常数和形常数。
结构力学形常数和载常数表

结构力学形常数和载常数表1. 形常数形常数是指描述材料在变形过程中的力学行为的常数。
在结构力学中,常见的形常数有弹性模量、剪切模量、泊松比等。
弹性模量是衡量材料抗弯曲和拉伸变形能力的常数。
它描述了材料在受力后产生的应力与应变之间的关系。
弹性模量越大,材料的刚度越高,抗弯曲和拉伸能力越强。
剪切模量是衡量材料抗剪切变形能力的常数。
它描述了材料在受到剪切力时产生的剪切应力与剪切应变之间的关系。
剪切模量越大,材料的刚度越高,抗剪切能力越强。
泊松比是衡量材料在受力时体积变化与横向应变之间的关系的常数。
它描述了材料在受到拉伸或压缩力时纵向应变与横向应变之间的比例关系。
泊松比的取值范围在0到0.5之间,常见材料的泊松比一般在0.25左右。
2. 载常数载常数是指结构在受到外部荷载时所产生的应力与应变之间的关系的常数。
在结构力学中,常见的载常数有抗弯强度、抗剪强度、抗压强度等。
抗弯强度是材料在受到弯曲力时能够抵抗变形和破坏的能力。
它描述了材料在弯曲过程中所能承受的最大应力。
抗弯强度越大,材料的抗弯能力越强。
抗剪强度是材料在受到剪切力时能够抵抗剪切变形和破坏的能力。
它描述了材料在剪切过程中所能承受的最大应力。
抗剪强度越大,材料的抗剪能力越强。
抗压强度是材料在受到压缩力时能够抵抗压缩变形和破坏的能力。
它描述了材料在压缩过程中所能承受的最大应力。
抗压强度越大,材料的抗压能力越强。
形常数和载常数是结构力学中非常重要的参数,它们直接影响着结构的性能和安全性。
在设计和分析结构时,我们需要准确地了解材料的形常数和载常数,以确保结构的稳定性和承载能力。
除了这些常见的形常数和载常数之外,还有许多其他的参数和常数在结构力学中起着重要的作用,如杨氏模量、体积模量、屈服强度等。
这些参数的取值与材料的性质和结构的要求有关,不同的材料和结构可能有不同的形常数和载常数。
形常数和载常数是结构力学中不可或缺的概念和参数。
它们描述了材料和结构在受力时的力学行为,对于结构的设计和分析起着重要的指导作用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
F QFAB=0 F QFBA=0
A
6
=
B
A
l
B
i
A
B
=
M
= F
AB
i
M
= F
BA
i
F QFAB=0 F QFBA=0
编号
简图
=
1A
l
1
A
2
l
变形图
弯矩图(图中i 称为线 刚度,i=EI /l)
杆端弯矩 (以顺时针
转向为正)
B A = = A
B
B A
拐点
4i
B
A
拐点
6i/l
2i
M
= F
AB
4i
B
M
= F
BA
2i
6i/l
M
= F
AB
6i l
B
M
= F
BA
6i l
杆端剪力
F
= F
QAB
6i l
F
= F
QBA
6i l
表7-1 等截面杆件的固端弯矩和固端剪力(载常数)
编号
1A 4A 6A
简图 q l
FP
l q
l
变形图
弯矩图
BA
拐点
BA
拐点
BA
拐点
ql 2 BA
拐点
ql 2
F Pl
B8 A
拐点
FPl
8
ql 2 B
A
固端弯矩 (以顺时针
转向为正)
ql 2
M
= F
AB
B
ql 2 12
M
= F
BA
ql 2 12
固端剪力
F
= F
QAB
ql 2
F
= F
QBA
ql 2
FPl
8
M
= F
AB
FPl 8
B
M
= F
BA
FPl 8
F
= F
QAB
FP 2
F
= F
QBA
FP 2
B
M
= F
AB
ql 2 8
F
= F
QAB
5ql 8
F
= F
QBA
3ql 8
A
10 12 A
FP l /2 l /2
BA
拐点
q B
l
A
拐点
13 A
FP
B
l /2 l /2
FQFBA=0
B
FPl 8
M
= F
AB
M
= F
BA
3FPl 8
FPl 8
F
= F
QAB
F
P
FQFBA=0
B
M
= F
AB
FPl 2
FPl
M
= F
BA
2
FPl 2
F
= F
QAB
F
P
F
= F
QBA
F
P
FQRB=0
M B
M
= F
AB
M 2
M
= F
BA
M
F
= F
QAB
3M 2l
F
= F
QBA
3M 2l
表7-2 等截面杆件由杆端位移(或支座位移)引起的杆端弯矩和杆端剪力(形常数)
F
= F
QAB
12 i l2
F
= F
QBA
12 i l2
=
3A
l
= BA
=
BA 3i
B
M
= F
AB
3i
F
= F
QAB
3i l
F
= F
QBA
3i l
A
4
BA
1
= A
B
A
5
l
=
B
A
3i/l
B
A
B
B i
M
= F
AB
3i l
M
= F
AB
i
M
= F
BA
i
F
= F
QAB
3i l2
F
= F
QBA
3i l2
A
拐点
14 A 16 A
FP
A B
拐点
l
M
拐点
B
A
l
3FPl B 16
A 5FPl 32
ql 2
B
3
A
3FPl
B
8
A
FPl
B
2
A
BA
M 2
B
M
= F
AB
3FPl 16
F
= F
QAB
11F 16
P
F
= F
QBA5FP 16来自Bql 2 6
M
= F
AB
ql 2 3
M
= F
BA
ql 2 6
F
= F
QAB
ql
